条件概率和相互独立事件导学案

年级：高二科目：数学授课人：
教 学 过
程
教 学 过 程
(|) B A P A B B AB B 在发生的条件下包含的样本点数＝
在发生的条件下样本点数包含的样本点数＝
包含的样本点数
AB P AB B P B 包含的样本点数/总数（）
＝
＝
包含的样本点数/总数（）例盒中
有球如表任取一球 玻璃 木质 总计
红 2 3 5
蓝 4 7 11
总计 6 10 16
若已知取得是蓝球,问该球是玻璃球的概率
例1 A:取得是蓝球,B:取得是玻璃球
例2
变式:
若已知取得是玻璃球,求取得是篮球的概率
例3
在5道题中有3道理科题和2道文科题。

如果不放回的依次抽取2道题，求：
（1） 第1次抽到理科题的概率；
（2） 第
1次和第2次都抽到理科题的概率；
)
|(A B P )
()
(A P AB P =
11
416
11164=
=
)
|(B A P )
()(B P AB P =
6
416
6164=
=
()
,()()r
r p AB n A m m p B A n
=⋅=
即p。

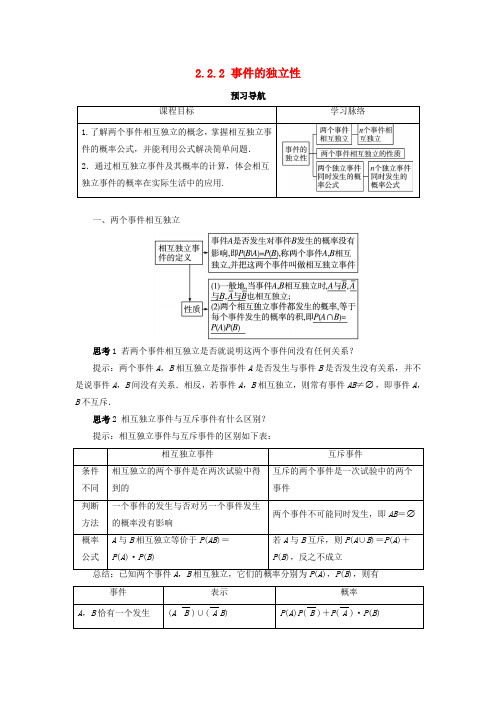
2.2.2 事件的独立性
预习导航
一、两个事件相互独立
思考1 若两个事件相互独立是否就说明这两个事件间没有任何关系？
提示：两个事件A ，B 相互独立是指事件A 是否发生与事件B 是否发生没有关系，并不是说事件A ，B 间没有关系．相反，若事件A ，B 相互独立，则常有事件AB ≠∅，即事件A ，
B 不互斥．
思考2 相互独立事件与互斥事件有什么区别？ 提示：相互独立事件与互斥事件的区别如下表：
1．对于n个事件A1，A2，…，A n，如果其中任一个事件发生的概率不受其他事件是否发生的影响，则称A1，A2，…，A n相互独立．
2．如果事件A1，A2，…，A n相互独立，那么这n个事件都发生的概率等于每个事件发生的概率的积，即P(A1∩A2∩…∩A n)＝P(A1)×P(A2)×…×P(A n)，并且上式中任意多个事件A i换成其对立事件后等式仍成立．。

-2.2.2 条件概率与事件独立性课堂导学三点剖析一、条件概率【例1】一个家庭中有两个小孩，假定生男、生女是等可能，这个家庭有一个是女孩，问这时另一个小孩是男孩概率是多少？解析：一个家庭两个小孩子只有4种可能：{两个都是男孩子}，{第一个是男孩，第二个是女孩}，{第一个是女孩，第二个是男孩}，{两个都是女孩}，由题目假定可知这4个根本领件发生是等可能.根据题意，设根本领件空间为Ω，A=“其中一个是女孩〞，B=“其中一个是男孩〞，那么Ω={〔男，男〕，〔男，女〕，〔女，男〕，〔女，女〕}， A={〔男，女〕，〔女，男〕，〔女，女〕}，B={〔男，男〕，〔男，女〕，〔女，男〕}，AB={〔男，女〕，〔女，男〕}，问题是求在事件A 发生情况下，事件B 发生概率，即求P 〔B|A 〕.由上面分析可知P 〔A 〕=43，P 〔AB 〕=42. 由公式②可得P 〔B|A 〕=, 因此所求条件概率为32. 温馨提示关键是弄清楚P 〔A·B〕及P 〔A 〕.二、事件独立性应用【例2】甲、乙两名篮球运发动分别进展一次投篮，如果两人投中概率都是0.6，计算： 〔1〕两人都投中概率；〔2〕其中恰有一人投中概率；〔3〕至少有一人投中概率.思路分析：甲、乙两人各投篮一次，甲〔或乙〕是否投中，对乙〔或甲〕投中概率是没有影响，也就是说，“甲投篮一次，投中〞与“乙投篮一次，投中〞是相互独立事件.因此，可以求出这两个事件同时发生概率.同理可以分别求出，甲投中与乙未投中，甲未投中与乙投中，甲未投中与乙未投中同时发生概率，从而可以得到所求各个事件概率.解：〔1〕设A=“甲投篮一次，投中〞，B=“乙投篮一次，投中〞，那么AB=“两人各投篮一次，都投中〞.由题意知，事件A 与B 相互独立，根据公式③所求概率为 P 〔AB 〕=P 〔A 〕·P(B)=0.6×0.6=0.36.(2)事件“两人各投篮一次，恰好有一人投中〞包括两种情况：一种是甲投中、乙未投中〔事件A∩B 发生〕，另一种是甲未投中、乙投中〔事件A∩B 发生〕。

条件概率与事件的独立性一、学习目标1. 理解条件概率的定义.2. 掌握条件概率的计算方法．3. 利用条件概率公式解决一些简单的实际问题．4. 在具体情境中，了解两个事件相互独立的概念.5. 能利用相互独立事件同时发生的概率公式解决一些简单的实际问题．二、导学方案1、抛掷红蓝骰子的实验，记事件A="蓝骰子的点数为3或6"，事件B=" 两颗骰子点数之和大于8"，当蓝骰子的点数为3或6时，两颗骰子点数之和大于8的概率是多少？(I)事件A=蓝色骰子的点数为3或6,则P(A)=(II)事件B=两颗骰子的点数之和大于8.则P(B)=(III)事件C=已知蓝色骰子的点数为3或6的前提下,两颗骰子的点数之和大于8,则P(C)= （1）请通过画图的方式解决以上三个问题（2）你能根据上面的实例得出条件概率的公式吗?（3）阅读48页,总结条件概率的含义、记法和计算公式。

2、集合A＝{1,2,3,4,5,6}，甲、乙两人各从A中任取一个数，若甲先取(不放回)，乙后取，在甲抽到奇数的条件下，求乙抽到的数比甲抽到的数大的概率．缩小基本事件范围求条件概率，通过缩小范围可以求条件概率，这是求条件概率最朴素的方法。

3、现有6个节目准备参加比赛，其中4个舞蹈节目，2个语言类节目，如果不放回地依次抽取2个节目，求：在第1次抽到舞蹈节目的条件下，第2次抽到舞蹈节目的概率．利用缩小范围求条件概率的过程中深入理解条件概率的概念和公式。

4、阅读50页回答下列问题：什么情况下两个事件叫做相互独立事件，请举出生活中相互独立事件的例子（2）相互独立事件的概念与性质（3）若事件A，B相互独立，则P(A∩B)＝5 、红队队员甲、乙、丙与蓝队队员A，B，C进行围棋比赛，甲对A，乙对B，丙对C各一盘.已知甲胜A、乙胜B、丙胜C的概率分别为0.6,0.5,0.5，假设各盘比赛结果相互独立.求红队至少两名队员获胜的概率；6、改革开放以来，人们的支付方式发生了巨大转变。

9.2.条件概率与事件的独立性（学案） 姓名【概念与方法】1.定义：设A ，B 是两个事件，且0)(>A P ，称)()()|(A P AB P A B P = 为在事件A 发生的条件下，事件B 发生的条件概率。

特别注意．．．．：()P AB 是指A 、B 同时发生的概率，①当A 、B 为互相独立事件时()P AB ＝()()P A P B ⋅；②当事件A 与事件B 有公共部分，或有包含关系时，就要单独算()P AB 。

2.相互独立事件①定义：设A ，B 是两个事件，如果)()()(B P A P AB P =，则称事件A 与事件B 相互独立. ②性质：如果事件A 与事件B 相互独立，那么A 与B ，A 与B ，A 与B 也都是相互独立的。

【题组一：条件概率】1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2 道题，求：(l ）第1次抽到理科题的概率；(2）第1次和第2次都抽到理科题的概率；(3）在第 1 次抽到理科题的条件下，第2次抽到理科题的概率．2.一张储蓄卡的密码共位数字，每位数字都可从0～9中任选一个．某人在银行自动提款机上取钱时，忘记了密码的最后一位数字，求：(1）任意按最后一位数字，不超过 2 次就按对的概率；(2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率．3.袋中有6个黄色、4个白色的乒乓球，作不放回抽样，每次任取一球，取2次，求:（1）第二次才取到黄色球的概率．（2）在发现其中之一是黄色的条件下，另一个也是黄色的概率4.甲、乙两城市都位于长江下游，根据一百余年气象记录，知道甲、乙两市一年中雨天占的比例分别为20%和18%，两地同时下雨的比例为12%，求：（1）乙市为雨天时，甲市也为雨天的概率；（2）甲市为雨天时，乙市也为雨天的概率.【题组二：事件的独立性】5.甲, 乙两人同时向敌机发射导弹,已知甲击中敌机的概率为0.6, 乙击中敌机的概率为0.5, 求敌机被击中的概率.6.设A、B、C三人投篮命中的概率分别为0.9、0.8、0.7，且他们相互之间投篮是没有影响的。

【主问题的提出】：独立性与条件概率的关系是什么？（1）求抽到的人有自主创业打算的概率；（2）求抽到的人是女生的概率；（3）若已知抽到的人是女生，求她有自主创业打算的概率；（4）判断“抽到的人是女生”与“抽到的人有自主创业打算”是否独立.小结1：两个事件是否独立的判断(1)直接法:由事件本身的性质直接判定两个事件发生是否相互影响.(2)定义法:当P (AB )=P (A )P (B )时,事件A ,B 独立.(3)条件概率法:当P (A )>0时,可用P (B|A )=P (B )判断.变式1：将上题中有自主创业打算的女生人数由原来的15人改成16人，判断“抽到的人是女生”与 “抽到的人有自主创业打算”是否独立.例 2已知甲、乙、丙3人参加驾校考试时，通过的概率分别为0.8，0.9,0.7，而且这3人之间的考试互不影响.求：（1）甲、乙、丙通过的概率；（2）甲、乙通过且丙未通过的概率.小结2：与相互独立事件有关的概率问题求解策略明确事件中的“至少有一个发生”“至多有一个发生”“恰好有一个发生”“都发生”“都不发生”“不都发生”等词语的意义.一般地,已知两个事件A ,B ,它们的概率分别为P (A ),P (B ),那么:(1)A ,B 中至少有一个发生为事件A+B. (2)A ,B 都发生为事件AB.(3)A ,B 都不发生为事件A B . (4)A ,B 恰有一个发生为事件A B +A B.(5)A ,B 中至多有一个发生为事件A B +A B+A B .变式2. 小王某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:(1)这三列火车恰好有两列正点到达的概率;(2)这三列火车至少有一列正点到达的概率.例3 在一个系统中，每一个部件能正常工作的概率称为部件的可靠度，而系统能正常工作的概率成为系统的可靠度.现有甲、乙、丙3个部件组成的一个如图所示的系统，已知当甲正常工作且乙、丙至少有一个能正常工作时，系统就能正常工作，各部件的可靠度均为()10<<r r ，而且甲、乙、丙互不影响，求系统的可靠度.例4 两射手彼此独立地向同一目标射击，设甲射中目标的概率为0.9，乙射中目标的概率为0.8，求目标被击中的概率是多少？归纳小结：归纳本节课所学的知识点及易错点：本节课你学到了什么？你的疑惑：。

主备人：审核：包科领导：年级组长：使用时间：3.条件概率与独立事件【学习目标】1、在具体情境中，了解条件概率的意义；2、学会应用条件概率及相互独立事件的概率解决实际问题3、理解独立事件概念以及其与互斥，对立事件的区别与联系．【重点、难点】条件概率、独立事件的理解与运用【使用说明与学法指导】1、根据学习目标，自学课本内容，限时独立完成导学案；2、用红笔勾画出疑难点，提交小组讨论；3、带※为选做题;【自主探究】1、在事件A发生的情况下事件B发生的条件概率为：)BP=(A2、设BA,为两个事件，如果，则称事件A与事件B的相互独立．【合作探究】1、在5道题中有3道理科题和2道文科题．如果不放回地依次抽取2道题，求：（1）第1次抽到理科题的概率；（2）第1次和第2次都抽到理科题的概率；（3）在第1次抽到理科题的条件下，第2次抽到理科题的概率．变式：在第1次抽到理科题的条件下，第2次抽到文科题的概率？2、天气预报，在元旦假期甲地的降雨概率是2.0，乙地的降雨概率是3.0，假定在这段时间内两地是否降雨相互之间没有影响，计算在这段时间内：（1）甲、乙两地都降雨的概率；（2）甲、乙两地都不降雨的概率；（3）其中至少一个地方降雨的概率．3、一张储蓄卡的密码共有6位数字，每位数字都可从0～9中任选一个．某人在银行自动提款机上取钱时，忘记了密码的最后一位数字．求：（1）任意按最后一位数字，不超过2次就按对的概率；（2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率．变式：任意按最后一位数字，第3次就按对的概率？【巩固提高】1、下列事件中，哪些是互斥事件，哪些是相互独立事件？（1）“掷一枚硬币，得到正面向上”与“掷一枚骰子，向上的点是2点”；（2）“在一次考试中，张三的成绩及格”与“在这次考试中李四的成绩不及格”；（3）在一个口袋内有3白球、2黑球，则“从中任意取1个球得到白球”与“从中任意取1个得到黑球2、某地区气象台统计，该地区下雨的概率是154，刮三级以上风的概率为52，既刮风又下雨的概率为101，设A 为下雨，B 为刮风，求：（1）)(B A P ； （2）)(A B P ．3、100件产品中有5件次品，不放回地抽取2次，每次抽1件．已知第1次抽出的是次品，求第2次抽出正品的概率．4、某同学参加科普知识竞赛，需回答3个问题．竞赛规则规定：答对第一、二、三问题分别得100分、100分、200分，答错得零分．假设这名同学答对第一、二、三个问题的概率分别为6.0,7.0,8.0，且各题答对与否相互之间没有影响．（1）求这名同学得300分的概率；（2）求这名同学至少得300分的概率．课堂小结————————————————————————————。