当前位置：文档之家 › 西华大学常用数学模型5_微分方程模型

西华大学常用数学模型5_微分方程模型

  • 格式：ppt
  • 大小：1.06 MB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

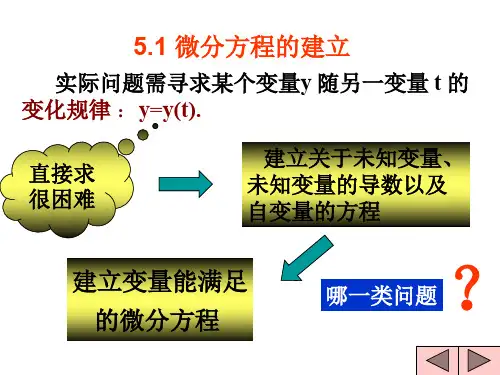
微分方程模型

微分方程模型

6.1 微分方程模型的建模步骤 6.2 作战模型
6.3 传染病模型 习题
6.1 微分方程模型的建模步骤
例1 某人的食量是10467焦/天，其中5038焦/天用于基本的新
陈代谢（即自动消耗）。在健身训练中，他每天大约每千克
体重消耗69焦的热量。 假设以脂肪形式贮藏的热量100%地有效，而1千克脂肪含 热量41868焦，试研究此人的体重随时间变化的规律。
模型分析
甲乙两支部队互相交战，在整个战争期间，双方的兵力 在不断发生变化，而影响兵力变化的诸多因素转化为数量非 常困难。为此，我们作如下假定把问题简化。
模型假设
1. x(t) , y(t) 表示甲乙双方在时刻 t 的人数， x(0)=x0 ,y(0)=y0 表示甲乙双方开战时的人数，x0 > 0, y0 >0； 2.设x(t) , y(t)是连续变化的，并且充分光滑； 3.每一方的战斗减员率取决于双方的兵力，不妨以f(x,y) ,
投入多大的初始兵力。不妨设 100 x0
S 活动区域 x 0.1
p， 0.1 rx， x
ry 2
， 平
平方千米，乙方射击的有效面积 1 sy
y0 2 0.1 0.1 106 100 x 2 1 100 0
2
方米，则可得乙方获胜的条件为：
a
时甲方兵力
降为“零”，从而乙方获胜。同理可知，K 0
甲方获胜。而当 K 0 时，双方战平。 2 2 甲方获胜的充要条件为 bx0 ay0 0
时，
代入a 、b 的值，有甲方获胜的充要条件为
2 2 rx p x x 0 r y p y y 0
故可找到一个用于正规作战部队的综合战斗力的评价函数：

微分方程模型(数学建模)

微分方程模型(数学建模)
利用模拟近似法建模
3
2019年1月8日
开普勒三大定律：
《数学的实践与认识》 2005.12
• 太阳系每一颗行星的轨道皆以太阳为一 焦点的椭圆;
• 行星的向径在单位时间扫过的面积是一 个常数；
• 行星运动周期之平方与平均距离之立方 成正比。
4
2019年1月8日
动态 模型
• 描述对象特征随时间(空间)的演变过程 • 分析对象特征的变化规律 • 预报对象特征的未来性态 • 研究控制对象特征的手段 • 根据函数及其变化率之间的关系确定函数 • 根据建模目的和问题分析作出简化假设 • 按照内在规律或用类比法建立微分方程
5 2019年1月8日
微分 方程 建模
一、微分方程建模的思想和方法
当我们用微观的眼光观察实际问题时一般遵循如下的模式
净变化率=输入率-输出率
（1）根据已知规律：利用数学、物理、力学、化学等经 过实践检验的规律和定理； （2）利用微元法 （3）利用模拟近似法：在社会科学、生物学、医学、经 济学的学科中一些现象的规律性我们不太清楚，需要在不 同的假设下去模拟实际现象。如此建立的模型从数学上求 解或分析后再与实际对比，观察看这个模型是否能够模拟、 近似这些现象。
现代战争的特点是多兵种的协同作战，根据不 同兵种的特点,在不同的区域参加战斗，都对战争的 结果产生一定的影响．
20 2019年1月8日
战争的预测与评估问题
１．问题的提出 现在要求建立数学模型讨论的问题： (1) 分析研究引起军备竞赛的因素，并就诸多 因素之间的相互关系进行讨论； (2) 在多兵种的作战条件下，对作战双方的战 势进行评估分析. （3）分析研究作战双方的兵力消耗，并预测初 始总兵力和战斗力变化对作战结果的影响。

第五章__微分方程模型_数学建模资料

第五章__微分方程模型_数学建模资料
微分方程模型
一、简单的微分方程模型
微分方程模型是数学模型中一类比较普遍而且非常有用 模型. 许多模型都与此模型密切相关. 在微积分课程中, 我
们就遇到了大量的微分方程模型.
例如在微积分中的问题: 弹簧震动问题就涉及到一个微 分方程问题.
再看一个简单的问题.
一个较热的物体置于室温为 50 C 的大房间内, 设物体最 初的温度是 80
Bn : 年龄在1岁之前的幼虫总数; An : 年龄在1—2岁之间的壮年虫总数; Cn : 年龄在2岁以上的老年虫总数;
不同年龄段的此种生物的繁殖和死亡率有下表所示:
组别
繁殖率
死亡率
B
0
0.3 0.1
0.1
0.2 0.3
A
C
由此得到状态转移矩阵及关系表达式
Bn1 0 0.3 0.1 Bn A 0.9 0 A . 0 n n1 C 0 0.8 0.7 C n n1
即有
kt
T 5 75e
t 2 ln 5 3
.
在MatLab下, 输入相应的命令可解此微分方程:
方程求解命令
定解条件
特解
确定方程中的参数
即方程的解为
T 5 75e
t 13.5476 分钟.
⑵在20分钟时的温度为
t 2 ln 5 3
.
则:⑴物体温度下降到30度时所需要的时间为:
最高阶与最低阶的差值. 例如一个二阶线性方程为
X n1 aX n bX n1 f n .
所谓同类线性差分方程指的是方程具有形式
X n1 aX n bX n1 0.
⑷
而方程

微分方程模型

微分方程模型
当 σ > 1 表示传染病的日接触率>日治愈率, 表示传染病的日接触率>日治愈率, i(t)>0,反映传染病在蔓延, i(t)>0,反映传染病在蔓延,感染人数不断上 升; 如SARS这类高传染性的传染病,日接触率 SARS这类高传染性的传染病, 远大于日治愈率, i(t)→1,反映传染病迅速 远大于日治愈率, i(t)→1,反映传染病迅速 爆发; 爆发; 当 σ ≤ 1 表示传染病的日接触率≤日治愈率, 表示传染病的日接触率≤日治愈率, i(t)=0,反映传染病传染受到控制; i(t)=0,反映传染病传染受到控制;
模型评价
隔离病人和在传染病爆发前对易感人群接 种疫苗都是有效降低日接触率λ 种疫苗都是有效降低日接触率λ, 使σ减小, 减小, 从而使病人比例减小; 从而使病人比例减小; 研发特效药是有效提高日治愈率 使使σ 研发特效药是有效提高日治愈率;使使σ 减小,从而使病人比例减小; 减小,从而使病人比例减小;
微分方程模型
常微分方程
常微分方程是最简单的微分方程之一，也 是在建模中经常使用的方程； 常微分方程就是各项系数为常数的微分方 程； y '+ y + xy 2 = 0 微分方程的解就是满足这个式子的函数 y=f(x,C)； y=f(x,C)；
Mathematica解常微分方程 Mathematica解常微分方程
SIS模型问题描述 SIS模型问题描述
有些传染病如流行性感冒、伤风等愈后免 疫力很低，于是病人被治愈后变成健康者， 健康者还可以被感染再变成病人。 传染病的传播是有一定范围的，在传染病 传播期内所考察地区的总人口数相对稳定。
SIS模型变量假设 SIS模型变量假设
传染病区总人口设为N 传染病区总人口设为N； 传染病区人群分为健康者和病人，它们在 人口所点比例分别为s(t)和i(t)； 人口所点比例分别为s(t)和i(t)； 日接触率：每个病人每天有效传染的平均 人数百分比λ 人数百分比λ，当病人与健康者接触，一 部分健康者就会被感染变为病人； 日治愈率：每天被治愈的病人点总病人总 数的百分比 数的百分比；

微分方程模型

微分方程模型

解
1、翻译或转化：
2、配备物理单位：
3、建立表达式： 4、确定条件：
1、‚每天‛：体重的变化＝输入一输出 其中输入指扣除了基本新陈代谢之后的净重量 吸收；输出是进行健身训练时的消耗．
2、上述陈述更好的表示结构式： 取天为计时单位，记W(t)为t天时体重(kg)，则： 每天的净吸收量＝2500 – 1200 ＝1300（cal) 每天的净输出量＝16(cal)×W＝16W(cal) 转换成脂肪量＝1300 – 16W（cal）
有一艘走私船正以匀速度a沿直线向北行驶，缉
私舰立即以最大的速度b追赶，若用雷达进行跟
踪，保持船的瞬时速度方向始终指向走私船，试 求缉私舰追逐路线和追上的时间。
图2 走私船与缉私舰的位置关系
走私船
R(0,at)
缉私艇 D(x,y)
O
(c,0)
x
几何关系
dy y at tg dx x dy 即 x y at dx
模型的解：
k k dy 1 x c p dx 2 c x
y (c ) 0
解的进一步讨论
（1）若a<b，从而k<1，由积分式得
c 1 x y 2 1 k c
y 当x=0时，
W (t ) 81.25 C3e
C3 23.9968
则
0.0016t
初始条件为： W (4) 57.40625，代入解出
W (t ) 81.25 23.9968e
0.0016t
最后得到不同阶段的微分方程是：
81.25 24.0974e , 0t 3 0.0016t W (t ) 143.75 86.8981e , 3t 4 81.25 23.9968e0.0016t , t 4

《微分方程模型》课件

《微分方程模型》课件
f '(x) 2x,
即 f (x) 2xdx C x2 C.
又由条件: 曲线过(1,3), 即 f (1) 3,
于是得 C 2. 故所求的曲线方程为:
y x2 2.
第一章 绪论
常微分方程是现代数学的一个重要分支,是人们解决各 种实际问题的有效工具,它在几何,力学,物理,电子技术,自 动控制,航天,生命科学,经济等领域都有着广泛的应用,本 章将通过几个具体例子,粗略地介绍常微分方程的应用,并 讲述一些最基本概念.
§1.1 微分方程模型
微分方程:
联系着自变量,未知函数及其导数的关系式.
解: 设t时刻时镭元素的量为R(t),
由于镭元素的衰变律就是R(t)对时间的变化律dR(t) , dt
依题目中给出镭元素的衰变律可得:
dR kR, dt
R(0) R0
这里k 0,是由于R(t)随时间的增加而减少 .
解之得: R(t) R0ekt
即镭元素的存量是指数规律衰减的.
例2 物理冷却过程的数学模型
物体的温度与其所在的介质的温度之差成正比.
解: 设物体在时刻 t 的温度为 u(t). 根据导数的物理意义, 则
温度的变化速度为 du . 由Newton冷却定律, 得到 dt
du dt
k (u
ua ),
其中 k 0 为比例系数. 此数学关系式就是物体冷却过程的数
学模型.
注意:此式子并不是直接给出u 和 t 之间的函数关系,而只是
（3.2）
（3.2）的解为: θ(t)= θ0cosωt
当 t T 时,θ(t)=0 4
故有
g T
l4 2
其中 g
l
由此即可得出
T 2 gБайду номын сангаас

数学建模---微分方程模型简介

数学建模---微分方程模型简介
N rN x 0 x* £ µ Í É » à ¬ ´ ³ Ï ² À Í hm ¬ ¤ º ªà Ø é ï Õ ð ò ¾ ª 2 4 E 当 x ＝x* N 时， E E * r x 0 N (1 ) 0 2 2 r r 结论：当捕捞强度控制在 E * 时, 鱼量保持在最大 2 鱼量 N 的一半, 可获得最大持续产量, i.e.,
Malthus模型特点: 在有限的时间内, 在生存空间和食物供应充足 的环境下, Malthus人口模型是比较准确的; 但是, 由于生存空间 有限、食物短缺、战争、疾病、自然灾害, 以及人为控制人口增 长等等原因, Malthus人口模型不能准确地反映出人口的实际增 长情况.
11
上页 下页 返回
Logistic阻滞增长模型
hR £ ¹
r c E R (1 ) 2 pN
N c xR 2 2p
比较：
è ò ¾ £ Ì ªÎ ¬ Ø ¬ï ¬ï §æ à ­ î Á ¬ Ò ² À Ã Ï Ç ¼ £ Ó «Æ é ´ Ï Ñ µ Ó Ó Î £ ¶ Ë ¾ Ç ©Õ ð ò ¾ ñ Ï ñ î × ¬ ð æ ¡ ß ¾ æ È ª ² ¿ Æ ¶ » ³ Ï ² À ½ Ò Ê » È £ ¶ Ò ³ Ò À Ê ³ ½ c à ï Ò ð ï Ò ¬ «Î µ É ° ï £ µ Ó » ¶ Ó » £ ñ ¹ É » Æ ¾ ¡
x
上页 下页 返回
§2 、人口模型
设 t 时刻人口数为 x(t ) ，经过 t 时间后，人数变为
x 则从 t 时刻到 t t 时刻的平均增长速度为 ， x( t ) x ， t x x( t )。 相对增长率为 t
t ªË à ­ Ó ï ¤É ¹ É ¾ µ Î ¶ Ó ³ Á £

数学建模第五章微分和微分方程模型

数学建模第五章微分和微分方程模型

在解决实际问题时，弄清问题中的变量之间的函数关系或其转变趋势是相当重要的，而在一些较为复杂的转变进程中，变量之间的函数关系无法直接取得。

可是，在许多情形下，咱们往往能够在理论或体会的基础上找到问题中的一些变量及其导数之间的关系。

也确实是找出一个或几个含有未知函数及其导数所知足的方程，那个（些）方程就称为微分方程（组）。

然后通过求解微分方程（组）取得变量之间的函数关系，或在微分方程（组）的基础上进行数值计算和渐进性态研究，从而了解整个系统的进展转变规律。

为了研究一些实际问题的转变规律，往往需要对所研究的问题进行适当的简化和假设，再成立数学模型，当问题中涉及变量的转变率时，就能够够通过微分方程来建模。

微分方程模型主若是解决与导数，也即转变率相关的问题，可是；实际问题中一样并非会直接显现“导数”或“转变率”等词语，这时，就需要咱们认真分析，从中找出这些信息，一样来讲，若是问题中涉及到“速度”、“增加”、“改变”、“转变”、“增加”、“减少”、“衰变”（在放射性问题中）、“扩散”、“边际的”（在经济学中）等问题时，往往就能够够用微分方程（组）来建模。

微分方程模型的类型很多，在解决实际问题时，要依照具体情形选择不同的模型，成立模型时，应第一将实际问题概念化为文字方程，许多问题都遵循下面的模式：总讯宗勋净转变率=净增加率━净减少率若是变量之间的关系能够用这种形式来描述，咱们就不难给出相应的微分方程（组）了。

在成立了微分方程模型以后，咱们固然希望能取得微分方程的解，可是，关于大多数微分方程而言，要想直接求解往往是困难的，乃至是不可能的，现在咱们能够通过对方程的定性分析取得有关的一些有效信息。

§1 确信性存贮模型为了使生产和销售有条不紊地进行，一样的工商企业总需要存贮必然数量的原料或商品，但是大量的库存不但积存了资金，而且会使仓库的保管费用增加。

因此，寻求合理的库存量乃是现代企业治理的一个重要课题。

需要注意的是，存贮问题的原型能够是真正的仓库存货，水库存水，也能够是运算机的存贮器的设计问题，乃至是大脑的存贮问题。

微分方程模型

微分方程模型

图示
y 敌艇 R=(0,at)
D(x,y)
x (c,0)
几何关系
dy tg y at
dx
x
即 x dy y at dx
如何消去时间t?
1、求导：
2、速度与路程的关系： b ds
dt
dt
3、分解 dx 得：
（这里有负号是因为s随x的减小而增大） 4、将第2、3步代入第1步，可得模型
注入浓度为c1的同样溶液，假定溶液立即被搅 匀，并以v2的流量流出这种混合后的溶液，试 建立容器中浓度与时间关系的数学模型。
模型的建立
参数设定：设容器中溶液溶质的质量为x(t)，原 来的初始质量为x0，t＝0时溶液的体 积为v0。
在△t的时间间隔内，容器内溶质的改变量：
其中c1：输入溶液浓度， c2：t时刻溶液浓度
2gy
（2）弧微分公式： ds 1 (y/ )2 dx
（3）下降的时间： dt ds ds 1 ( y/ )2 dx
v 2gy
2gy
模型：
2、追线问题
我缉私舰雷达发现，距c海里处有一艘走私 船正以匀速度a沿直线行驶，缉私舰立即以最大 的速度b追赶，若用雷达进行跟踪，保持船的瞬 时速度方向始终指向走私船，试求缉私舰追逐 路线和追上的时间。
令t 0,得 dp rp(N p), r 0, dt

p(0) 1
解
p(t)
N
为
1 (N 1)erNt
当t无穷大时，p(t)的趋向及范围？ 还有当？时变化率最大？
如果考虑广告的效应呢？
考虑单位时间内使用该技术的企业数增量 时应把示范效应和广告效应一起考虑。而 广告只对没采用该技术的企业起作用。假 设其引起的增量与（N-p）成正比

5微分方程模型

5微分方程模型
第五章 微分方程模型
5.1 传染病模型 5.2 经济增长模型 5.3 正规战与游击战 5.4 药物在体内的分布与排除 5.5 香烟过滤嘴的作用 5.6 人口预测和控制 5.7 烟雾的扩散与消失 5.8 万有引力定律的发现
动态 模型
• 描述对象特征随时间(空间)的演变过程 • 分析对象特征的变化规律 • 预报对象特征的未来性态 • 研究控制对象特征的手段
K w L 1 r
w , r ,
K/L
3) 经济(生产率)增长的条件 (动态模型)
要使 Q(t) 或 Z(t)=Q(t)/L(t) 增长, K(t), L(t)应满足的条件
模型 • 投资增长率与产值成正比 假设 (用一定比例扩大再生产)
dK Q, 0
dt
• 劳动力相对增长率为常数
dL L
i0 0, s0 1
x 1 ln(1 x ) 0
s0
i
x<<s0
x(1
1
s0
x
2s02
)
0
x
2s0
(s0
1
)
P1
0 s 1/ s0
s
s0 - 1/ = x 2
小, s0 1
提高阈值1/ 降低 被传染人数比例 x
5.2 经济增长模型
增加生产 发展经济 增加投资 增加劳动力 提高技术
• 建立产值与资金、劳动力之间的关系 • 研究资金与劳动力的最佳分配，使投资效益最大
dt
L(t) L0et
Q f Lg( y) g(y) y 0
dK f Ly
dt
0
y K , K Ly L
dK L dy Ly
dt dt
dK f Ly

微分方程模型详解

微分方程模型详解
Malthus模型与Logistic模型虽然都是为了研究种群数量 的增长情况而建立的，但它们也可用来研究其他实际问题， 只要这些实际问题的数学模型有相同的微分方程即可。
范. 梅格伦（Van Meegren）伪造名画案
第二次世界大战比利时解放后，荷兰保安机关开始搜 捕纳粹分子的合作者，发现一名三流画家H.A.Vanmeegren 曾将17世纪荷兰著名画家Jan.Vermeer的一批名贵油画盗卖 给德寇，于1945年5月29日通敌罪逮捕了此人。
所以Malthus模型假设的人口净增长率不可能始终保 持常数，它应当与人口数量有关。
阻滞增长（Logistic）模型
人口净增长率应与人口数量有关，即反应 了自然因素对人口增长的影响，令r=r(N)
从而有：
其中，
故
注：设环境能供养的种群数量的上界为K（近似地将K 看成常数），N表示当前的种群数量，K-N为环境还能 供养的种群数量，则(K-N )/K为还能供养比例。
做出了如下假设：单位时间内人口增长量与人口
总数成正比，即人口净增长率 基本上是一常
数，
, 为出生率， 为死亡率。
设时刻 的人口总数为 人口增长量为：
，时间从 到
马尔萨斯（Malthus）模型
等式两边同时除以 t ，有
再运用极限的思想，令
有
由初始条件ห้องสมุดไป่ตู้
，即为初始
时刻的人口数，故解方程得
马尔萨斯（Malthus）模型
典型微分方程 • Malthus人口方程： • 虎克定律
典型微分方程 • 牛顿万有引力方程
• 波动方程
• 热传导方程
典型微分方程
• 势方程或 Laplace 方程
人口增长模型

数学建模之微分方程模型

数学建模之微分方程模型
看，在种群的发展初期种群数的变化是和指 数增长模型大致吻合的（甚至可能出现年
增长率递增的现象），但是随着人口数的 增加，人口的年增长率将呈现逐年递减的 现象。再考虑到环境适应程度的制约，想 象人口的增长不可能超过某个度。
（2）对于其中常数增长率r 的估计可以使用 拟合或者参数估计的方法得到。
（3）在实际情况下，可以使用离散的近似 表达式 N(t) N0 (1 r)t 作为人口的预测表 达式。
人口模型
人口数量以及和次类似的动植物种群 的个体数量都是离散变量，不具有连续可 微性。但由于短时间内改变的是少数个体， 与整体数量相比，这种变化是很微小的。 基于此原因，为了成功应用数学工具，我 们通常假定大规模种群的个体数量是时间 的连续可微函数。此假设条件在非自然科 学的问题中常常用到。
指数增长模型（Malthus 人口模型）
（程2可）以注看意到到，NddN(tt
0 ，并且从最终的人口方
)
N m，以及
lim
t
N
(t)
N m，
（这人3说口）dd明 的2tN2人增口 长r(随速1着 度2N时 最/间 快Nm的 ，) 增 从0加 而表递 可明增以当地得N趋到 于人N2mN口时m。
曲线上的一个拐点。
（4） 模型中所涉及到的两个参数 r, Nm 的估
模型假设：
（1）人口的增长率r 是当前人口数的减函 数 r r(N) r(N)' 0 。
（2） r(N) r sN ，其中r 是人口的固有增长
率，而s 决定了所能容纳的最大人口量 Nm 。
当 N Nm 时，人口的增长速度将降为0，从而 可以得到 s r / N。m 这样可以得到
r(N) r(1 N / Nm ) 。

西华大学应用数学系朱雯

西华大学应用数学系朱雯

f (x) f (x) cos x
则有
f (0) 0
利用公式可求出
f (x) 1 (cos x sin x ex ) 2
四、伯努利方程
伯努利(Bernoulli)方程的标准形式
dy P( x) y Q( x) yn (n 0,1)
dx 当n 0,1时， 方程为线性微分方程. 当n 0,1时，方程为非线性微分方程.
x x
原方程是齐次方程.
练习 题
一、求下列微分方程的通解: 1、 y y cos x e sin x ； 2、 y ln ydx ( x ln y)dy 0； 3、( y 2 6x) dy 2 y 0 . dx
二、求下列微分方程满足所给初始条件的特解:
1、dy dx
y cot x 5e cos x
提示:
y 1dy dx
y
x
可分离 变量方程
dy y ln y
齐次方程
dx x x
dy 1 y x2 线性方程
dx 2x
2
dx 1 x y2 线性方程
dy 2y
2
dy 2 y sin x y2 dx x x
伯努利 方程
例11 用适当的变量代换解下列微分方程:
1. 2 yy 2xy2 xex2 ;
dx
dx
dz dx
y
x(
x
1 sin 2
(
xy
)
y) x
1 sin 2
, z
分离变量法得 2z sin 2z 4x C,
将 z xy 代回,
所求通解为 2xy sin(2xy) 4x C.
3. dy 1 ; dx x y
解 令 x y u, 则 dy du 1, dx dx
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

下罪证。
西华大学数学与计算机学院
为了审理这一案件，法庭组织了一个由化学家、物理
学家、艺术史学家等参加的国际专门小组，采用了当时最
先进的科学方法，动用了X-光线透视等，对颜料成份进行
数 分析，终于在几幅画中发现了现代物质诸如现代颜料钴蓝
学 建
的痕迹。
模 课
这样，伪造罪成立， Vanmeegren被判一年徒刑。
培
训 衰变规律、溶液稀释规律等。
西华大学数学与计算机学院
2。模拟近似法。采用大量实验数据，提出各种假
设，在一定条件下模拟确定参数，再建立微分方程，
数 进行
在生物、经济等学科的实际问题中，许多现象
课 的规律性不很清楚，即使有所了解也是极其复杂
件
· 的，建模时在不同的假设下去模拟实际的现象，
的是变量之间的间接关系，因此，要得到直
件 ·
接关系，就得求微分方程。
竞
赛
培
训
西华大学数学与计算机学院
一、建模方法
建立微分方程模型很关键的一点就是要
数 掌握元素分析的方法，建模步骤如下：
学
建 1。理解表示导数的常用词：如经济学中的
模
课 “边际成本”、“边际收益”；生物学中的
件
· “增长速率”；化学反应中的“扩散速率”
常用数学模型
数
学
建 模
1 微分方程模型
课
件
· 竞
2 优化模型
赛
培
训
西华大学数学与计算机学院
数
常用数学模型
学
建
模 课
第5讲 微分方程模型
件
·
竞
赛
培
训
西华大学数学与计算机学院
在研究实际问题时，常常会联系到某些变
数 量的变化率或导数，这样所得到变量之间的
学 建
关系式就是微分方模型。微分方程模型反映
模 课
件 ·
属于铀系,2.地壳中几乎所有岩石中均含有微
竞 赛
量的铀,铀系中各种放射性元素在衰减而产生
培 训
新的元素,从而保持放射性平衡.3.铅矿中提炼
铅时,铅210和铅206被作为铅留下,其余物质
西华大学数学与计算机学院
90%-95%被留在矿渣中,从而打破了原有
的放射性平衡.
数
学 建 模
铀 238
T4。5108年2镭26
竞 赛
建立能近似反映问题的微分方程，然后从数学上
培 求解或分析所建方程及其解的性质，再去同实际
训 情况对比，检验此模型能否刻画、模拟某些实际
现象。
西华大学数学与计算机学院
二、几种微分方程模型
1。赝品的鉴定(Vanmeegren伪造名画
数
学 建
案 有)关知识:1.艺术家们用铅白作为颜料之一已
模 课
达2000多年.铅白中含有微量放射铅210.铅
建
模 方程为:
课 件 · 竞
dy y r dt
赛
为铅的分解率
培
训 镭分解为铅210,铅210分解为铅.
西华大学数学与计算机学院
其解为:
y (t )
r [1 e (t t0 ) ]
y e (t t0 ) 0
数 故:
学
建 模
y0 y(t)e(tt0 ) r[e(tt0 ) 1]
课 件
若画是真品, t t0 300,画中每克铅白中
T1600年2铅10
T22年2铅06
课
件 原理:著名物理学家卢瑟福:物质的放射性正
·
竞 比于物质的原子数.即N(t)表示t时刻的原子
赛
培 数,则(负号表示原子数减少)
训
dN N dt
西华大学数学与计算机学院
建模:
设t时刻1克铅白中铅210含量为y(t),而镭
数
学 的单位时间分解数为r(常数),则y(t)的微分
竞 赛
等等，表示变化速度的量。
培
训 2。建立瞬时表达式，根据 t有微小变化时，
的变化y ，得到 的表达d式y 。
dt
西华大学数学与计算机学院
3。根据已给的实际问题的边界条件，确
数 定有关常数。
学
建 模
此外，还常用下面两种方法建模：
课
件 ·
1。由已知的变化规律直接建模，如牛顿
竞
赛 第二定律、物体冷缺规律、放射性物质
·
竞 赛
含铅210目前的分子数为 y(t) ,镭目前的
培 训
分子数为r均可用仪器测出,从而可算出
y0 ,判断出铅210的分解数是否合理.
西华大学数学与计算机学院
范. 梅格伦（Van Meegren）伪造名画案
数
第二次世界大战后，荷兰保安机关开始搜捕纳粹分子的
学 合作者，发现一名三流画家H.A.VanMeegren曾将17世纪荷兰
平均吸引k个顾客.(3)若已知t=0时,电饭
数 学
煲销售数量为x0只.
建
模 课
建模:x(t)应满足微分方程:
件
· 竞
dx kx
赛
dt
培 训
x(0) x0
求解:
x(t) x0e k t
西华大学数学与计算机学院
结果分析:
调查情况表明,实际销售量在开始阶段
数 学
的增长情况与上式十分相符.问题是当t趋
建 模
于无穷大时,销售量达到无穷大与实际不
课 件
符.应该有上限限制.
·
竞
赛
培
训
西华大学数学与计算机学院
模型二:
假设: 需求量有一个上界N, 则尚未使用的人
数
学 数为(N-x),于是有
建
模 课
dx x(N x)
件
dt
·
x
竞 赛 培
即有: dx kx(N x)
dt
N N/2
训
解得: x
N
x0
建 模
著名画家Jan.Vermeer的一批名贵油画盗卖给德寇，于1945
课 年5月29日通敌罪逮捕了此人。
件
·
VanMeegren被捕后宣称他从未出卖过荷兰的利益，所有
竞
赛 的油画都是自己伪造的，为了证实这一切，在狱中开始伪造
培 训
Vermeer的画《耶稣在学者中间》。当他的工作快完成时，
又获悉他可能以伪造罪被判刑，于是拒绝将画老化，以免留
件 1947年11月30日他在狱中心脏病发作而死去。
·
竞
但是，许多人还是不相信其余的名画是伪造的，因为，
赛
培 Vanmeegren在狱中作的画实在是质量太差，所找理由都
训 不能使怀疑者满意。直到20年后，1967年，卡内基梅隆大
学的科学家们用微分方程模型解决了这一问题。
西华大学数学与计算机学院
2。新产品的推销与广告
1 CeN k t
t
西华大学数学与计算机学院
结论:
当销出量<最大需求量的一半时，销售速
数 学
度不断增大，销出量达到一半时，该产品最
建 模
为畅销，其后销售速度将开始下降。实际调
课
件 查表明，销售曲线在销售后期，几乎完全吻
问题1: 新立品推销速度
数 学
第二次世界大战后日本家用电器业建
建 模
立的饭煲销售模型:
课 件
模型一:
·
竞 赛
假设(1)记t时刻已售出的电饭煲总数为连续
培 训
函数x(t);(2)由于使用方便,已在使用的电饭
煲实际上起宣传品的作用,吸引着尚未购
西华大学数学与计算机学院
买的顾客.设每一个电饭煲在单位时间内