初中数学23种数学模型汇总

初中数学模型归纳大全初中数学模型归纳大全近年来，初中数学的课程安排越来越注重将数学的思维方法和现实生活相结合，让学生在数学学习中掌握丰富的实际应用技能。

其中一个重要的教学方式就是数学建模。

初中数学模型归纳大全，决是一篇非常有用的参考资料。

这篇文章将会对初中数学中的各种数学模型进行归纳介绍，供初中生及学科教师们参考学习。

模型一：生活中的数学模型物质交换、能量转化、社会相互作用、周期变化等生活中的各种现象都可以用数学模型来描述和研究，例如：1.物质平衡模型：糖果换水果的比例；汽油和尾气的关系。

2.周期变化模型：季节变换图；一天的时间变换图。

3.变化速率模型：打车计价器；电费计算表。

模型二：图形化数学模型在初中数学中，一些图形化的数学模型可以帮助学生更好地理解和掌握一些抽象的数学概念。

以下是几种常见的图形化数学模型：1.函数图像模型：介绍函数图像的概念，如y=x^2、y=|x|等等。

2.平面几何模型：为学生介绍平面几何中的各种概念，如直线、角度和三角形等等。

3.三维几何模型：三维几何不仅可以帮助学生更好地理解三维空间的概念，同时还可以培养学生的空间想象力和建模能力。

模型三：奥数模型奥数一直以来都是中国教育中的一大特色，在初中数学中也有一些与奥数相关的数学模型，例如：1.排列组合模型：介绍排列组合的概念，如A(4,2)、C(4,2)等等。

2.数学归纳模型：帮助学生更好地掌握数学归纳的思路，如猴子吃桃、阶乘问题等等。

3.数形结合模型：利用具体的图形问题结合数学解法，例如数轴上的问题、目测问题等等。

模型四：工程数学模型在工程领域中，数学模型的运用是不可或缺的。

初中数学中也有一些与工程相关的数学模型，例如：1.自然增长模型：介绍自然增长的概念，如人口增长、金融投资等等。

2.传热模型：帮助学生了解传热的基本原理，如热力学等等。

3.循环流动模型：帮助学生了解循环流动的规律和应用，例如水循环、风循环等等。

总结初中数学模型的归纳总结可以为学生提供更多的实践题材，培养学生发掘问题并解决问题的能力，更重要的是，可以加深学生对数学知识的理解和应用。

初中数学几何模型大全初中数学几何模型大全全等变换：平移：平移是指将平行等线段（平行四边形）沿着相同的方向平移相同的距离。

这种变换可以用来构造平行四边形。

对称：对称变换可以通过角平分线、垂直线或半角来进行。

这种变换可以用来构造对称全等的图形。

旋转：旋转变换是指将相邻等线段绕公共顶点进行旋转。

这种变换可以用来构造旋转全等的图形。

对称全等模型：这种模型是以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型：这种模型是通过翻折构造对称全等的图形。

可以通过上图中的45°、30°、22.5°、15°及有一个角是30°直角三角形的对称来实现。

翻折后可以得到正方形或者等腰直角三角形、等边三角形、对称全等的图形。

旋转全等模型：半角：这种模型是指相邻等线段所成角含1/2角及相邻线段。

通过旋转将另外两个和为二分之一的角拼接在一起，形成对称全等的图形。

自旋转：这种模型是指有一对相邻等线段，需要构造旋转全等。

可以通过遇到60度旋60度，造等边三角形；遇到90度旋90度，造等腰直角；遇到等腰旋顶点，造旋转全等；遇中点旋180度，造中心对称的方法来实现。

共旋转：这种模型是指有两对相邻等线段，直接寻找旋转全等中点。

通过旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

可以通过“8”字模型来证明。

模型变形：这种变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，可以先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：这种模型是指通过两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

初中数学196个模型篇一：初中数学是学生学习数学知识的重要阶段，也是培养他们数学思维能力和解决问题能力的关键时期。

在初中数学学习中，掌握数学模型是非常重要的，因为它能帮助学生将抽象的数学概念与现实生活中的问题相联系，使数学知识更加具体和实用。

在初中数学学习中，有许多重要的数学模型，下面将介绍其中的一些。

1. 几何模型：几何模型是初中数学中最基本的模型之一，它涉及到点、线、面、体等几何图形的性质和关系。

学生通过学习几何模型，可以掌握几何图形的特点，如直线的特性、平行线的性质、三角形的分类等，并能够运用几何模型解决实际问题。

2. 等式模型：等式模型是初中代数学习中的核心模型之一，它包括一元一次方程、一元一次不等式、二元一次方程等。

学生通过学习等式模型，可以掌握代数运算的基本规律，如加减乘除的计算，以及解方程、解不等式的方法，从而能够解决与等式相关的实际问题。

3. 概率模型：概率模型是初中数学学习中的一个重要模型，它涉及到随机事件的发生概率和统计推断等内容。

学生通过学习概率模型，可以了解事件发生的可能性，并能够运用概率模型解决与概率相关的实际问题，如掷硬币、抽卡片等。

4. 数列模型：数列模型是初中数学学习中的一个重要模型，它涉及到数列的概念、性质和应用等内容。

学生通过学习数列模型，可以了解数列的规律和特点，如等差数列、等比数列等，并能够运用数列模型解决与数列相关的实际问题，如找规律、预测未知数等。

5. 图形模型：图形模型是初中数学学习中的一个重要模型，它涉及到平面图形的性质和关系等内容。

学生通过学习图形模型，可以了解平面图形的分类、性质和变换等，并能够运用图形模型解决与图形相关的实际问题，如面积计算、图形的相似性等。

总之，初中数学学习中有许多重要的数学模型，通过学习这些模型，学生不仅可以增加对数学知识的理解和掌握，还可以培养数学思维能力和解决问题能力，为将来的学习和生活打下坚实的数学基础。

篇二：初中数学是学习和掌握数学基础知识的重要阶段。

初中数学四十八个几何模型1. 直线与角直线是任意两点之间的最短路径。

角是由两条射线共享一个端点而形成的图形。

直线与角是几何学的基本概念。

线段是直线上两个点之间的部分。

线段具有长度，可以进行比较。

射线是由一个端点和延伸的直线组成的。

射线有起点，但没有终点，可以无限延伸。

4. 平面与平行线平面是一个没有边界的二维图形。

平行线是在同一个平面上，永远不会相交的直线。

三角形是由三条线段连接而成的图形。

三角形的内角和为180度。

6. 等腰三角形等腰三角形是具有两条边长度相等的三角形。

等腰三角形的底角也相等。

7. 直角三角形直角三角形是具有一个内角为90度的三角形。

直角三角形的斜边是其他两条边的平方和的开方。

8. 锐角三角形锐角三角形是所有内角都小于90度的三角形。

9. 钝角三角形钝角三角形是具有一个内角大于90度的三角形。

10. 正方形正方形是四条边相等且四个角都是直角的四边形。

11. 长方形长方形是具有两对相等且每一对内角都是直角的四边形。

12. 平行四边形平行四边形是具有两对平行边的四边形。

梯形是具有一对平行边的四边形。

梯形的非平行边也可以不等长。

菱形是具有四个边相等且对角线相等的四边形。

圆是具有相同半径的所有点的集合。

圆上任意两点与圆心构成的线段称为弦。

16. 圆心角圆心角是以圆心为顶点的角。

弧是圆上两个点之间的部分。

弦是圆上任意两点之间的线段。

切线是与圆只有一个交点的直线。

弧长是圆上一部分的长度。

扇形是以圆心为顶点的角所对应的圆上的区域。

22. 对称与相似对称是指一个图形通过某条线、点或平面进行折叠后与自身完全重合。

相似是指两个图形的形状相同但大小不同。

23. 二维几何体二维几何体包括平面图形。

24. 立体几何体立体几何体是具有实体和体积的图形。

25. 正方体正方体是六个面都是正方形的立体几何体。

26. 长方体长方体是六个面都是矩形的立体几何体。

27. 正圆柱体正圆柱体是圆和矩形结合形成的立体几何体。

初中数学全部解题模型汇总
初中数学涉及的解题模型有很多，以下是部分初中数学中常见的解题模型：
1. 方程模型：方程是数学中描述数量之间关系的重要工具。

一元一次方程、二元一次方程、一元二次方程等都是常见的方程模型。

2. 函数模型：包括一次函数、二次函数、反比例函数等。

这些函数模型用于描述变量之间的关系，是解决实际问题的重要工具。

3. 几何模型：包括三角形、四边形、圆等。

这些模型用于研究图形的性质，如边长、角度、面积等。

4. 代数模型：代数模型用于解决代数问题，如合并同类项、解方程等。

5. 概率模型：概率模型用于解决与概率相关的问题，如排列组合、概率计算等。

这些模型不是孤立的，它们之间有很多交叉点，一个问题的解决可能需要多种模型的联合运用。

希望这些信息能帮助你更好地学习初中数学。

初中数学定理模型大全
初中数学是数学学习的重要阶段，涉及的定理和模型也越来越多。

以下是一些初中数学中常用的定理和模型，供参考。

一、定理
1. 勾股定理
在直角三角形中，勾股定理表述了两条直角边的平方和等于斜边的平方。

即，如果直角三角形的两条直角边长度分别为a和b，斜边长度为c，那么
a²+b²=c²。

2.等腰三角形定理
等腰三角形两边的长度相等，且两边的夹角也相等。

如果等腰三角形的两个底角分别为α和β，那么α=β。

3.平行线定理
如果两条直线平行于同一条直线，那么这两条直线的内错角相等。

即，如果两条直线a和b都平行于直线c，那么a和b的内错角相等。

二、模型
1. 方程模型
方程是解决数学问题的一种重要方法。

初中数学中常见的方程模型包括一元一次方程、一元二次方程、二元一次方程等。

这些方程模型都可以用来解决实际问题中的数量关系问题。

2.函数模型
函数是描述变量之间关系的一种重要方式。

初中数学中常见的函数模型包括一次函数、二次函数、反比例函数等。

这些函数模型都可以用来描述实际问题中的变量之间的关系。

3.几何模型
几何是初中数学的一个重要内容。

初中数学中常见的几何模型包括三角形、四边形、圆形等。

这些模型都可以用来描述实际生活中的空间形状和位置关系。

1。

中考数学常见的11种几何模型一、三角形的不等关系模型：A字型、K字型、X字型1. 三角形两边之和大于第三边；2. 三角形两边之差小于第三边；3. 直角三角形斜边上的中线等于斜边的一半；4. 直角三角形中30度所对的直角边等于斜边的一半；5. 三角形三个内角之和等于180度。

二、全等、相似模型模型：A字型全等、A字型相似、8字型全等、8字型相似、蝴蝶型全等、蝴蝶型相似、平行型全等、平行型相似、等积模型等。

三、平行四边形模型模型：平行四边形ABCD中，E为AB中点，则：AC、DE互相平分；模型：平行四边形ABCD中，AC、BD交于O，则：AO=CO，BO=DO；模型：平行四边形ABCD中，AC平分角BAD，则：四边形ABCD为菱形。

四、梯形模型模型：梯形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：BE=FE；模型：梯形ABCD中，A、B在直线EF上，则：延长DC交AB延长线于F，则：梯形ABCD面积等于三角形面积的2倍；模型：梯形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：EF=FC。

五、矩形模型模型：矩形ABCD中，E为BC中点，则：AE平分角BAD；模型：矩形ABCD中，E为AD中点，则：AF平分角ABC；模型：矩形ABCD中，AC平分角BAD，则：四边形ABCD为菱形。

六、多边形模型模型：任意多边形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：BF=FE；模型：任意多边形ABCD中，E为AD中点，延长BE交DC延长线于F，则：EF=FC。

七、燕尾模型模型：在三角形ABC中，BD平分角ABC，CE平分角ACB，则：点D、E在BC同旁，则：三角形ADE的面积等于三角形ABC面积的一半。

八、风筝模型模型：在三角形ABC中，点D、E在BC上，且AD平分角BAE，则：三角形ABC与三角形ADE的面积相等。

九、铅笔模型模型：在矩形ABCD中，点E、F分别在AB、CD上，则：EF平行于AD，则：矩形ABFE与矩形EFCD相似。

初中数学所有模型总结
初中数学是学生们学习最基础的数学知识和技能的阶段，其中模型是数学的重要组成部分。

数学模型是将现实问题转化为数学问题的过程，通过建立模型来解决实际问题。

在初中数学中，学生学习了多种不同类型的数学模型，如下所述：
1. 比例模型：比例模型是最常见的数学模型之一。

比例模型可以用来解决实际生活中的各种问题，如物品的价格、长度、时间等等。

学生需要对比例模型的基本概念和计算方法有深入的了解。

2. 几何模型：几何模型是在几何图形中建立的数学模型，如三角形、正方形、圆形等等。

几何模型可以用来解决实际问题，如计算面积、周长、角度等等。

3. 代数模型：代数模型是将实际问题抽象到代数符号中，建立代数方程来解决问题。

在初中数学中，学生需要学习代数符号的基础知识和代数方程的解法。

4. 统计模型：统计模型是用来分析和解释数据的数学模型。

在初中数学中，学生需要学习统计学基础知识和统计模型的使用方法。

5. 概率模型：概率模型是用来预测结果的数学模型。

在初中数学
中，学生需要学习概率基础知识和概率模型的使用方法。

总之，初中数学的模型种类繁多，每种模型都有其独特的应用和使用方法。

了解和掌握这些模型对于学生未来的学习和职业生涯都是非常重要的。

初中数学48个解题模型数学是一门需要理解和掌握的学科，而解题模型则是数学学习中非常重要的一部分。

解题模型是指在解决数学问题时，根据问题的特点和要求，采用合适的方法和步骤，运用数学知识进行分析、计算和推理的一种解题方式。

在初中数学学习中，掌握一定的解题模型，可以更好地提高数学解题的能力和效率。

下面，我们将介绍初中数学中常用的48个解题模型，其中包括了初中数学的各个方面，希望对初中数学学习有所帮助。

1. 等式变形模型：根据等式变形的性质，对等式进行变形，使其更加简单易解。

2. 分式化简模型：根据分式化简的原理，对分式进行化简，使其更加简单易解。

3. 去括号模型：根据去括号的原理，将括号内的式子进行展开，使其更加简单易解。

4. 合并同类项模型：根据合并同类项的原理，将同类项进行合并，使其更加简单易解。

5. 因式分解模型：根据因式分解的原理，将式子进行因式分解，使其更加简单易解。

6. 基本不等式模型：根据基本不等式的原理，对不等式进行变形，使其更加简单易解。

7. 二次函数解析式模型：根据二次函数解析式的原理，求出二次函数的解析式。

8. 三角函数解析式模型：根据三角函数解析式的原理，求出三角函数的解析式。

9. 解方程模型：根据解方程的原理，对方程进行变形，求出方程的解。

10. 解不等式模型：根据解不等式的原理，对不等式进行变形，求出不等式的解。

11. 平面几何基本定理模型：根据平面几何基本定理的原理，对几何问题进行求解。

12. 空间几何基本定理模型：根据空间几何基本定理的原理，对几何问题进行求解。

13. 三角形的性质模型：根据三角形的性质，对三角形问题进行求解。

14. 相似三角形模型：根据相似三角形的原理，对相似三角形问题进行求解。

15. 同余模型：根据同余的原理，对同余问题进行求解。

16. 勾股定理模型：根据勾股定理的原理，对勾股定理问题进行求解。

17. 三角函数基本关系式模型：根据三角函数的基本关系式，对三角函数问题进行求解。

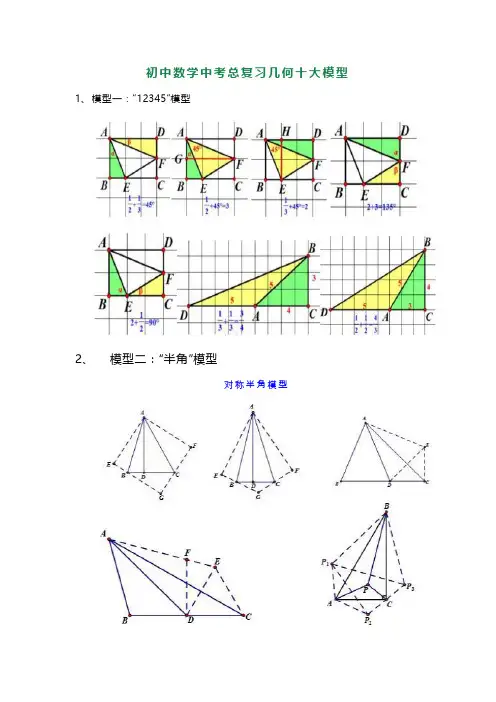
初中数学中考总复习几何十大模型1、模型一：“12345”模型
2、模型二：“半角”模型
对称半角模型
旋转半角模型
3、模型三：“角平分线”模型
角平分线定理角平分线+垂线=等腰三角
形
角分线+平行线=等腰三角必呈现
角平分线+垂线=等腰三角形
4、模型四：“手拉手”模型
条件：1、两个等腰三角形；2、顶角相等；3、顶点重合。

结论：1、手相等；2、三角形全等；3、手的夹角相等；
4、顶点连手的交点得平分。

5、模型五：“将军饮马”模型
6、模型六：“中点”模型
【模型1】倍长
1、倍长中线；
2、倍长类中线；
3、中点遇平行延长相交
【模型2】遇多个中点，构造中位线
1.直接连接中点；
2.连对角线取中点再相连
7、模型七：“邻边相等的对角互补”模型
【模型1】
【条件】如图，四边形ABCD中，AB=AD，∠BAD+∠BCD=∠ABC+∠ADC=180°【结论】AC平分∠BCD
【模型2】
【条件】如图，四边形ABCD中，AB=AD，∠BAD=∠BCD=90°
【结论】①∠ACB=∠ACD=45°②BC+CD=V2AC
8、模型八：“一线三角”模型
【条件】∠EDF=∠B=∠C，且DE=DF
【结论】△BDE=△CFD
9、模型九：“弦图”模型
【条件】正方形内或外互相垂直的四条线段
【结论】新构成了同心的正方形
10、模型十：费马点。

初中数学54个几何模型初中数学中的几何模型是指在几何学中用来描述和表示几何概念的模型。

下面将介绍54个常见的几何模型。

1. 点：几何中最基本的概念，没有大小和形状。

2. 直线：由无数个点连成的路径，无限延伸，没有宽度。

3. 射线：由一个起点出发，无限延伸的路径。

4. 线段：两个点之间的路径，有特定的长度。

5. 面：由无数个点连成的平面，有长度和宽度，没有厚度。

6. 圆：由同一平面上距离圆心相等的点组成的闭合曲线。

7. 椭圆：平面上到两个焦点的距离之和恒定的点的轨迹。

8. 椭圆弧：椭圆上的一段曲线。

9. 双曲线：平面上到两个焦点的距离之差恒定的点的轨迹。

10. 双曲线弧：双曲线上的一段曲线。

11. 抛物线：平面上到一个焦点的距离等于到直线的距离的点的轨迹。

12. 抛物线弧：抛物线上的一段曲线。

13. 球：由空间中到一个固定点的距离恒定的点组成的集合。

14. 圆锥：由平面和母线（与平面交于一点的直线）构成的几何体。

15. 圆柱：由平面和平行于平面的两个母线构成的几何体。

16. 圆台：由平面和平行于平面的两个母线及它们之间的曲面构成的几何体。

17. 球台：由平面和球的一部分构成的几何体。

18. 球梯：由平面和球的一部分及它们之间的曲面构成的几何体。

19. 直角三角形：有一个内角为90度的三角形。

20. 等腰三角形：有两边相等的三角形。

21. 等边三角形：三边长度均相等的三角形。

22. 直角梯形：有一个内角为90度的梯形。

23. 等腰梯形：有两边平行且相等的梯形。

24. 矩形：四个内角均为90度的四边形。

25. 正方形：四边长度均相等且内角均为90度的四边形。

26. 平行四边形：有两组对边平行的四边形。

27. 菱形：有四个边相等的四边形。

28. 六边形：有六个边的多边形。

29. 正六边形：六边形的六个内角均为120度。

30. 五边形：有五个边的多边形。

31. 正五边形：五边形的五个内角均为108度。

32. 正多边形：所有边和内角均相等的多边形。

初中数学I23种模型汇总办一数学模型三线八角同位儡找F型内错角：找Z型同旁内角二找U型拐角模型一.锯齿型ZI+Z3=Z2Z1+Z2=Z3+Z4左和=右和鹰嘴+小=大三.铅笔头型ZI+N2+N3=360°N1十Z2+Z3+Z4=540"等积变换模型S AACD=S ABCD初二数学模型八字模型角:zA+zB=zC+zD边：AD+BOAB+CD飞镖模型内内角平分线模型角：zD=zB+zC+zA 边！AB+AOBD+CD2内外角平分线模型ZD=-ZA2外外角平分线模型上D4角分线构造全等模型，比平分线垂两边二,角平分线;垂中间三角平分线构埴轴对称三垂模型手拉手模型大小等边三角虚线相等,FI夹布为60。

1全等，八字形）四.大小等腰三角形（顶角为口）（全等,八字结论工虚线相等.且夹角为a三.大小等腰宜角三角形结诒；虚线相等.且夹角为9。

口（全等『八字形）二.大小正方形结论：虚线相等，且央饱为90”C全等，八字形）半角模型条件:正方游ABCQ/EDFG证：EF=AE+CF条件才CD=AQ/ADr9TzEDF=4S c^A+zC=180*造叨二EF=AE+CF条件*AB=AD/B〜D=180口^EAF=lzBAD£证明:EF=BE十DF条件：AB=ACzBAC=90°zDAE-45t证明：DEz二BD"CEz△CEF为自用1角将军饮马模型PA十PB最小CA+AB+BC最小日边形ARCD】周氏故小六边形AIM I*冏k最小斜边中线模型2、平移他5四工等腰直珅△对称构造全等模型时称半角模型初三数学模型模则二.卮帖!•公共用模例 喷网网、射影定理模型①CD 』二ADDB ；②BC 三@AC 2-ADABi@AC-BC=AB'CD桢型…军产基相似八大模型模型、丸二次函数中等积变换模型A找到点。

，使得工即=曷|[/A。

在红线上H))/'P①求直线8端析式...t②求过点/直线解析式，求交点坐川标③求过点々直线解析式，求交点坐标二次函数中线段最值模型2ra 在平面声角坐标案中，己知盛物法F ・T 。

数学模型是数学的一个重要组成部分，它可以用来描述和解决实际问题，提高我们的分析和解决问题的能力。

以下是初中三年常用的数学模型大汇总：1.距离、速度和时间模型：-车辆行驶模型：根据速度和时间计算距离，根据距离和时间计算速度。

-管道水流模型：根据水流速度和时间计算水流的距离，根据水流的距离和时间计算水流的速度。

2.面积和体积模型：-图形面积模型：根据给定的图形的边长或半径计算面积，如矩形、正方形、圆等。

-几何体积模型：根据给定的几何体的边长或半径计算体积，如长方体、正方体、圆柱体等。

3.百分比模型：-增长和减少比例模型：根据增长或减少的百分比计算最终的值。

-打折模型：根据打折的百分比计算最终的价格。

4.比例模型：-直接比例模型：根据两个变量之间的比例关系求解未知数。

-间接比例模型：根据两组变量之间的间接比例关系求解未知数。

5.利息模型：-简单利息模型：根据给定的本金、利率和时间计算最终的利息。

-复利模型：根据给定的本金、利率和时间计算最终的本利和。

6.概率模型：-可能性模型：根据事件的可能性和总数，计算特定事件发生的概率。

-样本空间模型：根据样本空间和事件发生的可能性，计算事件的概率。

7.频率模型：-直方图模型：根据给定的数据集，绘制直方图，以展示数据的频率分布。

8.函数模型：-线性函数模型：根据给定的线性函数表达式，求解未知数。

-二次函数模型：根据给定的二次函数表达式，求解未知数。

9.排列和组合模型：-排列模型：根据一组元素的排列方式，计算排列的总数。

-组合模型：根据一组元素的组合方式，计算组合的总数。

10.进制模型：-十进制模型：根据十进制表示法，进行数学运算。

-二进制模型：根据二进制表示法，进行数学运算。

这些数学模型涵盖了初中三年数学学习的各个方面，通过运用这些模型，我们可以更好地理解和解决实际问题。

同时，这些模型也为我们打下了解决更复杂数学问题的基础。

以下是初一数学几何模型的一些汇总：
1.三角形：三角形是最基本的几何图形，它的性质、分类、定理和推论都是学
习的重点。

2.四边形：四边形是日常生活中常见的图形，其性质、分类、定理和推论也是
学习的重点。

3.圆形：圆是一种曲线图形，其性质、分类、定理和推论也是学习的重点。

4.轴对称：轴对称是指沿着一条直线折叠后两边完全重合，其性质、分类、定
理和推论是学习的重点。

5.全等三角形：全等三角形是指两个三角形的三条边和三个角都相等，其性质、
分类、定理和推论是学习的重点。

6.等腰三角形：等腰三角形是指两条边相等的三角形，其性质、分类、定理和
推论是学习的重点。

7.直角三角形：直角三角形是指有一个角为90度的三角形，其性质、分类、
定理和推论是学习的重点。

8.平行线：平行线是指永不相交的两条直线，其性质、分类、定理和推论是学
习的重点。

9.勾股定理：勾股定理是指直角三角形的三条边满足a^2 + b^2 = c^2的关系，
其性质、分类、定理和推论是学习的重点。

初中数学模型总结
初中数学模型有二元一次方程，平面几何、直线和圆、三角力学及其性质、等差数列和等比数列、解一元二次方程和二元一次不等式等。

它们都有自己的特点，其求解方法和运算步骤如下：
一、二元一次方程：
（1）把方程化为两边同乘以同一个数。

（2）把变量的符号都统一。

（3）把相同项合并在一起。

（4）用算法求出解，最后取得根。

二、平面几何：
（1）判断几何图形的主体、边、角、边界。

（2）计算图形的边长、面积、周长等。

三、直线和圆：
（1）判断圆外一点是否在直线上或圆上。

（2）给定圆和直线上任意点，求其他点的位置。

四、三角力学及其性质：
（1）确定采用的三角力学定理，根据定理求出边和角的数值。

（2）利用角边关系进行分析。

五、等差数列和等比数列：
（1）分析题目，确定序列的公差或公比，在给定的前几项中计算出求和式或通项公式。

（2）根据特定等差数列或等比数列的性质求出求和值或通项值。

六、解一元二次方程和二元一次不等式：
（1）将一元二次方程和不等式用图像表示出来。

（2）利用不等式的特性确定解的位置。

（3）根据求根公式求出二次方程的解。