下载文档原格式
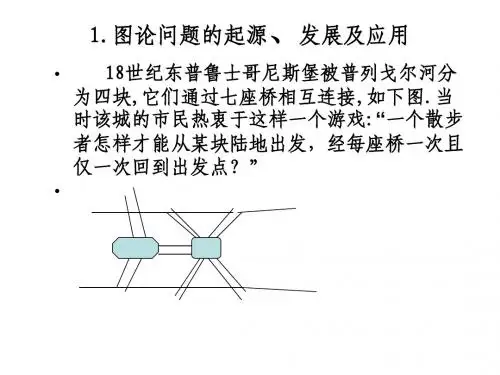
第五章图与网络模型及方法§1 概论图论起源于18 世纪。
第一篇图论论文是瑞士数学家欧拉于1736 年发表的“哥尼斯堡的七座桥”。
1847 年，克希霍夫为了给出电网络方程而引进了“树”的概念。
1857 年，凯莱在计数烷C n H2n+2 的同分异构物时，也发现了“树”。
哈密尔顿于1859 年提出“周游世界”游戏，用图论的术语，就是如何找出一个连通图中的生成圈、近几十年来，由于计算机技术和科学的飞速发展，大大地促进了图论研究和应用，图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、运筹学，生物遗传学、心理学、经济学、社会学等学科中。
图论中所谓的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物，用连接两点的线段（直的或曲的）表示两个事物的特定的联系，就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型，借助于图论的概念、理论和方法，可以对该模型求解。
哥尼斯堡七桥问题就是一个典型的例子。
在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与河岸联结起来，问题是要从这四块陆地中的任何一块开始通过每一座桥正好一次，再回到起点。
图 1 哥尼斯堡七桥问题当然可以通过试验去尝试解决这个问题，但该城居民的任何尝试均未成功。
欧拉为了解决这个问题，采用了建立数学模型的方法。
他将每一块陆地用一个点来代替，将每一座桥用连接相应两点的一条线来代替，从而得到一个有四个“点”，七条“线”的“图”。
问题成为从任一点出发一笔画出七条线再回到起点。
欧拉考察了一般一笔画的结构特点，给出了一笔画的一个判定法则：这个图是连通的，且每个点都与偶数线相关联，将这个判定法则应用于七桥问题，得到了“不可能走通”的结果，不但彻底解决了这个问题，而且开创了图论研究的先河。
图与网络是运筹学（Operations Research）中的一个经典和重要的分支，所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
第7章 图论图论是建立和处理离散型数学模型的重要数学工具，它已发展成具有广泛应用的一个数学分支。
图论的发展已有200多年的历史，它最早起源于一些数学游戏的难题研究。
1736年瑞士数学家欧拉（L.Eluer ）发表了关于解决哥尼斯堡七桥问题的一篇文章，标志着图论的正式诞生。
从19世纪中叶到20世纪中叶，图论问题大量出现，如汉密尔顿图问题、四色猜想等。
这些问题的出现进一步促进了图论的发展。
1847年，克希霍夫（Kirchhoff ）用图论分析电网络，这是图论最早应用于工程科学的一个例子。
随着计算机科学的迅猛发展，在现实生活中的许多问题，如交通网络问题，运输的优化问题，社会学中某类关系的研究，都可以用图论进行研究和处理。
图论在计算机领域中，诸如算法、语言、数据库、网络理论、数据结构、操作系统、人工智能等方面都有重大贡献。
本章主要介绍图论的基本概念、基本性质和一些典型应用。
7.1 图的基本概念7.1.1 图的基本概念1.图的定义图在现实生活中随处可见，如交通运输图、旅游图、流程图等。
此处我们只考虑由点和线所组成的图。
这种图能够描述现实世界的很多事情。
例如，用点表示球队，两队之间的连线代表二者之间进行比赛，这样，各支球队的比赛情况就可以用一个图清楚地表示出来。
到底什么是图呢？可用一句话概括：图是用点和线来刻划离散事物集合中的每对事物间以某种方式相联系的数学模型。
因为上述描述太过于抽象，难于理解，因此下面给出图作为代数结构的一个定义。
定义7.1.1 一个图（Graph ）是一个三元组〈)(G V ，)(G E ，G ϕ〉，其中)(G V 是一个非空的节点集合，)(G E 是有限的边集合，G ϕ是从边集合E 到点集合V 中的有序偶或无序偶的映射。
例7.1.1 图G =〈)(G V ，)(G E ，G ϕ〉，其中)(G V =},,,{d c b a ，)(G E =},,,,,{654321e e e e e e ，),()(1b a e G =ϕ，),()(2c a e G =ϕ，),()(3d b e G =ϕ，),()(4c b e G =ϕ，),()(5c d e G =ϕ，),()(6d a e G =ϕ。
大 众 文 艺大34摘要：图论是数学领域中发展最快的分支之一，数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的！这是拓扑学研究的先声。
图的染色问题一直是图论研究的焦点问题。
数学家赫伍德（Hedwood）成功地运用肯普的方法证明了五色定理，即一张地图能够用五种或者更少的颜色染色。
美国伊利诺斯大学的黑肯（W.Haken）和阿佩尔（Appel），经过四年的艰苦工作，终于完成了四色猜想的证明。
正是上述那些似乎没有多大意义的游戏的抽象与论证的方法，开创了图论科学的研究。
关键词：团论；染色体；四色猜想图论是组合数学的—个分支，与其他的数学分支，如群论、矩阵论、概率论、拓扑学、数值分析等有着密切的联系（参见文献[1]）。
图论中以图为研究对象，图形中我们用点表示对象，两点之间的连线表示对象之间的某种特定的关系。
事实上，任何一个包含了某种二元关系的系统都可以用图形来模拟，而且它具有形象直观的特点。
由于我们感兴趣的是两对象之间是否有某种特定关系，所以图形中两点间连接与否尤为重要，而图形的位置、大小、形状及连接线的曲直长短则无关紧要。
20世纪后，图论的应用渗透到许多其他学科领域。
从20世纪50年代以后，由于计算机的迅速发展，有力地推动了图论的发展，使图论成为数学领域中发展最快的分支之一。
一、图论的起源图论是一个古老的但又十分活跃的数学学科，也是一门很有实用价值的学科，它在自然科学、社会科学等各领域均有很多应用。
近年来它受计算机科学蓬勃发展的刺激，发展极其迅速。
应用范围不断拓广，已渗透到诸如语言学、逻辑学、物理学、化学、电讯工程、计算机科学以及数学的其它分支中。
1736年是图论的历史元年。
这一年，欧拉（L•Euler）研究了哥尼斯堡城（Königsberg）的七桥问题，发表了图论的首篇论文。
欧拉也因此被称为图论之父。
古老而美丽的哥尼斯堡城濒临蓝色的波罗的海，是著名的哲学家康德（Immanuel Kant）的出生地，城中有一条普莱格尔（Pregel）河，河的两条支流在这里汇合，然后横穿全城，流入大海。
河水把城市分成4块，于是，人们建造了7座各具特色的桥，把哥尼斯堡城连成一体，如图1．1(a)所示。
早在18世纪，这些形态各异的小桥吸引了众多的游客，游人在陶醉于美丽风光的同时，不知不觉间，脚下的桥触发了人们的灵感，一个有趣的问题在居民中传开。
谁能够从两岸A，B或两个小岛C，D中任一个地方出发一次走遍所有的7座桥，而且每座桥都只通过一次？这个问题似乎不难，谁都乐意用这个问题来测试一下自己的智力。
可是，谁也没有找到一条这样的路线。
这个问题极大的刺激了德意志人的好奇心，许多人热衷于解决这个问题，然而始终未能成功。
“七桥问题” 难住了哥尼斯堡城的所有居民。
哥尼斯堡城也因“七桥问题” 而出了名。
这就是数学史上著名的七桥问题。
问题看来不复杂，但谁也解决不了，也说不出其所以然来。
1736年，当时著名的数学家欧拉仔细研究了这个问题，他将上述四块陆地与七座桥间的关系用一个抽象图形来描述(见图1．1(b))，其中A、B、C、D分别用四个点来表示，而陆地之间有桥相连者则用连接两个点的连线来表示，这样，上述的哥尼斯堡七桥问题就变成了由点和边所组成的如下问题：试求从图中的任一点出发，通过每条边一次，最后返回到该点，这样的路径是否存在？于是问题就变得简洁明了多了，同时也更一般、更深刻。
这样一来，七桥问题就转变为图论中的一个一笔画问题。
即能不能一笔不重复的画出图1．1(b)中的这个图形。
原先人们是要求找出一条不重复的路线，欧拉想，成千上万的人都失败了，这样的路线也许根本不存在。
于是，欧拉接下来着手判断：这样不重复的路线究竟存不存在？由于这么改变了一下提问的角度，欧拉抓住了问题的实质。
最后，欧拉认真考虑了一笔画图形的结构特征。
欧拉发现，凡是能用一笔画成的图形，都有这样一个特点：每当用笔画一条线进入中间的一个点时，还必须画一条线离开这个点。
否则，整个图形就不可能用一笔画出。
也就是说，单独考察图中的任何一点（起点和终点除外），这个点都应该与偶数条线相连；如果起点与终点重合，那么，连这个点也应该与偶数条线相连。
在七桥问题的几何图中，A、B、D三点分别与3条线相连，C 点与5条线相连。
连线都是奇数条。
因此，欧拉断定：一笔画出这个图形是不可能的。
也就是说，不重复地通过7座桥的路线是根本不存在的！天才的欧拉只用了一步就证明了这个难题，从这里我们也可以看到图论的威力有多么的强大！欧拉对七桥问题的研究，是拓扑学研究的先声。
1750年，欧拉又发现了一个有趣的的现象。
欧拉得到了后人以他的名字命名的“多面体欧拉公式”。
正4面体有4个顶点、6条棱，它的面数加顶点数减去棱数等于2；正6面体有8个顶点、12条棱，它的面数加顶点数减去棱数也等于2。
接着，欧拉又考察了正12面体、正24面体，发现都有相同的结论。
于是继续深入研究这个问题，终于发现了一个著名的定理：这个公式证明了多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。
这个定理成为拓扑学的第一个定理，这个公式被认为开启了数学史上新的一页，促成了拓扑学的发展。
二、图论的发展从19世纪中叶开始，图论进入第二个发展阶段。
这一时期图论问题大量出现，诸如关于地图染色的四色问题、由“周游世界”游戏发展起来的哈密顿(W.Hamilton)问题等。
图的染色问题一直是图论研究的焦点问题。
最早记载染色问题的是英国伦敦大学（University of London）的数学教授德•摩根（D.Morgan）。
1852年，一位刚从伦敦大学毕业的学生费南西斯•古色利（F.Guthrie）在研究英国地图时想到了一个奇怪的问题。
这个问题被称为世界近代三大数学难题之一，这就是著名的“四色猜想”。
问题的起源是这样的：古色利望着挂在墙上的英国地图发呆，他边数着英国的行政区域，边查找它们的位置，同时还注意各区域的地图着色，看着看着他突然发现，该地图仅用四种不同的颜色便可以将地图中相邻的区域分开。
古色利无法解释这一现象，于是他写信给仍在大学读书的弟弟，让他向该校有名的数学家德•摩根请教。
摩根首先注意到：区分地图上的不同区域少于四种颜色不行。
但遗憾的是摩根本人也未能解决这个问题。
于是向自己的好友、著名数学家哈密顿爵士请教。
哈密顿接到摩根的信后，对四色问题进行论证。
但直到1865年哈密顿逝世，问题也没有能够解决。
1878年，英国数学家凯莱（Cayley）在伦敦数学年会上正式提出该问题——平面或球面上的地图仅需四种颜色可以将任何相邻的两区域分开——且征求解答，人称“四色猜想” 的问题便引起了世界数学界的重视。
许多一流的数学家纷纷参加了四色猜想的大会战。
1878—1880年，著名的律师兼数学家肯普（Kempe）和泰勒（Taylor）两人分别提交了证明四色猜想的论文，宣布证明了四色定理，大家都认为四色猜想从此也就解决了。
但是数学家赫伍德（Hedwood）仍然花费毕生精力致力于四图论的起源和发展李 冰 （河北省唐山第五中学 063000）图1．1(a)ADC 图1．1(b)理论研究大 众 文 艺35摘要：发表于文学杂志《江南》的小说《崽崽》是一篇颇具创意的意识流小说，该作是作者朱振武根据自己的亲身经历创作而成，讲述了一家三口和一只名叫崽崽的宠物小白兔之间感人至深的温情故事。
作者创作时有意在形式上进行探索，在内容上将“感情”进行到底，并以颇富哲理意味的方式对人世间的种种现象发起思索与争鸣。
本文试图从形式上的锐意尝试、表层中的以情动人，以及深层下的思辨色彩这三个方面对《崽崽》进行浅尝辄止的解读。
关键词：意识流；崽崽；朱振武一个睿智的爸爸、一个温柔的妈妈、一个活泼的姐姐，以及一只调皮可爱的小白兔，构成了《崽崽》[1]最令人难忘和动容的画面。
小说是作者朱振武[2]根据自己的亲身经历创作而成，讲述了一家三口和一只名叫崽崽的宠物小白兔之间感人至深的温情故事。
作者创作时有意在形式上进行探索，大胆运用了意识流文体，并借鉴了通俗小说中设置悬念的手法。
在内容上，朱振武一方面将“感情”进行到底，使全文弥漫了浓浓的爱的气息，令人感动；另一方面，则充分展开思辨的翅膀，以颇富哲理意味的方式对人世间的种种现象发起思索与争鸣。
因此，本文试图从形式上的锐意尝试、表层中的以情动人，以及深层下的思辨色彩这三个方面对《崽崽》进行浅尝辄止的解读。
形式上的锐意尝试作为全球畅销小说《达•芬奇密码》的中文译者，朱振武在解读该作品时指出了其成功的关键在于顺应了当下文学创作的雅俗合流的趋势。
秉承这一见解，朱振武在《崽崽》的创作中选择了文学性较浓的意识流文体与通俗性较重的悬念手法相结合的外观形式。
对于形式方面的探索是文学创作的一个重要组成部分，作为世界文学中的一员，中国当代作家也积极参与其中。
自改革开放以来，西方的书籍和思想像其他东西一样大量地涌入国门，人们，尤其是作家、学者开始如饥似渴地阅读这些于他们而言是万分新鲜宝贵的图书资源，那一代的人都潜移默化地受到了不同程度的影响。
作家莫言曾说，他“这种年纪的作家毫无疑问都受到了西方文学的影响，因为在80年代以前中国是封闭的，……改革开放以后大量的西方文学被翻译进来，我们有一个两三年的疯狂阅读时期，这种影响就自然而然地产生了，从而不知不觉地就把某个作家的创作方式转移到自己的作品中来了。
”[3]朱振武作为莫言的同龄人，也是被西方文学滋润的一份子，加之又是研究美国文学的教授，因此他的创作也较多地带有西方文学影响的痕迹。
在《崽崽》这部作品中，最明显的一点则非意识流莫属。
朱振武有意借鉴了意识流小说这一文体形式。
小说通篇都是按照小兔子的心理活动的轨迹进行组织行文。
作品伊始就是爸爸和妈妈的对话，但是却没有引号。
而且不仅这里的对话没有引号，全文中的对话都没有使用引号。
这不是作者忘记了，或是编辑不细心，而是作者有意舍弃了引号。
一方面，因为文中的一切都是小兔子的意识，记述的是小兔子的所见所闻所思所想，所以为了强化作品是小兔子的心理活动这一特点，作者有意识地回避了服务于对话的引号，将小兔子置于一种思想自由驰骋的状态之中。
另一方面，朱振武回避引号是和同样“摒弃”引号的女作家赵玫分享了相似的感受，引号的缺席能令作者的创作没有束缚，令作品的表述更加协调紧密，插叙对话和自然描述之间的转换更加灵活，同时也让读者的阅读更为流畅。
由于小说的主体内容是小兔子对于往昔的生活片段的回忆，因此意识流的使用完美地解决了文章中的碎片化内容的拼接问题，使散置的回忆自然地串联起来。
在意识流作品中，视角是比较重要的一个因素。
在《崽崽》中，作者选择了以一个亡灵的视角来讲述故事，但这个亡灵却不是人，而是一只聪慧伶俐的小白兔，同时还辅以儿童的口吻和心理态势。
