随机过程电子科大考博试题

§2.2 维纳过程维纳过程是最基本、最简单同时又是最重要的随机过程, 而且许多过程可以看成是它在某种意义下的推广, 现已广泛应用于物理、经济、通信、生物、管理科学与数理统计中.维纳过程的研究成果应用于计量经济学，使其方法论产生了一次飞跃，成功地应用于非平稳的经济过程，如变化激烈的金融商品价格的研究等.12将一个小球投入无限大高尔顿钉板内,小球各以的概率向左或向右移动一格.21EX.1(高尔顿钉板模拟试验)演示随机游动数学模型3⎩⎨⎧−=.1;,1)(层向左位移一格在第，层向右位移一格在第k k k X P {X (k )=i }－1 1X (k )2/12/1{X (k ), k ∈N +}是一个独立随机过程,令∑==n k k X n Y 0),()(小球在第n 次碰撞后所处位置{Y(n),n ∈N +}是一个平稳独立增量过程.4(),0][)]([1==∑=nk k X E n Y E 均值函数为,)]([)]([1∑===nk n k X D n Y D 方差函数为由独立同分布中心极限定理知)()()(1y y n k X P y n n Y P n k Φ→⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤=⎭⎬⎫⎩⎨⎧≤∑=∞→n as ",2,1,)()(*==n nn Y n Y 即依分布收敛于标准正态分布随机变量.2.2.1 维纳过程的数学模型及定义维纳过程是英国植物学家罗伯特.布朗在观察漂浮在液面的花粉运动—布朗运动规律时建立的随机游动数学模型.在一条直线上的简单对称的随机游动.设一粒质点(花粉)每隔时间Δt, 随机地以概率p =1/2向右移动Δx(>0), 以概率q =1/2向左移动一个Δx, 而且每次移动相互独立. 56x t x t +Δxx t －Δx p =1/2q =1/2",2,1.,1,,1=⎩⎨⎧−=i i i X i ，次向左移动第次向右移动第记则t 时刻质点的位置为)(][21t t t X X X x X ΔΔ+++="取整运算()0,i E X =因()0,t E X =故2()()[]t t D X x t =ΔΔ2()()1,1,2i i D X E X i ==="7][)()(,0)(2tt x X D X E t t ΔΔ==故实际粒子的不规则运动是连续进行的, 考虑的情形.0→t Δ由物理实验结论,可假定0).x t c Δ=Δ>为常数(1)有并令代入上式0,→t Δt c tt t c t t x X D t t t t 220200][lim ][)(lim )(lim ===→→→ΔΔΔΔΔΔΔ0)(lim 0=→t t X E Δ和显然X 0= 0.(2)8又因由泛函中心极限定理, 对任意的有对任意t >0 )(][21t t t X X X x X ΔΔ+++="可看为个相互独立同分布的随机变量之和,][t tΔ(3)0,[]t t tΔ→→∞Δ时0,>∈t R x }0,{>t X t 故过程是平稳独立增量过程.)(Φ}0{lim }{lim 2][0020x x tc X x P x t c X P i t t i t t t =≤−=≤∑=→→ΔΔΔΔ即当时, X t 趋于正态分布N (0, c 2t ).0→t Δ(4)9定义2.2.1若随机过程满足}0,{≥t W t (1) 平稳独立增量过程;(2) 对任意t >0, );0(),0(~2>σ，σt N W t 1}0{)3(0==W P 称{W t ,t ≥0}是参数为σ2的维纳过程.D (W t )随时间的推移而增大特别当σ=1，称{W t ,t ≥0}是参数为σ2的标准维纳过程.101.一维分布：W t ～N (0,σ2t )；2.增量分布：W t －W s ～N (0,σ2|t －s |);设t ＞s,因W 0=0, 且W t 是平稳独立增量过程，故有相同分布N (0,σ2(t－s )).2.2.2 维纳过程的分布及性质ss s t s t W W W W −=−+−0t s t sW W W −−−=与11证设维纳过程{ W ( t ),t ≥0}的参数是σ2，,121n t t t n <<<≥"及任取nk W W X W X k k t t k t ,,3,2,ˆ,ˆ111"=−==−n k t t N X k k k ,,2,1)),(,0(~12"=−−σX 1, X 2…, X n 相互独立, 且k t X X X W k +++="21则有独立增量过程是可加过程定理2.2.1维纳过程是正态过程.分析需证对任意的,0121n t t t n <<<<≥"及T t t t nW W W ),,,(21"服从n 为联合正态分布.12⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=000O #⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−=−)()(B 1212212n n t t t t t σσσ%随机向量可表示为T t t t n W W W ),,,(21"T n X X X ),,,(21"的满秩线性变换:其中故服从n 维联合正态分布N (O,B). T n X X X ),,,(21"13⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡n t t t W W W #21⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111001110001100001#####⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n X X X #21由正态分布的线性变换不变性可知Tt t t n W W W ),,,(21"或CXW =满秩矩阵是非退化n 维正态随机向量.14由维纳过程的定义可得1. E (W t )=0, D (W t ) =σ2t ;2. C (s, t )=R (s,t )=σ2min (s,t )维纳过程是平稳独立增量过程(性质1.3.1)根据定理2.1.3之推论1可知的均值向量为CO=O, 协方差矩阵为Tt t t n W W W ),,,(21"ΓW = CBC T ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n t t t t t t t t t 22212222212121212σσσσσσσσσ"#%##""维纳过程的数字特征15故维纳过程的n 维联合概率密度为=),,,(21,,,21n t t t x x x f n ""⎭⎬⎫⎩⎨⎧−−X X 1W 21W2Γτ21exp Γ2π1n 其中.),,,(21T n x x x "=X 一维概率密度为R x t x t x f t ∈−=},2exp{21)(22σσπ16EX.2设{W (t ), t ≥0}是参数为σ2的维纳过程, 求下列过程的均值函数和相关函数.1) X (t )=W 2(t ), t ≥0；.0),1()()2>=t t tW t X 解1）m X (t )=E [X (t )]=E [W 2(t )]=D [W (t )]+{E [W (t )]}2= σ2t.)]()([)]()([),(22t W s W E t X s X E t s R X ==})]()()()[({22s W s W t W s W E +−=( s <t )17)]}()()[({2)]([})]()()[({3422s W t W s W E s W E s W t W s W E −++−=)]([})]()({[)]([422s W E s W t W E s W E +−=独立增量)),(min 2(),(24t s st t s R X +σ=故)2(3)(242422s st s s t s +=+−=σσσσ)]()([)]()([),(22t W s W E t X s X E t s R X ==})]()()()[({22s W s W t W s W E +−=( s <t )另因若X ～N (0,σ2), 有⎪⎩⎪⎨⎧=−−σ=="""6,4,2,1)3)(1(,5,3,1,0)(n n n n X E n n18.0,0)]1([)]([)()2>===t t W tE t X E t m X )]1()1([)]1()1([),(t W s W stE t tW s sW E t s R X ==).,min()1,1min(22t s t s st σσ==EX.2设{W (t ), t ≥0}是参数为σ2的维纳过程, 求下列过程的均值函数和相关函数.1) X (t )=W 2(t ), t ≥0；.0),1()()2>=t ttW t X19定理2.2.2 (判断正态过程是否为维纳过程的充分必要条件)0),,min()(2>=C t s C W W E t s 且轨道连续, 则{Wt , t ≥0}是维纳过程, 反之亦然.轨道连续: 过程的样本函数是连续函数.结论维纳过程{W t ,t ≥0}几乎所有样本函数都是连续的. 即存在A Ω, P (A )=1, 使ω∈Ω时,W t (ω)在[0, ∞)上连续.⊂设{W t , t ≥0}是正态过程, W 0= 0, 对任意t , s >0 有E (W t )= 0 及20思考题设是参数为σ2的维纳过程，a 为一正常数，令}0),({≥t t W 0)()()(≥−+=t t W a t W t X 试讨论是否为正态过程, 是否为维纳过程.}0),({≥t t X21泛函中心极限定理(functional central limit zheorem) 设随机变量序列{X t ,t =1,2, …}是相互独立同分布的，且满足：;0)()1=t X E ;)()()222∞<==σt t X E X D 设r 为闭区间[0, 1]上的任一正实数，则统计量∑==][1)(Tr t tT X r R ).()(,r W r R T as T 弱收敛于∞→r满足：rW其中]1,0[),(∈（1）W(0)=0;（2）E{W(t)}=0;（3）W(t)～N(0,σ2t ), (σ＞0).（4）具有独立平稳增量;22。

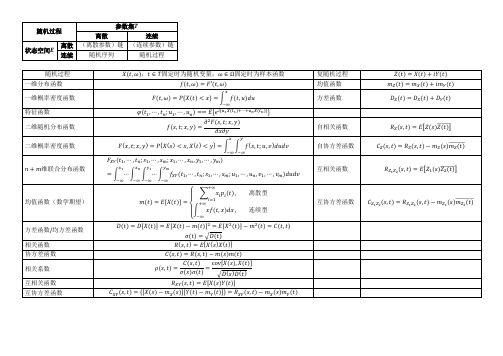
课程编号： 0721001 考试日期：考试日期： 2012 年 1 月 4 日考试时间： 150 分) 任课教师：任课教师：任课教师： 班号班号-saa a a a wE X l.i.ml.i.m X X lim )2C T T t -ò))22C TTTT-=-òò(2) 求状态5的首达概率(2)55f 和(5)55f以及计算511j jjm =å。

七. （12 分） 设j 为一齐次马尔可夫链的常返状态且周期为d ，则一定有，则一定有()lim nd jjn jjdp m ®¥=，其中jj m 为状态j 的平均返回时间。

的平均返回时间。

证明下面的问题：证明下面的问题：(1) 状态j 为零常返当且仅当()lim 0n jjn p®¥=。

(2) 状态j 为遍历的当且仅当()1lim 0n jjn jjpm®¥=>。

八. （12 分）分）设齐次马尔可夫链设齐次马尔可夫链{},0,1,2,...n X X n ==的状态空间{1,2,3,4,5,6}S =，且其且其 一步转移概率矩阵为一步转移概率矩阵为0.60.400.6000.400.10.10.10.10.50.1 00.20.20.40.2 0 00.2 0 00.8 00.4 0 0 0 00.6P éùêúêúêú=êúêúêúêúëû （1）试对状态空间进行分解。

）试对状态空间进行分解。

（2）问平稳分布是否存在？如果存在试求出所有的平稳分布。

（3）设初始分布0(), i P X i i S p ==Î，其中{}1261111,,...,,,0,0,,4634p p p ìü=íýîþ，求概率，求概率(1)?, =1,2,n P X n ==和概率1(1,2)?, =1,2,3,...=1,2,3,...n n P X X n +===。

西安电子科技大学研究生课程考试试题考试科目：随机过程考试日期：2015年1月13日考试时间：150分考试方式：（闭卷）任课教师：班号：学生姓名：学号：一．（10分）在华为公司上班的小吉某日（t=0）开通了支付宝账户，在时间段[0,t]内他向该账户内转了N t次账。

假设N={N t:t≥0}是参数为λ的Poisson过程，每次转账的金额相互独立，转账次数和转账金额也独立。

根据经验，一次转账为1000元、1200元和1500元的概率分别为1/2、1/3和1/6。

若Y t表示到t时刻为止小吉转入支付宝账户的总金额。

求（1）Y t的特征函数φt(u)。

（2）Y={Y t:t≥0}的均值函数m Y(t)。

二．（20分）设W={W t:t≥0}是一个标准布朗运动，即初值为0，具有平稳独立增量性，t(t>0)时刻的状态W t:N(0,t)。

若设X t=e−αW t（实常数α≠0），称X={X t:t≥0}是几何布朗运动。

（1）求X的自协方差函数C x(s,t)(s<t)。

（2）问X是否具有平稳增量性，并给出证明。

三．（20分）1.设某天文台观察到的流星流是一个泊松过程，据以往资料统计为每小时平均观察到3颗流星。

试求（1）在上午8点到12点期间，该天文台没有观察到流星的概率。

（2）下午（12点以后）该天文台观察到第一颗流星的时间的分布函数。

2.设脉冲到达计数器的规律符合到达率为λ的泊松过程。

每个到达的脉冲被记录的概率为p，且脉冲是否被记录是相互独立的。

令X t表示直到t(t≥0)时刻已被记录的脉冲数。

（1）计算P(X t=k),k=0,1,2,⋯。

（2）X={X t,t≥0}是否为泊松过程？若是请给出证明。

四．（20分）设实平稳过程X={X t,t≥0}的均值函数为零，相关函数为R x(τ)=e−|τ|,τ∈(−∞,+∞)。

令Y t=X t+cos(ωt+θ)，其中ω为常数，θ是与随机过程X独立的且服从[0,2π]上均匀分布的随机变量。

2004年秋季电子科技大学考博英语真题试卷(题后含答案及解析)题型有：1. Structure and V ocabulary 2. Reading Comprehension 3. Cloze 4. English-Chinese Translation 5. WritingStructure and V ocabulary1．Obviously these are all factors affecting smooth operation, but the underlying problem is still to be identified.A．operationalB．fundamentalC．operatingD．underneath正确答案：B解析：本题中，underlying的意思是“在下面的，根本的，潜在的”。

四个选项中，fundamental的意思是“基础的，根本的”，如：a fundamental difference between their aims(他们目标的根本差异)。

operational的意思是“操作的”；operating的意思是“运行的，操作的”；underneath的意思是“下面的”。

只有B 项符合题意。

2．If you can convince the interviewer of your special qualifications, your chance of being accepted will be greatly enhanced.A．appreciatedB．encouragedC．frustratedD．increased正确答案：D解析：本题中，enhanced的意思是“提高，增强”。

四个选项中，increased 的意思是“增强的”，如：My wages have increased this year．(我的工资今年增加了)。

5.4 齐次马氏链的状态为揭示齐次马氏链的基本结构，需对其状态按概率特性进行分类，状态分类是研究n 步转移概率的极限状态的基础.EX.1设系统有三种可能状态E={1, 2 ,3},“1”表示系统运行良好, “2”表示系统运行正常，“3”表示系统失效.电子科技大学电子科技大学以X (n )表示系统在n 时刻的状态, 并设{X (n ),n ≥0}是一马氏链. 在没有维修及更换的条件下, 其自然转移概率矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=10010110902012022017333231232221131211p p p p p p p p p P 由矩阵P 可见，从“1”或“2”出发经有限次转移后总能到达“3”状态，而一旦到达“3”状态则永远停留在“3”.状态“1”, “2”与状态“3”有不同的概率特性.状态“1”, “2”与状态“3”有不同的概率特性.一、刻画状态特性的几个特征量二、状态类型分类三、状态类型判别条件四、状态间的关系五、状态空间的分解电子科技大学一、刻画状态特性的几个特征量定义5.4.4，记及对1,≥∈∀n E j i },)0(11,)(,)({ˆ)(i X n k j k X j n X P f n ij =−≤≤≠==称为(n 步)首达概率.系统从状态“i ”出发经过n 步转移后首次到达状态“j ”的概率特别地称)(n ii f 为首返概率；5.4 齐次马氏链的状态电子科技大学∑∞==1)(n n ijf称为最终概率.定义5.4.5 自状态i 出发迟早(最终)到达j 的概率为})0()(,1{i X j n X n P f ij ==≥=使存在定理5.4.1(首达概率表示式)有，及对1,≥∈∀n E j i ;10)1)(≤≤n ij f 2) 首达概率可以用一步转移概率表示为为状态i 的最终返回概率.ii f ji i i j i j i i i j i n ij n n p p p f 1211112)(−−∑∑∑≠≠≠=电子科技大学j i i i j i ji i i j i n ij n n p p p f 1211112)(−−∑∑∑≠≠≠= 证1）显然ii 1i 2j2）分析示意图如下})0(1,,2,1,)(,)({)(i X n k j k X j n X P f n ij =−=≠== .)0(1,,2,1,})({,)(⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=−====∈≠i X n k i k X j n X P E i j i k k k ∪第1步第2步第n 步()01;n ij f ≤≤电子科技大学⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧===−==−≠≠≠−i X j n X i n X i X P n j i j i j i n )0(})(,)1(,,)1({11112 ∪∪∪()(),{()},1,2,,1(0).k n ij k i j f P X n j X k i k n X i ≠⎧⎫⎪⎪====−=⎨⎬⎪⎪⎩⎭∪∑∑∑≠≠≠−=j i ji j i n 112 })0()(,)1(,,)1({11i X j n X i n X i X P n ===−=− ji i i j i j i ii j i n n p p p 1211112−−∑∑∑≠≠≠=定义5.4.2 对j ∈E , 称})0(,)(,1:min{i X j n X n n T ij ==≥=为从i 到达j 的首达时间.注：若右边是空集, 则令T ij =∞.随机变量EX.2在股票交易过程中令状态空间为E ={－1, 0, 1}各状态分别代表“下跌”,“持平”,“上升”.若X (0)=0, 有使<<<<k n n n 21电子科技大学 ,1)(,,1)(,1)(21===k n X n X n X }0)0(,1)(:min{01===X n X n t k 则121},,,,min{n n n n k == 注1T ij 表示从i 出发首次到达j 的时间.T ii 表示从i 出发首次回到i 的时间.注2 T ij 与首达概率之间有关系式：,2,1,,,},)0({)1)(∞=∈===n E j i i X n T P f ij n ij.,},)0({)2E j i i X T P f ij ij ∈=∞<=若X (0)=0, 有使 <<<<k n n n 21续EX.1设系统有三种可能状态E ={1, 2 ,3}, “1”表示系统运行良好, “2”表示系统运行正常,“3”表示系统失效.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=10010110902012022017333231232221131211p p p p p p p p p P T 13(1)1313{1(0)1}f P T X ====131,20p =ji i i j i j i i i j i n ij n n p p p f 1211112)(−−∑∑∑≠≠≠= 系统的工作寿命，有电子科技大学(2)1313{2(0)1}f P T X ===13{(0)1}P T n X ≥=研究首达概率和首达时间有实际工程意义.……13{(0)1}P T n X ≥=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=10010110902012022017333231232221131211p p p p p p p p p P [0,],n 是系统在内运行的可靠性有1113122321,400p p p p =+=13{(0)1}k nP T k X ∞====∑()13n k nf∞==∑电子科技大学定理5.4.2概率与首达概率有关系式，任意步转移及对1,≥∈∀n E j i ∪∞==⊂==1}{})(,)0({m ij m T j n X i X 因证:⎭⎬⎫⎩⎨⎧====∞=∪∩1}{})(,)0({m ij m T j n X i X })(,)0({j n X i X ==故.)(1)()(m n jjnm m ijn ijpfp−=∑=电子科技大学})0()({)(i X j n X P P n ij===⎭⎬⎫⎩⎨⎧=====i X j n X m T P nm ij )0(})(,{1∪},)0()({})0({1m T i X j n X P i X m T P ij nm ij ======∑=⎭⎬⎫⎩⎨⎧====∞=∪∩1}{})(,)0({m ij m T j n X i X ∪nm ij m T j n X i X 1},)(,)0({=====})(,)0({j n X i X ==故电子科技大学马氏性})()({})0(,11,)(,)({1j m X j n X P i X m k j k X j m X P nm ==⋅=−≤≤≠==∑=})()({1)(j m X j n X P f nm m ij ===∑=()1{(0)}{()(0),}nn ijij ij m P P T m X i P X n j X i T m =======∑.)(1)(m n jjnm m ijpf−=∑=定义5.4.1使，若存在对1,,≥∈∀n E j i ,0)(>n ijp称自状态i 可达状态j ,记为.j i →定理5.4.3的充分必要条件是0>ij f .j i →证:必要性因01)(>=∑∞=m m ijij ff 至少存在一个n 使,有)(>n ijf ()()()1nn m n m ijijjjm pfp−==∑()(0)0n ijjj fP ≥>定义5.4.3称若,,0}{E j T P ij ∈=∞=∑∞===1)(][n n ijij ij nfT E μ为从状态i 出发, 到达状态j 的平均时间(平均步数).充分性因j i →使，存在1≥n 01)()()(>=∑=−nm m n jjm ijn ijpfp则在中至少有一个大于零，故)()1(,,n ijijff 01)(>=∑∞=m m ijij ff 特别当i=j 称jj μ为状态j 的平均返回时间.电子科技大学二、状态类型分类状态分类是研究n 步转移概率的极限状态的基础, 能有效地揭示其深刻的统计规律.续EX.1设系统有三种可能状态E ={1, 2 ,3},“1”表示系统运行良好, “2”表示系统运行正常，“3”表示系统失效.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∞→100100100lim )(n n P该系统的状态“3”是吸收态, 经有限步均会被吸收, 直观分析可得有必要分析各种状态的类型.电子科技大学定义5.4.6对状态i ∈E , 最终返回概率为f ii ，若f ii <1，称状态i 是非常返的(或瞬时的).若f ii =1，称状态i 是常返的；若马氏链的每个状态都是常返的, 则称为常返马氏链.f ii =1表示系统从状态i 出发几乎必定会返回状态i .定义5.4.7对常返状态i ∈E , 平均返回时间为μii ，若μii <+∞, 称状态i 是正常返的；进一步, 根据常返状态的平均返回步数再划分为两类.注若μii = +∞, 称状态i 为零常返的。

电⼦科技⼤学随机信号分析中期考题2006随机（A）1.设随机过程21)(cos )(2-Θ+=t t X ω，Θ是随机变量，其特征函数为)(υφΘ。

证明：)(t X 是⼴义平稳随机过程的充要条件是0)4()2(==ΘΘφφ。

证明：（1）)(t X 的均值为：()21()[()][cos ()]2111[1cos 2()][cos(22)]22211cos(2)[cos(2)]sin(2)[sin(2)]22X m t E X t E t E t E t t E t E ωωωωω==+Θ-=++Θ-=+Θ=Θ-Θ由上式可知，当且仅当0)]2sin()2[cos(][)2(2=Θ+Θ==ΘΘj E e E j φ时，()0X m t =，才与t ⽆关。

（2）)(t X 的相关函数为：22(,)[()()]11[(cos ())(cos ())]2211[cos(222)cos(22)]22[cos(2)][cos(424)]811cos(2)cos(42)[cos(4)]881sin(42)][sin(4)]8X R t t E X t X t E t t E t t E E t t E t E ττωωτωωωτωωτωωτωτωωτωωτ+=+=++Θ-+Θ-=++Θ?+Θ+++Θ==++Θ-+Θ同理可得，当且仅当0)]4sin()4[cos(][)4(4=Θ+Θ==ΘΘj E eE j φ时，)cos(21),(ωττ=+t t R X 与t ⽆关。

2.设随机过程)sin()(0Θ+Ω=t A t X ，其中0A 为常数，ΘΩ和为相互独⽴的随机变量，Ω在]2010[ππ内均匀分布，Θ在]20[π内均匀分布。

证明：（1） )(t X 是⼴义平稳随机信号；（2） )(t X 的均值是各态历经的。

解：（1）00000[()][sin()][sin()cos()cos()sin())][sin()][cos()][cos()][sin())]0E X t E A t E A t A t A E t E A E t E =Ω+Θ=ΩΘ+ΩΘ=ΩΘ+ΩΘ= 202020(,)[()()][sin()sin()]cos()cos(22)2cos()2X R t t E X t X t A E t t t A E A E ττττττ+=+=Ω+Ω+ΘΩ+ΘΩ-Ω+Ω+Θ??=Ω??=所以)(t X 是⼴义平稳随机信号（2）[]00000001[()][sin()]lim sin()lim sin()lim cos()|0TT T T T T A X t A A t A t dtT A A t d t t T T →+∞→+∞→+∞=Ω+Θ=Ω+Θ=Ω+ΘΩ=-Ω+Θ=ΩΩ时间平均等于统计平均，所以)(t X 的均值是各态历经的。

随机过程习题及部分解答习题一1.若随机过程X(/)为X(0 = A?,-oo<r<+oo,式中4为(0, 1)上均匀分布的随机变量，求X(/)的一维概率密度Px(x；t)。

2.设随机过程X(/) = 4cos(初+ 其中振幅A及角频率①均为常数,相位&是在[-兀,刃上服从均匀分布的随机变量，求X(/)的一维分布。

习题二1.若随机过程X(/)为X(t)=At -00 < r < +00 ,式中4为(0,1)上均匀分布的随机变量，求E[xa)],7?xa』2)2.给定一随机过程X(/)和常数Q,试以X(/)的相关函数表示随机过程y(0 = X(/ + a) —X(/)的自相关函数。

3.已知随机过程X(/)的均值阪⑴和协方差函数Cx (爪© , 0(/)是普通函数，试求随机过程丫⑴=X(/) + 0(/)是普通函数，试求随机过程丫⑴=X(/) + 0(/)的均值和协方差函数。

4.设X(t) = A cos at + B sin at,其中A, B是相互独立且服从同一高斯(正态)分布N(0Q2)的随机变量，a为常数，试求X(/)的值与相关函数。

习题三1.试证3.1节均方收敛的性质。

2.证明:若X(t),twT;Y(t),twT均方可微，a0为任意常数,则aX(t) + bY(t) 也是均方可微，且有[aX (?) + b Y(/)]' = aX'(/) + b Y'(/)3.证明：若X⑴,twT均方可微，/X/)是普通的可微函数，则f(Z)X(Z)均方可微且[f(ox(or-/w(o+/(ox,(o4.证明:设X⑴在[a,b]上均方可微，且X0)在[a,切上均方连续，则有X'⑴ dt = X(b) — X(a)J a5•证明，设X(t\t eT =[a,b];Y{t\t eT = [a,b]为两个随机过程，且在T上均方可积，a和0为常数，则有(*b (*b (*bf [aX(/) + 0Y(/)M = a [ Xit)dt + /3\ Y⑴ dtJ a J a J aeb rc rbaX (t)dt = X (t)dt + XQ) dt,aWcWbJ a J a Jc6.求随机微分方程X'(/) + aX ⑴二丫⑴ze[0,+oo]'X(0) = 0的X(t)数学期望E [X(0]。

1． 两个联合平稳的随机过程为：()()()()00X cos Y sin t a t t b t ωω=+Θ=+Θ其中a 、b 、0ω皆为常数，Θ是在[]0,2π上均匀分布的随机变量。

试求互相关函数()()XY YX R R ττ和，并说明互相关函数在0τ=时的值具有什么意义。

解：()()()()()()()()()()()()()0000000Y X 0c o s s i n s i n 22s i n 2sin 2sin 2XY XY R E X t Y t E a t b t abE t ababR R ττωωτωωωτωτωτττωτ=+⎡⎤⎣⎦⎡⎤=++Θ+Θ⎣⎦=++Θ-⎡⎤⎣⎦=--==()()YX 000XY R R ==，说明()()X t Y t 和在同一时刻正交，对于本题，()()0E X t E Y t =⎡⎤⎡⎤⎣⎦⎣⎦=，说明()()X t Y t 和在同一时刻还互不相关。

3、 设有平稳过程()cos()X t a t =Ω+Θ，其中a 为常数，Θ是在[0,2]π上服从均匀分布的随机变量，Ω是概率密度函数满足()()f f ωω=-的随机变量，且Ω与Θ相互独立。

求证()X t 的功率谱密度2()()X S a f ωπω=。

解：[](,)cos()cos()X R t t E a t a t ττ+=Ω+Ω+ΘΩ+Θ[]2cos(22)cos()2a E t ττ=Ω+Ω+Θ+Ω 由于Ω与Θ相互独立[]2,()0cos(22)cos(22)(,)0E t t f d d πωτωωτθωθθωΩΦ∴Ω+Ω+Θ=++=⎰⎰[][]22(,)cos(22)cos()=cos()22X a a R t t E t E ττττ∴+=Ω+Ω+Θ+ΩΩ2cos()()2a f d ωτωω∞Ω-∞'''=⎰由于()()X X R S τω⇔，所以2()cos()()2X a S f d ωωτωω∞Ω-∞⎧⎫'''=⎨⎬⎩⎭⎰F 2cos()()2j a f d e d ωτωτωωτ∞∞-Ω-∞-∞⎡⎤'''=⎢⎥⎣⎦⎰⎰ 2cos()()2j a e d f d ωτωττωω∞∞-Ω-∞-∞⎡⎤'''=⎢⎥⎣⎦⎰⎰()()2()2a f d πδωωδωωωω∞Ω-∞''''=-++⎡⎤⎣⎦⎰由于(), ()f δωωΩ''为偶函数，所以()()20()a f d πδωωδωωωω∞Ω''''=-++⎡⎤⎣⎦⎰()20()a f d πδωωωω∞Ω''=-⎰2()a f πωΩ=得证。

电子科技大学电子科大16秋《随机信号与系统》在线作业3一、单选题（共10 道试题，共40 分。

）1. 随机信号X（t，w）当时间变量t固定是，此函数为（）。

A. 随机信号B. 随机变量C. 样本函数D. 随机过程正确答案：2. 连续投两次硬币，两次的结果是一样的概率是（）。

A. 1/4B. 1/8C. 1/2D. 1正确答案：3. 若N(t)是方差为a的零均值独立高斯过程，则它在不同的两个时刻的相关函数是（）。

A. 0B. aC. 不确定正确答案：4. 已知X(t)=Acos(wt+θ),其中θ在[0,2*pi]上均匀分布，A为常数，则X(t)的均值为（）。

A. 1B. AC. 0D. w正确答案：5. 随机变量X~N(0,a),那么Y=2X的均值为（）。

A. aB. 0C. 4aD. 不确定正确答案：6. 均值为零的白噪声通过LTI系统后的输出噪声的均值为（）。

A. 2B. 0C. 1D. 不确定正确答案：7. 已知X(t)=Acos(wt+θ),其中θ在[0,2*pi上均匀分布，A服从均值为0的高斯分布，A与θ相互独立，则X(t)的均值为（）。

A. 0B. AC. 1D. w正确答案：8. 高斯信号X(t)的均值为u,方差d2,Y(t)=3X(t),Y(t)的方差为（）。

A. uB. d2C. 3uD. 9d2正确答案：9. 随机信号X(t)均值为2，通过一个LTI系统H(jw)=1/(jw+2),则输出Y(t)的均值为（）。

A. 2B. 1C. 1/2D. 0正确答案：10. 已知一随机信号X(t)是平稳的，则其均值可能是（）。

A. 2tB. t+2C. 2D. 以上都不可能正确答案：16秋《随机信号与系统》在线作业3二、多选题（共5 道试题，共30 分。

）1. 以下哪个信号不是随机信号？A. sin(2t)B. cos(2t+θ),θ~U[0,2*pi)C. t+a,a是常数D. 2t正确答案：2. 随机变量X1和X2都是服从均值为0，方差为1的高斯分布的且它们相互独立，Y=X1+X2，对于随机变量Y，下列说法正确的是（）。