直方图统计表模板

“健力芬达682.00%雪碧9100.00% 二、用Excel作数值数据的频数分布表和直方图例2 某班50名学生的统计学原理考试成绩数据如下：798878507090547258728091959181726173978374616263747499846475657566758567697586597688697787步骤一：输入数据并排序（一）打开Excel工作簿，把本例中的数据输入到A1至A50单元格中。

（二）对上述数据排序。

结果放到B1至B50。

具体步骤如下：1.拖曳鼠标选中A1：A50单元格区域。

在该处，单击鼠标右键，选中“复制”命令。

2.拖曳鼠标选中B1：B50单元格区域。

在该处，单击鼠标右键，选中“粘贴”命令。

3.再次选中B1：B50，选择“数据”下拉菜单中的“排序”选项。

出现对话框，选中按递增 排序即可。

4.单击确定。

步骤二：指定上限在C3至C7单元格中输入分组数据的上限59，69，79，89，100。

I 提示：Excel在作频数分布表时，每一组的频数包括一个组的上限值。

这与统计学上的“上限不在组”做法不一致。

因此50-60这一组的上限为59。

以此类推。

步骤三：生成频数分布表和直方图（一）选择“工具”下拉菜单中的“数据分析”选项。

出现该对话框。

（二）在“数据分析”对话框种选择“直方图”。

（三）当出现直方图对话框时，1.在“输入区域”方框中输入数据所在单元格区域B1：B50。

2.在“接受区域”方框中输入分组数据上限所在单元格区域C3：C7。

3.在“输出区域”方框中输入D3，表示输出区域的起点。

4.在输出选项中，选择“输出区域”、“累计百分比”和“图表输出”。

（四）点击确定。

（五）为了便于阅读，单击频数分布表中的有“接受”字样的单元格，输入“考试成绩”；同样，用50-60代替频数分布表中的第一个上限值59，60-70代替第二个上限值69，以此类推，最后，用90-100代替频数分布表中最后一个上限值100。

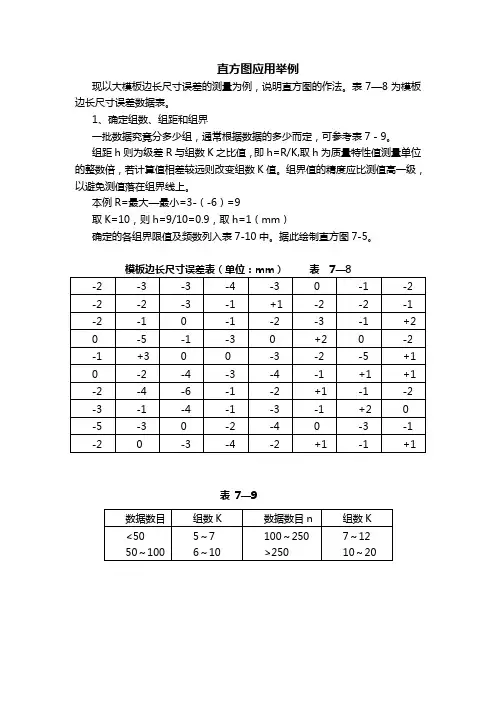
直方图应用举例现以大模板边长尺寸误差的测量为例，说明直方图的作法。

表7—8为模板边长尺寸误差数据表。

1、确定组数、组距和组界一批数据究竟分多少组，通常根据数据的多少而定，可参考表7－9。

组距h则为级差R与组数K之比值，即h=R/K,取h为质量特性值测量单位的整数倍，若计算值相差较远则改变组数K值。

组界值的精度应比测值高一级，以避免测值落在组界线上。

本例R=最大—最小=3-（-6）=9取K=10，则h=9/10=0.9，取h=1（mm）确定的各组界限值及频数列入表7-10中。

据此绘制直方图7-5。

模板边长尺寸误差表（单位：mm）表 7—8表 7—9一、直方图观察分析对照典型直方图（图7-6）分析形状。

图(a)正常型。

图(b)孤岛型，生产过程中出现了异常因素，如原材料变化，或有不熟练的工人操作或测量仪器出现偏差等。

图(c)双峰型，有两个中心出现，可能是数据统计或数据取得有误，比如将两个不同班组的数据混为一批，或将用不同设备和不同材料加工的产品混在一起造成的。

图(d)偏向型及图(f)陡壁型，可能是对一侧控制过严或是有意剔除了不合格数据。

图(e)平顶型，可能是将多个母体混在了一起或是生产过程中有缓慢变化的因素在起作用所造成的，如操作者的疲劳或机械的过度磨损等。

图(g)锯齿型，可能不是生产上的原因，而是由于绘图是数据分组过多或测量数据时失误而造成的。

图7-5 频数直方图图7-6 常见直方图形式图7-7 与标准对照的直方图对照标准比较范围：当工序处于稳定状态时（即直方图为正常型），还需进一步将直方图与规格标准进行比较，以判断工序满足标准要求的程度。

其主要是分析直方图的平均值X与质量标准中心重合程度，比较直方图分布范围B与公差范围T的关系.。

图7—7在直方图中标出了标准范围T，标准的上下偏差T U和T L ，实际尺寸范围B。

对照直方图图形可以看出实际产品分布与实际要求标准的差异。

统计表；条形图； 折线图；扇形图； 频数分布直方图； 频数折线图.
例:为了考察某种大麦穗长的分布情况，在一块实验田里
抽取了100个麦穗，量得它们的长度如下表（单位：cm）
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6 5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8 6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5 6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4 6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 7.0 6.4 6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6 5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0 5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7 5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0 6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
问题1解答
2．决定组距和组数 把所有数据分成若干组，每个小组的两 个端点之间的距离称为组距.
（最大值－最小值）÷组距 ＝ 23 7 2 , 33
所以要将数据分成8组：149≤x＜152， 152≤x＜155，… 170≤x＜173．这里组数和 组距分别是8和3．
3．列频数分布表 对落在各个小组内的数据进行累计，得到各
个小组内的数据的个数（叫做频数）．整理可以 得到频数分布表，见教材164页表10-4．
组数：分成的组的个数称为组数。
组距：每一组两个端点的差称为 组距
从表中可以看出，身高在155≤x ＜158，158≤x＜161，161≤x＜164三

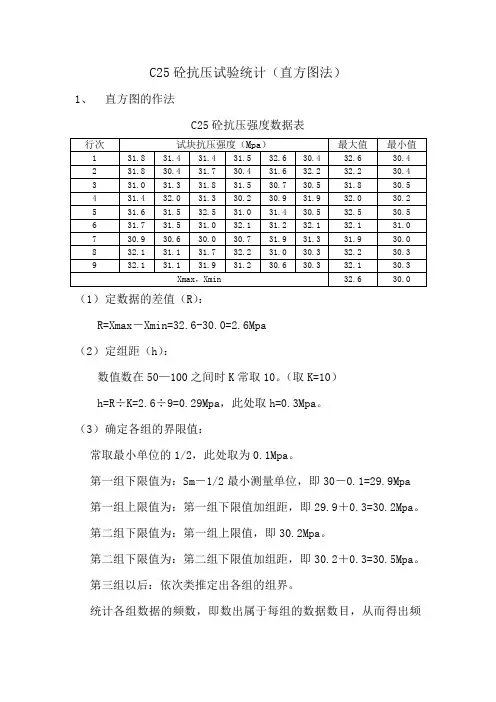
C25砼抗压试验统计（直方图法）1、直方图的作法C25砼抗压强度数据表（1）定数据的差值（R）：R=Xmax－Xmin=32.6-30.0=2.6Mpa（2）定组距（h）：数值数在50—100之间时K常取10。

（取K=10）h=R÷K=2.6÷9=0.29Mpa，此处取h=0.3Mpa。

（3）确定各组的界限值：常取最小单位的1/2，此处取为0.1Mpa。

第一组下限值为：Sm－1/2最小测量单位，即30－0.1=29.9Mpa 第一组上限值为：第一组下限值加组距，即29.9＋0.3=30.2Mpa。

第二组下限值为：第一组上限值，即30.2Mpa。

第二组下限值为：第二组下限值加组距，即30.2＋0.3=30.5Mpa。

第三组以后：依次类推定出各组的组界。

统计各组数据的频数，即数出属于每组的数据数目，从而得出频数分布表，见下表：组号组区间值组中值（b）频数统计频数（f）μiμi2 f iμi f iμi2①②③④⑤⑥⑦⑧⑨1 29.9～30.2 30.0511 2 -4 16 -8 322 30.2～30.5 30.3511111 5 -3 9 -15 453 30.5～30.8 30.65111111 6 -24 -12 244 30.8～31.1 30.951111111 7 -1 1 -8 85 31.1～31.4 31.25111111111 9 0 0 0 06 31.4～31.7 31.55111111111 9 1 1 9 97 31.7～32.0 31.851111111 7 2 4 14 288 32.0～32.3 32.15111111 6 3 9 18 549 32.3～32.6 32.4511 2 4 16 8 32总计54 0 60 6 232 （4）画直方图：以纵坐标表示各组发生频数，横坐标表示质量特性指标值，并以组距为各组区间底宽，绘出直方图，如下2、平均值X和标准差S的计算根据频数分布表，将位置居中且频数较大的一组的组中值定为全体数据的中心值b。

第二章 定量资料的统计描述四、统计表和统计图主要内容 n统计表n统计图u直方图u累计频率分布图u箱式图u直条图n小结(一）统计表（statistical table ）基线指标 试验组 对照组 男(n =61) 女(n =59) 男(n =27) 女(n =33) 年龄/岁 *50.82±9.99 49.59±10.92 54.19±10.87 56.12±10.84 体重/k g *70.03±10.39 55.70±9.42 68.90±7.85 61.80±11.95 身高/cm *170.16±4.37 158.86±6.52 169.81±4.05 160.61±5.62 血红蛋白/（g∙L ­1 ） *128.57±18.03 122.71±14.00 129.52±21.14 128.64±16.12 红细胞计数/(10 12 L ­1 ） ** 4.20(3.50~4.94) 4.16(3.39~4.65) 5.13(4.17~5.69) 4.40(3.65~5.01) 白细胞计数/（10 9 L ­1 ） ** 6.50(5.30~8.06) 6.30(5.60~8.42)8.16(4.95~9.10)5.14(4.40~6.24) 血小板计数/（10 9 L ­1 ）**228.00(171.00~284.00)223.00(188.00~304.00)221.00(190.00~384.00)176.00(162.00~228.00)表2­7 试验组和对照组不同性别受试对象的基线指标SX ± ： * )~ ( * * 75 25 P P M ：统计表的组成：表号及标题: 一个表号；标题简明扼要；表号及标题位于表上方中央标目: 横标目 纵标目线条 : 常用“三线表”，包括顶线、底线和纵标目分隔线。

频数
组距
组距
等距分组时，各小长方 形的面积与高的比是常数.
频数的大小 身高
画等距分组的频数分布直方图时，为了画 图与看图的方便、通常直接用小长方形的高表 示频数.
频数 思 考
通过频数分布直方图，你能发 现数据的分布有什么规律吗？
思考
对“问题”中的数据，如果取组距为 2 cm，那么数据应分成几组？如何选出需 要的 40 名同学？如果取组距为 4 cm 呢？ 结合 5 种不同分组选出需要的 40 名同学 的情况，说明哪种分组最合适.
（4）
（5）这个班每分钟跳 绳次数在100-120的学 生最多（还有很多结 论，同学自己观察）.
4. 一个面粉批发商统计了前 48 个星期的销售量 （单位：t）：
24.4 19.1 22.7 20.4 21.0 21.6 22.8 20.9 21.8 18.6 24.3 20.5 19.7 23.5 21.6 19.8 20.3 22.4 20.2 22.3 21.9 22.3 21.4 19.2 23.5 20.5 22.1 22.7 23.2 21.7 21.1 23.1 23.4 23.3 21.0 24.1 18.5 21.5 24.4 22.6 21.0 20.0 20.7 21.5 19.8 19.1 19.1 22.4
4
180≤ x＜ 200
1
次数
60≤ x＜
80
80≤x ＜100
100≤ x＜Hale Waihona Puke 120120≤ x＜
140
140≤ x＜
160
160≤ x＜
180
180≤ x＜
200
频数 2 4 21 13 8
4
1

由于身高数据具有连续性，因此我们应采用直方图来描述频数分布。
155 165 155 156 148 168 155 170 158 150 155 153 159 160 153 156 160 159 150 156 161 160 162 156 150 155 145 155 166 149 160 145 142 154 165 142 156 156 145 163 165 155 164 160 155 170 165 156 145 142 156 162 162 160 150
谢谢！
第十章 数据的收集、整理与描述
10.2 直方图
10.2 直方图
我们学习了条形图、折线图、扇形图等描述数据的方法， 下面介绍另一种常用来描述数据的统计图——直方图.
10.2 直方图
问题 为了参加全校各年级之间的广播体操比赛，七年级准备从63名同学中 挑选身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高（单位： cm)如下：
10.2 直方图
探究 上面对数据进行分组时，组距取 3，把数据分成 8 组.如
果组距取 2 或 4，那么数据分成几个组？这样能否选出需要 的 40 名同学呢?
10.2 直方图
4.画频数分布直方图 如图，为了更直观形象地看出频数分布的情况，可以根 据上表画出频数分布直方图（histogram).
158 158 160 168 159 159 151 158 159 168 158 154 158 154 169 158 158 158 159 167 170 153 160 160 159 159 160 149 163 163 162 172 161 153 156 162 162 163 157 162 162 161 157 157 164 155 156 165 166 156 154 166 164 165 156 157 153 165 159 157 155 164 156 选择身高在哪个范围的同学参加呢?

THANKS FOR WATCHING
感谢您的观看
中心极限定理是统计学中的基本定理 之一，它说明了无论总体分布是什么， 只要样本量足够大，样本均值的分布 将趋近于正态分布。
本讲内容还介绍了如何使用Python 中的matplotlib和seaborn库来绘制 直方图和箱线图，以及如何对图形进 行美化。
对未来研究的展望
01
随着大数据时代的到来，数据可视化在数据分析和挖掘中的作用越来越重要。 未来可以进一步研究如何利用先进的数据可视化技术，如交互式可视化、3D可 视化等，更好地揭示数据的内在规律和特征。
总结词
比较多个数据集
详细描述
箱线图可以同时展示多个数据集，通过比较它们的箱体 和异常值，可以方便地比较不同数据集的分布特性和离 散程度。
总结词
识别异常值
详细描述
箱线图能够清晰地识别异常值，这些异常值可能是由于 测量误差或数据采集问题导致的，对于数据分析和挖掘 具有重要意义。
实例三：直方图与箱线图的综合应用
样本及中心极限定理6.2直方图和 箱线图
contents
目录
• 引言 • 样本和中心极限定理概述 • 直方图 • 箱线图 • 直方图与箱线图的比较与选择 • 实例分析 • 结论
01 引言
主题简介
直方图和箱线图是常见的统计图表， 用于展示数据的分布和中心趋势。
箱线图则通过展示数据的最大值、最 小值、中位数、平均数等统计指标， 来描述数据的中心趋势和离散程度。
箱线图的制作步骤
01
02
03
04
绘制箱体
根据四分位数和IQR绘制箱体 ，确定箱体的位置和宽度。
绘制箱须和箱帽
根据四分位距和数据范围绘制 箱须和箱帽。

76，81，79，94，61，69，89，
70，70，87，81，86，90，88， PPT模板：素材： PPT背景：图表： PPT下载：教程： 资料下载：范文下载： 试卷下载：教案下载： PPT论坛：课件： 语文课件：数学课件： 英语课件：美术课件： 科学课件：物理课件： 化学课件：生物课件： 地理课件：历史课件：
1、你认为谁得记录方式好？根据谁的纪录 的结果能很快说出购买哪种品牌饮料的人数最多？
2、通过对本超市一天销售饮料的调查结果， 能大概推算出各品牌的饮料在本地的市场占有率 吗？
3
K出现的频数是15，频率是 10 ．把各个类别及 其对应的频数用表格的形式表示出来，所得表格就是
频数分布表．
可以用图形直观表示各类别频数的分布情 况．如下图这样的统计图也叫做频数分布直方图．
画频数分布直方图的一般步骤:
(1) 计算极差 :95-53=42（分)
(2) 决定组距与组数. 极差/组距=42/10=4.2 数据分成5组.
(3) 决定分点.
49.5~59.5, 59.5~69.5,
…89.5~99.5
某班一次数学测验成绩如下：
63，84，91，53，69，81，61，
69，91，78，75，81，80，67，
2050年世界人口分布预测
亚洲 北美洲 欧洲 拉美/加勒比 非洲
条形统计图 可以清楚地 表示出每个 项目的具体 数目.
折线统计图 可以清楚地 反映事物变 化的情况.
扇形统计图 可以清楚地 表示各部分 在总体中所 占的百分比.
A宋慧乔
B刘亦菲
C张敏健
D小沈阳
明 星 人数（频数）百分比（频率）
A宋慧 乔
87.5~92.5
2

教你绘制频数分布直方图与折线图频数分布直方图和频数分布折线统计图是描述数据的两种重要统计图，用这两种统计图把数据描述出来，就以直观地了解数据的分布情况及变化规律下面谈谈这两种统计图的画法：一、频数分布直方图画频数分布直方图一般按下列步骤：1计算极差（最大值与最小值的差）2决定组数3列出频数分布表4画出频数分布直方图例小明调查了他们班54名学生的身高，结果（单位:cm）如下:4555请将数据适当分组,并绘制相应的频数分布直方图分析：要绘制频数分布直方图，需要把数据适当分组，数出每一组的频数，得出频数分布表，在此基础上绘制频数分布直方图解：通过观察得到上面数据的最大值是172cm,最小值是141cm,它们的差是（172-141）=31cm将该组数据按身高的范围分为141≤<145,145≤<149,≤…分成7组整理可得下列统计表:身高/cm频数统计学生数（频数）141≤<1453145≤<149正5149≤<153正8153≤<157正9157≤<161正正14161≤<165正7165≤<169正5169≤<1733用横轴表示身高,用纵轴表示频数,并在纵轴上等距离标出5,10,15,以各组学生人数为高画出与此组对应的长方形,得到频数分布直方图（如图1）图1二、频数折线图频数折线图画法如下：1在频数分布直方图的基础上画频数折线图（1）取频数分布直方图中每个长方形上边的中点；（2）在横轴上取两个频数为0的点，在直方图横轴的左边取点（139，0），在直方图横轴的右边取点（175，0）；（3）将这些点用线段依次连接起来就得到了频数折线图（如图2）图22根据已有的数据直接画频数折线图（1）把数据分组，求出每个小组两端点的平均数，这些平均数称为组中值，如图141≤<145这个小组的组中值为（141145）÷2=143（2）用横轴表示身高,用纵轴表示频数,以各小组的组中值为横坐标,各小组对应的频数为纵坐标描点,另取两个点（139,0）和（175,0）（3）依次连接这些点就得到了频数折线图（如图3）图3。

8
直方图基本概念及应用场景
直方图定义
直方图又称质量分布图，是一种 统计报告图，由一系列高度不等 的纵向条纹或线段表示数据分布
的情况。
2024/2/2
应用场景
适用于展示连续变量的分布情况， 如身高、体重等指标的频数分布。
优点
能够直观地展示数据的分布情况， 便于观察数据的集中趋势和离散程 度。
9
条形图与直方图绘制方法
11
03
折线图与散点图
2024/2/2
12
折线图基本概念及应用场景
折线图定义
通过线段的上升或下降来 表示数据的变动情况，反 映数据随时间或其他因素 的变化趋势。
2024/2/2
应用场景
适用于展示时间序列数据 ，如疾病发病率、患者体 温等随时间的变化情况。
优点
直观展示数据变化趋势， 易于理解。
13
实例二
展示某产品在不同地区的销售额占比 的环形图，通过对比不同扇形的面积 和颜色可以直观地了解各地区销售额 的差异和占比情况。
21
05
箱线图与误差条图
2024/2/2
22
箱线图基本概念及应用场景
箱线图定义
箱线图是一种用作显示一组数据分散情况资料的统计图，因形状如 箱子而得名。
应用场景
主要用于反映原始数据分布的特征，还可以进行多组数据分布特征 的比较。
根据分析结果，对数据的特征和规律进行解读和总结，为后续的统 计分析和决策提供支持和依据。
26
06
医学统计学中其他常用图表
2024/2/2
27
生存曲线图
定义与作用
生存曲线图主要用于展示生存分析的结果，描述不同组别 或不同条件下患者的生存概率随时间的变化情况。

备考2022年中考数学一轮复习-统计与概率_数据收集与处理_频数（率）分布直方图频数（率）分布直方图专训单选题：1、(2017西城.中考模拟) 某大型文体活动需招募一批学生作为志愿者参与服务，已知报名的男生有420人，女生有400人，他们身高均在150≤x＜175之间，为了解这些学生身高的具体分别情况，从中随机抽取若干学生进行抽样调查，抽取根据图表提供的信息，有下列几种说法①估计报名者中男生身高的众数在D组；②估计报名者中女生身高的中位数在B组；③抽取的样本中，抽取女生的样本容量是38；④估计身高在160cm至170cm（不含170cm）的学生约有400人其中合理的说法是（）A . ①②B . ①④C . ②④D . ③④2、(2017磴口.中考模拟) 某次考试中，某班级的数学成绩统计图如下．下列说法错误的是（）A . 得分在70～80分之间的人数最多B . 该班的总人数为40C . 得分在90～100分之间的人数最少D . 及格（≥60分）人数是263、(2017乌拉特前旗.中考模拟) 如图，某学校九年级（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）．由图可知，人数最多的一组是（）A . 2﹣4小时B . 4﹣6小时C . 6﹣8小时D . 8﹣10小时4、(2018福清.中考模拟) 下图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（）A . 该学校教职工总人数是50人B . 年龄在40≤x＜42小组的教职工人数占该学校总人数的20%C . 教职工年龄的中位数一定落在40≤x＜42这一组D . 教职工年龄的众数一定在38≤x＜40这一组5、(2017慈溪.中考模拟) 一名射击运动员连续打靶8次，命中的环数如图所示，则命中环数的众数与中位数分别为（）A . 9环与8环B . 8环与9环C . 8环与8.5环D . 8.5环与9环6、(2014温州.中考真卷) 如图是某班45名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（）A . 5～10元B . 10～15元C . 15～20元D . 20～25元7、(2012丽水.中考真卷) 为了解中学300名男生的身高情况，随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图（如图）．估计该校男生的身高在169.5cm～174.5cm之间的人数有（）A . 12B . 48C . 72D . 968、(2017安徽.中考真卷) 为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（）A . 280B . 240C . 300D . 2609、(2012崇左.中考真卷) 崇左市江州区太平镇壶城社区调查居民双休日的学习状况，采取了下列调查方式；a：从崇左高中、太平镇中、太平小学三所学校中选取200名教师；b：从不同住宅楼（即江湾花园与万鹏住宅楼）中随机选取200名居民；c：选取所管辖区内学校的200名在校学生．并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图．以下结论：①上述调查方式最合理的是b；②在这次调查的200名教师中，在家学习的有60人；③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人；④小明的叔叔住在该社区，那么双休日他去叔叔家时，正好叔叔不学习的概率是0.1．其中正确的结论是（）A . ①④B . ②④C . ①③④D . ①②③④10、(2017阜康.中考模拟) 某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论错误的是（）A . 样本中位数是200元B . 样本容量是20C . 该企业员工捐款金额的平均数是180元D . 该企业员工最大捐款金额是500元填空题：11、(2017杨浦.中考模拟) 某区从近期卖出的不同面积的商品房中随机抽取1000套进行统计，并根据结果绘出如图所示的统计图．从中可知卖出的110m2～130 m2的商品房________套．12、(2017普陀.中考模拟) 某班学生参加环保知识竞赛，已知竞赛得分都是整数．把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图（如图所示），根据图中的信息，可得成绩高于60分的学生占全班参赛人数的百分率是________．13、(2019襄阳.中考模拟) 某校为了了解全校400名学生参加课外锻炼的情况，随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查，结果如下：（单位：分）40 21 35 24 40 38 23 52 35 62 36 15 51 4540 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45分组频数频率4.5﹣22.5 2 0.05022.5﹣30.5 330.5﹣38.5 10 0.25038.5﹣46.5 1946.5﹣54.5 5 0.12554.5﹣62.5 1 0.025合计40 1.000（2）填空：在这个问题中，总体是，样本是．由统计结果分析的，这组数据的平均数是38.35（分），众数是，中位数是．（3）如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况，你认为用平均数、众数、中位数中的哪一个量比较合适？（4）估计这所学校有多少名学生，平均每天参加课外锻炼的时间多于30分？14、(2015黄石.中考真卷) 九年级（3）班共有50名同学，如图是该班一次体育模拟测试成绩的频数分布直方图（满分为30分，成绩均为整数）．若将不低于23分的成绩评为合格，则该班此次成绩达到合格的同学占全班人数的百分比是________ ．15、(2011河池.中考真卷) 某校为了了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐次数在20～25次之间的频数是________．16、(2020温州.中考真卷) 某养猪场对200头生猪的质量进行统计，得到频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中质量在77.5kg 及以上的生猪有________头。

本节测试1.经历由实际问题进行统计调查解决问题的过程，会用分好组的频数分布表整理数据，会根据表格画简单的频数分布直方图，会利用频数分布的图表解释数据中蕴含的信息，培养统计观念.2.了解组距、组数、频数、频数分布等概念.综合练习1．在统计应用中，会用到频数分布表和频数分布直方图，但更多的情况下会应用到频率分布表和频率分布直方图．未成年人思想道德建设越来越受到社会的关注．某青少年研究所随机调查了大连市内某校100名学生寒假中花零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．根据调查数据制成了频率分布表．分组频数频率0.5～50.5 ______ 0.150.5～______ 20 0.2100.5～150.5 ______ ___________200.5 30 0.3200.5～250.5 10 0.1250.5～300.5 5 0.05 合计100 ______ （1）补全频率分布表；（2）根据上面的频率分布表，作出相应的频率分布图；（3）研究所认为，应对消费150元以上的学生提出勤俭节约的建议．试估计应对该校1 000名学生中约多少名学生提出这项建议？2．初中学生的视力状况已受到全社会广泛关注．某市有关部门对全市20万名初中学生视力状况进行了一次抽样调查，从中随机抽查了10所中学全体初中学生的视力，图12-29、图12-30是2004年抽样情况统计图．请你据图解答以下问题：（1）2004年这10所中学初中学生的总人数有多少人？（2）2004年这10所中学的初中学生中，视力在4.75以上的学生人数占全市初中学生总人数的百分比是多少？（3）2004年该市参加中考的学生达66 000人，请你估计2004年该市这10所中学参加中考的学生共有多少人？3．初三（1）班某一次数学测验成绩如下：63，84，91，53，69，81，61，69，91，78，75，81，80，67，76，81，79，94，61，69，89，70，70，87，81，86，90，88，85，67，71，82，87，75，87，95，53，65，74，77．数学老师按10分的组距分段，统计每个分数段出现的频数，填入频数分布表，并绘制频数分布直方图．（1）请把频数分布表及频数分布直方图补充完整；（2）请说明哪个分数段的学生最多？哪个分数段的学生最少？（3）请你帮老师统计一下这次数学考试的及格率（60分以上含60分为及格）及优秀率（90分以上含90分为优秀）．成绩段49.5～59.5 59.5～69.5 69.5～79.579.5～89.5 89.5～99.5频数记录丅正正正频数 2 9 14 5 频数0.050 0.225 0.250 0.3504．如图12-32所示，A、B两个旅游点从2001年至2005年五一的旅游人数变化情况分别用实线和虚线表示．根据图中所示解答以下问题：（1）B 旅游点的旅游人数相对上一年，增长最快的是哪一年？（2）求A 、B 两个旅游点从2001到2005年旅游人数的平均数和方差，并从平均数和方差的角度，用一句话对这两个旅游点的情况进行评价；（3）A 旅游点现在的门票价格为每人80元，为保护旅游点环境和游客的安全，A 旅游点的最佳接待人数为4万人，为控制游客数量，A 旅游点决定提高门票价格．已知门票价格x （元）与游客人数y （万人）满足函数关系y ＝5－100x若要使A 旅游点的游客人数不超过4万人，则门票价格至少应提高多少？5．下表数据来源于国家统计局《国民经济和社会发展统计公报》． 2001～2004年国内汽车年产量统计表2001年 2002年 2003年 2004年 汽车（万辆） 233 325.1 444.39 507.41 其中轿车（万辆）70.4 109.2 202.01 231.40 （1）根据上表将下面的统计图补充完整：（2）请你写出三条从统计图中获得的信息；（3）根据2004年汽车年产量和目前销售情况，有人预测2006年国内汽车年产量应上升至650万辆．根据这一预测，假设这两年汽车年产量平均年增长率为x ，则可列出方程__________．6．2005年1月6日《东亚经贸》报道，我国人口已达到13亿．请你根据右边的统计图回答下列问题：（1）哪个阶段人口增加的最快？（2）按照统计图的规律，请你估计2010年我国人口总数？（3）从近几年人口增长的情况看，你还能获得哪些有效信息？7．查阅动物百科全书可以知道，喜鹊体长41～52 cm，营巢于高大乔木的中上层，每次产卵5～8枚；丹顶鹤体长约140 cm，营巢于周围环水的浅滩、深草丛中，每次产卵2枚；绿孔雀体长100～230 cm，营巢于灌木丛、竹丛间的地面，每次产卵4～8枚；鸳鸯体长38～44 cm，营巢于树洞中，每次产卵7～12枚．请用统计表整理上述信息，并根据表中信息回答下列问题：（1）绿孔雀体长的极差是__________．（2）丹顶鹤成为国家一级保护动物的原因之一是__________．参考答案与点拨1．（1）分组频数频率0.5～50.5 10 0.150.5～100.5 20 0.2100.5～150.5 25 0.25150.5～200.5 10 0.1200.5～250.5 10 0.1250.5～300.5 5 0.05 合计100 1 （2）（3）4502．（1）10 000 （2）2.75％ （3）3 300人 3．（1）成绩段 49.5～59.5 59.5～69.5 69.5～79.5 79.5～89.5 89.5～99.5 频数记录 正正 正 频数2 9 10 14 5 频数 0.050 0.225 0.250 0.350 0.125（2）从图中可以清楚地看出79.5分到89.5分这个分数段的学生数最多，49.5分到59.5分这个分数段的学生数最少．（3）及格率：40240－＝95％，优秀率：405＝12.5％．4．解：（1）B 旅游点的旅游人数相对上一年增长最快的是2004年．（2）554321＋＋＋＋＝A X ＝3（万人）554321＋＋＋＋＝B X ＝3（万人）S 2A ＝51[（－2）2＋（－1）2＋02＋12＋22]＝2S 2B ＝51[02＋02＋（－1）2＋12＋02]＝52从2001至2005年，A 、B 两个旅游点平均每年的旅游人数均为3万，但A 旅游点较B 旅游点的旅游人数波动大．（3）由题意，得5－100x≤4解得x ≥100 100－80＝20答：A 旅游点的门票至少要提高20元．5．（1）如图答-15，（2）①汽车年产量逐年递增；②轿车年产量逐年递增；③汽车年产量2003年增长量最大；④轿车年产量2003年增长量最大； ⑤汽车年产量相对于上一年的增长速度2004年减缓；⑥轿车年产量相对于上一年的增长速度2004年减缓；⑦轿车的年产量在汽车中所占的比重逐年加大；⑧轿车的年产量2004年是2001年的3倍多；……（3）507.41×（1＋x ）2＝650．6．（1）60～70年代（增长人数为16 785万人）；或答60年代到二十世纪末也可以；（2）大约135 000万人左右（答案接近此数即可）；（3）从2000年以来增长速度渐缓，每年不到1 000万人．（如有其他答案只要合理亦可） 7．鸟名 喜鹊 丹顶鹤 绿孔雀 鸳鸯 营巢环境 高大乔大 浅滩、深草丛 灌木丛 树洞 体长（cm ） 41～52 140 100～230 38～44 产卵枚数 5～8 2 4～8 7～12 （表格中营巢环境、体长、产卵枚数每缺一行扣2分）（1）极差是130 cm ．（不写单位不扣分）（2）①丹顶鹤产卵很少；②营巢环境要求较高（写出一条即可）。

美临达医疗器械备案注册网RD-BG-30-2020/A/0
统计分析报表
1.客诉情况统计分析
1.1客诉情况统计表
1.2客诉情况分析表（折线图/直方图）
2.来料检验情况统计分析
2.1客诉情况统计表
2.2客诉情况分析表（折线图/直方图）
3.制程序品质状况统计分析
3.1客诉情况统计表
3.2客诉情况分析表（折线图/直方图）
4.成品品质情况统计分析
4.1客诉情况统计表
4.2客诉情况分析表（折线图/直方图）
5.合格品退货率统计分析
5.1客诉情况统计表
5.2客诉情况分析表（折线图/直方图）
6.前期改善项目完成状况统计分析
6.1客诉情况统计表
6.2客诉情况分析表（折线图/直方图）
7.总结。

B
课堂训练
3. 一个样本有 100 个数据，最大值为 7.4，最小值为4.0，如果取组距为 0.3，那么这组数据可分成 ( ) A. 11 组 B. 12 组 C. 13 组 D. 以上答案均不对
B
4.某校开展捐书活动，七(1)班同学积极参与，现将捐书数量绘制成频数直方图(如图所示)，如果捐书数量在3.5～4.5组别的人数占总人数的30%，那么捐书数量在4.5～5.5组别的人数是________人。
新知探究
思考 （1）根据上面的绘图过程，你能总结出绘制频数直方图的一般步骤吗？
（2）你觉得频数直方图有什么特点？与条形统计图相比有哪些不同？与同伴进行交流。
新知探究
① 找出所给数据中的最大值和最小值，求最大值与最小值的差，确定统计量的范围；
绘制频数直方图的一般步骤：
② 确定组数和组距，选取分点进行分组；
新知探究
（3）你能统计出落在各组中的频数吗？用什么方法统计的？
用“正”字计数法统计，结果如下表：
分组
家庭数（频数）
分组
家庭数（频数）
2.0——6.0
20
18.0——22.0
2
6.0——10.0
15
22.0——26.0
4
10.0——14.0
13
26.0——30.0
1
14.0——18.0
5
新知探究
（4）你能根据统计的各组频数绘制出频数直方图吗？
新知探究
知识点 从频数直方图获取信息
2
典型例题
成绩/分
频数
频率
50——60
10
0.05
60——70
20
0.10
70——80
30

频率 fi
样本分布函数 Fn x的图形如图5－1所示
图5-1
对于任意的实数 x总体分布函数Fx是事件 X x
的概率；样本分布函数Fn x是事件 X x 的频
率。根据伯努利大数定理可知,
当n 时，对于任意的正数 ，有
lim
n
P
Fn
x
F
x
1
格利文科（Glivenko）进一步证明了
当n 时，样本分布函数 Fn x与总体分布函
为10个子区间
242.5～245.5
9
0.09
245.5～248.5
19
0.19
(236.5,239.5),
248.5～251.5
24
0.24
( 239.5，242.5),
251.5～254.5
22
0.22
254.5～257.5
11
0.11
…,
257.5～260.5
6
0.06
( 263.5,266.5)
例 测量100个某种机械零件的质量，得到样本观 测值如下（单位：g）
246 251 259 254 246 253 237 252 250 251 249 244 249 244 243 246 256 247 252 252 250 247 255 249 247 252 252 242 245 240 260 263 254 240 255 250 256 246 249 253 246 255 244 245 257 252 250 249 255 248 258 242 252 259 249 244 251 250 241 253 250 265 247 249 253 247 248 251 251 249 246 250 252 256 245 254 258 248 255 251 249 252 254 246 250 251 247 253 252 255 254 247 252 257 258 247 252 264 248 244

该怎样做 比赛。为此收集到这63名同学的身高（单位：cm）如下：
172 172 161 162 161 156 159 154 157
1.计算最大值与最小值的差 172—149=23cm 2.决定组距与组数 组距:每个小组的两个端点之间的距离
(组内数据的取值范围)
频数分布表
讨论：我们选择
身高在哪个范围 的学生参加呢？
频数与组 距的比值
155≤x＜158
158≤x＜161 161≤x＜164 164≤x＜167 167≤x＜170 170≤x＜173
正正T
正正正 正正 正
１２
１９ １０ ８ ４
3
2 1 0 149152 155158 161164 167170173身高/cm
T
２
组距 频数
小长方形面积=组距×
组距
身高分组 149≤x＜153 153≤x＜157 157≤x＜161 161≤x＜165 165≤x＜169 169≤x＜173 划 记 T 正正T 正正正正 频数 ２ ６ １２ １９ １０ ８ （图二）
正一
正T
6
7
157≤x＜159
159≤x＜161 161≤x＜163 163≤x＜165
正正
正正一 正T
户数大约有多少户？
频数分布表
分 组
600≤x＜800
800≤x＜1000 1000≤x＜1200 1200≤x＜1400 1400≤x＜1600 1600≤x＜1800
(8%+10%) ×500 频数分布直方图 =90人
（户数） 20 16 12
频数 百分比%
4
5 20 11 8 2
8%
10% 40% 22% 16% 4%