(五四制) 鲁教版数学 9年级下册 配套练习册 一课一练 同步练习册_53
- 格式:pdf
- 大小:276.22 KB
- 文档页数:3

*7切线长定理过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长(length of the tangent ).切线长定理 从圆外一点引圆的两条切线,它们的切线长相等.我们来证明切线长定理.已知:如图 5-46,P A ,PB 是 ⊙O 的两条切线,A ,B 是切点.求证:P A = PB .证明:连接 OA ,OB .∵ P A ,PB 是 ⊙O 的切线,∴ ∠P AO = ∠PBO = 90°.在 Rt △POA 和 Rt △POB 中,∵ OA = OB ,OP = OP ,∴ Rt △POA ≌ Rt △POB .∴ P A = PB .图 5-46如图 5-47,四边形 ABCD 的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴交流.想一想例 如图 5-48,Rt △ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为 D ,E ,F ,求 ⊙O的半径.图 5-47第五章圆知识技能习题 5.13解:连接 OD ,OE ,OF ,设 OD = r.在 Rt △ABC 中,AC = 10,BC = 24,∴ AB26.∵ ⊙O 分别与 AB ,BC ,CA 相切于点 D ,E ,F ,∴ OD ⊥AB ,OE ⊥BC ,OF ⊥AC ,BE = BD ,AF = AD ,CE = CF .又∵ ∠C = 90°,∴ 四边形 OECF 为正方形.∴ EC = FC = r.∴ BE = 24 - r ,AF = 10 - r.∴ AB = BD + AD = BE + AF = 34 - 2r .∴ 34 - 2r = 26.∴ r = 4,即 ⊙O 的半径为 4.1. 如图,P A ,PB 分别与 ⊙O 相切于 A ,B 两点.C 是 A ⌒B 上任意一点,过点C 作 ⊙O 的切线,分别与 P A ,PB 相交于D ,E 两点,若 P A = PB = 5 cm ,求△PDE 的周长.AF C图 5-48已知 ⊙O 的半径为 3 cm ,点 P 和圆心 O 的距离为 6 cm .过点 P 作 ⊙O 的两条切线,求这两条切线的切线长.随堂练习(第 1 题)P(第 2 题)B8正多边形和圆※2. △ABC 的内切圆 ⊙O 与 BC ,CA ,AB 分别相切于点 D ,E ,F ,且 AB = 9 cm ,BC = 14 cm ,CA = 13 cm ,求 AF ,BD ,CE 的长.3. 如图,过 ⊙O 外一点 P 作 ⊙O 的两条切线 P A 和 PB ,点 A ,B 为切点,∠P = 40°.点 D 在 AB 上,点 E 在 PB 上,点 F 在 P A 上,且 AD = BE ,BD = AF ,求 ∠EDF 的度数.4. 有一张如图所示的四边形纸片 ABCD ,AB = AD = 6 cm ,CB = CD = 8 cm ,且 ∠B = 90°.(1)要把该四边形纸片裁剪成一个面积最大的圆形纸片,你能否用折叠的方法找出圆心?若能,请你度量出圆的半径;(2)计算出最大的圆形纸片的半径.(第 3 题)OD BE FA 数学理解ABDC(第 4 题)你还记得什么叫做正多边形吗?你能举出正多边形的一些例子来吗?8正多边形和圆如图 5-49,A ,B ,C ,D ,E 都是⊙O 上的点,且∠AOB =∠BOC =∠COD =∠DOE.议一议。



5.7 切线长定理一.选择题1.如图,P A,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交P A,PB于点M,N,若P A=7.5cm,则△PMN的周长是()A.7.5cm B.10cm C.12.5cm D.15cm2.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD 于点N,M,若CM+CN=4,则⊙O的面积为()A.πB.2πC.4πD.0.5π3.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为()A.44B.42C.46D.474.如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=5,AC=3,则BD 的长是()A.4B.3C.2D.15.如图,一个菱形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿此菱形的四边做无滑动旋转,直至回到原出发位置时,这个圆共转了()A.6圈B.5圈C.4.5圈D.4圈6.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有()个:①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.A.1B.2C.3D.4二.填空题7.如图,从点P引⊙O的切线P A,PB,切点分别为A,B,DE切⊙O于C,交P A,PB于D,E.若△PDE的周长为20cm,则P A=cm.8.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是.9.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为.10.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为.11.如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.12.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为.13.已知:P A切⊙O于点A,PB切⊙O于点B,点C是⊙O上异于A、B的一点,过点C 作⊙O的切线分别交P A和PB于点D、E,若P A=10cm,DE=7cm,则△PDE的周长为cm.14.如图所示,P为⊙O外一点,P A、PB分别切⊙O于A、B,CD切⊙O于点E,分别交P A、PB于点C、D,若P A=15,则△PCD的周长为.15.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为.16.如果圆的外切四边形的一组对边的和是5cm,那么这个四边形的周长是cm.三.解答题17.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P 的度数.18.如图,AB为⊙O直径,P A、PC分别与⊙O相切于点A、C,PQ⊥P A,PQ交OC的延长线于点Q.(1)求证:OQ=PQ;(2)连BC并延长交PQ于点D,P A=AB,且CQ=6,求BD的长.19.如图,∠APB=52°,P A、PB、DE都为⊙O的切线,切点分别为A、B、F,且P A=6.(1)求△PDE的周长;(2)求∠DOE的度数.20.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.21.已知P A、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交P A于C、交PB于D.(1)若P A=6,求△PCD的周长.(2)若∠P=50°求∠DOC.22.如图,P A、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交P A、PB于点E、F,已知P A=12cm,∠P=40°①求△PEF的周长;②求∠EOF的度数.23.如图,P A、PB切⊙O于A、B两点,CD切⊙O于点E,分别交P A、PB于点C、D.若P A、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.24.已知:如图,P A、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O 的切线,交P A、PB于E、F点,已知P A=12cm,求△PEF的周长.25.已知:如图△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,过D作⊙O的切线交BC于点E,EF⊥AB,垂足为F.(1)求证:DE=BC;(2)若AC=6,BC=8,求S△ACD:S△EDF的值.参考答案一.选择题1.解:∵直线P A、PB、MN分别与⊙O相切于点A、B、C,∴MA=MC,NC=NB,∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=P A+PB=7.5+7.5=15(cm).故选:D.2.解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,连接OE,OF,则四边形OECF是正方形,∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,∵∠MON=90°,∴∠EOM=∠FON,∴△OEM≌△OFN(ASA),∴EM=NF,∴CM+CN=CE+CF=4,∴OE=2,∴⊙O的面积为4π,故选:C.3.解:∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=22,∴四边形ABCD的周长=AD+BC+AB+CD=44,故选:A.4.解:∵AC、AP为⊙O的切线,∴AC=AP=3,∵BP、BD为⊙O的切线,∴BP=BD,∴BD=PB=AB﹣AP=5﹣3=2.故选:C.5.解:∵菱形的边长与它的一边相外切的圆的周长相等∴圆在菱形的边上转了4圈∵圆在菱形的四个顶点处共转了360°,∴圆在菱形的四个顶点处共转1圈∴回到原出发位置时,这个圆共转了5圈.故选:B.6.解:∵⊙O是四边形ABCD的内切圆,∴AF=AE,BF=BG,CG=CH,DH=DE,∴AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC.①AF=BG;④BG<CG无法判断.正确的有②③故选:B.二.填空题7.解:∵P A、PB、DE分别切⊙O于A、B、C,∴P A=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=P A+PB=20;∴P A=PB=10,故答案为10.8.解:如图所示:连接圆心与各切点,在Rt△DEO和Rt△DFO中,∴Rt△DEO≌Rt△DFO(HL),∴∠1=∠2,同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,∴∠3=∠4,∠5=∠7,∠6=∠8,∴∠5+∠6=∠7+∠8=108°,∴2∠2+2∠3=360°﹣2×108°,∴∠2+∠3=∠DOC=72°.故答案为:72°.9.解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,∵⊙O内切于菱形ABCD,∴OE=OF,∴OB平分∠ABC,∵∠ABC=60°,∴∠ABO=30°,同理得∠BAO=60°,∴∠AOB=90°,∴AO=AB=2,OB=2,∴S△AOB=AB•OE=AO•OB,4OE=2×,OE=,故答案为:.10.解:设AE的长为x,正方形ABCD的边长为a,∵CE与半圆O相切于点F,∴AE=EF,BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,∵AD=CD=BC=AB,∴正方形ABCD的边长为4;在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,∵AE+EF+FC+BC+AB=14,∴直角梯形ABCE周长为14.故答案为:14.11.解:∵P A,PB是⊙O的切线,∴P A=PB,P A⊥OA,∴∠P AB=∠PBA,∠OAP=90°,∴∠PBA=∠P AB=90°﹣∠OAB=90°﹣38°=52°,∴∠P=180°﹣52°﹣52°=76°;故答案为:76.12.解:∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=22,∴四边形ABCD的周长=AD+BC+AB+CD=44,故答案为:44.13.解:分两种情况:①点C在劣弧AB上时,如图,当根据切线长定理得:AD=CD,BE=CE,P A=PB,则△PDE的周长=PD+DE+PE=PD+CD+CE+PE=PD+AD+PE+BE=P A+PB=2P A=20cm.②点C在优弧AB上时,如图,当根据切线长定理得:AD=CD,BE=CE,P A=PB,则△PDE的周长=PD+DE+PE=2P A+2DE=20+2×7=34cm.综上,△PDE的周长为20或34cm.故答案为:20或34.14.解:∵P A、PB切⊙O于A、B,∴P A=PB=15;同理,可得:EC=CA,DE=DB;∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=P A+PB=2P A=30.即△PCD的周长是:30.故答案为:30.15.解:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD =10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故答案是:20cm.16.解:∵四边形ABCD是圆的切线.∴AH=AE,BE=BF,CF=CG,DH=DG∴AH+DH+BF+CF=AE+BE+CG+DG即:AD+BC=AB+CD∴四边形的周长是10cm.故答案是:10.三.解答题17.解:根据切线的性质得:∠P AC=90°,所以∠P AB=90°﹣∠BAC=90°﹣20°=70°,根据切线长定理得P A=PB,所以∠P AB=∠PBA=70°,所以∠P=180°﹣70°×2=40°.18.(1)证明:连接OP.∵P A、PC分别与⊙O相切于点A,C,∴P A=PC,OA⊥P A,∵OA=OC,OP=OP,∴△OP A≌△OPC(SSS),∴∠AOP=∠POC,∵QP⊥P A,∴QP∥BA,∴∠QPO=∠AOP,∴∠QOP=∠QPO,∴OQ=PQ.(2)设OA=r.∵OB=OC,∴∠OBC=∠OCB,∵OB∥QD,∴∠QDC=∠B,∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,∵QO=QP,∴OC=DP=r,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,在Rt△PCQ中,∵PQ2=PC2+QC2,∴(6+r)2=62+(2r)2,r=4或0(舍弃),∴OP==4,∵OB=PD,OB∥PD,∴四边形OBDP是平行四边形,∴BD=OP=4.19.解:(1)∵P A、PB、DE都为⊙O的切线,∴DA=DF,EB=EF,P A=PB=6,∴DE=DA+EB,∴PE+PD+DE=P A+PB=12,即△PDE的周长为12;(2)连接OF,∵P A、PB、DE分别切⊙O于A、B、F三点,∴OB⊥PB,OA⊥P A,∠BOE=∠FOE=∠BOF,∠FOD=∠AOD=∠AOF,∵∠APB=52°,∴∠AOB=360°﹣90°﹣90°﹣52°=128°,∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.20.解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF =∠OCG;∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBE+∠OCF=90°,∴∠BOC=90°;(2)由(1)知,∠BOC=90°.∵OB=6cm,OC=8cm,∴由勾股定理得到:BC==10cm,∴BE+CG=BC=10cm.(3)∵OF⊥BC,∴OF==4.8cm.21.解:(1)连接OE,∵P A、PB与圆O相切,∴P A=PB=6,同理可得:AC=CE,BD=DE,△PCD的周长=PC+PD+CD=PC+PD+CE+DE=P A+PB=12;(2)∵P A PB与圆O相切,∴∠OAP=∠OBP=90°∠P=50°,∴∠AOB=360°﹣90°﹣90°﹣50°=130°,在Rt△AOC和Rt△EOC中,,∴Rt△AOC≌Rt△EOC(HL),∴∠AOC=∠COE,同理:∠DOE=∠BOD,∴∠COD=∠AOB=65°.22.解:①∵P A、PB是⊙O的切线,∴P A=PB,又∵直线EF是⊙O的切线,∴EB=EQ,FQ=F A,∴△PEF的周长=PE+PF+EF=PE+PF+EB+F A=P A+PB=2P A=24cm;②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)=(180°+40°)=110°,∴∠EOF=180°﹣110°=70°.23.解:∵P A、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,∴P A+PB=m,P A•PB=m﹣1,∵P A、PB切⊙O于A、B两点,∴P A=PB=,即•=m﹣1,即m2﹣4m+4=0,解得:m=2,∴P A=PB=1,∵P A、PB切⊙O于A、B两点,CD切⊙O于点E,∴AD=ED,BC=EC,∴△PCD的周长为:PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=P A+PB=2.24.解:∵P A、PB是⊙O的切线,切点分别是A、B,∴P A=PB=12,∵过Q点作⊙O的切线,交P A、PB于E、F点,∴EB=EQ,FQ=F A,∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,=PE+EB+PF+F A=PB+P A=12+12=24,答:△PEF的周长是24.25.(1)证明:∵EC、ED都是⊙O的切线,∴EC=ED,∠ECD=∠EDC.∵∠EDC+∠EDB=90°,∠ECD+∠B=90°,∴∠EDB=∠B.∴ED=BE.∴DE=BE=EC.∴DE=BC.(2)解:在Rt△ABC中,AC=6,BC=8,则AB=10,根据射影定理可得:AD=AC2÷AB=3.6,BD=BC2÷AB=6.4,∴S△ACD:S△BCD=AD:BD=9:16,∵ED=EB,EF⊥BD,∴S△EDF=S△EBD,同理可得S△EBD=S△BCD,∴S△EDF=S△BCD,∴S△ACD:S△EDF=.。

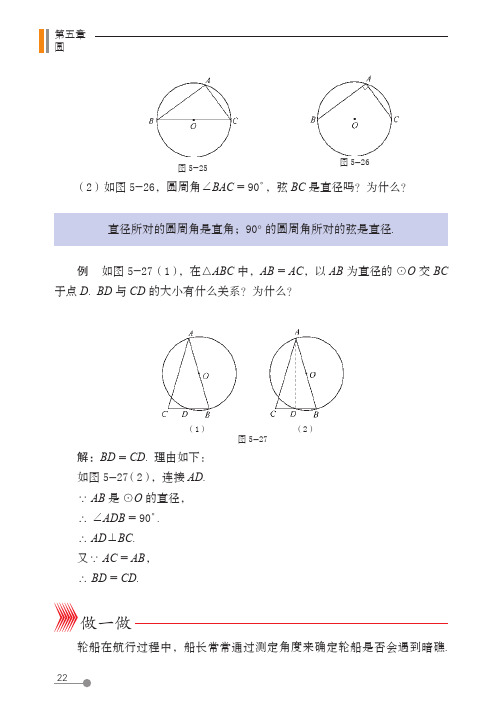
4圆周角和圆心角的关系已知:如图 5-24,∠ACB 是 A ⌒B 所对的圆周角,∠AOB 是 A ⌒B 所对的圆心角.求证:∠ACB = 12∠AOB .分析:根据圆周角和圆心的位置关系,分三种情况讨论:(1)圆心 O 在 ∠ACB 的一条边上,如图 5-24(1);(2)圆心 O 在 ∠ACB 的内部,如图 5-24(2);(3)圆心 O 在 ∠ACB 的外部,如图 5-24(3).议一议在图 5-23 中,改变 ∠AOB 的度数,上面的结论仍然成立吗?圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.在三种位置关系中,我们选择第(1)种情况给出证明,其他情况可以转化为(1)的情况进行证明.证明:圆心 O 在 ∠ACB 的一条边上,如图 5-24(1).∵ ∠AOB 是 △AOC 的外角,∴ ∠AOB = ∠CAO + ∠ACB .∵ OA = OC ,∴ ∠CAO = ∠ACB .(1) (2) (3)图 5-24O AB C OA B C OA B C第五章圆∴ ∠AOB = 2∠ACB ,即 ∠ACB= 12∠AOB .在得出本节结论的过程中,你用到了哪些方法?请举例说明,并与同伴交流.做一做你能将图 5-24(2)和图 5-24(3)这两种情况分别转化成图 5-24(1)的情况去解决吗?做一做,并与同伴交流.由圆周角定理,我们还可以得到下面的结论:圆周角的度数等于它所对弧的度数的一半.你能解决射门游戏中的问题了吗?当球员在 B ,D ,E 处射门时,他所处的位置对球门柱 A ,C 形成的三个张角∠ABC ,∠ADC ,∠AEC 的大小有什么关系?你能用圆周角定理去解决它吗?同弧或等弧所对的圆周角相等.议一议1. 如图,在 ⊙O 中,∠BOC = 50°,求∠BAC 的度数 .随堂练习(第 1 题)(第 2 题)想一想4圆周角和圆心角的关系2. 如图,在 ⊙O 中,∠A = 40°,求∠OBC 的度数.知识技能数学理解习题 5.5(1)如图 5-25,BC 是 ⊙O 的直径,它所对的圆周角有什么特点?你能证明吗?1. 如图,点 A ,B ,C ,D 在同一个圆上,四边形 ABCD 的对角线 AC 和 BD 相交于点 E . 在图中标出的 8 个角中,哪些是相等的角?2. 如图,OA ,OB ,OC 都是 ⊙O 的半径,∠AOB = 2∠BOC. ∠ACB 与∠BAC 的大小有什么关系?为什么?3. 如图,A ,B ,C ,D 是 ⊙O 上的四个点,且∠BCD = 100°,求∠BOD ( B ⌒CD 所对的圆心角)和∠BAD 的度数.4. 为什么有些电影的座位排列(横排)呈圆弧形?说一说这种设计的合理性.(第 2 题)(第 1题)(第 3 题)想一想12345678。
5. 3太阳光与影子♦基础训练一、选择题1.学校操场上有一棵大树和一棵小树,阳光照縫下,大树和小树的影子与它们的髙度之间关系,下列叙述不正确的是().A.在同一时刻,大树髙度与其影长之比等于小树高度与英影长之比「B.在同一时刻,大树和小树的高度之比等于其对应的影长之比C.在同一时刻,大树高度与其影长之差等于小树高度与英影长之差D.在同一时刻,大树的影长总不小于小树的影长2.某校大门附近有甲、乙两根木杆,某一时刻甲木杆在阳光下的影子如图所示,则此时乙木杆的影子是图中的().A . .BC D3.某天,小刚选择了三个不同的时间,在木杆南而的相同位垃给木杆照了三张照片,如图所示,那么三张照片照的先后顺序正确的是().①②c ③A. ®@®B.C.①③②”D.③①②二、填空题4.太阳光线可以看成_______ ,像这样的光线所形成的投影称为_________5.某学校操场上立着高度不同的甲、乙两种篮球架,那么在某一时刻,甲种篮球架的髙度与英影长的比一^_ (填'‘大于”、"小于”或“等于”)乙种篮球架的髙度与其影长的比.三、解答题6.如图,两人站在阳光下,请将他们的影子补充完整.7.如图,人和旗杆直立在操场上,其中人的影子已经画岀.(1)用线段表示这一时刻旗杆在阳光下的影子:-(2)比较旗杆与人影子的长短;(3)若将人看做一竖直线段,图中是否岀现了相似三角形?(4)在同一时刻,人站在操场不同的地方,会影响影子的长度和方向吗?♦能力提高一、填空题「8.在阳光下,将一三角形纸片平行于地而,观察英形成的影子,就会发现三角形纸片与貝形成的影子 ________ .9.小王同学想利用树影测量校园内的树高.他在某一时刻测得小树髙为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树的彫长时,因大树靠近教学楼,有一部分影子在墙上.经测虽:,地而部分彫长为6.4米,墙上影长为L.4米,那么这棵大树髙约为米.二、解答题10.一栋大楼髙40米,在某一时刻,大楼的影子长为20米,一身高1.80米的人,应站在距大楼多远的范囤内,太阳才照不到地?11.如图,AB、CD分别表示某市一小区的两幢楼房,高都为30m,两楼间的距离为24m.现了解到该市规左:在15: 00时,前楼在后楼上的影长不得低于16m (该地区15: 00时, 太阳光线与水平线的夹角为30°).(1)问该小区是否符合规泄?(2)如果要求1「5: 00时,前楼恰好不影响后楼的采光,那么两楼应相距多少米?♦拓「展训练12.一个矩形窗框被太阳照射后,留在地而上的影子是什么形状?它还是矩形吗?在不同的时刻,它的形状一样吗?如果窗框是圆形呢?假如影子不是落在地而上,而是落在与窗户平行的平而上,情况会怎样呢?参考答案I. C 2. C r3. C4.平行光线平行投影5.等于6.略7.路8.全等<:9. 9. 4米10.不超过19米II.(1)前楼在后楼的影长为(30-8弟)米>16米,该小区符合规泄.(2)应相距30的米.12.经过认真观察会发现:在太阳光照射下,矩形窗框被留在地而上的影子常”常是平行四边形,而且在不同的时刻,这些平行四边形的形状也不一样:圆形窗框在地而上的影子一般是椭圆形,如果影子落在与窗户平行的平而上,那么窗框与其影长全等.。