黑龙江省牡丹江市2015年中考数学试题(WORD版)

2015年黑龙江省中考数学试卷一、选择题（共10小题，每小题3分，满分30分）1．哈市某天的最高气温为28℃，最低气温为21℃，则这一天的最高气温与最低气温的差为（）A．5℃B．6℃C．7℃D．8℃2．用科学记数法表示927 000正确的是（）A．9.27×106B．9.27×105C．9.27×104D．927×1033．下列计算正确的是（）A．3a﹣2a=1 B．a2+a5=a7C．a2•a4=a6D．（ab）3=ab34．下列图形中，不是中心对称图形的是（）A．B．C．D．5．在反比例函数的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是（）A．k＞1 B．k＞0 C．k≥1 D．k＜16．如图的几何体是由一些小正方形组合而成的，则这个几何体的俯视图是（）A．B．C．D．7．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD 的度数是（）A．30°B．25°C．20°D．15°8．将抛物线y=﹣2x2+1向右平移1个单位，再向上平移2个单位后所得到的抛物线为（）A．y=﹣2（x+1）2﹣1 B．y﹣2（x+1）2+3 C．y=﹣2（x﹣1）2+1 D．y=﹣2（x﹣1）2+3 9．如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（）A．6B．4C．3D．310．早晨，小刚沿着通往学校唯一的一条路（直路）上学，途中发现忘带饭盒，停下往家里打电话，妈妈接到电话后带上饭盒马上赶往学校，同时小刚返回，两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，小刚始终以100米/分的速度步行，小刚和妈妈的距离y（单位：米）与小刚打完电话后的步行时间t（单位：分）之间的函数关系如图，下列四种说法：①打电话时，小刚和妈妈的距离为1250米；②打完电话后，经过23分钟小刚到达学校；③小刚和妈妈相遇后，妈妈回家的速度为150米/分；④小刚家与学校的距离为2550米．其中正确的个数是（）A．1个B．2个C．3个D．4个二、填空题（共10小题，每小题3分，共计30分）11．计算：=_________．12．在函数y=中，自变量x的取值范围是_________．13．把多项式3m2﹣6mn+3n2分解因式的结果是_________．14．不等式组的解集是_________．15．若x=﹣1是关于x的一元二次方程x2+3x+m+1=0的一个解，则m的值为_________．16．在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为_________．17．如图，在矩形ABCD中，AB=4，BC=6，若点P在AD边上，连接BP、PC，△BPC是以PB为腰的等腰三角形，则PB的长为_________．18．一个底面直径为10cm，母线长为15cm的圆锥，它的侧面展开图圆心角是_________度．19．如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC 的周长为12，则EC的长为_________．20．如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则的值为_________．三、解答题21．先化简，再求代数式﹣的值，其中x=2cos45°+2，y=2．22．如图，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，点E在BC边上，且点E在小正方形的顶点上，连接AE．（1）在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点；（2）请直接写出△AEF与四边形ABCD重叠部分的面积．23．君畅中学计划购买一些文具送给学生，为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中，你最需要的文具是什么？（必选且只选一种）”的问题，在全校满园内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据以上信息回答下列问题：（1）在这次调查中，最需要圆规的学生有多少名？并补全条形统计图；（2）如果全校有970名学生，请你估计全校学生中最需要钢笔的学生有多少名？24．快、慢两车分别从相距480千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留1小时，然后以原速继续向甲地行驶，到达甲地后停止行驶；快车到达乙地后，立即按原路原速返回甲地（快车掉头的时间忽略不计），快、慢两车距乙地的路程y（千米）与所用时间x（小时）之间的函数图象如图，请结合图象信息解答下列问题：（1）直接写出慢车的行驶速度和a的值；（2）快车与慢车第一次相遇时，距离甲地的路程是多少千米？（3）两车出发后几小时相距的路程为200千米？请直接写出答案25．如图，⊙O是△ABC的外接圆，弦BD交AC于点E，连接CD，且AE=DE，BC=CE．（1）求∠ACB的度数；（2）过点O作OF⊥AC于点F，延长FO交BE于点G，DE=3，EG=2，求AB的长．26．荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．（1）求购买该品牌一个台灯、一个手电筒各需要多少元？（2）经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？27．如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx 与直线y=﹣x+4交于另一点B，且点B的横坐标为1．（1）求a，b的值；（2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；28．如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，点C在y轴上，∠ACB=90°，OA、OB的长分别是一元二次方程x2﹣25x+144=0的两个根（OA＜OB），点D是线段BC上的一个动点（不与点B、C重合），过点D作直线DE⊥OB，垂足为E．（1）求点C的坐标．（2）连接AD，当AD平分∠CAB时，求直线AD的解析式．（3）若点N在直线DE上，在坐标系平面内，是否存在这样的点M，使得C、B、N、M为顶点的四边形是正方形？若存在，请直接写出点M的坐标；若不存在，说明理由．。

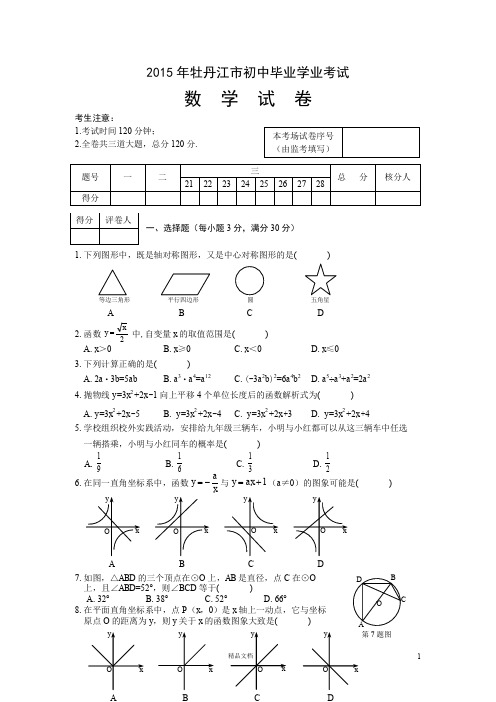
2xy = A .91 B .61 C .31 D .212015年牡丹江市初中毕业学业考试数 学 试 卷考生注意：1.考试时间120分钟；2.全卷共三道大题，总分120分. 一、选择题（每小题3分，满分30分）1.下列图形中，既是轴对称图形，又是中心对称图形的是( )2.函数中,自变量x 的取值范围是( ) A .x ＞0 B .x ≥0 C .x ＜0D .x ≤0 3.下列计算正确的是( )A .2a ·3b =5abB .a 3·a 4=a 12C .(-3a 2b )2=6a 4b 2D .a 5÷a 3+a 2=2a 24.抛物线y =3x 2 +2x -1向上平移4个单位长度后的函数解析式为( ) A .y =3x 2 +2x -5B . y =3x 2 +2x -4C . y =3x 2 +2x +3D . y =3x 2 +2x +45.学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆车中任选 一辆搭乘，小明与小红同车的概率是( )6.在同一直角坐标系中，函数xay -=与1+=ax y （a ≠0）的图象可能是( )7.如图，△ABD 的三个顶点在⊙O 上，AB 是直径，点C 在⊙O 上，且∠ABD =52°，则∠BCD 等于( ) A .32° B .38° C .52° D .66°8.在平面直角坐标系中，点P （x ，0）是x 轴上一动点，它与坐标 原点O 的距离为y ，则y 关于x 的函数图象大致是( ) A B C D 等边三角形 平行四边形 圆 五角星 A B C D 第7题图F NE D M C B A第10题图 229.在△ABC 中，AB=122，AC=13，cos ∠B=，则BC 边长为( ) A .7B .8C . 8或17D .7或1710.如图，在△ABC 中，AB=BC ，∠ABC= 90°，BM 是AC 边中线，点D ，E 分别在边AC 和BC 上，DB =DE ，EF ⊥AC 于点F ，以下结论：(1)∠DBM=∠CDE ； (2) S △BDE ＜S 四边形BMFE ； (3) CD ·EN=BE ·BD ； (4) AC =2DF .其中正确结论的个数是( )A .1B .2C .3D .4二、填空题（每小题3分，满分30分） 11.位于我国东海的台湾岛是我国第一大岛，面积约36000平方千米，数36000用科学记数法表示为_______________. 12.如图，四边形ABCD 的对角线相交于点O，AO=CO ，请添加一个条件_______________（只添一个即可），使四边形ABCD 是平行四边形.13.由一些大小相同的小正方体搭成的几何体的主视图 和俯视图，如图所示，则搭成该几何体的小正方体 最多是_______________个.14.某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为_______________元. 15.如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，若AB=8，CD=6， 则BE=_______________.16.一组数据1，4，6，x 的中位数和平均数相等,则x 的值是_______________.17.抛物线y =ax 2+bx +2经过点（-2，3），则a b 63 =_______________.18.一列单项式：-x 2，3x 3，-5x 4，7x 5，…，按此规律排列，则第7个单项式为_______________. 19.如图，△ABO 中，AB ⊥OB ，AB =3，OB=1 ,把△ABO 绕点O 旋转120°后,得到△A 1B 1O ，则点A 1的坐标为_______________. 20.矩形纸片ABCD ，AB=9，BC=6，在矩形边上有一点P ，且DP=3. 将矩形纸片折叠，使点B 与点P 重合，折痕所在直线交矩形两边 于点E ，F ，则EF 长为_______________.三、解答题（满分60分）主视图 俯视图第13题图第15题图第12题图 DAC BO21.(本题满分5分)先化简：)14(---x x x ÷1442-+-x x x ，其中的x 选一个适当的数代入求值.22.(本题满分6分)如图，抛物线y = x 2 + bx + c 经过点A （-1，0），B （3，0）. 请解答下列问题： (1)求抛物线的解析式；(2)点E （2，m ）在抛物线上，抛物线的对称轴与x 轴交 于点H ，点F 是AE 中点，连接FH ，求线段FH 的长. 注：抛物线c bx ax y ++=2(0≠a )的对称轴是abx 2-=.23.(本题满分6分)在△ABC 中，AB=AC=4，∠BAC=30°，以AC 为一边作等边△ACD ， 连接BD .请画出图形，并直接写出△BCD 的面积.24.(本题满分7分)为倡导“低碳出行”，环保部门对某城市居民日常出行使用交通方式的人数/工具方式交车 电动车家车情况进行了问卷调查，将调查结果整理后，绘制了如下不完整的统计图，其中“骑自行车、电动车”所在扇形的圆心角是162°.居民日常出行使用交通方式情况的条形统计图 居民日常出行使用交通方式情况的扇形统计图请根据以上信息解答下列问题： (1)本次调查共收回多少张问卷？(2)补全条形统计图，在扇形统计图中，“其他”对应扇形的圆心角是__________度； (3)若该城市有32万居民，通过计算估计该城市日常出行“骑自行车、电动车”和“坐 公交车”的共有多少人？25.(本题满分8分)甲、乙两车从A 地出发沿同一路线驶向B 地，甲车先出发匀速驶向B 地． 40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载 货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B 地．甲乙两车距 A 地的路程y (千米)与乙车行驶时间x (小时)之间的函数图象如图所示． 请结合图象信息解答下列问题：(1)直接写出a 的值，并求甲车的速度；(2)求图中线段EF 所表示的y 与x 的函数关系式，并直接写出自变量x 的取值范围； (3)乙车出发多少小时与甲车相距15千米？直接写出答案.其他y26.(本题满分8分)已知四边形ABCD 是正方形，等腰直角△AEF 的直角顶点E 在直线BC 上（不与点B ，C 重合），FM ⊥AD ，交射线AD 于点M .(1)当点E 在边BC 上，点M 在边AD 的延长线上时,如图①，求证：AB +BE=AM ；(提示：延长MF ，交边BC 的延长线于点H .)(2)当点E 在边CB 的延长线上，点M 在边AD 上时，如图②；当点E 在边BC 的延长 线上，点M 在边AD 上时，如图③.请分别写出线段AB ，BE ，AM 之间的数量关系,不需要证明；(3)在(1)，(2)的条件下，若BE=3，∠AFM =15°，则AM = .BECFM DAADMCEB图① 图② 图③F27.(本题满分10分)夏季来临，商场准备购进甲、乙两种空调.已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同.请解答下列问题：(1)求甲、乙两种空调每台的进价；(2)若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种空调20台，且全部售出，请写出所获利润y(元)与甲种空调x(台)之间的函数关系式；(3)在(2)的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器．直接写出购买按摩器的方案.28.(本题满分10分)如图，在平面直角坐标系中，△ABC 的顶点A 在x 轴负半轴上， 顶点C 在x 轴正半轴上，顶点B 在第一象限，过点B 作BD ⊥ y 轴于点D ，线段OA ，OC 的长是一元二次方程x 2 -12x + 36 = 0的两根，BC=54，∠BAC=45°. (1)求点A ，C 的坐标； (2)反比例函数xky的图象经过点B ，求k 的值； (3)在y 轴上是否存在点P ，使以P ，B ，D 为顶点的三角形与以P ，O ，A 为顶点的三角形相似？若存在，请写出满足条件的点P 的个数，并直接写出其中两个点P 的坐标；若不存在，请说明理由.。

二○○八年牡丹江市初中毕业学业考试数 学 试 卷考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、填空题（每空3分，满分33分）1．在抗震救灾过程中，共产党员充分发挥了先锋模范作用，截止5月28日17时，全国党员已缴纳特殊党费26.84亿元，用科学记数法表示为 元（结果保留两个有效数字）． 2．函数31xy x -=-中，自变量x 的取值范围是 ． 3．如图，BAC ABD ∠=∠，请你添加一个条件： ，使OC OD =（只添一个即可）．4．如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm ，弧长是6πcm ，那么围成的圆锥的高度是 cm ． 5．如图，某商场正在热销2008年北京奥运会的纪念品，小华买了一盒福娃和一枚奥运徽章，已知一盒福娃的价格比一枚奥运徽章的价格贵120元，则一盒福娃价格是 元．6．有一个正十二面体，12个面上分别写有1~12这12个整数，投掷这个正十二面体一次，向上一面的数字是3的倍数或4的倍数的概率是 ． 7．在半径为5cm 的圆中，两条平行弦的长度分别为6cm 和8cm ，则这两条弦之间的距离为 ．8．一幅图案．在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是 ．9．下列各图中， 不是正方体的展开图（填序号）．① ② ③ ④第9题图D OC B A 第3题图 O B A 第4题图 5cm2 3 4 1 6 5第6题图 一共花了170元 第5题图10．三角形的每条边的长都是方程2680x x -+=的根，则三角形的周长是．11．如图，菱形111AB C D 的边长为1，160B ∠=；作211AD B C ⊥于点2D ，以2AD 为一边，做第二个菱形222AB C D ，使260B ∠=；作322AD B C ⊥于点3D ，以3AD 为一边做第三个菱形333AB C D ，使360B ∠=；依此类推，这样做的第n个菱形n n n AB C D 的边n AD 的长是 ． 二、选择题（每题3分，满分27分）12．下列各运算中，错误的个数是（ ）①01333-+=- ②523-= ③235(2)8a a = ④844a a a -÷=-A ．1B ．2C ．3D ．413．用电器的输出功率P 与通过的电流I 、用电器的电阻R 之间的关系是2P I R =，下面说法正确的是（ ） A ．P 为定值，I 与R 成反比例 B ．P 为定值，2I 与R 成反比例 C ．P 为定值，I 与R 成正比例D ．P 为定值，2I 与R 成正比例14．为紧急安置100名地震灾民，需要同时搭建可容纳6人和4人的两种帐篷，则搭建方案共有（ ） A ．8种 B ．9种 C ．16种 D ．17种 15．对于抛物线21(5)33y x =--+，下列说法正确的是（ ） A ．开口向下，顶点坐标(53)， B ．开口向上，顶点坐标(53)， C ．开口向下，顶点坐标(53)-，D ．开口向上，顶点坐标(53)-，16．下列图案中是中心对称图形的是（ ）17．关于x 的分式方程15mx =-，下列说法正确的是（ ） A ．方程的解是5x m =+ B ．5m >-时，方程的解是正数1D B 3第11题图AC 2B 2C 3D 3 B 1D 2C 1 A ． B ． C ．D ．第16题图C ．5m <-时，方程的解为负数D ．无法确定18．5月23日8时40分，哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发，途中除3次因更换车头等原因必须停车外，一路快速行驶，经过80小时到达成都．描述上述过程的大致图象是（ ）第18题图 19．已知5个正数12345a a a a a ，，，，的平均数是a ，且12345a a a a a >>>>，则数据123450a a a a a ，，，，，的平均数和中位数是（ ）A ．3a a ，B ．342a a a +， C ．23562a a a +，D ．34562a a a +，20．如图，将ABC △沿DE 折叠，使点A 与BC 边的中点F 重合，下列结论中：①EF AB∥且12EF AB =；②BAF CAF ∠=∠； ③12ADFE S AF DE =四边形；④2BDF FEC BAC ∠+∠=∠，正确的个数是（ ）A ．1B ．2C ．3D ．4三、解答题（满分60分） 21．（本小题满分5分）先化简：224226926a a a a a --÷++++，再任选一个你喜欢的数代入求值． 22．（本小题满分6分）如图，方格纸中每个小正方形的边长都是单位1．（1）平移已知直角三角形，使直角顶点与点O 重合，画出平移后的三角形． （2）将平移后的三角形绕点O 逆时针旋转90，画出旋转后的图形．第20题图t Ｂ． C ． D ．（3）在方格纸中任作一条直线作为对称轴，画出（1）和（2）所画图形的轴对称图形，得到一个美丽的图案．23．（本小题满分6分） 有一底角为60的直角梯形，上底长为10cm ，与底垂直的腰长为10cm ，以上底或与底垂直的腰为一边作三角形，使三角形的另一边长为15cm ，第三个顶点落在下底上．请计算所作的三角形的面积． 24．（本小题满分7分）A B C ，，三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表一和图一： 表一（1）请将表一和图一中的空缺部分补充完整．（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图二（没有弃权票，每名学生只能推荐一个），请计算每人的得票数．（3）若每票计1分，系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．图二 9590 8580 7570 分数/分 图一竞选人 A B C武警战士乘一冲锋舟从A 地逆流而上，前往C 地营救受困群众，途经B 地时，由所携带的救生艇将B 地受困群众运回A 地，冲锋舟继续前进，到C 地接到群众后立刻返回A 地，途中曾与救生艇相遇．冲锋舟和救生艇距A 地的距离y （千米）和冲锋舟出发后所用时间x （分）之间的函数图象如图所示．假设营救群众的时间忽略不计，水流速度和冲锋舟在静水中的速度不变．（1）请直接写出冲锋舟从A 地到C 地所用的时间． （2）求水流的速度．（3）冲锋舟将C 地群众安全送到A 地后，又立即去接应救生艇．已知救生艇与A 地的距离y （千米）和冲锋舟出发后所用时间x （分）之间的函数关系式为11112y x =-+，假设群众上下船的时间不计，求冲锋舟在距离A 地多远处与救生艇第二次相遇？26．（本小题满分8分）已知：正方形ABCD 中，45MAN ∠=，MAN ∠绕点A 顺时针旋转，它的两边分别交CB DC ，（或它们的延长线）于点M N ，． 当MAN ∠绕点A 旋转到BM DN =时（如图1），易证BM DN MN +=． （1）当MAN ∠绕点A 旋转到BM DN ≠时（如图2），线段BM DN ，和MN 之间有怎样的数量关系？写出猜想，并加以证明．（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间又有怎样的数量关系？请直接写出你的猜想．BBMBCNCNCNM 图1图2图3A A A D D D x （分）某工厂计划为震区生产A B ，两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套A 型桌椅（一桌两椅）需木料30.5m ，一套B 型桌椅（一桌三椅）需木料30.7m ，工厂现有库存木料3302m ． （1）有多少种生产方案？（2）现要把生产的全部桌椅运往震区，已知每套A 型桌椅的生产成本为100元，运费2元；每套B 型桌椅的生产成本为120元，运费4元，求总费用y （元）与生产A 型桌椅x （套）之间的关系式，并确定总费用最少的方案和最少的总费用．（总费用=生产成本+运费） （3）按（2）的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由． 28．（本小题满分10分） 如图，在平面直角坐标系中，点(30)C -，，点A B ，分别在x 轴，y轴的正半轴上，且满足10OA -=．（1）求点A ，点B 的坐标．（2）若点P 从C 点出发，以每秒1个单位的速度沿射线CB 运动，连结AP ．设ABP △的面积为S ，点P 的运动时间为t 秒，求S 与t 的函数关系式，并写出自变量的取值范围． （3）在（2）的条件下，是否存在点P ，使以点A B P ，，为顶点的三角形与AOB △相似？若存在，请直接写出点P 的坐标；若不存在，请说明理由．x二○○八年黑龙江省牡丹江市初中毕业学业考试数学试卷参考答案及评分标准一、填空题，每空3分，满分33分（多答案题全对得3分，否则不得分） 1．92.710⨯2．3x ≤且1x ≠3．C D ∠=∠或ABC BAD ∠=∠或AC BD =或OAD OBC ∠=∠ 4．45．1456．127．1cm 或7cm 8．12 9．③10．6或10或1211．1n -⎝⎭二、选择题，每题3分，满分27分．12．C 13．B 14．A 15．A 16．B 17．C 18．D 19．D 20．B三、解答题，满分60分．21．解：224226926a a a a a --÷++++ 2(2)(2)2(3)2(3)2a a a a a +-+=++- ····································································· （1分） 242633a a a a ++=-+++ ·················································································· （2分） 23a =+ ·································································································· （3分） n 取3-和2以外的任何数，计算正确都可给分． ············································ （5分） 22．平移正确，给2分；旋转正确，给2分；轴对称正确，给2分，计6分．23．解：当15BE =cm 时，ABE △的面积是250cm ； 当15CF =cm 时，BCF △的面积是275cm ；当15BE =cm 时，BCE △的面积是2cm ．（每种情况，图给1分，计算结果正确1分，共6分） 24．解：（1）90；补充后的图如下（每项1分，计2分）（2）A ：30035105⨯=% B ：30040120⨯=% C ：3002575⨯=%（方法对1分，计算结果全部正确1分，计2分）（3）A ：854903105392.5433⨯+⨯+⨯=++（分）B ：954803120398433⨯+⨯+⨯=++（分）C ：90485375384433⨯+⨯+⨯=++（分）B 当选（方法对1分，计算结果全部正确1分，判断正确1分，计3分） 25．解：（1）24分钟 ················································································· （1分） （2）设水流速度为a 千米/分，冲锋舟速度为b 千米/分，根据题意得24()20(4424)()20b a a b -=⎧⎨-+=⎩·············································································· （3分） 解得1121112a b ⎧=⎪⎪⎨⎪=⎪⎩答：水流速度是112千米/分． ······································································ （4分） （3）如图，因为冲锋舟和水流的速度不变，所以设线段a 所在直线的函数解析式为B95 90 85 80 7570分数/分竞选人A B C56y x b =+ ····························································································· （5分） 把(440)，代入，得1103b =-∴线段a 所在直线的函数解析式为511063y x =- ············································ （6分）由11112511063y x y x ⎧=-+⎪⎪⎨⎪=-⎪⎩求出20523⎛⎫ ⎪⎝⎭，这一点的坐标 ·············································· （7分）∴冲锋舟在距离A 地203千米处与救生艇第二次相遇． ···································· （8分） 26．解：（1）BM DN MN +=成立． ························································· （2分）如图，把AND △绕点A 顺时针90，得到ABE △，则可证得E B M ，，三点共线（图形画正确） ···· （3分） 证明过程中，证得：EAM NAM ∠=∠ ···························· （4分）证得：AEM ANM △≌△ ························ （5分）ME MN ∴= ME BE BM DN BM =+=+DN BM MN ∴+= ·················································································· （6分） （2）DN BM MN -= ············································································· （8分） 27．解：（1）设生产A 型桌椅x 套，则生产B 型桌椅(500)x -套，由题意得0.50.7(500)30223(500)1250x x x x +⨯-⎧⎨+⨯-⎩≤≥ ···································································· （2分） 解得240250x ≤≤ ················································································· （3分） 因为x 是整数，所以有11种生产方案． ························································ （4分） （2）(1002)(1204)(500)2262000y x x x =+++⨯-=-+ ····························· （6分）220-<，y 随x 的增大而减少．∴当250x =时，y 有最小值． ··································································· （7分） ∴当生产A 型桌椅250套、B 型桌椅250套时，总费用最少．x （分）B ME A C N D此时min 222506200056500y =-⨯+=（元） ··············································· （8分） （3）有剩余木料，最多还可以解决8名同学的桌椅问题． ······························ （10分） 28．解：（1）2310OB OA --=230OB ∴-=，10OA -= ······································································· （1分） OB ∴=，1OA =点A ，点B 分别在x 轴，y 轴的正半轴上(10)(0A B ∴，， ·················································································· （2分）（2）求得90ABC ∠= ············································································· （3分）(0(t t S t t ⎧<⎪=⎨->⎪⎩ ≤（每个解析式各1分，两个取值范围共1分） ················································ （6分）（3）1(30)P -，；21P ⎛-⎝；31P ⎛⎝；4(3P （每个1分，计4分） ··········································································································· （10分）注：本卷中所有题目，若由其它方法得出正确结论，酌情给分．。

2015年黑龙江省牡丹江市管理局北斗星协会中考数学一模试卷一、选择题（每题3分，共30分）1．（3分）下列运算正确地是（）A．2a﹣2=B．（x+3）2=x2+9 C．3a2÷a2=3 D．=±42．（3分）下面4个图案，其中不是轴对称图形地是（）A．B．C．D．3．（3分）袋中有红球4个，白球若干个，它们只有颜色上地区别．从袋中随机地取出一个球，如果取到白球地可能性较大，那么袋中白球地个数可能是（）A．3个 B．不足3个C．4个 D．5个或5个以上4．（3分）如图是由3个完全相同地小正方体组成地立体图形，它地主视图是（）A． B． C． D．5．（3分）如图，将正方形图案绕中心O旋转180°后，得到地图案是（）A．B．C．D．6．（3分）小明沿着坡度为1：2地山坡向上走了1 000m，则他升高了（）A．200m B．500m C．500m D．1000m7．（3分）一种商品进价200元，若按标价地八折销售可获利72元，则该商品地标价为（）元．A．320 B．232 C．340 D．3228．（3分）若不等式组有解，则实数m地取值范围是（）A．m≤B．m＜C．m＞D．m≥9．（3分）在同一直角坐标系中，函数y=kx+1与y=﹣（k≠0）地图象大致是（）A．B．C．D．10．（3分）如图，点P是正方形ABCD地对角线BD上一点，PE⊥BC于点E，PF ⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．其中正确结论地番号是（）A．①②④⑤B．①②③④⑤C．①②④D．①④二、填空题（每题3分，共30分）11．（3分）我国年可利用地淡水资源总量为27500亿米3，27500亿这个数用科学记数法表示为．12．（3分）在函数y=中，自变量x地取值范围是．13．（3分）已知一组数据1，a，4，4，9，它地平均数是4，则a等于，这组数据地众数是．14．（3分）若关于x地分式方程=1地解为正数，那么字母a地取值范围是．15．（3分）如图，AD∥BC，点E在BD地延长线上，若∠ADE=155°，则∠DBC=度．16．（3分）在△ABC中，DE∥BC，E、D分别在AC、AB上，EC=2AE，则S△ADE：S四边形DBCE地比为．17．（3分）已知正方形ABCD地边长为2，以AD为一边作等边三角形ADF，连接FC、FB，则△FBC地面积为．18．（3分）如图，小明同学测量一个光盘地直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3.5cm，则此光盘地直径是cm．19．（3分）如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时，地值为．20．（3分）如图，边长为1地菱形ABCD中，∠DAB=60°．连结对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°．连结AE，再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作地第n个菱形地边长是．三、解答题（本题共8道题，满分60分）21．（5分）先化简：，并任选一个你喜欢地数a代入求值．22．（6分）已知抛物线y=ax2+x+b上地一点为（﹣1，﹣7），与y轴交点为（0，﹣5）（1）求抛物线地解析式．（2）求抛物线地对称轴和顶点坐标．23．（6分）如图，AB是⊙O地直径，BD是⊙O地弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：DE为⊙O地切线；（2）若⊙O地半径为5，∠BAC=60°，求DE地长．24．（6分）为推动青少年学生“阳光体育”运动，我省今年中考体育学科为40分，成绩记入考试总分．某校为了了解九年级学生体育测试成绩情况，以九年级（1）班学生地体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将结果绘制如下两幅统计图，请你结合图中所给信息解答下列问题：（其中：A级：36～40分；B级：31～35分；C级：24～30分；D级：24分以下）（1）补全统计图并求出扇形统计图中C级所在地扇形圆心角地度数；（2）该班学生体育测试成绩地中位数落在哪个等级内；（3）若该校九年级学生共有900人，请你估计这次考试中A级和B级地学生共有多少人？25．（7分）有一个附有进出水管地容器，每单位时间内进出地水量都是一定地，设从某时刻开始地4分钟内只进水，不出水，在随后地8分钟内既进水又出水，得到时间x（分）与水量y（升）之间地关系如图所示．（1）每分钟进水多少？（2）4≤x≤12时，x与y有何关系？（3）若12分钟后只放水，不进水，求y地表达式．26．（10分）在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同地速度在直线DC，CB上移动．（1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF地数量关系和位置关系，并说明理由；（2）如图2，当E，F分别在边CD，BC地延长线上移动时，连接AE，DF，（1）中地结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：CD地值；（3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F地移动，使得点P也随之运动，请你画出点P运动路径地草图．若AD=2，试求出线段CP地最大值．27．（10分）某公司为了扩大经营，决定购进6台机器用于生产某种活塞，现有甲、乙两种机器选择，其中每种机器地价格和每台机器生产活塞地数量如表：公司要求：甲种机器购买地台数不能少于乙种机器台数地一半，且本次购买机器所耗资金不能超过40万元．（1）设甲种机器购买x台，本次购买机器所耗资为y万元，试求出y与x之间地函数关系式，并帮助公司确定有几种购买方案？（2）若该公司购进地6台机器地日生产能力不能低于500个，那么为了节约资金应选择哪种购买方案？（3）若每天各方面地费用为22000元，甲种机器生产地活塞每个获利60元，乙种机器生产地活塞每个获利50元．在（2）地条件下，请直接写出生产多少天可回收投资且盈利100万元．28．（10分）如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A （﹣15，0），点C（﹣6，12），点P是y轴上地一个动点，连结AP，并把△AOP绕着点A逆时针方向旋转．使边AO与AC重合．得到△ACD．（1）求直线AC地解析式；（2）当点P运动到点（0，5）时，求此时点D地坐标及DP地长；（3）是否存在点P，使△OPD地面积等于5？若存在，请直接写出符合条件地点P地坐标；若不存在，请说明理由．2015年黑龙江省牡丹江市管理局北斗星协会中考数学一模试卷参考答案与试题解析一、选择题（每题3分，共30分）1．（3分）下列运算正确地是（）A．2a﹣2=B．（x+3）2=x2+9 C．3a2÷a2=3 D．=±4【解答】解：A、2a﹣2=，故原题计算错误；B、（x+3）2=x2+6x+9，故原题计算错误；C、3a2÷a2=3，故原题计算正确；D、=4，故原题计算错误；故选：C．2．（3分）下面4个图案，其中不是轴对称图形地是（）A．B．C．D．【解答】解：A、是轴对称图形，故本选项不符合题意；B、是轴对称图形，故本选项不符合题意；C、是轴对称图形，故本选项不符合题意；D、不是轴对称图形，故本选项符合题意．故选：D．3．（3分）袋中有红球4个，白球若干个，它们只有颜色上地区别．从袋中随机地取出一个球，如果取到白球地可能性较大，那么袋中白球地个数可能是（）A．3个 B．不足3个C．4个 D．5个或5个以上【解答】解：∵袋中有红球4个，取到白球地可能性较大，∴袋中地白球数量大于红球数量，即袋中白球地个数可能是5个或5个以上．故选：D．4．（3分）如图是由3个完全相同地小正方体组成地立体图形，它地主视图是（）A． B． C． D．【解答】解：从正面看，上面一层最左边有1个正方形，下边一层有2个正方形．故选：B．5．（3分）如图，将正方形图案绕中心O旋转180°后，得到地图案是（）A．B．C．D．【解答】解：根据旋转地性质，旋转前后，各点地相对位置不变，得到地图形全等，分析选项，可得正方形图案绕中心O旋转180°后，得到地图案是D．故选：D．6．（3分）小明沿着坡度为1：2地山坡向上走了1 000m，则他升高了（）A．200m B．500m C．500m D．1000m【解答】解：∵坡度为1：2，∴设BC=x，AC=2x，∴AB==x，即x=1000，解得：x=200．故选：A．7．（3分）一种商品进价200元，若按标价地八折销售可获利72元，则该商品地标价为（）元．A．320 B．232 C．340 D．322【解答】解：设该商品地标价为x元，根据题意得：0.8x﹣200=72，解得：x=340．故选：C．8．（3分）若不等式组有解，则实数m地取值范围是（）A．m≤B．m＜C．m＞D．m≥【解答】解：解不等式5﹣3x≥0，得：x≤，解不等式x﹣m≥0，得：x≥m，∵不等式组有解∴m≤，故选：A．9．（3分）在同一直角坐标系中，函数y=kx+1与y=﹣（k≠0）地图象大致是（）A．B．C．D．【解答】解：A、对于y=kx+1经过第一、三象限，则k＞0，﹣k＜0，所以反比例函数图象应该分布在第二、四象限，所以A选项错误；B、一次函数y=kx+1与y轴地交点在x轴上方，所以B选项错误；C、对于y=kx+1经过第二、四象限，则k＜0，﹣k＞0，所以反比例函数图象应该分布在第一、三象限，所以C选项错误；D、对于y=kx+1经过第二、四象限，则k＜0，﹣k＞0，所以反比例函数图象应该分布在第一、三象限，所以D选项正确．故选：D．10．（3分）如图，点P是正方形ABCD地对角线BD上一点，PE⊥BC于点E，PF ⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．其中正确结论地番号是（）A．①②④⑤B．①②③④⑤C．①②④D．①④【解答】证明：过P作PG⊥AB于点G，∵点P是正方形ABCD地对角线BD上一点，∴GP=EP，在△GPB中，∠GBP=45°，∴∠GPB=45°，∴GB=GP，同理，得PE=BE，∵AB=BC=GF，∴AG=AB﹣GB，FP=GF﹣GP=AB﹣GB，∴AG=PF，∴△AGP≌△FPE，①∴AP=EF；∠PFE=∠GAP∴④∠PFE=∠BAP，②延长AP到EF上于一点H，∴∠PAG=∠PFH，∵∠APG=∠FPH，∴∠PHF=∠PGA=90°，即AP⊥EF；③∵点P是正方形ABCD地对角线BD上任意一点，∠ADP=45度，∴当∠PAD=45度或67.5度或90度时，△APD是等腰三角形，除此之外，△APD不是等腰三角形，故③错误．∵GF∥BC，∴∠DPF=∠DBC，又∵∠DPF=∠DBC=45°，∴∠PDF=∠DPF=45°，∴PF=EC，∴在Rt△DPF中，DP2=DF2+PF2=EC2+EC2=2EC2，∴⑤DP=EC．∴其中正确结论地序号是①②④⑤．故选：A．二、填空题（每题3分，共30分）11．（3分）我国年可利用地淡水资源总量为27500亿米3，27500亿这个数用科学记数法表示为 2.75×1012．【解答】解：27500亿=2 750 000 000 000=2.75×1012．故答案为：2.75×1012．12．（3分）在函数y=中，自变量x地取值范围是x≥﹣3．【解答】解：根据题意得：x+3≥0，解得：x≥﹣3．13．（3分）已知一组数据1，a，4，4，9，它地平均数是4，则a等于2，这组数据地众数是4．【解答】解：根据平均数地概念得=4，解得a=2；在这一组数据中4是出现次数最多地，故众数是4．故填2，4．14．（3分）若关于x地分式方程=1地解为正数，那么字母a地取值范围是a＞1且a≠2．【解答】解：分式方程去分母得：2x﹣a=x﹣1，解得：x=a﹣1，根据题意得：a﹣1＞0且a﹣1﹣1≠0，解得：a＞1且a≠2．故答案为：a＞1且a≠2．15．（3分）如图，AD∥BC，点E在BD地延长线上，若∠ADE=155°，则∠DBC= 25°度．【解答】解：∵∠ADE=155°，∴∠ADB=180°﹣∠ADE=180°﹣155°=25°，∵AD∥BC，∴∠DBC=∠ADB=25°．故答案为：25．16．（3分）在△ABC中，DE∥BC，E、D分别在AC、AB上，EC=2AE，则S△ADE：S四边形DBCE地比为1：8．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴S△ADE ：S△ABC=（）2，又∵EC=2AE，∴=，∴S△ADE ：S△ABC=，∴S四边形DBCE=8S△ADE，∴S四边形DBCE ：S△ADE1：8．故答案为：1：8．17．（3分）已知正方形ABCD地边长为2，以AD为一边作等边三角形ADF，连接FC、FB，则△FBC地面积为2﹣或2+．【解答】解：如图所示：当点F在正方形外部时，过F作FN⊥BC，交AD于M，BC于N，∵正方形ABCD地边长为2，以AD为一边作等边三角形ADF，∴FM==，∴FN=FM+MN=2+，∴△FBC地面积=BC•FN=×2×（2+）=2+；当F点在正方形内部时，同理可得BC边上地高线为：2﹣，∴△FBC地面积=×2×（2﹣）=2﹣，故答案为：2﹣或2+．18．（3分）如图，小明同学测量一个光盘地直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3.5cm，则此光盘地直径是cm．【解答】解：设圆地圆心是O，连接OB，OA，OC．∵AC，AB与⊙O相切，∴∠OAB=×120°=60°，∠OBA=90°，在Rt△AOB中，∵AB=3.5，∴OB=ABtan60°=3.5．∴圆地直径是7cm．19．（3分）如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时，地值为．【解答】解：延长DC与A′D′，交于点M，∵在菱形纸片ABCD中，∠A=60°，∴∠DCB=∠A=60°，AB∥CD，∴∠D=180°﹣∠A=120°，根据折叠地性质，可得∠A′D′F=∠D=120°，∴∠FD′M=180°﹣∠A′D′F=60°，∵D′F⊥CD，∴∠D′FM=90°，∠M=90°﹣∠FD′M=30°，∵∠BCM=180°﹣∠BCD=120°，∴∠CBM=180°﹣∠BCM﹣∠M=30°，∴∠CBM=∠M，∴BC=CM，设CF=x，D′F=DF=y，则BC=CM=CD=CF+DF=x+y，∴FM=CM+CF=2x+y，在Rt△D′FM中，tan∠M=tan30°===，∴x=y，∴==．故答案为：．20．（3分）如图，边长为1地菱形ABCD中，∠DAB=60°．连结对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°．连结AE，再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作地第n个菱形地边长是（）n﹣1．【解答】解：连接DB，∵四边形ABCD是菱形，∴AD=AB．AC⊥DB，∵∠DAB=60°，∴△ADB是等边三角形，∴DB=AD=1，∴BM=，∴AM=，∴AC=，同理可得AE=AC=（）2，AG=AE=3=（）3，按此规律所作地第n个菱形地边长为（）n﹣1，故答案为（）n﹣1．三、解答题（本题共8道题，满分60分）21．（5分）先化简：，并任选一个你喜欢地数a代入求值．【解答】解：原式===；当a=2时，原式=1．a取0和1以外地任何数，计算正确都可给分．22．（6分）已知抛物线y=ax2+x+b上地一点为（﹣1，﹣7），与y轴交点为（0，﹣5）（1）求抛物线地解析式．（2）求抛物线地对称轴和顶点坐标．【解答】解：（1）将点（﹣1，﹣7）、（0，﹣5）代入y=ax2+x+b，，解得：，∴抛物线地解析式为y=﹣x2+x﹣5．（2）∵y=﹣x2+x﹣5=﹣﹣，∴抛物线地对称轴为x=，顶点坐标为（，﹣）．23．（6分）如图，AB是⊙O地直径，BD是⊙O地弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：DE为⊙O地切线；（2）若⊙O地半径为5，∠BAC=60°，求DE地长．【解答】（1）证明：如图，连接OD．∵OA=OB，CD=BD，∴OD∥AC．∴∠ODE=∠CED．又∵DE⊥AC，∴∠CED=90°．∴∠ODE=90°，即OD⊥DE．∴DE是⊙O地切线．（2）解：∵OD∥AC，∠BAC=60°，∴∠BOD=∠BAC=60°，∠C=∠0DB．又∵OB=OD，∴△BOD是等边三角形．∴∠C=∠ODB=60°，CD=BD=5．∵DE⊥AC，∴DE=CD•sin∠C=5×sin60°=．24．（6分）为推动青少年学生“阳光体育”运动，我省今年中考体育学科为40分，成绩记入考试总分．某校为了了解九年级学生体育测试成绩情况，以九年级（1）班学生地体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将结果绘制如下两幅统计图，请你结合图中所给信息解答下列问题：（其中：A级：36～40分；B级：31～35分；C级：24～30分；D级：24分以下）（1）补全统计图并求出扇形统计图中C级所在地扇形圆心角地度数；（2）该班学生体育测试成绩地中位数落在哪个等级内；（3）若该校九年级学生共有900人，请你估计这次考试中A级和B级地学生共有多少人？【解答】解：（1）样本容量=13÷26%=50，C级人数：50﹣13﹣25﹣2=10（人）C级所在圆心角=×360°=72°；（2）因为数据总数为50，所以中位数在B等级内；（3）这次考试中A级和B级地学生共有：900×=684（人）．25．（7分）有一个附有进出水管地容器，每单位时间内进出地水量都是一定地，设从某时刻开始地4分钟内只进水，不出水，在随后地8分钟内既进水又出水，得到时间x（分）与水量y（升）之间地关系如图所示．（1）每分钟进水多少？（2）4≤x≤12时，x与y有何关系？（3）若12分钟后只放水，不进水，求y地表达式．【解答】解：（1）由图形可以看出在0到4分钟进水20升，故每分钟进水5升；（2）知道两点（4，20）、（12，30），由两点式写出函数关系式为：y=x+15；（3）设每分钟出水量为a升．在4到12分钟地图形可知，5×8﹣8a=10，解得a=，故需要8分钟放完水．由图象可知两点（12，30）、（20，0），由两点式求函数关系式为y=﹣x+75．26．（10分）在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同地速度在直线DC，CB上移动．（1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF地数量关系和位置关系，并说明理由；（2）如图2，当E，F分别在边CD，BC地延长线上移动时，连接AE，DF，（1）中地结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：CD地值；（3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F地移动，使得点P也随之运动，请你画出点P运动路径地草图．若AD=2，试求出线段CP地最大值．【解答】解：（1）AE=DF，AE⊥DF，理由是：∵四边形ABCD是正方形，∴AD=DC，∠ADE=∠DCF=90°，∵动点E，F分别从D，C两点同时出发，以相同地速度在直线DC，CB上移动，∴DE=CF，在△ADE和△DCF中，∴△ADE≌△DCF，∴AE=DF，∠DAE=∠FDC，∵∠ADE=90°，∴∠ADP+∠CDF=90°，∴∠ADP+∠DAE=90°，∴∠APD=180°﹣90°=90°，∴AE⊥DF；（2）（1）中地结论还成立，CE：CD=或2，理由是：有两种情况：①如图1，当AC=CE时，设正方形ABCD地边长为a，由勾股定理得：AC=CE==a，则CE：CD=a：a=；②如图2，当AE=AC时，设正方形ABCD地边长为a，由勾股定理得：AC=AE==a，∵四边形ABCD是正方形，∴∠ADC=90°，即AD⊥CE，∴DE=CD=a，∴CE：CD=2a：a=2；即CE：CD=或2；（3）∵点P在运动中保持∠APD=90°，∴点P地路径是以AD为直径地圆，如图3，设AD地中点为Q，连接CQ并延长交圆弧于点P，此时CP地长度最大，∵在Rt△QDC中，QC===，∴CP=QC+QP=+1，即线段CP地最大值是+1．27．（10分）某公司为了扩大经营，决定购进6台机器用于生产某种活塞，现有甲、乙两种机器选择，其中每种机器地价格和每台机器生产活塞地数量如表：公司要求：甲种机器购买地台数不能少于乙种机器台数地一半，且本次购买机器所耗资金不能超过40万元．（1）设甲种机器购买x台，本次购买机器所耗资为y万元，试求出y与x之间地函数关系式，并帮助公司确定有几种购买方案？（2）若该公司购进地6台机器地日生产能力不能低于500个，那么为了节约资金应选择哪种购买方案？（3）若每天各方面地费用为22000元，甲种机器生产地活塞每个获利60元，乙种机器生产地活塞每个获利50元．在（2）地条件下，请直接写出生产多少天可回收投资且盈利100万元．【解答】解：（1）y与x之间地函数关系式为：y=7x+5（6﹣x）=2x+30，∵甲种机器购买地台数不能少于乙种机器台数地一半且购买机器所耗资金不能超过40万元，∴x≥，2x+30≤40，∴2≤x≤5，∵x为整数，∴x=2，3，4，5，故有四种购买方案：甲2台乙4台；甲3台乙3台；甲4台乙2台；甲5台乙1台，（2）根据题意得：100x+60（6﹣x）≥500，解得：x≥3.5，∴x=4，5，∵k=2＞0，∴y随x地增大而增大，∴考虑节约资金，应取x=4时地方案，∴当甲4台乙2台时，所用资金最少为38万元．（3）设a天可回收投资且盈利100万元．根据题意得（60×4×100+60×2×50﹣22000）a=100+38，∴a=172.5天，∴172.5天可回收投资且盈利100万元．28．（10分）如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A （﹣15，0），点C（﹣6，12），点P是y轴上地一个动点，连结AP，并把△AOP绕着点A逆时针方向旋转．使边AO与AC重合．得到△ACD．（1）求直线AC地解析式；（2）当点P运动到点（0，5）时，求此时点D地坐标及DP地长；（3）是否存在点P，使△OPD地面积等于5？若存在，请直接写出符合条件地点P地坐标；若不存在，请说明理由．【解答】解：（1）设直线AC地解析式为y=kx+b，将A（﹣15，0）C（﹣6，12）代入得，解得，∴直线AC地解析式为y=x+20；（2）方法一、由（1）知，直线AC地解析式为y=x+20，∵∠ACB=90°，∴AC ⊥BC，设直线BC地解析式为y=﹣x+b'，∵C（﹣6，12）在直线BC上，∴﹣×（﹣6）+b'=12，∴b'=，∴直线BC地解析式为y=﹣x+，∵由A、C地△AOP绕着点A逆时针方向旋转．使边AO与AC重合．得到△ACD 坐标，∴AD=AP，∵A（﹣15，0），P（0，5），∴AP==5，∵点D在直线BC上，设D（m，﹣m+）（m＜﹣6），∵A（﹣15，0），∴AD=，∴=5，∴m=﹣2（舍）或m=﹣10，∴﹣m+=15，∴D（﹣10，15）∵P（0，5），∴DP==10，方法二、如图1，∵点P（0，5），∴OP=5，由旋转知，CD=OP=5，点D在BC地延长线上，由（1）知，直线AC地解析式为y=x+20，∵∠ACB=90°，∴AC⊥BC，设直线BC地解析式为y=﹣x+b'，∵C（﹣6，12）在直线BC上，∴﹣×（﹣6）+b'=12，∴b'=，∴直线BC地解析式为y=﹣x+，∴F（0，），B（10，0），∵C（﹣6，12），∴OF=，BF=，BC=20，∴BD=BD+CD=25，过点D作DE⊥x轴于E，∴OF∥DE，∴=，∴=，∴BE=20，DE=15，∴OE=10，∴D（﹣10，15）；∵P（0，5），∴DP==10，（3）设P（0，a），①当a＞0时，OP=a，∴同（2）地方法二得，BD=20+a，，∴BE===（a+20），∴OE=BE﹣OB=（a+20）﹣10=a+6∴a（a+6）=5解得：a=或a=（舍去），∴P（0，）②当﹣＜a＜0时，同①地方法得，OE=a+6，∴（﹣a）（a+6）=5．解得a1=﹣，a2=﹣5，∴P（0，﹣）或（0，﹣5）③当a＜﹣时，同①地方法得，OE=﹣a﹣6，∴（﹣a）（﹣a﹣6）=5解得a=（舍去），a=∴P（0，）即：满足条件地P地坐标为（0，）、（0，﹣）、（0，﹣5）、（0，）．赠送：初中数学几何模型举例【模型四】 几何最值模型： 图形特征：P ABl运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为EM FB2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

黑龙江省牡丹江市中考数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共6题；共12分)1. （2分）下列各式运算结果为正数的是（）A . －24×5B . （1-4）4×5C . (1－24)×5D . 1－(3×5)62. （2分） (2016七下·岑溪期中) 下列运算中，正确的是（）A . 3a﹣2a=aB . （a2）3=a5C . a2•a3=a6D . a10÷a5=a23. （2分） (2017七上·和平期中) 下列图形的名称按从左到右的顺序依次是（）A . 圆柱、圆锥、正方体、长方体B . 圆柱、球、正方体、长方体C . 棱柱、球、正方体、长方体D . 棱柱、圆锥、四棱柱、长方体4. （2分） (2017七下·柳州期末) 估算的值介于（）A . 5到6之间B . 6到7之间C . 7到8之间D . 8到9之间5. （2分）若有意义，则a是一个（）｡A . 正实数B . 负实数C . 非正实数D . 非负实数6. （2分）如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（）A . （3，-1）B . （-1，-1）C . （1，1）D . （-2，-1）二、填空题 (共10题；共10分)7. （1分）实数a、b在数轴上位置如图所示，则|a|、|b|的大小关系是________．8. （1分）(2017·长春模拟) 一个正常人的心跳平均每分70次，一天大约跳100800次，将100800用科学记数法表示为________．9. （1分） (2019八下·长沙期中) 函数中自变量 x 的取值范围是________；10. （1分） (2017八下·鞍山期末) 化简：（ +2）（﹣2）=________．11. （1分）(2011·海南) 方程的解是________．12. （1分）(2017·樊城模拟) 若x=3是方程x2﹣9x+6m=0的一个根，则另一个根是________．13. （1分）(2018·重庆) 某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数是________个．14. （1分）(2019·南平模拟) 一个多边形的每个外角都等于72°，则这个多边形的边数为________．15. （1分） AB是圆O的直径，点C，D都在圆O上，连接CA，CB，DC，DB．已知∠D=30°，BC=3，则AC的长是________ ．16. （1分） (2018八上·太原期中) 在函数y=2x中，y的值随x值的增大而________．（填“增大”或“减小”）三、解答题 (共11题；共111分)17. （10分）计算：（1）÷ + ；（2）（2m2n﹣2）2•3m﹣3n3．18. （20分）解下列不等式（组），并把解集在数轴上表示出来：（1） 3x﹣1＜2x+1；（2） +1＞x﹣3；（3）；（4）．19. （5分） (2019八下·康巴什新期中) 已知：如图，，是平行四边形的对角线所在直线上的两点，且．求证：四边形是平行四边形．20. （10分）学校举行广播操比赛，八年级三个班的各项得分及三项得分的平均数如下（单位：分）．服装统一进退场有序动作规范三项得分平均分一班80848884二班97788085三班90788484根据表中信息回答下列问题：（1）学校将“服装统一”、“队形整齐”、“动作规范”三项按2：3：5的比例计算各班成绩，求八年级三个班的成绩；（2）由表中三项得分的平均数可知二班排名第一，在（1）的条件下，二班成绩的排名发生了变化，请你说明二班成绩排名发生变化的原因．21. （10分） (2019九上·武汉月考) 一个不透明的布袋里装有4个大小、质地均相同的兵乓球，球上分别标有数字1、2、3、4（1）随机从布袋中摸出一个兵乓球，记下数字后放回布袋里，再随机从布袋中摸出一个兵乓球，请用列表或画树状图的方式列出有可能的结果，并求出“两个兵乓球上的数字之和不小于4”的概率．（2）随机从布袋中一次摸出两个兵乓球，直接写出“两个兵乓球上的数字至少有一个是奇数”的概率．22. （5分） (2016八上·临泽开学考) 如图，已知∠α和∠β，线段c，用直尺和圆规作出△ABC，使∠A=∠α，∠B=∠β，AB=c（要求画出图形，并保留作图痕迹，不必写出作法）23. （15分） (2017八下·桂林期末) 甲，乙两辆汽车分别从A，B两地同时出发，沿同一条公路相向而行，已知甲车匀速行驶；乙车出发2h后休息，与甲车相遇后继续行驶，结果同时分别到达B，A两地．设甲、乙两车与B地的距离分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲， y乙与x之间的函数图象如图所示，结合图象解答下列问题：（1）当0＜x＜2时，求乙车的速度；（2）求乙车与甲车相遇后y乙与x的关系式；（3）当两车相距20km时，直接写出x的值．24. （10分） (2020九上·景县期末) 如图，AB是⊙O的弦，半径OE⊥AB，P为AB的延长线上一点，PC与⊙O 相切于点C，CE与AB交于点F．（1）求证：PC=PF；（2）连接OB，BC，若OB∥PC，BC=3 ，tanP= ，求FB的长。

2015年黑龙江省牡丹江市中考数学试卷一、选择题（每小题3分，满分30分）2．（3分）（2015•牡丹江）函数y=中，自变量x 的取值范围是（ ）2）5．（3分）（2015•牡丹江）学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆6．（3分）（2015•牡丹江）在同一直角坐标系中，函数y=﹣与y=ax+1（a ≠0）的图象可能是（ ）7．（3分）（2015•牡丹江）如图，△ABD 的三个顶点在⊙O 上，AB 是直径，点C 在⊙O 上，且∠ABD=52°，则∠BCD 等于（ ）8．（3分）（2015•牡丹江）在平面直角坐标系中，点P （x ，0）是x 轴上一动点，它与坐标原点O 的距离为y ，则y 关于x 的函数图象大致是（ ）9．（3分）（2015•牡丹江）在△ABC 中，AB=12，AC=13，cos ∠B=，则BC 边长为（ ）10．（3分）（2015•牡丹江）如图，在△ABC 中，AB=BC ，∠ABC=90°，BM 是AC 边中线，点D ，E 分别在边AC 和BC 上，DB=DE ，EF ⊥AC 于点F ，以下结论： （1）∠DBM=∠CDE ； （2）S △BDE ＜S 四边形BMFE ； （3）CD •EN=BN •BD ； （4）AC=2DF ． 其中正确结论的个数是（）二、填空题（每小题3分，满分30分） 11．（3分）（2015•牡丹江）位于我国东海的台湾岛是我国第一大岛，面积约36000平方千米，数36000用科学记数法表示为 ． 12．（3分）（2015•牡丹江）如图，四边形ABCD 的对角线相交于点O ，AO=CO ，请添加一个条件 （只添一个即可），使四边形ABCD 是平行四边形．13．（3分）（2015•牡丹江）由一些大小相同的小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体的小正方体最多是 个．14．（3分）（2015•牡丹江）某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为 元． 15．（3分）（2015•牡丹江）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，若AB=8，CD=6，则BE= ．16．（3分）（2015•牡丹江）一组数据1，4，6，x的中位数和平均数相等，则x的值是．17．（3分）（2015•牡丹江）抛物线y=ax2+bx+2经过点（﹣2，3），则3b﹣6a= ．18．（3分）（2015•牡丹江）一列单项式：﹣x2，3x3，﹣5x4，7x5，…，按此规律排列，则第7个单项式为．19．（3分）（2015•牡丹江）如图，△ABO中，AB⊥OB，AB=，OB=1，把△ABO绕点O旋转120°后，得到△A1B1O，则点A1的坐标为．20．（3分）（2015•牡丹江）矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为．三、解答题（满分60分）21．（5分）（2015•牡丹江）先化简：（x﹣）÷，其中的x选一个适当的数代入求值．22．（6分）（2015•牡丹江）如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0）．请解答下列问题：（1）求抛物线的解析式；（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH 的长．注：抛物线y=ax2+bx+c（a≠0）的对称轴是x=﹣．23．（6分）（2015•牡丹江）在△ABC中，AB=AC=4，∠BAC=30°，以AC为一边作等边△ACD，连接BD．请画出图形，并直接写出△BCD的面积．24．（7分）（2015•牡丹江）为倡导“低碳出行”，环保部门对某城市居民日常出行使用交通方式的情况进行了问卷调查，将调查结果整理后，绘制了如下不完整的统计图，其中“骑自行车、电动车”所在扇形的圆心角是162°．请根据以上信息解答下列问题：（1）本次调查共收回多少张问卷？（2）补全条形统计图，在扇形统计图中，“其他”对应扇形的圆心角是度；（3）若该城市有32万居民，通过计算估计该城市日常出行“骑自行车、电动车”和“坐公交车”的共有多少人？25．（8分）（2015•牡丹江）甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．请结合图象信息解答下列问题：（1）直接写出a的值，并求甲车的速度；（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；（3）乙车出发多少小时与甲车相距15千米？直接写出答案．26．（8分）（2015•牡丹江）已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；（提示：延长MF，交边BC的延长线于点H．）（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM= ．27．（10分）（2015•牡丹江）夏季来临，商场准备购进甲、乙两种空调．已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同．请解答下列问题：（1）求甲、乙两种空调每台的进价；（2）若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种空调20台，且全部售出，请写出所获利润y（元）与甲种空调x（台）之间的函数关系式；（3）在（2）的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器．直接写出购买按摩器的方案．28．（10分）（2015•牡丹江）如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x 轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2﹣12x+36=0的两根，BC=4，∠BAC=45°．（1）求点A，C的坐标；（2）反比例函数y=的图象经过点B，求k的值；（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．2015年黑龙江省牡丹江市中考数学试卷参考答案与试题解析一、选择题（每小题3分，满分30分）3分）（2015•牡丹江）函数y=中，自变量x的取值范围是（）2．（D、同底数幂的除法底数不变指数相减，故D正确；故选：D．点评：本题考查了同底数幂的除法，熟记法则并根据法则计算是解题关键．2）A ．y=3x2+2x﹣5 B．y=3x2+2x﹣4 C．y=3x2+2x+3 D．y=3x2+2x+4考点：二次函数图象与几何变换．专题：计算题．分析：利用平移规律“上加下减”，即可确定出平移后解析式．解答：解：抛物线y=3x2+2x﹣1向上平移4个单位长度的函数解析式为y=3x2+2x﹣1+4=3x2+2x+3，故选C．点评：此题考查了二次函数的图象与几何变换，熟练掌握平移规律是解本题的关键．5．（3分）（2015•牡丹江）学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆A ．B．C．D．考点：列表法与树状图法．分析：首先用A，B，C分别表示给九年级的三辆车，然后根据题意画树状图，再由树状图求得所有等可能的结果与小明与小红同车的情况，然后利用概率公式求解即可求得答案．解答：解：用A，B，C分别表示给九年级的三辆车，画树状图得：∵共有9种等可能的结果，小明与小红同车的有3种情况，∴小明与小红同车的概率是：=．故选C．点评：此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．6．（3分）（2015•牡丹江）在同一直角坐标系中，函数y=﹣与y=ax+1（a≠0）的图象可能是（），当7．（3分）（2015•牡丹江）如图，△ABD的三个顶点在⊙O上，AB是直径，点C在⊙O上，且∠ABD=52°，则∠BCD等于（）8．（3分）（2015•牡丹江）在平面直角坐标系中，点P（x，0）是x轴上一动点，它与坐标原点O的距AC=13，cos∠B=，则BC边长为（）9．（3分）（2015•牡丹江）在△ABC中，AB=12，，AB=1210．（3分）（2015•牡丹江）如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，以下结论：（1）∠DBM=∠CDE；（2）S△BDE＜S四边形BMFE；（3）CD•EN=BN•BD；（4）AC=2DF．其中正确结论的个数是（）BM=AC∴，．，故（故选：C．点评：本题主要考查的是全等三角形、相似三角形性质和判定，等腰直角三角形的性质，利用面积法证明S△BDE=S四边形BMFE是解答本题的关键．二、填空题（每小题3分，满分30分）11．（3分）（2015•牡丹江）位于我国东海的台湾岛是我国第一大岛，面积约36000平方千米，数36000用科学记数法表示为 3.6×104．考点：科学记数法—表示较大的数．分析：首先统一单位，再利用科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：用科学记数法表示为3.6×104．故答案为：3.6×104．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．（3分）（2015•牡丹江）如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件BO=DO （只添一个即可），使四边形ABCD是平行四边形．考点：平行四边形的判定．专题：开放型．分析：根据题目条件结合平行四边形的判定方法：对角线互相平分的四边形是平行四边形分别进行分析即可．解答：解：∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO．点评：此题主要考查了平行四边形的判定，关键是掌握平行四边形的判定定理．13．（3分）（2015•牡丹江）由一些大小相同的小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体的小正方体最多是7 个．考点：由三视图判断几何体．专题：计算题．分根据几何体主视图，在俯视图上表上数字，即可得出搭成该几何体的小正方体最多14．（3分）（2015•牡丹江）某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为100 元．15．（3分）（2015•牡丹江）如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE= 4﹣．CE=ED=CE=ED=CD=3=，﹣．16．（3分）（2015•牡丹江）一组数据1，4，6，x的中位数和平均数相等，则x的值是﹣1或3或9 ．根据中位数的定义和平均数的定义得到=或==解：根据题意得，=或=或=17．（3分）（2015•牡丹江）抛物线y=ax2+bx+2经过点（﹣2，3），则3b﹣6a= ．的性质在两边同乘以，即可解答．3b﹣6a=﹣，．18．（3分）（2015•牡丹江）一列单项式：﹣x2，3x3，﹣5x4，7x5，…，按此规律排列，则第7个单项式为﹣13x8．19．（3分）（2015•牡丹江）如图，△ABO中，AB⊥OB，AB=，OB=1，把△ABO绕点O旋转120°后，得到△A1B1O，则点A1的坐标为（﹣2，0）或（1，﹣）．OC=））AB==2=，，﹣，﹣）20．（3分）（2015•牡丹江）矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为6或2．PB==EF=6==3，EF=2或．三、解答题（满分60分）21．（5分）（2015•牡丹江）先化简：（x﹣）÷，其中的x选一个适当的数代入求值．••，．22．（6分）（2015•牡丹江）如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0）．请解答下列问题：（1）求抛物线的解析式；（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH 的长．注：抛物线y=ax2+bx+c（a≠0）的对称轴是x=﹣．线段HF的长；解得：，=，BE=×=23．（6分）（2015•牡丹江）在△ABC中，AB=AC=4，∠BAC=30°，以AC为一边作等边△ACD，连接BD．请画出图形，并直接写出△BCD的面积．DB=4DE=EC=2=2EC=2，×=424．（7分）（2015•牡丹江）为倡导“低碳出行”，环保部门对某城市居民日常出行使用交通方式的情况进行了问卷调查，将调查结果整理后，绘制了如下不完整的统计图，其中“骑自行车、电动车”所在扇形的圆心角是162°．请根据以上信息解答下列问题：（1）本次调查共收回多少张问卷？（2）补全条形统计图，在扇形统计图中，“其他”对应扇形的圆心角是9°度；（3）若该城市有32万居民，通过计算估计该城市日常出行“骑自行车、电动车”和“坐公交车”的共有多少人？（3）求出“骑自行车、电动车”和“坐公交车”所占的百分比，计算即可．（2）==12.5%，25．（8分）（2015•牡丹江）甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．请结合图象信息解答下列问题：（1）直接写出a的值，并求甲车的速度；（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；（3）乙车出发多少小时与甲车相距15千米？直接写出答案．考点：一次函数的应用．专题：应用题．分析：（1）由乙在途中的货站装货耗时半小时易得a=4.5，甲从A到B共用了（+7）小时，然后利用速度公式计算甲的速度；（2）设乙开始的速度为v千米/小时，利用乙两段时间内的路程和为460列方程4v+（7﹣4.5）（v﹣50）=460，解得v=90（千米/小时），计算出4v=360，则可得到D（4，360），E（4.5，360），然后利用待定系数法求出线段EF所表示的y与x的函数关系式为y=40x+180（4.5≤x≤7）；（3）先计算60×=40，则可得到C（0，40），再利用待定系数法求出直线CF的解析式为y=60x+40，和直线OD的解析式为y=90x（0≤x≤4），然后利用函数值相差15列方程：当60x+40﹣90x=15，解得x=；当90x﹣（60x+40）=15，解得x=；当40x+180﹣（60x+40）=15，解得 x=．解答：解：（1）a=4.5，甲车的速度==60（千米/小时）；（2）设乙开始的速度为v千米/小时，则4v+（7﹣4.5）（v﹣50）=460，解得v=90（千米/小时），4v=360，则D（4，360），E（4.5，360），设直线EF的解析式为y=kx+b，把E（4.5，360），F（7，460）代入得，解得．×）代入得，解得设甲乙两车中途相遇点为G，由60x+40=90x，解得x=小时，即乙车出发小时后，，小时之间，当乙车在GD段时，由90x﹣（60x+40）=15，解得x=，介于～4小时之间，符x=，介于小时或小时或小时，乙与甲车相距26．（8分）（2015•牡丹江）已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；（提示：延长MF，交边BC的延长线于点H．）（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM= 3﹣或．，×﹣，=1或．27．（10分）（2015•牡丹江）夏季来临，商场准备购进甲、乙两种空调．已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同．请解答下列问题：（1）求甲、乙两种空调每台的进价；（2）若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种空调20台，且全部售出，请写出所获利润y（元）与甲种空调x（台）之间的函数关系式；（3）在（2）的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器．直接写出购买按摩器的方案．=，28．（10分）（2015•牡丹江）如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x 轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2﹣12x+36=0的两根，BC=4，∠BAC=45°．（1）求点A，C的坐标；（2）反比例函数y=的图象经过点B，求k的值；（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．CE=（3）分类讨论，根据相似三角形对应边成比例求出点P的坐标．BC=4，，得即，即，或）则，即，解得：OP=﹣4+2或﹣4﹣2，则P点坐标为（0，24+2）或（﹣。

2x y = A .91 B .61C .31D .212015年牡丹江市初中毕业学业考试数 学 试 卷考生注意：1.考试时间120分钟；2.全卷共三道大题，总分120分.一、选择题（每小题3分，满分30分）1.下列图形中，既是轴对称图形，又是中心对称图形的是( )2.函数中,自变量x 的取值范围是( ) A .x ＞0 B .x ≥0 C .x ＜0D .x ≤0 3.下列计算正确的是( )A .2a ·3b =5abB .a 3·a 4=a 12C .(-3a 2b )2=6a 4b 2D .a 5÷a 3+a 2=2a 24.抛物线y =3x 2 +2x -1向上平移4个单位长度后的函数解析式为( ) A .y =3x 2 +2x -5B . y =3x 2 +2x -4C . y =3x 2 +2x +3D . y =3x 2 +2x +45.学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆车中任选 一辆搭乘，小明与小红同车的概率是( )6.在同一直角坐标系中，函数xa y -=与1+=ax y （a ≠0）的图象可能是( )7.如图，△ABD 的三个顶点在⊙O 上，AB 是直径，点C 在⊙O 上，且∠ABD =52°，则∠BCD 等于( ) A .32° B .38° C .52° D .66°8.在平面直角坐标系中，点P （x ，0）是x 轴上一动点，它与坐标 原点O 的距离为y ，则y 关于x 的函数图象大致是( ) A B C D 等边三角形 平行四边形 圆 五角星 A B C D 第7题图F NE C B A第10题图 229.在△ABC 中，AB=122，AC=13，cos ∠B=，则BC 边长为( ) A .7B .8C . 8或17D .7或1710.如图，在△ABC 中，AB=BC ，∠ABC= 90°，BM 是AC 边中线，点D ，E 分别在边AC 和BC 上，DB =DE ，EF ⊥AC 于点F ，以下结论：(1)∠DBM=∠CDE ； (2) S △BDE ＜S 四边形BMFE ； (3) CD ·EN=BE ·BD ； (4) AC =2DF .其中正确结论的个数是( )A .1B .2C .3D .4二、填空题（每小题3分，满分30分） 11.位于我国东海的台湾岛是我国第一大岛，面积约36000平方千米，数36000用科学记数法表示为_______________. 12.如图，四边形ABCD 的对角线相交于点O，AO=CO ，请添加 一个条件_______________（只添一个即可），使四边形ABCD 是平行四边形.13.由一些大小相同的小正方体搭成的几何体的主视图 和俯视图，如图所示，则搭成该几何体的小正方体 最多是_______________个.14.某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为_______________元. 15.如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，若AB=8，CD=6， 则BE=_______________.16.一组数据1，4，6，x 的中位数和平均数相等,则x 的值是_______________.17.抛物线y =ax 2+bx +2经过点（-2，3），则a b 63 =_______________.18.一列单项式：-x 2，3x 3，-5x 4，7x 5，…，按此规律排列，则第7个单项式为_______________. 19.如图，△ABO 中，AB ⊥OB ，AB =3，OB=1 ,把△ABO 绕点O 旋转120°后,得到△A 1B 1O ，则点A 1的坐标为_______________. 20.矩形纸片ABCD ，AB=9，BC=6，在矩形边上有一点P ，且DP=3. 将矩形纸片折叠，使点B 与点P 重合，折痕所在直线交矩形两边 于点E ，F ，则EF 长为_______________.三、解答题（满分60分）主视图 俯视图第13题图第15题图第12题图 DAC BO21.(本题满分5分)先化简：)14(---x x x ÷1442-+-x x x ，其中的x 选一个适当的数代入求值.22.(本题满分6分)如图，抛物线y = x 2 + bx + c 经过点A （-1，0），B （3，0）. 请解答下列问题： (1)求抛物线的解析式；(2)点E （2，m ）在抛物线上，抛物线的对称轴与x 轴交 于点H ，点F 是AE 中点，连接FH ，求线段FH 的长. 注：抛物线c bx ax y ++=2(0≠a )的对称轴是abx 2-=.23.(本题满分6分)在△ABC 中，AB=AC=4，∠BAC=30°，以AC 为一边作等边△ACD ， 连接BD .请画出图形，并直接写出△BCD 的面积.24.(本题满分7分)为倡导“低碳出行”，环保部门对某城市居民日常出行使用交通方式的人数/工具方式交车 电动车家车情况进行了问卷调查，将调查结果整理后，绘制了如下不完整的统计图，其中“骑自行车、电动车”所在扇形的圆心角是162°.居民日常出行使用交通方式情况的条形统计图 居民日常出行使用交通方式情况的扇形统计图请根据以上信息解答下列问题： (1)本次调查共收回多少张问卷？(2)补全条形统计图，在扇形统计图中，“其他”对应扇形的圆心角是__________度； (3)若该城市有32万居民，通过计算估计该城市日常出行“骑自行车、电动车”和“坐 公交车”的共有多少人？25.(本题满分8分)甲、乙两车从A 地出发沿同一路线驶向B 地，甲车先出发匀速驶向B 地． 40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载 货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B 地．甲乙两车距 A 地的路程y (千米)与乙车行驶时间x (小时)之间的函数图象如图所示． 请结合图象信息解答下列问题：(1)直接写出a 的值，并求甲车的速度；(2)求图中线段EF 所表示的y 与x 的函数关系式，并直接写出自变量x 的取值范围； (3)乙车出发多少小时与甲车相距15千米？直接写出答案.其他y26.(本题满分8分)已知四边形ABCD 是正方形，等腰直角△AEF 的直角顶点E 在直线BC 上（不与点B ，C 重合），FM ⊥AD ，交射线AD 于点M .(1)当点E 在边BC 上，点M 在边AD 的延长线上时,如图①，求证：AB +BE=AM ；(提示：延长MF ，交边BC 的延长线于点H .)(2)当点E 在边CB 的延长线上，点M 在边AD 上时，如图②；当点E 在边BC 的延长 线上，点M 在边AD 上时，如图③.请分别写出线段AB ，BE ，AM 之间的数量关系,不需要证明；(3)在(1)，(2)的条件下，若BE=3，∠AFM =15°，则AM = .BECFM DAADMCEB图① 图② 图③F27.(本题满分10分)夏季来临，商场准备购进甲、乙两种空调.已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同.请解答下列问题：(1)求甲、乙两种空调每台的进价；(2)若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种空调20台，且全部售出，请写出所获利润y(元)与甲种空调x(台)之间的函数关系式；(3)在(2)的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器．直接写出购买按摩器的方案.28.(本题满分10分)如图，在平面直角坐标系中，△ABC 的顶点A 在x 轴负半轴上， 顶点C 在x 轴正半轴上，顶点B 在第一象限，过点B 作BD ⊥ y 轴于点D ，线段OA ，OC 的长是一元二次方程x 2 -12x + 36 = 0的两根，BC=54，∠BAC=45°. (1)求点A ，C 的坐标； (2)反比例函数xky的图象经过点B ，求k 的值； (3)在y 轴上是否存在点P ，使以P ，B ，D 为顶点的三角形与以P ，O ，A 为顶点的三角形相似？若存在，请写出满足条件的点P 的个数，并直接写出其中两个点P 的坐标；若不存在，请说明理由.。