山东省德州夏津一中2018-2019学年上学期高三第一次月考理科数学试卷

夏津县高中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知复合命题p ∧（￢q ）是真命题，则下列命题中也是真命题的是（ ）A ．（￢p ）∨qB ．p ∨qC ．p ∧qD ．（￢p ）∧（￢q ）2． 在数列{}n a 中，115a =，*1332()n n a a n N +=-∈，则该数列中相邻两项的乘积为负数的项是 （ ）A ．21a 和22aB ．22a 和23aC ．23a 和24aD ．24a 和25a 3． 已知集合23111{1,(),,}122i A i i i i -=-+-+（其中为虚数单位），2{1}B x x =<，则A B =（ ）A ．{1}-B ．{1}C ．{-D ． 4． 已知空间四边形ABCD ，M 、N 分别是AB 、CD 的中点，且4AC =，6BD =，则（ ）A ．15MN <<B ．210MN <<C ．15MN ≤≤D ．25MN << 5． 四面体ABCD 中,截面 PQMN 是正方形， 则在下列结论中，下列说法错误的是（ ）A ．AC BD ⊥B ．AC BD =C.AC PQMN D ．异面直线PM 与BD 所成的角为456． 已知函数()cos()3f x x π=+，则要得到其导函数'()y f x =的图象，只需将函数()y f x =的图象（ ）A ．向右平移2π个单位 B ．向左平移2π个单位 C. 向右平移23π个单位 D ．左平移23π个单位7． 自圆C ：22(3)(4)4x y -++=外一点(,)P x y 引该圆的一条切线，切点为Q ，切线的长度等于点P 到原点O 的长，则点P 轨迹方程为（ ）A ．86210x y --=B ．86210x y +-=C ．68210x y +-=D ．68210x y --=【命题意图】本题考查直线与圆的位置关系、点到直线的距离，意在考查逻辑思维能力、转化能力、运算求解能力．8． 下列给出的几个关系中：①{}{},a b ∅⊆；②(){}{},,a b a b =；③{}{},,a b b a ⊆；④{}0∅⊆,正确的有（ ）个A.个B.个C.个D.个 9． 已知是虚数单位，若复数)(3i a i +-（R a ∈）的实部与虚部相等，则=a （ ）A ．1-B ．2-C ．D ．10．已知角的终边经过点()3P x ，()0x <且cos x θ=，则等于（ ）A ．1-B ．13- C ．3- D ．11．已知2->a ，若圆1O ：01582222=---++a ay x y x ，圆2O ：04422222=--+-++a a ay ax y x 恒有公共点，则a 的取值范围为（ ）.A ．),3[]1,2(+∞--B ．),3()1,35(+∞-- C ．),3[]1,35[+∞-- D ．),3()1,2(+∞-- 12．2016年3月“两会”期间，有代表提出适当下调“五险一金”的缴存比例，现拟从某工厂职工中抽取20名代表调查对这一提案的态度，已知该厂青年，中年，老年职工人数分别为350，500，150，按分层抽样的方法，应从青年职工中抽取的人数为（ ） A. 5 B.6 C.7D.10【命题意图】本题主要考查分层抽样的方法的运用，属容易题.二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知一组数据1x ，2x ，3x ，4x ，5x 的方差是2，另一组数据1ax ，2ax ，3ax ，4ax ，5ax （0a >）的标准差是a = ．14．如图为长方体积木块堆成的几何体的三视图，此几何体共由 块木块堆成．15．已知函数21,0()1,0x x f x x x ⎧-≤=⎨->⎩，()21xg x =-，则((2))f g = ，[()]f g x 的值域为 ．【命题意图】本题考查分段函数的函数值与值域等基础知识，意在考查分类讨论的数学思想与运算求解能力. 16．不等式0＜1﹣x 2≤1的解集为 ．三、解答题（本大共6小题，共70分。

德州市2018届高三第一次模拟考试数学（理）试题 第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 已知全集{}1,2,3,4,5,6U=，集合{}1,3A =，集合{}3,4,5B =，则集合()U A C B ⋂=（ ）A ．{}1,2,3,6B ．{}1C ．{}1,2D ．{}1,3,4,52.设i 为虚数单位，a R ∈，若()()11i ai --为纯虚数，则复数1ai -的模是（ ） AB ．2C ．1D ．03.已知命题():0,,sin p x x x ∀∈+∞>，命题121:,log 2xq x R x⎛⎫∃∈= ⎪⎝⎭，则下列命题中的真命题为（ ）A ．q ⌝B ．p q ∧C ．()p q ⌝∧D ．()()p q ⌝∨⌝ 4.已知双曲线()222210,0x y a b ab-=>>的一个焦点在抛物线216y x =的准线上，且双曲线的—条渐近线过点)，则双曲线的方程为（ ）A ．221420xy-= B ．221124xy-= C ．221412xy-= D ．221204xy-=5.已知ABC ∆的三边分别是,,a b c，设向量()()sin sin ,sin ,m B A c n C a b =-+=+，且//m n ，则B的大小是（ ）A ．6πB ．56π C ．3πD ．23π6.某几何体的三视图如图所示，则该几何体的表面积是（ ）A．162π+ B．164π++ C．164π+ D．162π++7.设()1,1XN ，其正态分布密度曲线如图所示，那么向正方形ABCD 中随机投掷100000个点，则落入阴影部分的点的个数的估计值是（ ） 注：若()2,XN μσ，则()0.6826P X μσμσ-<<+≈，()220.9544P X μσμσ-<<+≈A. 60380B.65870C.70280D.753908.已知不等式组210y x y kx y ≤-+⎧⎪≤+⎨⎪≥⎩所表示的平面区域为面积等于94的三角形，则实数k 的值为（ ）A ．1B ．2-C ．1或2-D ．29-9.函数()lncos f x x x=+（22x ππ-≤≤且0x ≠）的图象大致是（ ）A ．B ．C ．D ．10.已知公比不为1的等比数列{}n a 的前n 项和为n S ，且满足258,2,3a a a 成等差数列，则363S S =（ ） A ．134B ．1312C ．94D ．111211.已知函数()(](]111,1,012,0,1x x x f x x -⎧-∈-⎪+=⎨⎪∈⎩，且()()2g x f x mx m =-+在(]1,1-内有且仅有两个不同的零点，则实数m 的取值范围是（ ） A ．11,4⎛⎤--⎥⎝⎦B ．(]1,1,4⎛⎫-∞-⋃-+∞ ⎪⎝⎭ C ．11,4⎡⎫--⎪⎢⎣⎭ D ．()1,1,4⎡⎫-∞-⋃-+∞⎪⎢⎣⎭12．若关于x 的方程10x xxx em ex e+++=+有三个不等的实数解123,,x x x ，且1230x x x <<<，其中, 2.71828m R e ∈=为自然对数的底数，则1232312111x x x xx x e e e ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值为（ ）A ．2eB ．eC ．1m -D ．1m +第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.5名同学去参加2个不同的社团组织，每名同学只能参加其中一个社团组织，且甲乙两位同学不参加同一个社团组织，则共有 种可能（结果用数字表示）.14.在《九章算术》中记载着一道关于“持金出关”的题目，大意是：“在古代出关要交税.一天，某人拿钱若干出关，第1关交所拿钱数的12，第2关交所剩钱数的13，第3关交所剩钱数的14，”.现以这则故事中蕴含的数学思想，设计如图所示程序框图，则运行此程序，输出n 的值为 ．15.若圆22440x y x y +--=上至少有三个不同的点到直线:l y kx =l 的斜率的取值范围是 ．16.如图所示，坐标纸上的每个单位格的边长为1，由下往上的六个点：1,2,3,4,5,6的横、纵坐标分别对应数列{}()*n a n N ∈的前12项，其中横坐标为奇数项，纵坐标为偶数项，按如此规律，则2016201720182019a a a a +++=．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知函数()22sin cos f x x x x =-+（1）求()f x 的单调递增区间； （2）若11,324x ππ⎡⎤∈⎢⎥⎣⎦，且锐角ABC∆的两边长分别是函数()f x 的最大值和最小值，ABC ∆的，求ABC ∆的面积.18.某数学小组从医院和气象局获得今年1月至6月份每月20日的昼夜温差（,3x C x ︒≥）和患感冒人数（y 人）的数据，画出折线图.（1）由折线图看出，可用线性回归模型拟合y 与x 的关系，请用相关系数加以说明； （2）建立y 关于x 的回归方程（精确到0.01)，预测昼夜温差为4C ︒时患感冒的人数(精确到整数).参考数据：6154.9ii x ==∑，()()6194i i i x xy y =--=∑6= 2.646≈.参考公式:相关系数:nxxyyr --=，回归直线方程是y a bx =+，()()()121,niii nii xxyyb a y b xxx==--==-⋅-∑∑19. 如图1，在高为2的梯形ABCD中，//,25AB CD AB CD ==，，过A B、分别作,AE CD BF CD ⊥⊥，垂足分别为E F 、.已知1DE =，将D C 、沿AE BF 、折向同侧，得空间几何体ADE BCF -，如图2.（1）若AFBD ⊥，求证:DE BE ⊥；（2）若//,DE CF CD ，线段AB 的中点是P ，求CP 与平面ACD 所成角的正弦值.20.已知椭圆()2222:10x yC a b ab+=>>，点1⎛⎝⎭在椭圆上，,A B 分别为椭圆的右顶点与上顶点，过点,A B 引椭圆C 的两条弦AE BF 、交椭圆于点,E F .（1）求椭圆C 的方程；（2）若直线,AE BF 的斜率互为相反数， ①求出直线EF 的斜率；②若O 为直角坐标原点，求OEF ∆面积的最大值.21.已知函数()()ln 0f x ax x a =>在点()(),e f e 处的切线和直线210x y ++=垂直. （1）求a 的值；（2）对于任意的0x >，证明：()32f x x e -≥--； （3）若()f x b =有两个实根()1212,x x x x ≠，求证：12331122x x b e-<++.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程已知极坐标系的极点为直角坐标系xOy 的原点，极轴为x 轴的正半轴，两种坐标系中的长度单位相同.直线l cos 14πθ⎛⎫+= ⎪⎝⎭，曲线C的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数），设直线l 与曲线C 交于,A B 两点.（1）写出直线l 的普通方程与曲线C 的直角坐标方程，并求线段AB 的长； （2）已知点P 在曲线C 上运动，求点P 到直线l 距离的最大值. 23.选修4-5：不等式选讲 已知函数()3f x x a x =++-.（1）若()f x 的最小值为5，求实数a 的值； （2）当10x -≤≤时，不等式()4f x x ≤-恒成立，求实数a 的取值范围.。

山东省德州市夏津县一中2019届高三数学上学期第一次月考试题 文一．选择题：本大题共12小题，每小题5分1.在ABC ∆中，若AB ，120C ∠= ,则AC =（A ）1（B ）2（C ）3（D ）42.473sin17-的值为（A ） （B ）1-（C（D ）13. 已知点(0,1)A ，(3,2)B ，向量(4,3)AC =--，则向量BC =（A ）(7,4)-- （B ）(7,4) （C ） (1,4)- （D ） (1,4) 4. 已知函数()sin 2f x x =向右平移6π个单位后，得到函数()y g x =，下列关于()y g x =的说法正确的是 （A ）图象关于点,06π⎛⎫-⎪⎝⎭中心对称 （B ） 图象关于6x π=-轴对称（C ）在区间5,126ππ⎡⎤--⎢⎥⎣⎦单调递增（D ）在5,1212ππ⎡⎤-⎢⎥⎣⎦单调递增 5. 在ABC ∆中，,,a b c分别为内角,,A B C的对边，且()()2sin 2sin 2sin a A b c B c b C =+++，则A 的值为（A ）6π（B ）3π （C ）23π （D ）56π 6. 若等差数列{}n a 的前7项和721S =，且21a =-，则6a =( )A ．5B ．6C ．7D ．87. 设D 为ABC ∆所在平面内一点，1433AD AB AC =-+，若()BC DC R λλ=∈，则λ= （A ）2 （B ）3 （C ）-2 （D ）-3 8. 已知函数()()3sin 06f x x πωω⎛⎫=-> ⎪⎝⎭和()()2cos 21g x x ϕ=++的图象的对称轴完全相同，若0,2x π⎡⎤∈⎢⎥⎣⎦，则()f x 的取值范围是（A ） 3,32⎡⎤-⎢⎥⎣⎦（B ）[]3,3-（C ） 33,22⎡⎤-⎢⎥⎣⎦（D ） ,22⎡-⎢⎣⎦9. 已知数列{a n }满足a 1＝1，a n ＋1＝a 2n －2a n ＋1(n ∈N *)，则a 2 018＝( )A ．1B ．0C ．2 018D ．－2 01810. 已知ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，且CB Aa cbc sin sin sin +=--，则=B （A ）6π （B ）4π （C ）3π （D ）43π 11. 函数)2,0)(sin(2)(πϕϕ<>+=w wx x f 的部分图像如图所示，则17(0)()12f f π+的值为（A ）32- （B ）32+（C ）231-（D ） 231+ 12. 在ABC ∆中，内角C B A ,,的对边分别为c b a ,,，若ABC ∆的面积为S ，且226c b a S -+=）（，则C tan 等于（A ）125 （B ）125- （C ）125 （D ）125-二．填空题：本大题共5小题，每小题5分13. 若1tan 3α=，则2cos cos 22παα⎛⎫++= ⎪⎝⎭． 14. 等差数列{a n }与{b n }的前n 项和分别为S n 和T n ，若S n T n ＝3n －22n ＋1，则a 7b 7=___________15. 已知 a ＝4，b ＝3， ()()b a b a+⋅-232＝61.则b a + =___________________16. 设两个向量()222,cos ,,sin 2a b μλλθμθ⎛⎫=+-=+ ⎪⎝⎭，其中,,R λμθ∈． 若2a b =，则λμ的最小值为 ． 三．解答题：解答应写出必要的文字说明，证明过程或演算步骤 17. 在ABC ∆中，内角,,A B C 对的边为,,a b c .已知2cos 2c A a b +=.（Ⅰ）求角C 的值；（Ⅱ）若2c =，且ABC ∆，求,a b ．18. 在ABC ∆中，角A ，B ，C 的对边分别是a ，b ，c ，且向量(54,4)m a c b =-与向量(cos ,cos )n C B =共线. （Ⅰ）求cos B ；（Ⅱ）若b =5c =，a c <，且2AD DC =，求BD 的长度.19. 已知函数23()sin 22f x x x =+. （Ⅰ）求函数()f x 的单调递减区间；（Ⅱ）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若()2A f =ABC ∆的面积为a 的最小值.20. 已知函数1cos sin 32cos 2)(2-+=x x x x f ωωω,且)(x f 的周期为2 .（Ⅰ）当⎥⎦⎤⎢⎣⎡-∈21,21x 时，求)(x f 的最值； （Ⅱ）若41)2(=παf ，求)32cos(απ-的值.21. 已知向量)()2,1,sin ,cos m x n x x =-=u rr ，函数()12f x m n =⋅+u r r .（Ⅰ）若()0,,43x f x π⎡⎤∈=⎢⎥⎣⎦，求cos2x 的值；（Ⅱ）在ABC ∆中，角A,B,C 对边分别是,,a b c ，且满足2cos 2b A c ≤，求()f B 的取值范围．22. (重点文) (1）记等差数列{a n }的前n 项和为S n ，若a 1=21，S 4=20，求S 6 ; （2）已知等差数列{a n }的前n 项和为S n ，且满足且满足12323=-S S ， 求数列{a n }的公差。

夏津一中 2018—2019学年上学期高三开学摸底考试理 科 数 学本试卷共5页，23题(含选考题)．全卷满分150分．考试用时120分钟．★祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．写在试卷、草稿纸和答题卡上的非答题区域均无效．3．非选择题的作答：用黑色签字笔直接答在答题卡对应的答题区域内．写在试卷、草稿纸和答题卡上的非答题区域均无效．4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑．答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效． 5．考试结束后，请将本试卷和答题卡一并上交．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集{}6,5,4,3,2,1=U ，集合{}3,5,1=A ，集合{}Z x x x x B ∈≤--=,0)4)(2(|，则()U C A B = A ．{}1,6 B ．{}6 C ．{}63，D ．{}1,3 2．欧拉公式cos sin ixe x i x =+ (i 为虚数单位)是由瑞士著名数学家欧拉发明的，他将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．根据欧拉公式可知，3ie 表示的复数在复平面中位于 (A)第一象限(B)第二象限(C)第三象限(D)第四象限3．对任意非零实数b a ,，若b a ⊗的运算原理如图所示，则41log )21(22⊗-的值为（ ） A ．2 B ．2- C ．3 D ．3-4．2018年3月7日《科学网》刊登“动物可以自我驯化”的文章表明：关于野生小鼠的最新研究，它们在几乎没有任何人类影响的情况下也能表现出进化的迹象——皮毛上白色的斑块以及短鼻子．为了观察野生小鼠的这种表征，从有2对不同表征的小鼠（白色斑块和短鼻子野生小鼠各一对）的实验箱中每次拿出一只，不放回地拿出2只，则拿出的野生小鼠不是同一表征的概率为（ ） A ．14B ．13C ．23D ．345．()()6221x x -+的展开式中4x 的系数为（ ）A ．-160B ．320C ．480D ．6406．某几何体的三视图如图所示，其侧视图为等边三角形，则该几何体的体积为A ．3263+π B ．43+π C ．32123+π D ．432+π 7．()61211x x ⎛⎫+- ⎪⎝⎭的展开式中的常数项是（ ）A ．-5B ．7C ．-11D ．138．《九章算术》卷5《商功》记载一个问题“今有圆堡瑽，周四丈八尺，高一丈一尺．问积几何？答曰：二千一百一十二尺．术曰：周自相乘，以高乘之，十二而一”．这里所说的圆堡瑽就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”．就是说：圆堡瑽（圆柱体）的体积为112V =⨯（底面圆的周长的平方⨯高），则由此可推得圆周率π的取值为（ ） A ．3B ．3.1C ．3.14D ．3.29．已知向量,5=-=++的取值范围是A ．]5,0[B ．]25,5[C ．]7,25[D ．]10,5[10．如图，网格纸上小正方形的边长为2，粗实线及粗虚线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（ ）A BC ．41πD ．31π11．已知圆22:1C x y +=，点P 为直线240x y +-=上一动点，过点P 向圆C 引两条切线,,,PA PB A B 为切点，则直线AB 经过定点.（ ）A. 11,24⎛⎫ ⎪⎝⎭B. 11,42⎛⎫⎪⎝⎭C. ⎫⎪⎪⎝⎭D. ⎛ ⎝⎭12．已知定义在R 上的可导函数()f x 的导函数为()f x '，对任意实数x 均有()()()10x f x xf x '-+>成立，且()1e y f x =+-是奇函数，则不等式()e 0x xf x ->的解集是（ ）A ．(),e -∞B ．()e,+∞C ．(),1-∞D ．()1,+∞二、填空题：本题共4小题，每小题5分，共20分。

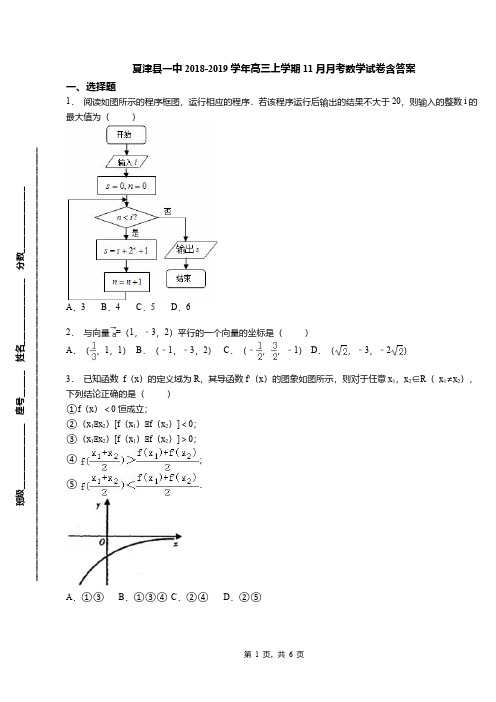
夏津县一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 阅读如图所示的程序框图，运行相应的程序．若该程序运行后输出的结果不大于20，则输入的整数i 的最大值为（）A ．3B ．4C ．5D ．62． 与向量=（1，﹣3，2）平行的一个向量的坐标是（）A ．（，1，1）B ．（﹣1，﹣3，2）C ．（﹣，，﹣1）D ．（，﹣3，﹣2）3． 已知函数 f （x ）的定义域为R ，其导函数f ′（x ）的图象如图所示，则对于任意x 1，x 2∈R （ x 1≠x 2），下列结论正确的是（ ）①f （x ）＜0恒成立；②（x 1﹣x 2）[f （x 1）﹣f （x 2）]＜0；③（x 1﹣x 2）[f （x 1）﹣f （x 2）]＞0；④；⑤．A ．①③B ．①③④C ．②④D ．②⑤班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________4． 如图，直三棱柱ABC ﹣A 1B 1C 1中，侧棱AA 1⊥平面ABC ．若AB=AC=AA 1=1，BC=，则异面直线A 1C与B 1C 1所成的角为（）A ．30°B ．45°C ．60°D ．90°5． 在某次测量中得到的A 样本数据如下：82，84，84，86，86，86，88，88，88，88．若B 样本数据恰好是A 样本数据都加2后所得数据，则A ，B 两样本的下列数字特征对应相同的是（ ）A ．众数B ．平均数C ．中位数D ．标准差6． 命题“∀a ∈R ，函数y=π”是增函数的否定是（ ）A ．“∀a ∈R ，函数y=π”是减函数B ．“∀a ∈R ，函数y=π”不是增函数C ．“∃a ∈R ，函数y=π”不是增函数D ．“∃a ∈R ，函数y=π”是减函数7． 定义运算：,,a a ba b b a b ≤⎧*=⎨>⎩．例如121*=，则函数()sin cos f x x x =*的值域为（ ）A ．⎡⎢⎣ B ．[]1,1- C ．⎤⎥⎦D ．⎡-⎢⎣8． 设奇函数f （x ）在（0，+∞）上为增函数，且f （1）=0，则不等式＜0的解集为（）A ．（﹣1，0）∪（1，+∞）B ．（﹣∞，﹣1）∪（0，1）C ．（﹣∞，﹣1）∪（1，+∞）D ．（﹣1，0）∪（0，1）9． 已知函数f （x ）=x 3+（1﹣b ）x 2﹣a （b ﹣3）x+b ﹣2的图象过原点，且在原点处的切线斜率是﹣3，则不等式组所确定的平面区域在x 2+y 2=4内的面积为（ ）A ．B ．C ．πD ．2π10．设集合A={x|2x ≤4}，集合B={x|y=lg （x ﹣1）}，则A ∩B 等于（ ）A ．（1，2）B ．[1，2]C ．[1，2）D ．（1，2]11．中，“”是“”的（）ABC ∆A B >cos 2cos 2B A >A. 充分必要条件 B. 充分不必要条件 C. 必要不充分条件D. 既不充分也不必要条件【命题意图】本题考查三角函数的性质与充分必要条件等基础知识，意在考查构造函数的思想与运算求解能力.12．若复数（2+ai ）2（a ∈R ）是实数（i 是虚数单位），则实数a 的值为（）A ．﹣2B ．±2C ．0D ．2二、填空题13．已知数列{a n }满足a n+1=e+a n （n ∈N *，e=2.71828）且a 3=4e ，则a 2015= ．14．如图是正方体的平面展开图，则在这个正方体中①与平行；②与是异面直线；BM ED CN BE ③与成角；④与是异面直线．CN BM 60︒DM BN 以上四个命题中，正确命题的序号是（写出所有你认为正确的命题）．15．已知a ，b 是互异的负数，A 是a ，b 的等差中项，G 是a ，b 的等比中项，则A 与G 的大小关系为 ．16．圆柱形玻璃杯高8cm ，杯口周长为12cm ，内壁距杯口2cm 的点A 处有一点蜜糖．A 点正对面的外壁（不是A 点的外壁）距杯底2cm 的点B 处有一小虫．若小虫沿杯壁爬向蜜糖饱食一顿，最少要爬多少 cm．（不计杯壁厚度与小虫的尺寸）17．阅读下图所示的程序框图，运行相应的程序，输出的的值等于_________. n 18．计算sin43°cos13°﹣cos43°sin13°三、解答题19．（本小题满分10分）选修4-1如图，点为圆上一点，.C O CP 3=（1）若交圆于点，PE O F 165EF =（2）若连接并延长交圆于的长.OP O ,A B20．在直角坐标系中，已知圆C的圆心坐标为（2，0），半径为，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．，直线l的参数方程为：（t为参数）．（1）求圆C和直线l的极坐标方程；（2）点P的极坐标为（1，），直线l与圆C相交于A，B，求|PA|+|PB|的值．21．某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：X1234Y51484542这里，两株作物“相近”是指它们之间的直线距离不超过1米．（I）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；（II）在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．22．（本小题满分10分）已知曲线的极坐标方程为，将曲线，（为参数），经过伸缩变C 2sin cos 10ρθρθ+=1cos :sin x C y θθ=⎧⎨=⎩α换后得到曲线．32x xy y'=⎧⎨'=⎩2C （1）求曲线的参数方程；2C （2）若点的在曲线上运动，试求出到曲线的距离的最小值．M 2C M C 23．在等比数列{a n }中，a 1a 2a 3=27，a 2+a 4=30试求：（1）a 1和公比q ；（2）前6项的和S 6．24．（本小题满分12分）设函数（）．mx x x x f -+=ln 21)(20>m （1）求的单调区间；)(x f （2）求的零点个数；)(x f （3）证明：曲线没有经过原点的切线．)(x f y =夏津县一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案B C DCDCDDBD题号1112答案A.C二、填空题13．　2016　． 14．③④15．　A ＜G ．16．　10　cm 17． 618． ．三、解答题19．（1）；（2）.4CE =CD =20． 21． 22．（1）（为参数）；（2.3cos 2sin x y θθ=⎧⎨=⎩23． 24．。

夏津县高级中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知向量(,2)a m =，(1,)b n =-（0n >），且0a b ⋅=，点(,)P m n 在圆225x y +=上，则|2|a b +=（ ）A ．34B ．C ．42D ．32 2． 如图是某几何体的三视图，则该几何体任意两个顶点间的距离的最大值为（ ）A ．4B ．5C ．32D ．333． 如图框内的输出结果是（ ）A ．2401B ．2500C ．2601D ．27044． 设集合{|12}A x x =<<，{|}B x x a =<，若A B ⊆，则的取值范围是（ ） A ．{|2}a a ≤ B ．{|1}a a ≤ C ．{|1}a a ≥ D ．{|2}a a ≥5． 已知函数x x x f 2sin )(-=，且)2(),31(log ),23(ln 3.02f c f b f a ===，则（ ）A ．c a b >>B ．a c b >>C ．a b c >>D ．b a c >>【命题意图】本题考查导数在单调性上的应用、指数值和对数值比较大小等基础知识，意在考查基本运算能力．6． 若圆心坐标为()2,1-的圆在直线10x y --=上截得的弦长为 ） A ．()()22210x y -++= B ．()()22214x y -++= C ．()()22218x y -++= D ．()()222116x y -++= 7． 将函数x x f ωsin )(=（其中0>ω）的图象向右平移4π个单位长度，所得的图象经过点 )0,43(π，则ω的最小值是（ ） A ．31 B ． C ．35D ．8． 等差数列{a n }中，a 1+a 5=10，a 4=7，则数列{a n }的公差为（ ） A ．1B ．2C ．3D ．49． 一个四边形的斜二侧直观图是一个底角为45°，腰和上底的长均为1的等腰梯形，那么原四边形的面积是（ ）A ．2+B ．1+C ．D ．10．若函数y=a x ﹣（b+1）（a ＞0，a ≠1）的图象在第一、三、四象限，则有（ ） A ．a ＞1且b ＜1 B ．a ＞1且b ＞0 C ．0＜a ＜1且b ＞0D ．0＜a ＜1且b ＜011．设函数()log |1|a f x x =-在(,1)-∞上单调递增，则(2)f a +与(3)f 的大小关系是（ ） A ．(2)(3)f a f +> B ．(2)(3)f a f +< C. (2)(3)f a f += D ．不能确定 12．S n 是等差数列{a n }的前n 项和，若3a 8－2a 7＝4，则下列结论正确的是（ ） A ．S 18＝72 B ．S 19＝76 C ．S 20＝80D ．S 21＝84二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．某工厂产生的废气经过过虑后排放，过虑过程中废气的污染物数量P （单位：毫克/升）与时间t （单位：小时）间的关系为0ekt P P -=（0P ，k 均为正常数）．如果前5个小时消除了10%的污染物，为了 消除27.1%的污染物，则需要___________小时.【命题意图】本题考指数函数的简单应用，考查函数思想，方程思想的灵活运用.14．已知点A 的坐标为（﹣1，0），点B 是圆心为C 的圆（x ﹣1）2+y 2=16上一动点，线段AB 的垂直平分线交BC 与点M ，则动点M 的轨迹方程为 ．15．若正数m 、n 满足mn ﹣m ﹣n=3，则点（m ，0）到直线x ﹣y+n=0的距离最小值是 ．16．设α为锐角，若sin （α﹣）=，则cos2α= ．三、解答题（本大共6小题，共70分。

高一年级2018-2019学年第二学期第一次月考数学试题2019.03.26第I卷（共52分）一、选择题（本大题共13小题，每小题4分，共52分）1.A. B. C. D.2、已知向量，，则A. B. C. D.3、如图，在平行四边形ABCD中，E为BC的中点，且，则A. ，B. ，C. ，D. ，4、下列计算正确的是A. B.C. D.5、已知平面向量是非零向量，，，则向量在向量方向上的投影为A. 1B.C. 2D.6、已知，，则A. B. C. D.7、设，向量，且，则A. B. C. D. 108、已知角，均为锐角，且，，则的值为A. B. C. D.9、函数的最小正周期为( )A. B. C. D.10、在中，，点P是所在平面内一点，则当取得最小值时，A. B. C. 9 D.（11-13为多选题）11、下列说法正确的有.若，则若，则A、B、C、D有可能构成平行四边形的四个顶点若，，则单位向量的模都相等12、已知，则下列结论正确的有A. 在区间上单调递增B. 的一个对称中心为C. 当时，的值域为D. 先将函数的图象的纵坐标不变，横坐标缩短为原来的倍，再向左平移个单位后得到函数的图象13、下列式子中结果为的有( )．，，C，第II卷（共98分）二、填空题（本大题共4小题，每小题4分，共16分）14、=______15、已知是锐角，，且，则为16、已知，则夹角为钝角时，取值范围为17、三、解答题：（本大题共6小题，共82分. 解答应写出文字说明、证明过程和演算步骤.）18、（本题12分）已知向量，．设与的夹角为，求的值；若与垂直，求实数的值19、（本题14分）如图，在平面直角坐标系xOy上，点，点B在单位圆上，．若点，求的值；若，，求．20、（本题14分）已知，，．若，求证：；设，若，求，的值．21、（本题14分）已知函数，．求函数的单调区间；若把向右平移个单位得到函数，求在区间上的最小值和最大值．22、（本题14分）在三角形ABC中，，，，D是线段BC上一点，且，F为线段AB 上一点．设，，设，求；求的取值范围；若F为线段AB的中点，直线CF与AD相交于点M，求．23、（本题14分）已知，，，，求的值．第一次月考数学试题参考答案1---5 D A D C B 6---10 A B C C D 11、 BCD 12、 ABD 13、ABCD14、零向量或且 17、18、解：向量，，则，且，；设与的夹角为，则；若与垂直，则，即，所以，解得．19、解：由点，，，．；，．，，解得，，．．20、解：由，，则，由，得．所以即；由得，得：．因为，所以．所以，，代入得：．因为所以．所以，．21、解：，下面分为单调增区间和单调减区间进行求解，令，得，可得函数的单调增区间为，；令，得，可得函数的单调减区间为，．若把函数的图象向右平移个单位，得到函数的图象，，，，．故在区间上的最小值为，最大值为1．22、解：，而，，；在三角形ABC中，，，，，，，不妨设，，式，，；为线段AB的中点，，不妨设，，，，A、M、D三点共线，，即，，解得，，．23、解：，，，，，，即．。

山东省夏津一中2019届高三数学10月月考试题文时间：120分钟满分：150分一．选择题（本大题共12个小题，每题5分共60分）1命题“x R,|x|x40”的否定是（）A．x R,|x|x40B．x R,|x|x40C．x R,|x|x40D．x R,|x|x402. 已知P{x|x24x30},Q{y|y42x}，则P Q（）A．(1,2)B．[0,2)C．(1,2]D．[0,1)3. 设，，，则（）a log0.2b log0.2c 1.20.2d 1.10.20.1 1.1A．c d a b B．c a d b C．d c a b D．a b d c 114. 若，则下列结论不正确的是()a bb aA.a2 ＜b 2 B .ab＜b2 C. 2 D.|a|＋|b|＞|a＋a bb|15 A ABC BD DA,CB a,CA b CD()在中，点D在边A B上，且设，则221 12A．B．a b a b33334334C．D．a b a b55556. “a0”是“函数f(x)|(ax1)x|在区间(0,)上单调递增”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件7. 函数f(x)= 的图象的大致形状是（）- 1 -8．将函数2sin(x)sin(x)的图象向左平移（>0)个单位，所得图象对应的函y36数恰为奇函数，则的最小值为( )A. B. C. D.612439. 在C中，角A,B,C所对的边分别为a,b,c，若sin B 2sin A cos C 0,则当cos Ba取最小值时，=（）c3A．2 B. 3C． D.32210.若0,，且sin 2cos 2，则tan等于（）21A．3 B.2C． D.213x21(x0)函数f(x)11．若方程f(x)=-x+a又且只有两个不等的实数根，则实数a的f (x1)(x0)取值范围为（）A．,0 B.0,1C．,1 D.0, 12. 已知定义在R上的偶函数y f(x)的导函数为f'(x)，函数f(x)满足：当x0时，2017x f'(x)f(x)1f(1)=2018f x，且.则不等式的解集是（）()1xA ．-1,1B.-，1C ．-1, 00,1D.-, -11，+二．填空题(本大题共 4小题，每小题 5分，共 20分) 13. 记a 的前 n 项和.若 S2a1，则 S_____________．S 为数列nnnn6- 2 -14.若向量AB与AC的夹角为，|AB |2,|AC |3,AMABAC (,R)，且3AMBC，则．15．已知实数x,y满足约束条1x yz2x y()2x y40的最小值为______件，则y 116. 已知函数f(x)满足f (1x)f(x 1)f(x 1)(x R)，且当0x 1时f cos x f(x)0[1,3](x)2x 1，则方程在上的所有根之和为_______二．解答题(17题10分，18-22题每题12分，共80分)17. （本小题满分10分）22设命题p：，命题，如果实数.满足120q:函数log(ax2ax 1)的定义域是Ra a ap q p q a是假命题，是真命题，求的取值范围.a,是两个单位向量．b18.. （本小题满分12分）已知（1）若3a2b 3，试求3a b的值；（2）若a,b的夹角为60o，试求向量m 2a b与n 2b a的夹角的余弦.19．（本小题满分12分）在ABC中，a,b,c分别为内角A,B,C所对的边，已知a cos A R，其中R为ABC外接圆的半径，S为ABC的面积，22243.a cb S3（1）求sin C；（2）若a b23，求ABC的周长．120．已知函数f x2a ln x2ax.x（1）当a2时，求函数f x的极值；（2）当a0时，求函数f x的单调增区间.21. （本小题满分12分）- 3 -某健身器材厂研制了一种足浴气血养身机,具体原理是在足浴盆的中心右侧离中心x厘米(0x20)处安装了臭氧发生孔,产生臭氧对双脚起保健作用.根据检测发现,该臭氧发生孔工作时会对泡脚的舒适度起到干扰作用,通过研究发现臭氧发生孔工作时,对左脚的干扰度与x2成反比,比例系数为4；对右脚的干扰度与400x2成反比,比例系数为k，且当x102时,对左脚和右脚的干扰度之和为0.065.（1）请将臭氧发生孔工作时对左脚和右脚的干扰度之和y表示为x的函数；（2）求臭氧发生孔工作时对左脚和右脚的干扰度之和y的最小值．22．（本小题满分12分）已知函数f x)ln x．(1xax（1）若f(x)0对x0恒成立，求a的值；12n1（2）求证：（）．ln(n1)...n N*23n222- 4 -高三理科数学参考答案：71-5 BAADB6-10 ACACB 11-12CC13.14.615. 216.11617解：若命题 p 是真时，由a 2 a 12得或a -4 a 3若命题 q 是真时，ax 2 ax 1>0① 当 a =0时，不等式成立。

山东省德州一中 高三上学期1月月考理科数学试题【试卷综析】本试卷是高三理科试卷，以基础知识为载体，以基本能力测试为主导，重视学生科学素养的考查.知识考查注重基础、兼顾覆盖面.试题重点考查：集合、导数、函数模型、函数的性质、三角函数，数列，椭圆，立体几何等；考查学生解决实际问题的综合能力，是份比力好的试卷.一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合标题问题要求的. 【题文】1.集合{}{}{}3,2,,4a A B a b A B A B==⋂=⋃，则，则等于A. {}234，，B. {}341，，C.{}0,1,2,3D.{}1,2,3,4【知识点】集合及其运算A1 【答案】A【解析】由A B ⋂={4},则24a=，a=2,b=4,所以A B ⋃={}234，，。

【思路点拨】按照交集求出a,b 值，再求并集。

【题文】2.已知a R ∈，则“2a a <”是“1a <”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 【知识点】充分条件、必要条件A2 【答案】A【解析】由2a a <得0<a<1,是1a <的充分而不必要条件。

【思路点拨】先求出a 的范围求出充分而不必要条件。

【题文】3.正项等比数列{}n a 的公比为2，若21016a a =，则9a 的值是A.8B.16C.32D.64【知识点】等比数列及等比数列前n 项和D3 【答案】C【解析】由21016a a ==26a ，64a =，3962a a =⨯=32.【思路点拨】按照等比数列的性质得。

【题文】4.已知命题4:0,4p x x x ∀>+≥：命题001:,22x q x R +∃∈=.则下列判断正确的是 A.p 是假命题B.q 是真命题C.()p q ∧⌝是真命题D.()p q ⌝∧是真命题【知识点】命题及其关系A2【答案】C【解析】由重要不等式得4:0,4 p x xx∀>+≥正确，122x=得01x=-不正确，则()p q∧⌝是真命题【思路点拨】先判断p,q的真假，再求结果。