GL1-小结与习题课
- 格式:ppt
- 大小:277.00 KB
- 文档页数:14


第 1 页 共 3 页选修1-1选修1-2知识点总结复习第三部分 导数及其应用1、函数()f x 从1x 到2x 的平均变化率:()()2121f x f x x x --2、导数定义:()f x 在点0x 处的导数记作xx f x x f x f y x x x ∆-∆+='='→∆=)()(lim)(00000;.3、函数()y f x =在点0x 处的导数的几何意义是曲线()y f x =在点()()00,x f x P 处的切线的斜率.4、常见函数的导数公式:①'C 0=;②1')(-=n n nx x ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a x x ln )('=;⑥xx e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 5、导数运算法则:()1 ()()()()f x g x f x g x '''±=±⎡⎤⎣⎦; ()2 ()()()()()()f x g x f x g x f x g x '''⋅=+⎡⎤⎣⎦;()3()()()()()()()()()20f x f x g x f x g x g x g x g x '⎡⎤''-=≠⎢⎥⎡⎤⎣⎦⎣⎦.6、在某个区间(),a b 内,若()0f x '>,则函数()y f x =在这个区间内单调递增; 若()0f x '<,则函数()y f x =在这个区间内单调递减.7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时:()1如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; ()2如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值.8、求函数()y f x =在[],a b 上的最大值与最小值的步骤是:()1求函数()y f x =在(),a b 内的极值;第 2 页 共 3 页()2将函数()y f x =的各极值与端点处的函数值()f a ,()f b 比较,其中最大的一个是最大值,最小的一个是最小值.9、导数在实际问题中的应用:最优化问题。

webgl笔记-1.模型视图矩阵和投影矩阵最近在学习WebGL技术的过程中,我补充了⼀些原本了解甚少的计算机图形学知识。
如果有同学和我⼀样,没有系统学过计算机图形学就接触了3D图形编程,⽽对不少略为艰深的概念有困惑,希望这些笔记能够帮助你。
模型矩阵我们必须考虑,当空间中点的位置会发⽣变化的时候,其坐标如何变化。
考虑三种基本的变换:平移、旋转和缩放。
“变换”的含义就是,将点的初始位置的坐标P映射到平移、旋转、缩放后的位置坐标P’,即:$$\begin{bmatrix}x\\y\\z\end{bmatrix}\rightarrow\begin{bmatrix}{x}'\\{y}'\\{z}'\end{bmatrix}$$平移变换是最简单的变换:$$\begin{bmatrix}{x}'\\{y}'\\{z}'\end{bmatrix}=\begin{bmatrix}x\\y\\z\end{bmatrix}+\begin{bmatrix}t_{x}\\t_{y}\\t_{z}\end{bmatrix}$$旋转变换有⼀些复杂,先看在⼆维平⾯上的旋转变换:很容易得到:$$\begin{matrix}x'=x\cos\theta-y\sin\theta\\y'=x\sin\theta+y\sin\theta\end{matrix}$$矩阵形式的表达更加简洁,后⾯⼤多使⽤这种形式:$$\begin{bmatrix}x'\\ y'\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$$推⼴到三维空间中:点绕z轴旋转:$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 &1\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$点绕x轴旋转:$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta &\cos\theta\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$点绕y轴旋转:$$\begin{bmatrix}x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}\cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin\theta & 0 &\cos\theta\end{bmatrix}\begin{bmatrix}x\\ y\\ z\end{bmatrix}$$绕指定的任意轴旋转变换是由⼏个绕坐标轴旋转变换和平移变换效果叠加⽽成的,后⽂会有详细叙述。

1.4小结与练习学习目标1、进一步理解因式分解的概念,能灵活的运用各种来进行因式分解。
2、通过因式分解综合练习,提高观察、分析问题的能力;通过应用因式分解方法进行简便运算、解决实际问题,体会到生活中数学无处不在。
学习重点综合应用各种方法进行因式分解。
学习难点根据多项式的特点,选择适当的方法分解因式。
【一】本章知识要点〔1〕、因式分解的定义:把一个含字母的多项式化为几个整式的乘积形式,叫做把这个多项式因式分解(分解因式).〔2〕、因式分解的方法和步骤:因式分解的常用方法有:1.提公因式法;2.运用公式法;3.分组分解法;4.十字相乘法。
把一个多项式因分解的步骤可简记为:一提二套三分组四交叉.〔3〕、因式分解应注意的几个问题:1.根据因式分解的定义,把一个多项式因式分解的结果必须是几个整式的乘积形式。
2.对一个多项式因式分解,首要考虑的方法是提公因式法,注意准确地找到多项式各项的公因式。
假设多项式各项没有公因式,那么根据多项式特点,选用平方差公式或完全平方公式,或其他方法。
3.对一个多项式的因式分解一定要进行到每一个因式不能再分解为止。
4.因式分解的结果中,如果有因式还能计算化简的,一定要计算化简。
因式分解的结果中,假设有常数因式,一定要写到最前面;假设有相同的因式,一定要写成幂的形式。
【二】合作交流1、选择题:(1)以下多项式的分解因式,正确的选项是〔〕A 、)34(391222xyz xyz y x xyz -=-B 、)2(363322+-=+-a a y y ay y a C 、)(22z y x x xz xy x -+-=-+-D 、)5(522a a b b ab b a +=-+ (2)以下各式不能继续因式分解的是〔〕A 、31x -B 、22y x -C 、2)(y x +D 、a a 22+(3)以下多项式中能用平方差公式分解因式的是〔〕A 、22)(b a -+B 、mn m 2052-C 、22y x --D 、92+-x(4)能用完全平方公式分解的是〔〕A 、2242x ax a ++B 、2244x ax a +--C 、2412x x ++-D 、2444x x ++(5)满足0106222=+-++n m n m 的是〔〕A 、3,1==n mB 、3,1-==n mC 、3,1=-=n mD 、3,1-=-=n m2、把以下多项式分解因式:〔1〕)3()3(2a a -+-〔2〕xy y x 81622-+ 〔3〕352281216xz z xy y x -+- 〔4〕n m n m -+-3922.3、在251010222++-+-b a b ab a 中,96=a ,92=b 。
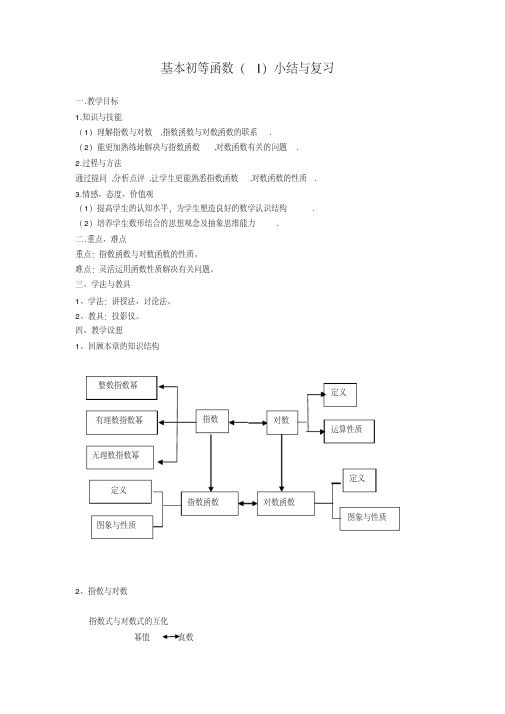

习题课:动量和能量的综合应用课后篇巩固提升必备知识基础练1.如图所示,木块A 、B 的质量均为2 kg,置于光滑水平面上,B 与一轻质弹簧的一端相连,弹簧的另一端固定在竖直挡板上,当A 以4 m/s 的速度向B 撞击时,由于有橡皮泥而粘在一起运动,那么弹簧被压缩到最短时,弹簧具有的弹性势能大小为( )A.4 JB.8 JC.16 JD.32 J、B 在碰撞过程中动量守恒,碰后粘在一起共同压缩弹簧的过程中机械能守恒。
由碰撞过程中动量守恒得m A v A =(m A +m B )v ,代入数据解得v=m A vAm A +m B=2 m/s,所以碰后A 、B 及弹簧组成的系统的机械能为12(m A +m B )v 2=8 J,当弹簧被压缩至最短时,系统的动能为0,只有弹性势能,由机械能守恒得此时弹簧的弹性势能为8 J 。
2.(多选)如图甲所示,在光滑水平面上,轻质弹簧一端固定,物体A 以速度v 0向右运动压缩弹簧,测得弹簧的最大压缩量为x 。
现让弹簧一端连接另一质量为m 的物体B (如图乙所示),物体A 以2v 0的速度向右压缩弹簧,测得弹簧的最大压缩量仍为x ,则( )A.A 物体的质量为3mB.A 物体的质量为2mC.弹簧达到最大压缩量时的弹性势能为32mv 02 D.弹簧达到最大压缩量时的弹性势能为m v 02,设物体A 的质量为M ,由机械能守恒定律可得,弹簧压缩量为x 时弹性势能E p =12Mv 02;对题图乙,物体A 以2v 0的速度向右压缩弹簧,A 、B 组成的系统动量守恒,弹簧达到最大压缩量时,A 、B 二者速度相等,由动量守恒定律有M×(2v 0)=(M+m )v ,由能量守恒定律有E p =12M×(2v 0)2-12(M+m )v 2,联立解得M=3m ,E p =12M×v 02=32mv 02,A 、C 正确,B 、D 错误。
3.如图所示,带有半径为R 的14光滑圆弧的小车的质量为m 0,置于光滑水平面上,一质量为m 的小球从圆弧的最顶端由静止释放,求小球离开小车时,小球和小车的速度。
酸化缓速剂GL-1的合成及在低黏低阻缓速酸液中的应用酸化缓速剂GL-1的合成及在低黏低阻缓速酸液中的应用一、引言酸化缓速剂广泛应用于石油开采行业中,通过控制酸性液体的反应速率,实现对储层的有效酸化处理。
本文旨在介绍一种名为GL-1的酸化缓速剂的合成方法,并探讨其在低黏低阻缓速酸液中的应用。
二、酸化缓速剂GL-1的合成方法1. 原料准备合成GL-1所需要的原料主要包括二甲基二(十二烷基硅烷基)氯硅烷、三丙氨乙醇、去离子水和氢氧化钠。
2. 反应步骤(1) 将二甲基二(十二烷基硅烷基)氯硅烷加入反应釜中,加热至80°C左右。
(2) 在搅拌下,将三丙氨乙醇缓慢滴加到反应釜中,保持温度在80°C左右。
(3) 在反应结束后,将产物冷却至室温,并用去离子水稀释。
(4) 使用氢氧化钠调节溶液的酸碱度,直至达到适宜的PH值。
三、酸化缓速剂GL-1在低黏低阻缓速酸液中的应用1. 酸液配方优化将GL-1与其他酸液成分进行配方优化,以得到低黏低阻的缓速酸液。
通常,低黏低阻的酸液可以通过添加界面活性剂,如适量的十二烷基苯磺酸钠、十二烷基苯磺酸钠等来实现。
2. 复杂储层酸化处理酸化缓速剂GL-1在低黏低阻缓速酸液中的应用使其特别适合用于复杂储层的酸化处理。
这些储层通常有较高的渗透率和多孔结构,而且容易受到溶液的侵彻和渗透。
使用低黏低阻缓速酸液,可以控制酸液的扩散速率,提高处理效果。
3. 缓慢酸化作用GL-1作为酸化缓速剂,可以控制酸液的反应速率,使其在储层中形成缓慢酸化作用。
这种缓慢酸化能够有效地防止酸液的过早失效,并保证酸液在储层中的长时间留存,从而提高酸化处理的效果。
4. 温度适应性GL-1在低黏低阻缓速酸液中的应用还具有良好的温度适应性。
无论是在高温还是低温条件下,GL-1都能保持稳定性和活性,确保酸液的长时间有效作用。
四、总结酸化缓速剂GL-1的合成方法简单,成本低廉。
其在低黏低阻缓速酸液中的应用可以实现对复杂储层的有效酸化处理。
1 过梁:GL-11.1 基本资料1.1.1 工程名称:工程一1.1.2 过梁类型:钢筋混凝土过梁砌体种类:烧结普通砖1.1.3 施工质量控制等级:B 级水泥砂浆砌筑砌块的强度等级:MU10砂浆的强度等级:M51.1.4 过梁的净跨 Ln = 1800mm 过梁梁端的实际支承长度 a = 240mm截面宽度 b = 240mm 截面高度 h = 180mm1.1.5 墙体宽度 bw = 240mm 墙体高度 hw = 2100mm每平米墙体的自重标准值 pk = 5.4kN/m1.1.6 混凝土强度等级:C25 fc = 11.94N/mm ft = 1.27N/mm1.1.7 钢筋抗拉强度设计值 fy = 300N/mm Es = 200000N/mm受拉纵筋最小配筋率ρmin = 0.20% 箍筋抗拉强度设计值 fyv = 210N/mm纵筋合力点至近边的距离 as = 40mm1.2 过梁的荷载1.2.1 墙体荷载对砖砌体,当过梁上的墙体高度 hw ≥ Ln/3 = 600mm 时,应按高度为 Ln/3 墙体的均布自重采用。
gki = 0.6*5.4 = 3.24kN/m1.2.2 过梁自重过梁截面面积 A = b * h = 0.24*0.18 = 0.043mgki =γ * A = 27*0.043 = 1.17kN/m1.3 砌体的计算指标1.3.1 按砌体规范第 3.2.1 条确定的砌体强度设计值砌体的抗压强度设计值 f = 1.5MPa1.3.2 按砌体规范第 3.2.3 条,下列情况的各类砌体,其砌体强度设计值应乘以调整系数γa:(1)、当砌体用水泥砂浆砌筑时,对第 3.2.1 条各表中的数值,γa = 0.9γa = 0.9 f = 1.35MPa1.4 受弯承载力1.4.1 弯矩标准值 Mki永久均布荷载作用下: Mk1 = 3.24*(1.05*1.8)^2/8 = 1.447kN·m永久均布荷载作用下: Mk2 = 1.166*(1.05*1.8)^2/8 = 0.521kN·m1.4.2 弯矩设计值 M由可变荷载效应控制的弯矩组合值 M(L) = 2.36kN·m由永久荷载效应控制的弯矩组合值 M(D) = 2.66kN·m弯矩设计值 M = Max{M(L), M(D)} = 2.66kN·m1.4.3 受弯承载力计算As = 65mm ρ = 0.19% ρmin = 0.20% As,min = 86mm1.5 受剪承载力1.5.1 剪力标准值 Vki永久均布荷载作用下: Vk1 = 3.24*1.8/2 = 2.9kN永久均布荷载作用下: Vk2 = 1.166*1.8/2 = 1.0kN1.5.2 剪力设计值 V由可变荷载效应控制的剪力组合值 V(L) = 4.8kN由永久荷载效应控制的剪力组合值 V(D) = 5.4kN剪力设计值 V = Max{V(L), V(D)} = 5.4kN1.5.3 受剪承载力计算当 S = 200mm 时,Asv = 0 (V≤0.7×ft×b×ho),Dmin = 6、Smax = 2001.6 局部受压ψ * No + Nl ≤η * γ * f * Al 砌体规范式 5.2.4-11.6.1 梁端有效支承长度 ao = 10 * (hc / f) ^ 0.5 = 10*(180/1.35)^0.5 = 115mm1.6.2 局部受压面积 Al = ao * b = 0.115*0.24 = 0.028m1.6.3 影响砌体局部抗压强度的计算面积 Ao = (a + bw) * bw = (0.24+0.24)*0.24 = 0.115m 1.6.4 砌体局部抗压强度提高系数γ = 1 + 0.35 * (Ao / Al - 1) ^ 0.5 = 1+0.35*(0.115/0.028-1)^0.5 = 1.62当γ > 1.25 时,取γ = 1.251.6.5 梁端底面压应力图形完整系数η,对于过梁可取η = 1.01.6.6 验算过梁下砌体局部受压承载力时,可不考虑上层荷载的影响。