大学物理同步训练第2版第六章真空中的静电场详解
- 格式:pdf
- 大小:1.05 MB
- 文档页数:8
x解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取 dq1dl , dq 在带电圆环轴线上x 处产生的场强大小为dEdq4(x R )根据电荷分布的对称性知,E y E z 0dE x dE cos1 xdq4(x 2 R 2)'2第6章 真空中的静电场 习题及答案1.电荷为 q 和 2q 的两个点电荷分别置于 x 1m 和x 1m 处。
一试验电荷置于 x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷 q 0位于点电荷 q 的右侧,它受到的合力才可能为0,所以2qq o qq o2 24 n o (x 1)4 n o (x 1)故 x 3 2 22.电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2这种平衡与三角形的边长有无关系 ?解:(1)以A 处点电荷为研究对象,由力平衡知, q 为负电荷,所以(2)与三角形边长无关。
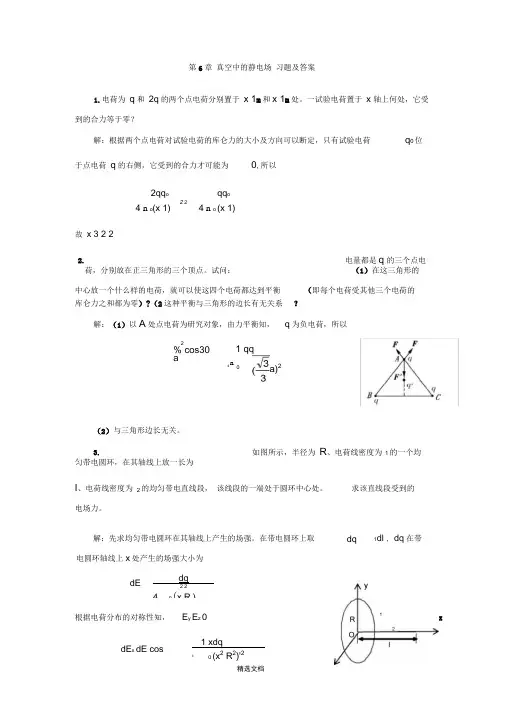
3.如图所示,半径为 R 、电荷线密度为 1的一个均匀带电圆环,在其轴线上放一长为I 、电荷线密度为 2的均匀带电直线段, 该线段的一端处于圆环中心处。
求该直线段受到的电场力。
2% cos30 a1 qqa)24nE xsin d4n 0R 2n 0R式中:为dq 到场点的连线与x 轴负向的夹角。
---------------------------------- 3dq4 o (x 2 R 2) 2x 1 2 R 1R x40 (x 2 R 2)'2 2 0(x 2 R 2)'2下面求直线段受到的电场力。
在直线段上取 dq2dx , dq受到的电场力大小为dF E x dq1 2只 ------- x ———dx2 0(x 2 R 2),2方向沿x 轴正方向。

第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷 q 位于点电荷 0q 的右侧,它受到的合力才可能为0,所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放 一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解:(1)以A 处点电荷为研究对象,由力平衡知,q 为负电荷,所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
3.如图所示,半径为R 、电荷线密度为1的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1,dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知,yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中:为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2,dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
4.一个半径为R的均匀带电半圆环,电荷线密度为。
求:(1)圆心处O点的场强;(2)将此带电半圆环弯成一个整圆后,圆心处O点场强。

②场强的方向:规定正电荷在电场中某点的受力 方向为该点的场强方向.(说明:电场中某点的场强与放入场中的试探电 荷无关,而是由该点的位置和场源电何来决定. )考纲要览考向预测电场是电学的基础,也是高考的重点.电荷守恒定律,库仑定律,电场线性质,带电体在静电场中的平衡,带电 粒子在匀强电场中的偏转等是考查热点•这部分内容一般采用选择题或计算题进行考查.也可与力学、磁场等知识进行综合.第1课时库仑定律电场强度基础知识回顾1 .电荷、电荷守恒⑴自然界中只存在两种电荷: 正电荷、负电荷.使 物体带电的方法有摩擦起电、接触起电、感应起电.⑵静电感应:当一个带电体靠近导体时,由于电 荷间的相互吸引或排斥,使导体靠近带电体的一端带 异号电荷,远离带电体的一端带同号电荷.⑶电荷守恒:电荷即不会创生,也不会消失,它 只能从一个物体转移到另一个物体,或从物体的一部 分转移到另一部分;在转移过程中,电荷总量保持 ______________ 变.(一个与外界没有电荷交换的系统, 电荷的代数和保持不变)⑷元电荷:指一个电子或质子所带的电荷量,用r . -19e 表示.e =x 10 C2 .库仑定律⑴真空中两个点电荷之间相互作用的电场力,跟 它们电荷量的乘积成正比,跟它们的距离的二次方成 其中k 为静电力常量,k =x 10 9N nf/c 2⑵成立条件① 真空中(空气中也近似成立),②点电荷, 电体的形状和大小对相互作用力的影响可以忽略不 计.(对带电均匀的球, r 为球心间的距离).3 .电场强度⑴电场:带电体的周围存在着的一种特殊物质, 它的基本性质是对放入其中的电荷有力的作用,这种 力叫电场力.电荷间的相互作用就是通过电场发生作 用的•电场还具有能的性质.⑵电场强度 E :反映电场强弱和方向的物理量,曰牛日 疋矢量.① 定义:放入电场中某点的试探电荷所受的电场 力F 跟它的电荷量q 的比值,叫该点的电场强度.单位:V/ m ,N / C第六章静电场即带即:②场强的方向:规定正电荷在电场中某点的受力 方向为该点的场强方向.(说明:电场中某点的场强与放入场中的试探电 荷无关,而是由该点的位置和场源电何来决定. )反比,作用力的方向在它们的连线上.即: Fkq^ 2 r⑶点电荷的电场强度: E = kp ,其中Q 为场 r—7源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导体 球间的库仑力时,要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧,此时r 将大于两球球 心间的距离.3 .库仑定律是长程力,当r 0时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的【解析】 设两小球的电量分别为 q 与7q ,则原来相 距r 时的相互作用力F k 空® 7k-q 2r r⑴若两球电性相同.相互接触时两球电量平均分布、每球带电量为-一也 4q ,放回原处后的相互作用22亠斗4q 4q qF 1 16 力为:F 1 k r 2 16k 笃,所以——r rF7(2)若两球电性不同.相互接触时电荷先中和再平分, 每球带电量为 四一q 3q ,放回原处后的相互作用22力为:F 1 k 3^ 9心,所以旦? r r F 7【答案】C D.【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1- 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0两球刚好发生接触, 然后两球又分别向相反方向运动.设A B 返回M N两点所经历的时间分别为t 1、t 2.则( )图 6- 1- 1A. t 1 t 2 B .t 1 t 2C. t 1 t 2 t °D. t 1t 2t °【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小r相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 出发点.相撞后因电量均分使得库仑力4q 4q(F k 2)变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次 返回时t 1 t 2 t 0 【答案】C二、与电场力相关的力学综合的问题电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电A.4B. C.16【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度: E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777Q源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该 点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电 场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、 负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导.体.球间的库仑力时, 要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧 , 此时 r 将大于两球球 心间的距离.3. 库仑定律是长程力, 当 r 0 时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例 1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的距r 时的相互作用力F k q [q 7k q 2r 2 r 2 ⑴若两球电性相同.相互接触时两球电量平均分布、 每球带电量为 q 7q 4q , 放回原处后的相互作用224q 4qqF 1 16 力为:F 1 k 216k 2 , 所以 1rrF 7(2)若两球电性不同. 相互接触时电荷先中和再平分, 每球带电量为7q q 3q ,放回原处后的相互作用22力为: F 1 k 3q 23q 9k q 22 , 所以 F 1 9r 2 r 2 F7【 答案 】 C 、 D .【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1 — 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0 两球刚好发生接触, 然后两球又分别向相反方向运动.设A 、B 返回 M 、 N两点所经历的时间分别为 t 1 、 t 2. 则( )图 6— 1— 1A . t 1t 2B . t 1 t 2C .t 1t 2 t 0 D . t 1t 2 t 0【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小 r 相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 岀 发 点 . 相 撞 后 因 电 量 均 分 使 得 库 仑 力4q 4q(F k 2 )变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次返回时t 1 t 2t 0【 答案 】 C二、与电场力相关的力学综合的问题【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度:E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起 产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 77779D 16【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度: E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777Q源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该 点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电 场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、 负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导.体.球间的库仑力时, 要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧 , 此时 r 将大于两球球 心间的距离.3. 库仑定律是长程力, 当 r 0 时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例 1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的距r 时的相互作用力F k q [q 7k q 2r 2 r 2 ⑴若两球电性相同.相互接触时两球电量平均分布、 每球带电量为 q 7q 4q , 放回原处后的相互作用224q 4qqF 1 16 力为:F 1 k 216k 2 , 所以 1rrF 7(2)若两球电性不同. 相互接触时电荷先中和再平分, 每球带电量为7q q 3q ,放回原处后的相互作用22力为: F 1 k 3q 23q 9k q 22 , 所以 F 1 9r 2 r 2 F7【 答案 】 C 、 D .【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1 — 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0 两球刚好发生接触, 然后两球又分别向相反方向运动.设A 、B 返回 M 、 N两点所经历的时间分别为 t 1 、 t 2. 则( )图 6— 1— 1A . t 1t 2B . t 1 t 2C .t 1t 2 t 0 D . t 1t 2 t 0【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小 r 相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 岀 发 点 . 相 撞 后 因 电 量 均 分 使 得 库 仑 力4q 4q(F k 2 )变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次返回时t 1 t 2t 0【 答案 】 C二、与电场力相关的力学综合的问题【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度:E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起 产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 77779D 16【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度: E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777Q源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该 点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电 场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、 负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导.体.球间的库仑力时, 要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧 , 此时 r 将大于两球球 心间的距离.3. 库仑定律是长程力, 当 r 0 时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例 1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的距r 时的相互作用力F k q [q 7k q 2r 2 r 2 ⑴若两球电性相同.相互接触时两球电量平均分布、 每球带电量为 q 7q 4q , 放回原处后的相互作用224q 4qqF 1 16 力为:F 1 k 216k 2 , 所以 1rrF 7(2)若两球电性不同. 相互接触时电荷先中和再平分, 每球带电量为7q q 3q ,放回原处后的相互作用22力为: F 1 k 3q 23q 9k q 22 , 所以 F 1 9r 2 r 2 F7【 答案 】 C 、 D .【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1 — 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0 两球刚好发生接触, 然后两球又分别向相反方向运动.设A 、B 返回 M 、 N两点所经历的时间分别为 t 1 、 t 2. 则( )图 6— 1— 1A . t 1t 2B . t 1 t 2C .t 1t 2 t 0 D . t 1t 2 t 0【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小 r 相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 岀 发 点 . 相 撞 后 因 电 量 均 分 使 得 库 仑 力4q 4q(F k 2 )变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次返回时t 1 t 2t 0【 答案 】 C二、与电场力相关的力学综合的问题【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度:E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起 产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 77779D 16【解析】 设两小球的电量分别为 q 与7q ,则原来相⑶点电荷的电场强度: E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777Q源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该 点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电 场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、 负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导.体.球间的库仑力时, 要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧 , 此时 r 将大于两球球 心间的距离.3. 库仑定律是长程力, 当 r 0 时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例 1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的距r 时的相互作用力F k q [q 7k q 2r 2 r 2 ⑴若两球电性相同.相互接触时两球电量平均分布、 每球带电量为 q 7q 4q , 放回原处后的相互作用224q 4qqF 1 16 力为:F 1 k 216k 2 , 所以 1rrF 7(2)若两球电性不同. 相互接触时电荷先中和再平分, 每球带电量为7q q 3q ,放回原处后的相互作用22力为: F 1 k 3q 23q 9k q 22 , 所以 F 1 9r 2 r 2 F7【 答案 】 C 、 D .【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1 — 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0 两球刚好发生接触, 然后两球又分别向相反方向运动.设A 、B 返回 M 、 N两点所经历的时间分别为 t 1 、 t 2. 则( )图 6— 1— 1A . t 1t 2B . t 1 t 2C .t 1t 2 t 0 D . t 1t 2 t 0【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小 r 相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 岀 发 点 . 相 撞 后 因 电 量 均 分 使 得 库 仑 力4q 4q(F k 2 )变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次返回时t 1 t 2t 0【 答案 】 C二、与电场力相关的力学综合的问题⑶点电荷的电场强度:E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起 产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777⑶点电荷的电场强度: E = k 2,其中Q 为场r 2电场力可以和其它力平衡,也可以和其它力一起产生加速度,因此这类问题实质上仍是力学问题,仍 是按力学问题的基本思路来解题,只不过多了一个电C.A.B. 7777源电荷,E 为场中距Q 为r 的某点处的场强大小•对 于求均匀带电的球体或球壳外某点的场强时, r 为该 点到球心的距离.⑷电场强度的叠加:当存在多个场源电荷时,电 场中某点的场强为各个点电荷单独在该点产生的电场 强度的矢量和.⑸电场线:为形象描述电场而引入的假想曲线. ① 电场线从正电荷或无限远岀发,终止于无限远 或负电荷.② 电场线不相交,也不相切,更不能认为电场就 是电荷在电场中的运动轨迹.③ 同一幅图中,场强大的地方电场线较密,场强 小的地方电场线较疏.⑹匀强电场:电场中各点场强大小处处相等,方 向相同,匀强电场的电场线是一些平行的等间距的平 行线.重点难点例析一、电荷守恒、库仑定律的理解1. 两个完全相同的金属球接触后, 所带正、 负电 荷先"中和"然后"平均分配"于两球. 分配前后正、 负电荷之和不变.2.当求两个导.体.球间的库仑力时, 要考虑电荷的重新分布,例:当两球都带正电时,电荷相互非斥而 使电荷主要分布于两球的外侧 , 此时 r 将大于两球球 心间的距离.3. 库仑定律是长程力, 当 r 0 时,带电体不能 看成质点,库仑定律不再适用.4. 微观粒子间的库仑力远大于它们之间的万有引 力,当计算微观粒子间的相互作用时可忽略粒子间的 万有引力.5. 计算库仑力时,先将电荷量的绝对值代入进行 计算,然后根据电性来判断力的方向.【例 1】 两个半径相同的金属小球,带电量之比为 1 : 7,相距为r (可视为点电荷),两者相互接触后再 放回原来的位置上,则相互作用力可能为原来的距r 时的相互作用力F k q [q 7k q 2r 2 r 2 ⑴若两球电性相同.相互接触时两球电量平均分布、 每球带电量为 q 7q 4q , 放回原处后的相互作用224q 4qqF 1 16 力为:F 1 k 216k 2 , 所以 1rrF 7(2)若两球电性不同. 相互接触时电荷先中和再平分, 每球带电量为7q q 3q ,放回原处后的相互作用22力为: F 1 k 3q 23q 9k q 22 , 所以 F 1 9r 2 r 2 F7【 答案 】 C 、 D .【点拨】本题的计算渗透着电荷守恒的思想,即正负 电荷的总和分配前后保持不变.拓展如图6- 1 — 1,A B 是两个完全相同的带电金属 球,它们所带的电荷量分别为 +3Q 和+5Q 放在光滑绝 缘的水平面上..若使金属球A 、B 分别由M N 两点以 相等的动能相向运动,经时间 t 0 两球刚好发生接触, 然后两球又分别向相反方向运动.设A 、B 返回 M 、 N两点所经历的时间分别为 t 1 、 t 2. 则( )图 6— 1— 1A . t 1t 2B . t 1 t 2C .t 1t 2 t 0 D . t 1t 2 t 0【解析】两球电量虽不同,但其相互作用力总是等大 反向(F k 3q 25q ),故AB 两球靠近时加速度大小 r 相等,又两球具有相同的质量、相同的初动能,由此 可知两球初速度相同,所以相同时间内两球的位移大 小一定相同,必然在连线中点相遇,又同时返回岀发 点.由动量观点看,系统动量守恒,两球的速度始终 等值反向,也可得岀结论:两球必将同时返回各自的 岀 发 点 . 相 撞 后 因 电 量 均 分 使 得 库 仑 力4q 4q(F k 2 )变大,排拆时加速度(相比之前r同一位置处)变大.因而运动时间将变小.所以再次返回时t 1 t 2t 0【 答案 】 C二、与电场力相关的力学综合的问题。






第六章 真空中的静电场1、电量为-5×10-9 C 的试验电荷放在电场中某点时,受到 20×10-9 N 的向下的力,求该点的电场强度大小和方向。
解:由q E F = 得C N q F E /4105/1020/99-=⨯-⨯==--方向向上2、一个带负电荷的质点,在电场力作用下从A 点 经C 点运动到B 点,其运动轨迹如图所示.已知质点运动的速率是递减的,试定性画出电场E的方向。
解:速率是递减→τa 为负→切向力与v相反做曲线运动→有n a →受合力方向如图→即电场E-的方向3、一均匀静电场,电场强度()j i E 600400+=V ·m -1,求点a (3,2)和点b (1,0)之间的电势差U ab .(点的坐标x ,y 以米计) 解:⎰⋅=baab l d E U)()600400(⎰+⋅+=baj dy i dx j i +=⎰13400dx ⎰2400dy=-2×103 V4、如图所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度.解:设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为λ=q / L ,在x 处取一电荷元d q = λd x = q d x / L ,它在P 点的场强: ()204d d x d L qE -+π=ε()204d x d L L xq -+π=ε 2分总场强为 ⎰+π=Lx d L xL q E 02)(d 4-ε()d L d q +π=04ε 3分方向沿x 轴,即杆的延长线方向.-qEO5、A 、B 为真空中两个平行的“无限大”均匀带电平面,已知两平面间的电场强度大小为E 0,两平面外侧电场强度大小都为E 0/3,方向如图.求A 、B 两平面上的电荷面密度σA , σB . 解:设电荷面密度为σA , σB由场强迭加原理,平面内、外侧电场强度由σA , σB 共同贡献: 外侧:32200E BA=+-εσεσ内侧:0022E BA=+εσεσ联立解得:3/200E Aεσ-= 3/400E Bεσ=6、半径为R 的半球面置于场强为E的均匀电场中,其对称轴与场强方向一致,如图所示.求通过该半球面的电场强度通量。

⼤学物理课后答案第六章真空中的静电场习题66-1 解:以x 轴上的点电荷Q 作为研究对象,其受q 的作⽤⼒具有对称性,所受合⼒沿x 轴,即F=qx Q x F F F 2+=其中:202)2(4a Q F Q πε=;02045cos 4aqQ F qx πε=所以:02020245cos 42)2(4a qQ a Q F πεπε+=令上式为零可得:q Q 22-= 6-2 解:据分析,3E 只能取垂直⽅向,D 点的场强如图所⽰:xa1q q 3(1)D 点的合场强的垂直分量为零,0cos 32=+E E θ,即32co s E E -=θ带⼊点电荷场强关系式,得203220422)2(41aq a q πεπε-=?C q 9310*9.9--= (2)22201021?+=+=a q a q E E E πεπε =m v /10*79.16-6-3 长l =15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m -1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强.解:如题6-3图所⽰(1)在带电直线上取线元x d ,其上电量q d 在P 点产⽣场强为20)(d π41d x a xE P -=λε 222)(d π4d x a xE E l l P P -==?-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ0.5-?=λ1m C -?, 5.12=a cm 代⼊得21074.6?=P E 1C N -? ⽅向⽔平向右(2)同理 2220d d π41d +=x xE Q λε⽅向如题8-6图所⽰由于对称性?=l Qx E 0d ,即Q E只有y 分量,∵ 22222220dd d d π41d ++=x x xE Qyλε22π4d d ελ?==lQyQy E E ?-+2223222)d (d l l x x2220d4π2+=l lελ0.5-?=λ1cm C -?, 15=l cm ,5d 2=cm 代⼊得21096.14?==Qy Q E E 1C N -?,⽅向沿y 轴正向6-4 ⼀个半径为R 的均匀带电半圆环,电荷线密度为λ,求环⼼处O 点的场强.解: 如6-4图在圆上取?Rd dl =题6-4图λλd d d R l q ==,它在O 点产⽣场强⼤⼩为 20π4d d R R E ε?λ=⽅向沿半径向外则 ??ελd sin π4sin d d 0RE E x ==ελπd cos π4)cos(d d 0RE E y -=-=积分RR E x 000π2d sin π4ελελπ==0d cos π400=-=?ελπRE y∴ RE E x 0π2ελ=6-5解:如图所⽰,将半球⾯分割成⽆数半径不等环⾯与X 轴垂直的细圆环,图中圆环所带电荷量θθπλλγd ds dq sin 22==,该带电细圆环在O 点产⽣的电场强度为E d =()i xdqy x o224123+επ由⼏何关系,θγcos =x θγs i n =yγ222=+yx有 E d=()i xdq y x o224123+επ = επo41i dθθπσθγγγsin 2cos 2=i d oθθθσεcos sin 2球⼼处的电场强度:i i d E d E o oεεσθθθσπ4cos sin 220===??6-6解:将球⾯沿垂直于X轴的⽅向分割成⽆数半径不等的细圆环,圆中阴影环的带电荷量为:ααπσσRd R ds dq sin 2==在P 点的场强为:θααπσπεθπεαcos sin 241cos 42020r Rd R r d dE ?==(1)⽅向沿X 轴正⽅向(设0>α)如图由余弦定理θc o s 2222xy r x R -+=得: xrR r x 2cos 222-+=θ(2)⼜由余弦定理得:(3)式两边微分得:ααd Rx rdr sin 22= 得:xr dd R =ααs i n(4)将(1)、(2)、(3)式代⼊(1)式得:dr rR x x R rx R r x xr Rrdr E d 2222022220142241-+=-+?=εσπσπε(1)球⾯外(R x >)任⼀点P 的场强值+-= ?-+==x R x R x qdr r R x x R dE E 2022220414πεεσ(2)球⾯内:(R x <)+-=?-+==x R x R dr r R x x R dE E 01422220εσ6-7均匀带电的细线弯成正⽅形,边长为l ,总电量为q .求这正⽅形轴线上离中⼼为r 处的场强E .解: 如6-7图⽰,正⽅形⼀条边上电荷4q在P 点产⽣物强P E d ⽅向如图,⼤⼩为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=π4d 22220l r l l r E P ++=ελP Ed 在垂直于平⾯上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题6-7图由于对称性,P 点场强沿OP ⽅向,⼤⼩为2)4(π44d 422220l r l r lrE E P ++==⊥ελE P ++=ε⽅向沿OP6-8如题6-8)图所⽰,在点电荷q 的电场中取半径为R 的圆平⾯.q 在该平⾯轴线上的A 点处,求:通过圆平⾯的电通量.解:题6-8图∵通过半径为R 的圆平⾯的电通量等于通过半径为22x R +的球冠⾯的电通量,球冠⾯积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq=[221xR x +-]*关于球冠⾯积的计算:见题8-9(c)图ααα)cos 1(π22α-=r6-9 解: ⾼斯定理0d ε∑?=?q S E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E15r =cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=3.98≈1C N -?,⽅向沿半径向外. 50r =cm 时,3π4∑=ρq -3(外r )内3r∴ ()33204π3 1.064πr r E r ρε-=≈外内 1C N -? 沿半径向外. 6-10 解:由⾼斯定理得:= dv s d E Sρε0球体内: E(r)? 4πr 2='rr k 041πεr d r ''2=4r k επ r e kr r E24)(ε= ,0球体外:4202414)(R R r d r r k r r E Rεππεπ=''?'=2044)(r rkR r Eε= (r>R ) 6-11 半径为1R 和2R (2R >1R )的两⽆限长同轴圆柱⾯,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: ⾼斯定理0d ε∑?=q S E s取同轴圆柱形⾼斯⾯,侧⾯积rl S π2=则 rl E S E Sπ2d =??对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >题6-12图6-12 两个⽆限⼤的平⾏平⾯都均匀带电,电荷的⾯密度分别为1σ和2σ,试求空间各处场强.解: 如题6-12图⽰,两带电平⾯均匀带电,电荷⾯密度分别为1σ与2σ,两⾯间, n E)(21210σσε-=1σ⾯外, n E)(21210σσε+-= 2σ⾯外, n E)(21210σσε+= n:垂直于两平⾯由1σ⾯指为2σ⾯.6-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去⼀块半径为r <R 的⼩球体,如题8-13图所⽰.试求:两球⼼O 与O '点的场强,并证明⼩球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀⼩球的组合,见题6-13图(a).(1) ρ+球在O 点产⽣电场010=E,ρ- 球在O 点产⽣电场'dπ4π3430320OO r E ερ=∴ O 点电场'd33030OO r E ερ= ; (2) ρ+在O '产⽣电场'd π4d 3430301OO E ερπ=' ρ-球在O '产⽣电场002='E∴ O ' 点电场 003ερ='E'OO题6-13图(a) 题6-13图(b)(3)设空腔任⼀点P 相对O '的位⽮为r',相对O 点位⽮为r (如题6-13(b)图)E PO =,3ερr E O P '-=' ,∴ 0003'3)(3ερερερdOO r r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.6-15解:将这⼀平⾯看作是由⼀系列环带所组成,取以O 为圆⼼,半径为r, 宽度为dr 的环带作为⾯元,该⾯元所带电量为rdrds dq πσσ2=?=rdr dq πσ2=该带电圆环在其轴线上P 点处的电场强度E d的⽅向沿X 轴正向,其⼤⼩为2322023220)(2)(41r x rdrx r x xdqdE +??=+?=εσπε做积分可得轴线上P 点的总场强:+2122023220)(2)(2x R xr x rdr x E R +?=+?=?∞εσεσ6-16解:① aqa q a q a q U 0002334πεπεπεπε-=-+-+=② aqQQ U U A 0023)(πε-=?-=∞题6-17图6-17 如题6-17图所⽰,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另⼀正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场⼒作的功.解: 如题6-17图⽰0π41ε=O U 0)(=-RqR q0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=6-18 如题6-18图所⽰的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中⼼O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产⽣的场强互相抵消,取θd d R l =则θλd d R q =产⽣O 点Ed 如图,由于对称性,O 点场强沿y 轴负⽅向题6-18图θεθλππcos π4d d 222R E E y R 0π4ελ=[)2sin(π-2sin π-]R0π2ελ-=(2) AB 电荷在O 点产⽣电势,以0=∞U===AB200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产⽣ 2ln π40 2ελ=U半圆环产⽣ 0034π4πελελ==R R U ∴ 0032142ln π2ελελ+=++=U U U U O 6-19解:⑴如图所⽰,建⽴坐标V ala x dx U la ap 300105.2ln 44?=+==?+πελπελV x b dxU l l Q 32220103.44?=+=?-πελ6—22解:⑴在板状圆环上取半径为为1r ,宽为dr 的环带作为⾯元,该⾯元的带电量为:rdr rdr ds dq πσπσσ22=?==该带电圆环在轴线上P 点的电势为21)(2)(42221220r x rdr r x dq dU +?=+=πσπε积分可得点P 的总电势+-+=+=+=212222022021222|2)(22121R x R x r x r x rdr U R R R R P εσεσεσ⑵⼩球在下落过程中,电场⼒和重⼒都在对⼩球做功,我们对⼩球应⽤质点动能定理,则有221mv A A =+电重下落过程中重⼒的做功为:mgx A =重电场⼒能做的功为:)(00U U q l d E q A p p--=?-=?电由第⼀问得的结果可知,环⼼处的电势为:)(21200R R U -=εσ由此可知,)(2)(2121221200R x R x R R q U U q A p +++--=--=εσ电将上述结果带⼊动能定理中得由此可得⼩球到环⼼O 处的速度为()121222212022??+++--+=R x R x R R gx v εσ6—23解:参考6—19题i xa ar x U E x z dzU p p aap 220220244+?=??-=+=?-πελπεσ。
第六章真空中的静电场习题选解6-1 三个电量为 q 的点电荷各放在边长为r 的等边三角形的三个顶点上,电荷f 1Q(Q 0) 放在三角形的重心上。
为使每个-q 负电荷受力为零, Q 之值应为多大? f 2解:以三角形上顶点所置的电荷( q)Q-q -q为例,其余两个负电荷对其作用力的合力为 f1,方向如图所示,其大小为题 6-1 图f1 2q 22 cos303q22 4r4 0r中心处 Q 对上顶点电荷的作用力为f2 ,方向与 f1 相反,如图所示,其大小为f2Qq3Qq43 24 0 r203r由 f1f2,得Q3 q 。
36-2 在某一时刻,从 U 238的放射性衰变中跑出来的粒子的中心离残核 Th 234的中心为 r 9.0 10 15 m 。
试问:(1)作用在粒子上的力为多大?( 2)粒子的加速度为多大?解:(1)由反应23892 U23490Th+ 24 He ,可知粒子带两个单位正电荷,即Q12e 3.2 10 19 CTh 离子带 90 个单位正电荷,即Q290e 144 10 19 C它们距离为 r 9.0 10 15 m由库仑定律可得它们之间的相互作用力为:Q Q 2 9 3.2 10 19 144 10 19F 1 (9.0 10 ) 512N 4 0r 2 (9.0 10 15 ) 2(2) 粒子的质量为:m2(m p m n )2 (1.67 10 271.67 10 27) 6.68 10 27Kg 由牛顿第二定律得:a F 512 7.66 1028m s 2m 6.68 10 276-3 如图所示,有四个电量均为 q 10 6 C 的点电荷,分别放置在如图所示的 1,2,3,4 点上,点 1 与点 4 距离等于点1 与点2 的距离,长 1m ,第3 个电荷位于 2、4 两电荷连线中点。
求作用在第 3 个点电荷 上的力。
解:由图可知,第 3 个电荷与其它各题 6-3 图 电荷等距,均为 r2m 。