sps非参数检验K多个独立样本检验(KruskalWallis检验)案例解析
- 格式:doc
- 大小:182.50 KB
- 文档页数:5

spss-非参数检验-K多个独立样本检验
(Kruskal-Wallis检验)案例解析Kruskal-Wallis检验,也称为KW检验,是一种非参数检验方法,用于比较两个或多个独立样本的中位数是否相等。
它利用秩(等级)来进行统计分析,而不是直接使用原始数据。
假设有一个关于人们在不同饮料中的品尝体验的数据集。
数据集中包含了人们在红酒、白酒和啤酒中品尝的感受,包括甜度、酸度、苦度等。
现在想要比较这三种饮料在甜度方面的中位数是否有显著差异。
首先,对每种饮料的甜度进行排序,得到每个人的秩。
然后,将每个人的秩平均分到他们所对应的饮料中,得到每个饮料的平均秩。
接着,对这些平均秩进行比较。
如果红酒、白酒和啤酒的平均秩存在显著差异,则说明这三种饮料在甜度方面的中位数存在显著差异。
如果平均秩没有显著差异,则说明这三种饮料在甜度方面的中位数没有显著差异。
下面是一个具体的案例数据:
根据上述数据,我们可以计算出每种饮料的平均秩:
红酒: (2+1)/2 = 1.5
白酒: (4+3)/2 = 3.5
啤酒: (6+5)/2 = 5.5
然后对这些平均秩进行比较。
由于红酒的平均秩最小,白酒的平均秩次之,啤酒的平均秩最大,因此可以得出结论:这三种饮料在甜度方面的中位数存在显著差异,其中啤酒的甜度最高,白酒次之,红酒最低。
需要注意的是,KW检验的前提假设是各个样本是独立同分布的,且样本容量足够大。
如果样本不满足这些条件,可能会导致检验结果出现偏差。
此外,KW检验只能告诉我们是否存在显著差异,但不能告诉我们差异的具体原因。
如果想要了解更多信息,需要进行后续的统计分析。

多样本尺度参数的非参数检验
非参数统计方法是一种不基于数据分布假设的统计推断方法,因此适用于各种类型和
尺度的数据。
在研究中,我们经常需要对多个样本进行比较,这时就需要用到多样本尺度
参数的非参数检验方法。
本文将介绍多样本尺度参数的非参数检验方法,包括
Kruskal-Wallis检验、Friedman检验和Page趋势检验。
Kruskal-Wallis检验是一种用于比较三个或更多个独立样本的方法,它是一种秩和检验统计方法,基本思想是将数据合并为一个总体,然后根据秩次进行比较。
Kruskal-Wallis检验的零假设是各样本总体的位置参数相等,即它们来自相同的总体分布。
计算Kruskal-Wallis检验统计量的步骤如下:
1. 对所有样本的数据合并,并按照大小排序;
2. 计算每个样本的秩次和;
3. 计算秩次和的平方和;
4. 根据样本量和秩次和的平方和计算Kruskal-Wallis检验的统计量。
以上三种非参数检验方法都是基于秩和的统计方法,它们都不需要对数据的分布做出
假设,适用于各种类型和尺度的数据。
在研究中,我们需要根据具体情况选择合适的非参
数检验方法,以便对多个样本进行比较,并得出统计显著性结论。

2多独立样本Kr u s k a l-Wa llis检验的原理及其实证分析摘要:阐述了多独立样本Kruskal-Wallis检验的基本思想和如何构造K-W统计量,运用多独立样本Kruskal- Wallis检验方法进行了实例分析,并进行H检验的事后比较,给出应用Mathematica和SPSS 做出的相关图形。
关键词:Kruskal-Wallis检验;K-W统计量;Mathematica中图分类号:O212.7非参数检验在总体分布未知时有很大的优越性。
这时如果利用传统的假定分布已知的检验,就会产生错误甚至灾难。
非参数检验总是比传统检验安全。
但是在总体分布形式已知时,非参数检验就不如传统方法效率高。
这是因为非参数方法利用的信息要少些。
往往在传统方法可以拒绝零假设的情况,非参数检验无法拒绝。
但非参数统计在总体未知时效率要比传统方法高,有时要高很多。
是否用非参数统计方法,要根据对总体分布的了解程度来确定[1]。
笔者就K r uskal-Wal lis检验方法及其在经济研究中的应用进行分析,以期对经济分析领域的实证研究提供借鉴。
1多独立样本Kruskal-Wallis检验的基本思想多独立样本K r uskal-Wal lis检验(又称H检验)的实质上是两独立样本时的M ann-Whi tney U检验在多个独立样本下的推广,用于检验多个总体的分布是否存在显著差异。
其原假设是:多个独立样本来自的多个总体的分布无显著差异。
多独立样本K r uskal-Wal lis检验的基本思想是:首先,将多组样本数混合并按升序排序,求出各变量值的秩;然后,考察各组秩的均值是否存在显著差异。
如果各组秩的均值不存在显著差异,则认为多组数据充分混合,数值相差不大,可以认为多个总体的分布无显著差异;反之,如果各组秩的均值存在显著差异,则是多组数据无法混合,有些组的数值普遍偏大,有些组的数值普遍偏小,可认为多个总体的分布存在显著差异,至少有一个样本不同于其他样本。

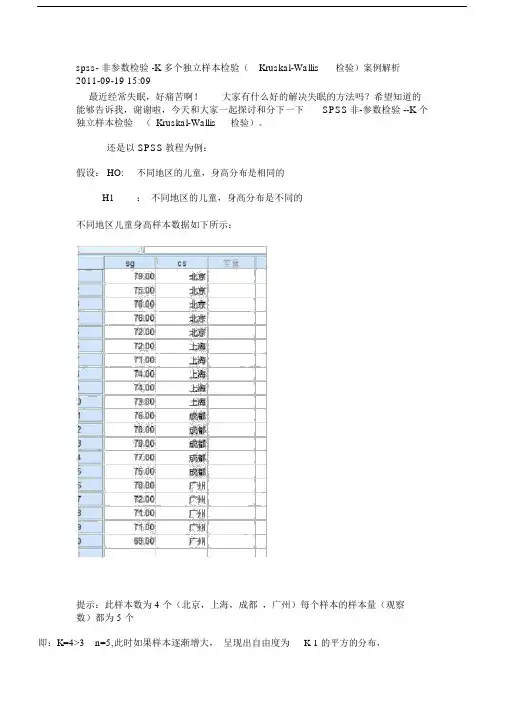
spss- 非参数检验 -K 多个独立样本检验(Kruskal-Wallis检验)案例解析2011-09-19 15:09最近经常失眠,好痛苦啊!大家有什么好的解决失眠的方法吗?希望知道的能够告诉我,谢谢啦,今天和大家一起探讨和分下一下SPSS非-参数检验 --K 个独立样本检验(Kruskal-Wallis检验)。
还是以 SPSS教程为例:假设: HO:不同地区的儿童,身高分布是相同的H1:不同地区的儿童,身高分布是不同的不同地区儿童身高样本数据如下所示:提示:此样本数为 4 个(北京,上海,成都,广州)每个样本的样本量(观察数)都为 5 个即:K=4>3 n=5,此时如果样本逐渐增大,呈现出自由度为K-1 的平方的分布,(即指:卡方检验)点击“分析”——非参数检验——旧对话框—— K 个独立样本检验,进入如下界面:将“周岁儿童身高”变量拖入右侧“检验变量列表”内,将“城市( CS)变量”拖入“分组变量”内,点击“定义范围” 输入“最小值”和“最大值”(这里的变量类型必须为“数字型”)如果不是数字型,必须要先定义或者重新编码。
在“检验类型”下面选择“秩和检验”(Kruskal-Wallis检验)点击确定运行结果如下所示:对结果进行分析如下:1:从“检验统计量a,b ”表中可以看出:秩和统计量为:13.900自由度为: 3=k-1=4-1下面来看看“秩和统计量”的计算过程,如下所示:假设“秩和统计量”为kw那么:其中: n+1/2为全体样本的“秩平均”Ri./ni为第i个样本的秩平均Ri. 代表第 i 个样本的秩和, ni 代表第 i 个样本的观察数)最后得到的公式为:北京地区的“秩和”为:秩平均 * 观察数( N) = 14.4*5=72上海地区的“秩和”为:8.2*5=41成都地区的“秩和”为:15.8*5=79广州地区的“秩和”为: 3.6*5=18接近 13.90 (由于中间的计算,我采用四舍五入,丢弃了部分数值,所以,会有部分误差)2:“检验统计量 a,b ”表中可以看出:“渐进显著性为0.003 ,由于0.003<0.01所以得出结论:H1:不同地区的儿童,身高分布是不同的。
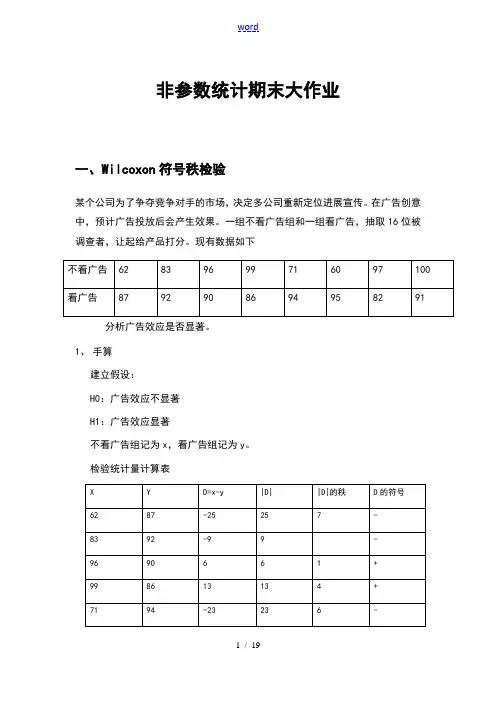
非参数统计期末大作业一、Wilcoxon符号秩检验某个公司为了争夺竞争对手的市场,决定多公司重新定位进展宣传。
在广告创意中,预计广告投放后会产生效果。
一组不看广告组和一组看广告,抽取16位被调查者,让起给产品打分。
现有数据如下分析广告效应是否显著。
1、手算建立假设:H0:广告效应不显著H1:广告效应显著不看广告组记为x,看广告组记为y。
检验统计量计算表60 95 -35 35 8 -97 82 15 15 5 +100 91 9 9 +由表可知:根据n=8,T+和T-中较大者T-=23.5,查表得,T+的右尾概率为0.230到0.273,在显著性水平下,P值显然较大,故没有理由拒绝原假设,明确广告效应不显著。
2、Spss在spss中输入八组数据〔数据1〕:选择非参数检验中的两个相关样本检验对话框中选择Wilcoxon,输出如下结果〔输出1〕:RanksN Mean Rank Sum of Ranks 看广告 - 不看广告Negative Ranks 4aPositive Ranks 4bTies 0cTotal 8a. 看广告 < 不看广告b. 看广告 > 不看广告RanksN Mean Rank Sum of Ranks看广告 - 不看广告Negative Ranks 4aPositive Ranks 4bTies 0cTotal 8a. 看广告 < 不看广告c. 看广告 = 不看广告由上表,负秩为4,正秩也为4,同分的情况为0,总共8。
负秩和为12.5,正秩和为23.5,与手算结果一致Test Statistics b看广告 - 不看广告Z aAsymp. Sig. (2-tailed) .441a. Based on negative ranks.b. Wilcoxon Signed Ranks Test由上表,Z为负,说明是以负秩为根底计算的结果,其相应的双侧渐进显著性结果为0.441,明显大于0.05,因此在的显著性水平下,没有理由拒绝原假设,即明确广告效应不显著,与手算的结论一致。

第十三章非参数统计分析统计推断方法大体上可分为两大类。
第一大类为参数统计方法。
常常在已知总体分布的条件下,对相应分布的总体参数进行估计和检验。
第二大类为非参数统计方法,着眼点不是总体参数,而是总体的分布情况或者样本所在总体分布的位置/形状。
非参数统计方法大约有8种,可被划分为两大类,处理各种不同情形的数据。
单样本情形:检验样本所在总体的位置参数或者分布是否与已知理论值相同。
①Chi-Square过程:针对二分类或者多分类资料例题1:见书P243。
检验样本分布情况是否与已知理论分布相同。
运用卡方检验过程。
②Binomial过程:针对二分类资料或者可转变为二分类问题的资料。
例题2 :见书P246。
检验某一比例是否与已知比例相等,运用二项分布过程。
练习:质量监督部门对商店里面出售的某厂家的西洋参片进行了抽查。
对于25包写明为净重100g的西洋参片的称重结果为(单位:克),数据见非参数。
Sav,人们怀疑厂家包装的西洋参片份量不足,要求进行检验。
③Runs过程:用于检验样本序列是否是随机出现的。
二分类资料和连续性资料均可。
游程检验:游程的含义:假定下面是由0和1组成的一个这种变量的样本:0 0 0 0 1 1 1 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0其中相同的0(或相同的1)在一起称为一个游程(单独的0或1也算)。
这个数据中有4个0组成的游程和3个1组成的游程。
一共是R=7个游程。
其中0的个数为m=15,而1的个数为n=10。
游程检验的原理判断数据序列是否是真随机序列。
该检验的原假设为数据是真随机序列,备择假设为非随机序列,在原假设成立的情况下,游程的总数不应太多也不应太少。
例题3:见书P247。
检验样本数据是否是随机出现的。
例题4:从某装瓶机出来的30盒化妆品的重量(单位克),数据见非参数.sav,为了看该装瓶机是否工作正常。
提示:实际需要验证大于和小于中位数的个数是否是随机的(零假设为这种个数的出现是随机的)。

Kruskal-Wallis检验的使用技巧Kruskal-Wallis检验是一种非参数检验方法,用于比较三个以上独立样本的中位数是否相同。
在实际应用中,Kruskal-Wallis检验常常被用于比较不同组别的样本的总体中位数是否有显著差异。
本文将介绍Kruskal-Wallis检验的使用技巧,包括数据准备、假设检验和结果解释等方面。
数据准备在进行Kruskal-Wallis检验之前,首先需要进行数据的准备工作。
具体而言,需要收集三个以上独立样本的数据,并对数据进行整理和清理。
在整理数据的过程中,需要注意检查数据是否符合Kruskal-Wallis检验的前提条件,即数据应当是来自对称分布的总体。
如果数据不符合这一前提条件,可能需要进行数据变换或者选择其他适合的统计方法。
假设检验进行Kruskal-Wallis检验时,需要先建立相应的假设。
在Kruskal-Wallis检验中,零假设是各组总体的中位数相等,备择假设是各组总体的中位数不全相等。
接着,进行检验统计量的计算,并根据该统计量的分布情况,计算P值以得出检验结果。
通常情况下,P值小于显著性水平(通常为)时,可以拒绝零假设,认为各组总体的中位数有显著差异。
结果解释在得出Kruskal-Wallis检验的结果之后,需要进行相应的结果解释。
如果P 值小于显著性水平,可以拒绝零假设,认为各组总体的中位数有显著差异。
此时,可以进一步进行事后比较分析,以确定具体哪些组别之间存在差异。
如果P值大于显著性水平,则不能拒绝零假设,即无法得出各组总体中位数有显著差异的结论。
应用技巧在进行Kruskal-Wallis检验时,需要注意一些应用技巧。
首先,应当注意样本量的大小。
当样本量较小的时候,Kruskal-Wallis检验可能会失去一些效应,因此在这种情况下可能需要考虑其他检验方法。
其次,需要注意分组的合理性。
在进行Kruskal-Wallis检验之前,需要对分组变量进行合理的划分,以确保各组之间存在一定的差异性。

Kruskal-Wallis检验是一种用于比较三个以上独立样本的非参数检验方法。
它通常用于检验多组数据的总体中位数是否相等。
与方差分析和t检验不同,Kruskal-Wallis检验不要求数据满足正态分布和方差齐性的假设,因此在数据不满足这些假设的情况下,Kruskal-Wallis检验是一个非常有用的统计方法。
首先,我们来看一下Kruskal-Wallis检验的基本原理。
该检验的原假设是各组样本来自同一总体分布,备择假设是各组样本来自不同的总体分布。
在进行检验之前,需要计算每组样本的秩和,然后根据秩和来计算检验统计量H。
H的计算方法较为复杂,通常需要使用统计软件进行计算。
在进行Kruskal-Wallis检验时,需要注意以下几点使用技巧。
首先,要注意选择合适的样本量。
Kruskal-Wallis检验对样本量的要求相对较高,较小的样本量可能导致检验结果不够可靠。
通常来说,每组样本的数量应该不少于5才能保证检验结果的准确性。
其次,要注意选择合适的统计软件进行计算。
由于Kruskal-Wallis检验需要进行秩和的计算,手动计算比较繁琐,容易出错。
因此建议使用专业的统计软件如SPSS、R或者Python进行计算,以确保结果的准确性和可靠性。
另外,Kruskal-Wallis检验的结果需要进行解释时,需要注意检验统计量H 的概念。
H的值越大,意味着样本之间的差异越大,备择假设的支持程度越高。
通常来说,当H的值显著大于临界值时,可以拒绝原假设,认为各组样本来自不同的总体分布。
此外,Kruskal-Wallis检验的结果也可以进行后续的多重比较分析。
当检验的结果显著时,可以使用多重比较方法如Dunn检验或者Conover-Iman检验来进一步比较各组样本之间的差异。
这有助于更加深入地理解各组样本之间的差异性。
最后,要注意Kruskal-Wallis检验的局限性。
虽然Kruskal-Wallis检验在数据不满足正态分布和方差齐性假设时仍然能够进行有效的比较,但是它对于样本量的要求较高,而且在样本量较小的情况下可能会导致结果的不稳定。

Kruskal-Wallis检验的使用技巧Kruskal-Wallis检验是一种非参数统计方法,用来比较三个或三个以上独立样本的中位数是否有差异。
它可以用于比较非正态分布的数据,同时也适用于等间隔或等级数据。
在实际应用中,Kruskal-Wallis检验的使用技巧对于正确的数据分析和解释非常重要。
一、数据的准备在进行Kruskal-Wallis检验之前,首先需要准备好要分析的数据。
确保样本数据是独立且来自不同总体。
同时,要对数据进行合理的筛选和整理,例如剔除异常值和缺失值。
另外,要对数据的分布进行初步探索,了解其特点,这有助于选择合适的统计方法。
二、检验假设的设定在进行Kruskal-Wallis检验时,需要明确所做的假设。
零假设是各组总体的中位数相等,备择假设是至少有一对总体的中位数不相等。
根据所得的检验结果,可以对假设进行推断,从而对不同组别之间的差异进行分析。
三、检验的执行执行Kruskal-Wallis检验时,需要使用统计软件来进行计算。
在R、Python 等统计软件中,有专门的函数可以进行Kruskal-Wallis检验的计算。
在进行计算时,需要输入相应的参数,包括样本数据和置信水平等。
完成计算后,可以得到检验的结果,包括检验统计量和P值等。
四、结果的解释在得到Kruskal-Wallis检验的结果后,需要对结果进行解释。
首先要对检验统计量进行解释,了解其代表的含义。
同时,要根据P值来进行假设检验的判断,确定是否拒绝零假设。
在解释结果时,需要注意结合实际问题,对不同组别之间的差异进行合理的解释。
五、进一步分析Kruskal-Wallis检验的结果可以作为进一步分析的基础。
在得到检验结果后,可以进行多重比较或进一步的分析,以深入了解不同组别之间的差异。
同时,也可以进行回归分析或其他统计方法的应用,对结果进行深入挖掘。
六、注意事项在使用Kruskal-Wallis检验时,还需要注意一些常见的问题。
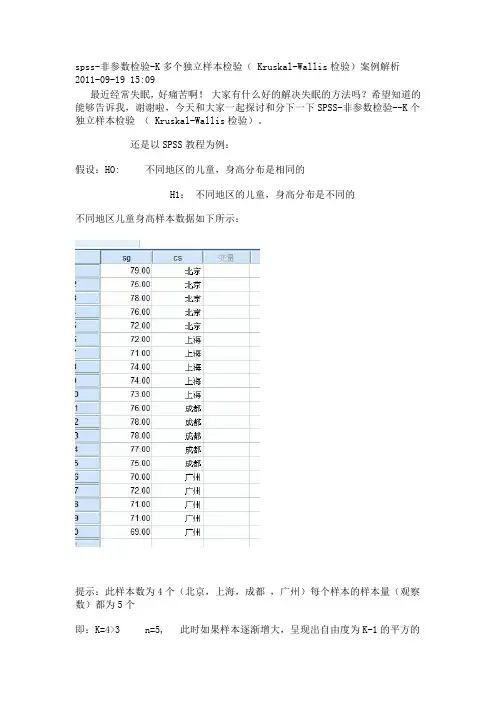
spss-非参数检验-K多个独立样本检验( Kruskal-Wallis检验)案例解析2011-09-19 15:09最近经常失眠,好痛苦啊!大家有什么好的解决失眠的方法吗?希望知道的能够告诉我,谢谢啦,今天和大家一起探讨和分下一下SPSS-非参数检验--K个独立样本检验( Kruskal-Wallis检验)。
还是以SPSS教程为例:假设:HO: 不同地区的儿童,身高分布是相同的H1:不同地区的儿童,身高分布是不同的不同地区儿童身高样本数据如下所示:提示:此样本数为4个(北京,上海,成都,广州)每个样本的样本量(观察数)都为5个即:K=4>3 n=5, 此时如果样本逐渐增大,呈现出自由度为K-1的平方的分布,(即指:卡方检验)点击“分析”——非参数检验——旧对话框——K个独立样本检验,进入如下界面:将“周岁儿童身高”变量拖入右侧“检验变量列表”内,将“城市(CS)变量” 拖入“分组变量”内,点击“定义范围” 输入“最小值”和“最大值”(这里的变量类型必须为“数字型”)如果不是数字型,必须要先定义或者重新编码。
在“检验类型”下面选择“秩和检验”( Kruskal-Wallis检验)点击确定运行结果如下所示:对结果进行分析如下:1:从“检验统计量a,b”表中可以看出:秩和统计量为:13.900自由度为:3=k-1=4-1下面来看看“秩和统计量”的计算过程,如下所示:假设“秩和统计量”为 kw 那么:其中:n+1/2 为全体样本的“秩平均” Ri./ni 为第i个样本的秩平均 Ri.代表第i个样本的秩和, ni代表第i个样本的观察数)最后得到的公式为:北京地区的“秩和”为:秩平均*观察数(N) = 14.4*5=72上海地区的“秩和”为:8.2*5=41成都地区的“秩和”为:15.8*5=79广州地区的“秩和”为:3.6*5=18接近13.90 (由于中间的计算,我采用四舍五入,丢弃了部分数值,所以,会有部分误差)2:“检验统计量a,b”表中可以看出:“渐进显著性为0.003,由于0.003<0.01 所以得出结论:H1:不同地区的儿童,身高分布是不同的(注:文档可能无法思考全面,请浏览后下载,供参考。
4.为研究烫伤后不同时间切痂对大鼠肝脏三磷酸腺苷(ATP)的影响,现将30只雄性大鼠随机分成3组,每组10只:A组为烫伤无切痂,B组为烫伤后24小时时切痂组,C组为烫伤后96小时切痂组,全部大鼠在烫伤168小时后测量其肝脏ATP含量。
试检验3组大鼠肝脏ATP总数均数是否相同。
表。
大鼠烫伤后肝脏ATP含量(mg)A组B组C组7.6711.2410.747.5311.708.688.3911.527.3210.1813.439.627.0314.198.7811.697.218.325.7412.879.856.7213.8911.317.0716.938.73解:由题意可知,通过分析多组独立样本的数据,推断样本来自多个总体的中位数或分布是否存在差异,所以可以选用多独立样本的Kruskal-Wallis检验数据的组织方式如下:Name Type Width Decimals Label Values Missing Columns Align Measure ATP Numeric82None None8Right Scale 分组Numeric82{1.00,A组None8Right ScaleATP分组17.67A组27.53A组38.39A组48.51A组510.18A组67.03A组711.69A组8 5.74A组9 6.72A组107.07A组1111.24B组1211.70B组1311.52B组1413.65B组1513.43B组1614.19B组177.21B组1812.87B组1913.89B组2016.93B组2110.74C组228.68C组237.32C组249.41C组259.62C组268.78C组278.32C组289.85C组2911.31C组308.73C组30只雄性大鼠的多独立样本非参数检验的基本操作步骤如下:(1)选择菜单:【Nnalyze】→【Nonparametric Tests】→【K Independent Samples】于是出现以下所示的窗口。
spss-非参数检验-K多个独立样本检验(-Kruskal-Wallis检验)案例解析spss-非参数检验-K多个独立样本检验( Kruskal-Wallis检验)案例解析2011-09-19 15:09最近经常失眠,好痛苦啊!大家有什么好的解决失眠的方法吗?希望知道的能够告诉我,谢谢啦,今天和大家一起探讨和分下一下SPSS-非参数检验--K 个独立样本检验( Kruskal-Wallis检验)。
还是以SPSS教程为例:假设:HO: 不同地区的儿童,身高分布是相同的H1:不同地区的儿童,身高分布是不同的不同地区儿童身高样本数据如下所示:提示:此样本数为4个(北京,上海,成都,广州)每个样本的样本量(观察数)都为5个即:K=4>3 n=5, 此时如果样本逐渐增大,呈现出自由度为K-1的平方的分布,(即指:卡方检验)点击“分析”——非参数检验——旧对话框——K个独立样本检验,进入如下界面:将“周岁儿童身高”变量拖入右侧“检验变量列表”内,将“城市(CS)变量” 拖入“分组变量”内,点击“定义范围” 输入“最小值”和“最大值”(这里的变量类型必须为“数字型”)如果不是数字型,必须要先定义或者重新编码。
在“检验类型”下面选择“秩和检验”( Kruskal-Wallis检验)点击确定运行结果如下所示:对结果进行分析如下:1:从“检验统计量a,b”表中可以看出:秩和统计量为:13.900自由度为:3=k-1=4-1下面来看看“秩和统计量”的计算过程,如下所示:假设“秩和统计量”为 kw 那么:其中:n+1/2 为全体样本的“秩平均” Ri./ni 为第i个样本的秩平均 Ri.代表第i个样本的秩和, ni代表第i个样本的观察数)最后得到的公式为:北京地区的“秩和”为:秩平均*观察数(N) = 14.4*5=72上海地区的“秩和”为:8.2*5=41成都地区的“秩和”为:15.8*5=79广州地区的“秩和”为:3.6*5=18接近13.90 (由于中间的计算,我采用四舍五入,丢弃了部分数值,所以,会有部分误差)2:“检验统计量a,b”表中可以看出:“渐进显著性为0.003,由于0.003<0.01 所以得出结论:H1:不同地区的儿童,身高分布是不同的。
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验是统计学中一种用于比较多个样本组之间差异的方法。
传统的参数检验方法假设数据符合特定的分布,而非参数检验方法不对数据的分布进行任
何假设,因此更适用于一些不满足正态分布的情况。
在进行多样本尺度参数的非参数检验之前,首先需要明确要比较的多个样本组的数量
和特征。
可以比较的多个样本组可以是两个以上,每个样本组内的数据可以是有序(连续),也可以是无序(离散)。
一种常见的多样本非参数检验方法是Kruskal-Wallis检验,也称为多样本方差分析的非参数版本。
Kruskal-Wallis检验的基本思想是比较多个样本组之间的中位数是否存在差异。
该检验的原假设是多个样本组的中位数相等,备择假设是多个样本组的中位数至少有
一个不相等。
Kruskal-Wallis检验的统计量是计算每个样本组的秩之和,然后与期望值进行比较。
如果计算得到的统计量值远大于期望值,则可以拒绝原假设,即认为多个样本组
之间存在差异。
需要注意的是,多样本尺度参数的非参数检验虽然不对数据的分布作出假设,但是仍
然对数据的独立性和随机性有一定的要求。
在进行检验之前,需要检查样本数据是否满足
这些要求。
多样本尺度参数的非参数检验是一种用于比较多个样本组之间差异的方法,常用的方
法有Kruskal-Wallis检验和Friedman检验。
在进行检验之前,需要明确要比较的多个样
本组的数量和特征,并对样本数据的独立性和随机性进行检查。
kruskal-wallis检验公式Kruskal-Wallis检验公式在统计学中,Kruskal-Wallis检验是一种用于比较三个或更多独立样本的非参数检验方法。
它可以判断多个样本是否来自同一总体分布。
Kruskal-Wallis检验公式的原理和应用将在本文中详细阐述。
我们要了解非参数检验的概念。
相对于参数检验,非参数检验不需要对总体的分布形态做出任何假设。
这使得非参数检验在样本数据缺乏正态分布或方差齐性的情况下仍然有效。
Kruskal-Wallis检验就是一种常用的非参数方法。
Kruskal-Wallis检验的原假设是:多个样本的中位数相等。
而备择假设则是:多个样本的中位数不全相等。
Kruskal-Wallis检验的计算步骤如下:1. 将所有样本的数据合并成一个大的数据集,并为每个数据点标记所属组别。
2. 对合并后的数据进行排序,计算每个数据点的秩次。
3. 计算每个组别的秩次和,得到各组的秩次和值。
4. 根据公式计算检验统计量H:H = (12 / (N(N+1))) * (∑(R_i^2 / n_i) - 3(N+1))其中,N为样本总数,R_i为第i组的秩次和,n_i为第i组的样本数。
5. 根据样本总数N和自由度k-1(k为组别数)查找Kruskal-Wallis检验的临界值。
6. 比较计算得到的检验统计量H和临界值,进行假设检验。
- 如果H小于临界值,则接受原假设,即多个样本的中位数相等。
- 如果H大于等于临界值,则拒绝原假设,即多个样本的中位数不全相等。
Kruskal-Wallis检验的应用广泛,特别适用于以下场景:1. 当样本数据不满足正态分布假设时,可以使用Kruskal-Wallis 检验替代方差分析(ANOVA)。
2. 当样本数据存在极端值或异常值时,Kruskal-Wallis检验更具鲁棒性。
3. 当样本数据的方差不满足齐性假设时,Kruskal-Wallis检验也是一种可靠的选择。
Kruskal-Wallis检验的使用技巧Kruskal-Wallis检验是一种非参数统计方法,用于比较两个或多个独立样本的中位数是否相等。
与方差分析不同,Kruskal-Wallis检验对数据的分布假设要求较低,适用于不满足正态分布的情况。
本文将从数据准备、检验原理和结果解释三个方面介绍Kruskal-Wallis检验的使用技巧。
数据准备在进行Kruskal-Wallis检验前,首先需要对数据进行准备。
假设我们有三组数据A、B和C,分别包含了不同组的观测值。
在进行检验前,需要对数据进行清洗和处理,确保数据的完整性和准确性。
同时,还需要对数据进行描述性统计分析,了解数据的分布情况和基本特征。
在进行描述性统计分析时,可以使用箱线图、直方图等方法对数据的分布进行可视化展示,以便更直观地了解数据的特点。
另外,还需要计算每组数据的中位数、四分位数等统计量,为后续的Kruskal-Wallis检验做准备。
检验原理Kruskal-Wallis检验的原理是基于秩和的比较。
首先,对所有的数据进行合并,并按照大小顺序进行排列,然后计算每个观测值的秩次。
接着,将每组数据对应的秩次相加,得到每组数据的秩和。
最后,比较各组数据的秩和是否存在显著差异,来判断各组数据的中位数是否相等。
在进行Kruskal-Wallis检验时,需要注意以下几点。
首先,需要设定显著性水平α,一般取。
其次,进行检验时需要进行多重比较校正,以避免多次检验导致的α错误累积。
最后,需要进行后续的事后分析,对检验结果进行解释和说明。
结果解释当进行Kruskal-Wallis检验后,我们可以得到相应的检验结果。
通常包括检验统计量H值和对应的显著性水平P值。
在进行结果解释时,首先需要对检验统计量H值进行比较,判断各组数据的秩和是否存在显著差异。
当H值显著小于α水平时,可以拒绝原假设,认为各组数据的中位数存在差异。
另外,在进行结果解释时,还需要进行事后分析。
Kruskal-Wallis H检验(多个独立样本)【详】-SPSS教程一、问题与数据某研究者认为工作年限多的人能更好地应对职场的压力。
为了验证这一假设,某研究招募了31名研究对象,调查了他们的工作年限,并测量了他们应对职场压力的能力。
根据工作年限,研究对象被分为4组:0-5年、6-10年、11-15年、>16年(变量名为working_time)。
利用Likert量表调查的总得分(CWWS得分)来评估应对职场压力的能力,分数越高,表明应对职场压力的能力越强(变量名为stress_score)。
部分数据如图1。
图1 部分数据二、对问题分析研究者想知道不同工作年限之间CWWS得分是否不同。
由于CWWS得分不服从正态分布(仅为模拟数据,实际使用时需要专业判断或结合正态性检验结果),因此可以使用Kruskal-Wallis H检验。
Kruskal-Wallis H检验(有时也叫做对秩次的单因素方差分析)是基于秩次的非参数检验方法,用于检验多组间(也可以是两组)连续或有序分类变量是否存在差异。
使用Kruskal-Wallis H test检验时,需要考虑以下3个假设。
假设1:有一个因变量,且因变量为连续变量或有序分类变量。
假设2:存在多个分组(≥2个)。
假设3:具有相互独立的观测值。
三、SPSS操作3.1 Kruskal-Wallis H检验在主界面点击Analyze→Nonparametric Tests→Independent Samples,出现Nonparametric Tests: Two or More Independent Samples对话框,默认选择Automatically compare distributions across groups。
如图2。
图2 Nonparametric Tests: Two or More Independent Samples点击Fields,在Fields下方选择Use custom field assignments,将变量stress_score放入Test Fields框中,将变量working_time放入Groups框中。
spss-非参数检验-K多个独立样本检验( Kruskal-Wallis检验)案例解析2011-09-19 15:09
最近经常失眠,好痛苦啊!大家有什么好的解决失眠的方法吗?希望知道的能够告诉我,谢谢啦,今天和大家一起探讨和分下一下SPSS-非参数检验--K个独立样本检验( Kruskal-Wallis检验)。
还是以SPSS教程为例:
假设:HO: 不同地区的儿童,身高分布是相同的
H1:不同地区的儿童,身高分布是不同的
不同地区儿童身高样本数据如下所示:
提示:此样本数为4个(北京,上海,成都,广州)每个样本的样本量(观察数)都为5个
即:K=4>3 n=5, 此时如果样本逐渐增大,呈现出自由度为K-1的平方的
分布,(即指:卡方检验)
点击“分析”——非参数检验——旧对话框——K个独立样本检验,进入如下界面:
将“周岁儿童身高”变量拖入右侧“检验变量列表”内,将“城市(CS)变量” 拖入“分组变量”内,点击“定义范围” 输入“最小值”和“最大值”(这里的变量类型必须为“数字型”)如果不是数字型,必须要先定义或者重新编码。
在“检验类型”下面选择“秩和检验”( Kruskal-Wallis检验)点击确定
运行结果如下所示:
对结果进行分析如下:
1:从“检验统计量a,b”表中可以看出:秩和统计量为:13.900
自由度为:3=k-1=4-1
下面来看看“秩和统计量”的计算过程,如下所示:
假设“秩和统计量”为 kw 那么:
其中:n+1/2 为全体样本的“秩平均” Ri./ni 为第i个样本的秩平均 Ri.代表第i个样本的秩和, ni代表第i个样本的观察数)
最后得到的公式为:
北京地区的“秩和”为:秩平均*观察数(N) = 14.4*5=72
上海地区的“秩和”为:8.2*5=41
成都地区的“秩和”为:15.8*5=79
广州地区的“秩和”为:3.6*5=18
接近13.90 (由于中间的计算,我采用四舍五入,丢弃了部分数值,所以,会有部分误差)
2:“检验统计量a,b”表中可以看出:“渐进显著性为0.003,由于
0.003<0.01 所以得出结论:
H1:不同地区的儿童,身高分布是不同的。