最小生成树 普里姆算法动画演示过程
- 格式:pptx
- 大小:121.88 KB
- 文档页数:2

1.实验目的(结出本次实验所涉及并要求掌握的知识点)最小生成树kruskal算法和prim算法的实现2.实验内容(结出实验内容具体描述)最小生成树kruskal算法和prim算法的实现3.算法描述及实验步骤(用适当的形式表达算法设计思想与算法实现步骤)数据结构:(MST也是图,所以实现用了邻接表表示)void union_v(LinkGraph*g,int index,int j){edgenode*p=g->adjlist[index].firstedge;g->adjlist[index].state=j;while(p){if(g->adjlist[p->adjvex].state!=j)union_v(g,p->adjvex,j);p=p->next;}}//(加边)对边按权排升序,每次考虑最小边,判断他两端是否是不同集合,是就把这边unionedges* Kruskal_MST(LinkGraph*g,int c){edges*head=creatEdgeList(g);edges*p;edgenode*s;int i,j;//判断每一条边,是否需要unionprintf("排序后的边结点:\n");p=head->next;while(p){printf("%d %d %d",p->leftv,p->rightv,p->weigth);printf("\n");p=p->next;}p=head->next;for(i=0;i<g->n;i++){g->adjlist[i].state=i;// 初始化点集,每个点都位于不同的连通分量}while(p){if(g->adjlist[p->leftv].state!=g->adjlist[p->rightv].state){// 只要这条边可以加入MST,就创建图结点// 把这些边当成图结点,创建图(MST树)p->flag=1;i=p->leftv;j=p->rightv;s=(edgenode *)malloc(sizeof(edgenode));s->adjvex=j;s->weigth=p->weigth;s->next=g->adjlist[i].firstedge; // 头插法创建邻接表g->adjlist[i].firstedge=s;if (c==0) { // c=0表示无向图s=(edgenode *)malloc(sizeof(edgenode));s->adjvex=i;s->next=g->adjlist[j].firstedge;g->adjlist[j].firstedge=s;}// union操作int m=g->adjlist[i].state;int n=g->adjlist[j].state;if(m<n){g->adjlist[j].state=m;union_v(g,j,m);}else{g->adjlist[i].state=n;}}p=p->next;}// 返回边结点链表return head;}Prim算法的实现:edges* Prim_MST(LinkGraph*g,int c){edges*head=creatEdgeList(g);edges*p;edgenode*s;int i,j;printf("排序后的边结点:\n");p=head->next;while(p){printf("%d %d %d",p->leftv,p->rightv,p->weigth);printf("\n");p=p->next;}for(i=0;i<g->n;i++){g->adjlist[i].state=0;// 初始化点集,所有点未在MST中}//从head的第一条边的顶点出发,逐个寻找需要union的int count=0;//用来记录目前MST中有多少个点p=head->next;g->adjlist[p->leftv].state=1;//选中第一个点加入count++;int l,r;while(count!=g->n){p=head->next;while(p){l=g->adjlist[p->leftv].state;r=g->adjlist[p->rightv].state;// 只有l,r一个在点集,一个不在点集,才unionif(l+r == 1){if(l*r==0){p->flag=1;count++;// 建MST树/图j=p->rightv;s=(edgenode *)malloc(sizeof(edgenode));s->adjvex=j;s->weigth=p->weigth;s->next=g->adjlist[i].firstedge; // 头插法创建邻接表g->adjlist[i].firstedge=s;if (c==0) { // c=0表示无向图s=(edgenode *)malloc(sizeof(edgenode));s->adjvex=i;s->next=g->adjlist[j].firstedge;g->adjlist[j].firstedge=s;}// union操作if(l==0)g->adjlist[p->leftv].state=1;else if (r==0)g->adjlist[p->rightv].state=1;break;}else{p=p->next;}}else{p=p->next;}}}// 返回边结点链表return head;}4.调试过程及运行结果(详细记录在调试过程中出现的问题及解决方法。

普里姆算法
普里姆算法(Prim's Algorithm)是用于求加权连通图的最小生成树的一种算法。
原理:从某个初始顶点开始,依次把它和它的最近邻居连起来,直到所有的顶点都连接起来。
每次选择最近的可连接的顶点加入到已有的最小生成树中,当所有的顶点都被收进集合中时,算法结束。
步骤:
1. 从一个顶点出发,将它加入最小生成树中;
2. 遍历未加入最小生成树中的顶点,找出与已加入最小生成树中的顶点相连接的边中权值最小的顶点,将其加入到最小生成树中;
3. 重复步骤2,直到所有顶点加入到最小生成树中,算法结束。

最⼩⽣成树Prim算法(邻接矩阵和邻接表) 最⼩⽣成树,普利姆算法.简述算法: 先初始化⼀棵只有⼀个顶点的树,以这⼀顶点开始,找到它的最⼩权值,将这条边上的令⼀个顶点添加到树中 再从这棵树中的所有顶点中找到⼀个最⼩权值(⽽且权值的另⼀顶点不属于这棵树) 重复上⼀步.直到所有顶点并⼊树中.图⽰:注:以a点开始,最⼩权值为1,另⼀顶点是c,将c加⼊到最⼩⽣成树中.树中 a-c在最⼩⽣成树中的顶点找到⼀个权值最⼩且另⼀顶点不在树中的,最⼩权值是4,另⼀个顶点是f,将f并⼊树中, a-c-f重复上⼀步骤,a-c-f-d, a-c-f-d-b, a-c-f-d-b-e.邻接矩阵的实现我⼜构建了⼀个邻接矩阵(prim_tree),将我们求出的最⼩⽣成树写⼊其中.我们还需要⼀个visited数组,来确定⼀个顶点是否已被纳⼊最⼩⽣成树中.1)初始化,visited数组,prim_tree节点信息,矩阵.1-11,41-55⾏2)将⼀个顶点并⼊树(prim_tree)中.以这个顶点开始,进⾏遍历寻找最⼩权值. 这⾥⽤了三层循环嵌套. i这⼀层的作⽤是遍历图的节点信息,我们要将所有节点都纳⼊树中. j这⼀层的作⽤是遍历树的节点信息.(我们是通过visited数组来确定⼀个节点是否属于最⼩⽣成树的,19⾏,if的作⽤) k这⼀层的作⽤是在j节点所在所在矩阵的⾏中找到最⼩权值. (注:j和k配合,找到树中的最⼩权值(最⼩权值的另⼀个节点没有被纳⼊树中,23⾏if的作⽤).j查找的节点信息的下标,但矩阵是正⽅形的,所以j既是节点信息的下标,⼜是该节点在矩阵中的列位置.⽽k则在j这⼀列查找最⼩权值.当j将树遍历⼀遍,这时会找到⼀个最⼩权值,这个最⼩权值的另⼀个顶点就是我们将要纳⼊树中的节点.)3)将上⾯获得的信息写⼊树中.(写⼊时也要判断该节点是否已被纳⼊树中.没有纳⼊树中的节点才会将其纳⼊树中.)1//最⼩⽣成树prim算法2static void init_prim(Graph * graph, Graph * prim_tree);3void Prim(Graph * graph, Graph * prim_tree)4 {5bool visited[graph->vertexs];6int i, j, k, h;7int power, power_j, power_k;89for ( i = 0; i < graph->vertexs; i++ )10 visited[i] = false;11 init_prim(graph, prim_tree);1213 visited[0] = true;14for ( i = 0; i < graph->vertexs; i++ )16 power = MAX_VALUE;17for ( j = 0; j < graph->vertexs; j++ )18 {19if ( visited[j] )20 {21for ( k = 0; k < graph->vertexs; k++ )22 {23if ( power > graph->arcs[j][k] && !visited[k] )24 {25 power = graph->arcs[j][k];26 power_j = j;27 power_k = k;28 }29 }30 }31 }32//min power33if ( !visited[power_k] )34 {35 visited[power_k] = true;36 prim_tree->arcs[power_j][power_k] = power;37 }38 }39 }4041static void init_prim(Graph * graph, Graph * prim_tree)42 {43int i, j;4445 prim_tree->vertexs = graph->vertexs;46for ( i = 0; i < prim_tree->vertexs; i++ )//初始化节点47 prim_tree->vertex[i] = graph->vertex[i];48for ( i = 0 ; i < prim_tree->vertexs; i++ )//初始化矩阵49 {50for ( j = 0; j < prim_tree->vertexs; j++ )51 {52 prim_tree->arcs[i][j] = MAX_VALUE;53 }54 }55 }上述代码适⽤于连通图.如果想运⾏这个程序,到/ITgaozy/p/5187483.html找源码,将上⾯的代码粘到⾥⾯就可以了.邻接表的实现算法和矩阵⼀样,只是由于数据结构不同,在代码上有些差别.static void init_prim(Graph * graph, Graph * prim_tree);void g_prim(Graph * graph, Graph * prim_tree){bool visited[graph->vertexs];int i, j, k;int power, pos;Arc_node * tmp;for ( i = 0; i < graph->vertexs; i++ )visited[i] = false;init_prim(graph, prim_tree);visited[0] = true;for ( i = 0; i < graph->vertexs; i++ ){power = INT_MAX;//limits.hfor ( j = 0; j < graph->vertexs; j++ ){if ( visited[j] ){tmp = graph->adjlist[j].next;while ( tmp != NULL ){if ( power > tmp->distance && !visited[tmp->pos] ){power = tmp->distance;pos = tmp->pos;k = j;}tmp = tmp->next;}}if ( !visited[pos] ){if ( prim_tree->adjlist[k].next == NULL ){prim_tree->adjlist[k].next = make_node(pos, power);}else{tmp = prim_tree->adjlist[k].next;while ( tmp->next != NULL )tmp = tmp->next;tmp->next = make_node(pos, power);}visited[pos] = true;}}}static void init_prim(Graph * graph, Graph * prim_tree){int i;for ( i = 0; i < graph->vertexs; i++ ){prim_tree->adjlist[i].info = graph->adjlist[i].info;prim_tree->adjlist[i].next = NULL;}prim_tree->vertexs = graph->vertexs;}到/ITgaozy/p/5187526.html⾥找到源码,将上述代码粘到源码中,就可以了.由于本⼈⽔平有限,不⾜之处还望⼤家不吝指教.。

简述prim算法的过程Prim算法是一种用于求解最小生成树的贪心算法,它把一个连通图分割成多个子图,使得每个子图都是一棵最小生成树,且这些子树的联合就是原连通图的最小生成树。
Prim算法是由安德鲁普里姆(Andrew.Prim)在1957年提出的,用于求解最短路径(解决连通度和权重问题)。
Prim算法一般步骤如下:(1)初始化:从图中任选一顶点,作为第一个顶点加入到最小生成树中;(2)循环:从剩余的顶点中,找到最小代价的边,将这条边加入到最小生成树中,并将这条边的顶点也加入到最小生成树中;(3)重复:重复步骤2,直到最小生成树中包括全部的顶点;(4)停止:最小生成树已经构造完成,停止算法的执行。
Prim算法是贪心算法的一种,它每次在可选的边中搜索代价最小的边,加入到最小生成树中,直至所有的顶点都在最小生成树中。
它的一般步骤可表示为:(1)从最小生成树中所有的顶点中,找出一个确定的顶点 u,它的邻居还未加入最小生成树;(2)从u的邻居v中,找出一个代价最小的边(u,v),将这条边加到最小生成树中;(3)将顶点v加入到最小生成树中;(4)重复步骤1到3,直到最小生成树中包括所有的顶点;深入分析Prim算法,我们可以发现它是一种贪心策略,它在设计上采用了“最优化原则”,即每次都选择代价最小的边加入到最小生成树中,而不管这个边是否有利于求解最小生成树的问题,因而贪心算法的实现对“最优策略”的选择是关键。
Prim算法的时间复杂度取决于边的存储结构,如果存储为邻接表,其时间复杂度为O(V2),如果存储为邻接矩阵,其时间复杂度为O(V2+E)。
其中,V为顶点数,E为边数。
Prim算法在现实生活中有着广泛的应用,比如电路设计时,需要求最小生成树,以此达到最短路径、最小花费的目的;另外,它还可以用于网络路由的设计,最小化网络的延迟;此外,它还可以用于求解旅行商问题,最小化客户的费用等等。
总之,Prim算法是一种有效的求解最小生成树的方法,它通过不断地在可选边中寻找代价最小的边,来构建最小生成树;在现实生活中,它也有着广泛的应用。

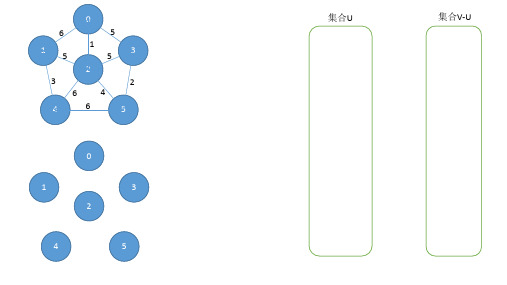
最⼩⽣成树---普⾥姆算法(Prim算法)和克鲁斯卡尔算法(Kruskal算法)最⼩⽣成树的性质:MST性质(假设N=(V,{E})是⼀个连通⽹,U是顶点集V的⼀个⾮空⼦集,如果(u,v)是⼀条具有最⼩权值的边,其中u属于U,v属于V-U,则必定存在⼀颗包含边(u,v)的最⼩⽣成树)普⾥姆算法(Prim算法)思路:以点为⽬标构建最⼩⽣成树1.将初始点顶点u加⼊U中,初始化集合V-U中各顶点到初始顶点u的权值;2.根据最⼩⽣成树的定义:从n个顶点中,找出 n - 1条连线,使得各边权值最⼩。
循环n-1次如下操作:(1)从数组lowcost[k]中找到vk到集合U的最⼩权值边,并从数组arjvex[k] = j中找到该边在集合U中的顶点下标(2)打印此边,并将vk加⼊U中。
(3)通过查找邻接矩阵Vk⾏的各个权值,即vk点到V-U中各顶点的权值,与lowcost的对应值进⾏⽐较,若更⼩则更新lowcost,并将k存⼊arjvex数组中以下图为例#include<bits/stdc++.h>using namespace std;#define MAXVEX 100#define INF 65535typedef char VertexType;typedef int EdgeType;typedef struct {VertexType vexs[MAXVEX];EdgeType arc[MAXVEX][MAXVEX];int numVertexes, numEdges;}MGraph;void CreateMGraph(MGraph *G) {int m, n, w; //vm-vn的权重wscanf("%d %d", &G->numVertexes, &G->numEdges);for(int i = 0; i < G->numVertexes; i++) {getchar();scanf("%c", &G->vexs[i]);}for(int i = 0; i < G->numVertexes; i++) {for(int j = 0; j < G->numVertexes; j++) {if(i == j) G->arc[i][j] = 0;else G->arc[i][j] = INF;}}for(int k = 0; k < G->numEdges; k++) {scanf("%d %d %d", &m, &n, &w);G->arc[m][n] = w;G->arc[n][m] = G->arc[m][n];}}void MiniSpanTree_Prim(MGraph G) {int min, j, k;int arjvex[MAXVEX]; //最⼩边在 U集合中的那个顶点的下标int lowcost[MAXVEX]; // 最⼩边上的权值//初始化,从点 V0开始找最⼩⽣成树Tarjvex[0] = 0; //arjvex[i] = j表⽰ V-U中集合中的 Vi点的最⼩边在U集合中的点为 Vjlowcost[0] = 0; //lowcost[i] = 0表⽰将点Vi纳⼊集合 U ,lowcost[i] = w表⽰ V-U中 Vi点到 U的最⼩权值for(int i = 1; i < G.numVertexes; i++) {lowcost[i] = G.arc[0][i];arjvex[i] = 0;}//根据最⼩⽣成树的定义:从n个顶点中,找出 n - 1条连线,使得各边权值最⼩for(int i = 1; i < G.numVertexes; i++) {min = INF, j = 1, k = 0;//寻找 V-U到 U的最⼩权值minfor(j; j < G.numVertexes; j++) {// lowcost[j] != 0保证顶点在 V-U中,⽤k记录此时的最⼩权值边在 V-U中顶点的下标if(lowcost[j] != 0 && lowcost[j] < min) {min = lowcost[j];k = j;}}}printf("V[%d]-V[%d] weight = %d\n", arjvex[k], k, min);lowcost[k] = 0; //表⽰将Vk纳⼊ U//查找邻接矩阵Vk⾏的各个权值,与lowcost的对应值进⾏⽐较,若更⼩则更新lowcost,并将k存⼊arjvex数组中for(int i = 1; i < G.numVertexes; i++) {if(lowcost[i] != 0 && G.arc[k][i] < lowcost[i]) {lowcost[i] = G.arc[k][i];arjvex[i] = k;}}}int main() {MGraph *G = (MGraph *)malloc(sizeof(MGraph));CreateMGraph(G);MiniSpanTree_Prim(*G);}/*input:4 5abcd0 1 20 2 20 3 71 2 42 3 8output:V[0]-V[1] weight = 2V[0]-V[2] weight = 2V[0]-V[3] weight = 7最⼩总权值: 11*/时间复杂度O(n^2)克鲁斯卡尔算法(Kruskal算法)思路:以边为⽬标进⾏构建最⼩⽣成树在边集中依次寻找最⼩权值边,若构建是不形成环路(利⽤parent数组记录各点的连通分量),则将其添加到最⼩⽣成树中。
c++普里姆算法最小生成树普姆算法 (Prim"s 算法) 是一种用于寻找最小生成树的算法。
它的时间复杂度为 $O(Elog E)$,其中 $E$ 是边数。
下面是 C++ 普姆算法的实现:```cpp#include <iostream>#include <vector>#include <cmath>using namespace std;// 定义边数const int E = 100010;// 定义最小生成树边权数组vector<int> adj[E];int weight[E];// 普姆算法int Prim(int u, vector<bool> &visited) {// 如果当前节点已经被访问过,则直接返回当前节点的值if (visited[u]) {return u;}// 计算当前节点到其他节点的最短路for (int v : adj[u]) {if (!visited[v]) {// 将当前节点添加到最小生成树中weight[u] += weight[v];adj[u].push_back(v);}}// 如果当前节点到其他节点的最短路长度小于当前的权值,则将当前节点的权值更新为最短路长度for (int v : adj[u]) {if (!visited[v]) {int dist = sqrt(pow(weight[u], 2) + pow(weight[v], 2)); weight[u] = dist;}}// 返回当前节点的值return u;}// 计算最小生成树vector<int> PrimTree(vector<int> &adj, int u) {// 如果当前节点已经被访问过,则直接返回当前节点的值vector<int> tree(adj.size(), -1);tree[u] = 0;// 辅助数组,记录每个节点到其他节点的最短路vector<int> pd(adj.size(), -1);for (int v : adj[u]) {if (!pd[v]) {pd[v] = u;}}// 循环遍历每个节点,并将当前节点添加到最小生成树中 for (int v = 0; v < adj.size(); v++) {int pdv = pd[v];if (pdv != -1 && weight[v] < weight[pdv]) {tree[v] = pdv;}}return tree;}int main() {// 读入边数cin >> E;// 读入边权数组for (int i = 0; i < E; i++) {cin >> weight[i];}// 初始化邻接表for (int i = 0; i < E; i++) {for (int j = 0; j < E; j++) {if (weight[i] < weight[j]) {adj[i].push_back(j);}}}// 计算最小生成树vector<int> tree = PrimTree(adj, 0);// 输出最小生成树for (int i = 0; i < tree.size(); i++) {cout << tree[i] << " ";}cout << endl;return 0;}```在上述代码中,我们首先定义了边数 `E`,然后读入边权数组`weight`。