湖南省201X年中考数学总复习 第七单元 图形与变换 课时29 视图与投影课件
- 格式:ppt
- 大小:1.74 MB
- 文档页数:32



视图与投影29视图与投影限时:30分钟夯实根底1.如图K29-1所示图形中,不可以作为一个正方体的展开图的是 ( )图K29-12.如图K29-2所示几何体中,其主视图不是中心对称图形的是 ( )图K29-23.[2021·菏泽] 如图K29-3,是两个等直径圆柱构成的“T 〞形管道,其左视图是 ( )图K29-3图K29-44.如图K29-5,是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )图K29-5A.主视图改变,左视图改变B.俯视图不变,左视图不变C.俯视图改变,左视图改变D.主视图改变,左视图不变5.三棱柱(图K29-6)的三视图如图K29-7所示,在△EFG中,EF=6 cm,∠EFG=45°,那么AB的长为 ()图K29-6图K29-7A.6 cmB.3√2 cmC.3 cmD.6√2 cm6.[2021·江西] 如图K29-8,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是.图K29-87.如图K29-9,是一个长方体的主视图与俯视图,由图示数据(单位:cm)可以得出该长方体的体积是cm3.图K29-98.图K29-10是一个食品包装盒的外表展开图.(1)请写出包装盒的几何体名称;(2)根据图中所标尺寸,用a,b表示这个几何体的全面积S(侧面积与底面积之和),并计算当a=1,b=4时S的值.图K29-10能力提升9.如图K29-11,在正方体的外表展开图中,A,B两点间的距离为6,折成正方体后,A,B两点是正方体的顶点,那么这两个顶点间的距离是()图K29-11A.3√2B.3√2C.6D.3210.如图K29-12,是某工件的三视图,那么此工件的外表积为()图K29-12A.15π cm2B.51π cm2C.66π cm2D.24π cm211.如图K29-13,长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长分别为AD=3,AA1=4,AB=5,那么从点A沿外表到C1的最短距离为()图K29-13A.5√2B.√74C.4√5D.3√1012.如图K29-14,直三棱柱ABC-A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,那么此直三棱柱左视图的面积为.图K29-1413.如图K29-15,在A时测得某树的影长为4 m,B时又测得该树的影长为16 m.假设两次日照的光线互相垂直,那么树的高度为.图K29-1514.如图K29-16,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,圆锥的高h为12 cm,OA=13 cm,那么扇形AOC中的AA⏜长是cm(计算结果保存π).图K29-16拓展练习15.问题探究:,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从点A (1)如图K29-17①所示是一个底面半径为32π出发,沿圆柱的侧面爬行一周到达点B,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线剪开,它的侧面展开图如图①中的矩形,那么蚂蚁爬行的最短路程即为线段AB'的长),母线长为4的圆锥和它的侧面展开图,AP是它的一条母线,一只蚂蚁从点A出发沿圆(2)如图②所示是一个底面半径为23锥的侧面爬行一周后回到点A,求蚂蚁爬行的最短路程.(3)如图③所示,在(2)的条件下,一只蚂蚁从点A出发沿圆锥的侧面爬行一周到达母线PA的中点,求蚂蚁爬行的最短路程.图K29-17参考答案1.C2.C3.B4.D5.B6.8 [解析] 所得几何体的俯视图是一个梯形:上底是1,下底是3,两腰长是2,周长是1+2+2+3=8,故答案为8.7.188.解:(1)长方体.(2)全面积S=(2a 2+ab+2ab )×2=4a 2+6ab. 当a=1,b=4时,S=4×12+6×1×4=28. 9.D 10.D 11.B12.2√3 [解析] 此直三棱柱左视图为矩形,长边为2,短边长为等边三角形ABC 中AB 边上的高,为√3,所以此直三棱柱左视图的面积为2√3.13.8 m [解析] 如图,过点C 作CD ⊥EF 于点D.那么∠EDC=∠CDF=90°.由题意,得△EFC 是直角三角形,∠ECF=90°.∴∠E+∠ECD=∠ECD+∠DCF=90°.∴∠E=∠DCF.∴Rt △EDC ∽Rt △CDF.∴AA AA =AAAA ,DC 2=ED ·FD.代入数据,可得DC 2=64,DC=8.14.10π15.解:(1)易知BB'=2π×32π=3,AB=4,那么蚂蚁爬行的最短路程为√32+42=5.(2)连接AA',那么AA'的长为蚂蚁爬行的最短路程.设r 1为圆锥的底面半径,r 2为侧面展开图(扇形)的半径,那么r 1=23,r 2=4.由题意,得2πr 1=A πA 2180,即2×π×23=A180×π×4.解得n=60.∴△PAA'是等边三角形.∴蚂蚁爬行的最短路程为AA'=PA=4.(3)如下图是圆锥的侧面展开图,设C 为A'P 的中点,连接AC ,那么线段AC 的长就是蚂蚁爬行的最短路程.∵△APA'为等边三角形,C 为A'P 的中点,∴AC ⊥A'P.∴AC=PA ·sin ∠APA'=4×sin60°=4×√32=2√3,即蚂蚁爬行的最短路程为2√3.。
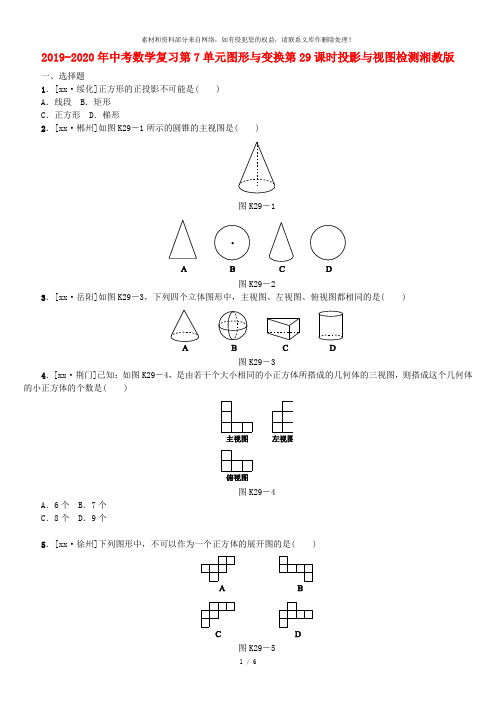
2019-2020年中考数学复习第7单元图形与变换第29课时投影与视图检测湘教版一、选择题1.[xx·绥化]正方形的正投影不可能是( )A.线段 B.矩形C.正方形 D.梯形2.[xx·郴州]如图K29-1所示的圆锥的主视图是( )图K29-1图K29-23.[xx·岳阳]如图K29-3,下列四个立体图形中,主视图、左视图、俯视图都相同的是( )图K29-34.[xx·荆门]已知:如图K29-4,是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )图K29-4A.6个 B.7个C.8个 D.9个5.[xx·徐州]下列图形中,不可以作为一个正方体的展开图的是( )图K29-56.[xx·咸宁]如图K29-6是某个几何体的三视图,该几何体是( )图K29-6A .三棱柱B .三棱锥C .圆柱D .圆锥 7.[xx·自贡] 如图K29-7是几何体的俯视图,所标数字为该位置小正方体的个数,则该几何体的主视图是( )图K29-7图K29-88.[xx·益阳]如图K29-9,空心卷筒纸的高度为12 cm ,外径(直径)为10 cm ,内径为4 cm ,在比例尺为1∶4的三视图中,其主视图的面积是( )图K29-9A.21π4 cm 2B.21π16cm 2C .30 cm 2D .7.5 cm 2二、填空题9.[xx·郴州]已知圆锥的母线长为5 cm ,高为4 cm ,则该圆锥的侧面积为________cm 2(结果保留π).K29-10图K29-1110.[xx·滨州]如图K29-11,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为________.11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于________.12.[xx·北京]如图K29-12,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为________m.图K29-12三、解答题13.如图K29-13是由几个相同的小正方体搭成的几何体的主视图和俯视图,求组成这个几何体的小正方体的个数.图K29-1314.小明用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小明看来看去觉得所拼图形似乎存在问题.(1)请你帮小明分析一下拼图是否存在问题.若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;(2)若图K29-14中的正方形边长为6 cm,长方形的长为8 cm,宽为6 cm,请直接写出修正后所折叠而成的长方体的表面积为________cm2.图K29-14|拓展提升|15.如图K29-15所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米.设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米.现有一只小猫睡在台阶的MN这层上晒太阳.(3取1.73)(1)求楼房的高度约为多少米?(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.图K29-15参考答案1.D [解析] 在同一时刻,平行物体的投影仍旧平行,得到的应是平行四边形或特殊的平行四边形或线段.故正方形的正投影不可能是梯形.2.A [解析] 主视图就是从几何体的正面得到的投影,本题中主视图反映的是圆锥的母线和底面圆的直径,∴A 符合.3.B [解析] 考查三视图,球体的主视图、俯视图、左视图是大小相等的圆,三视图相同.4.B [解析] 如图,以俯视图为基础,将另两个视图中小正方形的个数填写在俯视图的相应位置,即可得小正方体的个数是7.故选B.5.C 6.A 7.B8.D [解析] 圆柱的主视图是矩形,它的一边长是10 cm ,另一边长是12 cm.在比例尺为1∶4的主视图中,它的对应边长分别为2.5 cm ,3 cm ,因而矩形的面积为7.5 cm 2.因此选D.9.15π10.15π+12 [解析] 由三视图可以看出这是一个残缺的圆柱,侧面是由一个曲面和两个长方形构成,上下底面是两个扇形,S 侧=34×2π×2×3+2×3+2×3=9π+12,S 底面=2×34×π×22=6π,所以这个几何体的表面积为15π+12.11.144或384π [解析] 若圆柱底面周长为6,高为16π,则(62π)2×π×16π=π×9π2×16π=144;若圆柱的底面周长为16π,高为6,则π×(16π2π)2×6=π×64×6=384π.12.3 [解析] 由题意,画出示意图,如图所示.∵CD∥AB∥MN,∴△ABE∽△CDE,△ABF∽△MNF,∴CD∶AB=DE∶BE,MN∶AB=FN∶FB,即1.8∶AB=1.8∶(1.8+BD),1.5∶AB=1.5∶(1.5+2.7-BD),得AB=3 m.13.解:从俯视图可得最底层有4个小正方体,由主视图可得上面一层有2个或3个小正方体,则组成这个几何体的小正方体有6个或7个.14.解:(1)多余一个正方形如图所示.(2)表面积=6×8×4+6×6×2=192+72=264(cm2).15.解:(1)在Rt△ABE中,AB=AEtan60°=10 3≈17.3 (米).(2)如图,当α=45°时,AP=AB=17.3米,CP=AB-AC=17.3-17.2=0.1(米),∴CQ=CP=0.1<0.2,即CQ<CM,∴小猫能晒到太阳.-----如有帮助请下载使用,万分感谢。

