《平行线的特征》课件
- 格式:ppt
- 大小:1.21 MB
- 文档页数:11


平行线的特征平行线是几何学中重要的概念之一。
在二维欧几里得空间中,如果两条直线永远不相交,那么它们被称为平行线。
本文将介绍平行线的特征及相关的性质。
1. 平行线的定义给定二维欧几里得空间中的两条直线L1和L2,如果它们满足以下条件,则称L1和L2为平行线:•L1和L2不相交。
•L1和L2存在公共的平面。
2. 平行线的性质2.1 平行线的判定已知两条直线L1和L2,判断它们是否平行的方法有多种,这里介绍两种常见的判定方法:方法一:使用线性方程判断如果直线L1的斜率等于直线L2的斜率,那么L1和L2是平行线。
方法二:使用向量判断设直线L1上一点为点A,直线L2上一点为点B。
如果向量AB与L1的方向向量平行,则L1和L2是平行线。
2.2 平行线与夹角平行线之间不存在交点,因此它们之间的夹角为0度。
即使将两条平行线延长,无论延长多远,它们之间的夹角始终保持不变。
2.3 平行线与平行四边形平行线之间的性质与平行四边形的性质密切相关。
平行四边形是有四条边都平行的四边形。
性质一:对边平行平行四边形的对边是平行的。
即如果ABCD是一个平行四边形,那么线段AB和线段CD是平行线,线段AC和线段BD是平行线。
性质二:邻边互补平行四边形的邻边是互补的。
即如果ABCD是一个平行四边形,那么角A和角C是互补角,角B和角D是互补角。
性质三:对角线等长平行四边形的对角线等长。
即如果ABCD是一个平行四边形,那么线段AC和线段BD的长度相等。
2.4 平行线与转角当两条直线相交时,会形成四个角。
其中,相邻的两个角称为相邻角,非相邻的两个角称为转角。
如果两条直线分别与一条横穿它们的其他线相交,并且转角为等量,则这两条直线是平行线。
3. 平行线的应用平行线在几何学中有广泛的应用,下面简要介绍其中的几个应用领域。
3.1 地理学在地理学中,平行线常用于地图投影中的经纬度线。
地球上的纬线是平行于赤道的圆环状线,而经线是与纬线相交在地球上的两极的直线。


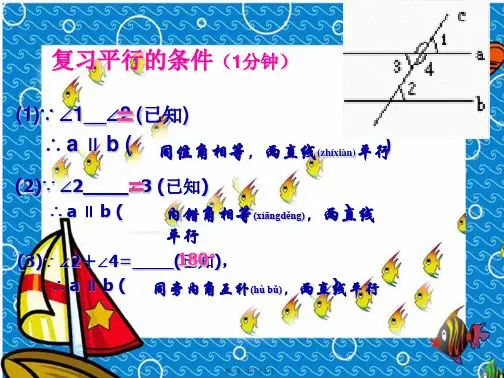






2.3 平行线特征在我们的数学世界中,平行线是一个十分重要的概念。
当两条直线在同一平面内,无论延伸多远都不会相交,我们就称它们为平行线。
那么,平行线究竟有哪些独特的特征呢?首先,平行线的同位角是相等的。
什么是同位角呢?比如说,有两条平行线被第三条直线所截,在截线的同侧,且在两条平行线的同一方的两个角,就是同位角。
我们可以通过简单的作图来理解。
假设这两条平行线是铁轨,第三条直线就像是横在铁轨上的一根枕木。
那么,在铁轨同一侧、枕木同一方所形成的角就是同位角。
不管这第三条直线怎么摆放,同位角的大小始终相等。
这就好像是两个双胞胎,无论身处何处,他们的某些特征总是一模一样的。
其次,平行线的内错角也是相等的。
内错角是在两条平行线之间,被截线错开的一对角。
还是用刚才铁轨和枕木的例子,位于两条铁轨之间,被枕木错开的角就是内错角。
它们就像是一对默契十足的伙伴,总是保持着相同的大小。
再者,平行线的同旁内角是互补的。
同旁内角是在两条平行线之间,在截线的同一旁的两个角。
想象一下,这就像是一个团队中的两个成员,虽然他们的角度不同,但加起来总是能形成一个完整的整体,其和为 180 度。
为什么我们要研究平行线的这些特征呢?这在我们解决实际的数学问题中可是大有用处的。
比如说,当我们要证明两条直线平行的时候,就可以通过证明同位角相等、内错角相等或者同旁内角互补来实现。
在日常生活中,平行线的特征也有着广泛的应用。
建筑工人在建造房屋时,需要确保墙壁与地面平行,地板的木板之间平行,这时就会用到平行线的知识。
工程师在设计桥梁、道路时,也需要考虑平行线的原理,以保证结构的稳定性和安全性。
我们再从几何图形的角度来看。
在平行四边形中,对边就是相互平行的,利用平行线的特征,我们可以很容易地得出平行四边形的对角相等,邻角互补等性质。
学习平行线的特征,还能帮助我们更好地理解和掌握其他数学知识。
比如在学习三角形、多边形的内角和时,平行线的知识往往能为我们提供解题的思路和方法。