数学建模培训_优化模型 PPT课件

2
3
4
• 制订月生产计划，使工厂的利润最大.
• 如果生产某一类型汽车，则至少要生产80辆，
那么最优的生产计划应作何改变？ 15
汽车厂生产计划
模型建立
设每月生产小、中、大型 汽车的数量分别为x1, x2, x3
小型 钢材 1.5 时间 280 利润 2
中型 3
250 3
大型 5
400 4
现有量 600 60000
p(t)w(t) p(t)w(t) 4
每天利润的增值 每天投入的资金
保留生猪直到利润的增值等于每天的费用时出售
由 S(t,r)=3 若 1.8 w 2.2(10%), 则 7 t 13（30%） 建议过一周后(t=7)重新估计 p, p, w, w, 再作计算。
13
研究 r, g变化时对模型结果的影响 估计r=2， g=0.1
• 设r=2不变
t 3 20 g , 0 g 0.15 g
t 对g的（相对）敏感度 30
t
S(t, g) Δ t / t dt g 20 Δ g / g dg t
S(t, g) 3 3 3 20 g
7
常用优化软件
1. LINGO软件 2. MATLAB优化工具箱 3. EXCEL软件的优化功能 4. SAS(统计分析)软件的优化功能 5. 其他
8
2.简单的优化模型
——生猪的出售时机
问 饲养场每天投入4元资金，用于饲料、人力、设 题 备，估计可使80千克重的生猪体重增加2公斤。
市场价格目前为每千克8元，但是预测每天会降 低 0.1元，问生猪应何时出售。
均为整数，重新求解. 17
模型求解 整数规划(Integer Programming,简记IP)

由上面三个表达式可求得：
r
1
4a 4,
cos
r1
4
r 2
r1
22
这也是在能量消耗最小原则下血管分岔处几何形状的 结果.由这个结果得：
a4
cos 2a 4
r 若取a＝1和a＝2可得 r1 和θ的大致范围约为：
r
1.26
1.32
r1
37
49
23
3.模型检验
记动物大动脉和最细的毛细血管半径分别为rmax和rmin
时刻为t＝t2，设t时刻森林烧毁面积为B(t)，则造成损失的森
林烧毁面积为B(t2)；单位时间烧毁的面积为 dB(t) (这 dt
也表示了火势蔓延的程度).在消防队员到达之前，即0≤t≤t1
期间，火势越来越大，从而
dB随(t )t的增加而增加 dt
；开始救火之后，即t1≤t≤t2期间，如果消防队员救火能力足
合来确定.式(3.3.2)还表明最优价格包括两部分：一部分为
成本的一半，另一部分与“绝对需求量”成正比，与市场
需求对价格的敏感系数成反比.
29
3.4 存贮模型
为了使生产和销售有条不紊地进行，一般的工商企业 总需要存贮一定数量的原料或商品，然而大量库存不但积 压了资金，而且会使仓库保管的费用增加.因此，寻求合理 的库存量乃是现代企业管理的一个重要课题.
min［订货费(或生产费)＋存贮费＋缺货损失费］
下面我们讨论几个重要的存贮模型.
31
3.4.1 不允许缺货的订货销售模型
为了使问题简化，我们作如下假设： (1)由于不允许缺货，所以规定缺货损失费为无穷大. (2)当库存量为零时，可立即得到补充. (3)需求是连续均匀的，且需求速度(单位时间的需求量) 为常数. (4)每次订货量不变，订货费不变. (5)单位存贮费不变.

投资组合优化
在风险和收益之间寻求平衡，通 过优化投资组合实现最大收益。
03
非线性规划模型
非线性规划问题的定义
目标函数
一个或多个非线性函数，表示 要最小化或最大化的目标。
约束条件
决策变量的取值受到某些限制 ，通常以等式或不等式形式给 出。
决策变量
问题中需要求解的未知数，通 常表示为x1, x2, ..., xn。
这是一种常用的求解整数规划问题的算法，通过不断将问题分解为更 小的子问题，并确定问题的下界和上界，逐步逼近最优解。
割平面法
该方法通过添加割平面来限制搜索区域，从而逼近最优解。
迭代改进法
该方法通过不断迭代和改进当前解，逐步逼近最优解。
遗传算法
这是一种基于生物进化原理的优化算法，通过模拟自然选择和遗传机 制来寻找最优解。
定义域
决策变量的取值范围，通常是 一个闭区间或开区间。
非线性规划问题的求解方法
梯度法
利用目标函数的梯度信息，通过迭代方法寻 找最优解。
共轭梯度法
结合梯度法和牛顿法的思想，通过迭代方法 寻找最优解。
牛顿法
利用目标函数的二阶导数信息，通过迭代方 法寻找最优解。
信赖域方法
在每次迭代中，通过限制搜索步长来保证求 解的稳定性。
02
线性规划模型
线性规划问题的定义
01
02
03
线性规划问题
在给定一组线性约束条件 下，求一组线性函数的最 大值或最小值的问题。
约束条件
包括资源限制、物理条件 等，通常以等式或不等式 形式给出。
目标函数
需要最大化或最小化的线 性函数，通常表示为决策 变量的线性组合。
线性规划问题的求解方法

题的求解过程。
混合整数线性规划问题求解
要点一
混合整数线性规划问题的复杂性
混合整数线性规划问题是指包含整数变量的线性规划问题 。由于整数变量的存在，混合整数线性规划问题的求解变 得更加困难，需要采用特殊的算法和技术来处理。
要点二
混合整数线性规划模型的求解方 法
为了解决混合整数线性规划问题，可以采用一些特殊的算 法和技术，如分支定界法、割平面法等。这些方法能够将 问题分解为多个子问题，并逐步逼近最优解，从而提高求 解效率。
目标函数的类型
常见的目标函数类型包括最小化、最大化等。
确定约束条件
约束条件
01
约束条件是限制决策变量取值的条件，通常表示为数学不等式
或等式。
确定约束条件的原则
02
根据问题的实际情况，选择能够反映问题约束条件的条件作为
约束条件。
约束条件的类型
03
常见的约束条件类型包括等式约束、不等式约束等。
线性规划模型的建立
也可以表示为
maximize (c^T x) subject to (A x geq b) and (x leq 0)。
线性规划的应用场景
生产计划
物流优化
在制造业中，线性规划可以用于优化生产 计划，确定最佳的生产组合和数量，以满 足市场需求并降低成本。
在物流和运输行业中，线性规划可以用于 优化运输路线、车辆调度和仓储管理，降 低运输成本和提高效率。
初始基本可行解
在线性规划问题中，一个解被称为基 本可行解，如果它满足所有的约束条 件。
在寻找初始基本可行解时，可以采用 一些启发式算法或随机搜索方法，以 快速找到一个可行的解作为起点。
初始基本可行解是线性规划问题的一 个起始点，通过迭代和优化，可以逐 渐逼近最优解。

数学建模案例解析
04
经济学案例：供需平衡模型
供需平衡理论
通过数学语言描述市场需求与供给之间的平衡关 系，涉及价格、数量等关键变量。
建模过程
收集相关数据，建立需求函数和供给函数，通过 求解方程组找到均衡价格和均衡数量。
模型应用
预测市场趋势，分析政策对市场的影响，为企业 决策提供支持。
物理学案例：热传导模型
Lingo在数学建模中的应 用案例
展示Lingo在数学建模中的实 际应用，如线性规划、整数规 划、非线性规划等优化问题的 求解。
其他数学建模相关软件与工具简介
Mathematica软件
简要介绍Mathematica的特点和功能，以及其 在数学建模中的应用。
SAS软件
简要介绍SAS的特点和功能，以及其在数学建模 中的应用。
数据预处理
包括数据清洗、缺失值处 理、异常值检测等，保证 数据质量。
数据可视化
利用图表、图像等手段展 示数据，便于理解和分析 。
数据分析方法
如回归分析、时间序列分 析、聚类分析等，用于挖 掘数据中的信息和规律。
数学建模常用方法
03
回归分析
线性回归
通过最小二乘法拟合自变量和因 变量之间的线性关系，得到最佳
模型应用
预测舆论走向，分析社会热点问题，为政府和企业提供决策支持。
数学建模软件与工
05
具介绍
MATLAB软件介绍及使用技巧
MATLAB概述
简要介绍MATLAB的历史、功能和应用领域 。
MATLAB常用函数
列举并解释MATLAB中常用的数学函数、绘 图函数、数据处理函数等。
MATLAB基础操作
详细讲解MATLAB的安装、启动、界面介绍 、基本语法和数据类型等。

6米钢管根数 0 1 0 2 1 3 0
8米钢管根数 0 0 1 0 1 0 2
余料(米) 3 1 3 3 1 1 3
为满足客户需要，按照哪些种合理模式，每种模式
切割多少根原料钢管，最为节省？
两种 1. 原料钢管剩余总余量最小 标准 2. 所用原料钢管总根数最少
18
决策 变量 xi ~按第i 种模式切割的原料钢管根数(i=1,2,…7) 目标1（总余量） Min Z1 3x1 x2 3x3 3x4 x5 x6 3x7
模型建立
xij--第i 种货物装入第j 个货舱的重量
目标 函数 (利润)
Max Z 3100(x11 x12 x13) 3800(x21 x22 x23) 3500(x31 x32 x33) 2850(x41 x42 x43)
货舱 x11 x21 x31 x41 10 重量 x12 x22 x32 x42 16
3
货机装运
模型建立
xij--第i 种货物装入第j 个货舱的重量
约束
平衡 要求
x11 x21 x31 x41 10
x12 x22 x32 x42 16
10； 6800
16； 8700
8； 5300
条件
x13 x23 x33 x43 8
货物 供应
x11 x12 x13 18 x21 x22 x23 15
如何装运， 使本次飞行 获利最大？
1
货机装运
模型假设
每种货物可以分割到任意小； 每种货物可以在一个或多个货舱中任意分布； 多种货物可以混装，并保证不留空隙；
模型建立
决策 xij--第i 种货物装入第j 个货舱的重量(吨） 变量 i=1,2,3,4, j=1,2,3 (分别代表前、中、后仓)

用Matlab编程求解程序如下：
[X,FVAL,EXITFLAG,OUTPUT] = LINPROG(f,A,b) f = -[10 5]; A = [0.3 0.4;0.5 0.2]; B = [9;8];
[X,FVAL,EXITFLAG,OUTPUT] = LINPROG(f,A,b)
X= 10.0000
2
建立无约束优化模型为：min y =- ( 3 2 x ) x ， 0< x <1.5
2
先编写M文件fun0.m如下: function f=fun0(x) f=-(3-2*x).^2*x; 主程序为wliti2.m: [x,fval]=fminbnd('fun0',0,1.5); xmax=x fmax=-fval
控制，计划聘请两种不同水平的检验员.一级检验员的标准为： 速度25件/小时，正确率98%，计时工资4元/小时；二级检验员 的标准为：速度15件/小时，正确率95%，计时工资3元/小时.检 验员每错检一次，工厂要损失2元.为使总检验费用最省，该工 厂应聘一级、二级检验员各几名？
解 设需要一级和二级检验员的人数分别为x1、x2人, 则应付检验员的工资为：
综上得，
函数f(x)在x=4取得在[-3,4]上得最大值f(4)=142，在 x=1处取得在[-3,4]上取得最小值f(1)=7
用MATLAB解无约束优化问题
1. 一元函数无约束优化问题: min f ( x )
常用格式如下： （1）x= fminbnd (fun,x1,x2) （2）x= fminbnd (fun,x1,x2 ，options) （3）[x，fval]= fminbnd（…） （4）[x，fval，exitflag]= fminbnd（…）

245

7
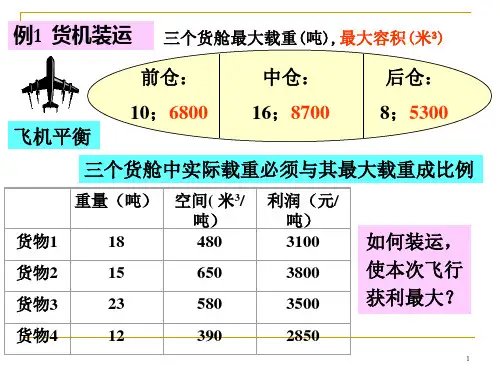
线性规划模型
结合存量限制和需量限制得数学模型：
m f 1 i x 1 n 2 2 x 2 4 8 x 3 3 x 4 0 1 x 5 2 2 x 64
x1 x2 x3 4
x4 x5 x6 8
s .t .
x1 x4 2 x2 x5 4

5
线性规划模型
运输问题
有两个粮 A1,库 A2向三个粮 B1,站 B2,B3调运大, 米 两个粮库现存大为米 4吨分 ,8吨 别,三个粮站至少需要 大米分别 2,4为 ,5吨,两个粮库到三个距粮离 (站 单的 位 :公里 )如下 ,问如何调运使运。费最低
距离 粮站
粮库
B1 B2 B3
在很多实际问题中,解题思想和运输问题同出一辙, 也就是说我们可以用运输模型解决其他问题.

10
线性规划模型
分派问题
设有n件工作B1, B2, … Bn,分派给n人A1, A2, … An去
做完成,每B人j的只工做时一为件c工ij,问作应且如每何件分工派作才只能派完一成个全人部去工做变作,设量的故Axii只建取立0和1,
原单材位料消耗 产品
Ⅰ
Ⅱ
现有原 材料

A1
21 8
A2
10 3
A3
01 4
4
线性规划模型
解:设生 ,产 两 种产品 x1,x分 2吨 ,别为
max f= 5x1 +2x2
求最大利润
2x1 + x2 8
s.t .
x1 3
三种材料量的限制
x2 4
x1，x2 0
生产量非负
数学建模
优化专题
--数学建模基地系列课件--

（二）优化模型的分类
1.根据是否存在约束条件 有约束问题和无约束问题。
2.根据设计变量的性质 静态问题和动态问题。
3.根据目标函数和约束条件表达式的性质 线性规划，非线性规划，二次规划，多目标规划等。
第3页/共29页
（1）非线性规划
目标函数和约束条件中，至少有一个非线性函数。
minu f (x) x
配件厂为装配线生产若干种部件，轮换生 产不同的部件时因更换设备要付生产准备费 （与生产数量无关），同一部件的产量大于需 求时因积压资金、占用仓库要付存贮费。今已 知某一部件的日需求量100件，生产准备费5000 元，存贮费每日每件1元。如果生产能力远大于 需求，并且不允许出现缺货，试安排该产品的 生产计划，即多少天生产一次（称为生产周 期），每次产量多少，可使总费用最小。
由相对变化量衡量对参数的敏感程度。
T 对c1 的敏感程度记为 S(T, c1) 2
S(T , c1)
T c1
T c1
dT d c1
c1 T
1 2
c2r c1 1 2c1 T 2
c2r
1
1
S (T , c2 ) 2
S(T , r) 2
第19页/共29页
S (T , c1)
1 2
S
(T
,
一 优化模型的一般意义
（一）优化模型的数学描述
将一个优化问题用数学式子来描述，即求函数
u f ( x) x (x1, x2, x3,...,xn ) 在约束条件 hi (x) 0,i 1,2,...,m.
和 gi (x) 0(gi (x) 0),i 1,2,...,p.
下的最大值或最小值，其中
工厂定期订购原料，存入仓库供生产之用； 车间一次加工出一批零件，供装配线每天生产之用； 商店成批购进各种商品，放在货柜里以备零售； 水库在雨季蓄水，用于旱季的灌溉和发电。