第1章 晶体结构基础04
- 格式:pdf
- 大小:1.97 MB
- 文档页数:35

第1章晶体的结构(1)固体物质是由大量的原子、分子或离子按照一定方式排列而成的,这种微观粒子的排列方式称为固体的微结构。
(2)按照微结构的有序程度,固体分为晶体、准晶体和非晶体三类。
其中,晶体的研究已经非常成熟,而非晶体和准晶体则是固体研究的新领域。
(3)晶体的结构和特性决定了它在现代科学技术上有着及其广泛的应用,因此,固体物理学以晶体作为主要的研究对象。
§1.1 晶体的基本性质一、晶体的特征1.长程有序*虽然不同的晶体具有各自不同的特性,但是,在不同的晶体之间仍存在着某些共同的特征,这主要表现在以下几个方面。
*具有一定熔点的固体,称为晶体。
*实验表明:在晶体中尺寸为微米量级的小晶粒内部,原子的排列是有序的。
在晶体内部呈现的这种原子的有序排列,称为长程有序。
*长程有序是所有晶体材料都具有的共同特征,这一特性导致晶体在熔化过程中具有一定的熔点。
*晶体分为单晶体和多晶体。
在单晶体内部,原子都是规则地排列的。
单晶体是个凸多面体,围成这个凸多面体的面是光滑的,称为晶面。
(1)单晶体( Single Crystal )由许多小单晶(晶粒)构成的晶体,称为多晶体。
多晶体仅在各晶粒内原子才有序排列,不同晶粒内的原子排列是不同的。
(2)多晶体( Multiple Crystal )由许多小单晶(晶粒)构成的晶体,称为多晶体。
多晶体仅在各晶粒内原子才有序排列,不同晶粒内的原子排列是不同的。
*晶面的大小和形状受晶体生长条件的影响,它们不是晶体品种的特征因素。
2.解理(Cleavage)(1)晶体具有沿某一个或数个晶面发生劈裂的特征,这种特征称为晶体的解理。
解理的晶面,称为解理面。
(2)有些晶体的解理性比较明显,例如,NaCl晶体等,它们的解理面常显现为晶体外观的表面。
(3)有些晶体的解理性不明显,例如,金属晶体等。
(4)晶体解理性在某些加工工艺中具有重要的意义,例如,在划分晶体管管芯时,利用半导体晶体的解理性可使管芯具有平整的边缘和防止无规则的断裂发生,以保证成品率。

第一章晶体结构(一)章节要求1、 掌握晶体的特征晶格周期性的描述方法:基元、布拉菲格子、原胞、基矢 的概念。
简单格子与复式格子,原胞、晶胞的概念与选取。
常 见晶格结构及其代表晶体。
2、 掌握晶列与晶面,晶向指数与晶面指数(密勒指数)的含义与 确定方法。
3、 掌握倒格子和布里源区的概念,正空间和倒空间的联系和转换,会计算倒格子体积等量4、 熟悉晶体的对称操作、对称素的概念,晶体点群的基本知识。
七大晶系与十四种布拉菲格子。
5、 熟悉晶体衍射理论,会推导劳厄定理和布拉格定理的等价关系6、 理解基于衍射理论的晶体结构计算方法匕4.金刚石结构(二)章节结构 1.长程有序•晶体共性2•自限性和晶面角守恒定律 3. 各向异性 4. 固定熔点 5. 非晶体与准晶体厂1.简单立方晶体结构(sc )2. 体心立方晶体结构(bcc )•常见晶体结构3.密堆积-六角密排(hcp )'面心立方(ccp )•晶体结构模型化研究:晶体结构 =晶格+基元(转化为晶格研究)-分类:简单格子;复式格子晶格 丿组成:原胞与原胞基矢;晶胞;常见晶体结构的原胞或晶胞描述方法:晶列和晶面指数;晶面和密勒指数广1.晶体的对称性 2•晶体的对称操作和对称元素四•晶体的宏观对称性 S 3.点群和空间群4.七大晶系和十四种布拉菲格子五.晶体结构计算1.布拉格定理2.劳厄定理 3.两者等价(2)倒格子1.倒矢量,倒格矢和倒格子2. 倒矢量和倒格矢的性质1. 布里渊衍射条件⑶布里渊区 Y2.布里渊区:一维,二维,简立方,面心立方,体心立方3. 布里渊区的性质(4)基于衍射理论的晶体结构计算(三)基础知识-、晶体的共性定义内部质点在三维空间呈周期性重复排列的固体为晶体。
1、长程有序一一晶体中的原子都是按一定规则排列的,这种至少在微米量级范围的有序 排列,称为晶体的长程有序。
晶体可以分为单晶体和多晶体,多晶体是由许多单晶体构成的。
单晶体,在整体范围内原子排列都是规则的。


第一章晶体结构1 布喇菲点阵和初基矢量晶体结构的特点在于原子排列的周期性质。
布喇菲点阵是平移操作112233R n a n a n a =++所联系的诸点的列阵。
布喇菲点阵是晶体结构周期性的数学抽象。
点阵矢量112233R n a n a n a =++,其中,1n ,2n 和3n 均为整数,1a ,2a 和3a 是不在同一平面内的三个矢量,叫做布喇菲点阵的初基矢量,简称基矢。
初基矢量所构成的平行六面体是布喇菲点阵的最小重复单元。
布喇菲点阵是一个无限的分立点的列阵,无论从这个列阵中的哪个点去观察,周围点的分布和排列方位都是完全相同的。
对一个给定的布喇菲点阵,初级矢量可以有多种取法。
2 初基晶胞(原胞)初基晶胞是布喇菲点阵的最小重复单元。
初基晶胞必定正好包含布喇菲点阵的一个阵点。
对于一个给定的布喇菲点阵,初基晶胞的选取方式可以不只一种,但不论初基晶胞的形状如何,初基晶胞的体积是唯一的,()123c V a a a =⋅⨯。
3 惯用晶胞(单饱)惯用晶胞是为了反映点阵的对称性而选用的晶胞。
惯用晶胞可以是初基的或非初基的。
惯用晶胞的体积是初基晶胞体积的整数倍,c V nV =。
其中,n 是惯用晶胞所包含的阵点数。
确定惯用晶胞几何尺寸的数字叫做点阵常数。
4 维格纳—赛兹晶胞(W-S 晶胞)维格纳—赛兹晶胞是另一种能够反映晶体宏观对称性的晶胞,它是某一阵点与相邻阵点连线的中垂面(或中垂线)所围成的最小体积。
维格纳—赛兹晶胞是初基晶胞。
5 晶体结构当我们强调一个实际的晶体与布喇菲点阵的抽象几何图案的区别时,我们用“晶体结构”这个名词[1]。
理想的晶体结构是由相同的物理单元放置在布喇菲点阵的阵点上构成的。
这些物理单元称为基元,它可以是原子、分子或分子团(有时也可以指一组抽象的几何点)。
将基元平移布喇菲点阵的所有点阵矢量,就得到晶体结构,或等价地表示为基元十点阵=晶体结构[2]当选用非初基的惯用晶胞时,一个布喇菲点阵可以用带有基元的点阵去描写。

第一章 晶体结构本章首先从晶体结构的周期性出发,来阐述完整晶体中离子、原子或分子的排列规律。
然后,简略的阐述一下晶体的对称性与晶面指数的特征,介绍一下倒格子的概念。
§1.1晶体的周期性一、晶体结构的周期性1.周期性的定义从X 射线研究的结果,我们知道晶体是由离子、原子或分子(统称为粒子)有规律地排列而成的。
晶体中微粒的排列按照一定的方式不断的做周期性重复,这样的性质成为晶体结构的周期性。
周期性:晶体中微粒的排列按照一定的方式不断的做周期性重复,这样的性质成为晶体结构的周期性。
晶体结构的周期性可由X-Ray 衍射直接证实,这种性质是晶体最基本或最本质的特征。
(非晶态固体不具备结构的周期性。
非晶态的定义等略),在其后的学习中可发现,这种基本性质对固体物理的学习具有重要的意义或是后续学习的重要基础。
2.晶格 格点和点阵晶格:晶体中微粒重心,做周期性的排列所组成的骨架,微粒重心所处的位置称为晶格的格点(或结点)。
格点的总体称为点阵。
整个晶体的结构,可看成是由格点沿空间三个不同方向, 各自按一定距离周期性平移而构成。
每个平移的距离称为周期。
在某一特定方向上有一定周期,在不同方向上周期不一定相同。
晶体通常被认为具有周期性和对称性,其中周期性最为本质。
对称性其实质是来源于周期性。
故周期性是最为基本的对称性,即“平移对称性”(当然,有更为复杂或多样的对称性,但周期性或平移对称性是共同的)。
3.平移矢量和晶胞据上所述,基本晶体的周期性,我们可以在晶体中选取一定的单元,只要将其不断地重复平移,其每次的位移为a 1,a 2,a 3,就可以得到整个晶格。
则→1a ,→2a ,→3a 就代表重复单元的三个棱边之长及其取向的矢量,称为平移矢量,这种重复单元称为晶胞,其基本特性为:⑴晶胞平行堆积在一起,可以充满整个晶体⑵任何两个晶胞的对应点上,晶体的物理性质相同,即:()⎪⎭⎫⎝⎛+++=→→→332211anananrQrQ其中→r为晶胞中任一点的位置矢量。


晶体结构知识点晶体结构是凝聚态物理学中的重要基础概念,它描述了晶体内部的原子或离子排列方式。
晶体结构的研究对于理解物质性质以及材料科学的发展具有重要意义。
本文将介绍晶体结构的基本概念、常见的晶体结构类型以及晶体结构的表征方法。
一、晶体结构的基本概念晶体是一种具有高度有序排列的固体物质,其内部的原子、离子或分子按照一定的规则排列。
晶体结构主要包括晶胞、晶格、晶格常数和晶体中的基元等概念。
1. 晶胞晶胞是晶体结构中的最小重复单元,它是通过平移操作进行重复填充整个晶体空间的基本单位。
晶胞可以是立方体、正交体、单斜体、菱形体等不同形状。
2. 晶格晶格是由晶胞堆积形成的空间结构,描述了晶体内原子或离子排列的规则性、周期性和对称性。
晶格对称性的不同将决定晶体的晶系,包括立方晶系、正交晶系、单斜晶系、菱形晶系、三斜晶系、四方晶系和六方晶系等。
3. 晶格常数晶格常数是指晶体结构中晶胞的参数,包括晶格常数a、b、c和晶胞间的夹角α、β、γ。
它们的数值可以通过实验测量或者计算得到,是描述晶体几何结构的重要参量。
4. 基元基元是指晶体结构中的最小组成单位,可以是原子、离子或分子。
晶胞中的所有基元通过晶格的平移操作进行重复填充,形成整个晶体。
二、常见的晶体结构类型根据晶体中原子、离子或分子的排列方式,可以将晶体结构分为多种类型。
以下介绍几种常见的晶体结构类型:1. 立方晶系最简单的晶体结构类型是立方晶系,其晶胞为正方体。
立方晶系包括简单立方晶体、体心立方晶体和面心立方晶体。
在简单立方晶体中,原子只位于晶胞的角点;在体心立方晶体中,除了角点上的原子,还有一个原子位于晶胞的中心;而在面心立方晶体中,除了角点上的原子,还有六个原子位于晶胞的六个面心。
2. 正交晶系正交晶系的晶胞为长方体,晶胞中的边长和夹角可以不相等。
正交晶系包括了许多工程材料,如金属、陶瓷等。
3. 六方晶系六方晶系是由六边形晶胞构成的晶体结构,其中晶胞的底面为六边形,晶胞高度可以与底面边长不同。


第一章 晶体结构【教学目的】了解晶体结构,掌握晶体基本概念及性质,对称性,紧密堆积原理,典型结构类型等。
【教学内容】晶体的基本概念及性质、晶体的宏观对称性、布拉维点阵与晶系、点阵几何元素的表示法、微观对称和空间群、结晶化学原理、典型结构类型硅酸盐晶体结构。
【教学重点】晶体的对称性、布拉维点阵、晶体的配位及鲍林规则、硅酸盐晶体结构。
【教学方法及手段】多媒体课件展示图、表第一节 几何结晶学基本概念一、 晶体的定义1、定义晶体是内部质点在三维空间作有规则的周期性重复排列的固体,是具有格子构造的固体。
晶体的这一定义表明,不论晶体的组成如何不同,也不论其表观是否具有规则的几何外形,晶体的共同特征是内部质点在三维空间按周期性的重复排列。
不具备这一特征的物体就不是晶体。
2、空间点阵(空间格子)在三维空间按周期性重复排列的几何点的集合称为空间点阵(空间格子)。
空间点阵(空间格子)中的结点是抽象的几何点并非实际晶体中的质点。
阵点或结点:空间点阵中的几何点称为阵点或结点。
等同点:同一套空间格子中的结点叫等同点。
实际晶体是由组成晶体的离子或原子去占据一套或几套穿插在一起的空间格子的结点位置而构成。
实际晶体的内部质点是有实际内容的原子或离子。
实际晶体中化学组成相同、结晶化学环境相同的质点占据的结点构成一套等同点。
所谓结晶化学环境相同是指质点周围在相同方位上离开相同距离有相同的质点。
晶体中有几套空间格子就有几套等同点,判断晶体中有几套空间格子的方法是看晶体中有几套等同点。
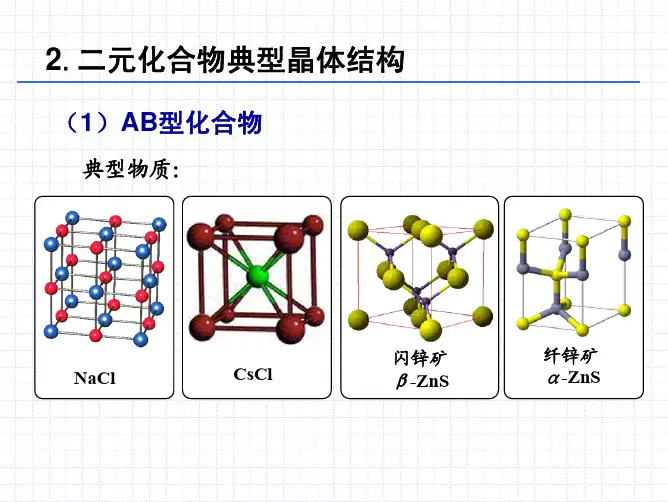
NaCl晶体有2套空间格子,Na+ 离子和Cl-离子各构成一套空间格子。
CsCl晶体有2套空间格子,Cs+ 离子和Cl-离子各构成一套空间格子。
晶体有3套空间格子,Ca2+离子构成一套空间格子;F-离子 CaF2有两套空间格子。
3、晶体的性质:结晶均一性、各向异性、自限性、对称性、最小内能性。
二、晶系:根据晶体的对称性,将晶体分为三大晶族、七大晶系。
高级晶族:立方晶系(等轴晶系)中级晶族:六方晶系、三方晶系(菱方晶系)、四方晶系(正方晶系)低级晶族:斜方晶系(正交晶系)、单斜晶系、三斜晶系三、 晶胞晶胞是晶体中重复出现的最小结构单元,它包含了整个晶体的特点。