连杆机构运动分析
- 格式:doc
- 大小:121.82 KB
- 文档页数:10





平面连杆机构及其分析与设计平面连杆机构是由连杆和连接点组成的机械结构,广泛应用于各种机械设备中。
它的功能是将输入的旋转运动转化为输出的直线运动或者将输入的直线运动转化为输出的旋转运动。
本文将对平面连杆机构的分析与设计进行介绍。
首先,对平面连杆机构进行分析。
平面连杆机构的主要组成部分是连杆和连接点。
连杆是连接点之间的刚性杆件,可以是直杆、曲杆或者具有其他特殊形状的杆件。
连接点是连杆的两个端点或者连杆与其他机构的连接点,可以是支点、铰链等。
平面连杆机构的运动可以分为三种基本类型:平动、转动和复动。
平动是指连杆的一端保持固定,另一端进行直线运动;转动是指连杆的一端保持固定,另一端进行旋转运动;复动是指连杆的一端进行直线运动,另一端同时进行旋转运动。
进行平面连杆机构的设计时,需要考虑以下几个要点。
首先,确定机构的类型和功能。
根据机构的动作要求和功能要求,选择适合的连杆类型和连接点类型。
其次,进行机构的运动分析。
根据机构的运动要求,确定连杆的长度和连接点的位置,使连杆能够实现所需的运动。
然后,进行机构的力学分析。
根据机构的受力情况,确定连杆的截面尺寸和材料,保证机构的刚度和强度。
最后,进行机构的优化设计。
考虑机构的性能要求和制造要求,对机构进行优化设计,提高机构的工作效率和使用寿命。
在平面连杆机构的设计中,还需要考虑机构的动力学问题。
机构的动力学分析包括静力学分析和动力学分析两个方面。
静力学分析是指在机构静止或静力平衡状态下,对机构受力和力矩进行分析。
动力学分析是指在机构进行运动时,对机构的加速度、速度和位移进行分析。
通过对机构的动力学分析,可以确定机构的惯性力和惯性矩,从而确定机构的动态特性和振动特性。
总之,平面连杆机构的分析与设计是一项复杂而重要的工作。
在进行分析与设计时,需要考虑机构的类型和功能,进行运动分析和力学分析,优化设计和动力学分析。
通过合理的分析与设计,可以使机构具有较好的工作性能和使用寿命,满足各种工程应用的要求。
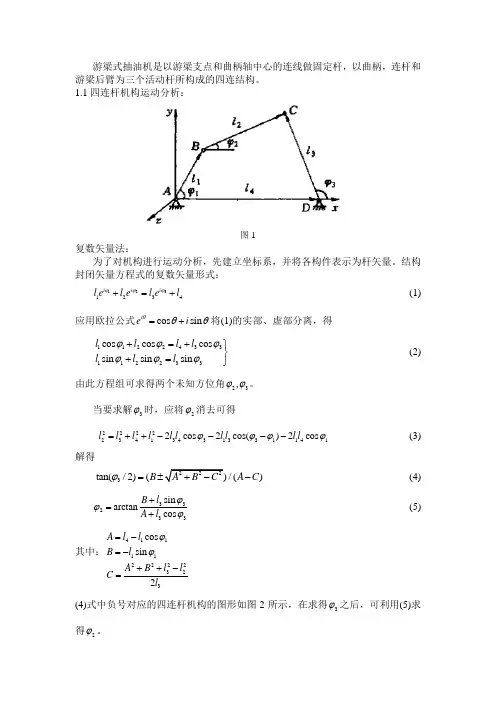
游梁式抽油机是以游梁支点和曲柄轴中心的连线做固定杆,以曲柄,连杆和游梁后臂为三个活动杆所构成的四连结构。
1.1四连杆机构运动分析:图1复数矢量法: 为了对机构进行运动分析,先建立坐标系,并将各构件表示为杆矢量。
结构封闭矢量方程式的复数矢量形式:3121234i i i l e l e l e l ϕϕϕ+=+ (1)应用欧拉公式cos sin i e i θθθ=+将(1)的实部、虚部分离,得1122433112233cos cos cos sin sin sin l l l l l l l ϕϕϕϕϕϕ+=+⎫⎬+=⎭(2)由此方程组可求得两个未知方位角23,ϕϕ。
当要求解3ϕ时,应将2ϕ消去可得2222234134313311412cos 2cos()2cos l l l l l l l l l l ϕϕϕϕ=++---- (3)解得2223tan(/2)()/()B A B C A C ϕ=+-- (4)33233sin arctancos B l A l ϕϕϕ+=+ (5)其中:411112222323cos sin 2A l l B l A B l l C l ϕϕ=-=-++-=(4)式中负号对应的四连杆机构的图形如图2所示,在求得3ϕ之后,可利用(5)求得2ϕ。
图2由于初始状态1ϕ有个初始角度,定义为01ϕ,因此,我们可以得到关于011t ϕϕω=+,ω是曲柄的角速度。
而通过图形3分析,我们得到OA 的角度0312πθϕϕ=--。
因此悬点E 的位移公式为||s OA θ=⨯,速度||ds d v OA dt dtθ==,加速度2222||dv d s d a OA dt dt dtθ===。
图3已知附录4给出四连杆各段尺寸,前臂AO=4315mm ,后臂BO=2495mm ,连杆BD=3675mm ,曲柄半径O ’D=R=950mm ,根据已知条件我们推出''||||||||OO O D OB BD +>+违背了抽油系统的四连结构基本原则。

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是关于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确信从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,因此机构的运动分析是机械设计进程中必不可少的重要环节。
以运算机为手腕的解析方式,由于解算速度快,精准度高,程序有必然的通用性,已成为机构运动分析的要紧方式。
连杆机构作为在机械制造专门是在加工机械制造中要紧用作传动的机构型式,同其他型式机构专门是凸轮机构相较具有很多优势。
连杆机构采纳低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构能够将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,知足给定的运动要求,完成机械的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的操纵。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,现在要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的阻碍。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度和刨刀C点的位移、速度和加速度的转变情形。

四连杆机构运动分析
1、组装零件:
---放置第一个零件常采用缺省;
---连接零件可采用销钉连接方式(机构能运动);
2、进入机构运动环境
---应用程序|机构---
---编辑|重新连接--- /检查装配情况
---运行(连接组件)---是(确认)---
3、观察机构中的体
---视图|加亮主体--- /绿色表示为地体
4、拖动模型
---单击‘拖动’按钮---
---任选四连杆上一点,拖动鼠标进行拖动---
---单击中建,结束拖动---
5、建立伺服电机
---选择‘伺服电动机’按钮---
---定义电机名称,运动轴--- /若装配正确,运动处都会出现
运动轴
---定义电机速度、加速度--- /可单击图像查看
6、仿真运动过程
---单击‘机构分析’按钮---
---选择‘运动学’分析类型,单击‘运行’观察运动情况---
7、回放并保存结果
单击‘回放’按钮可以进行回放;
8、产生分析测量结果
---分析|测量,打开‘测量结果’---
---单击‘新建’按钮(在测量栏中),打开‘测量定义’--- ---选择测量点,测量分量,坐标系---确定---
/测量点可以是零件端点,基准点,几何点
---单击画图,可以绘制结果图形---
9、产生轨迹曲线
---插入|轨迹曲线---
---选择点---确定---
/零件顶点,几何点可以产生轨迹,基准点不能产生轨迹,可以在模型树种中右键零件‘打开’|草绘,绘制几何点;。

多连杆机构的运动学分析与合理设计多连杆机构作为机械系统中常见的一种形式,广泛应用于各种工程领域。
它由多个连杆和铰接连接的节点构成,能够实现复杂的运动路径。
在机器人技术、汽车工程和航天领域等众多应用中,多连杆机构的运动学分析和合理设计是至关重要的。
在进行多连杆机构的运动学分析时,需要首先确定各个连杆的长度、连杆的连接方式以及铰接的位置等。
通过这些参数的确定,可以进一步推导出机构的运动方程和运动学限制条件。
常见的多连杆机构包括摇杆机构、曲柄滑块机构和平面四杆机构等。
以摇杆机构为例,它由一个直杆和两个转轴构成。
当一个转动的驱动件作用于摇杆机构时,整个机构的运动路径可以被描述为抛物线形状。
通过分析抛物线的特性,可以确定驱动件的转速和转动角度对机构运动轨迹的影响,从而实现对机构运动的控制。
曲柄滑块机构是另一种常见的多连杆机构,它由一个转动的曲柄和一个滑块构成。
曲柄滑块机构的运动轨迹通常是椭圆形状,可以通过改变曲柄的转动角度和滑块位置来实现不同的运动路径。
在实际应用中,曲柄滑块机构常被用于发动机和机械传动系统中,其运动学分析对于提高机构的效率和可靠性至关重要。
平面四杆机构是一种更为复杂的多连杆机构,它由四个连杆和四个铰接节点组成。
平面四杆机构的运动学分析涉及到大量的几何关系和运动学方程的推导,需要利用刚体座标系和几何约束条件进行求解。
通过解析解或数值解的方法,可以求得平面四杆机构的运动轨迹、速度和加速度等运动学参数,为机构的合理设计提供了重要依据。
在多连杆机构的合理设计中,除了运动学分析以外,还需要考虑机构的结构刚度、平衡性和可靠性等因素。
合理的机构设计可以提高机构的性能,并确保机构能够承受预期的载荷和工作环境。
此外,还需要考虑机构的制造成本和装配难度等实际因素,以实现设计与制造的良好平衡。
总之,多连杆机构的运动学分析和合理设计是一项复杂而重要的任务。
通过分析机构的运动学特性和设计要求,可以实现对机构运动路径和性能的优化控制。
实验二平面连杆机构设计分析及运动分析综合实验一、实验目的:1、掌握机构运动参数测试的原理和方法。
了解利用测试结果,重新调整、设计机构的原理。
2、体验机构的结构参数及几何参数对机构运动性能的影响,进一步了解机构运动学和机构的真实运动规律。
3、熟悉计算机多媒体的交互式设计方法,实验台操作及虚拟仿真。
独立自主地进行实验内容的选择,学会综合分析能力及独立解决工程实际问题的能力,了解现代实验设备和现代测试手段。
二、实验内容1、曲柄滑块机构及曲柄摇杆机构类型的选取。
2、机构设计,既各杆长度的选取。
(包括数据的填写和调整好与“填写的数据”相对应的试验台上的杆机构的各杆长度。
)3、动分析(包括动态仿真和实际测试)。
4、分析动态仿真和实测的结果,重新调整数据最后完成设计。
三、实验设备:平面机构动态分析和设计分析综合实验台,包括:曲柄滑块机构实验台、曲柄摇杆机构实验台,测试控制箱,配套的测试分析及运动仿真软件,计算机。
四、实验原理和内容:1、曲柄摇杆机构综合试验台①曲柄摇杆机构动态参数测试分析:该机构活动构件杆长可调、平衡质量及位置可调。
该机构的动态参数测试包括:用角速度传感器采集曲柄及摇杆的运动参数,用加速度传感器采集整机振动参数,并通过A/D板进行数据处理和传输,最后输入计算机绘制各实测动态参数曲线。
可清楚地了解该机构的结构参数及几何参数对机构运动及动力性能的影响。
②曲柄摇杆机构真实运动仿真分析:本试验台配置的计算机软件,通过建模可对该机构进行运动模拟,对曲柄摇杆及整机进行运动仿真,并做出相应的动态参数曲线,可与实测曲线进行比较分析,同时得出速度波动调节的飞轮转动惯量及平衡质量,从而使学生对机械运动学和动力学,机构真实运动规律,速度波动调节有一个完整的认识。
③曲柄摇杆机构的设计分析:本试验台配置的计算机软件,还可用三种不同的设计方法,根据基本要求,设计符合预定运动性能和动力性能要求的曲柄摇杆机构。
另外还提供了连杆运动轨迹仿真,可做出不同杆长,连杆上不同点的运动轨迹,为平面连杆机构按运动轨迹设计提供了方便快捷的虚拟实验方法。
连杆机构的动力学分析与优化设计连杆机构是一种常见的机械传动装置,它由若干个连杆组成,通过铰链连接在一起。
连杆机构广泛应用于各个领域,如发动机、泵浦、机床等,对于实现复杂运动和力学传递起到重要的作用。
本文将对连杆机构的动力学分析与优化设计进行探讨。
一、连杆机构的动力学分析连杆机构的动力学分析是研究其运动规律和受力分布的过程。
在动力学分析中,我们可以通过构建连杆机构的运动学方程和受力方程来描述其运动和受力情况。
1. 运动学方程运动学方程描述了连杆机构中各个连杆的位置和速度之间的关系。
通过连杆机构的几何形状和运动特点,我们可以推导出各个连杆的位置和速度方程。
运动学方程的求解可以帮助我们了解连杆机构的运动规律和运动参数。
2. 受力方程受力方程描述了连杆机构中各个连杆受力的情况。
通过对各个铰链点的受力平衡条件的分析,我们可以得到连杆机构中各个连杆的受力方程。
受力方程的求解可以帮助我们了解连杆机构中各个连杆的力学特性,为优化设计提供基础。
二、连杆机构的优化设计连杆机构的优化设计旨在提高其性能和效率。
在连杆机构的优化设计中,我们可以从以下几个方面进行改进。
1. 结构优化连杆机构的结构优化包括选取合适的连杆尺寸和形状,以及确定连杆的连接方式。
通过对连杆机构结构的优化设计,可以减小其重量和体积,提高其刚度和强度,从而提高整个机构的性能。
2. 运动特性优化连杆机构的运动特性优化包括提高其运动平稳性和运动精度。
在优化设计过程中,可以通过调整连杆的长度比例和位置布局,以及选用合适的铰链点来改善连杆机构的运动特性。
运动特性优化可以使连杆机构实现更加精确和稳定的运动。
3. 动力优化连杆机构的动力优化包括提高其传动效率和降低能耗。
在优化设计过程中,可以选用合适的传动形式和传动参数,以及减小传动过程中的能量损失来改善连杆机构的动力性能。
动力优化可以提高连杆机构的整体效率,并减少对能源的消耗。
三、连杆机构的应用领域连杆机构广泛应用于各个领域,如发动机、泵浦、机床等。
基于SolidWorks的连杆机构的运动分析与仿真共3篇基于SolidWorks的连杆机构的运动分析与仿真1基于SolidWorks的连杆机构的运动分析与仿真引言机械工程是一门涵盖广泛领域的学科,而其核心是机械设计。
机械设计在现代化社会中具有举足轻重的地位,是实现生产自动化、机械化和数字化的必不可少的手段。
在机械设计中,连杆机构是一种非常重要的机械构件,因其能够将单向的直线运动转换为复杂的曲线运动。
因此,了解和掌握连杆机构的运动特点对于机械工程师和设计师具有非常大的实用价值。
本文将介绍基于SolidWorks的连杆机构的运动分析与仿真。
正文SolidWorks是目前应用最广泛的三维计算机辅助设计(CAD)软件之一,其主要功能是建立三维模型和进行工程分析。
在SolidWorks中,连杆机构是一种常用的机构,在机械设计中有着广泛的应用。
通过 SolidWorks 可以进行连杆机构的建模、运动分析和仿真等全过程,以便更好地理解该机构的运动特点,为机械设计提供便利。
连杆机构是一种具有连杆、销轴和铰链等构件相互连接而成的复杂机械结构。
通过连杆机构可以将旋转运动和直线运动相互转换,实现有效的动力传递和力量转换。
对于机械设计师而言,了解连杆机构的运动特点是非常重要的。
在SolidWorks中,连杆机构的建模首先需要考虑构件的建立。
构件的建立应符合物理规律和机械原理,并使得机构具有合适的运动特性。
比如,在连杆机构中,需要考虑杆件的长度、销轴的直径、铰链的设计等因素。
在建模过程中,需要给予合适的参数设定,从而实现模型的运动模拟。
模型建立完毕后,可进行三维建模、组装和运动仿真。
通过连杆机构的仿真,可以深入地理解机械运动规律和性能特点,为机械设计提供便利。
此外,连杆机构的运动分析也是非常重要的一步。
通过对运动分析的深入研究,可以了解动力学和运动学的相关规律,为机械设计提供依据。
具体地,运动分析包括以下几个方面:速度和加速度分析、运动轨迹分析、力学分析等。
连杆机构的运动分析报告连杆机构的运动分析报告连杆机构是一种常见的机械结构,由连杆和铰链组成。
通过连杆的连接和铰链的运动,连杆机构可以实现复杂的机械运动。
在本篇文章中,我们将对连杆机构的运动进行分析。
首先,我们需要了解连杆机构的基本组成。
连杆机构通常由两个或多个连杆组成,这些连杆通过铰链连接。
在连杆机构中,至少有一个连杆是固定的,称为固定连杆,其他连杆可以通过铰链连接进行运动,称为运动连杆。
接下来,我们需要确定连杆机构的运动目标。
连杆机构可以用于实现各种运动,例如直线运动、旋转运动、摆动运动等。
在分析时,我们需要明确机构的运动目标是什么,以便更好地理解和分析机构的运动性质。
然后,我们可以通过建立连杆机构的几何模型来进行运动分析。
连杆机构的几何模型是通过连杆的长度、连杆之间的连接方式以及铰链的位置来确定的。
通过几何模型,我们可以计算出各个连杆的位置、速度和加速度等参数,从而分析机构的运动性质。
在进行运动分析时,我们需要应用运动学原理。
根据连杆机构的特点,我们可以使用欧拉方程或拉格朗日方程来描述机构的运动。
通过这些方程,我们可以得到机构的运动方程,从而进一步分析和预测机构的运动。
此外,我们还可以使用计算机辅助分析工具来进行连杆机构的运动分析。
通过使用计算机软件,我们可以建立机构的数学模型,并进行模拟计算,从而更准确地分析机构的运动性质。
这种方法可以大大提高分析的效率和准确性。
最后,我们可以根据运动分析的结果对连杆机构进行设计和优化。
通过分析连杆机构的运动性质,我们可以了解机构的工作原理和特点,从而进一步改进和优化机构的设计。
通过优化设计,可以提高机构的性能和效率,实现更好的运动控制和工作效果。
总之,连杆机构的运动分析是理解和设计机械结构的重要方法。
通过逐步分析连杆机构的运动特性,我们可以深入了解机构的工作原理,为机构的设计和优化提供有力的支持。
机械原理大作业一课程名称:机械原理设计题目:连杆机构运动分析1 、题目如图所示机构,一只机构各构件的尺寸为AB=100mm,BC=4.28AB,CE=4.86AB,BE=8.4AB,CD=2.14AB,AD=4.55AB,AF=7AB,DF=3.32AB,∠BCE=139˚。
构件1的角速度为ω1=10rad/s,试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度,并对计算结果进行分析。
ABCDEF123452、机构结构分析该机构由6个构件组成,4和5之间通过移动副连接,其他各构件之间通过转动副连接,主动件为杆1,杆2、3、4、5为从动件,2和3组成Ⅱ级RRR基本杆组,4和5组成Ⅱ级RPR基本杆组。
如图建立坐标系ABCD EF12345YX3、各基本杆组的运动分析数学模型1) 位置分析⎩⎨⎧+=+=i AB A B iAB A B l y y l x x ϕϕsin cos 2) 速度和加速度分析将上式对时间t 求导,可得速度方程:sin cos BAB B A i iB AB B A i i dx x x l dtdy y y l dtϕϕϕϕ⎧==-⎪⎪⎨⎪==+⎪⎩ 将上式对时间t 求导,可得加速度方程:222222cos sin cos cos BAB AB B A i i i i B AB AB B A i i i id x x x l l dtd y y y l l dt ϕϕϕϕϕϕϕϕ⎧==--⎪⎪⎨⎪==-+⎪⎩RRR Ⅱ级杆组的运动分析如下图所示 当已知RRR 杆组中两杆长L BC 、L CD 和两外副B 、D 的位置和运动时,求内副C 的位置、两杆的角位置、角运动以及E 点的运动。
CXY1) 位置方程cos cos sin sin BC CD C B i D jBC CD C B i D jx x l x l y y l y l ϕϕϕϕ=+=+⎧⎪⎨=+=+⎪⎩ 由移项消去j ϕ后可求得i ϕ:002arctan i ϕ=⎝⎭式中,()()00222022BC D B BC D B BC BD CDBDA l x xB l y yC l l l l ⎧=-⎪=-⎪⎪⎨=+-⎪⎪=⎪⎩可求得j ϕ:2arctan C D j C D y y x x ϕ⎛⎫-=⎪-⎝⎭E 点坐标方程:()()cos sin BE E B i BE E B i x x l y y l ϕθϕθ=+-⎧⎪⎨=+-⎪⎩ 其中222cos 2i k ji k l l l l l θ⎛⎫+-= ⎪ ⎪⎝⎭2) 速度方程两杆角速度方程为()()()()11//i i j D B j D B j j i D B i D B C x x S y y G C x x S y y G ωϕωϕ⎧⎡⎤==-+-⎪⎣⎦⎨==-+-⎡⎤⎪⎣⎦⎩ 式中,1cos cos sin sin i j j i BC i i CD j j BC i i CD j jG C S C S C l C l S l S l ϕϕϕϕ=-====点E 速度方程为()()()()sin sin cos cos Ex B i BE i Bx i BE i EyB i BE i By i BE i v x l v l v y l v l ϕϕθωϕθϕϕθωϕθ=--=--⎧⎪⎨=+-=+-⎪⎩ 3) 加速度方程两杆角加速度为()()231231//i i j j j j i i G C G S G G C G S G αϕαϕ⎧==+⎪⎨==+⎪⎩ 式中,222223D B i i j j D B i i j j G x x C C G y y S S ϕϕϕϕ⎧=-+-⎪⎨=-+-⎪⎩点E 加速度方程为()()()()()()()()2222sin cos sin cos cos sin cos sin ex B i BE i i BE i Bx i BE i i BE i ey B i BE i i BE i By i BE i i BE i a x l l a l l a y l l a l l ϕϕθϕϕθαϕθωϕθϕϕθϕϕθαϕθωϕθ⎧=----=----⎪⎨=+---=+---⎪⎩RPR Ⅱ级杆组的运动分析(1) 位移方程arctanE FiE Fx x y y ϕ-=-(2)速度方程()sin cos /i Ex i Ey i iv v l ωϕϕ=-+其中i l =(3)加速度方程()sin cos /i Ex i Ey i i a a l αϕϕ=-+4、 计算编程利用MATLAB 软件进行编程,程序如下:% 点B 和AB 杆运动状态分析 >>r=pi/180; w 1=10; e 1=0; l 1=100; Xa=0; Ya=0; Vax=0; Vay=0; aax=0; aay=0;f1=0:1: 360; % B 点位置Xb=Xa+l1*cos(r*f1); Yb=Ya+l1*sin(r*f1); % B 点速度Vbx=V ax-w1*l1*sin(r*f1);Vby=Vay+w1*l1*cos(r*f1);% B点加速度abx=aax-l1*w1.^2.*cos(r*f1);aby=aay-l1*w1.^2.*sin(r*f1);% RRR2级杆组运动分析% 输入D点参数l2=428;l3=214;Xd=455;Yd=0;Vdx=0;Vdy=0;adx=0;ady=0;% 计算E点、2杆、3杆运动参数lbe=840;lce=486;a0=2*l2*(Xd-Xb);b0=2*l2*(Yd-Yb);c0=l2^2+(Xb-Xd).^2+(Yb-Yd).^2-l3^2;f2=2*atan((b0+sqrt(a0.^2+b0.^2-c0.^2))./(a0+c0)); % C点位置Xc=Xb+l2*cos(f2);Yc=Yb+l2*sin(f2);% 2杆、3杆运动参数计算dX=Xc-Xd;dY=Yc-Yd;for n=1:length(dX)if dX(n)>0&dY(n)>=0f3(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f3(n)=pi/2;elseif dX(n)<0&dY(n)>=0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f3(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f3(n)=2*pi+atan(dY(n)/dX(n));endendC2=l2*cos(f2);C3=l3*cos(f3);S2=l2*sin(f2);S3=l3*sin(f3);G1=C2.*S3-C3.*S2;w2=(C3.*(Vdx-Vbx)+S3.*(Vdy-Vby))./G1;w3=(C2.*(Vdx-Vbx)+S2.*(Vdy-Vby))./G1;G2=adx-abx+(w2.^2).*C2-(w3.^2).*C3;G3=ady-aby+(w2.^2).*S2-(w3.^2).*S3;e2=(G2.*C3+G3.*S3)./G1;% E点位置w=acos((l2^2+lbe^2-lce^2)/(2*l2*lbe));Xe=Xb+lbe*cos(f2-w);Ye=Yb+lbe*sin(f2-w);Vex=Vbx-lbe*w2.*sin(f2-w);Vey=Vby+lbe*w2.*cos(f2-w);aex=abx-lbe*(e2.*sin(f2-w)+w2.^2.*cos(f2-w));aey=aby+lbe*(e2.*cos(f2-w)-w2.^2.*sin(f2-w));% 计算杆5运动参数Xf=646.2912088;Yf=-268.9008617;l5=sqrt((Xe-Xf).^2+(Ye-Yf).^2);dX=Xe-Xf;dY=Ye-Yf;for n=1:length(dX)if dX(n)>0&dY(n)>=0f5(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f5(n)=pi/2;elseif dX(n)<0&dY(n)>=0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f5(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f5(n)=2*pi+atan(dY(n)/dX(n));endendw5=(-Vex.*sin(f5)+Vey.*cos(f5))./l5;a5=(-aex.*sin(f5)+aey.*cos(f5))./l5;% 画出各参数曲线figure(1);plot(Xe,Ye,'k');xlabel('Xe/\mm');ylabel('Ye/mm');grid on;title('E点位置'); figure(2);plot(f1,f5,'k');xlabel('f/\circ');ylabel('f5/\circ');grid on;title('5杆角位移'); figure(3);plot(f1,w5,'k');xlabel('f/\circ');ylabel('w5/rad/s');grid on;title('5杆角速度'); figure(4);plot(f1,a5,'k');xlabel('f/\circ');ylabel('a5/rad/s2');grid on;title('5杆角加速度'); Warning: Unable to interpret TeX string "Xe/\mm"5、计算结果图一:E点的运动轨迹图二:5杆角位移图三:5杆角速度图四:5杆角加速度6、计算结果分析由E点位置图像可看出,构件4做周期往复运动,由图二、三、四可看出,构件5的角位移、角速度、角加速度均成周期性变化。