大话多旋翼飞行器--欧拉角与四元数

X型四旋翼无人机建模及四元数控制
丁少宾;肖长诗;刘金根;文元桥
【期刊名称】《系统仿真学报》
【年(卷),期】2015(0)12
【摘要】对X型四旋翼无人机做了合理假设以及受力分析,推导并建立了X型四旋翼无人机全面的动力学数学模型,考虑了无人机平动、转动空气阻力,并且将转子、螺旋桨和机体看成多刚体系统。

在Solidworks软件中,建立了无人机实物模型以获得无人机惯性参数。

直接以四元数作为反馈控制量,设计出多通道双回路矢量PD 控制系统。

以Matlab/Simulink为平台,对四元数反馈控系统和欧拉角反馈控制系统进行对比控制仿真。

从仿真结果来看,这2种反馈模式都能对无人机模型进行位置、姿态跟踪等控制,但是四元数反馈控制系统具有过渡时间短、计算量少以及无奇点产生的优点。

【总页数】6页(P3057-3062)
【作者】丁少宾;肖长诗;刘金根;文元桥
【作者单位】湖北省内河航运技术重点实验室;武汉理工大学信息工程学院光纤传感技术与信息处理教育部重点实验室
【正文语种】中文
【中图分类】V249.1
【相关文献】
1.四旋翼无人机建模与PID控制器设计
2.超/特高压输电线路巡检四旋翼无人机的建模与回馈递推控制
3.自主巡线四旋翼无人机建模及姿态控制器设计
4.四旋翼无人机的控制原理及建模
5.带单关节机械臂四旋翼无人机的建模与控制
因版权原因，仅展示原文概要，查看原文内容请购买。

飞行器姿态动力学建模方法比较综述飞行器姿态动力学建模是飞行器设计和控制的重要工作之一。

姿态动力学模型描述了飞行器在空中运动过程中的导航、姿态变化和动力学响应。

准确建模飞行器的姿态动力学对于飞行控制系统的设计、性能评估和飞行安全至关重要。

在飞行器姿态动力学建模中，主要涉及到飞行器的姿态表示、运动方程和控制输入等方面。

根据姿态表示的方法可以将姿态动力学模型分为欧拉角、四元数和旋转矩阵等不同的表示形式。

同时，在建模过程中也需要考虑到飞行器的非线性特性，以及可能存在的不确定性和扰动。

常见的飞行器姿态动力学建模方法包括欧拉角方法、四元数方法、旋转矩阵方法和仿射变换方法等。

每种方法都有其特点和适用范围。

下面将对这些方法进行综述和比较。

1. 欧拉角方法欧拉角方法是最常见和直观的姿态表示方法之一。

它将飞行器的姿态分解为绕三个相互垂直的轴（通常是roll、pitch和yaw轴）的旋转角度。

然而，由于欧拉角存在奇异点和万向锁等问题，这种方法在某些情况下不够精确和稳定。

2. 四元数方法四元数方法通过四元数数值来表示飞行器的姿态，它具有无奇异性和唯一性的特点，能够准确描述飞行器的旋转。

四元数方法相对于欧拉角方法在计算上更加高效和精确，因此在飞行控制中得到广泛应用。

3. 旋转矩阵方法旋转矩阵方法使用一个3x3的矩阵来表示姿态，该矩阵描述了飞行器的旋转变换。

旋转矩阵方法在计算上相对复杂，但可以提供更多的姿态信息，适用于需要高精度姿态表示的任务。

4. 仿射变换方法仿射变换方法是一种灵活的建模方法，可以通过旋转、平移和缩放等变换来描述飞行器的姿态。

这种方法可以较好地处理复杂姿态动力学建模问题，但也需要更多的计算资源和数学基础。

综合比较这些方法可以发现，四元数方法是最受欢迎和实用的飞行器姿态动力学建模方法之一。

四元数方法相比于其他表示方法具有更高的计算效率和数值稳定性，并且可以避免奇异性和万向锁问题。

因此，在飞行器姿态动力学建模中，四元数方法可以作为首选方法使用。

四元数与欧拉角刚体动力学数值积分算法及其比较徐小明;钟万勰【摘要】为推广四元数保辛积分在工程中的应用,对欧拉角表示的状态方程数值积分与四元数的保辛积分进行比较.重陀螺的数值仿真结果表明四元数保辛积分的数值结果明显优于欧拉角状态方程积分.与欧拉角状态方程积分相比,四元数保辛积分在刚体动力学的数值仿真中更具优势.【期刊名称】《计算机辅助工程》【年(卷),期】2014(023)001【总页数】6页(P59-63,75)【关键词】四元数;欧拉角;刚体动力学;保辛;重陀螺【作者】徐小明;钟万勰【作者单位】大连理工大学工程力学系,辽宁大连116024;大连理工大学工业装备结构分析国家重点实验室,辽宁大连116024;大连理工大学工程力学系,辽宁大连116024;大连理工大学工业装备结构分析国家重点实验室,辽宁大连116024【正文语种】中文【中图分类】TP391.9;O313.30 引言四元数、欧拉角和方向余弦［1］是描述刚体旋转最主要的3 种坐标形式.方向余弦法需要9 个参量，应用较少;而另外2 种则应用广泛，如航天器姿态控制和捷联式惯性导航系统［1］等，对于两者的研究也卷帙浩繁，但对两者优劣的评价却褒贬不一.描述刚体在三维空间中的运动姿态可采用2 类12 种欧拉角系统，分别对应于不同的旋转轴先后次序.目前公认的用欧拉角描述旋转的固有缺陷是奇异性问题［2］，即:无论采用哪种欧拉角系统，都不可避免地会含有奇异点，使得在该点附近区域进行的数值积分精度不高.对于小角度旋转，只要采用适当的欧拉角系统便可避开奇异点;而在大角度旋转时，若想避开奇异点，必须提供2 套欧拉角系统交替进行计算.据此，黄雪樵［3］提出一种“双欧法”的计算方法;近几年仍有学者［4］在继续研究该方法.双欧法虽然解决奇异性问题，但是计算过程较复杂.四元数用于描述刚体旋转，没有奇异性问题，可很好地描述刚体的全角度旋转.然而，四元数需要满足长度等于1 的单位约束，这成为制约其应用的限制.在实际应用中，经常采用的正交化修正等方法只能缓解长度的偏移，无法从根本上解决问题;黄雪樵［3］在其双欧法中也有所讨论.目前，对于单位约束最佳的解决方案是将四元数表示的刚体动力学方程导入微分代数方程范畴，近年来逐渐有学者［5-7］展开相关问题的研究.徐小明等［8］提出一种基于四元数理论描述刚体旋转的保辛数值积分方法.该方法先将问题导入微分-代数方程系统，然后利用分析结构力学理论［9］进行逐步积分，该积分保辛.该方法在积分点上严格满足四元数长度等于1 的约束条件，而在区段内部则由插值近似，属于祖冲之类方法［10］.数值算例表明仿真效果优异.本文简要介绍四元数和欧拉角的基本理论，以重陀螺为例对2 种表示形式的数值积分进行比较.对于欧拉角表述，应用比较普遍的状态方程表述.研究表明，以欧拉角和角速度为状态变量形成的1 阶微分方程在使用差分近似积分时，精度损失很大，能量不守恒;该现象被周江华等［11］称为“睡陀螺”.这是一个值得注意的问题，却未得到广泛关注;而采用文献［8］给出的保辛格式，四元数单位长度约束条件得到满足，仿真结果优异，能量也达到守恒.1 刚体旋转及其运动学表示刚体运动由质心平动和绕质心转动组成.如果刚体上有一固定点，则称为刚体定点转动问题.假设Oxyz 为系统的惯性坐标系，O 为原点，亦为固定点.Ox'y'z'为随体坐标系，固定于刚体上.若将刚体的随体坐标轴取为与固定点有关的主轴，则刚体定点转动可由式(1)描述.式中:I1，I2和I3为将定点选为参考点的主转动惯量;ω1，ω2和ω3为绕3 个主轴的角速度分量;N1，N2和N3为外力矩沿3 个主轴的分量.式(1)中的3 个方程称为刚体定点转动的欧拉方程.要求解式(1)的微分方程，还需将描述旋转的坐标与角速度联系起来.如果采用欧拉角描述刚体运动，可设φ，θ 和Ψ 分别代表绕z 轴、转动后的x 轴及二次转动后的z 轴的三次旋转，即采用12 种欧拉角系统中的z-x-z 模式，则角速度分量与欧拉角之间的微分关系可以表示为式(2)称为刚体定点转动的运动方程.将式(2)与式(1)联立，将(φ，θ，Ψ)作为广义位移，将(ω1，ω2，ω3)作为广义速度，构成系统的状态方程.对于此状态方程，应用欧拉差分格式或者龙格库塔格式等可进行数值积分.本文将在第2 节对其应用辛-欧拉格式［12］进行研究.另一方面，若采用单位四元数描述旋转，则有四元数的运动学方程可以定义四元数向量式(3)隐含着四元数单位长度的约束条件将式(3)与式(1)联立可得状态方程，对其应用数值算法求解，约束条件无法很好地满足，往往导致结果失真.反对称群是正交矩阵群的李代数［8］，据此在群上定义微商，可将式(3)等价成式中:通过式(6)便可得到刚体的动能，进而得到系统的Lagrange 函数，然后通过作用量的变分原理进行数值离散求解，具体算法见第2 节.2 数值积分算法首先给出2 种表示形式的积分格式.对于欧拉角，采用辛-欧拉差分格式［12］.为此，可将式(2)和(1)写为式中:则欧拉差分格式为对式(11)进行迭代便可逐步积分求解.根据文献［12］，将式(11)应用于Hamilton 正则方程可达到保辛效果.显然式(8)仅是状态方程表述，不能达到保辛效果.然而，式(8)应用十分广泛，形式也较为简单，对其数值积分进行比较研究具有一定的现实意义.对于四元数的数值积分，首先需要刚体系统的Lagrange 函数式中:U(q)为系统的势能为系统的动能.根据式(6)，式(12)可以写为式中:q 参见式(4).要进行数值积分，首先要对系统进行有限元离散.具体来说，取离散时间区段η，t0=0，t1=η，t2=2η，…，tk=kη，….可假设tk-1时的位移与速度是已知，并满足的约束.现在的问题是通过tk-1步的已知量计算下一个时间步的qk和为此，首先在［tk-1，tk］时间段内做有限元离散.为计算简便，假设区段内的位移和速度分别为则根据式(12)与四元数约束条件可以得到离散的区段作用量(含约束)式中:λk-1和λk为Lagrange 乘子.根据分析结构力学理论［9］给出四元数的保辛积分格式，对式(16)进行迭代便可逐步积分求解.对于式(16)的具体推导以及作为参考的具体算法见文献［8］.3 重陀螺的数值模拟3.1 算例1图1 对称重陀螺Fig.1 Symmetric heavy top考察如图1 所示的对称重陀螺绕其尖点O 的运动.该尖点固定于惯性空间;取陀螺的对称轴为随体坐标Ox'y'z'的z'轴;陀螺质心与尖点的距离为l，陀螺的基本参数为:m=1 kg，l=0.04 m，I1=I2=0.002 0 kg·m2，I3=0.000 8 kg·m2.取重力加速度g=9.8 m/s2.对于此例，可以写出式(10)对应的重力矩的具体表达式以及式(12)对应的重力势能的具体形式对于初始时刻，选取对应于式(16)的初始条件为对于式(4)在k=1 时的p0，结合式(12)和(20)，则由Legendre 变换给出具体见文献［8］.这一初始条件对应于陀螺运动中的“尖点运动”.设陀螺对称轴(z'轴)与单位球面的交点为A，则任意时刻A 点的位置由式(22)确定.采用四元数表示则为对称重陀螺的z'轴与单位球面交点A 的z 坐标-时间曲线见图2.对于对称重陀螺，是有椭圆函数解的，z 随时间应该呈周期变化.由图2 可知，唯有当时间间隔非常小时，用欧拉角表示刚体旋转的辛-欧拉差分格式的数值解才与解析解拟合得较好，步长较大时呈现发散现象;而基于四元数的保辛积分，不论大步长还是小步长，均与解析解吻合得很好.其中，当步长取Δt=10-2 s 时，1 个周期内仅有15 个左右的积分点，与解析解相比，仅仅相位略微超前，表明在大步长下数值积分的结果仍然可信.图2 对称重陀螺的z＇轴与单位球面交点A 的z 坐标-时间曲线Fig.2 z coordinate vs time curves of point A of intersection of symmetric heavytop axis z＇ and unit sphere对称重陀螺A 点长时间轨迹沿x-y 平面的投影见图3.由于是保守系统，z'轴应以z 轴为轴绕其转动，周而复始，所以A 点沿x-y 平面的投影应该限制在一个圆环内.图3(b)表明四元数的保辛积分很好地模拟这一现象;图3(a)表明，在Δt=10-3 s 时，欧拉角的保辛积分结果完全失真，实际上如果继续减小步长至Δt=10-4 s，为四元数积分步长的1/100，这一现象仍未得到缓解.本文采用的是辛-欧拉格式，文献［11］中采用4 阶龙格库塔法，同样出现此现象，被称之为“睡陀螺”.图3 对称重陀螺A 点长时间轨迹沿x-y 平面的投影Fig.3 x-y plane projectionof long time trajectory of point A for symmetric top2 种数值积分的系统能量随时间变化情况见图4.在欧拉角表示中，虽然采用辛-欧拉格式进行数值积分，但是能量却保持得不好，这验证对状态方程应用辛-欧拉格式并不能保辛.与之相反，四元数的数值积分保辛，其能量保持得很好，这也是保辛积分的优势所在.四元数保辛积分的约束误差见图5，表明在时间积分过程中单位长度约束条件满足得很好.3.2 算例2将算例1 中转动惯量改为I1=0.002 25 kg·m2，I2=0.001 75 kg·m2，I3不变，其他参数以及初始条件与算例1 相同.不对称重陀螺A 点长时间轨迹沿x-y 平面的投影见图6，采用的是基于四元数的保辛积分.与图2(b)对比可看出，其轨迹一直限制在一圆环内，这也是保守系统的特点.本例表明，四元数保辛积分，不论对于对称陀螺还是不对称陀螺，均能达到较好的仿真效果.图4 两种数值积分的系统的能量随时间变化情况Fig.4 Energy variation with respect to time for two numerical integration systems图5 四元数保辛积分的约束误差Fig.5 Constraint error of symplectic preservation integration of quaternion图6 不对称重陀螺A 点长时间轨迹沿x-y 平面的投影Fig.6 x-y plane projection of long time trajectory of point A for asymmetric top注：时间间隔Δt=10-2 s，时间长度t=50 s4 结束语介绍2 种刚体旋转的数值积分，一种基于欧拉角表示，另一种基于四元数表示.以重陀螺的高速旋转为例，对2 种数值积分进行比较发现:以欧拉角、角速度组成状态变量，然后直接使用辛-欧拉格式不能保辛，能量衰减很快，数值积分存在缺陷;与之相反，采用四元数表示，根据分析结构力学的保辛积分方法，并结合祖冲之类方法的思想，可以很好地避免约束违约，仿真效果令人满意，可作为陀螺等仿真分析的有力工具.本文仅对以欧拉角、角速度组成状态变量的数值积分进行研究，对其他形式并未涉及，对其积分效果不佳的成因亦未研究，还有很多工作有待展开.参考文献:【相关文献】［1］张树侠，孙静.捷联式惯性导航系统［M］.北京：国防工业出版社，1992：48-80.［2］赵晓颖，温立书，么彩莲.欧拉角参数表示下姿态的2 阶运动奇异性［J］.科学技术与工程，2012，12(3) ：634-637.ZHAO Xiaoying，WEN Lishu，YAO Cailian.The second-order kinematic singularity of orientation in Euler parameters representation［J］.Sci Technol ＆Eng，2012，12(3) ：634-637.［3］黄雪樵.克服欧拉方程奇异性的双欧法［J］.飞行力学，1994，12(4) ：28-37.HUANG Xueqiao.The dual-Euler method for overcoming the singularity of Euler equation［J］.Flight Dynamics，1994，12(4) ：28-37.［4］李跃军，阎超.飞行器姿态角解算的全角度双欧法［J］.北京航空航天大学学报，2007，33(5) ：505-508.LI Yuejun，YAN Chao.Improvement of dual-Euler method for full scale Eulerian angles solution of aircraft［J］.J Beijing Univ Aeronautics ＆Astronautics，2007，33(5) ：505-508.［5］NIKRAVESH P E，WEHAGE R A，KWON K.Euler parameters in computational kinematics and dynamics：Part 1［J］.J Mechanisms，Transmissions ＆ Automation Des，1985，107(3) ：358-365.［6］BETSCH P，SIEBERT R.Rigid body dynamics in terms of quaternions：Hamiltonian formulation and conserving numerical integration［J］.Int J Numer Methods Eng，2009，79(4) ：444-473.［7］UDWADIA F E，SCHUTTE A D.An alternative derivation of the quaternion equationsof motion for rigid-body rotational dynamics［J］.J Appl Mech，2010，77(4) ：44505. ［8］徐小明，钟万勰.刚体动力学的四元数表示及保辛积分［J］.应用数学和力学，2014，35(1) ：1-11.XU Xiaoming，ZHONG Wanxie.Symplectic integration of rigid body motion by quaternion parameters［J］.Appl Math ＆ Mech，2014，35(1) ：1-11.［9］钟万勰，高强.约束动力系统的分析结构力学积分［J］.动力学与控制学报，2006，4(3) ：193-200.ZHONG Wanxie，GAO Qiang.Integration of constrained dynamical system via analytical structrural mechanics［J］.J Dynamics ＆ Contr，2006，4(3) ：193-200.［10］钟万勰，高强，彭海军.经典力学辛讲［M］.大连：大连理工大学出版社，2013：202-241. ［11］周江华，苗育红，李宏，等.四元数在刚体姿态仿真中的应用研究［J］.飞行力学，2000，18(4) ：28-32.ZHOU Jianghua，MIAO Yuhong，LI Hong，et al.Research of attitude simulation using guaternion［J］.Flight Dynamics，2000，18(4) ：28-32.［12］HAIRER E，LUBICH C，WANNER G.Geometric numerical integration：structure-preserving algorithms for ordinary differential equations［M］.Berlin：Springer，2006：189.。

1.欧拉角在四元数出现之前先看下欧拉角：对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。

为了后面的角度不混乱，我们要先区分参考系和坐标系的概念。

参考系即为大地参考系，是静止不动的。

而坐标系则固定于四轴飞行器，随着四轴飞行器的旋转而旋转。

按照右图所示。

设定xyz-轴为四轴上的参考轴，XYZ-轴则是大地的参考轴。

右图即为四轴相对地面进行了一定旋转，xy-平面与XY-平面的相交线为交点线，用英文字母（N）代表。

我们可以这样定义欧拉角：α是x-轴与交点线的夹角β是z-轴与Z-轴的夹角γ是交点线与X-轴的夹角这样我们就可以用三个欧拉角：(α，β，γ)其取值为0-360来描述四轴飞行器相对于大地的参考系的姿态角度了。

三个欧拉角：(α，β，γ)。

蓝色的轴是xyz-轴，红色的轴是XYZ-坐标轴。

绿色的线是交点线(N) 。

2.轴角欧拉角使用roll，pitch，yaw来表示这些分量的旋转值。

需要注意的是，这里的旋转是针对大地参考系说的，这意味着第一次的旋转不会影响第二、三次的转轴，简单的说，三角度系统无法表现任意轴的旋转，只要一开始旋转，物体本身就失去了任意轴的自主性，这也就导致了万向节锁（Gimbal Lock）的问题。

什么是Gimbal Lock？正如前面所说，因为欧拉描述中针对x,y,z的旋转描述是世界坐标系下的值，所以当任意一轴旋转90°的时候会导致该轴同其他轴重合，此时旋转被重合的轴可能没有任何效果，这就是Gimbal Lock，还有一种是轴角的描述方法，这种方法比欧拉描述要好，它避免了Gimbal Lock，它使用一个3维向量表示转轴和一个角度分量表示绕此转轴的旋转角度，即(x,y,z,angle)，一般表示为(x,y,z,w)或者(v,w)。

(x,y,z)为旋转轴，w为旋转角度。

但这种描述法却不适合插值。

轴角的表示方法：那么轴、角的描述方法又有什么问题呢？虽然轴、角的描述解决了Gimbal Lock，但这样的描述方法会导致差值不平滑，差值结果可能跳跃，欧拉角描述同样有这样的问题。

（转）四轴飞⾏器6050六轴传感器软件姿态解算使⽤MPU6050硬件DMP解算姿态是⾮常简单的，下⾯介绍由三轴陀螺仪和加速度计的值来使⽤四元数软件解算姿态的⽅法。

我们先来看看如何⽤欧拉⾓描述⼀次平⾯旋转(坐标变换)：设坐标系绕旋转α⾓后得到坐标系,在空间中有⼀个⽮量在坐标系中的投影为,在内的投影为由于旋转绕进⾏，所以Z坐标未变，即有。

转换成矩阵形式表⽰为：整理⼀下：所以从旋转到可以写成上⾯仅仅是绕⼀根轴的旋转，如果三维空间中的欧拉⾓旋转要转三次:上⾯得到了⼀个表⽰旋转的⽅向余弦矩阵。

不过要想⽤欧拉⾓解算姿态，其实我们套⽤欧拉⾓微分⽅程就⾏了：上式中左侧,,是本次更新后的欧拉⾓,对应row,pit,yaw。

右侧，是上个周期测算出来的⾓度，，，三个⾓速度由直接安装在四轴飞⾏器的三轴陀螺仪在这个周期转动的⾓度，单位为弧度，计算间隔时T陀螺⾓速度，⽐如0.02秒0.01弧度/秒=0.0002弧度。

间因此求解这个微分⽅程就能解算出当前的欧拉⾓。

前⾯介绍了什么是欧拉⾓，⽽且欧拉⾓微分⽅程解算姿态关系简单明了，概念直观容易理解，那么我们为什么不⽤欧拉⾓来表⽰旋转⽽要引⼊四元数呢？⼀⽅⾯是因为欧拉⾓微分⽅程中包含了⼤量的三⾓运算，这给实时解算带来了⼀定的困难。

⽽且当俯仰⾓为90度时⽅程式会出现神奇的“GimbalLock”。

所以欧拉⾓⽅法只适⽤于⽔平姿态变化不⼤的情况，⽽不适⽤于全姿态飞⾏器的姿态确定。

四元数法只求解四个未知量的线性微分⽅程组，计算量⼩，易于操作，是⽐较实⽤的⼯程⽅法。

我们知道在平⾯(x,y)中的旋转可以⽤复数来表⽰，同样的三维中的旋转可以⽤单位四元数来描述。

我们来定义⼀个四元数：我们可以把它写成,其中,。

那么是⽮量，表⽰三维空间中的旋转轴。

w是标量，表⽰旋转⾓度。

那么就是绕轴旋转w度，所以⼀个四元数可以表⽰⼀个完整的旋转。

只有单位四元数才可以表⽰旋转，⾄于为什么，因为这就是四元数表⽰旋转的约束条件。

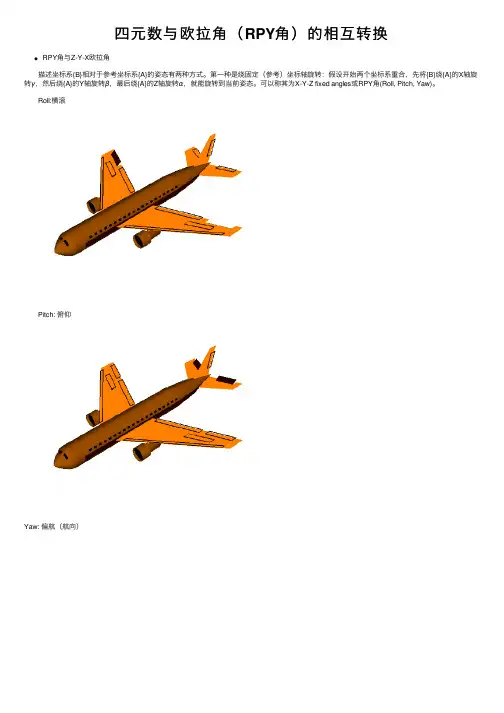
四元数与欧拉⾓（RPY⾓）的相互转换RPY⾓与Z-Y-X欧拉⾓ 描述坐标系{B}相对于参考坐标系{A}的姿态有两种⽅式。

第⼀种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转γ，然后绕{A}的Y轴旋转β，最后绕{A}的Z轴旋转α，就能旋转到当前姿态。

可以称其为X-Y-Z fixed angles或RPY⾓(Roll, Pitch, Yaw)。

Roll:横滚 Pitch: 俯仰Yaw: 偏航（航向） 由于是绕固定坐标系旋转，则旋转矩阵为（cα is shorthand for cosα, sα is shorthand for sinα,and so on.）R XYZ(γ,β,α)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 另⼀种姿态描述⽅式是绕⾃⾝坐标轴旋转：假设开始两个坐标系重合，先将{B}绕⾃⾝的Z轴旋转α，然后绕Y轴旋转β，最后绕X轴旋转γ，就能旋转到当前姿态。

称其为Z-Y-X欧拉⾓，由于是绕⾃⾝坐标轴进⾏旋转，则旋转矩阵为：R Z′Y′X′(α,β,γ)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 可以发现这两种描述⽅式得到的旋转矩阵是⼀样的，即绕固定坐标轴X-Y-Z旋转(γ,β,α)和绕⾃⾝坐标轴Z-Y-X旋转(α,β,γ)的最终结果⼀样，只是描述的⽅法有差别⽽已。

In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.Axis-Angle与四元数 绕坐标轴的多次旋转可以等效为绕某⼀转轴旋转⼀定的⾓度。

四元数旋转举证转欧拉角四元数是一种描述三维空间旋转的数学工具，它是由一个标量和三个虚数构成的，可以视为在四维空间中的点。

与欧拉角相比，四元数旋转具有更好的可靠性和稳定性，并且能够避免万向锁问题（Gimbal lock）。

然而，在实际应用中，许多场景仍然需要将四元数转换为欧拉角进行使用。

那么，如何将四元数转化为欧拉角呢？首先需要明确的是，四元数存在多种表示方式，如单位四元数表示旋转的角度和旋转轴，而其他形式的四元数则不一定具有相同的意义。

因此，在进行四元数与欧拉角转换时，需要根据具体的物理问题和数学约定来选择适当的表示方式。

在将四元数转换为欧拉角时，通常可以采用两种方法，分别为转轴-角度法和旋转矩阵法。

对于两种方法，都需要先将四元数转换为旋转轴和旋转角度或旋转矩阵。

其中，转轴-角度法可以较为简便地进行转换，但存在无法唯一确定欧拉角的问题。

而旋转矩阵法能够确定唯一的欧拉角，但其计算较为繁琐。

对于转轴-角度法，首先需要使用四元数求出旋转轴和旋转角度。

具体方法为将四元数表示为$q=(cos\theta,sin\theta n)$，其中$\theta$为旋转角度，$n$为旋转轴的单位向量。

然后，可以通过反三角函数求出欧拉角，如pitch=$arctan(2(q_wq_x+q_yq_z),(1-2(q_x^2+q_y^2)))$，yaw=$arcsin(2(q_wq_y-q_xq_z))$，roll=$arctan(2(q_wq_z+q_xq_y),(1-2(q_y^2+q_z^2)))$。

在进行转换时，需要注意欧拉角的计算顺序，常见的有Z-Y-X顺序（即roll-pitch-yaw）和X-Y-Z顺序（即yaw-pitch-roll）等。

对于旋转矩阵法，需要求出四元数对应的旋转矩阵，然后通过将旋转矩阵分解为三个正交基向量再计算出欧拉角。

具体方法为将四元数表示为$q=(q_w,q_x,q_y,q_z)$，则其对应的旋转矩阵为：$$\begin{bmatrix}1-2(q_y^2+q_z^2) & 2(q_xq_y-q_zq_w) & 2(q_xq_z+q_yq_w)\\2(q_xq_y+q_zq_w) & 1-2(q_x^2+q_z^2) & 2(q_yq_z-q_xq_w)\\2(q_xq_z-q_yq_w) & 2(q_yq_z+q_xq_w) & 1-2(q_x^2+q_y^2)\end{bmatrix}$$然后，可以利用正交矩阵的特点来分解出三个正交基向量。

多旋翼飞行器设计与控制_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.欧拉转动中，将地球固联坐标系绕固定点转动（）次可以使它与机体坐标系的三轴指向一致。

参考答案:三次2.螺旋桨桨盘倾斜安装的好处是（）参考答案:前飞时可以不倾斜机身3.多旋翼动力学模型的输出不包括（）参考答案:位置4.同等条件下，飞行距离最远的飞行器是（）。

参考答案:固定翼飞行器5.多旋翼超声波测距仪检测不到反射波的原因可能有哪些？（）参考答案:机体俯仰角过大_机体距离地面过远_机体滚转角过大6.一个飞行控制系统(FCS)或者自动驾驶仪除了需要底层控制模块，还需要什么( )参考答案:决策模块7.遥控器上可设置的飞行参数包括（）参考答案:油门的正反_摇杆灵敏度大小_摇杆功能设定8.判断系统【图片】的可观性（）参考答案:可观9.对于带光流传感器的半自主自驾仪多旋翼的自稳定模式，关于水平位置通道的描述正确的是（）参考答案:水平位置通道是不稳定的_水平速度通道是稳定的10.而在（）实验中，输入信号可以任意选择，因此能获得更多的系统信息。

参考答案:开环11.理论上加速度计可以测量下列哪些量？（）参考答案:比力_滚转角_俯仰角12.姿态控制的目标是（）参考答案:_13.稳定性和飞行性能之间是什么关系（）参考答案:稳定性越高飞行性能越差14.避障技术包括（）参考答案:声呐系统_激光雷达15.多旋翼的建模包含哪些部分？（）参考答案:刚体运动学模型_动力系统模型_控制效率模型_刚体动力学模型16.不考虑动力系统动态特性时，电机模型中可忽略的有（）参考答案:电感17.一般情况下，空载电流对悬停时间的影响（）参考答案:有影响，但是影响较小18.单目视觉系统（）获取绝对尺度信息参考答案:不能19.下列多旋翼构型，当有任意一个旋翼失效时，哪些构型可以采用放弃偏航的方式实现安全着陆（）参考答案:__20.表示材料或结构在外力作用下抵抗破坏的能力的物理量为（）参考答案:强度21.当电子罗盘不健康时，则多旋翼无法实现以下哪个功能（）参考答案:定点悬停22.多旋翼可靠性高主要是因为（）参考答案:无刷直流电机_没有活动关节23.如果得到的误差传递函数为【图片】，其中【图片】而是频率为幅值为1的正弦信号，那么关于最终误差表述正确的是（）参考答案:收敛到 024.在做系统辨识时，传递函数阶数的选取应（）参考答案:尽可能小25.水平速度通道中的速度是指（），这样才能与偏航角无关参考答案:机体系下的速度26.工具箱( )在多种真实飞机的系统辨识中得到了广泛的应用参考答案:CIFER27.对于半自主自驾仪的多旋翼，遥控指令能直接控制多旋翼的以下变量( )参考答案:俯仰角和滚转角_垂直高度方向的速度_偏航角速度28.在多旋翼控制模型系统辨识中，下列（）先验知识对系统辨识有用参考答案:有无速度反馈_偏航通道的模型形式_水平位置通道的模型形式_高度通道的模型形式29.系统辨识方法包括( )参考答案:最小二乘方法_子空间辨识方法_PEM（Prediction-Error Minimization）方法_最大似然率方法30.对于半自主自驾仪的多旋翼的自稳定模式，关于高度通道的描述正确的是（）参考答案:高度方向的速度通道是稳定的_高度通道是不稳定的31.对于半自主自驾仪的多旋翼的自稳定模式，关于偏航通道的描述正确的是（）参考答案:偏航角速度通道是稳定的_偏航通道是不稳定的32.多旋翼在悬停下主要受到（）参考答案:重力_拉力33.直升机的升力主要由（）控制参考答案:油门_总距操纵杆34.多旋翼“刷锅”其实指的以一个目标为中心点，飞行器围着它转圈拍摄。