大角度范围内四元数转化为欧拉角的算法_辛岩

欧拉角四元数转换欧拉角和四元数都是用于描述物体在三维空间中的旋转状态的数学表示方法。

欧拉角是一个由三个角度组成的向量，而四元数是一个由四个实数组成的向量。

在计算机图形学和机器人学等领域中，这两种方法都被广泛使用。

欧拉角和四元数之间的转换可以帮助我们在不同的数学表示方法中进行转换，从而更方便地进行计算和应用。

下面是欧拉角和四元数之间的转换公式：欧拉角转四元数：给定欧拉角向量 [α, β, γ]，我们可以通过以下公式将其转换为对应的四元数 [q0, q1, q2, q3]：q0 = cos(α/2)cos(β/2)cos(γ/2) + sin(α/2)sin(β/2)sin(γ/2)q1 = sin(α/2)cos(β/2)cos(γ/2) - cos(α/2)sin(β/2)sin(γ/2)q2 = cos(α/2)sin(β/2)cos(γ/2) + sin(α/2)cos(β/2)sin(γ/2)q3 = cos(α/2)cos(β/2)sin(γ/2) - sin(α/2)sin(β/2)cos(γ/2)四元数转欧拉角：给定四元数 [q0, q1, q2, q3]，我们可以通过以下公式将其转换为对应的欧拉角向量 [α, β, γ]：α = atan2(2(q0q1 + q2q3), 1 - 2(q1^2 + q2^2))β = asin(2(q0q2 - q3q1))γ = atan2(2(q0q3 + q1q2), 1 - 2(q2^2 + q3^2))其中，atan2() 是一个带有两个参数的反正切函数，它可以根据两个参数的正负关系来确定结果的正负号。

通过以上公式，我们可以方便地在欧拉角和四元数之间进行转换，从而更加灵活地描述物体在三维空间中的旋转状态。

旋转矩阵、欧拉⾓、四元数理论及其转换关系1. 概述旋转矩阵、欧拉⾓、四元数主要⽤于表⽰坐标系中的旋转关系，它们之间的转换关系可以减⼩⼀些算法的复杂度。

本⽂主要介绍了旋转矩阵、欧拉⾓、四元数的基本理论及其之间的转换关系。

2、原理2.1 旋转矩阵对于两个三维点p1(x1,y1,z1)，p2(x2,y2,z2)，由点 p1 经过旋转矩阵 R 旋转到 p2，则有注：旋转矩阵为正交矩阵RR^T=E任意旋转矩阵：任何⼀个旋转可以表⽰为依次绕着三个旋转轴旋三个⾓度的组合。

这三个⾓度称为欧拉⾓。

三个轴可以指固定的世界坐标系轴，也可以指被旋转的物体坐标系的轴。

三个旋转轴次序不同，会导致结果不同。

2.2 欧拉⾓欧拉⾓有两种：静态：即绕世界坐标系三个轴的旋转，由于物体旋转过程中坐标轴保持静⽌，所以称为静态。

动态：即绕物体坐标系三个轴的旋转，由于物体旋转过程中坐标轴随着物体做相同的转动，所以称为动态。

使⽤动态欧拉⾓会出现万向锁现象；静态欧拉⾓不存在万向锁的问题。

对于在三维空间⾥的⼀个参考系，任何坐标系的取向，都可以⽤三个欧拉⾓来表现。

参考系⼜称为实验室参考系，是静⽌不动的。

⽽坐标系则固定于刚体，随着刚体的旋转⽽旋转。

如图1，设定xyz-轴为参考系的参考轴。

称xy-平⾯与XY-平⾯的相交为交点线，⽤英⽂字母（N）代表。

zxz顺规的欧拉⾓可以静态地这样定义：α是x-轴与交点线的夹⾓，β是z-轴与Z-轴的夹⾓，γ是交点线与X-轴的夹⾓。

图中三个欧拉⾓分别为：(α,β,γ)；蓝⾊的轴为：xyz轴红⾊的轴为：XYZ轴绿⾊的线为交线：Nα∈[0,2π],β∈[0,π],γ∈[0,2π]很可惜地，对于夹⾓的顺序和标记，夹⾓的两个轴的指定，并没有任何常规。

科学家对此从未达成共识。

每当⽤到欧拉⾓时，我们必须明确的表⽰出夹⾓的顺序，指定其参考轴。

实际上，有许多⽅法可以设定两个坐标系的相对取向。

欧拉⾓⽅法只是其中的⼀种。

此外，不同的作者会⽤不同组合的欧拉⾓来描述，或⽤不同的名字表⽰同样的欧拉⾓。

欧拉角和四元数是在计算机图形学和游戏开发中常用的两种旋转表示方法，它们可以相互转化，用于描述物体的旋转姿态。

gl-matrix 是一种专门用于线性代数的JavaScript 库，提供了便利的函数来处理矩阵、向量、旋转等操作。

在 gl-matrix 中，也提供了欧拉角和四元数相互转化的函数，方便开发者在使用这两种表示方法时进行转换。

本文将介绍 gl-matrix 中欧拉角和四元数的相互转化方法，并结合实际案例进行详细讲解。

1. 欧拉角和四元数的概念在计算机图形学和游戏开发中，欧拉角和四元数是用来描述物体旋转的常用方法。

欧拉角是通过旋转顺序和旋转角度来描述物体在三维空间中的旋转姿态，一般包括绕 x 轴、y 轴和 z 轴的旋转角度。

而四元数是一种复数的扩展，可以用来表示三维空间中的旋转，其具有较好的数学性质和计算性能。

2. gl-matrix 中的欧拉角和四元数表示gl-matrix 是一种快速、轻量级且又开放源代码的数学库，用于矢量和矩阵运算。

在 gl-matrix 中，欧拉角和四元数都是以数组的形式来表示的。

欧拉角可以用一个包含三个旋转角度的数组来表示，而四元数则可以用包含四个元素的数组来表示。

3. 欧拉角和四元数相互转化的原理欧拉角和四元数是两种不同的旋转表示方法，它们之间存在着一定的转换关系。

在 gl-matrix 中，提供了方便的函数来实现欧拉角和四元数的相互转化。

欧拉角转四元数的原理是先将欧拉角转化为旋转矩阵，再将旋转矩阵转化为四元数；而四元数转欧拉角的原理是先将四元数转化为旋转矩阵，再将旋转矩阵转化为欧拉角。

4. 在 gl-matrix 中实现欧拉角和四元数的相互转化接下来，我们将通过一个具体的案例来演示在 gl-matrix 中如何实现欧拉角和四元数的相互转化。

假设我们有一个物体，其初始的欧拉角为 [0, 0, 0]，我们需要将其转化为四元数表示。

我们可以使用 gl-matrix 提供的函数 'quat.create()' 来创建一个四元数：```javascriptvar quaternion = quat.create();```我们可以使用 gl-matrix 提供的函数 'quat.fromEuler()' 来将欧拉角转化为四元数：```javascriptvar euler = [0, 0, 0];quat.fromEuler(quaternion, euler[0], euler[1], euler[2]);```通过上述操作，我们就可以将初始的欧拉角 [0, 0, 0] 转化为对应的四元数表示。

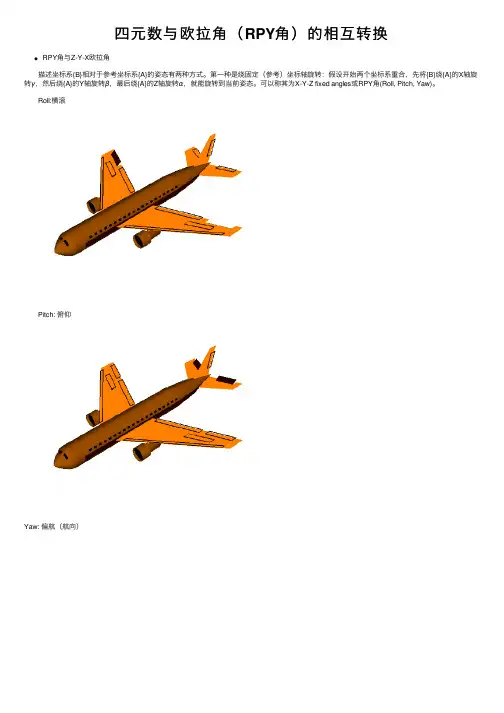
四元数与欧拉⾓（RPY⾓）的相互转换RPY⾓与Z-Y-X欧拉⾓ 描述坐标系{B}相对于参考坐标系{A}的姿态有两种⽅式。

第⼀种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转γ，然后绕{A}的Y轴旋转β，最后绕{A}的Z轴旋转α，就能旋转到当前姿态。

可以称其为X-Y-Z fixed angles或RPY⾓(Roll, Pitch, Yaw)。

Roll:横滚 Pitch: 俯仰Yaw: 偏航（航向） 由于是绕固定坐标系旋转，则旋转矩阵为（cα is shorthand for cosα, sα is shorthand for sinα,and so on.）R XYZ(γ,β,α)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 另⼀种姿态描述⽅式是绕⾃⾝坐标轴旋转：假设开始两个坐标系重合，先将{B}绕⾃⾝的Z轴旋转α，然后绕Y轴旋转β，最后绕X轴旋转γ，就能旋转到当前姿态。

称其为Z-Y-X欧拉⾓，由于是绕⾃⾝坐标轴进⾏旋转，则旋转矩阵为：R Z′Y′X′(α,β,γ)=R Z(α)R Y(β)R X(γ)=cαcβcαsβsγ−sαcγcαsβcγ+sαsγsαcβsαsβsγ+cαcγsαsβcγ−cαsγ−sβcβsγcβcγ 可以发现这两种描述⽅式得到的旋转矩阵是⼀样的，即绕固定坐标轴X-Y-Z旋转(γ,β,α)和绕⾃⾝坐标轴Z-Y-X旋转(α,β,γ)的最终结果⼀样，只是描述的⽅法有差别⽽已。

In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.Axis-Angle与四元数 绕坐标轴的多次旋转可以等效为绕某⼀转轴旋转⼀定的⾓度。

四元数和欧拉角
四元数与欧拉角：
1、四元数
四元数是一种数学物体，它由ONE个实部和THREE个虚部组成。

实部是非负实数，其余的THREE个部分是虚数。

四元数的表达式可以表示为：Q=a+bi+cj+dk (a、b、c、d是实实部）。

它们有助于以三维空间中的方式表示方向和旋转。

离散空间中表示四元数，当旋转发生时，它们保持一致。

2、欧拉角：
欧拉角是一种三维旋转矢量，可以用来表示不同方向之间的关系。

它将旋转分成THREE个不同的轴，分别为X轴、Y轴和Z轴。

每个轴都有自己的旋转角度，比如X轴有X角度，Y轴有Y角度，Z轴有Z角度。

欧拉角的表达式可以写作：[X,Y,Z]，其中X、Y、Z分别表示每个轴的旋转角度。

欧拉角与四元数之间的差别在于欧拉角表示的是不同方向间的关系，而四元数表示的是不同方向的空间旋转。

可以说四元数和欧拉角均是用来表示旋转有关信息的，但是又是有所差别的。

下面我们来总结下它们两者之间的区别：
1）表示方式不同：欧拉角表示的是不同方向间的关系，而四元数是表
示不同方向的空间旋转；
2）用途不同：欧拉角被广泛应用于3D图形学处理领域，可以很方便
地实现3D模型的几何变换；而四元数方便地表示空间任意的旋转变换，是用来表达机器人的运动控制中的基本角度表示方式；
3）值域不同：欧拉角的值域为[0,2π)，而四元数的值域为[-1,1]；
4）叠加角度表示方法不同：四元数是可以用乘法表达累加旋转；而欧
拉角只能使用加法来表达叠加旋转。

我们要找出欧拉角（Euler angles）对四元数（quaternion）的导数。

首先，我们需要了解欧拉角和四元数的基本定义和关系。

欧拉角是用来描述三维空间中物体方向的一组角度，通常表示为(φ, θ, ψ)。

四元数是一种复数扩展，用于表示三维空间中的旋转，通常表示为(q0, q1, q2, q3)。

欧拉角和四元数之间的关系可以通过一系列的转换公式来表示。

为了简化问题，我们假设使用Z-Y-X欧拉角。

根据Z-Y-X欧拉角到四元数的转换公式，我们有：q0 = cos(ψ/2) * cos(θ/2) * cos(φ/2) + sin(ψ/2) * sin(θ/2) * sin(φ/2)q1 = sin(ψ/2) * cos(θ/2) * cos(φ/2) - cos(ψ/2) * sin(θ/2) * sin(φ/2)q2 = cos(ψ/2) * sin(θ/2) * cos(φ/2) + sin(ψ/2) * cos(θ/2) * sin(φ/2)q3 = cos(ψ/2) * cos(θ/2) * sin(φ/2) - sin(ψ/2) * sin(θ/2) * cos(φ/2)为了找到欧拉角对四元数的导数，我们需要对上述每个四元数组件分别求导。

这将涉及到对cos和sin函数的求导，并使用链式法则。

针对q0的求导示例：δq0/δφ = -1/2 * sin(ψ/2) * cos(θ/2) * sin(φ/2) - 1/2 * cos(ψ/2) * sin(θ/2) * cos(φ/2)同理，我们可以求出δq0/δθ和δq0/δψ，以及其他q1, q2, q3对欧拉角的导数。

注意，这是一个相对复杂的过程，涉及到多个三角函数的求导和组合。

最终结果会是一系列与欧拉角相关的三角函数表达式。

四元数转欧拉角公式1 四元数简介四元数是一种数学上的扩张，它可以用来表示旋转、仿射变换、坐标变换等多种数学表示。

四元数由一个标量和一个三维向量组成，其中标量称为实部，三维向量称为虚部。

2 四元数转欧拉角欧拉角是指绕三个坐标轴的旋转角度，分别称为滚动角、俯仰角和偏向角。

将四元数转换为欧拉角可以用以下公式：psi = atan2(2(q0*q1 + q2*q3), 1 - 2(q1*q1 + q2*q2))theta = asin(2(q0*q2 - q3*q1))phi = atan2(2(q0*q3 + q1*q2), 1 - 2(q2*q2 + q3*q3))其中psi、theta、phi分别对应欧拉角的偏向角、俯仰角和滚动角，q0、q1、q2、q3为四元数的四个分量。

3 四元数转欧拉角的原理通过四元数和欧拉角的定义，我们可以知道，欧拉角相当于描述了三个坐标轴的旋转，而四元数可以表示任意旋转。

因此，我们可以使用四元数来表示欧拉角相应的旋转，然后通过比较四元数和欧拉角的定义，推出它们之间的关系式。

4 四元数转欧拉角的应用四元数转欧拉角常常用于3D游戏、计算机图形学等领域。

在3D 游戏中，我们需要获取角色的坐标和旋转信息，通过四元数转换欧拉角可以获得相应的旋转角度；在计算机图形学中，我们需要将三维模型转换为投影到二维屏幕上的二维图像，通过四元数转换欧拉角可以对三维对象进行旋转变换。

5 结论四元数和欧拉角是两种不同的数学表达方式，但它们之间存在一定的关系，通过转换可以实现相互转换。

四元数转换为欧拉角的公式虽然有些复杂，但是在实际应用中可以轻松地进行计算，并且可以提高程序的效率和可读性。

四元数与欧拉角之间的转换早在1843年哈米尔顿就提出了四元数的基本概念[138]，但当时仅停留在理论概念的讨论上。

20世纪以来，随着航天、航空工业的发展，四元数得到了广泛地实际应用[139-142]。

四元数的定义为[143]4q ⎛⎫≡ ⎪⎝⎭Q q（0-1）式中：123(,,)sin 2T q q q α≡=Q e （0-2）4cos2q α= （0-3）其中，e 是沿旋转轴的单位向量，α是旋转角度。

四元数满足约束条件1T =q q（0-4）四元数与姿态矩阵具有如下关系：224334222212341234132422221234123423142222132423141234()22[]()()2()2()2()2()2()2()T T q I q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q ⨯=-+-⨯=Ξψ⎛⎫--++-⎪=--+-++ ⎪⎪+---++⎝⎭A Q QQ Q q q q（0-5）其中，33⨯I 是33⨯单位矩阵，433[]()T q ⨯+⨯⎛⎫Ξ≡ ⎪-⎝⎭I Q q Q（0-6）433[]()T q ⨯-⨯⎛⎫ψ≡ ⎪-⎝⎭I Q q Q（0-7）3231210[]00q q q q q q -⎛⎫ ⎪⨯=- ⎪ ⎪-⎝⎭Q （0-8）地面坐标系Axyz 和弹体坐标系O 1x 1y 1z 1的关系可以用下式来表示=b Ar（0-9）其中，b 、r 分别为某向量在弹体坐标系和地面坐标系中的表示形式，A 的表达形式见错误！未找到引用源。

，具体为cos cos sin cos sin sin cos cos sin sin cos cos sin sin cos cos sin sin cos sin sin cos cos sin sin sin sin cos cos ϑψϑϑψϑψγψγϑγϑψγψγϑψγψγϑγϑψγψγ-⎛⎫⎪=-++ ⎪ ⎪+--+⎝⎭A（0-10）比较式（0-5）和式（0-10），得到姿态角的四元数表示131324222211123412123432231422222212342()arctan arctan arcsin arcsin 2()2()arctan arctan q q q q q q q q q q q q q q q q q q q q ψθφ⎧-=-=-⎪--+⎪⎪==+⎨⎪-⎪=-=-⎪-+-+⎩q q q q q A A A A A （0-11）也可以用姿态角来表示四元数q ，即(cossinj)(cossinj)(cos sin j)222222ψψθθφφ=+⊗+⊗+q（0-12）其中，符号⊗表示四元数乘法，其定义如下[144-145]41234123(i j k)(i j k)A A A A B B B B ⊗=+++⊗+++A B44123114322341232143B A A A A B A A A A A A A A B A A A A B ---⎛⎫⎛⎫ ⎪ ⎪- ⎪⎪= ⎪⎪- ⎪ ⎪ ⎪-⎝⎭⎝⎭44112233144132232431421334211243()()i ()j ()kA B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B =---++-++++-+-++（0-13）其中，4123i j k A A A A =+++A 和4123i j k B B B B +++B =均为四元数。

四元数与旋转一．四元组基础Q(x,y,z,w)，其中x，y，z用来确定旋转轴，w为旋转的角度Q=w+xi+yj+zk，i，j，k为三个虚轴的单位分量I*j=kJ*k=i;K*i=j;叉乘：c=a × b=| i j k||a1 b1 c1||a2 b2 c2|=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)c也为一个向量，且c的长度为|a||b|sin(theta)，垂直于a和b所在的平面，方向由右手法则来判定，用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c 的方向1．四元组相乘：Q1=w1+x1i+y1j+z1k=(w1,v1)Q2=w2+x2i+y2j+z2k=(w2,v2)Q1*Q2=(w1*w2-<v1,v2>,w1*v2+w2*v1+v1xv2)( w1+x1i+y1j+z1k)*( w2+x2i+y2j+z2k)=w1*w2-x1*x2-y1*y2-z1*z2+(W1*x2+x1*w2+y1*z2-z1-y2)i+(y1*w2+w1*y2+z1*x2-x1*z2)j+(w1*z2+z1*w2+x1*y2-y1*x2)k对于其中的轴部分，假如v1//v2，则有v1 x v2=0（平行向量的叉乘结果为0）2．四元组的点乘，点乘积为数值：Q1.*Q2=w1*w2+<v1,v2>=w1*w2+x1*x2+y1*y2+z1*z2;3．数乘s为一实数，q为四元组，则有sq=qs4．共轭p=(w,v)，则p*=(w,-v)(pq)*=q*p*N(q)=w2+x2+y2+z2q-1=q*/N(q)---------------显然可得qq-1=(1,0)二．使用四元数旋转向量假如有一表示向量的四元组q=(w,v)，对其应用旋转量p后的结果为：q’=pqp-1=(w,v’)从上可以看出，计算的结果q’的实部和q的实部是相等的，并且有N(v)=N(v’)如果N(q)=1，则可以令q=(cosa,usina)，u也为一个单位向量，则q’是q绕u旋转2a个弧度的结果假如S(q)表示q的实部，则有2S(q)=q+q*2S(pqp-1)= pqp-1+( pqp-1)*=pqp*+(pqp*)*=pqp*+pq*p*=p(q+q*)p*=2S(q)（这里由于p是单位四元数，所以有p-1等于p*）欧拉角到四元数的转换定义pitch, yaw, roll分别为绕X轴、Y轴、Z轴的旋转弧度float p = pitch * PIOVER180 / 2.0;float y = yaw * PIOVER180 / 2.0;float r = roll * PIOVER180 / 2.0;float sinp = sin(p);float siny = sin(y);float sinr = sin(r);float cosp = cos(p);float cosy = cos(y);float cosr = cos(r);this->x = sinr * cosp * cosy - cosr * sinp * siny;this->y = cosr * sinp * cosy + sinr * cosp * siny;this->z = cosr * cosp * siny - sinr * sinp * cosy;this->w = cosr * cosp * cosy + sinr * sinp * siny;normalise();三．使用matlab进行相关计算计算两个向量v1和v2之间的旋转量四元数p，使得v1应用p后到达v2假如v1转到v2的旋转轴为v，旋转角为theta，则q=[v*cos(theta/2)sin(theta/2)]Matlab代码：function q=vector2q(v1,v2)%..normalize....len1=sqrt(v1*v1');len2=sqrt(v2*v2');v1=v1/len1;v2=v2/len2;angle=v1*v2';axis=cross(v1,v2);alen=sqrt(axis*axis');axis=axis/alen;t=acos(angle);t=t/2;q(1)=axis(1)*sin(t);q(2)=axis(2)*sin(t);q(3)=axis(3)*sin(t);q(4)=cos(t);end计算出了q之后，可以获得对应的旋转矩阵，旋转矩阵的计算Matlab里面的矩阵是以列为主顺序的function r=q2rot(q)w=q(4);x=q(1);y=q(2);z=q(3);r=zeros(3,3);r(1,1)=1-2*y*y-2*z*z;r(1,2)=2*x*y+2*w*z;r(1,3)=2*x*z-2*w*y;r(2,1)=2*x*y-2*w*z;r(2,2)=1-2*x*x-2*z*z;r(2,3)=2*z*y+2*w*x;r(3,1)=2*x*z+2*w*y;r(3,2)=2*y*z-2*w*x;r(3,3)=1-2*x*x-2*y*y;r=r';end同时，也可以根据四元数来计算欧拉角function R=q2euler(q)w=q(4);x=q(1);y=q(2);z=q(3);t11=2*(w*x+y*z);t12=1-2*(x*x+y*y);R(1)=atan2(t11,t12);t2=2*(w*y-z*x);R(2)=asin(t2);t31=2*(w*z+x*y);t32=1-2*(y*y+z*z);R(3)=atan2(t31,t32);end计算出来的欧拉角rx，ry，rz，分别为绕X轴、Y轴和Z轴的旋转角，假如有：Rotq=q2rot(q)R=q2euler(q)[rotx roty rotz]=Rotation(R)可以发现Rotq==rotz*roty*rotx从这里可以看出，上面使用四元数这样计算出来的旋转矩阵的旋转顺序分别是X轴、Y轴和Z轴的ra=pi/4;qz=[0 0 -sin(ra) cos(ra)] %绕z旋转-90度qy=[0 sin(ra) 0 cos(ra) ] %绕y旋转90度qyz=qmult(qy,qz)r=q2euler(qyz)上面的r得出的结果为r = -1.5708 0.0000 -1.5708也就是说其几何意义变成先绕X轴旋转-90度，再绕Z轴旋转-90度，而根据qy和qz的相乘我们实际进行的操作却是先绕Z轴旋转-90度，再绕Y轴旋转90度，但是结果却是这两种操作等价，这说明由四元数到欧拉角可以有多个解两个四元数，假如它们的方向是相反的，用它们作用于向量得到的新向量的值仍然相等q1=[0.024666 -0.023954 0.504727 0.862594];arm=[-8.881719 6.037597 -2.36776];q2=-q1;rot1=q2rot(q1);rot2=q2rot(q2);v1=rot1*arm'v2=rot2*arm'上面计算出来的v1等于v2四元数的余弦值为它们的内积假如余弦值小于0，则需要将其中的一个取反，因为上面我们知道一个四元数和它的反方向的四元数对一个向量起相同的作用四元数的相乘，代表旋转的累积pq=p*q;rotp=q2rot(p);rotq=q2rot(q);rotpq=q2rot(pq);rotmul=rotp*rotq;这里rotpq与rotmul相等四． OGRE中Quaternion类的几个函数1.四元数到旋转向量void Quaternion::ToRotationMatrix (Matrix3& kRot) const1 - 2*qy2 -2*qz22*qx*qy -2*qz*qw2*qx*qz +2*qy*qw2*qx*qy + 2*qz*qw 1 - 2*qx2 -2*qz22*qy*qz -2*qx*qw2*qx*qz -2*qy*qw 2*qy*qz +2*qx*qw1 - 2*qx2 -2*qy22.旋转量到四元数根据1中的表格，有：4 *(1-qx2-qy2-qz2) = 1 + m00 + m11 + m22又qw2=1-qx2-qy2-qz2，可得4 *qw2= 1 + m00 + m11 + m22这里解qw必须保证1 + m00 + m11 + m22>=0，如果不是的话，就构造其他的等式来计算，OGRE中分成两种情况，一种是m00 + m11 + m22>=0，就可以直接先解出qw，否则的采用另外的等式计算3．Local axisVector3 xAixs(void) const;取得旋转矩阵的第一列，旋转矩阵和一个向量相乘的话，第一列的数据均和向量的x分量相乘Vecotr3 yAxis(void) const;取得旋转矩阵的第二列，旋转矩阵和一个向量相乘的话，第二列的数据均和向量的y分量相乘Vecotr3 zAxis(void) const;取得旋转矩阵的第三列，旋转矩阵和一个向量相乘的话，第三列的数据均和向量的z分量相乘。

四元数转化成欧拉角笔者：奋斗 修改时间：2015.11.23一． 姿态解算（以匿名版程序为例）首先，程序中一般用了两种求解姿态的方法，一种为欧拉角法，一种为四元数法。

由四元数法将MPU6050的值融合成四元，再由欧拉角法把四元转换成欧拉角送入串级PID 控制器。

（1）欧拉角法静止状态，或者总加速度只是稍微大于g 时，由加计算出的值比较准确。

使用欧拉角表示姿态，令Φ,θ和Φ代表ZYX 欧拉角，分别称为偏航角、俯仰角和横滚角。

载体坐标系下的 加 速 度(a x B,a y B ,a z B )和参考坐标系下的加速度(a x N, a y N, a z N)之间的关系可表示为(1)。

其中 c 和 s 分别代表 cos 和 sin 。

axB,ayB,azB 就是mpu 读出来的三个值。

这个矩阵就是三个旋转矩阵相乘得到的，因为矩阵的乘法可以表示旋转。

axB c c c s s axN ayB c s s s c c c s s s s c ayN azB s s c s c s c c s s c c azN θψθψθφψφθψφψφθψφθφψφθψφψφθψφθ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+-+⎣⎦⎣⎦⎣⎦ (1) 飞行器处于静止状态，此时参考系下的加速度等于重力加速度，即00xN yN zN a a g a ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦（2）把（2）代入（1）可以解得arctg θ=（3）yB zB a arctg a φ⎛⎫= ⎪⎝⎭（4） 即为初始俯仰角和横滚角，通过加速度计得到载体坐标系下的加速度即可将其解出，偏航角可以通过电子罗盘求出。

（2）四元数法（通过处理单位采样时间内的角增量(mpu的陀螺仪得到的就是角增量)，为了避免噪声的微分放大，应该直接用角增量）void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az){float norm;// float hx, hy, hz, bx, bz;float vx, vy, vz; // wx, wy, wz;float ex, ey, ez;// 先把这些用得到的值算好float q0q0 = q0*q0;float q0q1 = q0*q1;float q0q2 = q0*q2;// float q0q3 = q0*q3;float q1q1 = q1*q1;// float q1q2 = q1*q2;float q1q3 = q1*q3;float q2q2 = q2*q2;float q2q3 = q2*q3;float q3q3 = q3*q3;if(ax*ay*az==0)return;norm = sqrt(ax*ax + ay*ay + az*az); //acc数据归一化ax = ax /norm;ay = ay / norm;az = az / norm;// estimated direction of gravity and flux (v and w)vx = 2*(q1q3 - q0q2); //四元素中xyzvy = 2*(q0q1 + q2q3);vz = q0q0 - q1q1 - q2q2 + q3q3 ;// error is sum of cross product between reference direction of fields and direction measured by sensorsex = (ay*vz - az*vy) ; //向量外积在相减得到差分就是误差ey = (az*vx - ax*vz) ;ez = (ax*vy - ay*vx) ;exInt = exInt + ex * Ki; //对误差进行积分eyInt = eyInt + ey * Ki;ezInt = ezInt + ez * Ki;// adjusted gyroscope measurementsgx = gx + Kp*ex + exInt; //将误差PI 后补偿到陀螺仪，即补偿零点漂移 gy = gy + Kp*ey + eyInt;gz = gz + Kp*ez + ezInt; //这里的gz 由于没有观测者进行矫正会产生漂移，表现出来的就是积分自增或自减// integrate quaternion rate and normalise //四元素的微分方程 q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;// normalise quaternionnorm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);q0 = q0 / norm;q1 = q1 / norm;q2 = q2 / norm;q3 = q3 / norm;//Q_ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yawQ_ANGLE.Y = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitchQ_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll}下面对上面的程序逐条解释。

旋转矩阵四元数欧拉角旋转矩阵是在三维空间中表示旋转的一种方法，它通过一个三阶正交矩阵来描述。

这个矩阵可以用来表示一个点或向量绕某个轴旋转一定的角度。

在3D图形学、计算机视觉和机器人领域中，旋转矩阵被广泛应用。

旋转矩阵的大小为3×3，可以表示绕x轴、y轴、z轴旋转的三个角度。

例如，绕z轴旋转θ角度的旋转矩阵为：cosθ -sinθ 0sinθ cosθ 00 0 1四元数是另一种描述旋转的方法，它是一个具有四个实数的向量，通常被写作q = a + bi + cj + dk，其中a、b、c、d是实数。

四元数具有叠加和乘法运算，并且可以表示旋转和转动等复杂的运动。

四元数与旋转矩阵之间有一个简单的关系。

任何一个旋转矩阵都可以用一个四元数来表示，并且一个四元数也可以转换成一个旋转矩阵。

这个转换过程中，四元数和旋转矩阵的元素之间有一个固定的关系。

欧拉角是一种描述物体在三维空间中的方向的方法。

欧拉角通常由三个角度（yaw、pitch、roll）组成，用于描述物体相对于旋转参考系的旋转。

这些角度通常是绕物体的三个轴，通常是z、y、x，在类飞行器航空学中也称为偏转、俯仰和滚转。

欧拉角是最常见的描述物体方向的方法之一，但也存在一些问题。

一个主要的问题是欧拉角的旋转顺序，相同的三个角度可能会导致不同的旋转结果。

这个问题称为欧拉角万向锁问题。

总之，旋转矩阵、四元数和欧拉角都是用于描述物体在三维空间中的方向和位置的方法。

它们各有优缺点，并且在不同的领域和应用中具有不同的优势。

了解这些方法的特点和用途，有助于我们在设计和实现3D图形、机器人和计算机视觉应用时做出更合适的决策。

四元数与旋转一．四元组基础Q(x,y,z,w)，其中x，y，z用来确定旋转轴，w为旋转的角度Q=w+xi+yj+zk，i，j，k为三个虚轴的单位分量I*j=kJ*k=i;K*i=j;叉乘：c=a × b=| i j k||a1 b1 c1||a2 b2 c2|=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)c也为一个向量，且c的长度为|a||b|sin(theta)，垂直于a和b所在的平面，方向由右手法则来判定，用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向1．四元组相乘：Q1=w1+x1i+y1j+z1k=(w1,v1)Q2=w2+x2i+y2j+z2k=(w2,v2)Q1*Q2=(w1*w2-<v1,v2>,w1*v2+w2*v1+v1xv2)( w1+x1i+y1j+z1k)*( w2+x2i+y2j+z2k)=w1*w2-x1*x2-y1*y2-z1*z2+(W1*x2+x1*w2+y1*z2-z1-y2)i+(y1*w2+w1*y2+z1*x2-x1*z2)j+(w1*z2+z1*w2+x1*y2-y1*x2)k对于其中的轴部分，假如v1//v2，则有v1 x v2=0（平行向量的叉乘结果为0）2．四元组的点乘，点乘积为数值：Q1.*Q2=w1*w2+<v1,v2>=w1*w2+x1*x2+y1*y2+z1*z2;3．数乘s为一实数，q为四元组，则有sq=qs4．共轭p=(w,v)，则p*=(w,-v)(pq)*=q*p*N(q)=w2+x2+y2+z2q-1=q*/N(q)--------------- 显然可得qq-1=(1,0)二．使用四元数旋转向量假如有一表示向量的四元组q=(w,v)，对其应用旋转量p后的结果为：q’=pqp-1=(w,v’)从上可以看出，计算的结果q’的实部和q的实部是相等的，并且有N(v)=N(v’)如果N(q)=1，则可以令q=(cosa,usina)，u也为一个单位向量，则q’是q绕u旋转2a个弧度的结果假如S(q)表示q的实部，则有2S(q)=q+q*2S(pqp-1)= pqp-1+( pqp-1)*=pqp*+(pqp*)*=pqp*+pq*p*=p(q+q*)p*=2S(q)（这里由于p是单位四元数，所以有p-1等于p*）欧拉角到四元数的转换定义pitch, yaw, roll分别为绕X轴、Y轴、Z轴的旋转弧度float p = pitch * PIOVER180 / 2.0;float y = yaw * PIOVER180 / 2.0;float r = roll * PIOVER180 / 2.0;float sinp = sin(p);float siny = sin(y);float sinr = sin(r);float cosp = cos(p);float cosy = cos(y);float cosr = cos(r);this->x = sinr * cosp * cosy - cosr * sinp * siny;this->y = cosr * sinp * cosy + sinr * cosp * siny;this->z = cosr * cosp * siny - sinr * sinp * cosy;this->w = cosr * cosp * cosy + sinr * sinp * siny;normalise();三．使用matlab进行相关计算计算两个向量v1和v2之间的旋转量四元数p，使得v1应用p后到达v2假如v1转到v2的旋转轴为v，旋转角为theta，则q=[v*cos(theta/2) sin(theta/2)] Matlab代码：function q=vector2q(v1,v2)%..normalize....len1=sqrt(v1*v1');len2=sqrt(v2*v2');v1=v1/len1;v2=v2/len2;angle=v1*v2';axis=cross(v1,v2);alen=sqrt(axis*axis');axis=axis/alen;t=acos(angle);t=t/2;q(1)=axis(1)*sin(t);q(2)=axis(2)*sin(t);q(3)=axis(3)*sin(t);q(4)=cos(t);end计算出了q之后，可以获得对应的旋转矩阵，旋转矩阵的计算Matlab里面的矩阵是以列为主顺序的function r=q2rot(q)w=q(4);x=q(1);y=q(2);z=q(3);r=zeros(3,3);r(1,1)=1-2*y*y-2*z*z;r(1,2)=2*x*y+2*w*z;r(1,3)=2*x*z-2*w*y;r(2,1)=2*x*y-2*w*z;r(2,2)=1-2*x*x-2*z*z;r(2,3)=2*z*y+2*w*x;r(3,1)=2*x*z+2*w*y;r(3,2)=2*y*z-2*w*x;r(3,3)=1-2*x*x-2*y*y;r=r';end同时，也可以根据四元数来计算欧拉角function R=q2euler(q)w=q(4);x=q(1);y=q(2);z=q(3);t11=2*(w*x+y*z);t12=1-2*(x*x+y*y);R(1)=atan2(t11,t12);t2=2*(w*y-z*x);R(2)=asin(t2);t31=2*(w*z+x*y);t32=1-2*(y*y+z*z);R(3)=atan2(t31,t32);end计算出来的欧拉角rx，ry，rz，分别为绕X轴、Y轴和Z轴的旋转角，假如有：Rotq=q2rot(q)R=q2euler(q)[rotx roty rotz]=Rotation(R)可以发现Rotq==rotz*roty*rotx从这里可以看出，上面使用四元数这样计算出来的旋转矩阵的旋转顺序分别是X轴、Y轴和Z轴的ra=pi/4;qz=[0 0 -sin(ra) cos(ra)] %绕z旋转-90度qy=[0 sin(ra) 0 cos(ra) ] %绕y旋转90度qyz=qmult(qy,qz)r=q2euler(qyz)上面的r得出的结果为r = -1.5708 0.0000 -1.5708也就是说其几何意义变成先绕X轴旋转-90度，再绕Z轴旋转-90度，而根据qy和qz的相乘我们实际进行的操作却是先绕Z轴旋转-90度，再绕Y轴旋转90度，但是结果却是这两种操作等价，这说明由四元数到欧拉角可以有多个解两个四元数，假如它们的方向是相反的，用它们作用于向量得到的新向量的值仍然相等q1=[0.024666 -0.023954 0.504727 0.862594];arm=[-8.881719 6.037597 -2.36776];q2=-q1;rot1=q2rot(q1);rot2=q2rot(q2);v1=rot1*arm'v2=rot2*arm'上面计算出来的v1等于v2四元数的余弦值为它们的内积假如余弦值小于0，则需要将其中的一个取反，因为上面我们知道一个四元数和它的反方向的四元数对一个向量起相同的作用四元数的相乘，代表旋转的累积pq=p*q;rotp=q2rot(p);rotq=q2rot(q);rotpq=q2rot(pq);rotmul=rotp*rotq;这里rotpq与rotmul相等四．OGRE中Quaternion类的几个函数1.四元数到旋转向量void Quaternion::ToRotationMatrix (Matrix3& kRot) const1 - 2*qy2 - 2*qz22*qx*qy - 2*qz*qw2*qx*qz + 2*qy*qw2*qx*qy + 2*qz*qw 1 - 2*qx2 - 2*qz22*qy*qz - 2*qx*qw2*qx*qz - 2*qy*qw2*qy*qz + 2*qx*qw 1 - 2*qx2 - 2*qy22.旋转量到四元数根据1中的表格，有：4 *(1-qx2-qy2-qz2) = 1 + m00 + m11 + m22又qw2=1-qx2-qy2-qz2，可得4 *qw2= 1 + m00 + m11 + m22这里解qw必须保证1 + m00 + m11 + m22>=0，如果不是的话，就构造其他的等式来计算，OGRE中分成两种情况，一种是m00 + m11 + m22>=0，就可以直接先解出qw，否则的采用另外的等式计算3．Local axisVector3 xAixs(void) const;取得旋转矩阵的第一列，旋转矩阵和一个向量相乘的话，第一列的数据均和向量的x分量相乘Vecotr3 yAxis(void) const;取得旋转矩阵的第二列，旋转矩阵和一个向量相乘的话，第二列的数据均和向量的y分量相乘Vecotr3 zAxis(void) const;取得旋转矩阵的第三列，旋转矩阵和一个向量相乘的话，第三列的数据均和向量的z分量相乘。

1.欧拉角在四元数出现之前先看下欧拉角：对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。

为了后面的角度不混乱，我们要先区分参考系和坐标系的概念。

参考系即为大地参考系，是静止不动的。

而坐标系则固定于四轴飞行器，随着四轴飞行器的旋转而旋转。

按照右图所示。

设定 xyz-轴为四轴上的参考轴，XYZ-轴则是大地的参考轴。

右图即为四轴相对地面进行了一定旋转， xy-平面与XY-平面的相交线为交点线，用英文字母（N）代表。

我们可以这样定义欧拉角：α是 x-轴与交点线的夹角β是 z-轴与Z-轴的夹角γ是交点线与X-轴的夹角这样我们就可以用三个欧拉角：(α，β，γ)其取值为0-360来描述四轴飞行器相对于大地的参考系的姿态角度了。

三个欧拉角：(α，β，γ)。

蓝色的轴是 xyz-轴，红色的轴是 XYZ-坐标轴。

绿色的线是交点线 (N) 。

2.轴角欧拉角使用roll，pitch，yaw来表示这些分量的旋转值。

需要注意的是，这里的旋转是针对大地参考系说的，这意味着第一次的旋转不会影响第二、三次的转轴，简单的说，三角度系统无法表现任意轴的旋转，只要一开始旋转，物体本身就失去了任意轴的自主性，这也就导致了万向节锁（Gimbal Lock）的问题。

什么是Gimbal Lock？正如前面所说，因为欧拉描述中针对x,y,z的旋转描述是世界坐标系下的值，所以当任意一轴旋转90°的时候会导致该轴同其他轴重合，此时旋转被重合的轴可能没有任何效果，这就是Gimbal Lock，还有一种是轴角的描述方法，这种方法比欧拉描述要好，它避免了Gimbal Lock，它使用一个3维向量表示转轴和一个角度分量表示绕此转轴的旋转角度，即(x,y,z,angle)，一般表示为(x,y,z,w)或者(v,w)。

(x,y,z)为旋转轴，w为旋转角度。

但这种描述法却不适合插值。

轴角的表示方法：那么轴、角的描述方法又有什么问题呢？虽然轴、角的描述解决了Gimbal Lock，但这样的描述方法会导致差值不平滑，差值结果可能跳跃，欧拉角描述同样有这样的问题。

欧拉角与四元数之间的转换数学公式欧拉角和四元数是两种广泛应用于机器人、航空、姿态控制等领域的旋转表示方法。

它们之间的转换是非常有用的，在实际应用中经常需要将一个旋转表示方法转换成另一个。

本文将介绍欧拉角和四元数之间的转换数学公式，以及它们的应用。

欧拉角是一种旋转表示方法，它将旋转分解成三个轴向旋转的组合。

欧拉角共有12种表示方式，其中最常用的是ZYZ方式。

它将一个旋转分解为绕Z轴旋转一个角度，绕新的Y轴旋转一个角度，再绕新的Z轴旋转一个角度。

欧拉角的转换公式如下：$$begin{bmatrix} alpha beta gamma end{bmatrix} =begin{bmatrix} atan2(r_{23},r_{33}) asin(-r_{13})atan2(r_{12},r_{11}) end{bmatrix}$$其中，r是旋转矩阵，α、β、γ是绕Z、Y、Z轴旋转的角度。

四元数是一种用四元组表示旋转的方法。

它比欧拉角更为简洁、稳定，并且没有万向锁问题。

四元数的转换公式如下：$$begin{bmatrix} q_w q_x q_y q_z end{bmatrix} =begin{bmatrix} cos(theta/2) sin(theta/2) * n_x sin(theta/2) * n_y sin(theta/2) * n_z end{bmatrix}$$其中，q是四元数，θ是旋转角度，n是旋转轴向量。

四元数的逆转换公式如下：$$begin{bmatrix} theta n_x n_y n_z end{bmatrix} = begin{bmatrix} 2 * acos(q_w) q_x / sqrt{1-q_w^2} q_y /sqrt{1-q_w^2} q_z / sqrt{1-q_w^2} end{bmatrix}$$ 欧拉角和四元数之间的转换可以通过以下公式实现：$$begin{bmatrix} q_w q_x q_y q_z end{bmatrix} = begin{bmatrix} cos(alpha/2) * cos(beta/2) * cos(gamma/2) + sin(alpha/2) * sin(beta/2) * sin(gamma/2) sin(alpha/2) * cos(beta/2) * cos(gamma/2) - cos(alpha/2) * sin(beta/2) * sin(gamma/2) cos(alpha/2) * sin(beta/2) * cos(gamma/2) + sin(alpha/2) * cos(beta/2) * sin(gamma/2) cos(alpha/2) * cos(beta/2) * sin(gamma/2) - sin(alpha/2) * sin(beta/2) * cos(gamma/2) end{bmatrix}$$$$begin{bmatrix} alpha beta gamma end{bmatrix} = begin{bmatrix} atan2(2(q_w*q_x+q_y*q_z),1-2(q_x^2+q_y^2)) asin(2(q_w*q_y-q_z*q_x))atan2(2(q_w*q_z+q_x*q_y),1-2(q_y^2+q_z^2)) end{bmatrix}$$ 通过欧拉角和四元数之间的转换，可以方便地在不同领域应用中进行旋转表示的转换。

四元数转欧拉角奇异值问题四元数和欧拉角作为常见的表示方法，在计算机图形学和机器人领域中广泛应用。

在四元数表示角度时，存在着一些奇异值问题，会使得欧拉角的转换结果出现异常，本文将对此进行详细的阐述。

一、四元数简介四元数是一种扩充了实数的数学结构，它包括一个实数部分和三个虚数部分，可以表示旋转和剪切等变换。

四元数形式上可以写成 $q = w + xi + yj + zk$，其中 $w, x, y, z$ 都是实数，$i, j, k$ 是三个虚数单位，它们的平方分别等于-1。

四元数通过旋转的方式来表示角度。

例如，单位四元数可以表示3D中的转动180度绕轴 $(1,1,1)$，则可以写成：$$q = [\cos(\theta/2),\sin(\theta/2)\frac{1}{\sqrt{3}},\sin(\theta/2)\frac{1}{\sqrt{3}},\sin(\theta/2)\frac{1}{\sqrt{3}}]$$其中，$\theta$ 是旋转的角度。

二、欧拉角简介欧拉角是一种表示旋转的方式，它通过描述旋转的三个角度来确定旋转的方向。

欧拉角可以通过任何航向、俯仰、翻转（yaw-pitch-roll）的组合来表示。

例如，将 3D 物体绕 X 轴旋转30度，然后绕 Y 轴旋转45度，再绕 Z 轴旋转 60 度，这个过程可以用以下的欧拉角表示：$$\alpha = 30^\circ,\beta = 45^\circ,\gamma = 60^\circ$$当然，在欧拉角的表示中也存在固有的问题，例如欧拉角的万向锁问题等。

但是，在本文中，我们主要探讨的问题是四元数转为欧拉角时可能会遇到的问题。

三、四元数转换为欧拉角在将四元数转换为欧拉角时，我们可以首先计算对应的旋转矩阵，然后通过该矩阵计算欧拉角。

假设四元数为$q = [w, x, y, z]$，则相应的旋转矩阵可以表示为：$$\left[\begin{matrix} 1 - 2(y^2+z^2)& 2(xy-wz)& 2(xz+wy)\\ 2(xy+wz)& 1-2(x^2+z^2)& 2(yz-wx)\\ 2(xz-wy)& 2(yz+wx)& 1 - 2(x^2+y^2)\end{matrix}\right]$$根据四元数到旋转矩阵的转换方法，我们可以通过这个矩阵计算出欧拉角，例如：$$\alpha = \tan^{-1}(\frac{-m_{23}}{m_{33}})$$$$\beta = \sin^{-1}(m_{13})$$$$\gamma = \tan^{-1}(\frac{-m_{12}}{m_{11}})$$其中 $m_{ij}$ 表示旋转矩阵中的第 $i$ 行第$j$ 列的元素。

四元数转欧拉角奇异值
四元数是一种表示旋转的方法，而欧拉角则是另一种。

在将四元数转换为欧拉角时，有时会遇到奇异值的问题，这时需要进行特殊处理。

奇异值出现的原因是欧拉角的定义域有限，而四元数的定义域无限。

当四元数的某些元素超出欧拉角的定义域时，就会出现奇异值。

为了解决奇异值问题，可以使用雅可比矩阵方法进行转换。

这种方法可以通过计算雅可比矩阵的特征值来确定是否存在奇异值，并进行相应的处理。

另外，还可以使用另一种方法来避免奇异值，即使用欧拉角的另一种定义方式。

这种方式可以将欧拉角的定义域扩展到无限，从而避免奇异值的出现。

总之，在将四元数转换为欧拉角时，需要注意奇异值的问题，并选择合适的方法进行处理。

- 1 -。