平面向量专题讲座

平面向量专题讲座一：平面向量的概念例1.1=b a =； ②若A 、B 、C 、D 是不共线的四点，则DC AB =是四边形为平行四边形的等价条件； ③若c b b a ==,，则c a =； ④b a ==a ∥b ； ⑤若a ∥b ，b ∥c ，则a ∥c 。

其中，正确命题的序号是____________答案：②③。

变式训练1：判断下列各命题：（1）若a ≠0，a ·b =a ·c ，则b =c ；（2）若a ·b =a ·c ，则b ≠c 当且仅当a =0时成立；（3）（a ·b ）c =a （b ·c ）对任意向量a 、b 、c 都成立； （4）对任一向量a ，有a 2=|a |2.其中，正确命题的序号是____________ 二：向量的基本运算例2．已知△ABC 中，D 为BC 的中点，E 为AD 的中点．设aAB =，bAC=，求BE ．解：BE ＝AE －AB ＝41(AB ＋AC )－AB ＝－43a＋41b变式训练2.如图所示，D 是△ABC 边AB 上的中点，则向量CD 等于（ ） A ．－BC ＋BA21 B ．－BC －BA21C ．BC －BA 21D ．BC ＋BA21 解:A例3. 已知向量2132e e a -=，2132e e b+=，2192e e c-=，其中1e 、2e 不共线，求实数λ、μ，使ba cμλ+=．解:c ＝λa ＋μb⇒21e －92e ＝(2λ＋2μ)1e ＋(－3λ＋3μ)2e ⇒2λ＋2μ＝2，且－3λ＋3μ＝－9⇒λ＝2，且μ＝－1变式训练3：已知平行四边形ABCD 的对角线相交于O 点，点P 为平面上任意一点，求证：POPD PC PB PA 4=+++证明PA＋PC ＝2PO ，PB ＋PD ＝2PO⇒PA＋PB ＋PC ＋PD ＝4PO三：共线向量定理、平面向量基本定理及应用例5. 设a ，b 是两个不共线向量，若a 与b 起点相同，t ∈R ，t 为何值时，a ，t b ，31(a ＋b )三向量的终点在一条直线上？ 解：设])(31[b a a b t a+-=-λ (λ∈R)化简整理得：0)31()132(=-+-b t a λλBC∵不共线与b a ，∴⎪⎪⎩⎪⎪⎨⎧==⇒⎪⎪⎩⎪⎪⎨⎧=-=-2123030132t t λλλ故21=t时，)(31,,b a b t a +三向量的向量的终点在一直线上．变式训练5：已知,,,,O A a O B b O C c O D d O E e ===== ，设t R ∈，如果3,2,a c b d ==()e t a b =+，那么t 为何值时，,,C D E 三点在一条直线上？解：由题设知，23,(3)C D d c b a C E e c t a t b =-=-=-=-+，,,C D E 三点在一条直线上的充要条件是存在实数k ，使得C E k C D = ，即(3)32t a t b k a k b -+=-+，整理得(33)(2)t k a k t b -+=-.①若,a b共线，则t 可为任意实数；②若,a b 不共线，则有33020t k t k -+=⎧⎨-=⎩，解之得，65t =.综上，,a b 共线时，则t 可为任意实数；,a b 不共线时，65t =.四：平面向量的坐标运算例6.已知点A （2，3），B （－1，5），且AC ＝31AB，求点C 的坐标． 解AC ＝31AB＝(－1，32)，OC ＝ACOA+＝(1,311)，即C(1,311)变式训练6.若(2,8)O A = ，(7,2)O B =- ，则31A B= . 解: (3,2)--提示：(9,6)A B O B O A =-=--例7.已知a －2b ＝(－3，1)，2a ＋b ＝(－1，2)，求a ＋b ． 解a＝(－1，1)，b ＝(1，0)，∴a ＋b ＝(0，1)变式训练7.已知向量a ＝(1, 2)，b ＝(x, 1)，1e ＝a ＋2b ，2e ＝2a －b ，且1e ∥2e ，求x ． 解:1e ＝(1＋2x ，4)，2e ＝(2－x ，3)，1e ∥2e ⇒3(1＋2x)＝4(2－x)⇒x ＝21五：平面向量数量积运算例9. 已知|a |＝4，|b |＝5，且a 与b 的夹角为60°，求：(2a ＋3b )·(3a －2b )． 解:(2a ＋3b )(3a －2b )＝－4变式训练9.已知|a |＝3，|b |＝4，|a ＋b |＝5，求|2a －3b |的值． 解:56六：平面向量的数量积解决夹角问题例10. 已知向量a ＝(sin θ，1)，b ＝(1，cos θ)，－22πθπ<<．(1) 若a ⊥b ，求θ； (2) 求|a ＋b |的最大值． 解：(1)若ba ⊥，则0cos sin =+θθ即1tan -=θ而)2,2(ππθ-∈，所以4πθ-=(2))4sin(223)cos (sin 23πθθθ++=++=+b a当4πθ=时，ba +的最大值为12+七：平面向量的数量积解决垂直问题例11：已知(cos ,sin )a αα= ，(cos ,sin )b ββ=，其中0αβπ<<<． (1)求证：a b + 与a b -互相垂直；(2)若ka →+→b 与a k →-→b 的长度相等，求βα-的值(k 为非零的常数)．证明：222222()()(cos sin )(cos sin )0a b a b a b ααββ+⋅-=-=+-+=a b ∴+ 与a b -互相垂直（2）k a →+(cos cos ,sin sin )b k k αβαβ→=++,a k →-(co s co s ,sin sin )b k k αβαβ→=--,k a b →+=a kb →-=,而=cos()0βα-=，2πβα-=八：平面向量的数量积解决三角形的形状的问题例12. 已知O 是△ABC 所在平面内一点，且满足(OB －OC )·(OB ＋OC －2OA )＝0，判断△ABC 是哪类三角形． 解:设BC 的中点为D ，则(OCOB-)(OAOC OB2-+)＝0⇒2BC ·AD ＝0⇒BC ⊥AD ⇒△ABC 是等腰三角形变式训练：若(1,2),(2,3),(2,5)A B C -，则△ABC 的形状是 .解: 直角三角形.提示：(1,1),(3,3),0,A B A C A B A C A B A C ==-⋅=⊥九：高考题体验1.(广东卷)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( ) A 平行于x 轴 B.平行于第一、三象限的角平分线 C.平行于y 轴 D.平行于第二、四象限的角平分线答案 C2.(山东卷)设P 是△ABC 所在平面内的一点，2B C B A B P +=，则（ ）A.0P A P B +=B.0P C P A +=C.0P B P C +=D.0P A P B P C ++=答案 B3.（全国卷）已知向量()2,1,10,||a a b a b =⋅=+=，则||b =( )5 D. 25 答案 C4.（辽宁）平面向量a 与b 的夹角为060，(2,0)a =，1b = 则2a b +=( )答案 B5.（宁夏）已知O ，N ，P 在A B C ∆所在平面内，且,0O A O B O C N A N B N C ==++=，且P A P B P B P C P C P A ∙=∙=∙，则点O ，N ，P 依次是A B C ∆的( )A.重心 外心 垂心B.重心 外心 内心C.外心 重心 垂心D.外心 重心 内心 答案 C6.（湖北）若向量a=（1，1），b=（-1,1），c=（4，2），则c=( )A.3a+bB. 3a-bC.-a+3bD. a+3b 答案 B 十．选讲选做题例1.2.下列命题:①如果非零向量,a b 的方向相同或相反, 那么a b + 的方向必与,a b之一的方向相同;②在A B C ∆中, 必有0A B B C C A ++= ; ③若0A B B C C A ++=,则,,A B C 为一个三角形的三个顶点;④若,a b均为非零向量,则a b a b +=+ 其中真命题的个数为（ ）A.0个B. 1个C.2个D.3个解析：选B.只有②是真命题.对于①②③关于向量的加减法运算除掌握法则外,还应注意一些特殊情况,例4. 已知ABCD 是一个梯形，AB 、CD 是梯形的两底边，且AB ＝2CD ，M 、N 分别是DC 和AB 的中点，若aAB=，b AD =，试用a 、b表示BC 和MN ．解：连NC ，则b AD NC==ba CN AB CN MC MN -=+=+=4141；ab NB NC BC21-=-=变式训练4：如图所示，OADB 是以向量OA ＝a ，OB ＝b 为邻边的平行四边形，又BM ＝31BC，CN ＝31CD，试用a 、b 表示OM ，ON ，MN ． 解:OM ＝61a＋65b，ON ＝32a＋32b，MN ＝21a－61b例8. 在平行四边形ABCD 中，A(1，1)，AB ＝(6，0)，(1) 若AD ＝(3，5)，求点C 的坐标；(2) 当|AB |＝|AD |时，求点D 的轨迹． 解：(1)设点C 的坐标为(x 0，y 0)，)5,1()5,9()0,6()5,3(00--==+=+=y x DB AD AC得x 0＝10 y 0＝6 即点C(10，6) (2) ∵ADAB=∴点D 的轨迹为(x －1)2＋(y －1)2＝36 (y ≠1)变式训练8.在直角坐标系x 、y 中，已知点A(0，1)和点B(－3，4)，若点C 在∠AOB 的平分线上，且|OC |＝2，求OC 的坐标． 解 ∴)5103,510(-=OC例13. .平面向量11),(,22a b =-=，若存在不同时为0的实数k 和t ，使2(3)x a t b =+- ,,y ka tb =-+ 且x y ⊥ ，试求函数关系式()k f t =.解：由11),(22a b =-=得0,||2,||1a b a b ⋅=== 22222[(3)]()0,(3)(3)0a t b k a t b k a t a b k t a b t t b +-⋅-+=-+⋅--⋅+-=33311430,(3),()(3)44k t t k t t f t t t -+-==-=-。

八年级数学平面向量新课讲义完整版(全8
讲)
第一讲：向量的概念
- 向量的定义
- 向量的表示方法
- 向量的性质
第二讲：向量的运算
- 向量的加法
- 向量的减法
- 向量的数乘
第三讲：向量的模与方向角
- 向量的模的概念
- 向量的方向角的概念
- 向量的模与方向角的计算
第四讲：向量坐标表示与平行四边形法则
- 向量的坐标表示方法
- 矢量和坐标的关系
- 平行四边形法则的应用
第五讲：向量共线与定比分点
- 向量共线的概念
- 共线向量的判定方法
- 向量的定比分点
第六讲：向量的数量积
- 数量积的定义
- 数量积的性质
- 数量积的计算方法
第七讲：向量的坐标表示与夹角公式- 向量的坐标表示与数量积
- 夹角的概念与计算方法
- 向量间的夹角公式
第八讲：平面向量的应用
- 向量的投影
- 向量的位移
- 向量的垂直与平行
以上是八年级数学平面向量的新课讲义完整版，共8讲，内容
包括向量的概念、运算、模与方向角、坐标表示与平行四边形法则、共线与定比分点、数量积、坐标表示与夹角公式以及向量的应用。

通过学习这些内容，学生将能够掌握平面向量的基本概念和运算方法，并能够应用于实际问题的解决中。

高中数学讲座 高考中的平面向量问题龚天勇考纲解读▪ 要掌握平面向量的概念与性质（共线、模、夹角、垂直等）； ▪ 在选择填空中要重视平面向量的几何运算,也要重视坐标运算（有时要自己建系）；要注意三角形的重心、垂心的向量判断； ▪ 在其它知识如解析几何中要注意平面向量的工具作用（如平行、垂直可转化向量的关系求解）。

一、平面向量基本概念与性质：1．向量的概念①向量：既有大小又有方向的量。

向量一般用c b a,,……来表示，或用有向线段的起点与终点的大写字母表示，如：AB a；坐标表示法),(y x j y i x a=+=。

向量的大小即向量的模（长度），记作|AB|｜a|。

向量不能比较大小，但向量的模可以比较大小。

②零向量：长度为0的向量，记为0，其方向是任意的，0与任意向量平行a是零向量⇔｜a｜＝0。

由于0 的方向是任意的，且规定0平行于任何向量，故在有关向量平行（共线）的问题中务必看清楚是否有“非零向量”这个条件。

注意零向量与0的区别③单位向量：模为1个单位长度的向量，向量0a为单位向量⇔｜0a｜＝1。

④平行向量（共线向量）：方向相同或相反的非零向量。

任意一组平行向量都可以移到同一直线上，方向相同或相反的向量，称为平行向量，记作a∥b。

由于向量可以进行任意的平移(即自由向量)，平行向量总可以平移到同一直线上，故平行向量也称为共线向量。

注意：（1）、数学中研究的向量是自由向量，只有大小、方向两个要素，起点可以任意选取，现在必须区分清楚共线向量中的“共线”与几何中的“共线”、的含义，（2）、理解平行向量中的“平行”与几何中的“平行”是不一样的。

⑤相等向量：长度相等且方向相同的向量叫相等向量；相等向量经过平移后总可以重合，记为ba =。

两个向量相等的充要条件是对应坐标相等；即：),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 。

2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法。

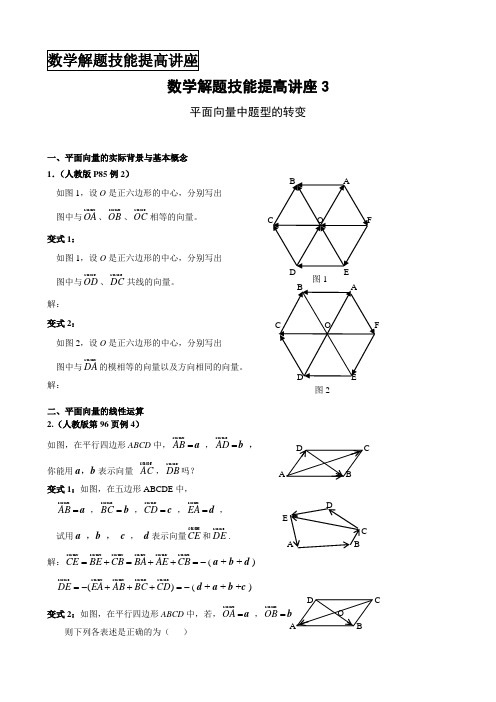
数学解题技能提高讲座3平面向量中题型的转变一、平面向量的实际背景与基本概念 1．（人教版P85例2）如图1，设O 是正六边形的中心，分别写出图中与OA 、OB 、OC相等的向量。

变式1：如图1，设O 是正六边形的中心，分别写出图中与OD 、DC共线的向量。

解： 变式2：如图2，设O 是正六边形的中心，分别写出图中与DA的模相等的向量以及方向相同的向量。

解：二、平面向量的线性运算 2.（人教版第96页例4）如图，在平行四边形ABCD 中，AB = a ，AD =b ，你能用a ，b 表示向量 AC ，DB吗？变式1：如图，在五边形ABCDE 中，AB = a ，BC = b ，CD = c ，EA =d ， 试用a ，b ， c ， d 表示向量CE 和DE.解：CE BE CB BA AE CB =+=++=-( a + b + d )()DE EA AB BC CD =-+++=-( d + a + b +c )变式2：如图，在平行四边形ABCD 中，若，OA = a ，OB =b则下列各表述是正确的为（ ）D EC A BC B AC OFD E图1图2A ．OA OB AB += B ．OC OD AB += C ．CD =- a + b D ．BC =-(a + b )正确答案：选D变式3：已知=a ，=b, =c ,=d , 且四边形ABCD 为平行四边形，则（ ）A. a +b +c +d =0B. a －b +c －d =0C. a +b －c －d =0D. a －b －c +d =0正确答案：选A变式4：在四边形ABCD 中，若12AB CD =-，则此四边形是( )A ．平行四边形B ．菱形C ．梯形D ．矩形 正确答案：选C变式5：已知a 、b 是非零向量，则|a |=|b |是(a +b )与(a －b )垂直的 （ ）A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件正确答案：选C变式6：在四边形ABCD 中，AB =a +2b ，BC =－4a －b ，CD =－5a －3b ，其中a 、b 不共线，则四边形ABCD为（ ）A.平行四边形B.矩形C.梯形D.菱形【解析】 ∵=++=－8a －2b =2，∴//.∴四边形ABCD 为梯形. 正确答案：选C变式7：已知菱形ABCD ，点P 在对角线AC 上（不包括端点A 、C ），则AP 等于（ ） A.λ(+),λ∈(0,1)B.λ(+),λ∈(0,22) C.λ(－),λ∈(0,1)D.λ(BC AB -),λ∈(0,22)【解析】 由向量的运算法则=+，而点P 在对角线AC 上，所以与同向，且||＜||,∴=λ(+),λ∈(0,1).正确答案：选 A变式8：已知D 、E 、F 分别是△ABC 的边BC 、CA 、AB 的中点，且=a ，=b，=c ,则下列各式：①EF =21c －21b②BE =a +21b③=－21a +21b④++=0其中正确的等式的个数为（ ）A.1B.2C.3D.4正确答案：选B 3．（人教版第98页例6）如图，已知任意两个非零向量a 、b ，试作OA = a + b ，OB =a + 2b ， OC =a + 3b ，你能判断A 、B 、C 三点之间的位置关系吗？为什么？变式1：已知OA = a + 2b ，OB = 2a + 4b ，OC =3a + 6b (其中a 、b 是两个任意非零向量) ，证明：A 、B 、C 三点共线．证明：∵AB OB OA =-= a + 2b ，AC OC OA =-=2a + 4b ，∴ 2AC AB =所以，A 、B 、C 三点共线．变式2：已知点A 、B 、C 在同一直线上，并且OA = a + b ，(2)OB m =- a + 2b ，(1)OC n =+a + 3b (其中a 、b 是两个任意非零向量) ，试求m 、n 之间的关系．解：(3)AB OB OA m =-=-a +b ，AC OC OA n =-= a + 2b 由A 、B 、C 三点在同一直线上可设AB k AC =，则 (3)21m kn k -=⎧⎨=⎩ 所以 1(3)2m n -= 即 260m n --=为所求．4．（人教版第102页第13题）已知四边形ABCD ，点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，求证：EF HG =变式1：已知任意四边形ABCD 的边AD 和BC 的中点分别为E 、F ，求证：2AB DC EF += .证明：如图，连接EB 和EC ， 由EA AB EB += 和EF FB EB += 可得，EA AB EF FB +=+（1）由ED DC EC += 和EF FC EC += 可得，ED DC EF FC +=+（2） （1）+（2）得， 2EA ED AB DC EF FB FC +++=++（3） ∵E 、F 分别为AD 和BC 的中点，∴0EA ED += ，0FB FC +=，代入（3）式得，2AB DC EF +=b a三、平面向量的基本定理及坐标表示 2.（人教版第109页例6）已知a = (4，2)，b = (6，y )，且a // b ，求 y ． 变式1：与向量a = (12，5) 平行的单位向量为（ ）A ．1251313⎛⎫⎪⎝⎭，- B ．1251313⎛⎫- ⎪⎝⎭-C ．1251313⎛⎫⎪⎝⎭， 或1251313⎛⎫- ⎪⎝⎭，- D ．1251313⎛⎫- ⎪⎝⎭， 或1251313⎛⎫ ⎪⎝⎭，-正确答案：选C变式2：已知a (1,2)=，b (),1x =，当a +2b 与2a －b 共线时，x 值为 （ ）A ．1B ．2C ．13D ．12正确答案：选D变式3：已知A (0,3) 、B (2,0) 、C (－1,3) 与2+方向相反的单位向量是( )A ．(0,1)B ．(0,－1)C ． (－1,1)D ．(1,－1) 正确答案：选A变式4：已知a = (1，0)，b = (2，1) ．试问：当k 为何实数时， k a －b 与a +3b 平行, 平行时它们是同向还是反向？ 解：因为 k a －b ()21k =--，，a +3b ()73=，．由已知得，()3270k -+= 解得 13k =-，此时，k a －b 713⎛⎫=-- ⎪⎝⎭，，a +3b ()73=，，二者方向相反． 2.（人教版第110页例8）设点P 是线段12PP 上的一点，1P 、2P 的坐标分别为()11y x ，，()22y x ，． (1) 当点P 是线段12PP 上的中点时，求点P 的坐标； (2) 当点P 是线段12PP 的一个三等分点时，求P 的坐标变式1：已知两点()3,2M ，()5,5N --，12MP MN =，则P 点坐标是 （ ）A ．()8,1-B ．31,2⎛⎫-- ⎪⎝⎭C ．31,2⎛⎫⎪⎝⎭D ．8,1-正确答案：选B变式2：如图，设点P 、Q 是线段AB 的三等分点，若OA ＝a ，OB ＝b ，则OP ＝ 2133+a b ，OQ ＝ 1233+a b (用a 、b 表示)四、平面向量的数量积 5．（人教版第116页例3）已知|a |＝6，|b | ＝4且a 与b 的夹角为60︒，求 (a + 2b)²(a 3-b ) ．变式1：已知()()3,4,223,a b a b a b ==++=那么a 与b 夹角为A 、60︒B 、90︒C 、120︒D 、150︒正确答案：选C变式2：已知向量a 和b 的夹角为60°，| a | ＝ 3，| b | ＝ 4，则（2a – b ）²a 等于 （A ）15 （B ）12 （C ）6 （D ）3 正确答案：选B变式3：在△ABC 中，已知||=4，|AC |=1，S △ABC =3，则²AC 等于（ ）A.－2B.2C.±2D.±4 正确答案：选C变式4：设向量2172e e t +与向量21e t e +的夹角为钝角，求实数t 的取值范围. 解：∵0))(72(2121<++e t e e e t ，故071522<++t t ，解之217-<<-t ． 另有λλt t ==7,2，解之14,214-=-=λt ， ∴)21,214()214,7(--⋃--∈t ．2.（人教版第116页例4）已知|a |＝3，|b | ＝4且a 与b 不共线，k 为何实数时，向量a + k b 与a k -b 互相垂直？变式1：已知a ⊥b ，|a |＝2，|b | ＝3，且向量3a + 2b 与k a -b 互相垂直，则k 的值为（ ）A ．32-B ．32C ．32± D ．1 正确答案：选B变式2：已知|a |＝1，|b | ＝2且（a －b ）⊥a ，则a 与b 夹角的大小为 45º ． 解：2.（人教版第119页 第11题）已知a = (4，2)，求与向量a 垂直的单位向量的坐标． 变式1：若i = (1,0), j =(0,1)，则与2i +3j 垂直的向量是 ( )A ．3i +2jB ．－2i +3jC ．－3i +2jD ．2i －3j正确答案：选C变式2：已知向量)1,1(=，)3,2(-=，若k 2-与垂直，则实数k =（ ）A ．1B ．－1C ．0D ．2正确答案：选B变式3：若非零向量,互相垂直，则下列各式中一定成立的是 （ ）A ．-=+B ．||||-=+C ．0))((=-+b a b aD ．0)(2=-b a正确答案：选B变式4：已知向量a ＝（3，－4），b ＝（2，x ）， c ＝（2，y ）且a ∥b ，a ⊥c ．求|b －c |的值． 解：∵ a ∥b ，∴ 3x ＋8＝0． ∴x ＝38-． ∴ b ＝（2， 38-） ． ∵ a ⊥c ， ∴ 6－4y ＝0． ∴ y ＝23． ∴ c ＝（2， 23）．而b －c ＝（2，38-）－（2，23）＝（0，－256），∴ |b －c |＝256．（人教版第118页例5）已知A (1，2)，B (2，3)，C (2-，5)，试判断ABC ∆的形状，并给出证明．变式1：O 是ABC ∆所在的平面内的一点，且满足()()0OB OC OC OA -⋅-=，则ABC ∆ 一定为（ ）A ．正三角形B ．等腰直角三角形C ．直角三角形D ．斜三角形 正确答案：选C变式2：已知A 、B 、C 三点不共线，O 是△ABC 内的一点，若＋＋＝0，则O 是△ABC 的（ ） A ． 重心 B ． 垂心C ． 内心D ． 外心正确答案：选A变式3：已知02=+⋅，则△ABC 一定是 （ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰直角三角形正确答案：选B变式4：四边形ABCD 中，)3,2(),,(),1,6(--===y x （1）若//，试求x 与y 满足的关系式；（2）满足（1）的同时又有⊥，求y x ,的值及四边形ABCD 的面积。

平面向量讲座一、向量的基本概念二、1.向量的定义：既有大小又有方向的量。

(注意与前面我们所讲的量的区别)2.向量的表示：。

(注意印刷体与手写体的关系)向量的长度(模)表示为：3.特殊向量：(1)零向量：长度为0的向量，方向为任意。

记作：。

(2)单位向量：长度为1的向量。

(3)相等向量：长度相等，方向一致的两个向量。

向量不能比较大小，向量的长度可以比较大小。

(4)平行向量(共线向量)：方向相同或相反的两个非零向量叫做平行向量，规定零向量与任一向量平行，平行向量也叫做共线向量。

(5)相反向量：长度相同，方向相反的向量。

例题：判断下列命题的对错：1.零向量与任意非零向量平行；(对)2.长度相等方向相反的向量共线；(对)3.若是两个单位向量，则相同；(错)4.若向量不共线，则都是非零向量；(对)5.若两个向量相等，则它们的起点、方向、长度必须相等；(错)6.“两个向量共线”是“这两个向量相等”的充分不必要条件；(错)7.若非零向量是共线向量，则A、B、C、D四点共线；(错)8.“四边形ABCD是平行四边形”的充要条件是“”；(错)9.共线的向量一定相等；(错)10.相等的向量一定共线；(对)二、向量的基本运算1.加法运算、减法运算：向量的加法运算满足平行四边形法则和三角形法则。

(1)平行四边形法则(2)三角形法则即首尾相接的两个向量的和是由第一个向量的起点指向第二个向量的终点的有向线段所示的向量。

由此，可推广到n个首尾相接的向量的和是由第一个向量的起点指向第n个向量的终点的有向线段所表示的向量。

规定：零向量与向量的和等向量向量加法的运算率：(1)两个向量的模的和、差与两向量和的模的关系：2.实数与向量的积：对于非零向量及实数λ，表示一个向量，其长度和方向规定如下：(1)长度：，即等于的λ绝对值与的长度的乘积。

(2)方向：①当λ＞0时，的方向相同；②当λ<0时，的方向相反；③当λ=0时，规定：零向量与任意实数相乘仍为零向量。

平面向量一、向量的相关概念：1.向量的概念：我们把既有大小又有方向的量叫向量2.向量的表示方法：几何表示法：①用有向线段表示；②用字母a 、b 等表示；③用有向线段的起点与终点字母：AB ；坐标表示法：,(y x yj xi a =+=3、向量的模：向量AB 的大小――长度称为向量的模，记作|AB |.4、特殊的向量：①长度为0的向量叫零向量，记作0的方向是任意的②长度为1个单位长度的向量，叫单位向量.说明：零向量、单位向量的定义都是只限制大小，不确定方向.5、相反向量：6、相等的向量：7、平行向量(共线向量)：方向相同或相反的向量，称为平行向量记作b a //平行向量也称为共线向量 规定零向量与任意向量平行。

8、两个非零向量夹角的概念：已知非零向量a 与b ，作OA ＝a ，OB ＝b ，则∠ＡＯＢ＝θ（０≤θ≤π）叫ａ与b 的夹角9、实数与向量的积：实数λ与向量a的积是一个向量，记作λa，它的长度与方向规定如下：（Ⅰ）a a λλ=； （Ⅱ）当0>λ时，λa的方向与a 的方向相同；当0<λ时，λa的方向与a 的方向相反；当0=λ时，0=a λ，方向是任意的10、两个向量的数量积：已知两个非零向量a 与b ，它们的夹角为θ，则a ·b =︱a ︱·︱b ︱cos θ 叫做a 与b 的数量积（或内积） 规定00=⋅a二、重要定理、公式：1、平面向量基本定理：1e ，2e 是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数21,λλ，使2211e e a λλ+=（1）．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的两个单位向量i 、j 作为基底a ，由平面向量基本定理知，有且只有一对实数x 、y ，使得yj xi a +=…………○1 我们把),(y x 叫做向量a 的（直角）坐标，记作),(y x a =…………○2 其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示 与．a 相等的向量的坐标也为．．．．．．．．．．,(y x 特别地，)0,1(=i ，)1,0(=j ，)0,0(0=（2） 若),(11y x A ，),(22y x B ，则()1212,y y x x AB --=一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标2、两个向量平行的充要条件向量共线定理：向量b 与非零向量a 共线的充要条件是：有且只有一个非零实数λ，使b =λaa∥b ⇔a＝λb⇔1221=-y x y x3、两个向量垂直的充要条件设),(11y x a =，),(22y x b =，则ba⊥ ⇔a·b ＝O ⇔02121=+y y x x4、平面内两点间的距离公式（1）设),(y x a =，则222||y x a +=或||a =（2）如果表示向量a的有向线段的起点和终点的坐标分别为A ),(11y x、B ),(22y x ，那么||AB =平面内两点间的距离公式)5、两向量夹角的余弦（πθ≤≤0） co s θ =||||b a b a ⋅⋅222221212121y x y x y y x x +++=特别注意：（1）结合律不成立： c b a c b a ⋅⋅≠⋅⋅)()(；（2）消去律不成立ca ba ⋅=⋅不能cb =（3）b a ⋅ = 0不能得到a =0或b =06、线段的定比分点公式: 设点P 分有向线段21P P 所成的比为λ，即P P 1＝λ2PP ，则⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式) 当λ＝1时，得中点公式：OP ＝21（1OP ＋2OP ）或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x7、平移公式： 设点P (x ，y )按向量a ＝（ｈ，ｋ）平移后得到点P ′（x ′，y ′），则P O '＝OP +a 或⎩⎨⎧+='+='.,k y y h x x曲线y ＝f （x ）按向量a ＝（ｈ，ｋ）平移后所得的曲线的函数解析式为：y －ｋ＝f （x －ｈ)8、正弦定理其中R 表示三角形的外接圆半径）： （1）2sin sin sin a b c R ABC===余弦定理（1）2b =222cos ac ac B +-（2）1sin 2S bc A =练习题：一、平面向量的概念及其运算1、若c AC b AB==,，则BC等于（ B ）A ．c b -B ．b c -C ．c b +D ．c b -- 2、正六边形ABCDEF 中，=++EF CD BA （ D ）A ．0B ．BEC ．CD D ．CF练习：3、在ABC ∆中，已知BD BC 3=，则AD 等于（ ） A ．)2(31AB AC + B ．)2(31AC AB + C ．)3(41AB AC + D ．)2(41AB AC +4、已知：向量b a , 同向，且7,3==b a ，则=-b a 2二、平面向量的基本定理及坐标表示5、若115,3e CD e AB-===ABCD 是（ C ）A ．是平行四边形B ．菱形C ．等腰梯形D ．不等腰梯形 6、已知向量)4,3(--=a ，则与a 同向的单位向量是（ A ） A ．)54,53(--B ．)54,53(C ．)4,3(--D ．)4,3(练习：7、若三点)9,(),4,2(),1,1(--x B A P 共线，求x8、若向量)43,3(2--==x x x a 与AB 相等地，已知)2,1(),2,1(B A -，则x 的值为（ ） A ．-1 B ．-1或-4 C ．4 D ．1或4三、线段的定比分点9、已知A 、B 、C 三点在同一条直线上，且A （3，-6），B （-5，2），若点C 的横坐标为6，求点C 分AB 所成的比及点C 的纵坐标（答案：9,113--=λ）练习：10：已知三个点)3,4(),4,1(),1,2(--D B A ，点C 在AB 上，且CBAC =2，连结DC 并延长至E ，使DECE 41=，则E 点的坐标为（ ） A ．（0，1） B ．（-8，35-） C ．（0，1）或)311,2( D ．（38-，311）四、平面向量的数量积11、已知，33,3,2=⋅==b a b a ，则a 与b 的夹角等于 o 3012、已知向量a 与b 的夹角为o 120，且2,4==b a ， （1）求a 在b 方向上的投影 （2）求b a 43+ （3）若向量kba+与ba+5垂直，求实数k 的值（答案：（1）-2，（2）74，（3）419）练习：13、已知 )3,2(,132-==b a ，且b a ⊥ ，求a 的坐标14、已知)5,5(),0,6(-==b a，则a 与b 的夹角为五、平移15、把点A （3，4），按)2,1(=a 平移，求对应点A '的坐标),(y x '' （答案（4，6））16、一个向量把点（2，-1）平移到（-2，1），它把点（-2，1）平移到（ A ） A ．)1,2(- B ．（-2，1） C ．（6，-3） D ．（-6，3）练习：17、若向量a 使点（3，-9）平移到点（1，1），则将函数21232+-=x x y 的图象，按a 平移后的解析式为（ A ）A ．23x y =B ．2)2(3-=x yC ．10)2(32--=x yD ．10)2(32++=x y 18、已知A （5，7）、B （2，3），将AB 按向量)1,4(=a 平移后的坐标为 （-3，-4）六、解斜三角形19、在ABC ∆中，已知22,30,45===a A C o o ，求b （ 答案：232+） 练习：20、在ABC ∆中，1,60,3===∆b A S oABC，则a的值为（ ）A ．13B ．13C ．3D ．9 例21、设函数)()(c b a x f +⋅=，其中向量Rx x x c x x b x x a ∈-=-=-=),sin ,cos (),cos 3,(sin ),cos ,(sin ，求函数)(x f 的最大值和最小正周期 （答案：（1）22+； （2）π。