2016年福建高职招考数学模拟试题：二次函数的图象与性质

2016年福建高职招考数学押题卷（一）（面向普通高中）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟。

第Ⅰ卷（选择题 共70分）一、选择题：本大题共14小题，每小题5分，共70分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知全集{}|2A x N x =∈<，{}0,1,2B =，则AB =( )A.{}1,2B.{}0,1,2C.{}1D.{}0,1 2. 若幂函数kx x f =)(在(0,)+∞上是减函数，则k 可能是（ ）A.1B.2C.12D.1- 3. "0"x =是"0"x =的（ ）.A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件 4．i 是虚数单位，复数21i+的共轭复数是（ ）A.1i +B.1i -C.22i +D.22i -5．圆2220x y x +-=的圆心和半径分别为（ ）A. (1,0),1-B. (1,0),1C. (2,0),2-D. (2,0),26. 若sin 2cos αα=，则sin cos sin cos αααα-+的值为（ ）A.1B.13-C.13D.1-7. 下列命题正确的是（ ）A ．平行于同一平面的两条直线一定平行B ．夹在两平行平面间的等长线段必平行C ．若平面α外的直线l 与α内的一条直线平行，则l 平行于平面αD ．若一个平面内的无数条直线平行于另一个平面，则该两个平面平行 8.下列函数)(x f 中，在()+∞,0上为增函数的是（ ）A.xx f 1)(=B.2)1()(-=x x fC ．x x f ln )(= D. x x f )21()(=9. x 0 1 2 3 y1357则y 与x 的线性回归方程为ˆybx a =+必过点（ ） A ．(2,2)B ．(1,2)C ．3(,4)2D ．3(,0)210. 若实数x y ，满足1000x y x y x -+≥⎧⎪+⎨⎪⎩≥≤，，，则2z x y =+的最小值是（ ）A ．0B ．12C ．1D ．211、在ABC ∆中，60A ∠=︒，23AC =，32BC =，则角B 等于（ ）A ．30 B.45 C. 90 D.135 12.下列各对向量,a b 中，共线的是（ ）A . (2,3),(3,2)a b ==-B . (2,3),(4,6)a b ==-C . (2,1),(1,2)a b =-=D . (1,2),(2,2)a b == 13．当03x <<时，则下列大小关系正确的是（ ）A.333log xx x <<B. 333log x x x <<C.33log 3xx x <<D.33log 3x x x <<14. 如图，直线AB 的方程为6340x y --=，向边长为2的正方形内随机地投飞镖，飞镖都能投入正方形内，且 投到每个点的可能性相等，则飞镖落在阴影部分（三角 形ABC 的内部）的概率是（ ）A 、14411 B 、14425 C 、14437 D 、144416340x y --=第Ⅱ卷（非选择题 共80分）二、填空题：本大题共4小题，每小题5分，共20分。

2016福建省高职招考数学模拟试卷六2016福建省高职招考（面向普高）统一考试数学模拟试题（六）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟。

第Ⅰ卷（选择题 共70分）一、选择题：本大题共14小题，每小题5分，共70分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．.已知集合{}{}3,5,6,8,1,3,5A B ==，那么A B U 等于（ ）A. {}3,5B. {}6,8C.{}1,6,8D. {}1,3,5,6,82()2xf x =A. B.C. D. 3．平面向量a v ，b v 满足2b a=v v ，如果(1,1)a =v，那么bv 等于( )1 x O yx O y 1 xO y1 x O yA. (2,2)- B.(2,2)C.(2,2)-D.(2,2)--4．已知3sin ,(,)52πααπ=∈，则cos α的值为（ ） A. 34B. 34-C. 45 D.45-5.某简单几何体的三视图如图所示，则该几何体为（ ）A. 圆柱B. 圆锥C. 圆台D. 棱锥6. 已知直线20x y --=与直线0mx y +=垂直，那么m 的值是（ ）A. 2- B.1- C. 1 D. 27. 在等比数列{}na 中，141,8a a==，那么{}na 的前5项和是（ ）A ．31B ．32C ．63D ．648.已知命题p ：三角形确定一个平面；命题q ：两两相交的三条直线确定一个平面．则下列命题为真命题的是A ．p q ∧B ．()p q ⌝∨C ．()p q ⌝∧D ．()p q ∨⌝ 9. 椭圆2212+=x y 与直线50x y +-=的位置关系为（ ）A. 相离B. 相切C. 相交D. 无法确定 10.已知实数,x y 满足条件20200x y x y y --≤⎧⎪++≥⎨⎪≤⎩，那么目标函数2z x y=+的最小值是（ ） A.6- B.4- C.2-D. 411. 在同一坐标系中，函数3xy =的图与1()3xy =的图象（ ）A ．关于x 轴对称；B ．关于y 轴对称；C ．关于原点y x =对称；D ．关于直线y x =对称．12. 在ABC ∆中，如果5,3,4AB AC BC ===，那么AB AC•u u u r u u u r等于（ ）A. 9B. 12C. 15D. 2013.将函数cos y x =的图象向左平移2π个单位，得到函数()y f x =的图象，则下列说法正确的是( ).A ．()y f x =的最小正周期为πB. ()=是偶函数y f xπ对称C. ()y f x=的图像关于点(,0)2D. ()=在区间[0,]2π上是减函数y f x14. 已知函数()1=-与()(1)f x ax=-的图象无交点，g x a x则实数的取值范围是（）A. (,0]-∞ B. 1(0,)2 C. 1[,1)2 D. [1,)+∞第Ⅱ卷（非选择题共80分）二、填空题：本大题共4小题，每小题5分，共20分。

2016福建省高职招考（面向普高）统一考试数学模拟试题（七）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟。

第Ⅰ卷（选择题 共70分）一、选择题：本大题共14小题，每小题5分，共70分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图，阴影部分表示的集合是（ ）A. A BB. A BC. A BD. ∅2．已知{}n a 为等差数列，且2=3a ,56=a , 则7S 的值为A. 42B. 28C. 24D. 343．设a ，b 是两个平面向量，则“a ＝b ”是“|a|＝|b|”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件 4．以点(0，1)为圆心，2为半径的圆的方程是( )A. x 2＋(y －1)2＝2B. (x －1)2＋y 2＝2C. x 2＋(y －1)2＝4D. (x －1)2＋y 2＝4 5. 函数y()6. 如果直线022=++y ax 与直线023=--y x 平行，则a 的值为（ ）A.3-B.6- C.23D.32 7. 下列函数是在（0，1）上为减函数的是（ ）A. 2y x =B. 1y x =+C. sin y x =D. cos y x =8. 已知回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为（ ）A. 23.108.0+=x yB.523.1+=x yC.423.1+=x yD.=1.23+0.08y x 9. 函数()1ln f x x =-的零点所在的区间是（ ）A. （1，2）B. （2，3）C. （3，4）D. （4，5）10.已知点()y x ，在如图所示的阴影部分内（含边界）运动，AB则2z x y =+的最大值是（ ）A.0B.2C.5D.611. 设椭圆)0(12222>>=+b a by a x 的左、右焦点分别为21F F 、，上顶点为B .若212F F BF ==2，则该椭圆的方程为（ ）A.13422=+y x B. 1322=+y x C. 1222=+y x D. 1422=+y x 12. 两根相距m 6的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于m 2的概率等于（ ） A.16 B. 13 C. 12D. 2313. 如图是王珊早晨离开家边走边背诵英语过程中离家距离y 与行走时间x 之间函数关系的图象．若用黑点表示王珊家的位 置，则王珊步行走的路线可能是（ ）A. B. C. D.14. 两直立矮墙成0135二面角，现利用这两面矮墙和篱笆围成一个面积为542m 的直角梯形菜园（墙足够长），则所 用篱笆总长度的最小值为（ ）A. m 16B. m 18C. m 5.22D. m 315第Ⅱ卷（非选择题 共80分）二、填空题：本大题共4小题，每小题5分，共20分。

2016年福建省高等职业教育入学考试模拟试卷(数学)(面向普通高中考生)参考公式：样本数据12,,...,n x x x 的标准差 锥体体积公式s =222121()()()n x x x x x x n ⎡⎤-+-++-⎣⎦ (13)V Sh = 其中x 为样本平均数 其中S 为底面面积，h 为高柱体体积公式 球的表面积、体积公式 V Sh =24S R =π，343V R =π其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题 共70分）一．单项选择题（本大题共14小题，每小题5分，共70分．在每小题给出的四个备选答案中，选出一个正确答案 ，并将答题卡上对应题目的答案标号涂黑） 1.设集合{}1,3,5A =，{}1,2B =，则B A ⋂等于（ ）A.{}1,2,3,5B.{}1,3,5C.{}2,3,5D.{}1 2.函数xx f 3)(=的图象大致为（ ）A. B. C. D.3.已知向量),3,2(),,1(-==b k a 且b a ⊥，则实数k 等于 （ ）A ．23 B ． 23- C ．32 D ．32- 4.已知)42cos(3)(π-=x x f 的最小正周期是（ ）A.23π B. 3πC.3πD.π 5.下列平面图形绕直线l 旋转一周，得到的几何体为圆台的是 （ ）A. B. C. D.6.圆0222=-+y y x 的圆心坐标为（ ）A.( 0 , 1 )B.( 2 , 0 )C.（1 , 0 )D.( 0 , 2 ) 7.“0)1)(1(=+-a a ”是“1=a ”的（ ）A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件8.双曲线1222=-y x 的离心率为（ ） A. 22 B. 25 C. 26 D. 369.函数322)(-+=x x f x的零点所在区间是 （ ） A ．)0,1(- B ．（0,1） C ．（1,2） D ．（2,3）10.设,x y 满足束条件,02⎪⎩⎪⎨⎧≥≤+≤x y x y x ，则y x z +-=2的最小值等于（ ）A.2-B.1C.0D.1-11.已知在△ABC 中，1=AB ，2AC =，内角3π=A ，则BC 等于（ ） A.3 B.2 C.1 D.212.如图，正方形ABCD 中，E 、F 、G 、H 分别是边AB 、BC 、 CD 、DA 的中点，在正方形ABCD 内随机撒一粒黄豆，则 它落到阴影部分的概率是 （ ）A ．41B ．21 C ．83 D ．8513.函数)1(11)(>-+=x x x x f 的最小值是（ ） A.2 B.3 C.4 D.514.设奇函数()f x 是定义在R 上的减函数，且不等式0)()2(2<++x f x a f 对一切x R ∈恒 成立，则实数a 的取值范围是（ ）A.(,1)-∞-B.(,1]-∞-C.(1,)+∞D.[1,)+∞第II 卷（非选择题 共80分）二.填空题（本大题共4小题，每小题5分，共20分．把答案填在答题卡的相应位置上） 15．=--1)2(i i ；16．某团队有男成员24人.女成员18人, 为了解团队成员的工作情况,用分层抽样的方法从 全体成员中抽出一个容量为7的样木,则抽取男成员的人数为____________； 17．已知函数⎩⎨⎧>≤-=1,log 1),2()(3x x x x x x f , 则=)]3([f f ___________________；18．一个有上、下底面的圆柱体的表面积为296cm π的易拉罐，则其高为 时易拉罐的体积最大.三.解答题（本大题共6 小题，共60分．解答应写出文字说明，证明过程或演算步骤） 19．（本小题满分8分）已知函数)sin 21(32sin )(2x x x f -+=.（Ⅰ）求)6(πf 的值；（Ⅱ）求函数()f x 的最小值.20. （本小题满分8分）已知等差数列{}n a 的前n 项和为n S ，公差1=d ,且513=-S S .（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若数列{}n b 满足2n a n b =，求321b b b ⋅⋅的值.21. （本小题满分10分）右下图是某公司5个销售店某月销售某机器的数量（单位：台）的茎叶图. （Ⅰ）求该公司5个销售店当月销售这种机器的平均台数；（Ⅱ）该公司若从这5个销售店中随机抽取2个进行分析，求抽到的2个销售店该月的销售量中有且仅有一个高于平均数的概率.22. （本小题满分10分）设直线l 过抛物线Γ：22y px =（0p >）的焦点F ，且与抛物线Γ相交于A ，B 两点，其中点)1,41(-B .（Ⅰ）求抛物线Γ的方程； （Ⅱ）求线段AB 的长.23. （本小题满分12分）某铁制零件是如图所示的几何体，其底面是边长为4cm 的正方形，高为3cm ，内孔圆柱的半径为lcm. (注: π取3.14 ，质量=密度×体积). (1)求该零件的体积;(2)已知铁的密度为7.8g/cm,问制造1000个这样的零件，需要铁多少千克?24.（本小题满分12分）已知函数32()231()f x x ax x =-+∈R ．（1）若()f x 在x =2处取得极值，求实数a 的值； （2）当0a >时,求()f x 的单调递增区间； （3）求函数()f x 在闭区间 [0,2] 内的最小值.2016年福建省高等职业教育入学考试数学试卷答案及评分参考（面向普通高中考生）一、单项选择题（本大题共14小题，每小题5分，共70分）1．D 2．B 3．C 4．D 5．B 6．A 7．A 8．C 9．B 10．D 11．A 12．C 13．B 14．C二、填空题（本大题共4小题，每小题5分，共20分）15．i 2 16．4 17．1- 18．8cm三、解答题（本大题共6小题，共60分．解答应写出文字说明，证明过程或演算步骤） 19. 解：（Ⅰ）因为x x x f 2cos 32sin )(+= ………………………………………2分)32sin(2π+=x ……………………………4分所以)6(πf )362sin(2ππ+⨯=32sin2π=3= ……………………………………………6分（Ⅱ）因为)(x f )32sin(2π+=x所以当Z k k x ∈-=,125ππ时，2)(min -=x f ……………………8分20. 解： （Ⅰ）因为 1=d ,且513=-S S .所以 5)2233(11=-⋅⨯+a d a 5321=+∴a解得 11=a ………………………2分则 ()11n a a n d n =+-= ……………………………4分（Ⅱ）由（Ⅰ）知,n a n =，得nn b 2= ……………………………6分 所以6422232321=⨯⨯=⋅⋅b b b ……………………………8分21. 解：（Ⅰ）该公司5个销售店当月销售这种机器的平均台数为30)3331362723(51=++++台 …………………………..4分（Ⅱ）设5个销售店中低于平均数的数量为12a a 、，高于平均数的数量分别为123b b b 、、，则从5个销售店中随机抽取2个进行分析的可能情况为：()()()()()1211121321,,,,,a a a b a b a b a b 、、、、、 ()()()()()2223121323,,,,,a b a b b b b b b b 、、、、 共10种情况，…………………………………..6分 记“从5个销售店中随机抽取2个进行分析，则抽到的2个销售店该月的销售量中有且仅有一个高于平均数”为事件A ，则可能的情况为：),(11b a 、),(21b a 、),(31b a 、),(12b a 、),(22b a 、),(32b a 共6种， …………8分所以53106)(==A P . …………………………………..10分22. 解：（Ⅰ）把点)1,41(-B 坐标代入抛物线Γ： 22y px = 得412)1(2⋅=-p ………………………..2分 解得2p =24y x ∴= ………………………..4分 （Ⅱ）抛物线Γ的焦点为F )0,1(-，直线AB 的方程为1411010--=---x y ，化简得 4340x y --= …………………………………..6分与抛物线方程24y x =联立可得241740x x -+= ………………………………….8分设点A 点的坐标为),(A A y x ，则141=⋅A x所以2414++=++=p x x AB B A425=则线段AB 的长为254. ………………………………….10分23.解：（Ⅰ）由三视图可得该几何体是一个底面是边长为4cm 的正方形，高为3cm 的长方体， 挖去一个半径为lcm 的圆柱孔.………………………..3分所以该零件的体积为：313442⨯⨯-⨯⨯=πV π348-=)(58.383cm ≈ ………………………..6分（Ⅱ）1000个这种零件需要铁为：8.758.381000⨯⨯≈P （克） ……………..9分 924.300=（千克） ……………..10分答：制造1000个这样的零件，约需要铁924.300千克. ……..12分24.解：（Ⅰ） 2()66f x x ax '=-，因为()f x 在2x =处取得极值，所以(2)0f '=，解得2a =． ……………..2分（Ⅱ）()6()f x x x a '=-，当0a >时，由()6(0f x x x a '=->）得x a >或0x <.即()f x 的单调增区间为(),0-∞和(),a +∞. ……………..6分 （Ⅲ）（1）当0a ≤时，由（Ⅱ）可知，()f x 在[]0,2上单调递增，所以()f x 的最小值为(0)1f =； ……………..8分（2）当02a <<时，可知，()f x 在[)0,a 上单调递减，在(],2a 上单调递增，所以()f x 的最小值为3()1f a a =-； ……………..10分 （3）当2a ≥时，可知，()f x 在[]0,2上单调递减，所以()f x 的最小值为(2)1712f a =-. 则 当0a ≤时，()f x 的最小值为(0)1f =； 当02a <<时，()f x 的最小值为3()1f a a =-；当2a ≥时，()f x 的最小值为(2)1712f a =-. ……………..12分。

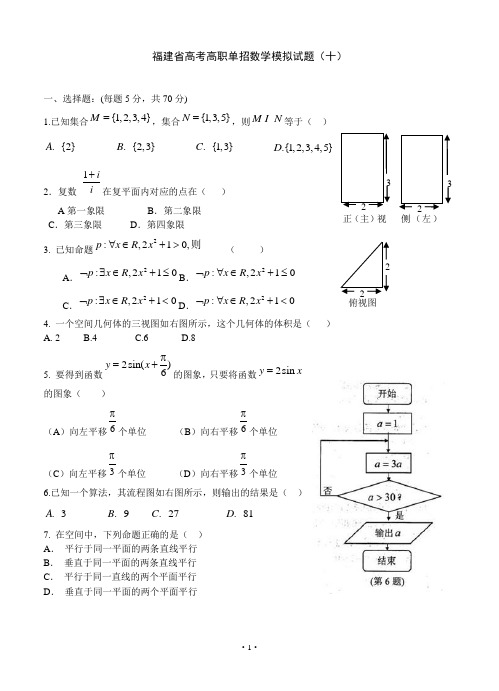
福建省高考高职单招数学模拟试题（十）一、选择题：(每题5分，共70分)1.已知集合{1,2,3,4}M =，集合{1,3,5}N =，则M N 等于（ ）.{2}A .{2,3}B .{1,3}C .{1,2,3,4,5}D2．复数 1ii +在复平面内对应的点在（ ）A 第一象限B ．第二象限C ．第三象限D ．第四象限3. 已知命题2:,210,p x R x ∀∈+>则 （ ） A ．2:,210p x R x ⌝∃∈+≤B ．2:,210p x R x ⌝∀∈+≤C ．2:,210p x R x ⌝∃∈+<D ．2:,210p x R x ⌝∀∈+< 4. 一个空间几何体的三视图如右图所示，这个几何体的体积是（ ） A. 2 B.4 C.6 D.85. 要得到函数2sin()6y x π=+的图象，只要将函数2sin y x =的图象（ ）（A ）向左平移6π个单位 （B ）向右平移6π个单位 （C ）向左平移3π个单位 （D ）向右平移3π个单位6.已知一个算法，其流程图如右图所示，则输出的结果是（ ）.3A .9B .27C .81D7. 在空间中，下列命题正确的是（ ） A ． 平行于同一平面的两条直线平行 B ． 垂直于同一平面的两条直线平行 C ． 平行于同一直线的两个平面平行 D ． 垂直于同一平面的两个平面平行正（主）视侧（左）俯视图8.若AD 为ABC ∆的中线，现有质地均匀的粒子散落在ABC ∆内，则粒子在ABD ∆内的概率等于（ ）4.5A 3.4B 1.2C 2.3D9. 计算sin 240︒的值为（）.A 1.2B - 1.2CD⒑"tan 1"α=是""4πα=的 （ ）A.必要而不充分条件B.充分而不必要条件C.充要条件D.既不充分也不必要条件 11. 下列函数中，在),0(+∞上是减函数的是（ ）.Ax y 1=.B 12+=x y .C xy 2= .D x y 3l o g =⒓已知直线的点斜式方程是21)y x -=-，那么此直线的倾斜角为（ ）.6A π.3B π2.3C π 5.6D π13.已知实数x 、y 满足04x y x y ⎧⎪⎨⎪+⎩≥≥0≥4，则z x y =+的最小值等于（ ）.0A .1B .4C .5D14、设椭圆的两焦点为F1、F2，过F2作椭圆长轴的垂线交椭圆于点P ，若△F1PF2为等腰直角三角形，则椭圆的离心率为（ ） A 、22B 、212-C 、22-D 、12-二、 填空题：本大题共4个小题，每小题5分，共20分。

考单招——上高职单招网X农业职业技术学院高职招考数学模拟试题〔附答案解析〕一、选择题〔本大题共12 小题，每题5 分，共 60 分〕1．集合M={x | x∈ N，且8-x∈ N}，那么M中只含二个元素的子集的个数为〔〕A、3B 、15C 、21D、422．函数 y= | lg 〔 x-1 〕 | 的图象是〔〕3．假设θ∈〔 0，〕，那么sinθ+cosθ的一个可能值是〔〕A、B、C、D、14．共轭双曲线的离心率分别为e1， e2，那么必有〔〕A、=1 B 、e1 =e 2 C 、e1·e2=1 D 、=15．直线 a⊥ b，且 a∥平面α，那么 b 与平面α的关系是〔〕A、bαB、 bαC、b∥α或 b αD、b 与α相交或 b ∥α或 b α6．如果把两条异面直线看作“一对〞，那么四棱锥的棱所在8 条直线中，异面直线共有〔〕A、4 B 、 8 C 、16 D 、247．A=3 是直线 ax+2y+3a=0和直线3x+〔a-1〕y=a-7平行且不重合的〔〕条件考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕考单招——上高职单招网A、充分不必要B、必要不充分C、充要D、不充分且不必要8．不等式组的解集是〔〕A、{x | 0 ＜ x＜3｝ B 、 {x | 0 ＜ x＜} C 、 {x | 0 ＜x＜ 2.5 ｝ D 、{x | 0 ＜ x＜2｝9．如图，等腰直角△ ABC，沿其斜边AB 上的高 CD 对折，使△ ACD 与△BCD 所在平面垂直，此时，∠ ACB 等于〔〕A、45°B、60°C、90°D、120 °10．复数的值是〔〕A、iB、 1 C 、 -i D-111．关于 x 的方程 x 2+ 〔 a2-1 〕 x+ 〔a-2 〕x=0的一个根比 1 大，另一根比1 小，那么有〔〕A、-2 ＜ a＜1 B 、-1 ＜ a＜ 1 C 、 a＜-2 或 a＞ 1D、a＜ -1 或 a＞ 212 ．f〔 x〕 =log 2〔-x 〕++2 ，假设 f〔 a〕=5 ，那么 f〔 -a 〕等于〔〕A、-5B 、5C 、7D、-1二、填空题〔本大题共4 小题，每题4 分，共 16 分〕。

2016年福建高职招考数学押题卷（二）（面向普通高中）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。

考试时间120分钟。

第Ⅰ卷(选择题 共70分)一、选择题：本大题共14小题，每小题5分，共70分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1。

已知全集{}1,2,3,4,5,6A =，{}21,B y y x x A ==-∈，则A B =( ）A.{}1,2,3,4 B 。

{}1,2,3 C.{}1,3,5 D.{}2,4,6 2．i 是虚数单位，若复数2333z i i +-=-,则z =（ ）A.5 5 C 。

61 613. 某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是（ ） A.抽签法 B 。

分层抽样法 C 。

系统抽样法D.随机数法4. 在等差数列{}na 中，若253,9aa ==，则其前6项和6S =（ )。

A. 12B. 24 C 。

36 D.485．若一个圆锥的轴截面是等边三角形，则该圆锥的侧面积与底面积的比等于（ ）A 。

3B 。

2C 。

3D 。

26。

若1sin()2πα-=,则tan α的值为（ ）A.3B.3-C 。

3±D 。

7. ABC ∆中，已知90,(,6),(2,3)A AB k AC ===-，则k 的值是( ）A ．4- B ．3- C ．4 D ．9 8. 已知抛物线22(0)y px p =>的准线经过点(1,1)-，则抛物线焦点坐标为( )A ．(1,0)B ．(1,0)-C ．(0,1)-D ．(0,1) 9.设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩，则((2))f f -=(）A ．1-B ．14C ．12D ．3210.下列函数中，最小正周期为π的奇函数是A. sin(2)2y x π=+B 。

2000 份高职单招试题，全部免费提供！育龙单招网，单招也能上大学zzzsxx 2021年XX高职招考数学模拟试题:常见函数、幂函数的导数及导数公式表【试题内容来自于相关和学校提供】1：对于三次函数〔〕，定义：设f″〔x〕是函数y＝ f′〔 x〕的导数，假设方程f″〔 x〕＝ 0 有实数解x0，那么称点〔x0，f〔 x0〕〕为函数的“拐点〞。

有同学发现: “任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心。

〞请你将这一发现为条件，假设函数，那么=〔〕A、2021B、2021C、2021D、20212：假设对任意，，，那么是〔〕A、B、C、D、A、0 秒B、1 秒末2000 份高职单招试题，全部免费提供！育龙单招网，单招也能上大学zzzsxxC、2 秒末D、1秒末和 2 秒末4：函数的导数为()A、B、C、D、5：定义方程的较大实数根叫做函数的“轻松点〞，假设函数，，的“轻松点〞分别为，那么的大小关系为〔〕6：曲线在点处的切线方程为_________。

2000 份高职单招试题，全部免费提供！育龙单招网，单招也能上大学zzzsxx7：求以下函数的导数：〔 1〕的导数为 _________ ；〔 2〕的导数为；（3〕的导数为_____________。

8：设函数，假设，那么的值等于。

9：函数的导数为 _______。

10：函数的导数是.11：求曲线在点处的切线方程。

2000 份高职单招试题，全部免费提供！育龙单招网，单招也能上大学zzzsxx12：〔此题 9 分〕函数，是的导函数〔 1〕求函数的最小正周期；〔 2〕假设，求的值。

13： (此题总分值12 分 )求以下函数的导数（1〕（2〕14：〔此题总分值15 分〕曲线C上的动点满足到点的距离比到直线的距离小1。

求曲线 C 的方程；过点F的直线l与曲线C交于A、B两点。

〔ⅰ〕过A、 B 两点分别作抛物线的切线，设其交点为M ，证明：〔；ⅱ〕是否在y轴上存在定点Q ，使得无论 AB怎样运动，都有？证明你的结论。

考单招——上高职单招网2016福建工程学院高职招考数学模拟试题（附答案解析）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．设等于（）A．{1,4} B．{1,6} C．{4,6} D．{1,4,6}2．已知点M（6，2）和M2（1，7）.直线y=mx—7与线段M1M2的交点M分有向线段M1M2的比为3：2，则m的值为（）A．B．C． D．43．已知函数的解析式可能为（）A． B．C．D．4．两个圆的公切线有且仅有（）A．1条B．2条C．3条D．4条5．若函数、三、四象限，则一定有（）A．B．C．D．6．四面体ABCD四个面的重心分别为E、F、G、H，则四面体EFGH的表面积与四面体ABCD的表面积的比值是（）A．B．C． D．考单招——上高职单招网7．已知为非零的平面向量.甲：（）A．甲是乙的充分条件但不是必要条件B．甲是乙的必要条件但不是充分条件C．甲是乙的充要条件D．甲既不是乙的充分条件也不是乙的必要条件8．已知有（）A．最大值B．最小值C．最大值1D．最小值19．已知数列{}的前n项和其中a、b是非零常数，则存在数列{}、{}使得（）A．为等差数列，{}为等比数列B．和{}都为等差数列C．为等差数列，{}都为等比数列D．和{}都为等比数列10．若则下列结论中不．正确的是（）A．B．C．D．考单招——上高职单招网11．将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子里，每个盒内放一个球，恰好3个球的标号与其在盒子的标号不．一致的放入方法种数为（）A．120B．240C．360D．72012．设是某港口水的深度y（米）关于时间t（时）的函数，其中.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：t03691215182124 y1215.112.19.111.914.911.98.912.1经长期观观察，函数的图象可以近似地看成函数的图象.在下面的函数中，最能近似表示表中数据间对应关系的函数是（）A．B．C． D．二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.13．Tan2010°的值为.14．已知的展开式中各项系数的和是128，则展开式中x5的系数是.（以数字作答）15．某校有老师200人，男学生1200人，女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人，则n= .16．设A、B为两个集合，下列四个命题：①A B对任意②A B考单招——上高职单招网③A B A B ④A B存在其中真命题的序号是.（把符合要求的命题序号都填上）三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知的值.18．（本小题满分12分）如图，在棱长为1的正方体ABCD—A1B1C1D1中，AC与BD交于点E，CB与CB1交于点F.（I）求证：A1C⊥平BDC1；（II）求二面角B—EF—C的大小（结果用反三角函数值表示）.考单招——上高职单招网19．（本小题满分12分）如图，在Rt△ABC中，已知BC=a.若长为2a的线段PQ以点A为中点，问的夹角θ取何值时的值最大？并求出这个最大值.20．（本小题满分12分）直线的右支交于不同的两点A、B.（Ⅰ）求实数k的取值范围；（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由.21．（本小题满分12分）为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率（记为P）和所需费用如下表：预防措施甲乙丙丁考单招——上高职单招网P0.90.80.70.690603010费用（万元）预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超过120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大.22．（本小题满分14分）已知的图象相切.（Ⅰ）求b与c的关系式（用c表示b）；（Ⅱ）设函数内有极值点，求c 的取值范围.参考答案一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．D 2．D 3．A 4．B 5．C 6．C 7．B 8．D 9．C 10．D 11．B 12．A 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13． 14．35 15．192 16．④考单招——上高职单招网17．本小题考三角函数的基本公式以及三角函数式的恒等基础知识和基本运算技能，满分12分.解法一：由已知得：由已知条件可知解法二：由已知条件可知考单招——上高职单招网18．本小题主要考查线面关系和正方体等基础知识，考查空间想象能力和推理能力.满分12分.解法一：（Ⅰ）∵A1A⊥底面ABCD，则AC是A1C在底面ABCD的射影.∵AC⊥BD.∴A1C⊥BD.同理A1C⊥DC1,又BD∩DC1=D,∴A1C⊥平面BDC1.（Ⅱ）取EF的中点H，连结BH、CH，又E、F分别是AC、B1C的中点，考单招——上高职单招网解法二：（Ⅰ）以点C为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0). D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)（Ⅱ）同（I）可证，BD1⊥平面AB1C.考单招——上高职单招网19．本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力，满分12分.解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.考单招——上高职单招网20．本小题主要考查直线、双曲线的方程和性质，曲线与方程的关系，及其综合应用能力，满分12分.解：（Ⅰ）将直线……①依题意，直线l与双曲线C的右支交于不同两点，故（Ⅱ）设A、B两点的坐标分别为、，则由①式得考单招——上高职单招网……②假设存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F（c,0）.则由FA⊥FB得：整理得……③把②式及代入③式化简得21．本小题考查概率的基础知识以及运用概率知识解决实际问题的能力，满分12分.解：方案1：单独采用一种预防措施的费用均不超过120万元.由表可知，采用甲措施，可使此突发事件不发生的概率最大，其概率为0.9.方案2：联合采用两种预防措施，费用不超过120万元，由表可知.联合甲、丙两种预防措施可使此突发事件不发生的概率最大，其概率为1—(1—0.9)(1—0.7)=0.97.方法3：联合采用三种预防措施，费用不超过120万元，故只能联合乙、丙、丁三种预防措施，此时突发事件不发生的概率为1—（1—0.8）(1—0.7)(1—0.6)=1—0.024=0.976.考单招——上高职单招网综合上述三种预防方案可知，在总费用不超过120万元的前提下，联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.22．本小题考查导数、切线、极值等知识及综合运用数学知识解决问题的能力.满分14分.解：（Ⅰ）依题意，令（Ⅱ）x x0 （+0+于是不是函数的极值点.的变化如下：x x1 （+0—0+由此，的极小值点.综上所述，当且仅当考单招——上高职单招网。