2017-2018学年人教A版高一数学热点专题高分特训必修1：第3章指数函数的概念及其性质 Word版含答案

对数运算一、单选题(共7道，每道10分)1.设，且，下列等式中正确的是( )A.B.C.D.答案：D解题思路：由对数的运算法则，，．故选D试题难度：三颗星知识点：对数的运算性质2.的值是( )A.1B.C. D.答案：B解题思路：故选B试题难度：三颗星知识点：对数的运算性质3.的值是( )A.1B.C. D.答案：A解题思路：故选A试题难度：三颗星知识点：对数的运算性质4.的值是( )A. B.C. D.答案：C解题思路：故选C试题难度：三颗星知识点：换底公式的应用5.的值是( )A. B.C. D.答案：B解题思路：故选B试题难度：三颗星知识点：换底公式的应用6.若，，则用含m，n的代数式可表示为( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：换底公式的应用7.已知，则的值的集合为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：对数的运算性质二、填空题(共3道，每道10分)8.已知，则的值为____．答案：100解题思路：试题难度：知识点：对数的运算性质9.已知，且，，，则的值____．答案：20解题思路：试题难度：知识点：指数式与对数式的互化10.已知，则的值为____．答案：1解题思路：试题难度：知识点：指数式与对数式的互化。

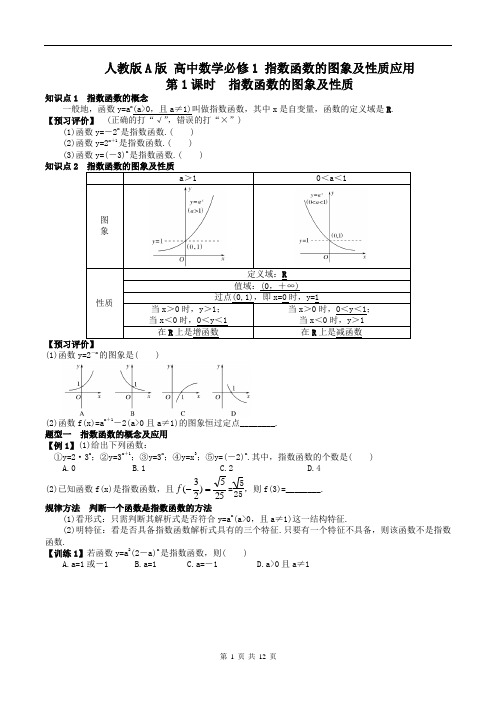
人教版A 版 高中数学必修1 指数函数的图象及性质应用第1课时 指数函数的图象及性质知识点1 指数函数的概念一般地，函数y=a x(a>0，且a ≠1)叫做指数函数，其中x 是自变量，函数的定义域是R . 【预习评价】 (正确的打“√”，错误的打“×”)(1)函数y=－2x是指数函数.( )(2)函数y=2x ＋1是指数函数.( )(3)函数y=(－3)x是指数函数.( ) 知识点2(1)函数y=2－x的图象是( )(2)函数f(x)=a x ＋1－2(a>0且a ≠1)的图象恒过定点________. 题型一 指数函数的概念及应用 【例1】(1)给出下列函数：①y=2·3x ；②y=3x ＋1；③y=3x ；④y=x 3；⑤y=(－2)x.其中，指数函数的个数是( ) A.0 B.1 C.2 D.4(2)已知函数f(x)是指数函数，且255)23(=-f =525，则f(3)=________. 规律方法 判断一个函数是指数函数的方法(1)看形式：只需判断其解析式是否符合y=a x(a>0，且a ≠1)这一结构特征.(2)明特征：看是否具备指数函数解析式具有的三个特征.只要有一个特征不具备，则该函数不是指数函数.【训练1】若函数y=a 2(2－a)x是指数函数，则( )A.a=1或－1B.a=1C.a=－1D.a>0且a ≠1题型二 指数函数图象的应用【例2】(1)函数f(x)=2a x ＋1－3(a>0，且a ≠1)的图象恒过的定点是________.(2)已知函数y=3x的图象，怎样变换得到2)31(1+=+x y 的图象？并画出相应图象.规律方法 处理函数图象问题的策略(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y 的值，即可得函数图象所过的定点.(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移). (3)利用函数的性质：奇偶性与单调性.【训练2】(1)函数y=2|x|的图象是( )(2)函数f(x)=ax －b的图象如图所示，其中a ，b 为常数，则下列结论正确的是( )A.a>1，b<0B.a>1，b>0C.0<a<1，b>0D.0<a<1，b<0 题型三 指数型函数的定义域、值域问题【例3】(1)函数f(x)=1－2x＋1x ＋3的定义域为( )A.(－3,0]B.(－3,1]C.(－∞，－3)∪(－3,0]D.(－∞，－3)∪(－3,1] (2)函数1)31()(-=xx f ，x ∈[－1,2]的值域为________. (3)函数y=4x＋2x ＋1＋1的值域为________.规律方法 指数型函数y=a f(x)定义域、值域的求法(1)定义域：函数y=a f(x)的定义域与y=f(x)的定义域相同. (2)值域：①换元，t=f(x). ②求t=f(x)的定义域为x ∈D. ③求t=f(x)的值域为t ∈M.④利用y=a t 的单调性求y=a t，t ∈M 的值域.【训练3】求函数4215-=x y 的定义域和值域.课堂达标1.若函数f(x)是指数函数，且f(2)=2，则f(x)=( )A.(2)xB.2xC.⎝ ⎛⎭⎪⎫12xD.⎝⎛⎭⎪⎫22x2.当x ∈[－2,2)时，y=3－x－1的值域是( )A.⎝ ⎛⎦⎥⎤－89，8B.⎣⎢⎡⎦⎥⎤－89，8C.⎝ ⎛⎭⎪⎫19，9 D.⎣⎢⎡⎦⎥⎤19，9 3.已知函数f(x)=2x，则f(1－x)的图象为( )4.函数f(x)=2·a x －1＋1的图象恒过定点________.5.函数f(x)=a x－1(a>0，且a ≠1)的定义域是(－∞，0]，求实数a 的取值范围.第2课时 指数函数及其性质的应用题型一 指数函数单调性的应用 方向1 比较两数的大小【例1－1】(1)下列大小关系正确的是( )A.0.43<30.4<π0B.0.43<π0<30.4C.30.4<0.43<π0D.π0<30.4<0.43(2)设a=0.60.6，b=0.61.5，c=1.50.6，则a ，b ，c 的大小关系是( ) A.a<b<c B.a<c<b C.b<a<c D.b<c<a 方向2 解简单的指数不等式 【例1－2】(1)不等式13)21(-x ≤2的解集为________.(2)已知a－5x>ax ＋7(a>0，且a ≠1)，求x 的取值范围.方向3 指数型函数的单调性 【例1－3】判断xx x f 22)31()(-=的单调性，并求其值域.规律方法：1.比较幂值大小的三种类型及处理方法2.解指数不等式的类型及应注意的问题(1)形如a x >a b 的不等式，借助于函数y=a x的单调性求解，如果a 的取值不确定，要对a 分为0<a<1和a>1两种情况分类讨论.(2)形如a x >b 的不等式，注意将b 转化为以a 为底数的指数幂的形式，再借助于函数y=a x的单调性求解.3.函数y=a f(x)(a>0，a ≠1)的单调性的处理技巧当a>1时，y=a f(x)与y=f(x)的单调性相同，当0<a<1时，y=a f(x)与y=f(x)的单调性相反.题型二 指数函数的实际应用【例2】某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若初始溶液含杂质2%，每过滤一次可使杂质含量减少13.(1)写出杂质含量y 与过滤次数n 的函数关系式；(2)过滤7次后的杂质含量是多少？过滤8次后的杂质含量是多少？至少应过滤几次才能使产品达到市场要求？规律方法：指数函数在实际问题中的应用(1)与实际生活有关的问题，求解时应准确读懂题意，从实际问题中提取出模型转化为数学问题. (2)在实际问题中，经常会遇到指数增长模型：设基数为N ，平均增长率为p ，则对于经过时间x 后的总量y 可以用y=N(1＋p)x来表示，这是非常有用的函数模型.【训练1】春天来了，某池塘中的荷花枝繁叶茂，已知每一天新长出荷叶覆盖水面面积是前一天的2倍，若荷叶20天可以完全长满池塘水面，当荷叶刚好覆盖水面面积一半时，荷叶已生长了________天.解析：假设第一天荷叶覆盖水面面积为1，则荷叶覆盖水面面积y 与生长时间x 的函数关系为y=2x －1，当x=20时，长满水面，所以生长19天时，荷叶布满水面一半.答案 19 题型三 指数函数性质的综合应用【例3】已知定义在R 上的函数f(x)=a ＋14x ＋1是奇函数.【训练2】已知函数3)21121()(x x f x ⋅+-= (1)求f(x)的定义域； (2)讨论f(x)的奇偶性； (3)证明：f(x)>0.课堂达标1.已知0.3m >0.3n，则m ，n 的大小关系为( )A.m>nB.m<nC.m=nD.不能确定2.已知xx f )21()(=，x ∈R ，那么f(x)是( )A.奇函数且在(0，＋∞)上是增函数B.偶函数且在(0，＋∞)上是增函数C.奇函数且在(0，＋∞)上是减函数D.偶函数且在(0，＋∞)上是减函数 3.函数xy -=1)21(的单调递增区间为( )A.(－∞，＋∞)B.(0，＋∞)C.(1，＋∞)D.(0,1) 4.不等式23－2x<0.53x －4的解集为________.5.比较下列各组值的大小：(1)1.8－0.1,1.8－0.2； (2)1.90.3,0.73.1； (3)a 1.3，a 2.5(a>0，且a ≠1).指数函数图象性质课时作业1.函数f(x)=3－x－1的定义域、值域分别是( ) A.定义域是R ，值域是RB.定义域是R ，值域是(0，＋∞)C.定义域是R ，值域是(－1，＋∞)D.以上都不对2.函数y=12x －1的值域是( )A.(－∞，1)B.(－∞，0)∪(0，＋∞)C.(－1，＋∞)D.(－∞，－1)∪(0，＋∞) 3.函数y=2x 2x ＋1的值域是( )A.(0，1)B.(0，1]C.(0，＋∞)D.[0，＋∞) 4.已知函数f(x)=5|x|，g(x)=ax 2－x(a ∈R )，若f[g(1)]=1，则a=( ) A.1 B.2 C.3 D.－1 5.函数y=110x －1－1的定义域为________.6.当x ∈[－1，1]时，函数f(x)=3x－2的值域为________.7.若函数f(x)=⎩⎪⎨⎪⎧f （x ＋2）（x<2），2－x （x ≥2），则f(－3)的值为________.8.若函数f(x)=a x－1(a>0且a ≠1)的定义域、值域都是[0，2]，则实数a 的值为________. 9.(1)函数y=(23)|x ＋1|的定义域是__________，值域是__________.(2)函数112+-=x x y 的定义域是________，值域是________.10.若函数y=a x(a ＞0且a ≠1)在[0，1]上的最大值与最小值的和为3，则a=________. 11.若集合A={y|y=2x，x ∈R }，B={y|y=x 2，x ∈R }，则A ∩B=________. 12.函数x y )21(2-=的定义域是______________，值域是____________.13.若正数a 满足a －0.1>a 0.2，则a 的取值范围是________.14.若x<0，f(x)=(a ＋1)x<1恒成立，则a 的取值范围是________. 15.求函数22)31(x x y -=的值域.16.已知函数f(x)=a x －1(x ≥0)的图像经过点(2，12)，其中a ＞0且a ≠1.(1)求a 的值；(2)求函数y=f(x)(x ≥0)的值域.参考答案第1课时 指数函数的图象及性质【预习评价】提示:(1)× 因为指数幂2x 的系数为－1，所以函数y=－2x不是指数函数；(2)× 因为指数不是x ，所以函数y=2x ＋1不是指数函数；(3)× 因为底数小于0，所以函数y=(－3)x不是指数函数.【预习评价】解析：(1)y=2－x =⎝ ⎛⎭⎪⎫12x是(－∞，＋∞)上的单减函数，故选B.(2)令x ＋1=0，则x=－1，f(－1)=a 0－2=－1，则f(x)的图象恒过点(－1，－1).答案 (1)B (2)(－1，－1) 题型一 指数函数的概念及应用【例1】解析:(1)①中，3x 的系数是2，故①不是指数函数；②中，y=3x ＋1的指数是x ＋1，不是自变量x ，故②不是指数函数；③中，3x 的系数是1，幂的指数是自变量x ，且只有3x一项，故③是指数函数；④中，y=x 3的底为自变量，指数为常数，故④不是指数函数.⑤中，底数－2＜0，不是指数函数.(2)设f(x)=a x (a>0且a ≠1)，由)23(-f =a －32 =5－32 ，故a=5，故f(x)=5x ，所以f(3)=53=125.答案 (1)B (2)125【训练1】解析 由条件知⎩⎪⎨⎪⎧a 2＝1，2－a>0，2－a ≠1，解得a=－1.答案 C题型二 指数函数图象的应用 【例2】(1)解析:因为y=a x 的图象过定点(0,1)，所以令x ＋1=0，即x=－1，则f(x)=－1，故f(x)=2a x ＋1－3的图象过定点(－1，－1).答案 (－1，－1) (2)解2)31(1+=+x y =3－(x ＋1)＋2.作函数y=3x的图象关于y 轴的对称图象得函数y=3－x的图象，再向左平移1个单位长度就得到函数y=3－(x ＋1)的图象，最后再向上平移2个单位长度就得到函数y=3－(x ＋1)＋2=2)31(1++x 的图象，如图所示.【训练2】解析 (1)y=2|x|=⎩⎪⎨⎪⎧2x，x ≥0，⎝ ⎛⎭⎪⎫12x，x<0，故选B.(2)从曲线的变化趋势，可以得到函数f(x)为减函数，从而有0<a<1；从曲线位置看，是由函数y=a x(0<a<1)的图象向左平移|－b|个单位长度得到，所以－b>0，即b<0.答案 (1)B (2)D题型三 指数型函数的定义域、值域问题【例3】解析:(1)由题意得自变量x 应满足⎩⎪⎨⎪⎧1－2x≥0，x ＋3>0，解得－3<x ≤0.(2)∵－1≤x ≤2，∴19≤⎝ ⎛⎭⎪⎫13x ≤3，∴－89≤⎝ ⎛⎭⎪⎫13x －1≤2，∴值域为⎣⎢⎡⎦⎥⎤－89，2. (3)函数的定义域为R ，又y=4x ＋2x ＋1＋1=(2x )2＋2·2x ＋1=(2x ＋1)2，易知2x>0，故y>1，即函数的值域为(1，＋∞).答案 (1)A (2)⎣⎢⎡⎦⎥⎤－89，2 (3)(1，＋∞) 【训练3】解:由2x －4>0，得x>2，故函数的定义域为{x|x>2}，因为12x －4>0，所以y=512x －4>1，故函数的值域为{y|y>1}.课堂达标1.解析:由题意，设f(x)=a x (a>0且a ≠1)，则由f(2)=a 2=2，得a=2，所以f(x)=(2)x.答案 A2.解析 y=3－x －1，x ∈[－2,2)上是减函数，∴3－2－1<y ≤32－1，即－89<y ≤8.答案 A3.解析 f(1－x)=21－x =⎝ ⎛⎭⎪⎫12x －1是减函数，故排除选项C ，D ，又当x=0时，⎝ ⎛⎭⎪⎫120－1=2，排除A ，故选B.4.解析:令x －1=0，得x=1，f(1)=2×1＋1=3，所以f(x)的图象恒过定点(1,3).答案 (1,3)5.解:由题意，当x ≤0时，a x≥1，所以0<a<1，故实数a 的取值范围是0<a<1. 第2课时 指数函数及其性质的应用 题型一 指数函数单调性的应用【例1－1】解析:(1)0.43<0.40=1=π0=30<30.4，故选B.(2)∵1.50.6>1.50=1,0.60.6<0.60=1，故1.50.6>0.60.6，又函数y=0.6x在(－∞，＋∞)上是减函数，且1.5>0.6，所以0.61.5<0.60.6，故0.61.5<0.60.6<1.50.6，选C.答案 (1)B (2)C【例1－2】(1)解析:∵2=⎝ ⎛⎭⎪⎫12－1，∴原不等式可化为⎝ ⎛⎭⎪⎫123x －1≤⎝ ⎛⎭⎪⎫12－1，∵函数y=⎝ ⎛⎭⎪⎫12x在R 上是减函数，∴3x －1≥－1，∴x ≥0，故原不等式的解集是{x|x ≥0}.答案 {x|x ≥0}(2)解:当a>1时，∵a －5x >a x ＋7，∴－5x>x ＋7，解得x<－76；当0<a<1时，∵a －5x >a x ＋7，∴－5x<x ＋7，解得x>－76.综上所述，x 的取值范围是：当a>1时，x<－76；当0<a<1时，x>－76.【例1－3】解：令u=x 2－2x ，则原函数变为y=⎝ ⎛⎭⎪⎫13u .∵u=x 2－2x=(x －1)2－1在(－∞，1]上递减，在[1，＋∞)上递增，又∵y=⎝ ⎛⎭⎪⎫13u 在(－∞，＋∞)上递减，∴y=⎝ ⎛⎭⎪⎫13x 2－2x 在(－∞，1]上递增，在[1，＋∞)上递减. ∵u=x 2－2x=(x －1)2－1≥－1，∴y=⎝ ⎛⎭⎪⎫13u ，u ∈[－1，＋∞)，∴0＜⎝ ⎛⎭⎪⎫13u ≤⎝ ⎛⎭⎪⎫13－1=3，∴原函数的值域为(0,3].【例2】解：(1)过滤1次后的杂质含量为2100×⎝ ⎛⎭⎪⎫1－13=2100×23；过滤2次后的杂质含量为⎝ ⎛⎭⎪⎫2100×23×⎝ ⎛⎭⎪⎫1－13=2100×⎝ ⎛⎭⎪⎫232；过滤3次后的杂质含量为⎣⎢⎡⎦⎥⎤2100×⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫1－13=2100×⎝ ⎛⎭⎪⎫233；…过滤n 次后的杂质含量为2100×⎝ ⎛⎭⎪⎫23n (n ∈N *).故y 与n 的函数关系式为y=2100×⎝ ⎛⎭⎪⎫23n (n ∈N *).(2)由(1)知当n=7时，y=2100×⎝ ⎛⎭⎪⎫237=6454 675>11 000，当n=8时，y=2100×⎝ ⎛⎭⎪⎫238=128164 025<11 000，所以至少应过滤8次才能使产品达到市场要求. 【例3】解 (1)∵f(x)的定义域为R ，且f(x)为奇函数，∴f(0)=0，即a ＋12=0，a=－12. (2)由(1)知f(x)=－12＋14x ＋1，故f(x)在R 上为减函数. (3)∵f(x)为奇函数，∴f(t 2－2t)＋f(2t 2－k)<0可化为f(t 2－2t)<f(k －2t 2)，由(2)知f(x)在R 上单调递减，∴t 2－2t>k －2t 2，即3t 2－2t －k>0对于一切t ∈R 恒成立，∴Δ=4＋12k<0，得k<－13，∴k 的取值范围是⎝⎛⎭⎪⎫－∞，－13. 【训练2】解：(1)由题意得2x －1≠0，即x ≠0，∴f(x)的定义域为(－∞，0)∪(0，＋∞).(2)令g(x)=12x －1＋12=2x ＋122x －1，φ(x)=x 3. ∵g(－x)=2－x ＋122－x －1=1＋2x 21－2x =－g(x)，∴g(x)为奇函数. 又∵φ(x)=x 3为奇函数，∴f(x)=⎝ ⎛⎭⎪⎫12x －1＋12·x 3为偶函数. (3)证明：当x>0时，2x >1，∴2x －1>0，∴12x －1＋12>0.∵x 3>0，∴f(x)>0. 由偶函数的图象关于y 轴对称，知当x<0时，f(x)>0也成立.故对于x ∈(－∞，0)∪(0，＋∞)，恒有f(x)>0.课堂达标1.解析 因为函数y=0.3x 是R 上的减函数，且0.3m >0.3n ，所以m<n.答案 B2.解析 由x ∈R 且f(－x)=f(x)知f(x)是偶函数，当x>0时，f(x)=⎝ ⎛⎭⎪⎫12x 是减函数.答案 D 3.解析 定义域为R .设u=1－x ，y=⎝ ⎛⎭⎪⎫12u . ∵u=1－x 在(－∞，＋∞)上为减函数.又∵y=⎝ ⎛⎭⎪⎫12u 在(－∞，＋∞)上为减函数， ∴y=⎝ ⎛⎭⎪⎫121－x 在(－∞，＋∞)上是增函数，∴选A.答案 A 4.解析 原不等式可化为23－2x <24－3x ，因为函数y=2x 是R 上的增函数，所以3－2x<4－3x ，解得x<1，则解集为{x|x<1}.答案 {x|x<1}5.解：(1)因为函数y=1.8x 是R 上的增函数，且－0.1>－0.2，所以1.8－0.1>1.8－0.2.(2)因为1.90.3>1.90=1,0.73.1<0.70=1，所以1.90.3>0.73.1.(3)当a>1时，函数y=a x 是R 上的增函数，又1.3<2.5，故a 1.3<a 2.5；当0<a<1时，函数y=a x 是R 上的减函数，又1.3<2.5，故a 1.3>a 2.5.指数函数图象性质课时作业1.答案 C2.答案 D3.答案 A 解析 y=2x＋1－12x ＋1=1－12x ＋1.而0<12x ＋1<1，所以0<y<1. 4.答案 A 解析 方法一：∵f[g(1)]=1，∴g(1)=0，∴a －1=0，∴a=1.选A.方法二：∵g(1)=a －1，f[g(1)]=f(a －1)=5|a －1|=1，∴|a －1|=0，∴a=1.选A.5.答案 {x|x ≠1}6.答案 [－53，1] 7.答案 188.答案 39.答案 (1)R ，(0，1]，(2){x|x ≠－1}，(0，2)∪(2，＋∞)解析：(1)由于|x ＋1|≥0，而0<23<1，∴y 有最大值1，∴值域为(0，1]. (2)∵x －1x ＋1=1－2x ＋1≠1，∴y ≠2.∴函数值域为(0，2)∪(2，＋∞). 10.答案：2；解析 由a 0＋a 1=3，得a=2.11.答案：{y|y>0}(或填A)；解析：∵A={y|y>0}，B={y|y ≥0}，∴A ∩B={y|y>0}.12.答案 [－1，＋∞)，[0，2)；解析：要使函数有意义，只需2－(12)x ≥0，即(12)x ≤(12)－1，∴x ≥－1，即定义域为[－1，＋∞). ∵y=2－（12）x 在[－1，＋∞)上是增函数，而(12)x >0，∴值域为[0，2). 13.答案 0<a<114.答案 a>015.解：令u=2x －x 2=－(x －1)2＋1≤1.又y=(13)u 为减函数，∴y ≥13，即函数的值域为[13，＋∞). 16.解：(1)函数图像经过点(2，12)，所以，a 2－1=12，则a=12. (2)f(x)=(12)x －1(x ≥0)，由x ≥0，得x －1≥－1.于是0＜(12)x －1≤(12)－1=2.所以函数的值域为(0，2].。

数学1（必修）第三章 函数的应用（含幂函数）[基础训练A 组]一、选择题 1 若)1(,,)1(,1,4,)21(,2522>==-=+====a a y x y x y x y x y y x y xx 上述函数是幂函数的个数是（ ） A 0个 B 1个 C 2个 D 3个 2 已知)(x f 唯一的零点在区间(1,3)、(1,4)、(1,5)内，那么下面命题错误的（ ） A 函数)(x f 在(1,2)或[)2,3内有零点 B 函数)(x f 在(3,5)内无零点 C 函数)(x f 在(2,5)内有零点 D 函数)(x f 在(2,4)内不一定有零点 3 若0,0,1a b ab >>>，12log ln 2a =，则log a b 与a 21log 的关系是（ ） A 12log log a b a < B 12log log a b a = C 12log log a b a > D 12log log a b a ≤ 4 求函数132)(3+-=x x x f 零点的个数为 （ ） A 1 B 2 C 3 D 4 5 已知函数)(x f y =有反函数，则方程0)(=x f （ ） A 有且仅有一个根 B 至多有一个根 C 至少有一个根 D 以上结论都不对 6 如果二次函数)3(2+++=m mx x y 有两个不同的零点，则m 的取值范围是（ ） A ()6,2- B []6,2- C {}6,2- D ()(),26,-∞-+∞ 7 某林场计划第一年造林10000亩，以后每年比前一年多造林20%，则第四年造林（ ） A 14400亩 B 172800亩 C 17280亩 D 20736亩二、填空题 1 若函数()x f 既是幂函数又是反比例函数,则这个函数是()x f =2 幂函数()f x 的图象过点（，则()f x 的解析式是_____________3 用“二分法”求方程0523=--x x 在区间[2,3]内的实根，取区间中点为5.20=x ，4 函数()ln 2f x x x =-+的零点个数为5 设函数)(x f y =的图象在[],a b 上连续，若满足 ，方程0)(=x f 在[],a b 上有实根三、解答题 1 用定义证明：函数1()f x x x=+在[)1,x ∈+∞上是增函数设1x 与2x 分别是实系数方程20ax bx c ++=和20ax bx c -++=的一个根，且1212,0,0x x x x ≠≠≠ ，求证：方程202a x bx c ++=有仅有一根介于1x 和2x 之间3 函数2()21f x x ax a =-++-在区间[]0,1上有最大值2，求实数a 的值4 某商品进货单价为40元，若销售价为50元，可卖出50个，如果销售单价每涨1元， 销售量就减少1个，为了获得最大利润，则此商品的最佳售价应为多少？数学1（必修）第三章 函数的应用 [基础训练A 组]参考答案一、选择题 1 C 2,y x y x ==是幂函数 2 C 唯一的零点必须在区间(1,3)，而不在[)3,5 3 A 12log ln 20,01,1a a b =><<>得，12log 0,log 0a b a <> 4 C 332()2312212(1)(1)f x x x x x x x x x =-+=--+=--- 2(1)(221)x x x =-+-，22210x x +-=显然有两个实数根，共三个； 5 B 可以有一个实数根，例如1y x =-，也可以没有实数根，例如2x y = 6 D 24(3)0,6m m m ∆=-+>>或2m <- 7 C 310000(10.2)17280+=二、填空题 1 1x设(),f x x α=则1α=- 2()f x =(),f x x α=图象过点（，34333,4αα===3 [2,2.5) 令33()25,(2)10,(2.5) 2.5100f x x x f f =--=-<=->4 2 分别作出()ln ,()2f x x g x x ==-的图象；5 ()()0f a f b ≤ 见课本的定理内容三、解答题 1 证明：设1212121211,()()()(1)0x x f x f x x x x x ≤<-=--< 即12()()f x f x <，∴函数1()f x x x =+在[)1,x ∈+∞上是增函数 2 解：令2(),2a f x x bx c =++由题意可知2211220,0ax bx c ax bx c ++=-++= 221122,,bx c ax bx c ax +=-+=2222111111(),222a a a f x x bx c x ax x =++=-=- 22222222223(),222a a a f x x bx c x ax x =++=+=因为120,0,0a x x ≠≠≠ ∴12()()0f x f x <，即方程202a x bx c ++=有仅有一根介于1x 和2x 之间 3 解：对称轴x a =，当[]0,0,1a <是()f x 的递减区间，max ()(0)121f x f a a ==-=⇒=-； 当[]1,0,1a >是()f x 的递增区间，max ()(1)22f x f a a ===⇒=；当01a ≤≤时2max 1()()12,2f x f a a a a ±==-+==与01a ≤≤矛盾； 所以1a =-或2 4 解：设最佳售价为(50)x +元，最大利润为y 元， (50)(50)(50)40y x x x =+---⨯240500x x =-++当20x =时，y 取得最大值，所以应定价为70元。

新编人教版精品教学资料指数函数的概念及其性质一、单选题(共11道，每道9分)1.若函数满足，则的值为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：指数函数的解析式及运算2.若函数是指数函数，则的值为( )A.2B.C. D.-2答案：B解题思路：试题难度：三颗星知识点：指数函数的解析式及运算3.函数的定义域是( )A.(-∞，2]B.["0，2"]C.(-∞，2)D.(0，2]答案：A解题思路：试题难度：三颗星知识点：指数函数的定义域4.函数的值域是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：指数函数的值域5.若，则函数的值域是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：指数函数的值域6.若函数的图象恒过定点(1，2)，则b的值为( )A.0B.1C.2D.3答案：C解题思路：试题难度：三颗星知识点：指数函数的图象与性质7.不论a是何值，函数恒过一定点，这个定点坐标是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：指数函数的图象与性质8.若函数的图象在第一、三、四象限，则有( )A.，B.，C.，D.，答案：D解题思路：试题难度：三颗星知识点：指数函数的图象与性质9.函数在上是( )A.单调递减无最小值B.单调递减有最小值C.单调递增无最大值D.单调递增有最大值答案：A解题思路：试题难度：三颗星知识点：指数函数单调性的应用10.函数在上的最小值为( )A.-1B.0C.2D.10答案：C解题思路：试题难度：三颗星知识点：指数函数单调性的应用11.已知函数，，若有，则b的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：指数函数综合题。

⼈教A版必修1指数函数及其性质知识点总结与例题讲解指数函数及其性质知识点总结本节知识点（1）指数函数的概念（2）指数函数的图象和性质（3）指数函数的定义域和值域（4）指数函数的单调性及其应⽤（5）指数函数的图象变换知识点⼀指数函数的概念⼀般地,函数xa y =（0>a 且1≠a ）叫做指数函数,其中x 是⾃变量,函数的定义域是R . 1.为什么规定“0>a 且1≠a ”?答:若0=a ,则当0>x 时,0=x a ,当x ≤0时,xa ⽆意义;若0值,xa ⽆意义,如函数()xy 2-=,当 41,21=x 时,函数⽆意义;若1=a ,则对任意的∈x R ,都有1=x a ,没有研究的必要.基于上⾯的原因,在指数函数的定义中,规定0>a 且1≠a .上⾯的定义,是形式定义. 2.为什么指数函数的定义域是R ?答:对于指数幂来说,当底数⼤于0时,指数已经由整数指数推⼴到了实数指数,所以在指数函数的定义⾥⾯,⾃变量的取值范围是全体实数,即函数的定义域为R . 3.指数函数的结构特征指数函数的定义是形式上的定义,其函数解析式的结构具有⾮常明显的特征,如下: （1）指数中只有⼀个⾃变量x ,⽽不是含⾃变量的多项式; （2）xa 的系数必须为1,不能是其它的数字,也不能含有⾃变量; （3）底数a 必须满⾜0>a 且1≠a 的⼀个常数.根据上⾯的三个特征,可以判断⼀个函数是否为指数函数,也可以在已知指数函数的前提下,求参数的值或参数的取值范围.例1. 已知函数()()x a a x f ?-=32是指数函数,求a 的值. 分析:本题考查指数函数的定义,指数函数的定义有三个特征: （1）指数的位置只有⼀个⾃变量,但不是含⾃变量的多项式; （2）底数是⼀个⼤于0且不等于1的常数;（3）x a 的系数必须为1.解:∵函数()()x a a x f ?-=32是指数函数∴??≠>=-10132a a a ,解之得:2=a . 例2. 已知指数函数()()32--+=a a a y x 的图象过点()4,2,则=a _________.解:由题意可得:()()≠>=--10032a a a a ,解之得:2=a 或3=a .∵函数的图象经过点()4,2 ∴2=a .例3. 若指数函数()x f 的图象经过点()9,2,求()x f 的解析式及()1-f 的值. 解:设函数()x a x f =.∵其图象经过点()9,2,∴2239==a ,∴3=a . ∴()x f 的解析式为()x x f 3=. ∴()31311==--f . 例4. 函数()x a a a y 442+-=是指数函数,则a 的值是【】（A ）4 （B ）1或3 （C ）3 （D ）1解:由题意可得:??≠>=+-101442a a a a ,解之得:3=a .∴x y 3=.选择【 C 】.例5. 若函数()xa y 12-=（x 是⾃变量）是指数函数,则a 的取值范围是_________.解:∵函数()xa y 12-=是指数函数∴≠->-112012a a ,解之得:21>a 且1≠a .∴a 的取值范围是?≠>121a a a 且.例6. 若函数()xa a y 32-=是指数函数,求实数a 的取值范围.解:∵函数()xa a y 32-=是指数函数∴≠->-130322a a a a ,解之得:±≠<>213303a a a 或. ∴实数a 的取值范围是?±≠<>213303a a a a 且或.知识点⼆指数函数的图象和性质⼀般地,指数函数xa y =（0>a 且1≠a ）的图象和性质如下表所⽰:指数函数函数值的特点:（1）当10<<a 时,若0<x="" ,则恒有1="" bdsfid="213">y ;若0>x ,则恒有10<a 时,若0x ,则恒有1>y . 1. 指数函数图象的画法。