运输问题及解法
- 格式:ppt
- 大小:643.50 KB
- 文档页数:42


运输问题的解法运输问题是一类特殊的线性规划问题,最早是从物质调运工作中提出的,后来又有许多其它问题也归结到这一类问题中。
正是由于它的特殊结构,我们不是采用线性规划的单纯方法求解,而是根据单纯形方法的基本原理结合运输问题的具体特性须用表上作业的方法求解。
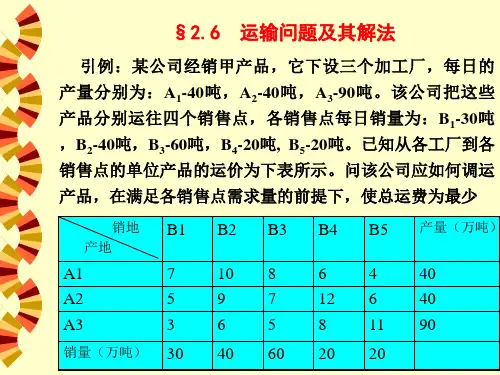
§1 运输问题的数学模型及其特性1.1 运输问题的数学模型设有 个地点(称为产地或发地) 的某种物资调至 个地点(称为销地或收地),各个发点需要调出的物资量分别为个单位,各个收点需要调进的物资量分别为 个单位。
已知每个发点到每个收点的物资每单位运价为 ,现问如何调运,才能使总的运费最小。
我们把它列在一张表上(称为运价表)。
设表示从产地运往销地的运价( =1,2,…, ; =1,2,…,)。
表3-1如果(总发量)(总收量),我们有如下线性规划问题:m mA A A ,,,21 n nB B B ,,,21 ma a a ,,,21 nb b b ,,,21 iA jB ijc ijx iA jB i m jn(3.1)(3.1)式称为产销平衡运输问题的数学模型。
当(总发量)(总收量)时。
即当产大于销()时,其数学模型为(3.2)当销大于产()时,其数学模型为(3.3)因为产销不平衡的运输问题可以转化为产销平衡的运输问题。
所以我们先讨论产销平衡的运输问题的求解。
运输问题有个未知量,个约束方程。
例如当≈40,=70时(3.1)式就有2800个未知量,110个方程,若用前面的单纯形法求解,计算工作量是相当大的。
我们必须寻找特殊解法。
∑∑===m i nj ijij x c z 11min ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥====∑∑==),,2,1;,2,1(0),,2,1(),,2,1(11n j m i x n j b x m I a x ij j mi ij i nj ij ∑∑==≠nj jm i i ba 11∑∑==>nj jm i i ba 11∑∑===m i nj ijij x c z 11min ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥===≤∑∑==),,2,1;,2,1(0),,2,1(),,2,1(11n j m i x n j b x m I a x ij j mi ij i nj ij ∑∑==<nj jm i i ba 11∑∑===m i nj ijij x c z 11min ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥=≤==∑∑==),,2,1;,2,1(0),,2,1(),,2,1(11n j m i x n j b x m I a x ij j mi ij i nj ij mn n m +m n1.2 运输问题的特性由于运输问题也是线性规划问题,根据线性规划的一般原理,如果它的最优解存在,一定可以在基可行解中找到。






运输问题1 运输问题提出运输问题是社会经济生活和军事活动中经常出现的优化问题。
在经济建设和国防建设中,经常遇到煤、钢铁、木材、粮食、武器装备等物资的调运问题。
如何制定调运方案,将物资运往指定地点,而且实现运输成本最小,即为运输问题。
运输问题是在1941年美国学者希奇柯克(Hitchcock )在研究生产组织和铁路运输方面的线性规划问题时提出的。
运输问题的提出,不仅可以求出物资的合理调运方案,其他类型的问题也都可以经过变换后转为运输问题来进行求解。
Hitchcock 运输问题如下:在m 个补给仓库处,分别有补给物品12,,,m a a a 个单位,这些物品要分发给n 个消费仓库,各消费仓库的需要量分别为12,,,n b b b 个单位。
从第i 个补给仓库到第j 个消费仓库运输一个单位的物品成本为ij c 元。
假设物品的总补给量等于总需求量,求使总运输成本最小的分配方案。
2 运输问题数学模型运输问题的一般提法: 有m 个生产地12,,,m A A A ,可供应某种物质,其产量分别为12,,,m a a a ,另有n 个销售地12,,,n B B B ,其销售量分别为12,,,n b b b ,从i A 到j B 运输单位物资的运价为ij c 。
问应如何组织调运,使调运方案的总运费最小。
建立数学模型:设从i A 到j B 的发运量为ij x ,则从i A 运出的物质总量应不大于i a ,ij x 应满足:1,1,2,,niji j xa i m =≤=∑ (1)同理运到j B 的物质总量应不大于j b ,ij x 应满足:1,1,2,,mijj i xb j n =≤=∑ (2)总运输成本为:11m nij ij i b Z c x ===∑∑(3)可建立运输问题的一般数学模型如下:11min mnij ij i b Z c x ===∑∑11..,1,2,,,1,2,,0&nij i j mijj i ij ij s t x a i m xb j n x x Z==≤=≤=≥∈∑∑(4)特别地,当11mni j i j a b ===∑∑时,称为产销平衡运输问题,也简称运输问题,其数学模型如下:1111min ..,1,2,,,1,2,,0&mnij iji b nij i j mijj i ij ij Z c x s t x a i m xb j nx x Z=========≥∈∑∑∑∑ (5)但在现实生活中多为产销不平衡运输问题,即产大于销:11m ni j i j a b ==≤∑∑,或销大于产:11mni ji j a b==≥∑∑。


运输问题的简化解法多数运筹学或物流管理教科书对运输问题(表上作业法)一般先采用最小元素法找出一个可行解,然后采用闭回路法或位势法计算“检验数”,验证这个可行解是否最优解。
如果不是最优解,再用闭回路法调整。
调整后还要用闭回路法或位势法计算“检验数”,直到验证表明调整后的方案是最优解才算完成。
解法可用如下程序图所示:注:不平衡的要虚设需方或产地,已有成熟方法,本文对此不加讨论在上述程序中,“采用闭回路法或位势法计算‘检验数’,验证这个可行解是否最优解”是一个比较复杂的过程。
当产地和销地数量较大时,闭回路寻找比较复杂。
多数运筹学或物流管理教科书采用位势法计算检验数,这要先分解运价,列出并求解一个联立方程(有时列出的联立方程还可能未知数与方程数不等,还要做技术处理),再计算每一个未使用的运价(空格)的检验数,要所有检验数不小于零才表明所得方案是最优解。
这个过程有时要重复多次,比较繁琐,能否简化呢?笔者从后面的闭回路法得到启示,是否可以这么认为:只要还存在可以用闭回路法调整优化的“回路”,原方案就不是最优解,一直到所有的“回路”都不能再调整优化时,该方案就是最优解。
并且笔者认为闭回路的寻找也可以从已采用的最大运价开始着手,便于使不合理的运价及时得到调整,这样上述程序图就可修改如下:在上述程序中,“判断所在运量闭回路是否可调整”可以用一个比较简单的“对角相加法”来加以判断,下面用一个例子来加以说明:设有5个产地A1,A2,A3,A4,A5和4个销地B1,B2,B3,B4的运输问题,它们的供应量与需求量及单位运费表如下:求解这个问题的第一步:按“最小元素法”根据运价从小到大满足需求得一可行解:注:在此用“P/M”表示以P运价运输量M,未打“/”的运价暂不采用第二步:找到所采用的最大运价20,找其所在的“运量闭回路”。
所谓的“运量闭回路”应满足以下条件:(1)“运量闭回路”是由水平线和垂线及其角上元素组成的矩形。
第三章运输问题在生产实际中,经常需要将某种物资从一些产地运往一些销地,因而存在如何调运使总的运费最小的问题。
这类问题一般可用线性规划模型来描述,当然可以用单纯形法求解。
但由于其模型结构特殊,学者们提供了更为简便和直观的解法—-表上作业法。
此外,有些线性规划问题从实际意义上看,并非运输问题,但其模型结构类似运输问题,也可以化作运输问题进行求解。
第一节运输问题及其数学模型首先来分析下面的问题。
例3。
1农产品经销公司有三个棉花收购站,向三个纺织厂供应棉花。
三个收购站A1、A2、A3的供应量分别为50kt、45kt和65kt,三个纺织厂B1、B2、B3的需求量分别为20kt、70kt和70kt。
已知各收购站到各纺织厂的单位运价如表3-1所示(单位:千元/kt),问如何安排运输方案,使得经销公司的总运费最少?设x ij表示从A i运往B j的棉花数量,则其运输量表如下表所示。
表3—2由于总供应量等于总需求量,因此,一方面从某收购站运往各纺织厂的总棉花数量等该收购站的供应量,即x11+x12+x13 = 50x21+x22+x23 = 45x31+x32+x33 = 65另一方面从各收购站运往某纺织厂的总棉花数量等该纺织厂的需要量,即x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70因此有该问题的数学模型为min f= 4x 11+8x 12+5x 13+6x 21+3x 22+6x 23+2x 31+5x 32+7x 33x 11+x 12+x 13 = 50 x 21+x 22+x 23 = 45 x 31+x 32+x 33 = 65 x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70x ij ≥0,i=1,2,3;j=1,2,3 生产实际中的一般的运输问题可用以下数学语言描述。