18.1.2_平行四边形的判定2---三角形中位线定理

课题：18.1.2.2平行四边形的判定（2）【学习目标】(一)知识与技能：1．理解三角形中位线的概念，掌握它的性质．2．能较熟练地应用三角形中位线性质进行有关的证明和计算．(二)数学思考：体会将三角形转化为四边形的思想方法。

(三)问题解决：初步学会利用三角形中位线定理证明线段间的数量和位置关系。

获得解决问题的思路方法。

(四)情感态度：培养发现意识和能力，具有强烈的好奇心和求知欲。

【学习重点】掌握和运用三角形中位线的性质．【学习难点】三角形中位线性质的证明（辅助线的添加方法）【课前预习案】1、平行四边形的判定方法：2、三角形中线的定义：【课中探究案】活动1:三角形的中位线定义:1.(1)定义:连接的线段叫做三角形的中位线.(2)符号表示:如图,点D、E分别为△ABC边AB、AC的中点,线段DE是△ABC的中位线.2.思考:(1)想一想:①一个三角形的中位线共有几条?②三角形的中位线与中线有什么区别?(2)三角形的中位线与第三边有怎样的关系?活动2:探索三角形中位线的定理:1.如图,点D、E分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=BC.证明:方法一:如图（1）方法二:如图(2),2.归纳:(1)三角形中位线的定理:三角形的中位线于第三边,且等于第三边的.(2)符号表示:如图,∵线段DE是△ABC的中位线.∴DE∥BC且DE=BC.总结:一个三角形中位线有3条,三角形的3条中位线构成的三角形的周长等于原三角形的周长的 ,面积等于原三角形的面积的.活动3:例题讲解【例1】如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5 m,他想把四边形BCFE用篱笆围成一个圈放养小鸡,则需要篱笆的长是()A.15 mB.20 mC.25 mD.30 m【例2】已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.证明:总结:顺次连接四边形四条边的中点,所得的四边形是.【课末达标案】1.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()A.50°B.60°C.70°D.80°2.如图,小明想用皮尺测量池塘A,B间的距离,但现用皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A,B两点的点O,连接OA,OB,分别在OA,OB上取中点C,D,连接CD,并测得CD=a,由此他即知道A,B间的距离是()A.aB.2aC.aD.3a3. 图所示,在△ABC中,点D,E分别是AB,AC的中点,连接DE,若DE=5,则BC=________.4.如图,▱ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为________.5.已知:三角形的各边分别为8 cm,10 cm和12 cm ,求连接各边中点所成三角形的周长.6.如图,△ABC的中线BF,CE相交于点O,点H,G分别是BO,CO的中点,试判断四边形EFGH的形状,并证明你的结论.7.如图,△ABC中,D,E,F分别是AB,AC,BC的中点,(1)若EF=5 cm,则AB=______ cm;若BC=9 cm,则DE=______ cm.(2)中线AF与中位线DE有什么特殊的关系?证明你的猜想.【课后拓展案】基础达标：1.如图1,在△ABC中,点D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于__ __.2.如图2,▱ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12.则△DOE的周长为__ __.3.如图3,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )A.8B.10C.12D.144.已知△ABC的各边长度分别为3 cm,4 cm,5 cm,则连接各边中点的三角形的周长为 ( )A.2 cmB.7 cmC.5 cmD.6 cm5如图,在△ABC中,点D,E,F,G分别是AB,AC,AD,AE的中点,若BC=8,则DE+FG等于( )A.4.5B.6C.7D.86如图,▱ABCD的对角线AC,BD相交于点O,点E是AB的中点,且AE+EO=4,则▱ABCD的周长为( )A.20B.16C.12D.8应用提高：5如图,要测定被池塘隔开的A,B两点之间的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E, 连接DE.现测得AC=30 m,BC=40 m,DE=24 m,则AB= ( )A.50 mB.48 mC.45 mD.35 m6所示,在△ABC中,点D是AB边的中点,点E是AC边上一点,若DE=5 cm,则BC的长( )A.等于5 cmB.等于10 cmC.等于15 cmD.无法确定思维拓展：7.在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形.(2)求证:∠DHF=∠DEF.。

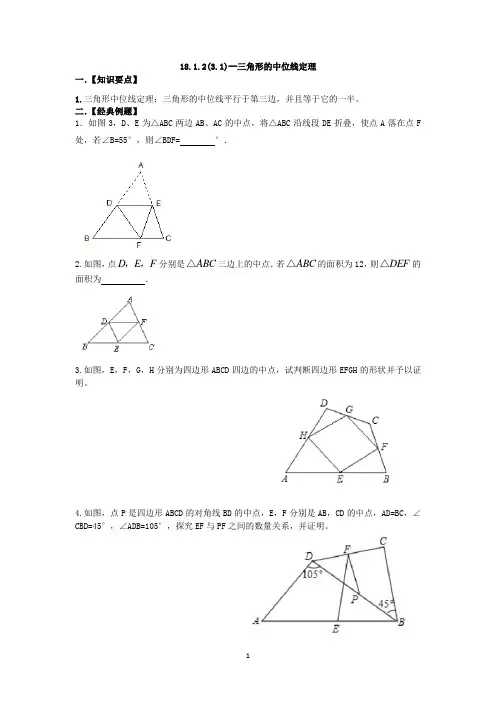
18.1.2(3.1)--三角形的中位线定理一．【知识要点】1.三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。

二．【经典例题】1．如图3，D 、E 为△ABC 两边AB 、AC 的中点，将△ABC 沿线段DE 折叠，使点A 落在点F 处，若∠B=55°，则∠BDF= °．2.如图，点分别是三边上的中点．若的面积为12，则的面积为 ．3.如图，E ，F ，G ，H 分别为四边形ABCD 四边的中点，试判断四边形EFGH 的形状并予以证明。

4.如图，点P 是四边形ABCD 的对角线BD 的中点，E ，F 分别是AB ，CD 的中点，AD=BC ，∠CBD=45°，∠ADB=105°，探究EF 与PF 之间的数量关系，并证明。

D E F ，，ABC △ABC △DEF△5.如图，∠ACB=∠BCD=90°，AC=BC，点E在BC上，CD=CE，点P，M，N分别为AB，AD，BE 的中点，试探究:PM与PN之间的数量关系和位置关系.6.如图，四边形ABCD中，∠A＝90°，AB＝8，AD＝6，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（）A．8B．7C．6D．57．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连接DC，点M，P，F分别为DE，DC，BC的中点，△ADE可以绕点A在平面内自由旋转，若AD＝4，AB＝10，则△PMF的面积S的变化范围是．三．【题库】【A】1.在ABCD中，点O是对角线AC.BD的交点，点E是边CD的中点，且AB=6，BC=10，则OE=______________．2．如图，要测量的A、C两点被池塘隔开，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得E、F两点间的距离等于23米，则A、C两点间的距离= ．3.如图，A.B两点被池塘隔开，在AB外选一点C ，连结AC 和BC，并分别找出AC 和BC的中点M.N，如果测得MN=20 m，那么 A.B两点的距离是，依据是．4.如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.【B】1．如图，在△ABC中，AB=5，AC=3，AD是角平分线，AE是中线，过点C作CG⊥AD于点F，AB CDO E交AB 于点G ，连接EF ，则线段EF 的长为 ．3．如图，△ABC 中，D 、E 分别是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，若BC=6，则DF 的长是（ ） A. 2 B. 3 C.25D. 4 4.已知：三角形的各边分别为8cm ,10cm 和12cm ，求连结各边中点所成三角形的周长_____. 5. 如图，ABCD 的周长为36，对角线AC ，BD 相交于点O ．点E 是CD 的中点，BD=12，则△DOE 的周长为 ．【C 】1.如图，在四边形ABCD 中，DC ∥AB ，CB ⊥AB ，AB=AD ，CD=12AB ，点E 、F 分别为AB 、AD 的中点，则△AEF 与多边形BCDFE 的面积之比为 （ ） A ．17B ．16C ．15D ．142．如图，在矩形ABCD 中，P 、Q 分别是BC 、DC 上的点，E 、F 分别是AP 、PQ 的中点．BC =12，第24题图FE DCBADQ =5，在点P 从B 移动到C （点Q 不动）的过程中，则下列结论正确的是 ( )A. 线段EF 的长逐渐增大,最大值是13B. 线段EF 的长逐渐减小，最小值是6.5C. 线段EF 的长始终是6.5D. 线段EF 的长先增大再减小，且6.5≤EF ≤133.如图，在四边形ABCD 中，AD ∥BC ，AB ＝AD ，∠C ＝60°，∠ABD ＝30°AE ⊥BD 于点E ，F 是CD 的中点. 求证：四边形AEFD 是平行四边形.3.如图①，已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为4cm ，E ，F ，G 分别是AB ，AA 1，AD 的中点，截面EFG 将这个正方体切去一个角后得到一个新的几何体（如图②），则图②中阴影部分的面积为 cm 2．4.如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，直角∠EPF 的顶点P 是BC 的中点，两边PE 、PF 分别交于点E ，F ，现给出一下四个结论：①AE ＝CF ，②△EPF 是等腰直角三角形，③S 四边形AEPF＝，④当∠EPF 在△ABC 内绕顶点P 旋转时始终有EF ＝AP （点E 不与A 、B 重合），上述结论中是正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【D 】1.已知,在平行四边形ABCD 中,连接对角线AC , ∠CAD 的平分线AF 交CD 于点F ，∠ACD 平分线CG 交AD 于点G, AF.CG 交于点O,点E 为BC 上一点,且 ∠BAE=∠GCD, （12分） (1)如图1,若△ACD 是等边三角形,OC=2 ,求平行四边形ABCD 的面积; (2)如图2,若△ACD 是等腰直角三角形∠CAD=90O, ,求证：CE + 2 OF = AC:2.（绵阳2018年第18题）如图，在△ABC 中，3=AC ，4=BC ,若AC ，BC 边上的中线BE ，垂直相交于O 点，则=AB __________。

《§18.1.2 平行四边形的判定(3)----三角形的中位线及定理》教学设计新疆维吾尔自治区克孜勒苏柯尔克孜州阿合奇县同心中学王全才课题：§18.1.2 平行四边形的判定----三角形的中位线及定理一、教材版本：义务教育教科书人民教育出版社出版八年级（下册）第18章p47—49页，§18.1 平行四边形中§18.1.2 平行四边形的判定中的第3课时的内容。

二、教材分析：三角形中位线是继三角形的角平分线、中线、高线后的第四条重要线段，是三角形、平行四边形知识的进一步应用和深化.采用由特殊的点——“中点”入手来研究，显示了其独到之处. 三角形中位线定理的证明更是与三角形的全等紧密相连，作为一种暗线贯穿于整个的平行四边形的知识中。

三角形中位线定理为解决直线平行和线段的倍分关系，提供了新的依据，拓宽了学生的证题思路.三角形中位线定理的证明和应用，对于培养学生的合情推理能力、发散思维能力以及探索、体验数学思维规律和用数学知识解决实际问题的能力方面起着重要的作用，因此地位非常重要.三、教学目标：1、理解三角形中位线的概念和三角形中位线定理，掌握它的性质，几何语言的表述，会用三角形中位线定理进行有关的论证和计算。

2、经历三角形中位线的概念和定理的探索、得出过程，培养学生观察、分析、探索知识的能力及归纳总结能力。

3、通过学生亲自参与定理的发现和证明，培养学生的参与、探索的意识，激发学生的学习兴趣，获得成功的体验。

四、教学重点：（1）三角形中位线的性质的探究与证明方法；（2）三角形中位线的性质的应用．五、教学难点：（1）猜想结论，实践探究，动手操作的效果与意义；（2）证明三角形中位线的性质的思维拓展与前后知识的贯穿联系，几何辅助线的添加画法。

六、难点的突破：（1）实践性的用动手剪，拼，度量以达验证；（2）证明思维中的拓展以联系平行四边形性的探讨方法，一题多解。

七、教学用具：多媒体、三角尺、学生作的三角形、学生用剪刀、彩色粉笔。