穿甲原理和各种主要的穿甲计算公式
- 格式:doc
- 大小:1.70 MB
- 文档页数:24

装甲倾角换算公式
装甲倾角是指战车等装甲车辆上装甲板与水平面的夹角。
它
的主要作用是提高战车的防护能力,减少来自敌方攻击的威胁。
在设计和评估装甲防护时,常常需要进行装甲倾角的换算。
下
面给出了装甲倾角的换算公式。
装甲倾角的换算公式如下:
cosα=1/(1+h^2/l^2*tan^2β)
其中,α为目标装甲板的实际倾角,β为目标装甲板的表面
倾角,l为弹丸打击装甲板的水平投影长度,h为弹丸打击装甲
板的垂直投影高度(即穿深)。
该公式适用于当战车受到垂直
方向的攻击时。
该公式的推导基于几何学原理和三角函数。
通过这个公式,
可以在已知目标装甲板的表面倾角和穿深的情况下,计算出实
际装甲板的倾角。
这对于评估装甲防护性能、设计和改进装甲
车辆具有重要意义。
需要注意的是,装甲倾角的换算公式是一个近似的计算公式,对于特定情况下的装甲防护效果可以提供参考,但实际效果还
需要通过实验和模拟验证。
另外,在实际的战斗中,常常需要
考虑各种不同的攻击角度和攻击方式,所以装甲倾角的选择也
需要综合考虑各种因素。


随着材料科学的发展,复合装甲、高强度陶瓷装甲、贫铀装甲的使用,以及爆炸反应装甲的出现,大大提高了装甲的抗毁能力,对破甲技术提出更高的要求。
为此,人们在相继研制出一系列新型破、穿甲战斗部的同时,也注意开发研究某些新概念超高速动能穿甲武器,电磁炮就是其中一种。
电磁炮的基本原理电磁炮是利用物理学中运动电荷或载流导体在磁场中受到电磁力(即洛伦兹力) 作用的基本原理来加速弹丸的。
根据加速方式,电磁炮可分为导轨炮和线圈炮。
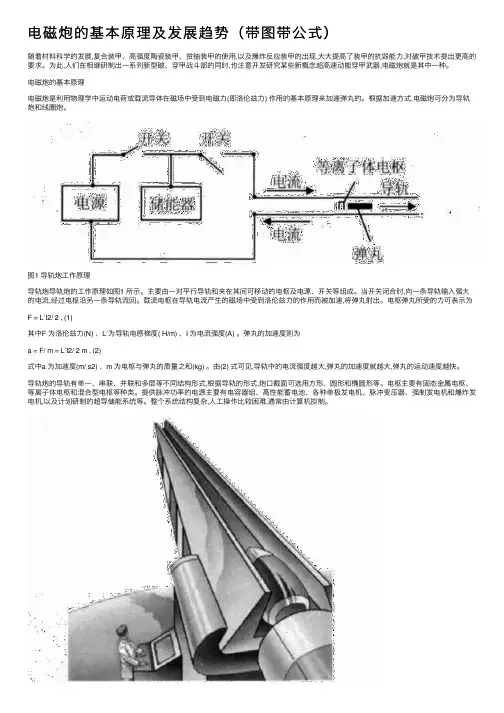
图1 导轨炮工作原理导轨炮导轨炮的工作原理如图1 所示。
主要由一对平行导轨和夹在其间可移动的电枢及电源、开关等组成。
当开关闭合时,向一条导轨输入强大的电流,经过电枢沿另一条导轨流回。
载流电枢在导轨电流产生的磁场中受到洛伦兹力的作用而被加速,将弹丸射出。
电枢弹丸所受的力可表示为F = L′I2/ 2 , (1)其中F 为洛伦兹力(N) 、L′为导轨电感梯度( H/m) 、I 为电流强度(A) 。
弹丸的加速度则为a = F/ m = L′I2/ 2 m , (2)式中a 为加速度(m/ s2) 、m 为电枢与弹丸的质量之和(kg) 。
由(2) 式可见,导轨中的电流强度越大,弹丸的加速度就越大,弹丸的运动速度越快。
导轨炮的导轨有单一、串联、并联和多层等不同结构形式,根据导轨的形式,炮口截面可选用方形、圆形和椭圆形等。
电枢主要有固态金属电枢、等离子体电枢和混合型电枢等种类。
提供脉冲功率的电源主要有电容器组、高性能蓄电池、各种单极发电机、脉冲变压器、强制发电机和爆炸发电机,以及计划研制的超导储能系统等。
整个系统结构复杂,人工操作比较困难,通常由计算机控制。
线圈炮线圈炮的工作原理如图3 所示。
主要由感应耦合的固定线圈、可动线圈、储能器以及开关等组成。
固定线圈相当于炮身,可动线圈相当于弹丸。
当固定线圈接通电源时,所产生的磁场与可动线圈上的感应电流相互作用,产生洛伦兹力,推动可动弹丸线圈加速射出。
弹丸所受的力可表示为F = I f·I p·d M/ d x , (3)其中F 为洛伦兹力(N) 、I f 为固定线圈中的电流强度(A) 、I p 为弹丸线圈中的电流强度(A) 、M 为固定与可动线圈的互感( H) 、d M/ d x 为互感梯度( H/m) 。

等效装甲计算公式 装甲是一种用于保护战斗车辆的重要措施,而等效装甲是用来计算和评估装甲对弹药的抵抗力的指标。
通过计算等效装甲,我们可以评估装甲是否足够坚固,能够在战斗中有效地保护车辆和士兵免受敌方的攻击。
等效装甲是指用于模拟和计算装甲防护效果的理想化表面。
它考虑到装甲材料的硬度、厚度和密度等因素,以及弹药进入装甲板后的变形和损伤程度。
通过使用等效装甲计算公式,我们可以估算出弹药在击中装甲板后能够穿透的深度,从而评估装甲的抵抗能力。
等效装甲计算公式的核心思想是将装甲材料的物理特性转化为数学模型,并通过一系列公式进行计算。
下面将介绍几种常见的等效装甲计算公式。
1、布鲁斯公式 布鲁斯公式是最早使用的等效装甲计算公式之一。
它是根据钢板的特性和弹药的特性来计算等效装甲的深度。
公式中考虑了钢板的硬度、厚度和弹性模量等因素,以及弹药的质量、初速度和直径等因素。
2、伯克曼公式 伯克曼公式是用于计算均匀装甲板对弹药的抵抗能力的一种公式。
该公式考虑了装甲板的材料特性,包括硬度、密度和抗拉强度等因素。
同时,它还考虑了弹药的特性,如质量、初速度和角度等因素。
3、荷马公式 荷马公式是用于计算非均匀装甲板对弹药的抵抗能力的一种公式。
装甲板通常由多层材料组成,不同层次的材料具有不同的性质。
荷马公式考虑了装甲板的层次结构和材料特性,以及弹药的特性,从而计算出装甲板的等效装甲深度。
4、达尔布尔公式 达尔布尔公式是用于计算复合装甲板对弹药的抵抗能力的一种公式。
复合装甲板由多层材料组成,每层材料具有不同的厚度和密度。
达尔布尔公式考虑了装甲板的材料组成和层次结构,以及弹药的特性,从而计算出装甲板的等效装甲厚度。
以上介绍的公式只是等效装甲计算中常见的一部分,实际使用时可能还会有一些修正系数和附加参数。
通过使用这些等效装甲计算公式,我们可以更好地评估和设计装甲,从而提高战斗车辆的保护能力和战斗效能。
虽然等效装甲计算公式提供了一种评估装甲抵抗力的方法,但仍需谨慎使用。
电磁炮的基本原理及发展趋势(带图带公式)随着材料科学的发展,复合装甲、⾼强度陶瓷装甲、贫铀装甲的使⽤,以及爆炸反应装甲的出现,⼤⼤提⾼了装甲的抗毁能⼒,对破甲技术提出更⾼的要求。
为此,⼈们在相继研制出⼀系列新型破、穿甲战⽃部的同时,也注意开发研究某些新概念超⾼速动能穿甲武器,电磁炮就是其中⼀种。
电磁炮的基本原理电磁炮是利⽤物理学中运动电荷或载流导体在磁场中受到电磁⼒(即洛伦兹⼒) 作⽤的基本原理来加速弹丸的。
根据加速⽅式,电磁炮可分为导轨炮和线圈炮。
图1 导轨炮⼯作原理导轨炮导轨炮的⼯作原理如图1 所⽰。
主要由⼀对平⾏导轨和夹在其间可移动的电枢及电源、开关等组成。
当开关闭合时,向⼀条导轨输⼊强⼤的电流,经过电枢沿另⼀条导轨流回。
载流电枢在导轨电流产⽣的磁场中受到洛伦兹⼒的作⽤⽽被加速,将弹丸射出。
电枢弹丸所受的⼒可表⽰为F = L′I2/ 2 , (1)其中F 为洛伦兹⼒(N) 、L′为导轨电感梯度( H/m) 、I 为电流强度(A) 。
弹丸的加速度则为a = F/ m = L′I2/ 2 m , (2)式中a 为加速度(m/ s2) 、m 为电枢与弹丸的质量之和(kg) 。
由(2) 式可见,导轨中的电流强度越⼤,弹丸的加速度就越⼤,弹丸的运动速度越快。
导轨炮的导轨有单⼀、串联、并联和多层等不同结构形式,根据导轨的形式,炮⼝截⾯可选⽤⽅形、圆形和椭圆形等。
电枢主要有固态⾦属电枢、等离⼦体电枢和混合型电枢等种类。
提供脉冲功率的电源主要有电容器组、⾼性能蓄电池、各种单极发电机、脉冲变压器、强制发电机和爆炸发电机,以及计划研制的超导储能系统等。
整个系统结构复杂,⼈⼯操作⽐较困难,通常由计算机控制。
线圈炮线圈炮的⼯作原理如图3 所⽰。
主要由感应耦合的固定线圈、可动线圈、储能器以及开关等组成。
固定线圈相当于炮⾝,可动线圈相当于弹丸。
当固定线圈接通电源时,所产⽣的磁场与可动线圈上的感应电流相互作⽤,产⽣洛伦兹⼒,推动可动弹丸线圈加速射出。




《穿甲爆破弹侵彻多层复合目标及毁伤效应研究》一、引言在现代战争中,精确打击与高穿透性武器的重要性日益凸显。
穿甲爆破弹作为一种典型的弹药类型,在攻击装甲目标和多层复合目标时发挥着关键作用。
本文将着重探讨穿甲爆破弹侵彻多层复合目标的过程以及其产生的毁伤效应。
研究该类武器,有助于更好地理解其作战效能,并为未来武器研发提供理论支持。
二、穿甲爆破弹的基本原理与结构穿甲爆破弹是一种利用高速冲击力穿透装甲目标的弹药。
其基本原理在于通过炸药的能量,使得弹体穿透目标后引发爆炸,对目标内部造成破坏。
穿甲爆破弹主要由弹体、引信、炸药等部分组成。
其中,弹体负责穿透装甲,引信控制炸药的起爆时间与方式,炸药则是主要的毁伤元件。
三、侵彻多层复合目标的过程在侵彻多层复合目标的过程中,穿甲爆破弹主要面临的是不同材料、不同厚度的装甲层。
这些装甲层可能包括金属、陶瓷、复合材料等。
在侵彻过程中,弹体首先需要克服装甲层的硬度和强度,通过高速冲击将装甲层穿透。
当弹体穿透一层装甲后,会继续对下一层装甲进行侵彻,直至达到目标内部或被阻止。
四、毁伤效应研究穿甲爆破弹的毁伤效应主要体现在两个方面:一是侵彻过程中的物理破坏,二是爆炸后的化学破坏。
在物理破坏方面,穿甲爆破弹通过高速冲击力将装甲层穿透,并在目标内部形成空腔效应和碎裂效应,导致目标结构损伤。
在化学破坏方面,当炸药起爆后,会产生高温、高压的爆炸产物,对目标内部造成毁灭性破坏。
五、研究方法与实验结果为了研究穿甲爆破弹侵彻多层复合目标及毁伤效应,可以采用理论分析、数值模拟和实验研究等方法。
其中,实验研究是最直接的方法。
通过在实验室中模拟实际战场环境,使用穿甲爆破弹对多层复合目标进行攻击,并观察其侵彻过程和毁伤效果。
此外,还可以利用数值模拟软件对穿甲爆破弹的侵彻过程进行模拟,以预测其毁伤效果。
实验结果表明,穿甲爆破弹在侵彻多层复合目标时,其毁伤效果与弹体的材料、形状、速度以及装甲层的材料、厚度等因素密切相关。

军武百科碎甲弹、破甲弹与穿甲弹的原理碎甲弹(HESH)是通过塑性炸药在装甲板上爆炸产生冲击波,利用超压崩落坦克装甲内层碎片来杀伤车内人员和毁伤设备的。
碎甲弹最初是由英国人发明的,而且一直使用至今。
碎甲弹用来对付二战坦克的均质钢装甲比较有效。
它的另一个优点是可以作为普通高爆弹使用。
碎甲弹里面装的是塑性炸药,只要弹丸命中坦克,薄薄的弹壳在巨大的冲击力作用下变形或破碎,里面的塑性炸药像膏药一样紧紧粘贴在装甲表面,既不破碎,也不飞散。
在延时引信的作用下,粘贴在装甲外面的炸药爆炸,产生的冲击波以几百亿帕压力作用在装甲上,巨大的力传递到装甲内,犹如用锤子敲打墙壁,墙壁未穿透,背面的墙皮却一块快剥落一样,致使内壁落一块几千克重的的蝶形碎片和数十块小碎片。
这些碎片在坦克里四处飞溅,将乘员杀伤,设备击坏,外形完好的坦克再也无法动弹。
破甲弹又称空心装药破甲弹,是以聚能装药爆炸后形成的金属射流穿透装甲的炮弹。
也称聚能装药破甲弹,是反坦克的主要弹种之一。
主要配用于坦克炮、反坦克炮、无坐力炮等。
用于毁伤坦克等装甲目标和混凝土工事。
射流穿透装甲后,以剩余射流、装甲破片和爆轰产物毁伤人员和设备。
破甲弹的使用,加强了对坦克的威胁,其主要特点是靠装药本身的能量来穿甲的,故不受初速和射距的限制,是一种发展潜力较大的弹种。
不过它的装药很有学问,因为空心装药破甲弹,主要靠把装药制成带锥形孔的空心圆柱体药柱,并在锥形孔药表面加上金属罩,这样,爆炸时即会聚成一股速度、温度和压力都很大的金属能射流,即“聚能效应”,摧毁装甲,反之,如果把装药制成实心,就不能达到破甲的目的。
穿甲弹主要依靠弹丸的动能穿透装甲摧毁目标的炮弹,俗称动能弹。
其特点为初速高,直射距离大,射击精度高,是坦克炮和反坦克炮的主要弹种,我们知道,穿甲弹的穿透能力主要来源于弹丸运动时的动能。
而要增大弹丸击中目标时的动能,就必须提高弹丸的速度。
我们现在使用的穿甲弹,用长管火炮发射(更高的身管长度与口径比可以形成更高的炮堂压力,从而使炮弹的初速度更快,动能更大),还将弹体做成流线型或长杆形,就是我们常说的脱壳超速穿甲弹,因为脱壳超速穿甲弹的弹丸形状像支长箭,所以,还有人称它为箭形超速穿甲弹。

穿甲原理和各种主要的穿甲计算公式1该文旨在使大家对于穿甲原理和主要的穿甲计算公式有个了解。
穿甲是可以依照公式进行计算的,因为这种公式本身就是从无数试验中归纳,并得到验证的。
摒弃所谓“一切通过试验”的说法,其实很多试验数据本身又隐藏了很多值,测试方是谁?装甲靶板是什么材料(两国装甲钢都不一样靶板会一样?)穿透标准是什么?贯穿率是多少?空气抵抗系数怎么取算?等等,很多网上二战坦克资料中从未给出,所以出入很大也就不奇怪了。
公式按原形式难以用文本书写,所以按照C语言的规范来写:§5.2穿甲现象和抗弹能力的表征各种穿甲弹都是利用长身管火炮发射它时所获得的高速飞行动能来穿透装甲和起杀伤作用的。
弹丸在冲击装甲前具有的动能为W=1/2*M*Vc^2 (5-1)公式中m——弹丸质量;Vc——弹丸冲击装甲的速度。
弹丸的动能在穿甲过程中消耗于许多方面,包括破坏装甲、弹丸本身的变形、装甲板的弹性振动、碰撞及摩擦发热等。
其中,破坏装甲做功是主要的。
从力学的观点看,装甲受破坏的应力可能有以下几种;延性挤压:σx=F/π*d^2环形剪切:τ=F/π*d*b张应力破裂:径向:σn周向:σm式中F——弹丸对装甲的作用力;d——弹丸直径;b——装甲厚度。
当弹丸碰撞装甲时,这几种应力都同时出现,但其中那一种首先达到极限值造成破坏,随弹丸和装甲的材料性质和尺寸等不同而不同。
实际的装甲损坏形式有如下的概约规律:1、延性扩孔:主要由于挤压应力σx起作用,金属受弹丸挤压塑性流动,有的堆集在入口处,有的从出口处挤出,孔径约等于弹径d。
这一般发生在装甲较厚而韧、弹较尖而硬,和装甲厚b稍大于d时。
2、冲塞穿孔:主要是超过剪切应力τ所起的破坏作用,装甲被弹丸冲出一块大体成圆柱形的塞子,其出口稍大于弹径d。
这一般发生在中等厚度的装甲具有相当硬度,弹头较钝,装甲板厚略小于弹径时。
3、花瓣形孔:主要是周向张应力σm的作用,出现径向裂纹,装甲板卷向孔后,孔径约等于弹径约等于弹径d。
穿甲弹的内部原理
穿甲弹的内部原理是通过利用高速运动和特殊设计的弹头来穿透目标的防护装甲。
具体的原理如下:
1. 弹头设计:穿甲弹的弹头一般采用较硬的材料,如钢、钨合金等,以提供足够的硬度和耐磨性。
弹头通常具有锥形或长形设计,以减小与目标的接触面积,集中冲击力。
2. 高速运动:穿甲弹的关键是通过高速运动来增加弹头冲击目标的能量。
通常通过使用极高的发射速度或者使用火药加速发射速度,以提高穿甲效果。
3. 软化外层装甲:穿甲弹还可以采用一些手段来软化目标的外层装甲,以增加穿透能力。
例如,使用化学性能较强的装药,使弹头与目标接触时产生爆炸能量,破坏目标表面的装甲。
4. 经高速运动穿越装甲:当穿甲弹以极高的速度冲击目标装甲时,弹头与装甲接触区域的高压会导致装甲材料发生断裂、碎裂,形成穿孔。
弹头通过装甲后,目标内外部之间的压力差进一步破坏目标结构。
总之,穿甲弹通过高速运动和特殊设计的弹头来增加冲击目标的能量,软化目标装甲,以及通过产生高压来破坏目标结构,从而实现有效穿透装甲。
武器精准度评判标准
第一个标准参数是武器的理论每秒伤害值(Damage Per Second)。
计算方式为武器每发伤害乘以每秒击发子弹数量,以AK47为例,其
射速为600RPM,即每秒射击10发子弹,每发子弹35.85点伤害,合计358.5约等于360点伤害。
第二个参数为穿甲系数,即命中护甲后伤害剩余百分之七七点五,这个系数不受距离影响,是固定值。
第三个参数标准是穿甲类型。
最比如AK47的穿甲类型为2,即
穿甲能力百分之二百。
CS:GO中武器穿甲类型分为四种,分别为0、1、2、2.5,分别对应穿甲能力百分之零、百分之一百、百分之二百、百分之二百五十。
穿甲类型为0的武器无法射穿任何物体,目前仅有Nova一种。
穿甲类型1的武器可以射穿木板和一层薄铁板(比如那
些废弃的车),穿透后造成和原伤害相比较低的伤害,这类枪包括除
沙鹰外的所有手枪、所有微型冲锋枪和除nova外的所有霰弹枪。
穿
甲类型为2的武器可以穿透木板或薄铁板并造成较高伤害,穿透铁门造成较低伤害,这类武器包括机枪和自动步枪还有手枪里的沙鹰。
穿甲类型为2.5的武器可以穿透木板几乎不会降低伤害,穿透铁门也能造成较高的伤害,这类武器包括狙击步枪。
地图内能穿透的物体很多,包括木板、薄墙、铁板、铁门、墙角等。
值得注意的是油桶等少数物体是无法穿透的。
战士护甲穿透计算公式在许多角色扮演游戏和多人在线游戏中,战士是一个非常受欢迎的角色类型。
他们通常拥有强大的护甲和防御能力,能够在战斗中承受更多的伤害。
然而,对于其他玩家或怪物来说,战士的护甲可能成为一个难以逾越的障碍。
在这种情况下,穿甲成为了一种非常重要的能力,它可以帮助战士们更有效地对抗敌人。
穿甲是一种能力,它可以帮助玩家或怪物无视目标的护甲值,直接对其造成更多的伤害。
对于战士来说,穿甲能力可以让他们更快地击败敌人,从而提高他们在游戏中的战斗能力。
因此,了解如何计算战士的穿甲能力是非常重要的。
战士护甲穿透计算公式可以通过以下方式来进行计算:穿甲值 = 护甲值 / (1 + 护甲穿透百分比)。
在这个公式中,护甲值是目标的护甲数值,护甲穿透百分比是战士的穿甲能力所提供的百分比。
通过这个公式,我们可以计算出战士的穿甲值,从而确定他们对目标造成的实际伤害。
举个例子来说,假设一个敌人拥有100点护甲值,而战士的穿甲能力提供了25%的穿甲百分比。
那么根据上面的公式,战士的穿甲值将会是100 / (1 + 0.25) = 80。
这意味着战士可以无视敌人80点护甲值,直接对其造成更多的伤害。
通过这个公式,玩家可以更好地了解战士的穿甲能力对战斗的影响,从而更有效地利用这一能力。
此外,玩家还可以根据目标的护甲值和自身的穿甲能力来调整战术,以便在战斗中取得更大的优势。
除了了解如何计算战士的穿甲能力外,玩家还应该考虑如何提高战士的穿甲能力。
有许多方式可以提高穿甲能力,例如装备特定的装备、使用特定的技能或者选择特定的天赋。
通过这些方式,玩家可以提高战士的穿甲能力,从而在战斗中取得更大的优势。
此外,玩家还应该注意,穿甲能力并不是万能的。
一些敌人可能会拥有免疫穿甲的能力,从而减少战士的穿甲效果。
因此,在战斗中,玩家还需要根据目标的特性来调整自己的战术,以便更好地利用穿甲能力。
总之,战士的穿甲能力是非常重要的,它可以帮助战士更有效地对抗敌人,从而在游戏中取得更大的优势。
穿甲原理和各种主要的穿甲计算公式1该文旨在使大家对于穿甲原理和主要的穿甲计算公式有个了解。
穿甲是可以依照公式进行计算的,因为这种公式本身就是从无数试验中归纳,并得到验证的。
摒弃所谓“一切通过试验”的说法,其实很多试验数据本身又隐藏了很多值,测试方是谁?装甲靶板是什么材料(两国装甲钢都不一样靶板会一样?)穿透标准是什么?贯穿率是多少?空气抵抗系数怎么取算?等等,很多网上二战坦克资料中从未给出,所以出入很大也就不奇怪了。
公式按原形式难以用文本书写,所以按照C语言的规范来写:§5.2穿甲现象和抗弹能力的表征各种穿甲弹都是利用长身管火炮发射它时所获得的高速飞行动能来穿透装甲和起杀伤作用的。
弹丸在冲击装甲前具有的动能为W=1/2*M*Vc^2 (5-1)公式中m——弹丸质量;Vc——弹丸冲击装甲的速度。
弹丸的动能在穿甲过程中消耗于许多方面,包括破坏装甲、弹丸本身的变形、装甲板的弹性振动、碰撞及摩擦发热等。
其中,破坏装甲做功是主要的。
从力学的观点看,装甲受破坏的应力可能有以下几种;延性挤压:σx=F/π*d^2环形剪切:τ=F/π*d*b张应力破裂:径向:σn周向:σm式中F——弹丸对装甲的作用力;d——弹丸直径;b——装甲厚度。
当弹丸碰撞装甲时,这几种应力都同时出现,但其中那一种首先达到极限值造成破坏,随弹丸和装甲的材料性质和尺寸等不同而不同。
实际的装甲损坏形式有如下的概约规律:1、延性扩孔:主要由于挤压应力σx起作用,金属受弹丸挤压塑性流动,有的堆集在入口处,有的从出口处挤出,孔径约等于弹径d。
这一般发生在装甲较厚而韧、弹较尖而硬,和装甲厚b稍大于d时。
2、冲塞穿孔:主要是超过剪切应力τ所起的破坏作用,装甲被弹丸冲出一块大体成圆柱形的塞子,其出口稍大于弹径d。
这一般发生在中等厚度的装甲具有相当硬度,弹头较钝,装甲板厚略小于弹径时。
3、花瓣形孔:主要是周向张应力σm的作用,出现径向裂纹,装甲板卷向孔后,孔径约等于弹径约等于弹径d。
这一般发生在装甲薄而韧,弹丸速度较低时。
4、整块崩落:当装甲不太厚和韧性比较差时,主要由于径向应力σn的作用,产生圆周形裂纹,装甲被穿成超过弹径若干倍的大洞。
5、背后碎块:当较厚装甲的强度足够而韧性不足时,弹丸命中所产生的震动应力波可使装甲背面崩落碎块,并飞出起杀伤作用。
这时板前的孔不大,也可能未穿透。
实际出现的穿甲现象也可能是以上几种情况的不同综合。
一般穿甲弹在一般装甲的厚度和硬度条件下,穿甲孔主要是前二种情况的综合。
即先延性扩孔,当穿甲弹进行到装甲剩余厚度略小于弹径时,继之以冲塞成孔。
对于薄装甲,穿孔一般以花瓣或冲塞为主,视弹丸直径与装甲厚度的相对比例而定。
整块崩落不常产生的原因是过分硬脆的薄装甲难于加工,易于出现裂纹,不适于切割和焊接成车体。
碎甲弹破坏装甲以背后碎块为主,属于不穿透装甲的特殊破坏形式。
在一般穿甲弹射击装甲时,除装甲背部有生产中的金属缺陷外,极少出现。
在研究装甲防止弹丸穿透时,为能计算和试验,需要有一种表示抗弹能力的计量标准。
实用表示方法是分别对每一定装甲板来表示的,即某板的抗弹能力为“对某炮某弹的Vc”为多少。
这种一定装甲以能承受一定最大命中速度(称为着速)的弹丸而不被穿透的表示方法,是在靶场大量射击实验中产生的。
试验时,用一定炮和弹射击一定的靶板,逐渐增加发射药量来提高弹丸速度,直到刚刚穿透该板(或弹落点在板后近处,例如5m之内)为止,该发弹的Vc就用来表示该装甲板的抗弹能力。
当然,板越厚、材料越好时,需要Vc越高才能穿透,表示一定装甲板抗不同口径弹丸的能力,这种表示方法能保证符合实际,准确可靠,所以一直沿用。
只要在靶场试验出少数准确值,对不同的板厚,弹径和速度,可以按规律推算。
计算的方法见下节。
2对于较薄的板,例如30mm以下的装甲板,一般用枪来试射(若口径过大,一定穿透,试不出临界速度)。
但枪弹不能改变发射药量,即弹丸离管口的初速为一定,不能改变。
因此,只好利用弹丸飞行中空气阻力造成较大的速度降,即改变距离S来得到不同的命中速度。
因此,这时的抗弹能力,就成了抗“某枪弹(击穿的)最小距离”来表示。
在试验中,有时改变距离不方便,也可以固定距离而改变靶板的命中角度。
命中角α越大,越难穿透靶板,因此,这时的抗弹能力又可以用“某枪弹某距离(击穿)的α角”来表示。
不管用以上哪一种方式来表示抗弹能力,需要明确解决的还有一个什么叫“穿透”的标准问题。
通常用两种标准:1、背面强度极限——装甲受弹丸冲击时,为损坏装甲板背面金属的连续行,即无裂纹、无突起等时的最大速度,用m/s表示或相应的距离(m)或角度表示。
2、击穿强度极限——装甲受弹丸冲击时,不被弹丸头部穿透,即消耗完能量而装甲不出现洞孔的最大速度,用m/s表示或相应的距离(m)或角度表示。
这里的前一种情况较多地与装甲板的韧性有关,而后一种情况更多与板强度有关,按后一标准的速度值一般大于前一标准的速度值,是开始具有杀伤后效的标准。
现在主要采用击穿强度极限。
§5.3抗弹能力计算的基本公式设计的坦克装甲车辆能不能防御敌人火炮击穿?所设计坦克装甲车辆的火炮能不能击毁敌人的装甲?设计时没有敌炮或敌装甲可以试射,也没有数据或曲线可查时,需要用公式来计算。
对于一些一定直径和速度的弹丸射击一些一定材料和厚度的装甲,有了试验数据以后,也可以通过计算而不必再对不同的弹丸和不同的装甲厚度及倾角都一一进行了破坏性试验,即可确定其穿甲能力或抗弹能力。
一、克虏伯(Krupp)公式由火炮生产历史上著名的德国克虏伯公司提出的穿甲公式,是按弹丸较大、装甲稍薄,即b/d值较小时,装甲被弹丸以冲塞方式破坏来考虑的。
按此假设,冲塞过程中的作用力R 每冲dx距离所作的功dW是一个变量式中,阻力R与装甲板在冲塞过程中的剩余厚度成正比,即R=π*d*(b-x)*τ由0到b积分,得到把塞子完全冲掉的总功。
W=π*d*τ∫b→0 xdx=τ*π*d*(b^2/2)但作功的动力来源是弹丸的动能如前面式(5-1)W=m*Vc^2得到所谓克虏伯公式Vc=sqrt(τ*π)*d^0.5*b*m^(-0.5)=K*d^0.5*b*m^(-0.5) (5-2)式中,K=sqrt(τ*π)称为装甲抗弹能力系数,随装甲材料而定。
由式可以分析弹丸和装甲的攻防光焰系。
如果整理式(5-2)将“矛”和“盾”分别表示在等号的两端Vc^2*m/d=K^2*b^2由于一般不同直径的弹丸形状近似,即m∝d^3,得Vc*d∝K*b可见,攻方应该加大左端的火炮口径和弹速,而防御的一方则应加大右端的装甲厚度和改善装甲材料,采用优质的特殊装甲钢。
如果式的左端值很大,一定能穿透装甲。
如果式的右端很大,一定能阻止穿透。
这两种情况都用不着计算。
一般需要计算的,是介于穿透与穿不透左右的情况,以便确定临界值,或作出判断。
这种情况对于普通穿甲弹和装甲来说,一般发生在装甲厚度略等于或稍大于弹径时。
克虏伯公式是较原始的穿甲计算公式,只适于低速弹丸在小b/d值时判断穿甲,现在已不使用,但是它是理解穿甲计算的基础。
可以指出,当弹丸改为细长形状,大体保持原质量而减小弹径,同时加大Vc时,由公式可见其攻击能力可以迅速提高,近代的穿甲弹,如次口径弹等,就是沿着这个方向发展的。
二、德马尔公式(Jacob de Marre)公式对于通常需要计算的装甲厚度大于弹径的情况,穿甲之初不是冲塞,而是挤压为主,穿甲过程中弹速下降,弹头形状也逐渐变钝,到剩余装甲略小于弹径时,才冲出塞子。
整个穿甲过程接近于挤压与冲塞的符合。
3若完全按挤压破坏考虑,破坏装甲的总功应为W=R*b=π*d^2/(4*σx*b)=m*Vc^2/2得Vc=sqrt(π*σx/2)*d*b^0.5*m^(-0.5)=K'*d*b^0.5*m^(-0.5) 比较克虏伯公式,除K有所不同外,(d^0.5)*b变成(d*b^0.5)。
因此,可以把德马尔公式理解为考虑冲塞与挤压二者的综合,即破坏阻力是和冲塞圆周长值(剪应力)与圆面积值(压应力)的几何平均值成比例,根据经验修改而成为Vc=K*b^0.7*d^0.75*m^(-0.5) (5-3)德马尔公式或可写成下列形式b=Vc^1.43*m^0.715/(K^1.43*d^1.07) (5-4)式中,b和d单位常用dm(=100mm),Vc用m/s,m用Kg计算。
这时的装甲抗弹能力系数K成为代表装甲材料物理性能的综合系数,应由射击试验决定,而不能按某一种应力计算。
资料推荐的K值如下:低碳钢板1530镍钢板1900一般均质装甲2000-2400(其中较低值适用于低碳或中硬度装甲,而较高值适用于高硬度的薄装甲)经过表面处理的装甲2400-2600德马尔公式广泛使用至今,是抗弹能力计算的主要基本公式。
若将德马尔公式的矛盾双方改写到等式的两端来分析b*K^1.43=Vc^1.47*m^0.715/d^1.05与原克虏伯公式比较b*K^1.43=Vc*m^0.5/d^0.5从不同的指数可见,增加K比增加b的防御效果显著。
对于弹丸,弹径一定时,提高Vc的效果显著,而增加m的效果小。
若m增加,弹在膛内加速慢,却又影响Vc减小。
当Vc和m为一定时,减小弹径d也能提高攻击能力。
三、乌波尔尼科夫(Упорников)公式由于德马尔公式中的指数不是整数,计算不太方便。
为此令b/d=Cb称为装甲相对厚度;m/d^3=Cm,称为弹丸相对质量。
代入式(5-3)Vc=K*Cb^0.7*Cm^(-0.5)*d^(-0.05) (5-5)称为乌波尔尼科夫公式。
§5.4倾斜装甲抗弹能力计算由于反坦克炮弹的初速高,弹道低伸,一般可考虑成水平命中目标。
当装甲与水平面成β角倾斜时,弹丸中心线也与装甲板法线之间的α角称“法线角”或“着角”,这是抗弹能力计算所常用的角度。
α和β角互为余角。
装甲板呈倾斜状态时,弹丸穿透装甲所经过的距离增长,有如装甲厚度增加到b/cosα,使装甲的抗弹能力增加。
对于倾斜装甲的抗弹能力公式为Vc=K*b^0.7*d^0.75/(m^0.5*cosα^n)使用乌波尔尼科夫公式时,比式(5-5)多一个因数secα^n。
Vc=K*Cb^0.7*Cm^(-0.5)*d^(-0.05)*secα^n试验证明式中n≠0.7,而与装甲相对厚度Cb,装甲类型和弹丸形状等有关。
为什么n>0.7并且是变化的呢?主要是因为有“跳弹”因素的影响,当弹丸接触并开始破坏倾斜装甲时,装甲对弹丸有反作用力,使弹丸减速,弹丸则有惯性力向前。
反作用力的合力与弹丸的惯性力组成力偶。
当α不大时,特别是对钝头穿甲弹,这个力偶将使弹丸向减小α角的方向转动,称为转正效应,这有利于穿甲不利于抗弹,当α角较大时,这个力偶的方向会使弹丸向增大α角方向转动,使穿透距离增长。