2019届九年级数学下册第1章直角三角形的边角关系1.1锐角三角函数课堂导练课件含2018中考真题新版北师大版
- 格式:ppt
- 大小:4.43 MB
- 文档页数:41

1.1.1 锐角三角函数预习案一、预习目标及范围:1.经历探索直角三角形中边的比值和角大小关系的过程;2.理解正切三角函数的意义和与现实生活的联系.3.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算.预习范围:P1-3二、预习要点1.直角三角形中边的比值与角的大小的关系是怎样的?2.正切三角函数的概念:3.利用直角三角形两直角边表示tanA。
三、预习检测1.判断是非:(1)如图 (1)( )(2)如图 (1) ( )(3)如图 (1) ( )(4)如图 (1) ( )(5)如图 (1) ( )(6)如图 (2) ( )2.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值()A.扩大100倍B.缩小100倍C.不变D.不能确定3.已知∠A,∠B为锐角(1)若∠A=∠B,则tanA tanB;(2)若tanA=tanB,则∠A ∠B.4.在下图中,若BD=6,CD=12.求tanA的值.探究案一、合作探究活动内容1:活动1:小组合作实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子的铅直高度与其水平距离的比相同时,梯子就一样陡。
比值大的梯子陡。
你能设法验证这个结论吗?问题:如图,小明想通过测量及,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量及,算出他们的比,也能说明梯子的倾斜程度,你同意小亮的看法吗?(1)直角三角形AB1C1和直角三角形AB2C2有什么关系?(2) 和有什么关系?(3)如果改变B2在梯子上的位置呢?由此你能得出什么结论?活动2:探究归纳注意:拓展:梯子的倾斜程度与tanB有什么关系?tanB的值越大,梯子越陡,∠B越大;活动内容2:典例精析例1如图表示两个自动扶梯,哪一个自动扶梯比较陡?解:例2 在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值.解:正切通常也用来描述山坡的坡度.(坡度:铅直高度与水平宽度的比,也称为坡比)试求tanA 的值。
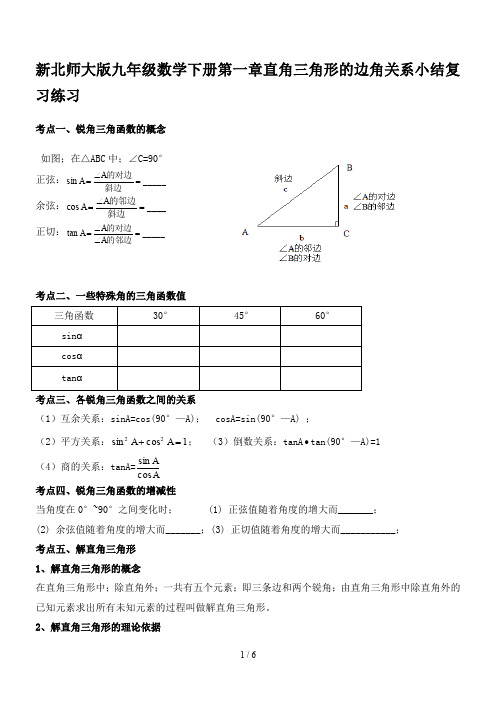
新北师大版九年级数学下册第一章直角三角形的边角关系小结复习练习考点一、锐角三角函数的概念如图;在△ABC 中;∠C=90° 正弦:_____sin =∠=斜边的对边A A余弦:____cos =∠=斜边的邻边A A正切:_____tan =∠∠=的邻边的对边A A A考点二、一些特殊角的三角函数值三角函数 30°45° 60° sin α cos α tan α考点三、各锐角三角函数之间的关系(1)互余关系:sinA=cos(90°—A); cosA=sin(90°—A) ;(2)平方关系:1cos sin 22=+A A ; (3)倒数关系:tanA ∙tan(90°—A)=1 (4)商的关系:tanA=AAcos sin 考点四、锐角三角函数的增减性当角度在0°~90°之间变化时; (1) 正弦值随着角度的增大而_______; (2) 余弦值随着角度的增大而_______;(3) 正切值随着角度的增大而___________; 考点五、解直角三角形 1、解直角三角形的概念在直角三角形中;除直角外;一共有五个元素;即三条边和两个锐角;由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
2、解直角三角形的理论依据在Rt △ABC 中;∠C=90°;∠A ;∠B ;∠C 所对的边分别为a ;b ;c(1)三边之间的关系:________(勾股定理);(2)锐角之间的关系:_______________ (3)边角之间的关系:正弦sinA=___________;余弦cosA=______;正切tanA=_______(4) 面积公式:c ch ab s 2121==(h c 为c 边上的高)考点六、解直角三角形应用1、将实际问题转化到直角三角形中;用锐角三角函数、代数和几何知识综合求解2、仰角、俯角、坡面 知识点及应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。

《锐角三角函数》锐角三角函数是义务教育课程标准实验教科书(北师版)《数学》九年级下册第一章第一节内容,本章主要研究直角三角形的边角关系;本节要求经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算。
;所以本节的重点是理解tanA的数学含义和公式。
【知识与能力目标】1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算。
【过程与方法目标】1.经历观察、猜想等数学活动过程,发展合情推理能力,能有条理地,清晰地阐述自己的观点。
2.体验数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题.提高解决实际问题的能力。
3.体会解决问题的策略的多样性,发展实践能力和创新精神。
【情感态度价值观目标】1.积极参与数学活动,对数学产生好奇心和求知欲。
2.形成实事求是的态度以及独立思考的习惯。
【教学重点】理解tanA的数学含义和公式。
【教学难点】现实情境中理解tanA的数学含义,以及公式的应用。
课前准备教师准备课件、多媒体;学生准备;练习本;教学过程第一课时创设情境引入课题[问题1]在直角三角形中,知道一边和一个锐角,你能求出其他的边和角吗?从而引出课题在活动1中教师应重点关注:(1) 学生是否能从实际生活中发现并提出数学问题。
(2)学生的审美意识及对演示图片倾注的情感。
通过熟悉的物体(梯子),不仅让学生感受到生活中数学无处不在,也为后面的探究活动作好了情感准备。
梯子是日常生活常见的物体,让学生比较如何比较梯子的倾斜度,有哪些办法?“陡”或“平缓”是用来描述梯子什么的?教师通过引导学生观察、讨论,通过步步设问,引发学生思考。
定义在在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA=∠A的对边/∠A的邻边从而引出正切的定义利用这个梯子模型引入,可以帮助学生直观理解正切的概念。



1.1 .2 锐角三角函数一、问题引入1.当Rt △ABC 中的锐角A 确定时,∠A 的对边与邻边的比便随之确定,此时,其他边之间的比也确定吗?2. 正弦的定义:在Rt △ABC 中,∠C=90°,我们把锐角A 的与的比叫做∠A 的正弦,记作sinA ,即sinA =A a A c∠=∠的对边的斜边, sinA 的值,梯子越陡. 3.余弦的定义:在Rt △ABC 中,∠C=90°,我们把锐角A 的与的比叫做∠A 的余弦,记作,即cosA 的值越,梯子越陡4.对于锐角A 的每一个确定的值,sinA 有唯一确定的值与它对应,所以sinA 是A 的函数.同样地,cosA ,tanA 也是A 的函数.二、基础训练1.在△ABC 中,∠C =900,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,如果a =9,b =12,则sinA=,sinB=.2.在Rt △ABC 中,∠C =900,AB =5㎝,BC=3㎝,则sinA= cosA= . 3.Rt △ABC 中,∠C =900,sinA=54,AB=10,则BC =4.在Rt △ABC 中,∠C = 90°,AC = 2, sin B =45,则AB = .三、例题展示B例1:在Rt △ABC 中,∠B = 90°,AC = 200,6.0sin =A ,求BC 的长.分析:本例是利用正弦函数的定义求对边的长.例2:如图,在Rt △ABC 中,∠C = 90°,AC = 10,1312cos =A , 求AB 的长及sinB .分析:通过正弦函数的定义求直角三角形其它边的长.四、课堂检测1.在等腰三角形ABC 中,AB=AC=5,BC=6,则sin B =, cos B = ,tan B =.2.在△ABC 中,∠C = 90°,sin A =45,BC=20,则AC = ,AB= ,△ABC 的面积为.3.在△ABC 中,∠C = 90°,AB = 3BC ,则sin B = ,cos B =;4.在△ABC 中,∠C = 90°,3BC = AC 3,则tan A =,sin A = .5.如图,已知Rt △ABC 中,AC=3,BC= 4,过直角顶点C 作CA 1⊥AB ,ACA B C垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去,得到了一组线段CA 1,A 1C 1,12C A ,…, 则CA 1=, 5554C A A C6.在Rt △ABC 中,∠C = 90°,cos B =35,AB=15,则BC 的长是( ) A. 3 B. 6 C. 9 D. 127.在Rt △ABC 中,∠BCA = 90°,CD 是AB 边上的中线,BC=8,CD=5,求sin ∠ACD ,cos ∠ACD 和tan ∠A CD 的值.8.在△ABC 中,∠BAC >90°,AB=5,BC=13,AD 是BC 边上的高,AD=4,求CD 和sinC.如果∠BAC <90°呢?A第5题图1.1.2锐角三角函数同步练习一、单选题(共15题)1.在Rt △ABC 中,∠C =90°,若斜边AB 是直角边BC 的3倍,则tanB 的值是( )A .13B .3C .4D .2. 如图,在△ABC 中,∠C =90°,AB =5,BC =3,则cosA 的值是( )( )A .2B .12 4. 如图,点A 为∠α边上的任意一点,作AC ⊥BC 于点C ,CD ⊥AB 于点D ,下列用线段比表示cos α的值,错误的是( )A .BD BCB .BC AB C .AD AC D .CD AC5.已知sin6°=a ,sin36°=b ,则sin 26°=( ) A .a 2B .2a C .b 2D .b6.在Rt △ABC 中,各边的长度都扩大两倍,那么锐角A 的各三角函数值( )A .都扩大两倍B .都缩小两倍C .不变D .都扩大四倍7.△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( )A.b cosB=c B.c sinA=a C.a tanA=b D.tanB=b c8. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是()A.b=a tanB B.a=c cosB C.c=asinAD.a=b cosA9. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=()A.513B.512C.1213D.12510. 如果∠A为锐角,且sinA=0.6,那么()A.0°<A≤30° B.30°<A<45° C.45°<A<60° D.60°<A≤90°11. 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值()A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化12. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinA的值越小,梯子越陡B.cosA的值越小,梯子越陡C.tanA的值越小,梯子越陡D.陡缓程度与上A的函数值无关13.sin70°,cos70°,tan70°的大小关系是()A.tan70°<cos70°<sin70° B.cos70°<tan70°<sin70°C.sin70°<cos70°<tan70° D.cos70°<sin70°<tan70°14.随着锐角α的增大,cosα的值()A.增大 B.减小 C.不变 D.增大还是减小不确定15.当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是()A.正弦和余弦 B.正弦和正切 C.余弦和正切 D.正弦、余弦和正切二、填空题(共5题)1. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=____________2. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=_______________.3.在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cosA的值等于_________4. 比较下列三角函数值的大小:sin40°___________sin50°三、解答题(共5题)1.如图,在Rt△ABC中,∠C=90°,AB=2BC,求sinB的值2. 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.3. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值4. Rt△ABC中,∠C=90°,AB=10,BC=8,求cosB的值5. 在Rt△ABC中,∠C=90°,如果AC:BC=3:4,求cosA的值。
九年级数学下第一章---直角三角形的边角关系复习与训练一 、锐角三角函数的定义1.在Rt △ABC 中,∠C=900,直角三角形边角之间的关系: (1)三边关系:_________________(即_______定理)(2)三角关系:_____________________(即_______________定理)____________________(性质:直角三角形两锐角______)(3)边角关系(即tanA ,sinA,cosA 与边的关系)锐角∠A 的正弦: ∠A 的( )边 ( ) ( )sinA= = =( )边 ( ) ( )锐角∠A 的余弦: ∠A 的( )边 ( ) ( )cosA= = =( )边 ( ) ( )锐角∠A 的正切: ∠A 的( )边 ( ) ( )tanA= = =∠A 的( )边 ( ) ( )注:① 锐角A 的______、______、______都是∠A 的三角函数....。
② 三角函数值是一个比值,没有.............单位....2.练习:1. 在Rt △ABC 中,∠C=900,AC=3,BC=4,求tanA 、sinA 和cosA 的值。
2. 在Rt △ABC 中,∠C=900, cosA=1312,AC=10, 求AB 、BC 的值。
3. 在Rt △ABC 中,∠C=900, cosA=0.6,BC=8, 求AB 、BC 的值。
4. 在Rt △ABC 中,∠C=900,sinA=43,求tanA 和cosA 的值。
5.如图,△ABC 是等腰三角形,AB=AC=5,BC=8,求tanB 、sinB 和cosB 。
AB C6. 在Rt △ABC 中,∠BCA=900,CD 是AB 边上的中线,BC=6,CD=5, 求sin ∠ACD,cos ∠ACD, tan ∠ACD ;BDA C7:坡度(坡比)与坡角:⑴坡面与水平面的夹角叫做________,⑵坡面的____________与____________的比称为坡度(或______)(用字母....i .表示)... ⑶坡度与坡角有什么关系?⑷正切在日常生活中的应用很广泛,例如建筑、工程技术等.正切经常用来描述山坡的_______、堤坝的_______.例:如图,有一山坡在水平方向上每前进100m 就升高60m,那么山坡的坡度是:( ) ( ) i=_______α= =( ) ( ) 60米二、特殊角的锐角三角函数值 100米1.⑴在Rt △ABC 中,∠C=900, 若∠A=300,设BC=a,则AB=______ AC=________ ⑵在Rt △DEF 中,∠F=900, 若∠D=450,设DF=a,则EF=______ DE=________ B EA C D F 2.利用上图,可求出下列特殊角的锐角三角函数值.3.锐角三角函数的大小比较(1) 正弦、正切的锐角三角函数值随角度的增大而_____ ,随角度的减小而____ _. (2)余弦的锐角三角函数值随角度的增大而_____ ,随角度的减小而____ _。
2018-2019学年九年级数学下册第一章直角三角形的边角关系1 锐角三角函数1.1.1 正切同步练习(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第一章直角三角形的边角关系1 锐角三角函数1.1.1 正切同步练习(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第一章直角三角形的边角关系1 锐角三角函数1.1.1 正切同步练习(新版)北师大版的全部内容。
课时作业(一)[第一章 1 第1课时正切]一、选择题1.在Rt△ABC中,∠C=90°,若BC=2AC,则∠A的正切值是()A。
错误! B。
错误! C。
错误! D.22.为测量山坡的倾斜度,小明测得数据如图K-1-1所示(单位:米),则该山坡的倾斜角α的正切值是()图K-1-1A.错误! B.4 C。
错误! D.错误!3。
如图K-1-2所示,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,已知CD=5,AC=6,则tan B的值为( )图K-1-2A.错误! B。
错误! C。
错误! D。
错误!4.如图K-1-3,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=错误!,则t的值是()A.1 B.1。
5 C.2 D.3图K-1-35。
2017·河北模拟如图K-1-4,△ABC的顶点都在正方形网格的格点上,则tan C的值为错误!()图K-1-4A.错误! B。
错误! C。
错误! D.错误!6.如图K-1-5,在Rt△ABC中,∠C=90°,AB=10,tan A=错误!,则AC的长是()图K-1-5A.3 B.4C.6 D.87.2017·湘潭期末如图K-1-6,已知山坡AB的坡度为1∶2,坡高BC=1,则坡长AB 为( )图K-1-6A。