2016年广西单招数学模拟试题：不等式的应用

高职高专自主单独招生数学模拟试题含答案一、选择题（本题有10小题，每小题4分，满分40分）1、（2011•台州）在、0、1、﹣2这四个数中，最小的数是（）A、B、0 C、1 D、﹣2考点：有理数大小比较。

分析：本题是对有理数的大小比较考查，根据任何负数都小于非负数，直接得出答案．解答：解：在有理数、0、1、﹣2中，最大的是1，只有﹣2是负数，∴最小的是﹣2．故选D．点评：此题主要考查了有理数的比较大小，解决此类问题的关键是根据负数的性质得出答案．2、（2011•台州）下列四个几何体中，主视图是三角形的是（）A、B、C、D、考点：简单几何体的三视图。

分析：主视图是从几何体的正面看，主视图是三角形的一定是一个锥体，是长方形的一定是柱体，由此分析可得答案．解答：解：主视图是三角形的一定是一个锥体，只有B是锥体．故选：B．点评：此题主要考查了几何体的三视图，主要考查同学们的空间想象能力．3、（2011•台州）要反映台州市某一周每天的最高气温的变化趋势，宜采用（）A、条形统计图B、扇形统计图C、折线统计图D、频数分布统计图考点：统计图的选择。

专题：分类讨论。

分析：根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．解答：解：根据题意，得要求直观反映台州市一周内每天的最高气温的变化情况，结合统计图各自的特点，应选择折线统计图．故选C．点评：此题主要考查统计图的选择，根据扇形统计图、折线统计图、条形统计图各自的特点来判断．4、（2011•台州）计算（a3）2的结果是（）A、3a2B、2a3C、a5D、a6考点：幂的乘方与积的乘方。

分析：根据幂的乘方：底数不变，指数相乘，计算后直接选取答案．解答：解：（a3）2=a3×2=a6．故选D．点评：此题主要考查的是幂的乘方，不要与同底数幂的乘法互相混淆；幂的乘方：底数不变，指数相乘；同底数幂的乘法：底数不变，指数相加．5、（2011•台州）若两个相似三角形的面积之比为1：4，则它们的周长之比为（）A、1：2B、1：4C、1：5D、1：16考点：相似三角形的性质。

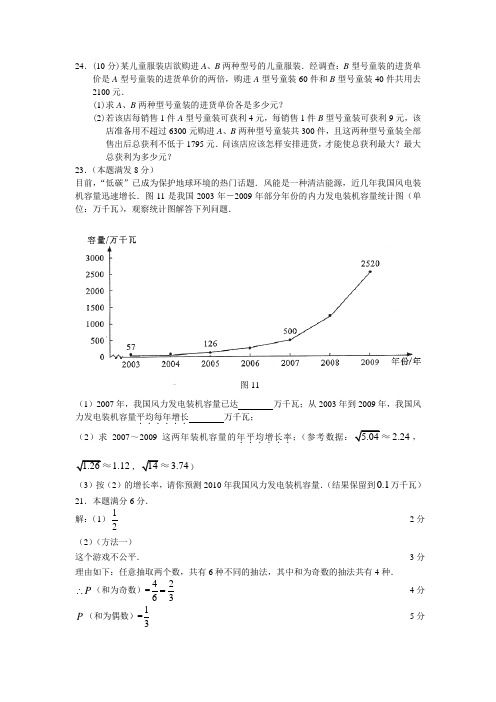
24．(10分)某儿童服装店欲购进A、B两种型号的儿童服装．经调查：B型号童装的进货单价是A型号童装的进货单价的两倍，购进A型号童装60件和B型号童装40件共用去2100元．(1)求A、B两种型号童装的进货单价各是多少元？(2)若该店每销售1件A型号童装可获利4元，每销售1件B型号童装可获利9元，该店准备用不超过6300元购进A、B两种型号童装共300件，且这两种型号童装全部售出后总获利不低于1795元．问该店应该怎样安排进货，才能使总获利最大？最大总获利为多少元？23．（本题满发8分）目前，“低碳”已成为保护地球环境的热门话题．风能是一种清洁能源，近几年我国风电装机容量迅速增长．图11是我国2003年－2009年部分年份的内力发电装机容量统计图（单位：万千瓦），观察统计图解答下列问题．（1）2007年，我国风力发电装机容量已达万千瓦；从2003年到2009年，我国风力发电装机容量平均每年增长．．．．．．万千瓦；（2）求2007～2009这两年装机容量的年平均增长率．．．．．．；（参考数据： 2.24，1.123.74）（3）按（2）的增长率，请你预测2010年我国风力发电装机容量．（结果保留到0.1万千瓦）21．本题满分6分．解：（1）12 ·····························································································································2分（2）（方法一）这个游戏不公平． ··················································································································3分理由如下：任意抽取两个数，共有6种不同的抽法，其中和为奇数的抽法共有4种．P∴（和为奇数）=4263= ·····································································································4分P（和为偶数）=13················································································································5分图11（方法二）设2008年的风力发电装机容量为a 万千瓦．5002520500a a a--= ·············································································································· 4分 21260000a = ················································································································0a >1122a ∴≈ ····················································································································· 5分经检验，1122a ≈是所列方程的根．则2007到2009这两年装机容量的年增长率为1122500 1.24124%500-=≈ ······················ 6分 答：2007到2009这两年装机容量的年平均增长率约为124%．（3）(1 1.24)25205644.8+⨯= ······················································································· 7分∴2010年我国风力发电装机容量约为5644.8万千瓦． ······················································· 8分24．（本题满分10分）某住宅小区计划购买并种植甲、乙两种树苗共300株．已知甲种树苗每株60元，乙种树苗每株90元．（1）若购买树苗共用21000元，问甲、乙两种树苗应各买多少株？（2）据统计，甲、乙两种树苗每株树苗对空气的净化指数分别为0.2和0.6，问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和不低于90而且费用最低？24．本题满分10分．解：（1）设甲种树苗买x 株，则乙种树苗买(300)x -株．················································· 1分 6090(300)21000x x +-= ·································································································· 3分200x = ········································································································ 4分300200100-= ····································································································· 5分答：甲种树苗买200株，乙种树苗买100株．（2）设买x 株甲种树苗，(300)x -株乙种树苗时该小区的空气净化指数之和不低于90．0.20.6(300)90x x +-≥ ····································································································· 6分 0.21800.690x x +-≥0.490x --≥225x ≤ ··································································································· 7分此时费用6090(300)y x x =+-3027000y x =-+ ·································································································· 8分 y 是x 的一次函数，y 随x 的增大而减少∴当225x =最大时，302252700020250y =-⨯+=最小（元） ······································· 9分 即应买225株甲种树苗，75株乙种树苗时该小区的空气净化指数之和不低于90，费用最小为20250元． ························································································································ 10分 （说明：其他解法参照此法给分）六、（本大题满分10分）24．2010年1月1日，全球第三大自贸区——中国——东盟自由贸易区正式成立，标志着该贸易区开始步入“零关税”时代.广西某民营边贸公司要把240吨白砂糖运往东盟某国的A 、B 两地，现用大、小两种货车共20辆，恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往A 地的运费为：大车630元/辆，小车420元/辆；运往B 地的运费为：大车750元/辆，小车550元/辆.（1）求这两种货车各用多少辆；（2）如果安排10辆货车前往A 地，某余货车前往B 地，且运往A 地的白砂糖不少于115吨.请你设计出使总运费最少的货车调配方案，并求出最少总运费.六、（本大题满分10分）24．解（1）解法一：设大车用x 辆，小车用y 辆.依据题意，得20x y x y +=⎧⎨⎩，15+10=240．…………………………………………………………………（2分） 解得812x y =⎧⎨=⎩，． ∴大车用8辆，小车用12辆.……………………………………………………（4分）解法二：设大车用x 辆，小车用()20x -辆.依题意，得()151020240x x +-=…………………………………………………………（2分）解得8x =.2020812x ∴-=-=．∴大车用8辆，小车用12辆.……………………………………………………（4分）（2）设总运费为W 元，调往A 地的大车a 辆，小车()10a -辆；调往B 地的大车()8a -辆，小车()2a +辆.则……………………………………………………………………（5分）()()()6304201075085502W a a a a =+-+-++，即：1011300W a =+ （0a a ≤≤8，为整数），………………………………（7分）()151010a a +-115≥．a ∴≥3．………………………………………………………………………………（8分）又W 随a 的增大而增大，∴当3a =时，W 最小.当3a =时，1031130011330W =⨯+ = ．…………………………………………（9分）因此，应安排3辆大车和7辆小车前往A 地；安排5辆大车和5辆小车前往B 地.最少24. (本小题满分12分)去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．（1）求饮用水和蔬菜各有多少件？（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部．．运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？24.解：（1）解法一: 设饮用水有x 件，则蔬菜有()80x -件. 依题意，得 …（1分）320)80(=-+x x ………………………………（3分）解这个方程，得 200=x ，12080=-x …………（4分） 答：饮用水和蔬菜分别为200件和120件． …………………………（5分）解法二：设饮用水有x 件，蔬菜有y 件. 依题意，得 ………（1分）⎩⎨⎧=-=+80320y x y x ………………………（3分） 解这个方程组，得 ⎩⎨⎧==120200y x ……………………（4分） 答：饮用水和蔬菜分别为200件和120件． ……………………（5分）（注：用算术方法解答正确同样本小题给满分．）（2）设租用甲种货车m 辆，则租用乙种货车()8m -辆.依题意，得 …（6分）4020(8)20010m 20(8)120m m m +-⎧⎨+-⎩≥≥ ………………………………………（8分） 解这个不等式组，得 24m ≤≤ ………………………（9分）m 为整数，∴m ＝2或3或4，安排甲、乙两种货车时有3种方案．设计方案分别为：①甲车2辆，乙车6辆；②甲车3辆，乙车5辆； ③甲车4辆，乙车4辆． （10分）（3）3种方案的运费分别为：①2×400+6×360＝2960元；②3×400+5×360＝3000元；③4×400+4×360＝3040元．∴方案①运费最少，最少运费是2960元．……………………………（12分）答:运输部门应选择甲车2辆，乙车6辆，可使运费最少，最少运费是2960元. ……（12分）21．（本题满分8分）某中学积极响应“钦州园林生活十年计划”的号召，组织团员植树300棵．实际参加植树的团员人数是原计划的1.5倍，这样，实际人均植树棵数比原计划的少2棵，求原计划参加植树的团员有多少人？21．解：设原计划参加植树的团员有x人. ··········································· 1分根据题意，得30030021.5x x-=. ·············································· 4分解这个方程，得x =50. ··············································· 6分经检验，x =50是原方程的根. ························································ 7分答：原计划参加植树的团员有50人. ··········································· 8分21．（6分）我市新城区环形路的拓宽改造工程项目，经投标决定由甲、乙两个工程队共同完成这一工程项目．已知乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程如果由甲队先做6天，剩下的工程再由甲、乙两队合作16天可以完成．求甲、乙两队单独完成这项工程各需要多少天？21．解：设乙工程队单独完成这项工程需要x天，则甲工程队单独完成这项工程需要2x天，由题意得：=1解得：x=17，经检验：x=17是分式方程的解，答：乙工程队单独完成这项工所需要17天．24．（8分）（2013•桂林）水源村在今年退耕还林活动中，计划植树200亩，全村在完成植树40亩后，某环保组织加入村民植树活动，并且该环保组织植树的速度是全村植树速度的1.5倍，整个植树过程共用了13天完成．（1）全村每天植树多少亩？（2）如果全村植树每天需2000元工钱，环保组织是义务植树，因此实际工钱比计划节约多少元？根据题意得：+=2522．为响应“美丽河池清洁乡村美化校园”的号召，红水河中学计划在学校公共场所安装温馨提示牌和垃圾箱。

2016年某某单招数学模拟试题:参数方程的应用【试题内容来自于相关和学校提供】1：直线被圆所截得的弦长为（）。

A、B、C、D、2：若直线与曲线（）有两个不同的公共点，则实数的取值X围为A、B、C、D、3：已知x2+y2＝10, 则3x+4y的最大值为（）A、5B、4C、3D、24：若动点（）在曲线上变化，则的最大值为（）A、B、C、D、25：下列在曲线上的点是（）A、B、C、D、6：若直线与曲线为参数，且有两个不同的交点，则实数的取值X围是__________。

7：参数方程中当为参数时，化为普通方程为_______________.8：椭圆C:，若椭圆C的焦点在x轴上，且a>0,则a的取值X围是_______________9：直线与圆相切，则_______________。

10：已知直线与圆相交于AB，则以AB为直径的圆的面积为 .11：已知直线经过点,倾斜角，设与圆相交与两点，求点到两点的距离之积。

12：（（本小题满分10分）选修4—4：坐标系与参数方程在直角坐标系xoy中，已知曲线C的参数方程是（是参数），现以原点O为极点，x轴正半轴为极轴建立极坐标系，⑴写出曲线C的极坐标方程。

⑵如果曲线E的极坐标方程是，曲线C、E相交于A、B两点，求.13：在平面直角坐标系xOy中，直线l的参数方程为 (t为参数)，它与曲线C：(y－2)2－x2＝1交于A、B两点。

(1)求|AB|的长；(2)以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为，求点P到线段AB中点M的距离。

14：（选修4—4 参数方程与极坐标）（本题满分7分）在极坐标系下，已知圆O：和直线，（Ⅰ）求圆O和直线的直角坐标方程；（Ⅱ）当时，求直线与圆O 公共点的一个极坐标.15：已知直线：为参数), 曲线（为参数）.（1）设与相交于两点,求；（2）若把曲线上各点的横坐标压缩为原来的倍,纵坐标压缩为原来的倍,得到曲线,设点是曲线上的一个动点,求它到直线的距离的最小值.答案部分1、C，把直线代入得，弦长为2、D略3、A解：因为x2+y2＝10, 则令x=则3x+4y=，因此可知其最大值为5，选A4、A设x=2cosα,y=bsinα,则x2+2y=4cos2α+2bsinα=-4sin2α+2bsinα+4=－2(sin2α－bsinα－2)=-2(sinα－)2+4+,∴的最大值为.5、B解：由，得到y2=1+x,利用逐一检验的方法可知满足参数方程的点为，选B6、解：因为作图可知当直线与曲线为参数，且有两个不同的交点则实数的取值X围是7、试题分析：由参数方程，两式平方作差得，。

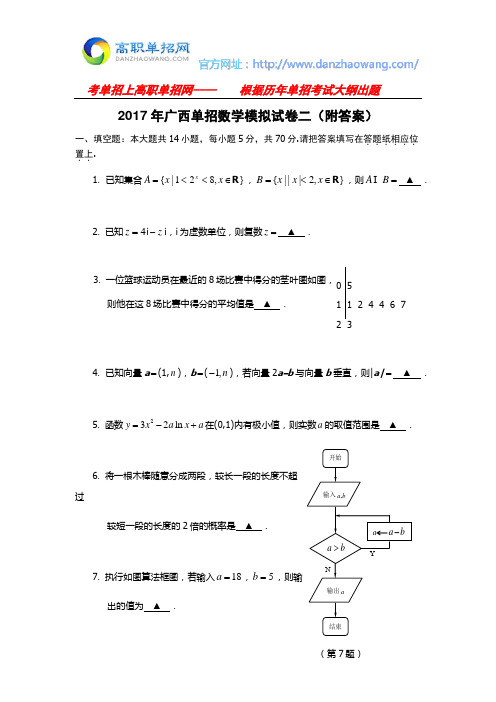
考单招上高职单招网---- 根据历年单招考试大纲出题（第7题）开始输入a ,bb a >结束 输出aa b a -YN2017年广西单招数学模拟试卷二（附答案）一、填空题：本大题共14小题，每小题5分，共70分.请把答案填写在答题．．纸．相应位．．．置上．．. 1. 已知集合∈<<=x x A x ,821|{R }，∈<=x x x B ,2|||{R }，则=B A ▲ ．2. 已知4=z i z -i ，i 为虚数单位，则复数=z ▲ ．3. 一位篮球运动员在最近的8场比赛中得分的茎叶图如图，则他在这8场比赛中得分的平均值是 ▲ ．4. 已知向量a =(1,n )，b =(1,n -)，若向量2a -b 与向量b 垂直，则|a|= ▲ ．5. 函数232ln y x a x a =-+在(0,1)内有极小值，则实数a 的取值范围是 ▲ ．6. 将一根木棒随意分成两段，较长一段的长度不超过较短一段的长度的2倍的概率是 ▲ ．7. 执行如图算法框图，若输入18=a ，5=b ，则输出的值为 ▲ ．0 51 12 4 4 6 7 2 3考单招上高职单招网---- 根据历年单招考试大纲出题8. 已知1F ，2F 是椭圆1122=++k y k x 的左、右焦点，经过1F 的直线与椭圆交于A ，B两点，若△2ABF 的周长为12，则椭圆的离心率为 ▲ ．9. 曲线x e y x cos =在0=x 处的切线方程为 ▲ ．10. 已知正四面体的表面积为34，则该四面体的体积为 ▲ ．11. 若函数2()2f x a x x a =-++-是偶函数，则实数a 的值为 ▲ ．12. 用)(n f 表示自然数n 的各位数字的和，例如202)20(=+=f ，02)2009(+=f1190=++，若对任意N n ∈，都有x n f n ≠+)(，满足这个条件的最大的两位数x 的值是 ▲ ．考单招上高职单招网---- 根据历年单招考试大纲出题13. 函数x x x x y 22sin cos cos sin 32+-=的图象在],0[m 上恰好有两个点的纵坐标为1，则实数m 的取值范围是 ▲ ．14. 设n S 为数列{}n a 的前n 项之和，若不等式222nS a n n+≥21a λ对任意等差数列{}n a 及任意正整数n 恒成立，则实数λ的最大值为 ▲ ．二、解答题：本大题共6小题，共计90分.请在答题．．纸．指定区域内．．．．．作答，解答时应写出文字说明、证明过程或演算步骤. 15. (本小题满分14分)已知在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边，tan (4C π-)23=-.(1) 求角C 的大小； (2) 若43sin sin =B A ，试判断△ABC 的形状，并说明理由．考单招上高职单招网---- 根据历年单招考试大纲出题16.(本小题满分14分)如图，在正三棱柱111C B A ABC -中，点D 在棱BC 上，D C AD 1⊥，点E ，F 分别是1BB ，11B A 的中点． (1) 求证：D 为BC 的中点； (2) 求证：//EF 平面1ADC ．（第16题） 17. (本小题满分14分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数p 与听课时间t 之间的关系满足如图所示的曲线．当]14,0(∈t 时，曲线是二次函数图象的一部分，当]40,14[∈t 时，曲线是函数()835log +-=x y a (0a >且1a ≠)图象的一部分．根据专家研究，当注意力指数p 大于80时听课效果最佳．(1) 试求()p f t =的函数关系式； (2) 老师在什么时段内安排核心内容能使得学生听课效果最佳？请说明理由．AA 1BCB 1C 1DEF 8100pO1200 140040008200 t考单招上高职单招网---- 根据历年单招考试大纲出题（第17题）18.(本小题满分16分)已知直线:与圆O (O 为坐标原点)相切，椭圆22122:1x y C a b +=(0)a b >>的离心率为33，短半轴长等于圆O 的半径． (1) 求椭圆的方程；(2) 抛物线的顶点为原点，焦点为椭圆的右焦点，点R ，S 是抛物线上不同的两点，且满足0OR RS ⋅=，求点S 的纵坐标的取值范围．19.(本小题满分16分)已知数列{}n a 的通项公式为an na n +=(,n a ∈N *)． (1) 若，，15a 成等比数列，求a 的值；(2) 是否存在k (k ≥3且k ∈N )，使得，2a ，k a 成等差数列，若存在，求出常数a的值；若不存在，请说明理由；(3) 求证：数列中的任意一项n a 总可以表示成数列中的其他两项之积．l 2y x =+1C 2C 1C 2C 1a 3a 1a考单招上高职单招网---- 根据历年单招考试大纲出题20.(本小题满分16分)已知正方形ABCD 的中心在原点，四个顶点都在曲线3y ax bx =+上． (1) 若正方形的一个顶点为(2,1)，求a 、b 的值；(2) 若1a =，求证：22b =-是正方形ABCD 唯一确定的充要条件．21.【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共计20分.请在答题纸指定区域内．．．．．．．．作答，解答应写出文字说明、证明过程或演算步骤. A .选修4-1：几何证明选讲如图，圆O 是△ABC 的外接圆，过点C 的切线交AB 的延长线于点D ，210CD =，3AB BC ==，求BD 以及AC 的长．B .选修4-2：矩阵与变换OABCD考单招上高职单招网---- 根据历年单招考试大纲出题已知变换T 把平面上的点)1,2(-，)1,0(分别变换成点)1,0(-，)1,2(-，试求变换T 对应的矩阵M .C .选修4-4：坐标系与参数方程 圆C ：2cos ρ=(4πθ-)，与极轴交于点A (异于极点O )，求直线CA 的极坐标方程.D .选修4-5：不等式选讲证明：n n12131211222-<++++(n ≥2，*n N ∈).【必做题】第22题、第23题，每小题10分，共计20分.请在答题纸指定区域内．．．．．．．．作答，解答应写出文字说明、证明过程或演算步骤.22. 某商场为促销设计了一个抽奖模型，一定数额的消费可以获得一张抽奖券，每张抽奖券可以从一个装有大小相同的4个白球和2个红球的口袋中一次性摸出3个球，至少摸到一个红球则中奖. (1) 求一次抽奖中奖的概率；(2) 若每次中奖可获得10元的奖金，一位顾客获得两张抽奖券，求两次抽奖所得的奖金额之和X (元)的概率分布和期望()E X .考单招上高职单招网---- 根据历年单招考试大纲出题23.函数2)1=xy的图象为曲线C，在C上有一点A的横坐标为)0(+t t，点P的(<坐标为)2,0(，直线AP与曲线C交于另一点B.(1) 试用t表示点B的横坐标；(2) 求直线AB与曲线C围成的封闭图形的面积的最小值.考单招上高职单招网---- 根据历年单招考试大纲出题参考答案一、填空题：本大题共14小题，每小题5分，共70分.1．{}20|<<x x 2．2+2i 3．14 4．2 5．(0,3) 6．31 7．38．31 9．01=+-y x 10．322 11．2 12．97 13．⎪⎭⎫⎢⎣⎡67,2ππ 14．51二、解答题：本大题共6小题，共计90分.解答时应写出文字说明、证明过程或演算步骤.15．(本题满分14分) 解：(1)32)4tan(-=-πC ，321tan 1tan -=+-∴C C ，3tan =C ……………4分π<<C 0 ，3π=∴C ．……………………………………………………6分(2)43sin sin =B A ，又23sin =C C B A 2sin sin sin =∴，由正弦定理得2c ab =……………………………10分由余弦定理得ab b a C ab b a c -+=-+=22222cos 2()02=-∴b a ，b a =∴， …………………………………………………12分又3π=C ，ABC ∆∴是正三角形．………………………………………14分16．(本题满分14分)解：(1) 正三棱柱111C B A ABC -，∴⊥C C 1平面ABC ，考单招上高职单招网---- 根据历年单招考试大纲出题又⊂AD 平面ABC ，∴AD C C ⊥1，又D C AD 1⊥，111C C C D C =∴⊥AD 平面11B BCC ，………………………………………………………3分又 正三棱柱111C B A ABC -，∴平面ABC ⊥平面11B BCC ，∴⊥AD BC ，D 为BC 的中点．………6分(2) 连接B A 1，连接C A 1交1AC 于点G ，连接DG矩形11ACC A ，∴G 为C A 1的中点，又由(1)得D 为BC 的中点，∴△BC A 1中，B A DG 1//…………………9分又 点E ，F 分别是1BB ，11B A 的中点，∴△B B A 11中，B A EF 1//，∴DG EF //，………12分又⊄EF 平面1ADC ，⊂DG 平面1ADC ，∴//EF 平面1ADC ．………14分17．(本题满分14分)解：（1）]14,0(∈t 时，设2()(12)82p f t c t ==-+(0<c )，将)81,14(代入得41-=c]14,0(∈t 时，21()(12)824p f t t ==--+…………………………2分]40,14[∈t 时，将)81,14(代入()835log +-=x y a ，得31=a ………4分 ∴2131(2)82(014)4()log (5)83(1440)t t p f t t t ⎧--+<<⎪==⎨-+≤≤⎪⎩． ………………………6分（2）]14,0(∈t 时，21(12)82804t --+≥解得22122212+≤≤-t ，AA 1BCB 1C 1DEF G考单招上高职单招网---- 根据历年单招考试大纲出题∴]14,2212[-∈t …………………………9分]40,14[∈t 时，8083)5(log 31≥+-t 解得325≤<t ，∴]32,14[∈t ， …………………………12分∴]32,2212[-∈t ，即老师在]32,2212[-∈t 时段内安排核心内容能使得学生听课效果最佳．…14分18．(本题满分16分) 解：（1）∵33==a c e ，∴223c a =，222cb =，∴2232b a =……………………3分 ∵直线相切， ∴∴∵椭圆的方程是 ………………………………………………6分 （2）设抛物线的方程为22y px =(0)p >， ∵椭圆的右焦点为(1,0)F ，∴12p=，∴2p =， ∴抛物线的方程为24y x =． ………………………………………………8分设 ∴222121121,,,44y y y OR y RS y y ⎛⎫⎛⎫-==- ⎪ ⎪⎝⎭⎝⎭ ， ∵0OR RS ⋅= ∴………………………………10分 ∵，化简得 ……………………………12分 22202:b y x y x l =+=--与圆2,2,222==∴=b b b 32=a 1C 12322=+y x 2C 1C 2C ),4(),,4(222121y y S y y R 0)(16)(121212221=-+-y y y y y y 0,121≠≠y y y )16(112y y y +-=考单招上高职单招网---- 根据历年单招考试大纲出题∴ 当且仅当 时等号成立 ……………………………14分 ∴当2y ≥8或2y ≤-8． ………………………………16分19．(本题满分16分) 解：(1)a a +=111，a a +=333，aa +=151515， ，，15a 成等比数列，∴23151)(a a a =，∴0=a 或9=a∵∈a N *，∴9=a ． ……………………………4分 (2)假设存在这样的k ，a 满足条件，a a +=111，a a +=222，ak ka k +=， ，2a ，k a 成等差数列，∴212a a a k =+，化简得2)3(=-a k∵k ，∈a N *，∴1=a 时，5=k ；或2=a 时，4=k ．……………………8分 (3)即证存在k ，t n ≠，使得t k n a a a = 即证：at ta k k a n n +⋅+=+ 即证：)1)(1(1ta k a n a ++=+ 即证：kta t k n ++=111 即证：ktak nk n k +=- 即证：ta k n n k +=-……………………12分 令1+=n k ，则)1()(a n n a k n t ++=+=6432256232256212122=+≥++=y y y 4,16,2561212121±===y y y y 1a 3a 1a考单招上高职单招网---- 根据历年单招考试大纲出题∴对任意n ，)1(1a n n n n a a a +++=即数列中的任意一项n a 总可以表示成数列中的其他两项之积．……………16分20．(本题满分16分)解：(1)∵一个顶点为(2,1)，∴必有另三个顶点(2,1)--，(1,2)-，(1,2)-， 将(2,1)，(1,2)-代入3y ax bx =+，得65=a ，617-=b ． ………………4分 (2) 设正方形在第一象限的顶点坐标为),(n m ，则必然有另一个顶点),(m n -…6分1充分性：若22b =-，x x y 223-=则⎪⎩⎪⎨⎧-=--=nn m m m n 222233，则有⎪⎪⎩⎪⎪⎨⎧-=--=222222n nm m m n ，即01)22)(22(22=+--n m ——① ……………8分令0222>=-t m ，则mt n =，代入①得01)22(22=+-t m t即01]22)22[(2=+-+t t t 化简得0)21(2=+-tt ， ……………10分又021=+-tt 有且仅有一个正根，∴),(n m 唯一确定，即正方形ABCD 唯一确定． ……………12分2必要性：若),(n m 唯一确定，则⎪⎩⎪⎨⎧+=-+=bn n m bmm n 33，即⎪⎪⎩⎪⎪⎨⎧+=-+=b n nm b m m n 22即01))((22=+++b n b m ——②考单招上高职单招网---- 根据历年单招考试大纲出题令02>=+t b m ，则mt n =，代入①得01)(22=++b t m t 即01])[(2=++-b t b t t 化简得0)1(122=--+t t b t t ，即02)1()1(2=+---tt b t t ——③ 又③有唯一解，∴82=b ，又∵02<--=n nmb ∴22b =-………16分21. 【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共计20分.请在答题纸指定区域内．．．．．．．．作答，解答应写出文字说明、证明过程或演算步骤. A .选修4-1：几何证明选讲(本题满分10分)解：由切割线定理得:2DB DA DC ⋅=， ………………………2分2()DB DB BA DC +=，04032=-+DB DB ，5=DB ． …………6分A BCD ∠=∠ ，∴DBC ∆∽DCA ∆， …………………………………8分∴BC DBCA DC =，得5106=⋅=DB DC BC AC ． ……………………………10分 B .选修4-2：矩阵与变换(本题满分10分)解：设⎥⎦⎤⎢⎣⎡=d c b a M ，则⎥⎦⎤⎢⎣⎡d c b a ⎥⎦⎤⎢⎣⎡-12⎥⎦⎤⎢⎣⎡-=10，⎥⎦⎤⎢⎣⎡d c b a ⎥⎦⎤⎢⎣⎡10⎥⎦⎤⎢⎣⎡-=12……………4分 ⎪⎪⎩⎪⎪⎨⎧-==-=-=-121202d b d c b a 0,1==∴c a ⎥⎦⎤⎢⎣⎡-=∴1021M ．…………………10分 C .选修4-4：坐标系与参数方程(本题满分10分)考单招上高职单招网---- 根据历年单招考试大纲出题解：圆C ：θρθρπθρρsin 2cos 24cos 22+=⎪⎭⎫⎝⎛-= 所以02222=--+y x y x …………………4分所以圆心⎪⎪⎭⎫⎝⎛22,22C ，与极轴交于()0,2A …………………6分直线CA 的直角坐标方程为2=+y x …………………8分 即直线CA 的极坐标方程为14cos =⎪⎭⎫⎝⎛-πθρ．…………………10分 D .选修4-5：不等式选讲(本题满分10分) 证明：n n n)1(13212111131211222-++⨯+⨯+<++++………5分 nn 11131212111--++-+-+= n12-=． ………10分 22. (本题满分10分)解：(1)设“一次抽奖中奖”为事件A ，则()5420163614222412==+=C C C C C A P 答：一次抽奖中奖的概率为54． …………………5分 (2)X 可取0，10，20()()04.02.002===X P ，()32.02.08.01012=⨯⨯==C X P ， ()()64.08.0202===X PX 的概率分布列为X 0 10 20 P0.040.320.64考单招上高职单招网---- 根据历年单招考试大纲出题1664.02032.01004.00)(=⨯+⨯+⨯=X E ． …………………10分23. (本题满分10分)解：(1)()()21,+t t A ，()2,0P ，t t t k AP122-+=，AP ∴：2122+-+=x tt t y 与()21+=x y 联立化简得：01122=--+x t t x 即()01=⎪⎭⎫ ⎝⎛+-t x t x 即t x =或t x 1-=，因为A 的横坐标为t ，所以B 的横坐标为t1-．……5分(2)dx x x x t t t tt⎰-⎪⎪⎭⎫ ⎝⎛---+-+12212212⎰-⎪⎪⎭⎫ ⎝⎛+-+-=t t dx x t t x 12211 t t x x t t x 12232131-⎪⎪⎭⎫ ⎝⎛+-+-=3161⎪⎭⎫ ⎝⎛+-=t t 当1-=t 时，最小值为34． …………………10分。

2016年对口升学考试数学模拟试卷(二)一、单选题（每小题给出的四个选项中只有一个符合题意。

）1.不等式220x x +-≤的解集.( )（A ）[]2,1- (B) （-1，2） (C) ()(,2)1,-∞-+∞ (D) (][),21,-∞-+∞ 2. =)16(log log 22 ( )A .1 B.2 C.4 D.83. 已知.tan a =,2a ππ<<则cosa 的值为 ( )A. 2-B. 2C. 12-D. 124. 直线0143=+-y x 与圆024222=+-++y x y x 的位置关系是 ( )A.相切B.相交C.相离D.不确定5. 下列等式成立的是（ ）A.0211log 022⎛⎫+= ⎪⎝⎭B.5155b a b a ⎛⎫= ⎪⎝⎭C. 2m m m a m a -=D. 132= 6. 经过点（-1,3）且与直线0532=-+y x 平行的直线的方程是 ( )A. 0732=++y xB. 0732=-+y xC. 0723=+-y xD. 0723=--y x7.设()3,2-=，则与共线的向量坐标是： （ ）（A ）()2,3 (B) ()3,1- (C) ()2,3- (D) ()6,4-8. 如果点M(3,4)与点N 关于点P(1,-2)对称，则点N 的坐标为 （ ）A. (-1，-8);B. (-1,0)C. (1，-8)D. (1，0)9．经过两点(3,5)和(-3,7),并且圆心在x 轴上的圆的方程是（ ）A ．9)1(22=++y xB ．26)2(22=+-y xC ．9)1()2(22=++-y xD ．50)2(22=++y x二、填空题：10.已知集合A={}|1|0x x ->，集合B={||1}x x ≥{，则A B .11. 若tan a =sin cos sin cos a a a a+-的值 12. 空间内平行于同一个平面的两条直线的位置关系有三、解答题：13. 一个圆经过点P （2，-1），和直线1=-y x 相切，并且圆心在直线x y 2-=求这个圆的方程.14. 已知直线L 过直线1L ：3x-5y-10=0和2L ：x+y+1＝0的交点，且平行于 直线3L ：x-2y-5=0求直线Ｌ的方程．15.已知等差数列}{n a 中，72=a ，154=a ，求数列}{n a 的首项1a 和前30项的和30s。

广西历年单招试题数学及答案一、选择题（每题3分，共30分）1. 下列哪个选项是最小的正整数？A. 0B. 1C. 2D. -1答案：B2. 函数f(x) = 2x^2 + 3x - 5在x = -1处的值是：A. -8B. -6C. -4D. -2答案：A3. 已知三角形ABC中，∠A = 90°，且AB = 3cm，BC = 4cm，那么AC的长度是：A. 5cmB. 6cmC. 7cmD. 8cm答案：A4. 一个数的60%加上它的40%等于：A. 100%B. 90%C. 80%D. 50%答案：A5. 以下哪个数是最小的正整数？A. 1B. 2C. 3D. 4答案：A6. 一个长方体的长、宽、高分别是10cm、8cm和6cm，它的体积是：A. 480cm³B. 600cm³C. 720cm³D. 800cm³答案：A7. 如果一个圆的半径是5cm，那么它的直径是：A. 10cmB. 15cmC. 20cmD. 25cm答案：A8. 一个数除以3的商是7，余数是2，那么这个数是：A. 23B. 25C. 27D. 29答案：A9. 以下哪个选项是最大的负整数？A. -1B. -2C. -3D. -4答案：A10. 一个数的75%等于它的1/3，那么这个数是：A. 3B. 4C. 5D. 6答案：B二、填空题（每题4分，共20分）11. 一个数的1/4加上它的1/2等于______。

答案：3/412. 如果一个数的1/5等于4，那么这个数是______。

答案：2013. 一个长方体的体积是120cm³，长是10cm，宽是6cm，那么它的高是______。

答案：2cm14. 一个数的3倍加上5等于这个数的2倍减去3，这个数是______。

答案：415. 一个圆的周长是2πr，其中r是圆的半径，如果一个圆的周长是12.56cm，那么它的半径是______。

2016年某某单招数学模拟试题:不等式的性质【试题内容来自于相关和学校提供】1：已知且，，则实数满足（）A、B、C、D、2：若，且，则下列不等式中，恒成立的是A、B、C、D、3：a，b，c，d均为实数，有下列命题正确的是（）①若ab>0，bc-ad>0，则->0；②若ab>0，->0，则bc-ad>0；③若bc-ad>0，->0，则ab>0.A、①②B、①③C、①②③D、②③4：已知a<0，－1<b<0，那么下列不等式成立的是()A、a>ab>ab 2B、ab 2>ab>aC、ab>a>ab 2D、ab>ab 2>a5：设不等式组表示的平面区域的面积为，若，则与满足A、B、C、D、6：若，则, , , 按由小到大的顺序排列为 7：定义“”是一种运算，对于任意的都满足，其中为正实数，，则取最大值时的值为 8：若对于任意非零实数,不等式恒成立,则实数的取值X围__________。

9：已知x,y,且x+2 y≥1,则二次函数式u= x2+ y2+4 x-2 y的最小值______. 10：如果，则把变量________的值增加1会使的值增加最大（填入中的某个字母）。

11：已知，，求的取值X围。

12：学生若干人，住若干宿舍，如果每间住4人，那么还余19人，如果每间住6人，那么一间不满也不空，求宿舍间数和学生人数。

13：设a，b，c为正实数，求证：＋abc≥2.14：（本小题12分）解不等式15：已知，，，，求的值。

（12分）答案部分1、D试题分析：因为，且，，所以，。

故选D。

考点：本题主要考查不等式的性质。

点评：简单题，由不等式的性质，“同号两数取倒数，不等号反向”。

2、C试题分析：A和B选项成立的条件是；D选项应该是；因此只有C正确. 考点：基本不等式.3、C由bc-ad>0得bc>ad，又ab>0，∴>，即>，∴->0，故①正确；由ab>0，->0，得ab>0，即bc-ad>0，故②正确；由->0，得>0，∵bc-ad>0，∴ab>0，故③正确.故选：C、4、D∵a<0，－1<b<0，∴ab 2－a＝a(b 2－1)>0，ab－ab 2＝ab(1－b)>0. ∴ab>ab 2>a. 也可利用特殊值法，取a＝－2，b＝－，则ab 2＝－，ab＝1，从而ab>ab 2>a. 故应选D.5、D略6、由糖水浓度不等式知，且，得，即7、3因为，所以；因为，所以，当且仅当，即时等号成立，所以当时，取最大值6.8、1>x解：已知对于任意非零实数m，不等式|2m-1|+|1-m|>|m|（|x|-|x-1|）恒成立变形为|2m-1|+|1-m|/|m|>|x|-|x-1| 因为：|2m-1|+|1-m|/|m|>|2m-1+1-m|/|m|=1 所以只需要1>|x|-|x-1|即可，利用分段函数求解得到9、因为x,y ,且x+2y≥1,所以表示的平面区域如下图所示：函数式u=x 2+y 2+4x-2y=(x+2) 2+(y-1) 2-5，当x=-2,y=1时，即取P（-2，1）时，u的值为最小，但是点P（-2，1）不在区域x+2y≥1内，所以函数u=x 2+y 2+4x-2y不在点P处取得最小值。

《数学》高职单招模拟试题入括号内。

本大题15小题，每小题3分，共45分）1、设集合A=｛0,3｝，B=｛1,2,3｝，C=｛0,2｝则A (B C)=( )A ｛0,1,2,3,4｝ B φ C ｛0,3｝D ｛0｝2、不等式()23+x ＞0的解集是( ).A ｛x ︱∞-＜x ＜∞+｝B ｛x ︱x ＞-3｝C ｛x ︱x ＞0｝D ｛x ︱x ≠-3｝ 3、已知0＜a ＜b ＜1，那么下列不等式中成立的是( ) Ab a 3.03.0log log <B ㏒3a ＜㏒3bC 0.3a ＜0.3bD 3a ＞3b4、已知角α终边上一点P 的坐标为(-5,12)，那么sin α=( ) A 135B 135-C 1312D 1312-的定义域是()+∞,4)6、已知a ＞0，b ＜0，c ＜0，那么直线0=++c by ax 的图象必经过（ ）。

A 第一、二、三象限 B第一、二、四象限C 第一、三、四象限 D第二、三、四象限 7、在等比数列｛n a ｝中，若1a ，9a 是方程02522=+-x x 的两根，则4a ·6a =（ ） A 5 B 25C 2D 1 8、函数y=x x cos sin 的最小正周数是( ) A π B 2πC 1D 2 9、已知两直线（m-2）x -y+3=0与x +3y-1=0互相垂直，则m=( ) A 35B 5C -1D 37 10、已知三点（2,-2），（4,2）及（5,2k）在同一条直线上，那么k 的值是( ) A 8B -8C 8±D 8或3姓名 班级 座号11、已知点A(-1,3)，B(-3,-1)，那么线段AB 的垂直平分线方程是（ ）。

A02=-y xB 02=+y xC 022=+-y xD 032=++y x12、五个人站成一排，甲、乙两人必须站在一起(即两人相邻)的不同站法共有（ ）。

A 48种B 24种C 12种D 120种 13、 14、若x 、y 为实数，则22y x =的充要条件是( ). Ax=y B ︱x ︱=︱y ︱Cx=y - D x =y =015、在空间中，下列命题正确的是( ).A 若两个平面有无数个公共点，则这两个平面重合B 若平面α内不共线的三点到平面β的距离相等，则α∥βC 两两相交的三条直线必共面D 若直线l 与平面a 垂直，则直线l 与平面a 上的无数条直线垂直11、在△ABC 中，若,32,2==c b ∠B=6π,则∠C=（ ）。

高职单考单招数学测试卷（一）试卷编号： 2015-YL — 09 姓名 _________ 报考专业 ________得分 _________一、选择题 (本大题共 18 小题每小题 2 分，共 36 分 )1. 设全集 Ux x 0 ,集合 A x x 3 ， Bx 2 x 8 ，则 C U A ∩ B =()A ． x 2 x 3B ． x 2 x 3C ． x 0 x 3D ． x 0 x 102. 已知函数 fxx 2 ax 5 ，的最小值为 1 ，则 a ．．．．．．．．．．．．．．．．．．．．（ ）A ．4B ． 2C ．4D ． 23.不等式2x 3 1）的解集为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（A ． ( ,2)B ． 1,C ． (1,2)D ． (,1) (2, )4. sinsin 是成立的．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）A ．充要条件B ．必要不充分条件C ．充分不必要条件D ．既不充分也不必要条件5.若 sin? tan 0 ，则 是．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）A ．第一，二象限角B ．第二，三象限角C ．第一，三象限角D ．第三、四象限角6. cos75 =．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）A ．5 1B ． 62C ． 6 2D ．5 144227.函数 y3sin(x) 的最大值和周期分别是． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．（ ）2 8A ． 3,4B ．3,4C ． 3,16D ． 3,168.角 的终边上有一点 P( 3,4) ，则 sincos 的值是．．．．．．．．．．．．．．．．．（）A ．3B ．4C ．11555D ．59.圆 x 2y 2 1上的点到 3x 4 y25 0的最短距离是． ．．．．．．．．．．．．．．．．．．． ()A ． 1B ． 5C ． 4D ． 610.已知点 M3,4 ,抛物线 y 24x 的焦点为 F ，则直线 FM 的斜率为．．．．．．（ ）A ．2 B ．4 C ．1D ．4311.已知 f 2xlog 3 4x11 ，则 f 1．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）A ． 1B ．C ．1 D ． log 3 72312. 若 sin()5 ，则 cos(22 ) ．．．．．．．．．．．．．．．．．．．．．．．．．．（ ）771616A 、B 、C 、D 、2525252513. 两圆 C 1：x 2＋ y 2＝4 与 C 2 ：x 2 ＋y 2－2x － 1＝ 0 的位置关系是． ．．．．．．．．． ( ) A ．相外切 B ．相内切 C ．相交 D ．外离14. 下列关系不成立是． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（ ）＞ ba ＋ c ＞b ＋ c＞ b 且 c ＞ da ＋ c ＞b ＋ d＞ b 且 b ＞ c a ＞ c＞ b ac ＞ bc15. 椭圆x 2 y 2 1离心率为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）9164B ．3C ．7 7A ．54 D ．5316. 若角 的终边经过点（ sin 30 , cos 30 ），则 sin 的值是．．．．．．．．．．．．（）11C.33A.22D. -2217. 设抛物线 y28x 的焦点为 F ，准线为 l ， P 为抛物线上一点， PAl ， A 为垂足，如果直线 AF 斜率为 3 ，那么 PF．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．（）A. 4 3C.8 3D. 1618. 化简1 cos2? 2sin 2)3sin 2等于．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． (cos2A ． tanB ． tan 21D ．1C ． tan 23 tan 2二、填空题 (本大题共 8 小题，每小题 3 分)19. 在等腰ABC 中，∠ B 为底角且 cos B3 ,则顶角 A 的正弦值为.520. 圆心为直线 xy 1 0 与直线 2x y 2 0 的交点，半径为 2 的圆的方程为.21. 直线经过点 A( 3,2) 和点 B(4, 5) ,则直线 AB 的距离 .22. 在ABC 中，若sin A 3 a 2c.sin C,则3c5函数 f ( x) { x 2 ( x0 )2 x 的图象的交点的 23. x 2 2 x 2 ( x0 ) 的图象和函数 g( x)个数有个。