中考数学总复习课后强化训练43图形折叠问题

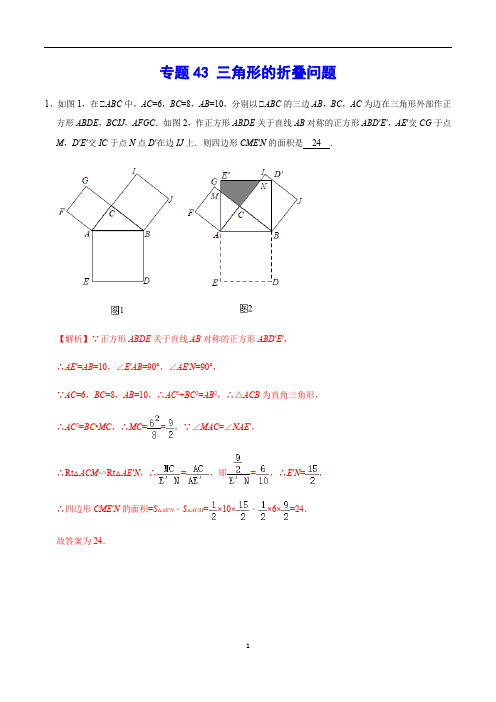
专题43 三角形的折叠问题1、如图1，在△ABC中，AC=6，BC=8，AB=10，分别以△ABC的三边AB，BC，AC为边在三角形外部作正方形ABDE，BCIJ，AFGC．如图2，作正方形ABDE关于直线AB对称的正方形ABD′E′，AE′交CG于点M，D′E′交IC于点N点D′在边IJ上．则四边形CME′N的面积是24．【解析】∵正方形ABDE关于直线AB对称的正方形ABD′E′，∴AE′=AB=10，∠E′AB=90°，∠AE′N=90°，∵AC=6，BC=8，AB=10，∴AC2+BC2=AB2，∴△ACB为直角三角形，∴AC2=BC•MC，∴MC==，∵∠MAC=∠NAE′，∴Rt△ACM∽Rt△AE′N，∴=，即=，∴E′N=，∴四边形CME′N的面积=S△AE′N﹣S△ACM=×10×﹣×6×=24．故答案为24．2、如图，在△ABC中，△C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B=．【解析】如图，连接BB′，∵△ABC绕点A顺时针方向旋转60°得到△AB′C′，∴AB=AB′，∠BAB′=60°，∴△ABB′是等边三角形，∴AB=BB′，在△ABC′和△B′BC′中，，∴△ABC′≌△B′BC′（SSS），∴∠ABC′=∠B′BC′，延长BC′交AB′于D，则BD⊥AB′，∵∠C=90°，AC=BC=，∴AB==2，∴BD=2×=，C′D=×2=1，∴BC′=BD﹣C′D=﹣1．故答案为：﹣13、如图，在Rt△ABC中，△ACB=90°，AC=3，BC=4，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，当线段AF=AC时，BE的长为．【解析】连接AD，作EG⊥BD于G，如图所示：则EG∥AC，∴△BEG∽△BAC，∴==，设BE=x，∵∠ACB=90°，AC=3，BC=4，∴AB==5，∴==，解得：EG=x，BG=x，∵点D是边BC的中点，∴CD=BD=2，∴DG=2﹣x，由折叠的性质得：DF=BD=CD，∠EDF=∠EDB，在△ACD和△AFD中，，∴△ACD≌△AFD（SSS），∴∠ADC=∠ADF，∴∠ADF+∠EDF=×1880°=90°，即∠ADE=90°，∴AD2+DE2=AE2，∵AD2=AC2+CD2=32+22=13，DE2=DG2+EG2=（2﹣x）2+（x）2，∴13+（2﹣x）2+（x）2=（5﹣x）2，解得：x=，即BE=；故答案为：．4、已知ABC 中， AC BC =， Rt C ∠=∠．如图，将ABC 进行折叠，使点A 落在线段BC 上（包括点B 和点C ），设点A 的落点为D ，折痕为EF ，当DEF 是等腰三角形时，点D 可能的位置共有（ ）．A ．2种B ．3种C ．4种D ．5种 【解析】（1）当点D 与C 重合时， ∵AC=BC ，AE=DE （即CE ），AF=DF （即CF ），∵此时∵AFC （即∵AFD ）是等腰直角三角形，点E 是斜边AC 的中点， ∵EF=DE ，∵∵EDF 为等腰三角形．（2）当点D 与B 点重合时，点C 与E 重合，∵AC=BC ，AF=DF （即BF ），∵此时EF=12AB=DF （即BF ）， ∵∵DEF 是等腰三角形；（3）当点D 移动到使DE=DF 的位置时，∵DEF 是等腰三角形． 综上所述，当∵DEF 为等腰三角形时，点D 的位置存在3中可能. 故选B.5、如图，在Rt △ABC 中，△A =90°，△B =30°，BC ，点E 、F 分别是BC 、AC 边上的动点，沿E 、F 所在直线折叠△C ，使点C 的落对应点C '始终落在边AB 上，若△BEC '是直角三角形时，则BC '的长为或1. 【解析】通过观察及分析可知，C 点不可能为直角顶点，分两种情况讨论. ①当∠CM B ′=90°时，如图例5-2所示.由折叠知：∠BMN =∠B ′MB =45°，又因为∠B =45°，所以∠BNM =90°，∠MNB ′=90° 即∠BNM +∠MN B ′=180°，所以B 、N 、B ′三点共线，此时B ′与点A 重合.所以，12BM BC ==①当∠CB ′M =90°时，如图例5-3所示.由折叠知∠B =∠B ′=45°，因为∠C =45°，可得∠B ′MC =45°，所以△B ′MC 是等腰直角三角形设BM = B ′M =x ，B ′C =x ，则MC =x因为BC +1所以x 解得：x =1，即BM =1.综上所述，BM 1. 【点睛】根据题意判断出C 点不可能为直角顶点，分两种情况讨论，利用等腰直角三角形的三边关系求解.6、如图，矩形ABCD中，点E为射线BC上的一个动点，连接AE，以AE为对称轴折叠△AEB，得到△AEB′，点B的对称点为点B′，若AB=5，BC=3，当点B′落在射线CD上时，线段BE的长为．【答案】5或.【解析】∵四边形ABCD为矩形，∴C D=AB=10，BC=AD=5，△矩形ABCD折叠，使点C落在边AB上的E处，折痕交DC边于点M，△△MEB=△C=90°，BC=BE=5，△四边形BCME为正方形，△ME=5，△AE=AB-BE=5，△点F在DM上运动，且△AEF是腰长为5的等腰三角形，△点F只能在点D或点M处，点F运动到点D时，EF=5当点F运动到点M时，EF=5．故答案为5或.7、如图例3-1，在Rt △ABC 中，△ACB =90°，△B =30°，BC =3，点D 是BC 边上一动点（不与点B 、C 重合），过点D 作DE △BC 交AB 边于点E ，将△B 沿直线DE 翻折，点B 落在射线BC 上的点F 处，当△AEF 为直角三角形时，BD 的长为图例3-1图例3-2图例3-38、如图例5-1，在Rt ABC ∆中，90A ∠=︒，AB AC =，1BC =，点M ，N 分别是边BC ，AB 上的动点，沿MN 所在的直线折叠B ∠，使点B 的对应点'B 始终落在边AC 上.若'MB C ∆为直角三角形，则BM 的长为 ．图例5-1图例5-2图例5-39、如图例6-1，在△MAN =90°，点C 在边AM 上，AC =4，点B 为边AN 上一动点，连接BC ，△A’BC 与△ABC 关于BC 所在直线对称. D 、E 分别为AC 、BC 的中点，连接DE 并延长交A’B 所在直线于点F ，连接A’E . 当△A’EF 为直角三角形时，AB 的长为.图例6-1图例6-2图例6-310、如图，在Rt△ABC中，△A=90°，△B=30°，BC+1，点E、F分别是BC、AC边上的动点，沿E、F 所在直线折叠△C，使点C的落对应点C'始终落在边AB上，若△BEC'是直角三角形时，则BC'的长为2.【解析】如图1，当△BEC'=90°时，图1 图2△△B=30°，△BE’E，又△CE=C'E，BC+1，△BE C'E=1，△Rt△BEC'中，BC'=2；如图2，当△BC'E=90°时，△△B=30°，△BE=2C'E=2CE又△BC+1，△BE=(213+，C'E=(113+△BC综上所述，BC'的长为2．。

中考数学二轮专题复习《折叠问题》培优练习一、选择题1.如图,有一条直的宽纸带,按图折叠,则∠α的度数等于 ( )A.50°B.60°C.75°D.85°2.如图，将长方形ABCD纸片沿对角线BD折叠，使点C落在点C/处，BC/交人D于点E，若∠DBC=22.5°，则在不添加任何辅助线的情况下，图中45°角(虚线也视为角的边)共有( )A.3个B.4个C.5个D.6个3.如图，将矩形ABCD沿EM折叠，使顶点B恰好落在CD边的中点N上.若AB＝6，AD＝9，则五边形ABMND的周长为( )A.28B.26C.25D.224.如图，有一块矩形纸片ABCD，AB＝8，AD＝6，将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△C EF的面积为( )A.12B.98C.2D.4 5.如图，在矩形ABCD 中，AB ＝8.将矩形的一角折叠，使点B 落在边AD 上的B ´点处，若AB /＝4，则折痕EF 的长度为( )A.8B.4 5C.5 5D.106.将矩形ABCD 按如图所示的方式折叠，BE ，EG ，FG 为折痕，若顶点A ，C ，D 都落在点O 处，且点B ，O ，G 在同一条直线上，同时点E ，O ，F 在另一条直线上，则AD ：AB 的值为( )A.65B. 2C.32 D. 37.如图矩形ABCD 中，AB ＝3，BC ＝33，点P 是BC 边上的动点，现将△PCD 沿直线PD 折叠，使点C 落在点C 1处，则点B 到点C 1的最短距离为( )A.5B.4C.3D.28.将一张宽为4cm 的长方形纸片(足够长)折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是( )A.833cm 2B.8cm 2C.1633cm 2 D.16cm 2二、填空题9.如图，在平面直角坐标系中，已知点A(0，4)，B(3，0)，连结AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A'处，折痕所在的直线交y轴的正半轴于点C，则直线BC所对应的函数表达式为.10.将正方形纸片ABCD按如图所示对折，使边AD与BC重合，折痕为EF，连接AE，将AE折叠到AB上，折痕为AH，则BH：BC的值是．11.如图，在矩形纸片ABCD中，AB＝6，BC＝10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG＝45°；②△DEF∽△ABG；③S△ABG ＝32S△FGH；④AG＋DF＝FG．其中正确的是．(把所有正确结论的序号都选上)12.如图，在矩形ABCD中，AB＝1，BC＝a，点E在边BC上，且BE＝35a．连接AE，将△ABE沿AE折叠，若点B的对应点B′落在矩形ABCD的边上，则a的值为．13.一张直角三角形纸片ABC，∠ACB＝90°，AB＝10，AC＝6，点D为BC边上的任一点，沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当△BDE是直角三角形时，则CD的长为．14.如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y 轴上，连接OB，将纸片OABC沿AC折叠，使点B落在D的位置上.若AC＝5，OC＝2BC，则点D的坐标 .三、解答题15.如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE折叠至△AFE，延长EF交BC于点G，连结AG.(1)求证：△ABG≌△AFG；(2)求BG的长．16.将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F，(1)求证：四边形AECF为菱形；(2)若AB＝4，BC＝8，求菱形的边长；(3)在(2)的条件下折痕EF的长．17.如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．(1)试找出一个与△AED全等的三角形，并加以证明；(2)若AB＝8，DE＝3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，试求PG＋PH的值，并说明理由．18.小王剪了两张直角三角形纸片，进行了如下的操作：操作一：如图1，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE．(1)如果AC＝6cm，BC＝8cm，可求得△ACD的周长为；(2)如果∠CAD：∠BAD＝4：7，可求得∠B的度数为；操作二：如图2，小王拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，若AC＝9cm，BC＝12cm，请求出CD的长．19.矩形AOBC中，OB＝8，OA＝4.分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B，C重合)，过点F的反比例函数y＝kx(k＞0)的图象与边AC交于点E.(1)当点F运动到边BC的中点时，求点E的坐标；(2)连接EF、AB，求证：EF∥AB；(3)如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式.20.将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G（如图）.（1）如果M为CD边的中点，求证：DE∶DM∶EM=3∶4∶5；（2）如果M为CD边上的任意一点，设AB=2a，问△CMG的周长是否与点M的位置有关？若有关，请把△CMG的周长用含DM的长x的代数式表示；若无关，请说明理由.21.如图，抛物线L：y=﹣x2+bx+c经过点A(1，0)和点B(5，0)，已知直线l的解析1式为y=kx﹣5.的解析式、对称轴和顶点坐标.(1)求抛物线L1(2)若直线l将线段AB分成1：3两部分，求k的值；(3)当k=2时，直线与抛物线交于M、N两点，点P是抛物线位于直线上方的一点，当△PMN面积最大时，求P点坐标，并求面积的最大值.在x轴上方的部分沿x轴折叠到x轴下方，将这部分图象与原抛物线(4)将抛物线L1剩余的部分组成的新图象记为L2①直接写出y随x的增大而增大时x的取值范围；有四个交点时k的取值范围.②直接写出直线l与图象L2答案1.C2.D3.A.4.C.5.C.6.B.7.C.8.B9.答案为：y＝﹣12x＋32.10.答案为：52﹣12．11.答案为：①③④．12.答案为：53或53.13.答案为：3或24 7．14.答案为：(﹣0.6，0.8)15.证明：(1)∵四边形ABCD是正方形，∴∠B＝∠D＝90°，AD＝AB.由折叠可知，AD＝AF，∠AFE＝∠D＝90°，∴∠AFG＝90°，AB＝AF.∴∠B＝∠AFG＝90°.又∵AG＝AG，∴Rt△ABG≌Rt△AFG(H.L.)．(2)解：∵△ABG≌△AFG，∴BG＝FG.设BG＝FG＝x，则GC＝6﹣x，∵E为CD的中点，∴EG＝x＋3，在Rt△CEG中，由勾股定理，得32＋(6﹣x)2＝(x＋3)2，解得x＝2，∴BG＝2.16.证明：(1)∵矩形ABCD折叠使A，C重合，折痕为EF，∴OA＝OC，EF⊥AC，EA＝EC，∵AD∥AC，∴∠FAC＝∠ECA，在△AOF和△COE中，∴△AOF≌△COE，∴OF＝OE，∵OA＝OC，AC⊥EF，∴四边形AECF为菱形；(2)①设菱形的边长为x，则BE＝BC﹣CE＝8﹣x，AE＝x，在Rt△ABE中，∵BE2＋AB2＝AE2，∴(8﹣x)2＋42＝x2，解得x＝5，即菱形的边长为5；②在Rt△ABC中，AC＝45，∴OA＝12AC＝25，在Rt△AOE中，AE＝5，OE＝5，∴EF＝2OE＝25．17.解：(1)△AED≌△CEB′证明：∵四边形ABCD为矩形，∴B′C＝BC＝AD，∠B′＝∠B＝∠D＝90°，又∵∠B′EC＝∠DEA，∴△AED≌△CEB′；(2)由折叠的性质可知，∠EAC＝∠CAB，∵CD∥AB，∴∠CAB＝∠ECA，∴∠EAC＝∠ECA，∴AE＝EC＝8﹣3＝5．在△ADE中，AD＝4，延长HP交AB于M，则PM⊥AB，∴PG＝PM．∴PG＋PH＝PM＋PH＝HM＝AD＝4．18.解：操作一：(1)14 (2)35º操作二：∵AC＝9cm，BC＝12cm，∴AB＝15(cm)，根据折叠性质可得AC＝AE＝9cm，∴BE＝AB﹣AE＝6cm，设CD＝x，则BD＝12﹣x，DE＝x，在Rt△BDE中，由题意可得方程x2＋62＝(12﹣x)2，解得x＝4.5，∴CD＝4.5cm．19.解：(1)∵四边形OACB是矩形，OB＝8，OA＝4，∴C(8，4)，∵AE＝EC，∴E(4，4)，∵点E在y＝kx上，∴E(4，4).(2)连接AB，设点F(8，a)，∴k＝8a，∴E(2a，4)，∴CF＝4﹣a，EC＝8﹣2a，在Rt△ECF中，tan∠EFC＝＝＝2，在Rt△ACB中，tan∠ABC＝＝2，∴tan∠EFC＝tan∠ABC，∴∠EFC＝∠ABC，∴EF∥AB.(3)如图，设将△CEF沿EF折叠后，点C恰好落在OB上的G点处，∴∠EGF＝∠C＝90°，EC＝EG，CF＝GF，∴∠MGE＋∠FGB＝90°，过点E作EM⊥OB，∴∠MGE＋∠MEG＝90°，∴∠MEG＝∠FGB，∴Rt△MEG∽Rt△BGF，∵点E(，4)，F(8，)，∴EC＝AC﹣AE＝8﹣，CF＝BC﹣BF＝4﹣，∴EG＝EC＝8﹣，GF＝CF＝4﹣，∵EM ＝4，∴＝，∴GB ＝2，在Rt △GBF 中，GF 2＝GB 2＋BF 2，即：(4﹣)2＝(2)2＋()2，∴k ＝12，∴反比例函数表达式为y ＝12x . 20.证明：(1)DE 为x ，则DM ＝1，EM ＝EA ＝2﹣x ，在Rt △DEM 中，∠D ＝90°，∴DE 2＋DM 2＝EM 2x 2＋12＝(2﹣x)2x ＝34，∴EM ＝54． (2)设正方形的边长为2，由(1)知，DE ＝34，DM ＝1，EM ＝54∴DE ：DM ：EM ＝3：4：5；(3)△CMG 的周长与点M 的位置无关．证明：设DM ＝x ，DE ＝y ，则CM ＝2a ﹣x ，EM ＝2a ﹣y ，∵∠EMG ＝90°，∴∠DME ＋∠CMG ＝90°．∵∠DME ＋∠DEM ＝90°，∴∠DEM ＝∠CMG ，又∵∠D ＝∠C ＝90°△DEM ∽△CMG ，∴△CMG 的周长为CM ＋CG ＋MG ＝. 在Rt △DEM 中，DM 2＋DE 2＝EM 2即x 2＋y 2＝(2a ﹣y)2整理得4a 2﹣x 2＝4ay ，∴CM＋MG＋CG＝＝4a．所以△CMG的周长为4a，与点M的位置无关．21.解：(1)∵抛物线L1：y=﹣x2+bx+c经过点A(1，0)和点B(5，0)∴y=﹣(x﹣1)(x﹣5)=﹣(x﹣3)2+4，∴抛物线L1的解析式为y=﹣x2+6x﹣5对称轴：直线x=3顶点坐标(3，4)；(2)∵直线l将线段AB分成1：3两部分，则l经过点(2，0)或(4，0)，∴0=2k﹣5或0=4 k﹣5∴k=52或k=54.(3)如图1，设P(x，﹣x2+6x﹣5)是抛物线位于直线上方的一点，解方程组，解得或不妨设M(0，﹣5)、N(4，3)∴0＜x＜4过P做PH⊥x轴交直线l于点H，则H(x，2x﹣5)，PH=﹣x2+6x﹣5﹣(2x﹣5)=﹣x2+4x，S△PMN =12PH•x N=(﹣x2+4x)×4=﹣2(x﹣2)2+8∵0＜x＜4∴当x=2时，SPMN最大，最大值为8，此时P(2，3) (4)如图2，A(1，0)，B(5，0).由翻折，得D(3，﹣4)， ①当x ≤1或3≤x ≤5时y 随x 的增大而增大②当y=kx ﹣5过D 点时，3k ﹣5=﹣4，解得k=13， 当y=kx ﹣5过B 点时，5k ﹣5=0，解得k=1，直线与抛物线的交点在BD 之间时有四个交点，即13＜k ＜1， 当13＜k ＜1时，直线l 与图象L 2有四个交点.。

2020年度初三数学专题复习中考 圆的折叠专题1. 如图①是半径为2的半圆，点C 是︵AB 的中点，现将半圆如图②方式翻折，使得点C 与圆心O 重合，则图中阴影部分的面积是（ ）A ．4π3B ．4π3 -3C ．23+π3D ．23-23π2. 如图，AB 是⊙O 的弦，AC 是⊙O 的直径，将︵ AB 沿着AB 弦翻折，恰好经过圆心O ．若⊙O 的半径为6，则图中阴影部分的面积等于（ ）A ．6πB ．93C ．9πD ．633. 如图，将⊙O 的劣弧︵AB 沿AB 翻折，D 为优弧︵ADB 上一点，连接AD ，交︵ AB 于点C ，连接BC 、BD ；若BC=5，则BD= ．4. 如图，AB 是⊙O 的直径，且AB=4，C 是⊙O 上一点，将弧AC 沿直线AC 翻折，若翻折后的圆弧恰好经过点O ，π≈314，2≈1.41，3≈1.73，那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是（ ）A ．3.2B ．3.6C ．3.8D ．4.25.如图，在扇形AOB中，∠AOB=90°，半径OA=6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，则整个阴影部分的面积为（）A．9π-9 B．9π-63C．9π-18 D．9π-1236.如图，是一个圆心角为90°的扇形，AO=2cm，点P在半径AO上运动，点Q在弧AB上运动，沿PQ将它以上的部分向下翻折，使翻折后的弧恰好过点O，则OP的最大距离为．7.如图，⊙O的半径为5，弦AB的长为8，将沿直线AB折叠，折叠后如右图，则⊙O到所作的圆的切线OC的长为（）A．22B．5C．3 D．118.如图，将半径为12的⊙O沿AB折叠，弧AB恰好经过与AB垂直的半径OC的中点D，则折痕AB长为（）A．42B．82C．6 D．629. 已知如图：⊙O 的半径为8cm ，把弧AmB 沿AB 折叠使弧AmB 经过圆心O ，再把弧AOB 沿CD 折叠，使弧COD 经过AB 的中点E ，则折线CD 的长为（ ）A ．8cmB ．38cmC ．72cmD ．47cm10. 如图，AB 是⊙O 的直径，且AB=4，C 是⊙O 上一点，将弧AC 沿直线AC 翻折，若翻折后的圆弧恰好经过点O ，π≈314，2≈1.41，3≈1.73，那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是（ ）A ．3.2B ．3.6C ．3.8D ．4.211. 如图，将弧BC 沿弦BC 折叠交直径AB 于点D ，若AD=6，DB=7，则BC 的长是（ ）A ．91B ．37C ．134D ．13012. 如图，在⊙O 中，点C 在优弧 AB ︵ 上，将弧︵BC 沿BC 折叠后刚好经过AB 的中点D ，连接AC ，CD ．则下列结论中错误的是（ ）A ．AC=CDB ．︵ AC +︵ BD =︵ BCC ．OD ⊥AB D ．CD 平分∠ACB13. 如图，点O 是半径为3的圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使弧AB 和弧BC 都经过圆心O ，则阴影部分的面积为（ ）A ．2πB ．3πC ．34πD ．5314. 如图，△ABC 内接于⊙O ，BC=22，∠BAC=45°，将劣弧︵ AB 和︵AC 分别沿直线AB 、AC 折叠后交于点M ，点S 、T 是弦AB 、AC 上的动点，则△MST 的周长的最小值为（ ）A ．22B ．4C ．24D ．815. 如图，在⊙O 中，点C 在优弧⌢ACB 上，将弧沿⌢BC 折叠后刚好经过AB 的中点D ，若⊙O 的半径为5，AB=4，则BC 的长是 ．16. 如图，AB 是半径为2的⊙O 的弦，将︵ AB 沿着弦AB 折叠，正好经过圆心O ，点C 是折叠后的︵AB 上一动点，连接并延长BC 交⊙O 于点D ，点E 是CD 的中点，连接AC ，AD ，EO ．则下列结论：①∠ACB=120°，②△ACD 是等边三角形，③EO 的最小值为1，其中正确的是 ．（请将正确答案的序号填在横线上）17. 如图，将︵ AB 沿着弦AB 翻折，C 为翻折后的弧上任意一点，延长AC 交圆于D ，连接BC ．（1）求证：BC=BD；（2）若AC=1，CD=4，︵AB=120°，求弦AB的长和圆的半径．18.如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将︵CD 沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC （1）求CD的长；（2）求证：PC是⊙O的切线；（3）点G为︵ADB 的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交︵BC 于点F（F与B、C不重合）．问GE•GF是否为定值？如果是，求出该定值；如果不是，请说明理由．19.如图1和图2，AB是⊙O的直径，AB=10，C是⊙O上的一点，将︵BC 沿弦BC翻折，交AB于点D．（1）若点D与圆心O重合，直接写出∠B的度数；（2）设CD交⊙O于点E，若CE平分∠ACB，①求证：△BDE是等腰三角形；②求△BDE的面积；（3）将图1中的︵BD 沿直径AB翻折，得到图2，若点F恰好是翻折后的︵BD 的中点，直接写出∠B的度数．20.如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC=3：5，AB=8．（1）求⊙O的半径；（2）点E为圆上一点，∠ECD=15°，将︵CE 沿弦CE翻折，交CD于点F，求图中阴影部分的面积．21.如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F两点，过点P（-1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于点B．抛物线y=ax2+bx+c 经过P、B、M三点．（1）求该抛物线的函数表达式；（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，并说明理由．2020年度初三数学专题复习中考 圆的折叠专题22. 如图①是半径为2的半圆，点C 是︵AB 的中点，现将半圆如图②方式翻折，使得点C 与圆心O 重合，则图中阴影部分的面积是（ ）A ．4π3B ．4π3 -3C ．23+π3D ．23-23π【分析】连接OC 交MN 于点P ，连接OM 、ON ，根据折叠的性质得到OP=12OM ，得到∠POM=60°，根据勾股定理求出MN ，结合图形计算即可．【解答】解：连接OC 交MN 于点P ，连接OM 、ON ，由题意知，OC ⊥MN ，且OP=PC=1，在Rt △MOP 中，∵OM=2，OP=1，∴cos ∠POM=OPOM=12，AC=22OP OM =3， ∴∠POM=60°，MN=2MP=23，∴∠AOB=2∠AOC=120°，则图中阴影部分的面积=S 半圆-2S 弓形MCN =12×π×22-2×（120π×22360 -12×23×1）=23-23π， 故选：D ．【点评】本题考查了轴对称的性质的运用、勾股定理的运用、三角函数值的运用、扇形的面积公式的运用、三角形的面积公式的运用，解答时运用轴对称的性质求解是关键．23. 如图，AB 是⊙O 的弦，AC 是⊙O 的直径，将︵AB 沿着AB 弦翻折，恰好经过圆心O ．若⊙O 的半径为6，则图中阴影部分的面积等于（ ）A ．6πB ．93C ．9πD ．63【分析】由题意△OBC 是等边三角形，弓形OnB 的面积=弓形BmC 的面积，根据S 阴=S △OBC 计算即可．【解答】解：如图，连接OB ，BC ．由题意△OBC 是等边三角形，弓形OnB 的面积=弓形BmC 的面积，∴S 阴=S △OBC=43×62=93， 故选：B ．【点评】本题考查扇形的面积的计算，垂径定理，翻折变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．24. 如图，将⊙O 的劣弧︵ AB 沿AB 翻折，D 为优弧︵ADB 上一点，连接AD ，交︵ AB 于点C ，连接BC 、BD ；若BC=5，则BD= ．【分析】根据圆周角定理、翻转变换的性质得到∠ADB=∠BCD ，根据等腰三角形的判定定理解答．【解答】解：由翻转变换的性质可知，∠ADB 所对的弧是劣弧︵AB ，∠CAB 所对的弧是劣弧︵ BC ，∠CBA 所对的弧是劣弧︵ AC ，∴∠ADB=∠CAB+∠CBA ，由三角形的外角的性质可知，∠BCD=∠CAB+∠CBA ，∴∠ADB=∠BCD，∴BD=BC=5，故答案为：5．【点评】本题考查的是翻转变换的性质、圆周角定理的应用，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．25.如图，AB是⊙O的直径，且AB=4，C是⊙O上一点，将弧AC沿直线AC翻折，若翻折后的圆弧恰好经过点O，π≈314，2≈1.41，3≈1.73，那么由线段AB、AC和弧BC所围成的曲边三角形的面积与下列四个数值最接近的是（）A．3.2 B．3.6 C．3.8 D．4.2【分析】作MN关于直线AN的对称线段M′N，交半圆于B'，连接AM、AM′，构造全等三角形，然后利用勾股定理、割线定理解答．【解答】解：如图，作MN关于直线AN的对称线段M′N，交半圆于B'，连接AM、AM′，可得M、A、M′三点共线，MA=M′A，MB=M′B′=4，M′N=MN=10．连接AB'，∵四边形AMNB'是圆内接四边形，∴∠M'AB'=∠M'NM，∵∠M'=∠M'，∴△M'AB'∽△M'NM，∴M′AM′N＝M′B′M′M∴M′A•M′M=M′B′•M′N，即M′A•2M′A=4×10=40．则M′A2=20，又∵M′A2=M′N2-AN2，∴20=100-AN2，∴AN=45．故选：B．【点评】此题将翻折变换、勾股定理、割线定理相结合，考查了同学们的综合应用能力，要善于观察图形特点，然后做出解答．26. 如图，在扇形AOB 中，∠AOB=90°，半径OA=6，将扇形AOB 沿过点B 的直线折叠，点O 恰好落在弧AB 上点D 处，折痕交OA 于点C ，则整个阴影部分的面积为（ ）A ．9π-9B ．9π-63C ．9π-18D ．9π-123【分析】首先连接OD ，由折叠的性质，可得CD=CO ，BD=BO ，∠DBC=∠OBC ，则可得△OBD 是等边三角形，继而求得OC 的长，即可求得△OBC 与△BCD 的面积，又在扇形OAB 中，∠AOB=90°，半径OA=6，即可求得扇形OAB 的面积，继而求得阴影部分面积．【解答】解：连接OD ．根据折叠的性质，CD=CO ，BD=BO ，∠DBC=∠OBC ，∴OB=OD=BD ，即△OBD是等边三角形，∴∠DBO=60°，∴∠CBO=12∠DBO=30°， ∵∠AOB=90°，∴OC=OB•tan ∠CBO=6×33=23， ∴S △BDC =S △OBC =12×OB×OC=12×6×23=63， S 扇形AOB =90360•π×62=9π， ∴整个阴影部分的面积为：S 扇形AOB -S △BDC -S △OBC =9π-63-63=9π-123．故选：D ．【点评】此题考查了折叠的性质、扇形面积公式以及直角三角形的性质．此题难度适中，注意数形结合思想的应用，注意辅助线的作法．27.如图，是一个圆心角为90°的扇形，AO=2cm，点P在半径AO上运动，点Q在弧AB上运动，沿PQ将它以上的部分向下翻折，使翻折后的弧恰好过点O，则OP的最大距离为．【分析】作O关于PQ的对称点O′，O′恰好落在⊙O上，于是得到OP=12Rcos∠POE，推出△OO′Q为等边三角形，根据等边三角形的性质得到OQ=O′Q=OO′=R，当cos∠POE最小时，∠POE最大，当∠QOB=0°时，∠POE=30°于是得到结论．【解答】解：作O关于PQ的对称点O′，O′恰好落在⊙O上，∴OP=12Rcos∠POE，∵△OO′Q为等边三角形，∴OQ=O′Q=OO′=R，∠POE+∠QOB=30°，当cos∠POE最小时，∠POE最大，当∠QOB=0°时，∠POE=30°，∴OP=1cos30°=332．故答案为：332．【点评】本题考查了翻折变换-折叠问题，等边三角形的判定和性质，正确的在才辅助线是解题的关键．28.如图，⊙O的半径为5，弦AB的长为8，将沿直线AB折叠，折叠后如右图，则⊙O到所作的圆的切线OC的长为（）A ．22B ．5C ．3D ．11【分析】根据题意先画出图形，可知翻转过后的弧AB 所在的圆和⊙O 全等，且两个圆的圆心相距为6，又已知圆的半径，故根据勾股定理即可求出答案．【解答】解：根据题意画出图形如下所示：BD=4，OB=5，点O′为翻转过后的弧AB 所在圆的圆心，则有O′D=OD=2245-=3．又O′C=5，O′O=6，∴OC=22C ′O O ′O -=2256-=11．故选：D ．【点评】本题考查了翻转变换、垂径定理及圆的切线的性质，难度不大，找出翻转过后的弧AB 所在圆的圆心是解题关键．29. 如图，将半径为12的⊙O 沿AB 折叠，弧AB 恰好经过与AB 垂直的半径OC 的中点D ，则折痕AB长为（ ）A ．42B ．82C ．6D ．62【分析】延长CO 交AB 于E 点，连接OB ，构造直角三角形，然后再根据勾股定理求出AB 的长【解答】解：延长CO 交AB 于E 点，连接OB ，∵CE ⊥AB ，∴E 为AB 的中点，∵OC=6，CD=2OD ，∴CD=4，OD=2，OB=6，∴DE=12（2OC-CD ）=12（6×2-4）=12×8=4， ∴OE=DE-OD=4-2=2，在Rt △OEB 中，∵OE 2+BE 2=OB 2，∴BE=22OE OB -=2246-42∴AB=2BE=82．故选：B ．【点评】本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．30. 已知如图：⊙O 的半径为8cm ，把弧AmB 沿AB 折叠使弧AmB 经过圆心O ，再把弧AOB 沿CD 折叠，使弧COD 经过AB 的中点E ，则折线CD 的长为（ ）A ．8cmB ．38cmC ．72cmD ．47cm【分析】连接OE 并延长交CD 于点F ，交C′D′于点F′，交弧AmB 于点G ，根据翻折的性质得出OF′=6，再由勾股定理得出．【解答】解：连接OE 并延长交CD 于点F ，交C′D′于点F′，交弧AmB 于点G ，∵OC′=8cm ，∴OF′=6cm ，∴C′F′=CF=2268-=27cm ，F∴CD=2CD=47cm ．故选：D ． 【点评】本题考查了垂径定理和勾股定理以及翻折的性质，是基础知识要熟练掌握． 31. 如图，AB 是⊙O 的直径，且AB=4，C 是⊙O 上一点，将弧AC 沿直线AC 翻折，若翻折后的圆弧恰好经过点O ，π≈314，2≈1.41，3≈1.73，那么由线段AB 、AC 和弧BC 所围成的曲边三角形的面积与下列四个数值最接近的是（ ）A ．3.2B ．3.6C ．3.8D ．4.2【分析】作OE ⊥AC 交⊙O 于F ，交AC 于E ，根据折叠的性质得到OE=12OF ，求出∠ACB 的度数即可解决问题．【解答】解：作OE ⊥AC 交⊙O 于F ，交AC 于E ．连接OB ，BC ．由折叠的性质可知，EF=OE=12OF ， ∴OE=12OA ，在Rt △AOE 中，OE=12OA ， ∴∠CAB=30°，∵AB 是直径，∴∠ACB=90°，∠BOC=2∠BAC=60°，∵AB=4，∴BC=12AB=2，AC=3BC=23， ∴线段AB 、AC 和弧BC 所围成的曲边三角形的面积为S=12•AC•B C+S 扇形OBC -S △OBC =12×23×2+60π•22360-43×22=3+23π≈3.8，故选：C ．【点评】本题考查的是翻折变换的性质、圆周角定理，折叠是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．32. 如图，将弧BC 沿弦BC 折叠交直径AB 于点D ，若AD=6，DB=7，则BC 的长是（ ）A ．91B ．37C ．134D ．130【分析】连接CA 、CD ，根据翻折的性质可得弧CD 所对的圆周角是∠CBD ，再根据AC 弧所得的圆周角也是∠CBA ，然后求出AC=CD ，过点C 作CE ⊥AB 于E ，根据等腰三角形三线合一的性质可得AE=ED=12AD ，根据直径所对的圆周角是直角可得∠ACB=90°，然后求出△ACE 和△CBE 相似，根据相似三角形对应边成比例求出CE 2，再求出BE ，然后利用勾股定理列式计算即可求出BC ．【解答】解：如图，连接CA 、CD ， 根据折叠的性质，弧CD 所对的圆周角是∠CBD ， ∵弧AC 所对的圆周角是∠CBA ，∠CBA=∠CBD ，∴AC=CD （相等的圆周角所对的弦相等），过点C 作CE ⊥AB 于E ， 则AE=ED=12AD=12×6=3， ∴BE=BD+DE=7+3=10， ∵AB 是直径，∴∠ACB=90°， ∵CE ⊥AB ，∴∠ACB=∠AEC=90°，∴∠A+∠ACE=∠ACE+∠BCE=90°，∴∠A=∠BCE ，∴△ACE ∽△CBE ，∴AE CE = CE BE， 即CE 2=AE•BE=3×10=30， 在Rt △BCE 中，BC=22CE BE + =30102+= 130，故选：D ．【点评】本题考查了翻折的性质，相似三角形的判定与性质，圆的性质，等腰三角形的判定与性质，作辅助线并求出AC=CD 是解题的关键．33. 如图，在⊙O 中，点C 在优弧 AB ︵ 上，将弧︵BC 沿BC 折叠后刚好经过AB 的中点D ，连接AC ，CD ．则下列结论中错误的是（ ）A ．AC=CDB ．︵ AC +︵ BD =︵ BCC ．OD ⊥AB D ．CD 平分∠ACB【分析】A 、作辅助线，构建折叠的性质可得AD=CD ；B 、相等两弧相加可作判断；C 、根据垂径定理可作判断；D 、延长OD 交⊙O 于E ，连接CE ，根据垂径定理可作判断．【解答】解：A 、过D 作DD'⊥BC ，交⊙O 于D'，连接CD'、BD'，由折叠得：CD=CD'，∠ABC=∠CBD'，∴AC=CD'=CD ，故①正确；B 、∵AC=CD'，∴︵ AC ＝︵ CD′ ，由折叠得：︵ BD ＝︵ BD ′，∴︵ AC+︵ BD=︵ BC ，故②正确；C 、∵D 为AB 的中点，∴OD ⊥AB ，故③正确；D 、延长OD 交⊙O 于E ，连接CE ，∵OD ⊥AB ，∴∠ACE=∠BCE ，∴CD 不平分∠ACB ，故④错误；故选：D ．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了圆周角定理和垂径定理．34. 如图，点O 是半径为3的圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使弧AB 和弧BC 都经过圆心O ，则阴影部分的面积为（ ）A ．2πB ．3πC ．34πD ．53【分析】作OD ⊥AB 于点D ，连接AO ，BO ，CO ，求出∠OAD=30°，得到∠AOB=2∠AOD=120°，进而求得∠AOC=120°，再利用阴影部分的面积=S 扇形AOC 得出阴影部分的面积是⊙O 面积的13，即可得出答案．【解答】解：作OD ⊥AB 于点D ，连接AO ，BO ，CO ，如图所示：∵OD=12AO ∴∠OAD=30°， ∴∠AOB=2∠AOD=120°，同理∠BOC=120°，∴∠AOC=120°，∴阴影部分的面积=S 扇形BOC =13×⊙O 面积=13×π×32=3π，故选：B ． 【点评】本题主要考查了翻折变换的性质、扇形面积以及圆的面积公式等知识；解题的关键是确定∠AOC=120°．35. 如图，△ABC 内接于⊙O ，BC=22，∠BAC=45°，将劣弧︵ AB 和︵AC 分别沿直线AB 、AC 折叠后交于点M ，点S 、T 是弦AB 、AC 上的动点，则△MST 的周长的最小值为（ ）A ．22B ．4C ．24D ．8【分析】作点M 关于AB 的对称点M ′，关于AC 的对称点M ″，根据折叠的性质得到点M ′，M ″在圆周上，连接M ′M ″，交AB 于S ，交AC 于T ，则△MST 的周长最小，连接AM ′，AM ″，OB ，OC ，根据圆周角定理得到M ′M ″是⊙O 的直径，即可得到结论．【解答】解：作点M 关于AB 的对称点M′，关于AC 的对称点M″，∵将劣弧AB 和AC 分别沿直线AB 、AC 折叠后交于点M ，∴点M′，M″在圆周上，连接M′M″，交AB 于S ，交AC 于T ，则△MST 的周长最小，连接AM′，AM″，OB ，OC ，则∠M′AM″=2∠BAC ，∵∠BAC=45°，∴∠M′AM″=∠BOC=90°，∵BC=22，∴OB=2，∴M′M″=2OB=4，∴△MST 的周长的最小值为4，故选：B ．【点评】本题考查了三角形的外接圆与外心，轴对称-最短路线问题，翻折变换（折叠问题），圆周角定理，勾股定理，正确的作出辅助线是解题的关键．36. 如图，在⊙O 中，点C 在优弧⌢ACB 上，将弧沿⌢BC 折叠后刚好经过AB 的中点D ，若⊙O 的半径为5，AB=4，则BC 的长是 ．【分析】连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图，利用垂径定理得到OD ⊥AB ，则AD=BD=12AB=2，于是根据勾股定理可计算出OD=1，再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆，则根据圆周角定理得到︵ AC=︵CD ，所以AC=DC ，利用等腰三角形的性质得AE=DE=1，接着证明四边形ODEF 为正方形得到OF=EF=1，然后计算出CF 后得到CE=BE=3，于是得到BC=32．【解答】解：连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图，∵D 为AB 的中点，∴OD ⊥AB ，∴AD=BD=12AB=2， 在Rt △OBD 中，OD=22BD OB -=222)5(-=1，∵将弧︵ BC 沿BC 折叠后刚好经过AB 的中点D ．∴︵ AC 和︵ CD 所在的圆为等圆，∴︵ AC=︵CD ，∴AC=DC ，∴AE=DE=1，易得四边形ODEF 为正方形，∴OF=EF=1，在Rt △OCF 中，CF=22OF CO -=221)5(-=2，∴CE=CF+EF=2+1=3，而BE=BD+DE=2+1=3，∴BC=32．故答案为32．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了圆周角定理和垂径定理．37. 如图，AB 是半径为2的⊙O 的弦，将︵ AB 沿着弦AB 折叠，正好经过圆心O ，点C 是折叠后的︵ AB 上一动点，连接并延长BC 交⊙O 于点D ，点E 是CD 的中点，连接AC ，AD ，EO ．则下列结论：①∠ACB=120°，②△ACD 是等边三角形，③EO 的最小值为1，其中正确的是 ．（请将正确答案的序号填在横线上）【分析】根据折叠的性质可知，结合垂径定理、三角形的性质、同圆或等圆中圆周角与圆心的性质等可以判断①②是否正确，EO 的最小值问题是个难点，这是一个动点问题，只要把握住E 在什么轨迹上运动，便可解决问题．【解答】解：如图1，连接OA 和OB ，作OF ⊥AB ．由题知：︵AB 沿着弦AB 折叠，正好经过圆心O ∴OF=OA=12OB∴∠AOF=∠BOF=60° ∴∠AOB=120°∴∠ACB=120°（同弧所对圆周角相等）∠D=12∠AOB=60°（同弧所对的圆周角是圆心角的一半）∴∠ACD=180°-∠ACB=60°∴△ACD 是等边三角形（有两个角是60°的三角形是等边三角形） 故，①②正确下面研究问题EO 的最小值是否是1 如图2，连接AE 和EF∵△ACD 是等边三角形，E 是CD 中点 ∴AE ⊥BD （三线合一） 又∵OF ⊥AB∴F 是AB 中点即，EF 是△ABE 斜边中线∴AF=EF=BF 即，E 点在以AB 为直径的圆上运动． 所以，如图3，当E 、O 、F 在同一直线时，OE 长度最小 此时，AE=EF ，AE ⊥EF∵⊙O的半径是2，即OA=2，OF=1∴AF=3（勾股定理）∴OE=EF-OF=AF-OF=3-1所以，③不正确综上所述：①②正确，③不正确．故答案为①②．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．38.如图，将︵AB沿着弦AB翻折，C为翻折后的弧上任意一点，延长AC交圆于D，连接BC．（1）求证：BC=BD；（2）若AC=1，CD=4，︵AB=120°，求弦AB的长和圆的半径．【分析】（1）作点C关于AB的对称点C′，连接AC′，BC′．利用翻折不变性，以及圆周角定理即可解决问题；（2）连接OA，OB，作OM⊥AB于M，AH⊥BC交BC的延长线于H．解直角三角形求出AB，OA即可；【解答】（1）证明：作点C关于AB的对称点C′，连接AC′，BC′．由翻折不变性可知：BC=BC′，∠CAB=∠BAC′，∴︵BD=︵BC′，∴BD=BC′，∴BC=BD．（2）解：连接OA，OB，作OM⊥AB于M，AH⊥BC交BC的延长线于H．∵︵AB=120°，∴∠D=12×120°=60°，∴∠AOB=∠ACB=2∠D=120°， ∵BC=BD ，∴△BCD 是等边三角形， ∴BC=DC=4，在Rt △ACH 中， ∵∠H=90°，∠ACH=60°，AC=1，∴CH=12，AH=23，∴AB=22BH AH +=22)29()23(+=21， ∵OM ⊥AB ， ∴AM=BM=221，在Rt △AOM 中， ∵∠OAM=30°，∠AMO=90°， ∴OA=AMcos30°=7【点评】本题考查圆心角、弧、弦之间的关系，垂径定理，勾股定理，翻折变换，等边三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．39. 如图，已知⊙O 的半径为2，AB 为直径，CD 为弦．AB 与CD 交于点M ，将︵CD 沿CD 翻折后，点A与圆心O 重合，延长OA 至P ，使AP=OA ，连接PC （1）求CD 的长；（2）求证：PC 是⊙O 的切线；（3）点G 为︵ADB 的中点，在PC 延长线上有一动点Q ，连接QG 交AB 于点E ．交︵BC 于点F （F 与B 、C 不重合）．问GE•GF 是否为定值？如果是，求出该定值；如果不是，请说明理由．【分析】（1）连接OC ，根据翻折的性质求出OM ，CD ⊥OA ，再利用勾股定理列式求解即可；（2）利用勾股定理列式求出PC ，然后利用勾股定理逆定理求出∠PCO=90°，再根据圆的切线的定义证明即可；（3）连接GA 、AF 、GB ，根据等弧所对的圆周角相等可得∠BAG=∠AFG ，然后根据两组角对应相等两三角相似求出△AGE 和△FGA 相似，根据相似三角形对应边成比例可得AG GE =FGAG ，从而得到GE•GF=AG 2，再根据等腰直角三角形的性质求解即可．【解答】（1）解：如图，连接OC ，∵︵CD 沿CD 翻折后，点A 与圆心O 重合， ∴OM=12OA=12×2=1，CD ⊥OA ，∵OC=2，∴CD=2CM=222OM OC -=22212-=23；（2）证明：∵PA=OA=2，AM=OM=1，CM=12CD=3，∠CMP=∠OMC=90°，∴PC=22PM MC +=223)3(+=23，∵OC=2，PO=2+2=4，∴PC 2+OC 2=（23）2+22=16=PO 2， ∴∠PCO=90°， ∴PC 是⊙O 的切线；（3）解：GE•GF是定值，证明如下，连接GO并延长，交⊙O于点H，连接HF∵点G为︵ADB 的中点∴∠GOE=90°，∵∠HFG=90°，且∠OGE=∠FGH ∴△OGE∽△FGH∴OGGF=GEGH∴GE•GF=OG•GH=2×4=8．【点评】本题是圆的综合题型，主要利用了翻折变换的性质，垂径定理，勾股定理，勾股定理逆定理，圆的切线的定义，相似三角形的判定与性质，难点在于（3）作辅助线构造出相似三角形．40.如图1和图2，AB是⊙O的直径，AB=10，C是⊙O上的一点，将︵BC 沿弦BC翻折，交AB于点D．（1）若点D与圆心O重合，直接写出∠B的度数；（2）设CD交⊙O于点E，若CE平分∠ACB，①求证：△BDE是等腰三角形；②求△BDE的面积；（3）将图1中的︵BD 沿直径AB翻折，得到图2，若点F恰好是翻折后的︵BD 的中点，直接写出∠B的度数．【分析】（1）如图所示：将⊙O沿BC翻折得到⊙O′，则⊙O与⊙O′为等圆，然后证明︵AC =︵CD =︵BD ，则可得到︵AC 的弧度，从而可求得∠B的度数；（2）①将⊙O沿BC翻折得到⊙O′，则⊙O与⊙O′为等圆，在⊙O′上取点E′，连接CE′，BE′．由等弧所对的圆周角相等可得到∠CEB=∠E′，依据圆内接四边形的性质可得到E′=∠BDE，故此可证明∠CEB=∠BDE ；②连接OE ．先证明∠BOE 为直角，依据勾股定理可求得BE 的长，从而得到BD 的长，最后依据△DBE 的面积=12BD•OE 求解即可；（3）将⊙O 沿BC 翻折得到⊙O′，将⊙O′沿BD 翻折得到⊙O″，则⊙O 、⊙O′、⊙O″为等圆．依据在同圆或等圆中相等的圆周角所对的弧相等可证明︵AC =︵CD =︵ DF=︵FB ，从而可得到弧AC 的度数，由弧AC 的度数可求得∠B 的度数．【解答】解：（1）如图所示：将⊙O 沿BC 翻折得到⊙O′，则⊙O 与⊙O′为等圆．∵︵AC 与︵CD 所对的角均为∠CBA ，⊙O 与⊙O′为等圆， ∴︵AC =︵ CD ． 又∵CD=BC ， ∴︵CD =︵ BD ．又∵︵ CDB =︵CO′B ，∴︵ AC =13︵ ACB ，∴∠ADC=13×180°=60°．∴∠B=30°．（2）①将⊙O 沿BC 翻折得到⊙O′，则⊙O 与⊙O′为等圆，在⊙O′上取点E′，连接CE′，BE′．由翻折的性质可知：︵ CFB=︵ CDB ，∴∠CEB=∠E′．∵四边形CDBE′是圆内接四边形， ∴∠E′=∠BDE ． ∴∠CEB=∠BDE ． ∴BE=BD ．∴△BDE 为等腰三角形．②如图2所示：连接OE ．∵AB 是⊙O 的直径，∴∠ACB=90°．∵CE 是∠ACB 的角平分线， ∴∠BCE=45°． ∴∠BOE=90°．在Rt △OBE 中，BE=22OB OE =52． ∴BD=52．∴△DBE 的面积=12BD•OE=12×52×5=2225．（3）将⊙O 沿BC 翻折得到⊙O′，将⊙O′沿BD 翻折得到⊙O″，则⊙O 、⊙O′、⊙O″为等圆．∵⊙O 与⊙O′为等圆，劣弧AC 与劣弧CD 所对的角均为∠ABC ， ∴︵AC =︵CD ． 同理：︵DF =︵CD ．又∵F 是劣弧BD 的中点， ∴︵DF =︵ BF ． ∴︵AC =︵CD =︵ DF =︵FB ．∴弧AC 的度数=180°÷4=45°． ∴∠B=12×45°=22.5°．【点评】本题主要考查的是圆的综合应用，解答本题主要应用了翻折的性质、弧、弦、圆周角之间的关系、圆内接四边形的性质，等腰三角形的判定，找出图形中的等弧是解题的关键．41. 如图，CD 是⊙O 的直径，AB 是⊙O 的弦，AB ⊥CD ，垂足为G ，OG ：OC=3：5，AB=8．（1）求⊙O 的半径；（2）点E 为圆上一点，∠ECD=15°，将︵CE 沿弦CE 翻折，交CD 于点F ，求图中阴影部分的面积．【分析】（1）根据AB ⊥CD ，垂足为G ，OG ：OC=3：5，AB=8，可以求得⊙O 的半径；（2）要求阴影部分的面积只要做出合适的辅助线，然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题．【解答】解：（1）连接AO ，如右图1所示，∵CD 为⊙O 的直径，AB ⊥CD ，AB=8， ∴AG=12AB=4，∵OG ：OC=3：5，AB ⊥CD ，垂足为G ， ∴设⊙O 的半径为5k ，则OG=3k ， ∴（3k ）2+42=（5k ）2， 解得，k=1或k=-1（舍去）， ∴5k=5，即⊙O 的半径是5；（2）如图2所示，将阴影部分沿CE 翻折，点F 的对应点为M ，∵∠ECD=15°，由对称性可知，∠DCM=30°，S 阴影=S 弓形CBM ， 连接OM ，则∠MOD=60°， ∴∠MOC=120°，过点M 作MN ⊥CD 于点N ， ∴MN=MO•sin60°=5×23＝235， ∴S 阴影=S 扇形OMC -S △OMC =120×π×52360 −12×5×235=25π3−435， 即图中阴影部分的面积是：25π3−435． 【点评】本题考查垂径定理、扇形的面积、翻折变换，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．42.如图1，在平面直角坐标系中，已知点M的坐标是（3，0），半径为2的⊙M交x轴于E、F两点，过点P（-1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于点B．抛物线y=ax2+bx+c 经过P、B、M三点．（1）求该抛物线的函数表达式；（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，并说明理由．【分析】【解答】【点评】本题考查了二次函数解析式的确定、图形面积的求法、圆心角定理、切线的性质与判定、特殊三角形的判定和性质等知识点．。

精选全中考数学中的折叠问题文完整版（可编辑修改）近年来，在各地中考数学命题时，十分重视对图形语言、文字语音、符号语言的理解运用及相互之间的关系，相互之间的转化能力以及动手操作能力的考查。

这样，图形的折叠问题就成为一个亮点，有关翻折的考题日趋增加。

翻折问题的解决方法，抓住翻折后与翻折的图形是以折痕为轴的轴对称图形这一关键，并运用代数方程，一般均可求得。

下面我们以中考题为例，谈谈翻折问题的几例类型及解法，供大家参考。

一、以矩形为母体的翻折这种类型最多，以折痕的不同位置又可分下面几种：1、沿对角线翻折例1、(2000年山西省)已知：如图1，将矩形ABCD沿直线BD折叠，使点C 落在C’处，BC’交AD于E，AD=8，AB=4，求△BED的面积。

分析：因为BD是对称轴，∴∠CBD=∠C’BD，又AD∥BC，∴∠CBD=∠ADB，得：∠C’BD=∠ADB，∴ED=EB设ED=x，∴AD=8-x在Rt△ABE中，AB2+AE2=BE2，即42+(8-x)2=x2，∴x=5，∴ED=EB=5又BD=∴S△BED==10方法2：过E作EF⊥BD，垂足F，在得到BE=5，BD=4后，在Rt△BEF中，EF=，得S△BED=BD×EF=×4×=10方法3：∵Rt△BEF∽Rt△BDC’，∴EF：DC’=BF：BC’，得EF==(以下略)2、沿一直线翻折，使一顶点落在对边上例2、(2000年山东省)已知矩形ABCD的两边AB与BC的比为4：5，E是AB 上一点，沿CE将△EBC向上翻折，若B点恰好落在边AD上的F点，如图2，则tg∠DCF=______。

A、B、C、D、分析：因为CF=CB，∴CF：CD=5：4，得CD：DF=4：3，∴tg∠DCF==，应选(A)。

例3、(1998年台州市)如图3，矩形ABCD的长、宽分别为5和3，将顶点C 折过来，使它落在AB上的C’点(DE为折痕)，那么阴影部分的面积是______。

二轮复习：图形变换（一）—折叠图形变换历来是中考必考点之一。

考试大纲要求：会运用图形变换的相关知识进行简单的作图与计算，并能解决相关动态需求数学问题，并能进行图案设计。

图形变换一般包括，折叠、平移、旋转、对称、位似和图形的探究。

在图形变换的考题中，最多题型是折叠、旋转。

在解决折叠问题时，应注意折叠前后相对应的边相等、角相等。

下面着重从三个方面进行讲述：三角形折折叠、特殊平行四边形折叠和在平面直角坐标系内的图形折叠三大类进行。

（一）三角形的折叠：题型1、一般三角形的折叠：1、如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A＝α，∠CEA′＝β，∠BDA'＝γ，那么下列式子中正确的是A．γ＝2α+βB．γ＝α+2βC．γ＝α+βD．γ＝180°﹣α﹣β2、（2019•江西）如图，在△ABC中，点D是BC上的点，∠BAD＝∠ABC＝40°，将△ABD沿着AD翻折得到△AED，则∠CDE＝°．3、如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为___．题型2、等腰或等边三角形的折叠：4、如图，在△ABC 中，AB =AC ，BC =24，tanC =2，如果将△ABC 沿直线l 翻折后，点B 落在边AC 的中点E 处，直线l 与边BC 交于点D ，那么BD 的长为_____.5、如图，D 是等边△ABC 边AB 上的点，AD=2，DB=4．现将△ABC 折叠，使得点C 与点D 重合，折痕为EF ，且点E 、F 分别在边AC 和BC 上，则CF CE=_______．（利用相似三角形周长的比等于相似比△AED 相似△DBF）题型3、直角三角形的折叠：6、如图，在Rt △ABC 中，∠ACB=90°，BC=6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于．7、如图，在等腰直角三角形ABC中，∠C=90°，D为BC的中点，将△ABC折叠，使点A与点D重合，EF为折痕，则sin∠BED的值是（二）特殊平行四边形的折叠：题型1、矩形折叠：1、（求角）.如图，将矩形沿对角线折叠，点落在处，交于点，已知,则的度为A. B. C. D.2、（求三角函数值）如图，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，如果AB：AD=2：3，那么tan∠EFC值是．3、（求边长）如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE 折叠，使点B落在矩形内点F处，连接CF，则CF的长为4、（求折痕长）如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为5、（求边的比）如下图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为。

专题复习(五) 图形的折叠问题折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．类型1 三角形中的折叠问题(宜宾)如图，一次函数的图象与x 轴、y 轴分别相交于点A 、B ，将△AOB 沿直线AB 翻折，得△ACB.若C(32，32)，则该一次函数的解析式为________．【思路点拨】 利用翻折变换的性质结合锐角三角函数关系得出CO ，AO 的长，进而得出A 、B 两点的坐标，再利用待定系数法求出直线AB 的解析式．【解答】 连接OC ，过点C 作CD⊥x 轴于点D ，∵将△AOB 沿直线AB 翻折，得△ACB，C(32，32)，∴AO ＝AC ，OD ＝32，DC ＝32，BO ＝BC ，则tan ∠COD ＝CD OD ＝33，故∠COD＝30°，∠BOC ＝60°，∴△BOC 是等边三角形，且∠CAD＝60°. 则sin60°＝CD AC ，则AC ＝DCsin60°＝1，故A(1，0)，sin30°＝CD CO ＝32CO ＝12.则CO ＝3，故BO ＝3，B 点坐标为(0，3)，设直线AB 的解析式为y ＝kx ＋3，把A(1，0)代入解析式可得k ＝－ 3. ∴直线AB 的解析式为y ＝－3x ＋ 3.折叠(翻折)意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．1．(绵阳)如图，D 是等边△ABC 边AB 上的一点，且AD∶DB＝1∶2，现将△ABC 折叠，使点C 与D 重合，折痕为EF ，点E ，F 分别在AC 和BC 上，则CE∶CF＝（ ）A.34B.45C.56D.672．(德阳)如图，△ABC 中，∠A ＝60°，将△ABC 沿DE 翻折后，点A 落在BC 边上的点A′处．如果∠A′EC ＝70°，那么∠A′DE 的度数为________．3．(宜宾)如图，在Rt△ABC 中，∠B ＝90°，AB ＝3，BC ＝4，将△ABC 折叠，使点B 恰好落在边AC 上，与点B′重合，AE 为折痕，则EB′＝________．4．(滨州)如图，在平面直角坐标系中，将矩形AOCD 沿直线AE 折叠(点E 在边DC 上)，折叠后顶点D 恰好落在边OC 上的点F 处，若点D 的坐标为(10，8)，则点E 的坐标为________．类型2 四边形及其他图形中的折叠问题(南充)如图，在矩形纸片ABCD 中，将△AMP 和△BPQ 分别沿PM 和PQ 折叠(AP ＞AM)，点A 和点B 都与点E 重合；再将△CQD 沿DQ 折叠，点C 落在线段EQ 上点F 处．(1)判断△AMP，△BPQ ，△CQD 和△FDM 中有哪几对相似三角形？(不需说明理由)(2)如果AM ＝1，sin ∠DMF ＝35，求AB 的长．【思路点拨】 (1)由矩形的性质得∠A ＝∠B ＝∠C ＝90°，由折叠的性质和等角的余角相等，可得∠BPQ ＝∠AMP ＝∠DQC ，所以△AMP∽△BPQ∽△CQD ；(2)设AP ＝x ，由折叠关系可得：BP ＝AP ＝EP ＝x ，AB ＝DC ＝2P∽△BPQ 得：AM BP ＝APBQ，即BQ ＝P∽△CQD得：AP CD ＝AM CQ，即CQ ＝2，从而得出AD ＝BC ＝BQ ＋CQ ＝＝x 2＋2－1＝中∠DMF 的正弦值得出P∽△BPQ∽△CQD.理由如下：∵四边形ABCD 是矩形， ∴∠A ＝∠B＝∠C＝90°.根据折叠可知：∠APM＝∠EPM，∠EPQ ＝∠BPQ，∴∠APM ＋∠BPQ＝∠EPM＋∠EPQ＝90°. ∵∠APM ＋∠AMP＝90°，∴∠BPQ ＝∠AMP，∴△AMP ∽△BPQ ， 同理：△BPQ∽△CQD. ∴△AMP ∽△BPQ ∽△CQD. (2)设AP ＝x ，∴由折叠关系，BP ＝AP ＝EP ＝P∽△BPQ 得，AM BP ＝AP BQ ，即1x ＝xBQ ，得BQ ＝P∽△CQD 得，AP CD ＝AM CQ ，即x 2x ＝1CQ ，得CQ ＝2.∴AD ＝BC ＝BQ ＋CQ ＝D ＝AD －1＝中，sin ∠DMF ＝35，∴2x x 2＋1＝35.解得x 1＝3，x 2＝13(不合题意，舍去)． 即AB ＝6.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图)，从而构造相似三角形，利用相似三角形求边或者角的度数．1．(南充)如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B′处，若AE ＝2，DE ＝6，∠EFB ＝60°，则矩形ABCD 的面积是（ ）A ．12B ．24C ．12 3D ．16 32．(泸州)如图，在△ABC 中，AB ＝AC ，BC ＝24，tanC ＝2，如果将△ABC 沿直线l 翻折后，点B 落在边AC 的中点E 处，直线l 与边BC 交于点D ，那么BD 的长为（ ）A ．13B.152C.272D ．123．(德阳)将抛物线y＝－x2＋2x＋3在x轴上方的部分沿x轴翻折至x轴下方，图象的剩余部分不变，得到一个新的函数图象，那么直线y＝x＋b与此新图象的交点个数的情况有（）A．6种 B．5种 C．4种 D．3种4．(成都)如图，在□ABCD中，AB＝13，AD＝4，将ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为________．5．(内江)如图，在四边形ABCD中，AD∥BC，∠C＝90°，E为CD上一点，分别以EA，EB为折痕将两个角(∠D，∠C)向内折叠，点C，D恰好落在AB边的点F处．若AD＝2，BC＝3，则EF的长为________．6．(南充)如图，有一矩形纸片ABCD，AB＝8，AD＝17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD(包括端点)，设BA′＝x，则x的取值范围是________．7．(绵阳)如图1，在矩形ABCD中，AB＝4，AD＝3，将矩形沿直线AC折叠，使点B落在点E处，AE交CD 于点F，连接DE.(1)求证：△DEC≌△EDA；(2)求DF的值；(3)如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其顶点Q落在线段AE上，顶点M、N落在线段AC上，当线段PE的长为何值时，矩形PQMN的面积最大？并求出其最大值．参考答案类型1 三角形中的折叠问题1．B 提示：∵△ABC 为等边三角形，∴∠A ＝∠B＝∠C＝60°.又∵折叠△ABC，使得点C 恰好与边AB 上的点D 重合，折痕为EF ，∴∠EDF ＝∠C＝60°，CE ＝DE ，CF ＝DF.∴∠ADE＋∠FDB＝120°.∴∠AED ＝∠FDB.∴△AED∽△BDF.∴AE BD ＝AD BF ＝DEFD .设等边△ABC 边长为6个单位，CE ＝x ，CF ＝y ，AE ＝6－x ，BC ＝6－y ，∴6－x 4＝26－y ＝x y ，解得x ＝145，y ＝72.∴x ∶y ＝4∶5，故选择B.2.65°3.1.54.(10，3)类型2 四边形及其他图形中的折叠问题1．D 2.A3.B 提示：由题意，易知y ＝－x 2＋2x ＋3与x 轴的两个交点坐标分别为(3，0)和(－1，0)，顶点坐标为(1，4)，顶点关于x 轴对称点的坐标为(1，－4)．当直线y ＝x ＋b 过(－1，0)时，b ＝1，此时直线与新的函数图象只有一个交点；当b>1时，此时直线与新的函数图象无交点；当直线y ＝x ＋b 过(3，0)时，b ＝－3，此时直线与新的函数图象有三个交点；观察图象，易知：当－3<b<1时，此时直线与新的函数图象有三个交点；当直线y ＝x ＋b 过(1，－4)时，b ＝－5，此时直线与新的函数图象有三个交点；观察图象，易知：当－5≤b<－3时，此时直线与新的函数图象有四个交点；观察图象，易知：当b<－5时，此时直线与新的函数图象有二个交点；综上，直线y ＝x ＋b 与此新图象的交点的个数的情况有5种，故选 B.4.35. 6 提示：作AH⊥BC 于H.∵分别以AE ，BE 为折痕将两个角(∠D，∠C)向内折叠，点C ，D 恰好落在AB 边的点F 处，∴DE ＝EF ，CE ＝EF ，AF ＝AD ＝2，BF ＝CB ＝3.∴DC＝2EF ，AB ＝5.∵AD∥BC，∠C ＝90°， ∴四边形ADCH 为矩形，∴AH ＝DC ＝2EF ，HB ＝BC －CH ＝BC －AD ＝1.在Rt△ABH 中，AH ＝AB 2－BH 2＝26，∴EF ＝ 6. 6.2≤x≤87.(1)证明：由矩形的性质可知△ADC≌△CEA，∴AD ＝CE ，DC ＝EA ，∠ACD ＝∠CAE. 在△CED 与△ADE 中，⎩⎪⎨⎪⎧CE ＝AD ，DE ＝ED ，DC ＝EA ，∴△DEC ≌△EDA.(2)∵∠ACD＝∠CAE，∴AF ＝CF.设DF ＝x ，则AF ＝CF ＝4－x ，在Rt△ADF 中，AD 2＋DF 2＝AF 2，即32＋x 2＝(4－x)2，解得x ＝78，即DF ＝78.(3)由矩形PQMN 的性质得PQ∥CA， ∴PE CE ＝PQCA. 又∵CE＝3，AC ＝AB 2＋BC 2＝5.设PE ＝x(0＜x ＜3)，则x 3＝PQ 5，即PQ ＝53x.过E 作EG⊥AC 于G ，则PN∥EG，∴CP CE ＝PN EG. 又∵在Rt△AEC 中，EG ·AC ＝AE·CE，解得EG ＝125.∴3－x 3＝PN 125，即PN ＝45(3－N 的面积为S ，则S ＝PQ·PN＝－43x 2＋4x ＝－43(x －32)2＋3(0＜x ＜3)． ∴当x ＝32，即PE ＝32时，矩形PQMN 的面积最大，最大面积为3.。

初中数学中的折叠问题折叠问题（对称问题）是近几年来中考出现频率较高的一类题型，学生往往由于对折叠的实质理解不够透彻，导致对这类中档问题失分严重。

本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析，从中抽象出基本图形的基本规律，找到解决这类问题的常规方法。

其实对于折叠问题，我们要明白：1、折叠问题（翻折变换）实质上就是轴对称变换．2、折叠是一种对称变换，它属于轴对称．对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、对于折叠较为复杂的问题可以实际操作图形的折叠，在画图时，画出折叠前后的图形，这样便于找到图形之间的数量关系和位置关系．4、在矩形（纸片）折叠问题中，重合部分一般会是一个以折痕为底边的等腰三角形5、利用折叠所得到的直角和相等的边或角，设要求的线段长为x，然后根据轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解．一、矩形中的折叠1．将一张长方形纸片按如图的方式折叠，其中BC，BD为折痕，折叠后BG和BH在同一条直线上，∠CBD= 度．BC、BD是折痕，所以有∠ABC = ∠GBC，∠EBD = ∠HBD则∠CBD = 90°折叠前后的对应角相等2．如图所示，一张矩形纸片沿BC折叠，顶点A落在点A′处，再过点A′折叠使折痕DE∥BC，若AB=4，AC=3，则△ADE的面积是．沿BC折叠，顶点落在点A’处，根据对称的性质得到BC垂直平分AA’，即AF = 12AA’，又DE∥BC，得到△ABC ∽△ADE，再根据相似三角形的面积比等于相似比的平方即可求出三角形ADE的面积= 24对称轴垂直平分对应点的连线3．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，得折痕DG ，求AG 的长．由勾股定理可得BD = 5，由对称的性质得△ADG ≌ △A ’DG ，由A ’D = AD = 3，AG ’ = AG ，则A ’B = 5 – 3 = 2，在Rt △A ’BG 中根据勾股定理，列方程可以求出AG 的值根据对称的性质得到相等的对应边和对应角，再在直角三角形中根据勾股定理列方程求解即可4．把矩形纸片ABCD 沿BE 折叠，使得BA 边与BC 重合，然后再沿着BF 折叠，使得折痕BE 也与BC 边重合，展开后如图所示，则∠DFB 等于（ ）根据对称的性质得到∠ABE=∠CBE ，∠EBF=∠CBF ，据此即可求出∠FBC 的度数，又知道∠C=90°，根据三角形外角的定义即可求出∠DFB = 112.5°注意折叠前后角的对应关系5．如图，沿矩形ABCD 的对角线BD 折叠，点C 落在点E 的位置，已知BC=8cm ，AB=6cm ，求折叠后重合部分的面积． ∵点C 与点E 关于直线BD 对称，∴∠1 = ∠2 ∵AD ∥BC ，∴∠1 = ∠3∴∠2 = ∠3 ∴FB = FD设FD = x ，则FB = x ，FA = 8 – x在Rt △BAF 中，BA 2 + AF 2 = BF 2∴62 + (8 - x)2 = x 2 解得x = 254所以，阴影部分的面积S △FBD = 12 FD ×AB = 12 ×254 ×6 = 754cm2重合部分是以折痕为底边的等腰三角形6．将一张矩形纸条ABCD 按如图所示折叠，若折叠角∠FEC=64°，则∠1= 度；△EFG 的形状 三角形．∵四边形CDFE 与四边形C ’D ’FE 关于直线EF 对称∴∠2 = ∠3 = 64°∴∠4 = 180° - 2 × 64° = 52° ∵AD ∥BC321F E D C B A54132G D‘FC‘DAGA'CA B D∴∠1 = ∠4 = 52°∠2 = ∠5又∵∠2 = ∠3∴∠3 = ∠5∴GE = GF∴△EFG是等腰三角形对折前后图形的位置变化，但形状、大小不变，注意一般情况下要画出对折前后的图形，便于寻找对折前后图形之间的关系，注意以折痕为底边的等腰△GEF7．如图，将矩形纸片ABCD按如下的顺序进行折叠：对折，展平，得折痕EF（如图①）；延CG折叠，使点B落在EF上的点B′处，（如图②）；展平，得折痕GC（如图③）；沿GH折叠，使点C落在DH上的点C′处，（如图④）；沿GC′折叠（如图⑤）；展平，得折痕GC′，GH（如图⑥）．（1）求图②中∠BCB′的大小；（2）图⑥中的△GCC′是正三角形吗？请说明理由．（1）由对称的性质可知：B’C=BC，然后在Rt△B′FC中，求得cos∠B’CF= 12，利用特殊角的三角函数值的知识即可求得∠BCB’= 60°；（2）首先根据题意得：GC平分∠BCB’，即可求得∠GCC’= 60°，然后由对称的性质知：GH是线段CC’的对称轴，可得GC’= GC，即可得△GCC’是正三角形．理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为四边形BCFE与四边形B′C′FE关于直线EF对称，则①②③④这四个三角形的周长之和等于正方形ABCD的周长折叠前后对应边相等9．如图，将边长为4的正方形ABCD沿着折痕EF折叠，使点B落在边AD的中点G处，求四边形BCFE的面积设AE = x，则BE = GE = 4 - x，在Rt△AEG中，根据勾股定理有：AE2 + AG2 = GE2即：x2 + 4 = (4 - x)2解得x = 1.5，BE = EG = 4 – 1.5 = 2.5∵∠1 + ∠2 = 90°，∠2 + ∠3 = 90°∴∠1 = ∠3又∵∠A = ∠D = 90°∴△AEG ∽△DGP∴AEDG=EGGP，则1.52=2.5GP，解得GP =103PH = GH – GP = 4 - 103=23∵∠3 = ∠4，tan∠3 = tan∠1 = 3 4∴tan∠4 = 34，FHPH=34，FH =34×PH =34×23=12∴CF = FH = 1 2∴S梯形BCFE = 12(12+52)×4 = 6注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等10．如图，将一个边长为1的正方形纸片ABCD折叠，使点B落在边AD上不与A、D 重合．MN为折痕，折叠后B’C’与DN交于P．(1)连接BB’，那么BB’与MN的长度相等吗？为什么？(2)设BM=y，AB’=x，求y与x的函数关系式；(3)猜想当B点落在什么位置上时，折叠起来的梯形MNC’B’面积最小？并验证你的猜想．(1)BB’ = MN过点N作NH∥BC交AB于点H），证△ABB’≌△HNM(2)MB’ = MB = y，AM = 1 – y，AB’ = x在Rt△ABB’中BB’ = AB2 + AB'2= 1 + x2因为点B与点B’关于MN对称，所以BQ = B’Q，则BQ = 12 1 + x2由△BMQ∽△BB’A得BM×BA = BQ×BB’PC'NB CA DMB'QPHC'NB CA DMB'∴y = 12 1 + x2× 1 + x2=12(1 + x2)(3) 梯形MNC′B′的面积与梯形MNCB的面积相等由(1)可知，HM = AB’ = x，BH = BM – HM = y – x，则CN = y - x∴梯形MNCB的面积为：12(y – x + y) ×1 = 12(2y - x)= 12(2×12(1 + x2) – x)= 12(x -12)2 +38当x = 12时，即B点落在AD的中点时，梯形MNC’B’的面积有最小值，且最小值是38二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）∵∠α= ∠1，∠2 = ∠1∴∠α= ∠2∴2∠α+∠ABE=180°，即2∠α+30°=180°，解得∠α=75°．题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为作CD⊥AB，∵CE∥AB，∴∠1=∠2，根据翻折不变性，∠1=∠BCA，故∠2=∠BCA．∴AB=AC．又∵∠CAB=45°，∴在Rt△ADC中，AC = 2 2 ，AB = 2 2S△ＡＢＣ＝12AB×CD = 2 2a2130°BEFACD在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm 的长方形纸条成如图所示的形状，那么折痕PQ 的长是如图，作QH ⊥PA ，垂足为H ，则QH=2cm ， 由平行线的性质，得∠DPA=∠PAQ=60° 由折叠的性质，得∠DPA =∠PAQ ， ∴∠APQ=60°，又∵∠PAQ=∠APQ=60°， ∴△APQ 为等边三角形， 在Rt △PQH 中，sin ∠HPQ = HQPQ∴32 = 2PQ ，则PQ = 433注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ14．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（ ）图c 图b图aCDGFEC GDFEFBCAEBB∵AD ∥BC ，∴∠DEF=∠EFB=20°，在图b 中，GE = GF ，∠GFC=180°-2∠EFG=140°， 在图c 中∠CFE=∠GFC-∠EFG=120°，本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b ∠GFC=140°，图c 中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm 的长方形纸片ABCD ，沿对称轴EF 折叠成如图的形状，若折叠后，AB 与CD 间的距离为60cm ，则原纸片的宽AB 是（ ）设AB=xcm ．右图中，AF = CE = 35，EF = x根据轴对称图形的性质，得AE=CF=35-x （cm ）． 则有2（35-x ）+x=60， x=10．16．一根30cm 、宽3cm 的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P 的长度相等，则最初折叠时，求MA 的长将折叠这条展开如图，根据折叠的性质可知，两个梯形的上底等于纸条宽，即3cm ， 下底等于纸条宽的2倍，即6cm ， 两个三角形都为等腰直角三角形， 斜边为纸条宽的2倍，即6cm ，故超出点P 的长度为（30-15）÷2=7.5， AM=7.5+6=13.5GEFD AE FD B C A B C 60cm三、三角形中的折叠17．如图，把Rt △ABC （∠C=90°），使A ，B 两点重合，得到折痕ED ，再沿BE 折叠，C 点恰好与D 点重合，则CE ：AE=18．在△ABC 中，已知AB=2a ，∠A=30°，CD 是AB 边的中线，若将△ABC 沿CD 对折起来，折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14 ．（1）当中线CD 等于a 时，重叠部分的面积等于 ；（2）有如下结论（不在“CD 等于a ”的限制条件下）：①AC 边的长可以等于a ；②折叠前的△ABC 的面积可以等于32a 2；③折叠后，以A 、B 为端点的线段AB 与中线CD 平行且相等．其中， 结论正确（把你认为正确结论的代号都填上，若认为都不正确填“无”）． (1)∵CD = 12 AB∴∠ACB = 90°∵AB = 2a ，BC = a ，∴AC = 3a ∴S △ABC = 12 ×AC ×BC = 32a 2∴重叠部分的面积为：14×32a 2 = 38a 2(2)若AC = a ，如右图∵AD = a ，∴∠2 = 180°- 30°2 = 75°∠BDC = 180°- 75°= 105° ∴∠B'DC = 105°∴∠3 = 105°- 75°= 30° ∴∠1 = ∠3 ∴AC ∥B'D∴四边形AB'DC 是平行四边形∴重叠部分△CDE 的面积等于△ＡＢＣ的面积的14若折叠前△ABC 的面积等于32a 2 过点C 作CH ⊥AB 于点H ，则 12 ×AB ×CH = 32a 2 B'CDAB231EB'CDBACH =32a 又tan ∠1 =CH AH∴AH = 32a∴BH = 12a则tan ∠B =CHBH，得∠B = 60° ∴△CBD 是等边三角形 ∴∠2 = ∠4∴∠3 = ∠4，AD ∥CB 2又CB 2 = BC = BD = a ，∴CB 2 = AD ∴四边形ADCB 2是平行四边形则重叠部分△CDE 的面积是△ABC 面积的14(3)如右图，由对称的性质得，∠3 = ∠4，DA = DB 3 ∴∠1 = ∠2又∵∠3 + ∠4 = ∠1 +∠2 ∴∠4 = ∠1 ∴AB 3∥CD注意“角平分线+等腰三角形”的基本构图，折叠前后图形之间的对比，找出相等的对应角和对应边19．在△ABC 中，已知∠A=80°，∠C=30°，现把△CDE 沿DE 进行不同的折叠得△C ′DE ，对折叠后产生的夹角进行探究：（1）如图（1）把△CDE 沿DE 折叠在四边形ADEB 内，则求∠1+∠2的和； （2）如图（2）把△CDE 沿DE 折叠覆盖∠A ，则求∠1+∠2的和；（3）如图（3）把△CDE 沿DE 斜向上折叠，探求∠1、∠2、∠C 的关系．（1）根据折叠前后的图象全等可知，∠1=180°-2∠CDE ，∠2=180°-2∠CED ，再根据三角形内角和定理比可求出答案；（2）连接DG ，将∠ADG+∠AGD 作为一个整体，根据三角形内角和定理来求；3241EHB 2DABC3412B 3DA BC在第一次折叠中可得到∠EAD = ∠FAD在第二次折叠中可得到EF是AD的垂直平分线，则AD⊥EF∴∠AEF = ∠AFE∴△AEF是等腰三角形(1)由折叠可知∠AEB = ∠FEB，∠DEG = ∠BEG而∠BEG = 45°+ ∠α因为∠AEB + ∠BEG + ∠DEG = 180°所以 45°+ 2（45°+∠α）= 180°∠α = 22.5°由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

专题：折叠类题目中的动点问题折叠问题是中考的热门也是难点问题，平时与动点问题联合起来，这种问题的题设平时是将某个图形按必定的条件折叠，经过分析折叠前后图形的变换，借助轴对称性质、勾股定理、全等三角形性质、相似三角形性质、三角函数等知识进行解答。

此类问题立意新奇，充满着变化，要解决此类问题，除了能依据轴对称图形的性质作出要求的图形外，还要能综合利用相关数学模型及方法来解答。

种类一、求折叠中动点运动距离或线段长度的最值例 1.着手操作：在矩形纸片ABCD 中， AB=3，AD =5.如图例1-1所示，折叠纸片，使点 A 落在 BC 边上的 A’处，折痕为PQ ，当点在BC边上挪动时，折痕的端点、也随之挪动 . 若限制点、分别在、边上挪动，则点A’A ’P Q P Q AB AD在 BC 边上可挪动的最大距离为.图例 1-1【答案】 2.【分析】此题依据题目要求正确判断出点A'的最左端和最右端地点.当点Q与点D重合时，A '的地点处于最左端，当点P 与点 B 重合时，点 A'的地点处于最右端. 依据分析结果，作出图形，利用折叠性质分别求出两种状况下的BA'或 CA'的长度，两者之差即为所求.①当点 Q 与点 D 重合时， A '的地点处于最左端，如图例1-2 所示 .确立点 A'的地点方法：由于在折叠过程中， A 'Q= AQ ，因此以点 Q 为圆心，以 AQ 长为半径画弧，与BC 的交点即为点A '.再作出∠ A' QA 的角均分线，与AB 的交点即为点P.图例 1-2图例1-3由折叠性质可知，AD = A' D=5，在 Rt△A' CD 中，由勾股定理得，A'C A' D2CD252324②当点 P 与点 B 重合时，点A'的地点处于最右端，如图例1-3 所示 .确立点 A'的地点方法：由于在折叠过程中， A 'P= AP，因此以点P 为圆心，以AP 长为半径画弧，与BC 的交点即为点A '.再作出∠ A' PA 的角均分线，与AD 的交点即为点Q.由折叠性质可知，AB= A' B=3，因此四边形AB A' Q 为正方形.因此 A'C= BC－A'B=5－3=2.综上所述，点 A 挪动的最大距离为4－2=2.故答案为： 2.【点睛】此类问题难度较大，主要观察学生的分析能力，作图能力。