图论问题起源

Dijkstra（迪克斯特拉算法）
算法思想： 是从一个顶点到其余各顶点的最短路径算法，解决的是有向 图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为 中心向外层扩展，直到扩展到终点为止，算法求最短路径的 步骤如下： G={V,E} 1. 初始时令 S={V0},T=V-S={其余顶点}，T中顶点对应的距 离值 若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值 若不存在<V0,Vi>，d(V0,Vi)为∞ 2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W， 加入到S中 3. 对其余T中顶点的距离值进行修改：若加进W作中间顶点， 从V0到Vi的距离值缩短，则修改此距离值 重复上述步骤2、3，直到S中包含所有顶点，即W=Vi为止。
解决图论的算法
Dijkstra（迪克斯特拉算法）——标号法，求一个顶 点（单源点）到其余各顶点的最短路径算法
Floyd（弗洛伊德算法） ——插点法，求任意一对 顶点（多源点）之间最短路径的方法
Prim(普里姆)算法——构造最小生成树的算法(与 点有关) Kruskal（克鲁斯卡尔）--构造最小生成树的算 法算法（只与边有关）
C (cij ) nn {0,1 } (i, j ) E, 1, cij (i, j ) E. 0,
也就是说，如果两顶点之间有边相连，则邻接矩阵 中对应的元素为1；否则为0。
n n
v v A= v v
1
0 1 2 3 1 4 1
v v vv
1
2 3
（1 ）
d (v) 2E
v V
（2） 任意一个图的奇顶点的个数是偶数。
奇/偶顶点：顶点的度数为奇数的顶点为奇顶点，度数为偶 数的顶点为偶顶点。 加权图：对图的边赋相应的权值（数值），权值可以代表 距离，费用，代价等一些实际的意义。 权值为 7

6
问题三：Ramsey 问题
几个事实：
1. 任意的6个人中，总有3个人互相认识或有3个人互不认 识。
2. 任意的9个人中，总有3个人互相认识或有4个人互不认 识。
3. 问题：
4.
对任意的自然数k和t，是否存在一个最小的正整
数r(k,t)，使得每个至少有r(k,t)个人的团体，总有k个
人互相认识或有t个人互不认识。
1
返回 结束
七桥问题
C
A
D
B
转化
Euler 1736年
包含两个要素：对象（陆 地）及对象间的二元关系 （是否有桥连接）
C
A
D
B 图论中讨论的图
问题：是否能从四块陆地中 的任一块开始，通过每座桥 恰好一次再回到起点？
转化 是否能从任意一个顶点开 始，通过每条边恰好一次 再回到起点？
2
返回 结束
问题一：四色问题
9
部分资料从网络收集整 理而来，供大家参考，
感谢您的关注！
3
1872年，英国当时最著名的数学家凯利正式向伦敦数学 学会提出了这个问题，于是四色猜想成了世界数学界关注的 问题。
1878～1880年两年间，著名的律师兼数学家肯普和泰勒 两人分别提交了证明四色猜想的论文，宣布证明了四色定理， 大家都认为四色猜想从此也就解决了。
1890年，在牛津大学就读的年仅29岁的赫伍德以自己的 精确计算指出了肯普在证明上的漏洞。不久，泰勒的证明也 被人们否定了。后来，人们开始认识到，这个貌似容易的题 目，其实是一个可与费马猜想相媲美的难题。
4
进入20世纪以来，科学家们对四色猜想的证明
基本上是按照肯普的想法在进行。后来美国数学家
富兰克林于1939年证明了22国以下的地图都可以用

6.基本的网络优化问题
基本的网络优化问题有:最短路径问题、最小生成树问 题、最大流问题和最小费用问题.图论作为数学的一个 分支,已经有有效的算法来解决这些问题.当然这当中 的有些问题也可以建立线性规划的模型,但有时若变量 特别多,约束也特别多,用线性规划的方法求解效率不 高甚至不能在可忍受的时间内解决.而根据这些问题的 特点,采用网络分析的方法去求解可能会非常有效.例 如,在1978年,美国财政部的税务分析部门在对卡特尔 税制改革做评估的过程中,就有一个100,000个约束以 上,25,000,000个变量的问题,若用普通的线性规划求 解,预计要花7个月的时间.他们利用网络分析的方法, 将其分解成6个子问题,利用特殊的网络计算机程序,花 了大约7个小时问题就得到了解决.
其他一些常见关系:
LA={<x,y>∣x,y Ax≤y},此处AR. DB={<x,y>∣x,y Ax整除y},此处BZ*.
R= {<x,y>∣x,y Fxy},此处F是集合簇.
例1.8.设A={1,2,3,4},下面定义的R都是A上的关系,试用列举法 表示R.(1)R={<x,y>∣x是y的倍数};(2)R={<x,y>∣(x-y)2A}; 1.3.二元关系的表示方法:给出一个关系的方法有三种:集合表达 式,关系矩阵和关系图.例1.5就是用集合表达式. 1. 关 系 矩 阵 表 示 法 : 设给定集合 A={a1 ， a2 ， … ， an} ，集合 B={b1 ， b2 ， … ， bm} ， R 为从 A 到 B 的一个二元关系，构造一个 n×m矩阵。用集合A的元素标注矩阵的行，用集合B的元素标注 矩阵的列，对于a∈A和b∈B，若 <a ，b>∈R，则在行 a 和列 b 交 叉处标1，否则标0。这样得到的矩阵称为R的关系矩阵。

实际应用Байду номын сангаас景
数模竞赛中的图论问题通常与实际应用紧密相关 ，要求选手具备将实际问题转化为数学模型的能 力，以及利用图论知识进行实际问题的优化和解 决的能力。
图论问题的发展趋势与展望
算法优化与数据结构创新
随着大规模数据的不断涌现，图论问题的解决需 要更加高效的算法和更加优化的数据结构。未来 研究将更加注重算法的时间和空间复杂度优化， 以及新型数据结构的开发和应用。
详细描述
最小生成树问题在数模竞赛中常以实际应用问题形式出现，如网 络设计、电路设计等。解决该问题通常采用Kruskal算法或Prim算 法，通过逐步添加边来构建最小生成树。
最短路径问题
总结词
最短路径问题是图论中的另一个基本问题，旨在找到连接两个顶点的最短路径。
详细描述
最短路径问题在数模竞赛中常见于诸如最佳路线规划、物流配送等问题。常用 的算法有Dijkstra算法和Bellman-Ford算法，它们能够处理带权重的图，并找 到最短路径。
总结词
旅行商问题是一个经典的组合优化问题，目标是在给定一系列城市和每对城市之间的距离的情况下， 找到一条旅行路线使得每个城市恰好经过一次并回到原点，且总距离最短。
详细描述
旅行商问题是数模竞赛中经常出现的图论问题之一。解决这类问题的方法包括暴力枚举、回溯算法、 遗传算法等。该问题在物流配送、路线规划等领域有广泛应用。
历史
图论起源于18世纪欧拉的研究， 后来在19-20世纪得到快速发展 ，成为组合数学的一个重要组成 部分。
图论的基本概念
01
02
03
04
05
节点（顶点）：图中的点 边：连接两个节点的线段 连通性：图中的节点或边 路径：一系列连续的边和

莱昂哈德· 欧拉
如何才能在所有桥都恰巧只走一遍的前提下，回到原出发点?
桥所连接的地区 视为点 A A
C
C D B B
D
每一座桥视为一 条线
求从图中任一点出发，通过每条边一次，最后回到起点。
如果通奇数座桥的地方不止两个，那麽 满足要求的路线便不存在了。
如果只有两个地方通奇数座桥，则可从 其中一地出发可找到经过所有桥的路线。 若没有一个地方通奇数座桥，则从任何 一地出发，所求的isberg七桥问题(Euler问题)
柯尼斯堡七桥问题是图论中的著名问题。 这个问题是基于一个现实生活中的事例: 位于当时东普鲁士柯尼斯堡(今日俄罗斯加里 宁格勒)有一条河，河中心有两个小岛。小岛 与河的两岸有七条桥连接。如何才能在所有 桥都恰巧只走一遍的前提下，回到原出发点？
如何才能在所有桥都恰巧只走一遍的前提下，回到原出发点?
图论的起源
图论诞生和孕育于民间游戏。 创生：1736年 瑞士数学家欧拉——图论之父； 进展：1936年，匈牙利数学家寇尼希(Konig)发 表名著 《有限图和无限图理论》 1930年，波兰数学家库拉托父斯基 (Kulatowsky)证明了平面图可以画在平面上。 其后，图论在现代数学、计算机科学、工程 技术、优化管理等领域有大用而得以大力发 展
不少数学家都尝试去解析这个事例。而 这些解析，最后发展成为了数学中的图论。 莱昂哈德· 欧拉(Leonhard Euler)在1736 年圆满地解决了这一问题，证明这种方法并 不存在。他在圣彼得堡科学院发表了图论史 上第一篇重要文献。欧拉把实际的抽象问题 简化为平面上的点与线组合，每一座桥视为 一条线，桥所连接的地区视为点。这样若从 某点出发后最后再回到这点，则这一点的线 数必须是偶数。

2) 在无向图中，两个结点间(包括结点自身间)若有几条 边，则这几条边称为平行边；
3) 两结点vi，vj间相互平行的边的条数称为边(vi，vj) 或<vi，vj>的重数；
4) 含有平行边的图称为多重图； 5) 非多重图称为线图； 6) 无自回路的线图称为简单图。
2020年3月14日
计算机科学与技术学院
G3＝<V3,E3>＝<{1,2,3,4,5},{<1,2>,(1,4),<4,3>,
<3,5>,<4,5>}>
2020年3月14日
计算机科学与技术学院
第9页
几个基本概念
1) 在一个图中，关联结点vi和vj的边e，无论是有向的 还是无向的，均称边e与结点vI和vj相关联，而vi和 vj称为邻接点，否则称为不邻接的；
设V＝{v1, v2,…,vn}为图G的结点集，称 (deg(v1),deg(v2),…,deg(vn))为G的度数序列。
上图的度数序列为（3,3,5,1,0）。
2020年3月14日
计算机科学与技术学院
第18页
例
1) （3,3,2,3），（5,2,3,1,4）能成为图的度数序列吗？ 为什么？
2) 已知图G中有10条边，4个度数为3的结点，其余结点 的度数均小于等于2，问G中至少有多少个结点？为什 么？
对任意e∈E，都有e与<u,v>∈VV或者
(u,v)∈V&V相对应。
2020年3月14日
计算机科学与技术学院
第6页
图的分类(按边的方向)
1) 若边e与无序结点对(u，v)相对应，则称边e为无向边, 记为e＝(u，v)，这时称u，v是边e的两个端点；

为弧的始结点(Initial Vertex), 称为弧的终结点(Terminal Vertex), 统称为的端点
(Endpoint)。
5
无向图 & 有向图
• 【定义】在图G中,
①如果每条边都是有向边, 该图G称为有向图(Directed Graph)
②若每条边都是无向边, 该图G称为无向图(Undirected Graph)
(Edge)；
③称为关联函数, 是从E到V中的有序对或无序对的映射。
•
若边∈E与无序结点对(, )相联系, 则()=(, ), 这时边称为无向边, 有时简称为边；
•
若边∈E与有序结点对<, >相联系, 则()=<, >, 此时边称为有向边或弧(Arc), 称
③如果有些边是有向边, 另一些边是无向边, 图G称为混合图(Mixed Graph)
• 【定义】一个有向图中, 如果将每条有向边都改为无向边, 便得到该有向图的
底图(Underlying Undirected Graph)或基础图。
6
图的表示
• 一个图可以用几何图形表示，方法与二元关系的表示法相同。
多重图(Multiple Graph): 含有平行边的图；
•Leabharlann 线 图: 非多重图称为线图；•
简单图(Simple Graph): 不含平行边和自回环的图。
简单图是一
个非常重要
的概念
13
图的分类(续)
• 3.按G的边有序, 无序分为有向图, 无向图和混合图。
• 有向图(Directed Graph): 每条边都是有向边的图称为有向图
图的基本概念
图论的前世今生
• 1736年，欧拉（L.Eular）发表了第一篇关于图论的论文，解决了哥尼斯

定义7.2.1 无向图G是一个二元组<V，E>
V
: vertex set 顶点集
常写作V(G)，也称点(point)，结点(node)，接点(junction) 非空有限集 它的元素，习惯上用数字或小写英文字母a,b,c,u,v,w,x,y,z等(或加 足标)表示


E : edge set 边集合

例
G'=<V',E'>=<{a,b,c,d,e,f},{<a,b>,<b,a>,<b,c >,<c,c>,<a,d>,<e,e>}>
简单图

只讨论V是有限集的情况
若#V(G)＝p，#E(G)＝q，则称G是一个(p.q)图
p称为图G的阶 (1,0)图——孤立点或平凡图
(p,0)图(p≥2)——空图或零图
uG
d (u) 2q
个数有什么特点？ 2. 是否存在奇数阶奇数 度正则图？
证明 图中顶点度之和是指图中与各个顶点相关联的边数 之和，每条边(包括自环线和平行线)都将恰好被计数两次， 所以定理成立。
推论1 在图中,次数为奇数的结点必为偶数个 推论2 不存在奇数阶奇数度正则图
思考题
p阶简单图中顶点的最大度数是多少？ 证明：在任何p(p≥2)阶简单图中，至少有两 个顶点具有相同的度 设G是一个有19条边的图，且图中顶点的度 至少是3，那么G的阶最大是多少？ 说明下面的序列中哪些不可能是图的度序 列，哪些不可能是简单图的度序列

结点数相等 边数相等 度数相同的结点数相等 注意：不是充分条件
G
G’

第7章 图论图论是建立和处理离散型数学模型的重要数学工具，它已发展成具有广泛应用的一个数学分支。

图论的发展已有200多年的历史，它最早起源于一些数学游戏的难题研究。

1736年瑞士数学家欧拉（L.Eluer ）发表了关于解决哥尼斯堡七桥问题的一篇文章，标志着图论的正式诞生。

从19世纪中叶到20世纪中叶，图论问题大量出现，如汉密尔顿图问题、四色猜想等。

这些问题的出现进一步促进了图论的发展。

1847年，克希霍夫（Kirchhoff ）用图论分析电网络，这是图论最早应用于工程科学的一个例子。

随着计算机科学的迅猛发展，在现实生活中的许多问题，如交通网络问题，运输的优化问题，社会学中某类关系的研究，都可以用图论进行研究和处理。

图论在计算机领域中，诸如算法、语言、数据库、网络理论、数据结构、操作系统、人工智能等方面都有重大贡献。

本章主要介绍图论的基本概念、基本性质和一些典型应用。

7.1 图的基本概念7.1.1 图的基本概念1.图的定义图在现实生活中随处可见，如交通运输图、旅游图、流程图等。

此处我们只考虑由点和线所组成的图。

这种图能够描述现实世界的很多事情。

例如，用点表示球队，两队之间的连线代表二者之间进行比赛，这样，各支球队的比赛情况就可以用一个图清楚地表示出来。

到底什么是图呢？可用一句话概括：图是用点和线来刻划离散事物集合中的每对事物间以某种方式相联系的数学模型。

因为上述描述太过于抽象，难于理解，因此下面给出图作为代数结构的一个定义。

定义7.1.1 一个图（Graph ）是一个三元组〈)(G V ，)(G E ，G ϕ〉，其中)(G V 是一个非空的节点集合，)(G E 是有限的边集合，G ϕ是从边集合E 到点集合V 中的有序偶或无序偶的映射。

例7.1.1 图G =〈)(G V ，)(G E ，G ϕ〉，其中)(G V =},,,{d c b a ，)(G E =},,,,,{654321e e e e e e ，),()(1b a e G =ϕ，),()(2c a e G =ϕ，),()(3d b e G =ϕ，),()(4c b e G =ϕ，),()(5c d e G =ϕ，),()(6d a e G =ϕ。

v∈V2 v∈V
D 是偶数之和，必为偶数， 是偶数。 由于∑ deg(v)是偶数之和，必为偶数，而2 E 是偶数。故得
v∈V2
C
是
v∈V1
偶数， ∑ deg(v) 偶数，即
V1 是偶数。 是偶数。
9
图的基本概念
（8）入度，出度：在有向图中，射入一个结点的边数称为该结 ）入度，出度：在有向图中， 点的入度。由一个结点射出的边数称为该结点的出度。 点的入度。由一个结点射出的边数称为该结点的出度。 结点的出度与入度和是该结点的度数。 结点的出度与入度和是该结点的度数。 度数 定理：在任何有向图中，所有结点的入度和等于所有结点的 定理：在任何有向图中，所有结点的入度和等于所有结点的 结点的入度和 出度之和。 出度之和。 a d 证：∵每一条有向边必对应一个入度和出度，若一个结点具有 每一条有向边必对应一个入度和出度， 一个入度或出度，则必关联一条有向边，所以， 一个入度或出度，则必关联一条有向边，所以，有向图中各 b 结点入度和等于边数，各结点出度和也是等于边数，因此， 结点入度和等于边数，各结点出度和也是等于边数，因此， c 任何有向图中，入度之和等于出度和。 任何有向图中，入度之和等于出度和。
10
图的基本概念
是平行的。 （9）连接于同一对结点间的多条边称为是平行的。 ）连接于同一对结点间的多条边称为是平行的 定义：含有平行边的任何一个图称为多重图。 定义：含有平行边的任何一个图称为多重图。 多重图 不含有平行边和环的图称作简单图。 不含有平行边和环的图称作简单图。 简单图
a b a b a b
1 n(n − 1) 2
证明：在有 个结点的无向完全图中 任意两点间都有边连接， 个结点的无向完全图中， 证明：在有n个结点的无向完全图中，任意两点间都有边连接， n个结点中任意取两点的组合为： 个结点中任意取两点的组合为： 个结点中任意取两点的组合为

图论的产生和发展经历了二百多年的历史，大体上可分为三个阶段：第一阶段是从1736年到19世纪中叶。

当时的图论问题是盛行的迷宫问题和游戏问题。

最有代表性的工作是著名数学家L.Euler于1736年解决的哥尼斯堡七桥问题(Konigsberg Seven Bridges Problem)。

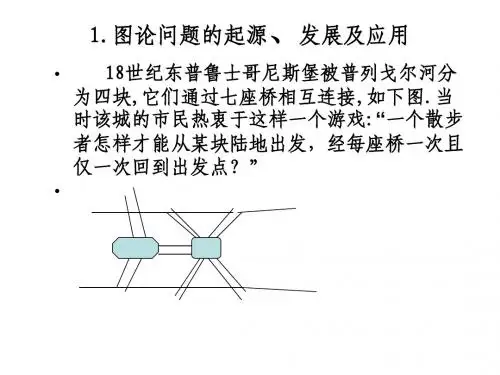
东普鲁士的哥尼斯堡城(现今是俄罗斯的加里宁格勒，在波罗的海南岸）位于普雷格尔(Pregel)河的两岸，河中有一个岛，于是城市被河的分支和岛分成了四个部分，各部分通过7座桥彼此相通。

如同德国其他城市的居民一样，该城的居民喜欢在星期日绕城散步。

于是产生了这样一个问题：从四部分陆地任一块出发，按什么样的路线能做到每座桥经过一次且仅一次返回出发点。

这就是有名的哥尼斯堡七桥问题。

哥尼斯堡七桥问题看起来不复杂，因此立刻吸引所有人的注意，但是实际上很难解决。

瑞士数学家(Leonhard Euler)在1736年发表的“哥尼斯堡七桥问题”的文章中解决了这个问题。

这篇论文被公认为是图论历史上的第一篇论文，Euler也因此被誉为图论之父。

欧拉把七桥问题抽象成数学问题---一笔画问题，并给出一笔画问题的判别准则，从而判定七桥问题不存在解。

Euler是这样解决这个问题的：将四块陆地表示成四个点，桥看成是对应结点之间的连线，则哥尼斯堡七桥问题就变成了：从A，B，C，D任一点出发，通过每边一次且仅一次返回原出发点的路线(回路)是否存在？Euler证明这样的回路是不存在的。

第二阶段是从19世纪中叶到1936年。

图论主要研究一些游戏问题：迷宫问题、博弈问题、棋盘上马的行走线路问题。

一些图论中的著名问题如四色问题(1852年)和Hamilton环游世界问题(1856年)也大量出现。

同时出现了以图为工具去解决其它领域中一些问题的成果。

1847年德国的克希霍夫(G.R.Kirchoff)将树的概念和理论应用于工程技术的电网络方程组的研究。

1857年英国的凯莱(A.Cayley)也独立地提出了树的概念，并应用于有机化合物的分子结构的研究中。

如果各条边都加上方向，则称为有向图，否则称为无向图。 如果有的边有方向，有的边无方向，则称为混合图。
如果任两顶点间最多有一条边，且每条边的两个端点皆 不重合的图，则称为简单图。
13 2018年6月26日
数学建模-图论
一、图的基本概念
图1
14
图2
2018年6月26日
数学建模-图论
一、图的基本概念
一个图会有许多外形不同的图解, 下面两个 图表示同一个图G = (V, E )的图解. 其中 V = {v1 , v2 , v3 , v4}, E = { v1v2 , v1v3 , v1v4 , v2v3 , v2v4 , v3v4}.
18
2018年6月26日
数学建模-图论
一、图的基本概念
几个基本定理：
1、对图G V，E ，有 d v 2 E .
vV
2、度为奇数的顶点有偶 数个。
3、设G V，E 是有向图， 则 d v d v E .
vV vV
19
2018年6月26日
支配集--仓库分区
7
• 将该图中所有顶点用不同颜色表示，最少需要几种颜色。
“点着色
• 将该图中所有边用不同颜色表示，最少需要几种颜色。
ห้องสมุดไป่ตู้
边着色 关键路径 最大流、最小流
8
问题2(哈密顿环球旅行问题): 十二面体的20个顶点代表世界上20个城市， 能否从某个城市出发在十二面体上依次经过每个 城市恰好一次最后回到出发点？
2、这3点至少2点不相邻，则 G包含3,0为子图。
数学建模-图论
一、图的基本概念(应用)
应用实例及解法分析
（设备更新问题）某企业每年年初,都要作出决定, 如果继续使用旧设备,要付维修费；若购买一台新设 备,要付购买费.试制定一个5年更新计划,使总支出 最少. 已知设备在每年年初的购买费分别为11,11, 12,12,13. 使用不同时间设备所需的维修费分别为 5,6,8,11,18.

若 H 是 G 的分图，则 H 首先必须是 G 的连通子图，并且 G 的任何其他子图（含 G），若它真包含 H，则它不是连通的。
若图 G 是连通图，则 G 只有一个分图。
27
用第二章“关系”的概念解释分图的概念如下：
设有图 G = (V, E)，其中 V 有 n 个结点。在 V 上定义一个二
元关系 ，当且仅当从 vi 到 vj 有路连接时，vi vj。 图 G 中结点之间的连接关系 是 V 上的一个等价关系。
要求的 V 到 V 的双射函数 h。
因为这两个图中边与结点的关联关系不相同。
例如，在 G 中度为 3 的 4 个结点构成一个长为 4 的环，而在
G 中度为 3 的 4 个结点没有构成长为 4 的环。
23
五、子图与分图
利用子集的概念可定义图 G 的子图。 定义8-7 设有图 G1 = (V1, E1) 和图 G2 = (V2, E2)， (1) 若 V2 V1，E2 E1，则称 G2 是 G1 的子图，或称 G1 包含 G2，记作 G2 G1； (2) 若 G2 G1 但 G2 G1（即 V2 V1 或 E2 E1），则称 G2 是 G1 的真子图，记作 G2 G1； (3) 若 V2 = V1，E2 E1，则称 G2 是 G1 的生成子图。 显然，任一图 G 都是自己的子图。
8
例2 (a), (b) 分别给出了例 1 中图 G 的图解方法5
(a)
矩阵表示法
v1 v2 v3 v4 v5 (b)
用矩阵的方法也可以表示一个图。在 8.2 节中我们再专门讨论。
9
二、完全图与补图
v1
(n, m) 图
具有 n 个结点和 m 条边的图称为 (n, m) 图。
例1 设 V = {v1, v2, v3, v4, v5}，

树支：组成树的支路。 树支数 nt n 1
连支：其余的支路。 连支 数 l b nt b n 1
第9页/共13页
X
2. 图论的一些基本概念
树支电压，连支电流
树支集合 2，5，6 连支集合 1，3，4
1
①
2② 3
③
5
4
6
④
2.9 基本回路：只含有一条连支的回路。
注
１，6，5，2 3，6，5 4，2，5
①
①
①
1
3
2
1 2
1
3
② 4③ 5 ④ ② 4 ③5 ④ ② 4③ 5 ④
图G
子图 G1
子 G2
图
第8页/共13页
X
2. 图论的一些基本概念
2.8 树(tree-T) ：树是连通图G的一个连通子图；包含
图G的所有的节点；不包含任何回路。
①
①
①
1
3
2
1
3
2
1
② 4③5 ④ ②
③
4
5
④②
③④
图G
T1
T2
2.1 拓扑(topology)：几何或联接性质。
2.2 图(Graph):电路（网络）的图由支路（线段）和节 点（点）组成，用G表示。每一支路代表一个电路元件 或一些电路元件的某种组合，每一支路都连接在图中 的两个节点之间。
标准支 ①
②①
②
路组合
i
u
第4页/共13页
X
2. 图论的一些基本概念
第5页/共13页
X
2. 图论的一些基本概念
2.4 路径(path)：从图G的某一节点出发，沿着一些支

一、图论的起源及发展（1）图论起源于著名的柯尼斯堡七桥问题。

在柯尼斯堡的普莱格尔河上有七座桥将河中的岛及岛与河岸联结起来问题是要从这四块陆地中任何一块开始，通过每一座桥正好一次，再回到起点。

然而无数次的尝试都没有成功。

欧拉在1736年解决了这个问题，他用抽像分析法将这个问题化为第一个图论问题：即把每一块陆地用一个点来代替，将每一座桥用联接相应的两个点的一条线来代替，从而相当于得到一个“图”。

欧拉证明了这个问题没有解，并且推广了这个问题，给出了对于一个给定的图可以某种方式走遍的判定法则。

这就是后来的欧拉路径和欧拉回路。

这项工作使欧拉成为图论〔及拓扑学〕的创始人。

（2）1859年，英国数学家汉密尔顿发明了一种游戏：用一个规则的实心十二面体，它的20个顶点标出世界著名的20个城市，要求游戏者找一条沿着各边通过每个顶点刚好一次的闭回路，即“绕行世界”。

用图论的语言来说，游戏的目的是在十二面体的图中找出一个生成圈。

这个生成圈后来被称为汉密尔顿回路。

这个问题后来就叫做汉密尔顿问题。

由于运筹学、计算机科学和编码理论中的很多问题都可以化为汉密尔顿问题，从而引起广泛的注意和研究。

（3）最著名问题在图论的历史中，还有一个最著名的问题－－四色猜想。

这个猜想说，在一个平面或球面上的任何地图能够只用四种颜色来着色，使得没有两个相邻的国家有相同的颜色。

每个国家必须由一个单连通域构成，而两个国家相邻是指它们有一段公共的边界，而不仅仅只有一个公共点，1976年数学家通过计算机运算得到证明而成为四色定理。

20世纪80-90年代曾邦哲的综合系统论（结构论）观将“四色猜想”命题转换等价为“互邻面最大的多面体是四面体”。

四色猜想有一段有趣的历史。

每个地图可以导出一个图，其中国家都是点，当相应的两个国家相邻时这两个点用一条线来连接。

所以四色猜想是图论中的一个问题。

它对图的着色理论、平面图理论、代数拓扑图论等分支的发展起到推动作用。

二、图论的基本概念图论〔Graph Theory〕是数学的一个分支。

图论任课教师：王磊基础教学部数学教研室图论发展史图论在现代科学技术中有着广泛的应用,如：网络设计、计算机科学、信息科学、密码学、DNA 的基因谱的确定和计数、工业生产和企业管理中的优化方法等都广泛的应用了图论及其算法。

首先我们通过图的发展过程来了解一下图论所研究的内容。

图论起源于1736年的一个游戏----哥尼斯城堡七桥问题。

七桥问题C包含两个要素：对象（陆地）及对象间的二元关系（是否有桥连接）C转化A DEuler1736年B A DB图论中讨论的图问题：是否能从四块陆地中的任一块开始，通过每座桥恰好一次再回到起点？转化是否能从任意一个顶点开始，通过每条边恰好一次再回到起点？问题一：四色问题四色问题是世界近代三大数学难题之一。

四色问题的内容是：任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。

它的提出来自英国。

1852年，毕业于伦敦大学的弗南西斯·格思里发现了一种有趣的现象：“看来，每幅地图都可以用四种颜色着色，使得有共同边界的国家都被着上不同的颜色。

”进入20世纪以来，科学家们对四色猜想的证明基本上是按照肯普的想法在进行。

后来美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。

1950年，有人从22国推进到35国。

1960年，有人又证明了39国以下的地图可以只用四种颜色着色；随后又推进到了50国。

1976年6月，美国伊利诺大学哈肯与阿佩尔在两台不同的电子计算机上，用了1200个小时，作了100亿判断，终于完成了四色定理的证明，轰动了世界。

然而，真正数学上的严格证明仍然没有得到！数学家仍为此努力，并由此产生了多个不同的图论分支。

问题二：Hamilton问题Hamilton问题源于1856年，英国数学家H amilton 设计了一个名为周游世界的游戏：他用一个正十二面体的二十个端点表示世界上的二十座大城市（见图），要求游戏者找一条沿着十二面体的棱通过每个端点恰好一次的行走路线。

浅析图论的起源及应用摘要：离散数学作为计算机科学与技术和相关专业的必修课程，在数据结构、算法设计与分析、操作系统、编译系统、人工智能、软件工程、网络与分布式计算得到了广泛应用。

并且是自动化、化学工程、生物学经济学等各个学科领域数学建模中的重要工具。

其中图论是其中重要的一部分，将对其起源到应用进行浅谈。

关键字：离散数学；计算机科学与技术；数据结构；图论一、图论的起源哥尼斯堡七桥是古老的数学游戏和趣题研究中最具代表性的一个。

普鲁士的古城哥尼斯堡（哲学家康德的故乡，今俄罗斯加里宁格勒）。

普瑞格尔河正好从市中心流过，河中心有两座小岛，岛和两岸之间建筑有七座古桥。

欧拉发现当地居民有一项消遣活动，就是试图每座桥恰好走过一遍并回到原出发点，但从来没人成功过。

首先能想到的证明方法是把走七座桥的走法都列出来，一个一个的试验，但七座桥的所有走法共用7！=5040种，逐一试验将是很大的工作量。

欧拉欧拉把两座岛和河两岸抽象成顶点，每一座桥抽象成连接顶点的一条边，假设每座桥都恰好走过一次（如图1）。

那么对于A、B、C、D四个顶点中的每一个顶点，需要从某条边进入，同时从另一条边离开。

这样问题就简洁明了多了。

欧拉想那么多人都失败了是不是这个问题本来就无解。

欧拉抓住了问题的本质，最终欧拉考虑了一笔画图像的结构特征：进入和离开顶点的次数是相同的，即每个顶点有多少条进入的边，就有多少条出去的边，也就是说，每个顶点相连的边是成对出现的，即每个顶点的相连边的数量必须是偶数。

七桥问题的几何图中，A、B、D三点分别与三条线相连，C点与5条线相连，连线都是奇数条，因此欧拉断定：一笔画出这个图形是不可能的。

也就是此题无解。

这不仅标志着图论的诞生，更是后来拓扑学的先声。

图1 哥尼斯堡七桥问题二、图论的发展从十九世纪中叶开始，图论进入了新的发展阶段。

这个时期，关于图论出现的大量的问题，其中最典型的是地图染色的四色问题和和“周游世界”发展来的哈密顿问题。