最大熵模型中的数学推导

证明开放系的最大熵原理开放系的最大熵原理可以通过最大化系统的熵来进行证明。

假设有一个开放系统，可以与外界交换物质和能量。

我们想要通过最大熵原理来推导系统的平衡状态。

首先，我们需要定义开放系统的熵。

对于一个开放系统，其熵可以表示为:S = -∑(pi * ln(pi))其中，pi表示系统处于第i个可能的状态的概率。

这个表示形式是基于信息论的熵的定义，它代表了系统的不确定性。

接下来，我们引入一些约束条件。

对于一个开放系统，通常有一些由外界施加的约束条件，如能量守恒、质量守恒等。

我们可以用一组约束条件的形式表示出来:∑(ci * pi) = Ci这里，ci是一个与约束条件相关的常数，Ci是一个特定的约束条件的值。

然后，我们引入拉格朗日乘子法来解决最大化熵的问题。

我们可以定义拉格朗日函数:L = -∑(pi * ln(pi)) + ∑(λi * (∑(ci * pi) - Ci))其中，λi是拉格朗日乘子，用于处理约束条件。

接下来，我们对L求解最大值。

我们将L对pi求偏导，并令其等于零:∂L/∂pi = -1 - ln(pi) - λi * ci = 0根据上面的偏导数等于零的方程，我们可以得到:pi = e^(-1 - λi * ci)然后，我们将所有的pi相加，得到:∑pi = ∑e^(-1 - λi * ci)= e^(-1) * ∑e^(-λi * ci)由于所有的pi都是概率，所以∑pi = 1。

将这个条件应用到上面的等式中，我们得到:1 = e^(-1) * ∑e^(-λi * ci)我们可以将上述等式改写为:e = ∑e^(-λi * ci)接下来，我们考虑约束条件∑(ci * pi) = Ci。

我们将其代入到L函数中，得到: -λi * Ci + ln(∑e^(-λi * ci)) = 0整理上面的等式，我们可以得到:λi = ln(∑e^(-λi * ci)) / Ci通过上面的方程，我们可以求出λi的值。

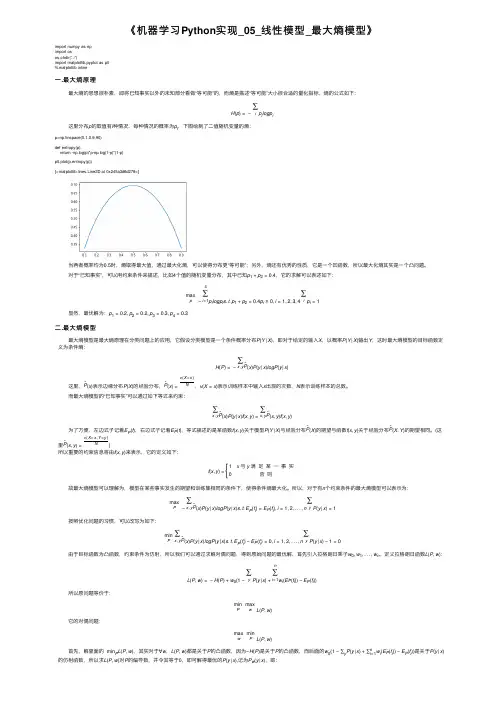
《机器学习Python 实现_05_线性模型_最⼤熵模型》import numpy as np import os os.chdir('../')import matplotlib.pyplot as plt %matplotlib inline⼀.最⼤熵原理最⼤熵的思想很朴素，即将已知事实以外的未知部分看做“等可能”的，⽽熵是描述“等可能”⼤⼩很合适的量化指标，熵的公式如下：H (p )=−∑i p i logp i这⾥分布p 的取值有i 种情况，每种情况的概率为p i ，下图绘制了⼆值随机变量的熵：p=np.linspace(0.1,0.9,90)def entropy(p):return -np.log(p)*p-np.log(1-p)*(1-p)plt.plot(p,entropy(p))[<matplotlib.lines.Line2D at 0x245a3d6d278>]当两者概率均为0.5时，熵取得最⼤值，通过最⼤化熵，可以使得分布更“等可能”；另外，熵还有优秀的性质，它是⼀个凹函数，所以最⼤化熵其实是⼀个凸问题。

对于“已知事实”，可以⽤约束条件来描述，⽐如4个值的随机变量分布，其中已知p 1+p 2=0.4，它的求解可以表述如下：maxp−4∑i =1p i logp i s .t .p 1+p 2=0.4p i ≥0,i =1,2,3,4∑i p i =1显然，最优解为：p 1=0.2,p 2=0.2,p 3=0.3,p 4=0.3⼆.最⼤熵模型最⼤熵模型是最⼤熵原理在分类问题上的应⽤，它假设分类模型是⼀个条件概率分布P (Y |X )，即对于给定的输⼊X ，以概率P (Y |X )输出Y ，这时最⼤熵模型的⽬标函数定义为条件熵：H (P )=−∑x ,y ˜P (x )P (y |x )logP (y |x )这⾥，˜P (x )表⽰边缘分布P (X )的经验分布，˜P (x )=v (X =x )N，v (X =x )表⽰训练样本中输⼊x 出现的次数，N 表⽰训练样本的总数。

高斯最大熵证明
高斯最大熵问题的证明可以通过以下步骤进行：
1. 定义问题：假设我们有一个连续随机变量X，其概率分布函数为p(x)。

我们希望找到一个概率分布函数p(x)，使得它满足
一些约束条件，并且熵H(p)最大。

2. 熵的定义：对于一个概率分布函数p(x)，其熵的表达式为
H(p) = -∫p(x)log(p(x))dx，其中积分是在整个定义域上进行的。

3. 约束条件：我们希望找到的概率分布函数p(x)需要满足一些约束条件，这些约束条件可以是概率为1，期望值等于一些给
定的值等等。

4. 构建拉格朗日函数：为了求解这个问题，我们可以构建拉格朗日函数L(p,λ) = -∫p(x)log(p(x))dx + ∑λi(gi(p) - bi)，其中λi是
拉格朗日乘子，gi(p)是约束条件。

5. 最大化熵：我们希望找到一个概率分布函数p(x)，使得熵
H(p) = -∫p(x)log(p(x))dx最大化。

因此，我们需要最大化拉格
朗日函数L(p,λ)。

6. 求解偏导数为零：为了找到最大化的概率分布函数p(x)，我们需要求解偏导数dL(p,λ)/dp(x) = 0和dL(p,λ)/dλi = 0。

这些方
程的解将给出最大化熵的概率分布函数p(x)和拉格朗日乘子λi。

7. 高斯概率分布分析：在实际应用中，我们通常假设随机变量
X服从高斯分布，即p(x) = (1/sqrt(2πσ^2)) * exp(-(x-
μ)^2/(2σ^2))，其中μ是均值，σ是标准差。

通过解上述方程，我们可以得到满足约束条件的高斯分布概率函数，使得熵最大化。

这就是高斯最大熵问题的一个证明过程。

最大信息熵计算公式
最大熵原理是一种选择随机变量统计特性最符合客观情况的淮则，也称为最大信息原理。

信息熵这个词是香农从热力学中借用过来的。

热力学中的热熵是表示分子状态混乱程度的物理量。

香农用信息熵的概念来描述信源的不确定度。

信息熵用于解决信息的量化问题，将原本模糊的信息概念进行计算得出精确的信息熵值，信息熵是描述消息中，不确定性的值。

信息熵的计算公式为H(x) = E[I(xi)] =
E[ log(2,1/P(xi)) ] = -∑P(xi)log(2,P(xi))
(i=1,2,..n)。

最大熵模型(MaxEnt: Maximum Entropy Model，又称MEM)， MaxEnt 是概率模型学习中一个淮则，其思想为：在学习概率模型时，所有可能的模型（即概率分布）中，熵最大的模型是最好的模型；
对一个随机事件的概率分布进行预测时，预测应当满足全部已知的约束，而对未知的情况不要做任何主观假设。

在这种情况下，概率分布最均匀，预测的风险最小，因此得到的概率分布的熵是最大。

若概率模型需要满足一些约束，则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。

最大熵模型算法今天我们来介绍一下最大熵模型系数求解的算法IIS算法。

有关于最大熵模型的原理可以看专栏里的这篇文章。

有关张乐博士的最大熵模型包的安装可以看这篇文章。

最大熵模型算法 1在满足特征约束的条件下，定义在条件概率分布P(Y|X)上的条件熵最大的模型就认为是最好的模型。

最大熵模型算法 23. IIS法求解系数wi先直接把算法粘贴出来，然后再用Python代码来解释。

这里也可以对照李航《统计学习方法》P90-91页算法6.1来看。

这个Python代码不知道是从哪儿下载到的了。

从算法的计算流程，我们明显看到，这就是一个迭代算法，首先给每个未知的系数wi赋一个初始值，然后计算对应每个系数wi的变化量delta_i，接着更新每个wi，迭代更新不断地进行下去，直到每个系数wi都不再变化为止。

下边我们一点点儿详细解释每个步骤。

获得特征函数输入的特征函数f1,f2,...,fn，也可以把它们理解为特征模板，用词性标注来说，假设有下边的特征模板x1=前词, x2=当前词, x3=后词 y=当前词的标记。

然后，用这个特征模板在训练语料上扫，显然就会出现很多个特征函数了。

比如下边的这句话，我/r 是/v 中国/ns 人/n用上边的模板扫过，就会出现下边的4个特征函数(start，我，是，r)(我，是，中国，v)(是，中国，人，ns)(中国，人，end，n)当然，在很大的训练语料上用特征模板扫过，一定会得到相同的特征函数，要去重只保留一种即可。

可以用Python代码得到特征函数def generate_events(self, line, train_flag=False):"""输入一个以空格为分隔符的已分词文本，返回生成的事件序列:param line: 以空格为分隔符的已分词文本:param train_flag: 真时为训练集生成事件序列；假时为测试集生成事件:return: 事件序列"""event_li = []# 分词word_li = line.split()# 为词语序列添加头元素和尾元素，便于后续抽取事件 if train_flag:word_li = [tuple(w.split(u'/')) for w inword_li if len(w.split(u'/')) == 2]else:word_li = [(w, u'x_pos') for w in word_li]word_li = [(u'pre1', u'pre1_pos')] + word_li + [(u'pro1', u'pro1_pos')]# 每个中心词抽取1个event，每个event由1个词性标记和多个特征项构成for i in range(1, len(word_li) - 1):# 特征函数a 中心词fea_1 = word_li[i][0]# 特征函数b 前一个词fea_2 = word_li[i - 1][0]# 特征函数d 下一个词fea_4 = word_li[i + 1][0]# 构建一个事件fields = [word_li[i][1], fea_1, fea_2, fea_4] # 将事件添加到事件序列event_li.append(fields)# 返回事件序列return event_li步进值 \delta_{i} 的求解显然delta_i由3个值构成，我们一点点儿说。

们对事物了解的不确定性的消除或减少。

他把不确定的程度称为信息熵。

假设每种可能的状态都有概率，我们⽤关于被占据状态的未知信息来量化不确定性，这个信息熵即为：
其中是以
扩展到连续情形。

假设连续变量的概率密度函数是，与离散随机变量的熵的定义类似，
上式就是我们定义的随机变量的微分熵。

当被解释为⼀个随机连续向量时，就是的联合概率密度函数。

4.2. ⼩概率事件发⽣时携带的信息量⽐⼤概率事件发⽣时携带的信息量多
证明略，可以简要说明⼀下，也挺直观的。

如果事件发⽣的概率为，在这种情况下，事件了，并且不传达任何
；反之，如果事件发⽣的概率很⼩，这就有更⼤的
对所有随机变量的概率密度函数，满⾜以下约束条件：
其中，是的⼀个函数。

约束
量的矩，它随函数的表达式不同⽽发⽣变化，它综合了随机变量的所有可⽤的先验知其中，是拉格朗⽇乘⼦。

对被积函数求的微分，并令其为。

高斯最大熵证明高斯最大熵（Gaussian Max-Entropy）是一种概率分布，其推导过程是基于一些假设和约束条件，如变量的方差和期望值等。

下面我们将通过数学推导来证明高斯最大熵的性质。

首先，我们假设有一个随机变量X，它是一个连续随机变量，并且服从均值为μ，方差为σ^2的正态分布。

那么，X的概率密度函数可以表示为：p(x|μ,σ^2) = (1/√(2πσ^2)) * exp(-(x-μ)^2/(2σ^2))现在，我们考虑一个与X相关的随机变量Y，它的概率分布是由X的概率分布和某个条件约束条件C所确定的。

假设条件约束条件C 是关于X的某个函数g(x)的约束，比如g(x)=x^2。

那么，Y的概率分布可以表示为：p(y|μ,σ^2,C) = ∫p(x|μ,σ^2) 1(y|x) dx其中1(y|x)是一个示性函数，如果满足条件约束C，则取值为1，否则取值为0。

接下来，我们考虑最大化Y的概率分布p(y|μ,σ^2,C)，即在满足约束条件的前提下，使得p(y|μ,σ^2,C)最大化。

为了解决这个问题，我们可以使用拉格朗日乘子法来求解。

首先，我们定义一个拉格朗日函数：L = log ∫p(x|μ,σ^2) 1(y|x) dx -λg(y)其中λ是一个拉格朗日乘子。

然后，我们可以通过求解下列方程来最大化L：L' = ∫p(x|μ,σ^2) 1(y|x) dx/∫p(x|μ,σ^2) dx -λg'(y) = 0由于这是一个积分方程，我们无法直接求解。

但是，我们可以使用一些近似方法来求解。

一种常用的方法是使用高斯分布来近似原始的分布p(x|μ,σ^2)，从而简化计算。

假设高斯分布的均值为μ，方差为σ^2，那么高斯分布的概率密度函数可以表示为：q(x|μ,σ^2) = (1/√(2πσ^2)) * exp(-(x-μ)^2/(2σ^2))于是，我们可以将原始的分布p(x|μ,σ^2)替换为q(x|μ,σ^2)，从而将复杂的积分方程转化为一个简单的微分方程。

最大熵模型的基本原理及其应用概述最大熵模型是一种常用的概率建模方法，广泛应用于自然语言处理、信息检索、图像识别等领域。

本文将介绍最大熵模型的基本原理，并探讨其在文本分类和情感分析中的应用。

一、最大熵模型的原理最大熵模型的核心思想是在给定一些已知条件的情况下，选择最平均、最不确定性的模型。

它通过最大化熵来选择概率模型，以保持模型的最大不确定性。

最大熵原理认为，当我们缺乏先验信息时，应该假设所有可能的结果都是等概率的，这样可以避免引入任何决策者的主观偏见。

二、最大熵模型的数学表示最大熵模型的数学表示可以通过最大熵优化问题来描述。

给定一些已知条件，最大熵模型要求找到满足这些条件的概率分布，使得该分布的熵最大。

通过求解最大熵优化问题，可以得到最大熵模型的参数估计。

三、最大熵模型在文本分类中的应用在文本分类任务中，最大熵模型可以用来训练一个分类器，将文本分类到事先定义好的类别中。

最大熵模型通过学习文本特征与类别之间的关系，自动挖掘特征的重要性，并据此进行分类。

最大熵模型的主要优点是能够处理大规模的特征空间和非线性问题，具有很强的表达能力。

四、最大熵模型在情感分析中的应用情感分析是研究文本情感倾向的任务，最大熵模型在情感分析中也具有广泛的应用。

最大熵模型可以学习文本特征与情感倾向之间的关系，从而实现情感分类的功能。

通过训练一个最大熵分类器，可以对文本进行情感分类，判断其是正面还是负面的情感。

最大熵模型在情感分析中的优势在于可以灵活地利用各种特征，并且能够处理多类别情感分类问题。

五、最大熵模型的应用挑战尽管最大熵模型在文本分类和情感分析中有广泛的应用，但也存在一些挑战。

首先，最大熵模型在处理大规模数据时要求计算量较大，需要考虑模型的训练和推断效率。

其次，最大熵模型对特征的表示非常敏感，需要合理选择和设计特征，以提高模型的性能。

此外，最大熵模型的参数估计问题也比较复杂，需要采用合适的算法和技巧来优化模型的参数。

一、熵物理学概念宏观上：热力学定律——体系的熵变等于可逆过程吸收或耗散的热量除以它的绝对温度（克劳修斯，1865）微观上：熵是大量微观粒子的位置和速度的分布概率的函数，是描述系统中大量微观粒子的无序性的宏观参数（波尔兹曼，1872）结论：熵是描述事物无序性的参数，熵越大则无序。

二、熵在自然界的变化规律——熵增原理一个孤立系统的熵，自发性地趋于极大，随着熵的增加，有序状态逐步变为混沌状态，不可能自发地产生新的有序结构。

当熵处于最小值, 即能量集中程度最高、有效能量处于最大值时, 那么整个系统也处于最有序的状态,相反为最无序状态。

熵增原理预示着自然界越变越无序三、信息熵（1）和熵的联系——熵是描述客观事物无序性的参数。

香农认为信息是人们对事物了解的不确定性的消除或减少，他把不确定的程度称为信息熵（香农，1948 ）。

随机事件的信息熵：设随机变量ξ，它有A1，A2，A3，A4，……，An共n种可能的结局，每个结局出现的概率分别为p1，p2，p3，p4，……，pn，则其不确定程度，即信息熵为（2）信息熵是数学方法和语言文字学的结合。

一个系统的熵就是它的无组织程度的度量。

熵越大，事件越不确定。

熵等于0，事件是确定的。

举例：抛硬币，p（head）=0.5，p（tail）=0.5H（p）=-0.5log2（0.5）+（-0.5l og2（0.5））=1说明：熵值最大，正反面的概率相等，事件最不确定。

四、最大熵理论在无外力作用下，事物总是朝着最混乱的方向发展。

事物是约束和自由的统一体。

事物总是在约束下争取最大的自由权，这其实也是自然界的根本原则。

在已知条件下，熵最大的事物，最可能接近它的真实状态。

五、基于最大熵的统计建模：建模理论以最大熵理论为基础的统计建模。

为什么可以基于最大熵建模？Jaynes证明：对随机事件的所有相容的预测中，熵最大的预测出现的概率占绝对优势。

Tribus证明，正态分布、伽马分布、指数分布等，都是最大熵原理的特殊情况。

最⼤熵1. 最⼤熵原理最⼤熵原理是概率模型学习的⼀个准则，其认为学习概率模型时，在所有可能的概率模型中，熵最⼤的模型是最好的模型。

通常⽤约束条件来确定概率模型的集合，然后在集合中选择熵最⼤的模型。

直观地，最⼤熵原理认为要选择的概率模型⾸先必须满⾜已有的事实，即约束条件。

在没有更多信息的情况下，那些不确定的部分都是等可能的。

最⼤熵原理通过熵的最⼤化来表⽰等可能性，因为当X服从均匀分布时熵最⼤。

2. 最⼤熵模型最⼤熵原理应⽤到分类得到最⼤熵模型。

给定训练集T=(x1,y1),(x2,y2),...,(x N,y N)，联合分布P(X,Y)以及边缘分布P(X)的经验分布都可以由训练数据得到：˜P(X=x,Y=y)=count(X=x,Y=y)N˜P(X=x)=count(X=x)N⽤特征函数f(x,y)描述输⼊x和输出y之间的某⼀个事实，特征函数是⼀个⼆值函数，当x与y满⾜某⼀事实时取1，否则取0。

例如，可以令特征x与标签y在训练集出现过时取1，否则取0。

特征函数f(x,y)关于经验分布˜P(X=x,Y=y)的期望值为：E˜P(f)=∑x,y˜P(x,y)f(x,y)特征函数f(x,y)关于模型P(Y|X)与经验分布˜P(x)的期望值为：E P(f)=∑x,y˜P(x)P(y|x)f(x,y)如果模型能够获取训练数据中的信息，那么就可以假设这两个期望值相等，即：∑x,y ˜P(x,y)f(x,y)=∑x,y˜P(x)P(y|x)f(x,y)将上式作为模型学习的约束条件，条件数量对应特征函数个数，设所有满⾜约束条件的模型集合为：C={P|∑x,y˜P(x,y)fi(x,y)=∑x,y˜P(x)P(y|x)fi(x,y),i=1,2,...,n}其中n为特征函数个数。

定义在条件概率分布P(Y|X)上的条件概率熵为：H(P)=−∑x,y˜P(x)P(y|x)ln P(y|x)模型集合C中条件熵H(P)最⼤的模型称为最⼤熵模型。

第五节最大熵模型最大熵模型（Entropy Model）也是随机概率模型之一。

典型的最大熵模型有Wilson模型和佐佐木(Sasaki)模型，以下分别讲述。

1．Wilson模型Wilson模型是由A.G.Wilson提出的方法，它以英国为中心，在区域科学方面的应用例较多，其模型如下式所示。

(4-5-1)式中，T：对象地区的生成交通量。

即，OD交通量的组合数由求E的最大得到。

例：发生小区Ｏ，吸引区AB，出行生成量为4。

能够发生的OD交通量状态如下。

OD交通量状态情况1 情况2 情况3 情况4情况5组合数E：,,,,发生概率：1/16, 4/16, 6/16, 4/16, 1/1616为可能发生的组合数。

从上述情况看,组合数为6的组合发生的概率最大,因此可以视为最容易发生。

Wilson模型的约束条件为：（4-5-2）（4-5-3）(4-5-4)式中，的交通费用；总交通费用。

最大熵模型一般用以下对数拉格朗日方法求解。

(4-5-5)式中，，，为拉格朗日系数。

应用Stirling公式近似，得，(4-5-6) 代入（4-5-5）式，并对求导数，得，令，得，(4-5-7)∵∴(4-5-8)同样，(4-5-9)这里，令，则（4-5-7）为：(4-5-10）可以看出，式(4-5-10）为重力模型。

Wilson模型的特点：(1)能表现出行者的微观行动；(2)总交通费用是出行行为选择的结果，对其进行约束脱离现实；(3)各微观状态的概率相等，即各目的地的选择概率相等的假设没有考虑距离和行驶时间等因素。

计算步骤：第1步给出第2步给出，求出第3步用求出的，求出第4步如果，非收敛，则返第2步；反之执行第5步。

第5步将，，代入式（4-5-7)求出，这时，如果总用条件（ 4-5-4）满足，则结束计算，反之，更新值返回第1步。

2．佐佐木(Sasaki)模型分别设定i区的发生概率和j区的吸引（选择）概率。

, （）－－发生守恒条件(4-5-11), （）－－吸引守恒条件(4-5-12), () (4-5-13)式中，为i区的发生交通量被j区有吸引的概率。