名校必备2009年普通高考重庆卷各科试卷基本结构及有关说明

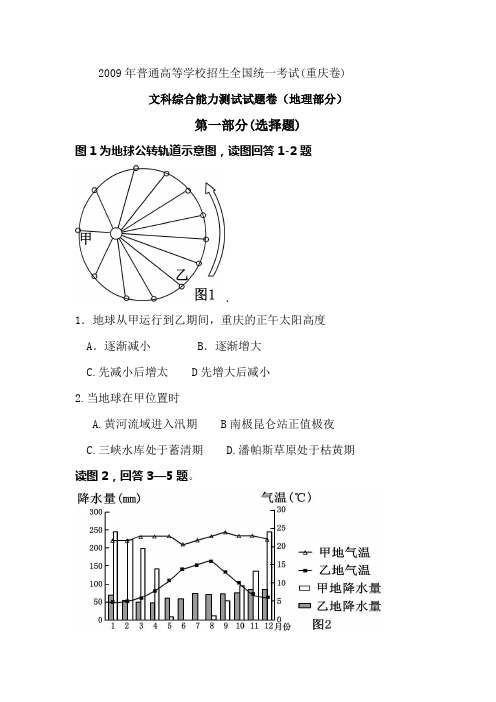
2009年普通高等学校招生全国统一考试(重庆卷)文科综合能力测试试题卷（地理部分）第一部分(选择题)图1为地球公转轨道示意图，读图回答1-2题．1．地球从甲运行到乙期间，重庆的正午太阳高度A．逐渐减小B．逐渐增大C.先减小后增太 D先增大后减小2.当地球在甲位置时A.黄河流域进入汛期 B南极昆仑站正值极夜C.三峡水库处于蓄清期D.潘帕斯草原处于枯黄期读图2，回答3—5题。

3下列地区气候类型与甲地相同的是A.德干高原 B．巴西高原 C.黄土高原 D.伊朗高原4.乙地气候类型区的地带性土壤是A．棕壤 B黑土 C.黄壤 D一红壤5甲、乙两地可能种植的主要经济作物分别是A，咖啡、甜菜 B．花生、咖啡C．甜菜、亚麻 D．亚麻、花生图3中，甲、乙两处景观所在地是我国著名旅游胜地。

读图回答6～7题。

6、游客在甲景观地可普遍观赏到A、奇松、云海B、石林、石牙 C.椰林孤峰 D、森林、冰川7、两地地貌形成主导外力作用与岩石组合正确的是A.甲——物理风化——风力侵蚀——砂岩B.乙——物理风化——风力侵蚀——砂岩C.甲——化学风化——流水侵蚀——石灰岩D.乙——化学风化——流水侵蚀——石灰岩图4是某城镇用地布局规划方案示意图。

读图回答8—9题。

8.该方案突出优点是规划中的A．居住区紧靠旧城、临近铁路B居住区环境好、建筑工程量小C.工业区靠近水源、铁路交通方便D.工业区地势平坦、位于主导风下风向9．适台布局在防护带的是A.停车场、日用品仓库B．幼儿园、日用品仓库C．幼儿园、医院D．医院、停车场图5是我国某盆地的局部地形剖面示意图。

读图回答l0—11题。

10.最适合形成天然绿洲的地带是A.①B.②C.③D.④11.该区域河流水文特征是A.夏季流量小B.补给以降水为主C.水量向下游增大D．径流年际变化小第二部分(综合题)36.（36）图6、图7是是两国跨流域调水工程局部示意图，图7中饼图是C城市的工业结构图。

A、B是两个水资源调入区代表性城市。

2009年重庆市高考数学试卷（理科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分）1．（5分）（2009•重庆）直线y=x+1与圆x2+y2=1的位置关系为（）A．相切 B．相交但直线不过圆心C．直线过圆心D．相离【考点】直线与圆的位置关系．【专题】计算题．【分析】求出圆心到直线的距离d，与圆的半径r比较大小即可判断出直线与圆的位置关系，同时判断圆心是否在直线上，即可得到正确答案．【解答】解：由圆的方程得到圆心坐标（0，0），半径r=1则圆心（0，0）到直线y=x+1的距离d==＜r=1，把（0，0）代入直线方程左右两边不相等，得到直线不过圆心．所以直线与圆的位置关系是相交但直线不过圆心．故选B【点评】此题考查学生掌握判断直线与圆位置关系的方法是比较圆心到直线的距离d与半径r的大小，灵活运用点到直线的距离公式化简求值，是一道中档题．2．（5分）（2009•重庆）已知复数z的实部为﹣1，虚部为2，则=（）A．2﹣i B．2+i C．﹣2﹣i D．﹣2+i【考点】复数的基本概念；复数代数形式的乘除运算．【专题】计算题．【分析】由题意求出复数z，代入，复数分子、分母同乘分母的共轭复数，化简为a+bi （a，b∈R）的形式，可得选项．【解答】解：因为由条件知z=﹣1+2i，则=，故选A．【点评】本题考查复数的基本概念，复数代数形式的乘除运算，考查计算能力，是基础题．3．（5分）（2009•重庆）（x+2）6的展开式中x3的系数是（）A．20 B．40 C．80 D．160【考点】二项式定理．【专题】计算题．【分析】利用二项展开式的通项公式求出通项，令x的指数为3求出展开式中x3的系数．【解答】解：设含x3的为第r+1，则Tr+1=C6r x6﹣r•2r，令6﹣r=3，得r=3，故展开式中x3的系数为C63•23=160．故选D．【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具．4．（5分）（2009•重庆）已知，则向量与向量的夹角是（）A．B．C．D．【考点】平面向量数量积的运算；数量积表示两个向量的夹角．【专题】计算题．【分析】利用向量的运算法则及向量模的平方即是向量的平方求出，再利用向量的数量积公式求出向量的夹角余弦，求出向量夹角．【解答】解：∵==2．又，∴=3．即cos＜a，b＞=3=1×6cos＜a，b＞，得cos＜a，b＞=，∴a与b的夹角为，故选项为C．【点评】本题考查向量的运算律；向量模的性质；利用向量的数量积公式求向量的夹角．5．（5分）（2009•重庆）不等式|x+3|﹣|x﹣1|≤a2﹣3a对任意实数x恒成立，则实数a的取值范围为（）A．（﹣∞，﹣1]∪[4，+∞）B．（﹣∞，﹣2]∪[5，+∞）C．[1，2]D．（﹣∞，1]∪[2，+∞）【考点】绝对值不等式的解法．【专题】计算题；转化思想．【分析】利用绝对值的几何意义，求出|x+3|﹣|x﹣1|的最大值不大于a2﹣3a，求出a的范围．【解答】解：因为|x+3|﹣|x﹣1|≤4对|x+3|﹣|x﹣1|≤a2﹣3a对任意x恒成立，所以a2﹣3a≥4即a2﹣3a﹣4≥0，解得a≥4或a≤﹣1．故选A．【点评】本题考查绝对值不等式的解法，绝对值的几何意义，以及恒成立问题，是中档题．6．（5分）（2009•重庆）锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同．从中任意舀取4个汤圆，则每种汤圆都至少取到1个的概率为（）A．B．C．D．【考点】等可能事件的概率；组合及组合数公式．【分析】本题考查的知识点是古典概型，我们计算出总的滔法种类，再计算满足条件“从中任意舀取4个汤圆，则每种汤圆都至少取到1个”所包含的基本事件个数，然后代入古典概型公式计算，即可得到答案．【解答】解：因为总的滔法C154，而所求事件的取法分为三类，即芝麻馅汤圆、花生馅汤圆、豆沙馅汤圆，取得个数分别按1，1，2；1，2，1；2，1，1三类，故所求概率P==．故选C．【点评】古典概型要求所有结果出现的可能性都相等，强调所有结果中每一结果出现的概率都相同．弄清一次试验的意义以及每个基本事件的含义是解决问题的前提，正确把握各个事件的相互关系是解决问题的关键．解决问题的步骤是：计算满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式进行求解．7．（5分）（2009•重庆）设△ABC的三个内角A，B，C，向量，，若=1+cos（A+B），则C=（）A．B．C．D．【考点】三角函数的化简求值．【专题】计算题．【分析】利用向量的坐标表示可求=1+cos（A+B），结合条件C=π﹣（A+B）可得sin（C+=，由0＜C＜π可求C【解答】解：因为=又因为所以又C=π﹣（B+A）所以因为0＜C＜π，所以故选C．【点评】本题主要以向量的坐标表示为载体考查三角函数，向量与三角的综合问题作为高考的热点，把握它的关键是掌握好三角与向量的基本知识，掌握一些基本技巧，还要具备一些运算的基本技能．8．（5分）（2009•重庆）已知，其中a，b∈R，则a﹣b的值为（）A．﹣6 B．﹣2 C．2 D．6【考点】极限及其运算．【专题】计算题．【分析】先通分得，然后由极限的性质知，由此可以求出a﹣b的值．【解答】解：∵已知==2，∴，∴a=2，b=﹣4；∴a﹣b=6．故选D．【点评】本题考查函数的极限，解题时注意函数极限的逆运算．9．（5分）（2009•重庆）三个互不重合的平面把空间分成六个部份时，它们的交线有（）条．A．1 B．2 C．3 D．1或2【考点】空间中直线与平面之间的位置关系．【专题】压轴题；分类讨论．【分析】三个互不重合的平面把空间分成六个部份有两种情形：一是其中两个平面平行，第三个平面都与它们相交；二是三个平面交于一条直线，考虑到两类即可解决．【解答】解：分两类：①当两个平面平行，第三个平面与它们相交时，有两条交线；②当三个平面交于一条直线时，有一条交线，故选D【点评】本题主要考查了空间中直线与平面之间的位置关系，考查空间想象能力和推理论证能力，属于基础题．10．（5分）（2009•重庆）已知三角函数f（x）=sin2x﹣cos2x，其中x为任意的实数．求此函数的周期为（）A．2πB．πC．4πD．﹣π【考点】函数的周期性；分段函数的解析式求法及其图象的作法；函数与方程的综合运用．【专题】计算题；压轴题．【分析】首先由题目中已知三角函数f（x）=sin2x﹣cos2x求周期，需要把函数化为标准型，然后根据周期公式求解即可得到答案．【解答】解：因为f（x）=sin2x﹣cos2x=，所以函数的周期T=，故答案选择B．【点评】此题主要考查三角函数周期性的求法，其中涉及到三角函数标准型的化法，涵盖知识点少，属于基础题目．二、填空题（共5小题，每小题5分，满分25分）11．（5分）（2009•重庆）若A={x∈R||x|＜3}，B={x∈R|2x＞1}，则A∩B={x|0＜x＜3}．【考点】交集及其运算．【专题】集合．【分析】要求A与B的交集，先要求出两个集合的区间，解出绝对值不等式得到集合A，根据指数函数的增减性得到集合B，然后取两集合的公共部分即可得到交集．【解答】解：由|x|＜3解得﹣3＜x＜3；由2x＞1=20，根据指数函数y=2x为增函数得到x＞0 ∴A={x|﹣3＜x＜3}，B={x|x＞0}，则A∩B={x|0＜x＜3}．故答案为：{x|0＜x＜3}【点评】此题考查学生会利用指数函数的增减性解不等式，理解交集的定义并会进行交集的运算．12．（5分）（2009•重庆）若f（x）=a+是奇函数，则a=﹣．【考点】奇函数；函数奇偶性的性质．【专题】常规题型．【分析】充分不必要条件：若奇函数定义域为R（即x=0有意义），则f（0）=0．或用定义：f（﹣x）=﹣f（x）直接求a．【解答】解：函数的定义域为R，且为奇函数，则f（0）=a+=0，得a+=0，得a=﹣，检验：若a=﹣，则f（x）=+=，又f（﹣x）==﹣=﹣f（x）为奇函数，符合题意．故答案为﹣．【点评】若定义域中包括0在内函数f（x）为奇函数⇒f（0）=0，注意是充分不必要条件，所以此类问题求解后需要检验，此题也可以直接采用奇偶性的定义f（﹣x）=f（x）求解．13．（5分）（2009•重庆）将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案有36种（用数字作答）．【考点】排列、组合及简单计数问题．【专题】计算题．【分析】由题意知将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，需要先从4个人中选出2个作为一个元素看成整体，再把它同另外两个元素在三个位置全排列排列，根据分步乘法原理得到结果．【解答】解：∵将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，∴先从4个人中选出2个作为一个元素看成整体，再把它同另外两个元素在三个位置全排列排列，共有C24A33=36．故答案为：36【点评】本题考查排列组合及简单的计数问题，是一个基础题，本题又是一个易错题，排列容易重复，注意做到不重不漏．14．（5分）（2009•重庆）设a1=2，，b n=，n∈N+，则数列{b n}的通项公式b n=2n+1．【考点】数列递推式．【专题】压轴题；创新题型．【分析】由题设条件得=，由此能够导出数列{b n}的通项公式b n．【解答】解：由条件得=且b1=4所以数列{b n}是首项为4，公比为2的等比数列，则b n=4•2n﹣1=2n+1．故答案为：2n+1．【点评】本题考查数列的性质和应用，解题时要认真审题，仔细解答，注意递推公式的合理运用．15．（5分）（2009•重庆）已知双曲线的左、右焦点分别为F1（﹣c，0），F2（c，0），若双曲线上存在一点P使，则该双曲线的离心率的取值范围是（1，）．【考点】双曲线的应用；双曲线的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】不防设点P（x o，y o）在右支曲线上并注意到x o＞a．利用正弦定理求得，进而根据双曲线定义表示出|PF1|和|PF2|代入求得e的范围．【解答】解：不防设点P（x o，y o）在右支曲线上并注意到x o＞a．由正弦定理有，由双曲线第二定义得：|PF1|=a+ex o，|PF2|=ex o﹣a，则有=，得x o=＞a，分子分母同时除以a2，易得：＞1，解得1＜e＜+1故答案为（1，）【点评】本题主要考查了双曲线的应用．考查了学生综合运用所学知识解决问题能力．三、解答题（共6小题，满分75分）16．（13分）（2009•重庆）设函数．（Ⅰ）求f（x）的最小正周期．（Ⅱ）若y=g（x）与y=f（x）的图象关于直线x=1对称，求当时y=g（x）的最大值．【考点】三角函数的最值；三角函数中的恒等变换应用；三角函数的周期性及其求法．【专题】计算题．【分析】（1）利用两角差的正弦公式及二倍角公式及化简三角函数；再利用三角函数的周期公式求出周期．（2）在y=g（x）上任取一点，据对称行求出其对称点，利用对称点在y=f（x）上，求出g （x）的解析式，求出整体角的范围，据三角函数的有界性求出最值．【解答】解：（1）f（x）===故f（x）的最小正周期为T==8（2）在y=g（x）的图象上任取一点（x，g（x）），它关于x=1的对称点（2﹣x，g（x））．由题设条件，点（2﹣x，g（x））在y=f（x）的图象上，从而==当时，时，因此y=g（x）在区间上的最大值为【点评】本题考查常利用三角函数的二倍角公式及公式化简三角函数、利用轴对称性求函数的解析式、利用整体角处理的思想求出最值．17．（13分）（2009•重庆）某单位为绿化环境，移栽了甲、乙两种大树各2株．设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响．求移栽的4株大树中：（1）两种大树各成活1株的概率；（2）成活的株数ξ的分布列与期望．【考点】离散型随机变量及其分布列；n次独立重复试验中恰好发生k次的概率．【专题】计算题．【分析】（1）甲两株中活一株符合独立重复试验，概率为，同理可算乙两株中活一株的概率，两值相乘即可．（2）ξ的所有可能值为0，1，2，3，4，分别求其概率，列出分布列，再求期望即可．【解答】解：设A k表示甲种大树成活k株，k=0，1，2B l表示乙种大树成活1株，1=0，1，2则A k，B l独立．由独立重复试验中事件发生的概率公式有P（A k）=C2k（）k（）2﹣k，P（B l）=C21（）l（）2﹣l．据此算得P（A0）=，P（A1）=，P（A2）=．P（B0）=，P（B1）=，P（B2）=．（1）所求概率为P（A1•B1）=P（A1）•P（B1）=×=．（2）解法一：ξ的所有可能值为0，1，2，3，4，且P（ξ=0）=P（A0•B0）=P（A0）•P（B0）=×=，P（ξ=1）=P（A0•B1）+P（A1•B0）=×+×=，P（ξ=2）=P（A0•B2）+P（A1•B1）+P（A2•B0）=×+×+×=，P（ξ=3）=P（A1•B2）+P（A2•B1）=×+×=．P（ξ=4）=P（A2•B2）=×=．综上知ξ有分布列ξ0 1 2 3 4P从而，ξ的期望为Eξ=0×+1×+2×+3×+4×=（株）．解法二：分布列的求法同上，令ξ1，ξ2分别表示甲乙两种树成活的株数，则ξ1：B（2，），ξ2：B（2，）故有Eξ1=2×=，Eξ2=2×=1从而知Eξ=Eξ1+Eξ2=．【点评】本题考查离散型随机变量的分布列、期望、独立重复试验的概率等知识，以及利用概率知识分析问题、解决问题的能力．18．（13分）（2009•重庆）设函数f（x）=ax2+bx+k（k＞0）在x=0处取得极值，且曲线y=f （x）在点（1，f（1））处的切线垂直于直线x+2y+1=0．（Ⅰ）求a，b的值；（Ⅱ）若函数，讨论g（x）的单调性．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【专题】计算题．【分析】（Ⅰ）因为”函数在x=0处取得极值“，则有f'（0）=0，再由“曲线y=f（x）在（1，f（1））处的切线与直线x﹣2y+1=0相互垂直”，则有f'（1）=2，从而求解．（Ⅱ）由（Ⅰ）可得到：，令g'（x）=0，有x2﹣2x+k=0，因为还有参数k，由一元二次方程，分三种情况讨论，（1）当△=4﹣4k＜0，函数g（x）在R上为增函数，（2）当△=4﹣4k=0，g（x）在R上为增函数（3）△=4﹣4k＞0，方程x2﹣2x+k=0有两个不相等实根，则由其两根来构建单调区间．【解答】解：（Ⅰ）因f（x）=ax2+bx+k（k＞0），故f'（x）=2ax+b又f（x）在x=0处取得极值，故f'（x）=0，从而b=0，由曲线y=f（x）在（1，f（1））处的切线与直线x+2y+1=0相互垂直可知该切线斜率为2，即f'（1）=2，有2a=2，从而a=1（6分）（Ⅱ）由（Ⅰ）知：、令g'（x）=0，有x2﹣2x+k=0（8分）（1）当△=4﹣4k＜0，即当k＞1时，g'（x）＞0在R上恒成立，故函数g（x）在R上为增函数（10分）（2）当△=4﹣4k=0，即当k=1时，，K=1时，g（x）在R上为增函数（12分）（3）△=4﹣4k＞0，即当0＜k＜1时，方程x2﹣2x+k=0有两个不相等实根当是g'（x）＞0，故g（x）在上为增函数当时，g'（x）＜0，故g（x）在上为减函数当时，g'（x）＞0，故g（x）在上为增函数（14分）【点评】本题主要考查导数的几何意义，函数的极值及函数的单调性．综合性较强，充分考查了函数方程不等式三者的内在联系与转化．19．（12分）（2009•重庆）如图，在四棱锥S﹣ABCD中，AD∥BC且AD⊥CD；平面CSD⊥平面ABCD，CS⊥DS，CS=2AD=2；E为BS的中点，CE=，求：（Ⅰ）点A到平面BCS的距离；（Ⅱ）二面角E﹣CD﹣A的大小．【考点】与二面角有关的立体几何综合题；点、线、面间的距离计算．【专题】计算题．【分析】（Ⅰ）根据线面平行的判定定理可知AD∥平面BCS，则从而A点到平面BCS的距离等于D点到平面BCS的距离，从而DS为点A到平面BCS的距离，在Rt△ADS中求出DS即可；（Ⅱ）过E点作EG⊥CD，交CD于点G，又过G点作GH⊥CD，交AB于H，根据二面角平面角的定义可知∠EGH为二面角E﹣CD﹣A的平面角，过E点作EF∥BC，交CS于点F，连接GF，在Rt△FEG中，求出此角即可．【解答】解：（Ⅰ）因为AD∥BC，且BC⊂平面BCS，所以AD∥平面BCS，从而A点到平面BCS的距离等于D点到平面BCS的距离．因为平面CSD⊥平面ABCD，AD⊥CD，故AD⊥平面CSD，从而AD⊥SD，由AD∥BC，得BC⊥DS，又由CS⊥DS知DS⊥平面BCS，从而DS为点A到平面BCS的距离，因此在Rt△ADS中（Ⅱ）如图，过E电作EG⊥CD，交CD于点G，又过G点作GH⊥CD，交AB于H，故∠EGH为二面角E﹣CD﹣A的平面角，记为θ，过E点作EF∥BC，交CS于点F，连接GF，因平面ABCD⊥平面CSD，GH⊥CD，易知GH⊥GF，故．由于E为BS边中点，故，在Rt△CFE中，，因EF⊥平面CSD，又EG⊥CD故由三垂线定理的逆定理得FG⊥CD，从而又可得△CGF～△CSD，因此而在Rt△CSD中，，在Rt△FEG中，可得，故所求二面角的大小为【点评】本题主要考查了点到平面的距离，以及二面角的度量等有关知识，同时考查了计算能力、推理能力、以及转化与划归的思想，属于中档题．20．（12分）（2009•重庆）已知以原点O为中心的椭圆的一条准线方程为，离心率，M是椭圆上的动点（Ⅰ）若C，D的坐标分别是，求|MC|•|MD|的最大值；（Ⅱ）如题（20）图，点A的坐标为（1，0），B是圆x2+y2=1上的点，N是点M在x轴上的射影，点Q满足条件：，、求线段QB的中点P的轨迹方程．【考点】直线与圆锥曲线的综合问题；轨迹方程．【专题】计算题；压轴题．【分析】（Ⅰ）由题设条件知焦点在y轴上，故设椭圆方程为（a＞b＞0）．设，由准线方程．由此能够求出椭圆方程．从而得到点M的坐标为（±1，0）时上式取等号，|MC|•|MD|的最大值为4．（Ⅱ）设M（x m，y m），B（x B，y B）Q（x Q，y Q）．因为，故x Q=2x N，y Q=y M，x Q2+y Q2=（2x M）2+y y=4．因为，（1﹣x Q﹣y Q）•（1﹣x N﹣y n）=（1﹣x Q）（1﹣x N）+y Q y N=0，所以x Q x N+y Q y N=x N+x Q﹣1．由此可导出动点P的轨迹方程为．【解答】解：（Ⅰ）由题设条件知焦点在y轴上，故设椭圆方程为（a＞b＞0）．设，由准线方程得．由得，解得a=2，c=，从而b=1，椭圆方程为．又易知C，D两点是椭圆的焦点，所以，|MC|+|MD|=2a=4从而|MC|•|MD|，当且仅当|MC|=|MD|，即点M的坐标为（±1，0）时上式取等号，|MC|•|MD|的最大值为4．（II）如图（20）图，设M（x m，y m），B（x B，y B）Q（x Q，y Q）．因为，故x Q=2x N，y Q=y M，x Q2+y Q2=（2x M）2+（y M）2=4 ①因为，（1﹣x Q﹣y Q）•（1﹣x N﹣y N）=（1﹣x Q）（1﹣x N）+y Q y N=0，所以x Q x N+y Q y N=x N+x Q﹣1．②记P点的坐标为（x P，y P），因为P是BQ的中点所以2x P=x Q+x P，2y P=y Q+y P由因为x N2+y N2=1，结合①，②得===故动点P的轨迹方程为【点评】本题考查圆锥曲线的综合应用，解题时要认真审题，仔细求解，知识方面注意椭圆的标准方程与焦点位置的关系以及向量与解析几何问题的综合运用．21．（12分）（2009•重庆）设m个不全相等的正数a1，a2，…，a m（m≥7）依次围成一个圆圈，（Ⅰ）若m=2009，且a1，a2，…，a1005是公差为d的等差数列，而a1，a2009，a2008，…，a1006是公比为q=d的等比数列；数列a1，a2，…，a m的前n项和S n（n≤m）满足：S3=15，S2009=S2007+12a1，求通项a n（n≤m）；（Ⅱ）若每个数a n（n≤m）是其左右相邻两数平方的等比中项，求证：a1+…+a6+a72+…+a m2＞ma1a2a m．【考点】等差数列的性质；数列的应用；等比数列的性质；反证法与放缩法．【专题】压轴题；反证法．【分析】（1）利用等比数列的性质，用a1、d表示出a2009、a2008，结合已知，列方程即可解出a1、d，进而求出a n．（2）通过探求数列的周期性或利用反证法求解．【解答】解：（I）因a1，a2009，a2008，a1006是公比为d的等比数列，从而a2009=a1d，a2008=a1d2，由S2009=S2007+12a1得a2008+a2009=12a1，解得d=3或d=﹣4（舍去）．∴d=3，又S3=3a1+3d=15．解得a1=2从而当n≤1005时，a n=a1+（n﹣1）d=2+3（n﹣1）=3n﹣1当1006≤n≤2009时，由a1，a2009，a2008，a1006是公比为d的等比数列得a n=a1d2009﹣（n﹣1）=a1d2010﹣n（1006≤n≤2009）因此（II）由题意a n2=a n﹣12a n+12（1＜n＜m），a m2=a m﹣12a12，a12=a m2a22得有①得④由①，②，③得a1a2a n=（a1a2a n）2，故a1a2a n=1．⑤又，故有．⑥下面反证法证明：m=6k若不然，设m=6k+p，其中1≤p≤5若取p=1即m=6k+1，则由⑥得a m=a6k+1=a1，而由③得，得a2=1，由②得，而④及⑥可推得a n=1（1≤n≤m）与题设矛盾同理若P=2，3，4，5均可得a n=1（1≤n≤m）与题设矛盾，因此m=6k为6的倍数由均值不等式得由上面三组数内必有一组不相等（否则a1=a2=a3=1，从而a4=a5═a m=1与题设矛盾），故等号不成立，从而a1+a2+a3++a6＞6又m=6k，由④和⑥得a72++a m2=（a72++a122）++（a6k﹣52++a6k2）=（k﹣1）（a12++a62）=因此由⑤得a1+a2+a3++a6+a72++a m2＞6+6（k﹣1）=6k=m=ma1a2a3a m【点评】本题考查了等差数列和等比数列的通项公式、性质及方程、解不等式的有关知识，考查运算能力和推理能力．。

2009年高考（重庆）理综物理试题分析09重庆卷物理试题的平均分69.2分,难度为0.58。

是一套命得成功的好题。

一、逐题研究14．考查的主要知识点：热力学第一定律、一定质量的理想气体其内能只与温度有关。

考查的主要能力：记忆能力、理解能力、推理能力。

考查的主要方法：直选法和推导法。

平均分：4.87，难度：0.81，易。

命题得失：本题考查热力学第一定律和理想气体的性质。

题意明确清晰，降低了对“理解能力”的要求，难度0.81，说明命题者对考纲要求和重庆市考生实际水平把握得很准，体现出“以人为本”的命题理念（即以考生为本）。

是一道命得非常成功的好题。

给高2010级的启示与复习建议：近四年重庆卷热学选择题考查的知识点几乎相同。

明年可能变考点，所以应加强对分子动理论的复习、热力学第二定律的复习。

15．考查的主要知识点：、波的频率在传播中保持不变、声波的折射。

考查的主要能力：记忆能力、理解能力、识图作图能力、推理能力。

考查的主要方法：直接法和推导法。

平均分：2.74 难度：0.46（中等）命题得失：本题考查、波的频率在传播中保持不变、声波的折射等知识点。

通过本题检验高中生是否明白机械波的折射和光的折射（即电磁波的折射）相同点和不同点。

本题得分率仅0.46，说明重庆市有54%的考生不明白机械波的折射和光的折射（电磁波的折射）相同点和不同点。

从波动图上读取已知条件，考查学生的识图能力。

命题者精心设计文、图结合的题目来考查高中物理学习中易混淆的知识点----机械波的折射和光的折射（电磁波的折射）相同点和不同点，体现了命题者高超的水准，是一道命得成功的好题。

给高2010级的启示与复习建议：加强对简谐运动（含单摆）受迫振动共振的复习。

16．考查的主要能力：记忆能力、理解能力、推理能力、应用数学的能力。

考查的主要方法：直选法、守恒法和推算法。

平均分：4.84 难度：0.81（易）命题得失：本题考查核反应方程应遵守质量数守恒、电荷数守恒、能量守恒。

00重庆09年高考大纲出炉各科考点无大变动[真诚为您服务]每年高考冲刺，考生十分紧张记者梁杰摄（资料图）昨日，市招办正式公布了2009年普通高等学校招生全国统一考试（重庆卷）各科试卷基本结构及有关说明。

今年高考跟去年相比，除了数学减少一题、英语考试单词词汇量有所增加之外，其他各科都没有什么变化。

理综选择题均单选，文综以中等难度题为主。

为了帮助考生理解大纲，备战高考，本报昨日在第一时间邀请名师，根据大纲逐科解读。

■语文备考优化简化知识点考纲今年题型主要是单选、古文翻译、填空、简答和写作。

考试内容包含：语言知识和语言表达，8题，28分；文学常识和名句名篇，1题，6分；古诗文阅读，5题，25分；现代文阅读，7题，31分；写作仍然是1题，60分。

重庆一中高三语文教师王海洋：今年的语文与去年相比没有变化，后期复习，要继续强化知识点的复习，但不再大面积地复习知识点，而要进行思维层面的优化。

要注重知识点的简化，要在各类题型特别是主观题中进行规模训练，针对每个板块的重点题型，归纳出其命题特点及答题思路。

写作题，要继续强化审题能力训练，多搜集经典素材。

■数学备考舍弃偏题难题考纲中，考试仍旧是选择、填空和解答三种题型。

文科数学考试的选择题从12题减少到10题，总题量减少一道题，理科数学试题量也减少了一道。

试题的减少，能让考生节约出更多时间来完成整张试卷。

重庆一中高三数学教师邹发明：今年题量发生变化，但试题的难易分布保持不变，高难度题所占比例不高。

今年的高考数学试卷更注重基础知识、基础技能的考查。

学生复习要跟着老师的节奏，舍弃偏、难、怪的习题，淡化特殊技巧。

■英语备考考生要多练习作文重庆一中高三年级英语老师成林：考纲中，英语试卷结构包括听力、英语知识运用、阅读理解、写作四个大题，今年的考试题型没有变化。

考生每周可以写一至二篇作文，将记忆词汇和阅读理解、完形填空、短文改错练习相结合。

■化学备考学会抠题规范解题步骤巴蜀中学高三化学教研组组长涂彬：今年的重庆考纲和试卷结构与前两年相比保持了稳定，基本没有变化，试题涉及的知识点比较多。

2009年重庆市高考数学试卷（文科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分）1．（5分）（2009•重庆）圆心在y轴上，半径为1，且过点（1，2）的圆的方程为（）A．x2+（y﹣2）2=1 B．x2+（y+2）2=1 C．（x﹣1）2+（y﹣3）2=1 D．x2+（y﹣3）2=1 【考点】圆的标准方程．【专题】计算题；数形结合．【分析】法1：由题意可以判定圆心坐标（0，2），可得圆的方程．法2：数形结合法，画图即可判断圆心坐标，求出圆的方程．法3：回代验证法，逐一检验排除，即将点（1，2）代入四个选择支，验证是否适合方程，圆心在y轴上，排除C，即可．【解答】解法1（直接法）：设圆心坐标为（0，b），则由题意知，解得b=2，故圆的方程为x2+（y﹣2）2=1．故选A．解法2（数形结合法）：由作图根据点（1，2）到圆心的距离为1易知圆心为（0，2），故圆的方程为x2+（y﹣2）2=1故选A．解法3（验证法）：将点（1，2）代入四个选择支，排除B，D，又由于圆心在y轴上，排除C．故选：A．【点评】本题提供三种解法，三种解题思路，考查圆的标准方程，是基础题．2．（5分）（2009•重庆）命题“若一个数是负数，则它的平方是正数”的逆命题是（）A．“若一个数是负数，则它的平方不是正数”B．“若一个数的平方是正数，则它是负数”C．“若一个数不是负数，则它的平方不是正数”D．“若一个数的平方不是正数，则它不是负数”【考点】四种命题．【专题】常规题型．【分析】将原命题的条件与结论进行交换，得到原命题的逆命题．【解答】解：因为一个命题的逆命题是将原命题的条件与结论进行交换，因此逆命题为“若一个数的平方是正数，则它是负数”．故选B．【点评】本题考查四种命题的互相转化，解题时要正确掌握转化方法．3．（5分）（2009•重庆）（x+2）6的展开式中x3的系数是（）A．20 B．40 C．80 D．160【考点】二项式定理．【专题】计算题．【分析】利用二项展开式的通项公式求出通项，令x的指数为3求出展开式中x3的系数．【解答】解：设含x3的为第r+1，则Tr+1=C6r x6﹣r•2r，令6﹣r=3，得r=3，故展开式中x3的系数为C63•23=160．故选D．【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具．4．（5分）（2009•重庆）已知向量=（1，1），=（2，x），若+与4﹣2平行，则实数x的值是（）A．﹣2 B．0 C．1 D．2【考点】平面向量共线（平行）的坐标表示．【分析】写出要用的两个向量的坐标，由+与4﹣2平行，根据向量共线的坐标形式的充要条件可得关于X的方程，解方程可得结果．【解答】解：∵=（1，1），=（2，x），∴+=（3，x+1），4﹣2=（6，4x﹣2），由于+与4﹣2平行，得6（x+1）﹣3（4x﹣2）=0，解得x=2．故选D【点评】本题也可以这样解：因为+与4﹣2平行，则存在常数λ，使+=λ（4﹣2），即（2λ+1）=（4λ﹣1），根据向量共线的条件知，向量与共线，故x=2．5．（5分）（2009•重庆）设{a n}是公差不为0的等差数列，a1=2且a1，a3，a6成等比数列，则{a n}的前n项和S n=（）A．B．C．D．n2+n【考点】等差数列的前n项和；等比数列的性质．【专题】计算题．【分析】设数列{a n}的公差为d，由题意得（2+2d）2=2•（2+5d），解得或d=0（舍去），由此可求出数列{a n}的前n项和．【解答】解：设数列{a n}的公差为d，则根据题意得（2+2d）2=2•（2+5d），解得或d=0（舍去），所以数列{a n}的前n项和．故选A．【点评】本题考查数列的性质和应用，解题时要认真审题，仔细解答．6．（5分）（2009•重庆）下列关系式中正确的是（）A．sin11°＜cos10°＜sin168°B．sin168°＜sin11°＜cos10°C．sin11°＜sin168°＜cos10° D．sin168°＜cos10°＜sin11°【考点】正弦函数的单调性．【专题】三角函数的图像与性质．【分析】先根据诱导公式得到sin168°=sin12°和cos10°=sin80°，再结合正弦函数的单调性可得到sin11°＜sin12°＜sin80°从而可确定答案．【解答】解：∵sin168°=sin（180°﹣12°）=sin12°，cos10°=sin（90°﹣10°）=sin80°．又∵y=sinx在x∈[0，]上是增函数，∴sin11°＜sin12°＜sin80°，即sin11°＜sin168°＜cos10°．故选：C．【点评】本题主要考查诱导公式和正弦函数的单调性的应用．关键在于转化，再利用单调性比较大小．7．（5分）（2009•重庆）已知a＞0，b＞0，则的最小值是（）A．2 B． C．4 D．5【考点】基本不等式．【分析】a＞0，b＞0，即，给出了基本不等式使用的第一个条件，而使用后得到的式子恰好可以再次使用基本不等式．【解答】解：因为当且仅当，且，即a=b时，取“=”号．故选C．【点评】基本不等式a+b，（当且仅当a=b时取“=”）的必须具备得使用条件：一正（即a，b都需要是正数）二定（求和时，积是定值；求积时，和是定值．）三等（当且仅当a=b时，才能取等号）8．（5分）（2009•重庆）12个篮球队中有3个强队，将这12个队任意分成3个组（每组4个队），则3个强队恰好被分在同一组的概率为（）A．B．C．D．【考点】等可能事件的概率．【专题】计算题．【分析】由题意知本题是一个古典概型，试验发生的所有事件是将12个组分成4个组的分法有种，而满足条件的3个强队恰好被分在同一组分法有，平均分组问题容易出错．【解答】解：由题意知本题是一个古典概型，∵试验发生的所有事件是将12个队分成4个组的分法有种，而满足条件的3个强队恰好被分在同一组分法有，根据古典概型公式∴3个强队恰好被分在同一组的概率为=，故选B．【点评】概率教学的核心问题是让学生了解随机现象与概率的意义，加强与实际生活的联系，以科学的态度评价身边的一些随机现象，尽量地让学生自己举出生活和学习中与古典概型有关的实例．9．（5分）（2009•重庆）在正四棱柱ABCD﹣A1B1C1D1中，顶点B1到对角线BD1和到平面A1BCD1的距离分别为h和d，则下列命题中正确的是（）A．若侧棱的长小于底面的边长，则的取值范围为（0，1）B．若侧棱的长小于底面的边长，则的取值范围为C．若侧棱的长大于底面的边长，则的取值范围为D．若侧棱的长大于底面的边长，则的取值范围为【考点】点、线、面间的距离计算．【专题】计算题；压轴题．【分析】设底面边长为1，侧棱长为λ，过B1作B1H⊥BD1，B1G⊥A1B，Rt△BB1D1中可知B1D1和B1D，进而利用三角形面积公式求得h，设在正四棱柱中，由于BC⊥AB，BC⊥BB1，进而可推断BC⊥平面AA1B1B，BC⊥B1G，B1G⊥平面AB1CD1，可知B1G为点到平面A1BCD1的距离，Rt△A1B1B中，又由三角形面积关系得d，进而可知的表达式，根据λ来确定其范围．【解答】解：设底面边长为1，侧棱长为λ（λ＞0），过B1作B1H⊥BD1，B1G⊥A1B．在Rt△BB1D1中，，由三角形面积关系得：设在正四棱柱中，由于BC⊥AB，BC⊥BB1，所以BC⊥平面AA1B1B，于是BC⊥B1G，所以B1G⊥平面AB1CD1，故B1G为点到平面A1BCD1的距离，在Rt△A1B1B中，又由三角形面积关系得于是，于是当λ＞1，所以，所以；故选C．【点评】本题主要考查了点到面得距离计算．点到平面的距离是近两年高考的一个热点问题，平时应注意强化训练．10．（5分）（2009•重庆）把函数f（x）=x3﹣3x的图象C1向右平移u个单位长度，再向下平移v个单位长度后得到图象C2、若对任意的u＞0，曲线C1与C2至多只有一个交点，则v的最小值为（）A．2 B．4 C．6 D．8【考点】函数单调性的性质；函数的图象；函数的零点与方程根的关系．【专题】计算题；压轴题．【分析】由平移规律得出平移后的曲线对应的解析式，因两曲线有交点，故相应方程有根，对方程（x﹣u）3﹣3（x﹣u）﹣v=x3﹣3x，进行变形，得出v关于u 的不等式，转化成恒成立的问题求参数v的范围．【解答】解：根据题意曲线C的解析式为y=（x﹣u）3﹣3（x﹣u）﹣v，由题意，方程（x﹣u）3﹣3（x﹣u）﹣v=x3﹣3x至多有一个根，即3ux2﹣3xu2+（u3﹣3u+v）=0至多有一个根，故有△=9u4﹣12u（u3﹣3u+v）≤0对任意的u＞0恒成立整理得对任意u＞0恒成立，令，则由此知函数g（u）在（0，2）上为增函数，在（2，+∞）上为减函数，所以当u=2时，函数g（u）取最大值，即为4，于是v≥4；故选B．【点评】考查据题意进行转化的能力，以及观察变形的能力，解本题过程中，把一个变量表示成另一个变量的函数，依据不等式恒成立的问题转化求求函数的最值来求出参数的范围，题型新颖．二、填空题（共5小题，每小题5分，满分25分）11．（5分）（2009•重庆）若U={n|n是小于9的正整数}，A={n∈U|n是奇数}，B={n∈U|n是3的倍数}，则∁U（A∪B）={2，4，8}．【考点】全集及其运算；补集及其运算．【专题】集合．【分析】先求出满足条件的全集U，进而求出满足条件的集合A与集合B，求出A∪B后，易根据全集U求出∁U（A∪B）．【解答】解：∵U={n|n是小于9的正整数}，∴U={1，2，3，4，5，6，7，8}，则A={1，3，5，7}，B={3，6，9}，所以A∪B={1，3，5，7，9}，所以∁U（A∪B）={2，4，8}．【点评】本题考查的知识点是并集运算和补集运算，运算的关键是准确列举出满足条件的集合．12．（5分）（2009•重庆）记f（x）=log3（x+1）的反函数为y=f﹣1（x），则方程f﹣1（x）=8的解x=2．【考点】反函数．【分析】容易看出，本题求解首先求出反函数y=f﹣1（x），然后通过令f﹣1（x）=8即可解得，求反函数需要利用指数式和对数式的互化．【解答】解：法1；由y=f（x）=log3（x+1），得x=3y﹣1，即f﹣1（x）=3x﹣1，于是由3x﹣1=8，解得：x=2法2：∵f﹣1（x）=8，∴x=f（8）=log3（8+1）=2故答案为：2．【点评】本题体现了小题综合化的特点，这里提供了2种解法，法一是直接法，过程完整，环节多；法二解法间简捷，环节少，值得借鉴．13．（5分）（2009•重庆）5个人站成一排，其中甲、乙两人不相邻的排法有72种（用数字作答）．【考点】排列、组合及简单计数问题．【专题】计算题；分析法．【分析】首先考虑求甲、乙两人不相邻的排法，可以联想到用插空法求解，先把除甲乙外的其他三人排好，将甲乙二人插入前三人形成的四个空隙中，求出排法相乘即可得到答案．【解答】解：求甲、乙两人不相邻的排法，可分两个步骤完成，第一步骤先把除甲乙外的其他三人排好，有A33种排法，第二步将甲乙二人插入前三人形成的四个空隙中，有A42种，则甲、乙两不相邻的排法有A33A42=72种．故答案为72．【点评】此题主要考查排列组合及简单的计数问题．题中应用到插空法，这种思想在求不相邻的问题中应用较广，需要同学们多加注意．14．（5分）（2009•重庆）从一堆苹果中任取5只，称得它们的质量为（单位：克）：125 124 121 123 127，则该样本标准差s=2（克）（用数字作答）．【考点】极差、方差与标准差．【专题】计算题；压轴题．【分析】根据题意，利用平均数、方差、标准差的公式直接计算即可．【解答】解：由题意得：样本平均数x=（125+124+121+123+127）=124，样本方差s2=（12+02+32+12+32）=4，∴s=2．故答案为2．【点评】本题考查用样本的平均数、方差、标准差来估计总体的平均数、方差、标准差，属基础题，熟记样本的平均数、方差、标准差公式是解答好本题的关键．15．（5分）（2009•重庆）已知椭圆=1（a＞b＞0）的左、右焦点分别为F1（﹣c，0），F2（c，0），若椭圆上存在一点P使，则该椭圆的离心率的取值范围为．【考点】椭圆的简单性质．【专题】计算题；压轴题．【分析】由“”的结构特征，联想到在△PF1F2中运用由正弦定理得：两者结合起来，可得到，再由焦点半径公式，代入可得到：a（a+ex0）=c（a﹣ex0）解出x0，由椭圆的范围，建立关于离心率的不等式求解．要注意椭圆离心率的范围．【解答】解：在△PF1F2中，由正弦定理得：则由已知得：，即：a|PF1|=c|PF2|设点（x0，y0）由焦点半径公式，得：|PF1|=a+ex0，|PF2|=a﹣ex0则a（a+ex0）=c（a﹣ex0）解得：由椭圆的几何性质知：x0＞﹣a则，整理得e2+2e﹣1＞0，解得：或，又e∈（0，1），故椭圆的离心率：，故答案为：．【点评】本题主要考查椭圆的定义，性质及焦点三角形的应用，特别是离心率应是椭圆考查的一个亮点，多数是用a，b，c转化，用椭圆的范围来求解离心率的范围．三、解答题（共6小题，满分75分）16．（13分）（2009•重庆）设函数f（x）=（sinωx+cosωx）2+2cos2ωx（ω＞0）的最小正周期为．（Ⅰ）求ω的值；（Ⅱ）若函数y=g（x）的图象是由y=f（x）的图象向右平移个单位长度得到，求y=g（x）的单调增区间．【考点】三角函数的周期性及其求法；函数y=Asin（ωx+φ）的图象变换．【分析】（1）先将函数化简为f（x）=sin（2ωx+），再由，可得答案．（2）根据g（x）=f（x﹣）先求出解析式，再求单调区间．【解答】解：（Ⅰ）f（x）=（sinωx+cosωx）2+2cos2ωx=sin2ωx+cos2ωx+sin2ωx+1+2cos2ωx =依题意得，故ω的值为．（Ⅱ）依题意得：由解得故y=g（x）的单调增区间为：．【点评】本题主要考查三角函数最小正周期的求法和单调区间的求法．做这种题首先要将原函数化简为y=Asin（ωx+φ）的形式再做题．17．（13分）（2009•重庆）某单位为绿化环境，移栽了甲、乙两种大树各2株、设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响、求移栽的4株大树中：（Ⅰ）至少有1株成活的概率；（Ⅱ）两种大树各成活1株的概率．【考点】互斥事件的概率加法公式；相互独立事件的概率乘法公式．【分析】（1）因各株大树是否成活互不影响，本题考查的是相互独立事件同时发生的概率，至少有1株成活包括的情况较多，所以从它的对立事件1株也不活来考虑．（2）应用独立重复试验中事件发生的概率公式，同时又有相互独立事件同时发生的概率，代入公式进行运算．【解答】解：设A k表示第k株甲种大树成活，k=1，2设B l表示第l株乙种大树成活，l=1，2则A1，A2，B1，B2独立，且（Ⅰ）至少有1株成活的概率为：（Ⅱ）由独立重复试验中事件发生的概率公式知，两种大树各成活1株的概率为：【点评】考查运用概率知识解决实际问题的能力，相互独立事件是指，两事件发生的概率互不影响，而对立事件是指同一次试验中，不会同时发生的事件，遇到求用至少来表述的事件的概率时，往往先求它的对立事件的概率．18．（13分）（2009•重庆）如图，在五面体ABCDEF中，AB∥DC，，CD=AD=2，四边形ABFE为平行四边形，FA⊥平面ABCD，，求：（Ⅰ）直线AB到平面EFCD的距离；（Ⅱ）二面角F﹣AD﹣E的平面角的正切值．【考点】与二面角有关的立体几何综合题；点、线、面间的距离计算．【专题】计算题．【分析】解法一：（几何法）（Ⅰ）AB到面EFCD的距离等于点A到面EFCD的距离，故可过A作平面EFCD的垂线，注意到面AFD⊥面EFDC，故只需过A作FD的垂线即可．（Ⅱ）由已知条件做出二面角F﹣AD﹣E的平面角，再求解．已知FA⊥AD，再可求证EA⊥AD，故，∠FAE为二面角F﹣AD﹣E的平面角，再解△AEF即可．解法二：（向量法）由AB、AD、AF两两垂直，故可通过向量法求解．（Ⅰ）求平面EFCD的法向量，则直线AB到平面EFCD的距离=（Ⅱ）分别求出两个面的法向量，再求两个法向量的余弦，即二面角F﹣AD﹣E的平面角的余弦，再求正切即可．【解答】解：法一：（Ⅰ）∵AB∥DC，DC⊂平面EFCD，∴AB到面EFCD的距离等于点A到面EFCD的距离，过点A作AG⊥FD于G，因AB∥DC，故CD⊥AD；又∵FA⊥平面ABCD，由三垂线定理可知，CD⊥FD，故CD⊥面FAD，知CD⊥AG，所以AG为所求直线AB到面EFCD的距离．在Rt△FCD中，由FA⊥平面ABCD，得FA⊥AD，从而在Rt△FAD中∴．即直线AB到平面EFCD的距离为．（Ⅱ）由己知，FA⊥平面ABCD，得FA⊥AD，又由，知AD⊥AB，故AD⊥平面ABFE∴DA⊥AE，所以，∠FAE为二面角F﹣AD﹣E的平面角，记为θ．在Rt△AED中，，由平行四边形ABCD得，FE∥BA，从而在Rt△AEF中，，故所以二面角F﹣AD﹣E的平面角的正切值为．法二：（Ⅰ）如图以A点为坐标原点，的方向为x，y，z的正方向建立空间直角坐标系数，则A（0，0，0）C（2，2，0）D（0，2，0）设F（0，0，z0）（z0＞0）可得，由．即，解得F（0，0，1）∵AB∥DC，DC⊂面EFCD，所以直线AB到面EFCD的距离等于点A到面EFCD的距离．设A点在平面EFCD上的射影点为G（x1，y1，z1），则因且，而，此即解得x1=0①，知G点在yoz面上，故G点在FD上.，故有②联立①，②解得，∴为直线AB到面EFCD的距离．而所以（Ⅱ）因四边形ABFE为平行四边形，则可设E（x0，0，1）（x0＜0），．由得，解得．即．故由，因，，故∠FAE为二面角F﹣AD﹣E的平面角，又∵，，，所以【点评】本题考查空间的角和空间距离的计算，考查空间想象能力和运算能力．注意几何法和向量法的应用．19．（12分）（2009•重庆）已知f（x）=x2+bx+c为偶函数，曲线y=f（x）过点（2，5），g （x）=（x+a）f（x）．（1）求曲线y=g（x）有斜率为0的切线，求实数a的取值范围；（2）若当x=﹣1时函数y=g（x）取得极值，确定y=g（x）的单调区间．【考点】导数的几何意义；利用导数研究函数的单调性；函数在某点取得极值的条件．【分析】（1）据偶函数的定义f（﹣x）=f（x）求出b值，将点（2，5）代入得c值，据导数在切点处的导数值为切线斜率，有g′（x）=0有实数解，由△≥0得范围．（2），函数在极值点处的导数值为0，导数大于0对应区间是单调递增区间；导数小于0对应区间是单调递减区间．【解答】解：（1）∵f（x）=x2+bx+c为偶函数，故f（﹣x）=f（x）即有（﹣x）2+b（﹣x）+c=x2+bx+c解得b=0又曲线y=f（x）过点（2，5），得22+c=5，有c=1∵g（x）=（x+a）f（x）=x3+ax2+x+a从而g′（x）=3x2+2ax+1，∵曲线y=g（x）有斜率为0的切线，故有g′（x）=0有实数解．即3x2+2ax+1=0有实数解．此时有△=4a2﹣12≥0解得a∈（﹣∞，﹣]∪[，+∞）所以实数a的取值范围：a∈（﹣∞，﹣]∪[，+∞）；（2）因x=﹣1时函数y=g（x）取得极值，故有g′（﹣1）=0即3﹣2a+1=0，解得a=2又g′（x）=3x2+4x+1=（3x+1）（x+1）令g′（x）=0，得x1=﹣1，x2=当x∈（﹣∞，﹣1）时，g′（x）＞0，故g（x）在（﹣∞，﹣1）上为增函数当时，g′（x）＜0，故g（x）在（﹣1，﹣）上为减函数当x∈（﹣）时，g′（x）＞0，故g（x）在上为增函数．【点评】本题考查偶函数的定义；利用导数几何意义求曲线切线方程；利用导数求函数单调区间．20．（12分）（2009•重庆）已知以原点O为中心的双曲线的一条准线方程为，离心率．（Ⅰ）求该双曲线的方程；（Ⅱ）如图，点A的坐标为，B是圆上的点，点M在双曲线右支上，|MA|+|MB|的最小值，并求此时M点的坐标．【考点】双曲线的标准方程；圆方程的综合应用；双曲线的应用；圆锥曲线的共同特征．【专题】计算题；压轴题．【分析】（Ⅰ）由题意可知双曲线的焦点在x轴上，双曲线的方程，根据准线方程和离心率求得a和c，进而求得b．（Ⅱ）设点D的坐标为，则点A、D为双曲线的焦点，根据双曲线的性质可得，|MA|﹣|MD|=2a，进而可|MA|+|MB|=2+|MB|+|MD|≥2+|BD|，又由B是圆上的点，推断出，进而通过直线方程与双曲线方程联立求得M的坐标．【解答】解：（Ⅰ）由题意可知，双曲线的焦点在x轴上，故可设双曲线的方程为，设，由准线方程为得，由得解得从而b=2，∴该双曲线的方程为；（Ⅱ）设点D的坐标为，则点A、D为双曲线的焦点，|MA|﹣|MD|=2a=2所以|MA|+|MB|=2+|MB|+|MD|≥2+|BD|，∵B是圆上的点，其圆心为，半径为1，故从而当M，B在线段CD上时取等号，此时|MA|+|MB|的最小值为∵直线CD的方程为，因点M在双曲线右支上，故x＞0由方程组解得所以M点的坐标为【点评】本题主要考查了双曲线的标准方程和双曲线与直线的关系．圆锥曲线问题是高考中必考的知识点，故应加强训练．21．（12分）（2009•重庆）已知，（Ⅰ）求b1，b2，b3的值；（Ⅱ）设c n=b n b n+1，S n为数列{c n}的前n项和，求证：S n≥17n；（Ⅲ）求证：．【考点】数列递推式；数列的求和；不等式的证明．【专题】计算题；证明题；压轴题．【分析】（Ⅰ）根据a2和a1及题设中递推式求得a3，进而求得a4，代入求得b1，b2，b3的值；（Ⅱ）整理a n+2=4a n+1+a n得，进而求得关于b n的递推式，进而推断出b n＞4，且c n=b n b n+1=4b n+1＞17进而推断出S n=c1+c2++c n≥17n．（Ⅲ）先看当n=1时把b1和b2代入结论成立；在看当n≥2时，把（2）中求得的递推式代入|b2n﹣b n|，进而根据（2）中S n≥17n的结论推断出|b2n﹣b n|＜，进而根据|b2n﹣b n|≤|b n+1﹣b n|+|b n+2﹣b n+1|+…+|b2n﹣b2n﹣1|使原式得证．【解答】解：（Ⅰ）∵a2=4，a3=17，a4=72，所以（Ⅱ）由a n+2=4a n+1+a n得即所以当n≥2时，b n＞4于是c1=b1，b2=17，c n=b n b n+1=4b n+1＞17（n≥2）所以S n=c1+c2++c n≥17n（Ⅲ）当n=1时，结论成立当n≥2时，有所以|b2n﹣b n|≤|b n+1﹣b n|+|b n+2﹣b n+1|+…+|b2n﹣b2n﹣1|【点评】本题主要考查了数列的递推式．数列的递推式与不等式，函数等知识综合考查是近几年高考的热点，平时的训练应注意知识的综合运用．。

2009年普通高等学校招生全国统一考试（重庆卷）理科综合能力测试试题卷理科综合能力测试试题分选择题和非选择题两部分，第一部分（选择题）1至5页，第二部分，（非选择题）6至12页，共12页，满分300分，考试时间150 分钟注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的地位置上2．大选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上作答无效。

5．考试结束后，将试题卷和答题卡一并交回以下数据可供解题时参考：相对原子质量：H 1 C 12 O 16 Na 23 Si 28 Cl 35.5第一部分（选择题共126分）1．下列有关酶的叙述，正确的是A．高温和低温均能破坏酶的结构使其失去活性B．酶是活细胞产生并具有催化作用的蛋白质C．细胞质基质中的催化葡萄糖分析的酶D．细胞质中没有作用于DNA的解旋酶2．下表有关基因表达的选项中，不可能的是A．大肠杆菌以复制方式进行繁殖，其你拟核实一个环状DNA分子B．在含葡萄糖和乳糖的培养基上，大肠杆菌首先利用乳糖作碳源C．用大肠杆菌工程菌生产干扰素时，应及时添加核算等生土长基因子D．处于队数期的大肠杆菌，常作为生产作用的菌种和科研的材料4．如果给人注射灭活的甲型H1N1流感病毒，可预防甲型H1N1流感，那么灭活病毒在体内引起的免疫反应，正确的是A．B细胞接受刺激后形成效应B细胞，能使靶细胞裂解B．T细胞接受刺激后形成效应T细胞，能释放淋巴因子C．吞噬细胞接受刺激后形成效应细胞，能产生相应的抗体D．淋巴细胞吞噬该病毒后形成记忆细胞，能释放白细胞介素5． 题图5是某森林生态系统物质和能量流向示意图，h 、i 、j 、k 表示不同用途的有机物（j是未利用部分），方框大小表示使用量，下列叙述正确的是A ． 进入该生态系统的2CO 量与各h 产生的2CO 总量相等B ． 生产者i 的量大于被初级消费者同化有机物的量C ． 流向分解者的k 可悲生产这直接吸收利用D ． 流经该生态系统的物质和能量可循环利用6． 材料与化学密切相关，表中对应系错误的是7． 有关实验的叙述，正确的是A ． 将固体加入容量瓶中溶解并稀释至刻度，配置成一定物质的量浓度的溶液B ． 用玻璃棒蘸取溶液，点在湿润的pH 是指上测定其pHC ． 用NaOH 溶液洗涤并灼烧铂丝后，再进行焰色反应D ． 读取滴定管内液体的体积，俯视读数导致读数偏小 8． 下列各组离子，能在溶液中大量共存的是A ．+2+--2Na Mg AlO Br 、、、 B +2+2--43H Fe SO NO 、、、 C ．++2--43K NH CO OH 、、、 D 2+3+--3Ca Al NO Cl 、、、 9．下列叙述正确的是A ．2SO 具有还原性，故可作漂白剂B ．Na 的金属活性比Mg 强，故可用Na 与2MgCl 溶液反应制MgC ．浓硝酸中的3HNO 见光辉份写，故有时在实验室看到的浓硝酸呈黄色D ．Fe 在2Cl 中燃烧生成3FeCl ，故在与其他金属反应的产物中的Fe 也显+3价 10．物质的量浓度相同的下列溶液，pH 由大到小排列正确的是A ．2233Ba(OH)Na SO FeCl KCl 、、、B 232334Na SiO Na SO KNO NH Cl 、、、C ．32342424NH H O H PO Na SO H SO 、、、、D 36525NaHCO C H C H OH HCl 、、、 11．下列对有机物结构或性质的描述，错误．．的是 A ．一定条件下，2Cl 可在甲苯的苯环或侧链上发生取代反应 B ．苯酚钠溶液中通入2CO 生成苯酚，则碳酸的酸性比苯酚弱 C ．乙烷和丙烯的物质的量功1mol ，完成燃烧生成3mol 2H O D ．光照下2，2-二甲基丙烷与2Br 反应其一溴取代物只有一种 12．下列热化学方程式数学正确的是（H 的绝对值均正确）A ．25222C H OH(1)+3O (g)=2CO (g)+3H O(g);ΔH=-1367.0kj/mol （燃烧热）B ．2NaOH(aq)+HCl(aq)=NaCl(aq)+H O(l);ΔH=+57.3kj/mol （中和热）C ．222S(s)+O (g)=SO (g)=SO (g;)ΔH=-269.kj/mol （反应热）D ．222NO =O +2NO;ΔH=+116.2kj/mol （反应热） 13．各可逆反应达平衡后，改变反应条件，其变化趋势正确的是14.密闭有空气的薄塑料瓶因降温而变扁，此过程中瓶内空气（不计分子势能） A ．内能增大，放出热量 B 内能减小，吸收热量C ．内能增大，对外界做功D 内能减小，外界对其做功15.同一音叉发出的声波同时在水和空气中传播，某时刻的波形曲线见题15图，以下说法正 确的是A ．声波在水中波长较大，b 是水中声波的波形曲线。

2009年普通高等学校招生全国统一考试（重庆卷）文科综合能力测试试题卷文科综合能力测试试题分选择题和综合题两部分。

第一部分（选择题）1至8页，第二部分（综合题）9至12页，共12页。

满分300分。

考试时间150分钟。

注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3.答综合题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在答题卷上答题无效。

5.考试结束后，将试题卷和答题卡一并交回。

第一部分（选择题）本部分共35题，每题4分，共140分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

图1为地球公转轨道示意图。

读图回答1-2题。

1.地球从甲运行到乙期间，重庆的正午太阳高度A.逐渐减小B.逐渐增大C.先减小后增大D.先增大后减小【解析】甲处位于近日点附近，为冬至日，从甲运行到乙期间，太阳直射点逐渐北移，因此重庆的正午太阳高度逐渐增大。

【答案】B2.当地球在甲位置时A.黄河流域进入汛期B.南极昆仑站正值极夜C.三峡水库处于蓄清期D.潘帕斯草原处于枯黄期【解析】当地球在甲位置时，为北半球的冬至日，太阳直射在南回归线，黄河流域进入枯水期，南极昆仑站正值极昼，潘帕斯草原处于夏季。

三峡水库在汛期6-9月“排浑”，讯末10月，开始蓄水，实现“蓄清”。

【答案】C读图2，回答3-5题。

3.下列地区气候类型与甲地相同的是A.德干高原B.巴西高原C.黄土高原D.伊朗高原4.乙气候类型区的地带性土壤是A.棕壤B.黑土C.黄壤D.红壤5.甲、乙两地可能种植的主要经济作物分别是A.咖啡、甜菜B.花生、咖啡C.甜菜、亚麻D.亚麻、花生【解析】甲地月均温都在15°C以上，为热带气候类型，降水季节分配不均，为南半球的热带草原气候，对应的地区是巴西高原。

绝密 ★ 启封前2009年普通高等学校招生全国统一考试（重庆卷）理科综合能力测试第一部分（选择题 共126分）14.密闭有空气的薄塑料瓶因降温而变扁，此过程中瓶内空气（不计分子势能）A ．内能增大，放出热量B 内能减小，吸收热量C ．内能增大，对外界做功D 内能减小，外界对其做功答案：D15.同一音叉发出的声波同时在水和空气中传播，某时刻的波形曲线见题15图，以下说法正确的是（ ）A ．声波在水中波长较大，b 是水中声波的波形曲线。

B ．声波在空气中波长较大，b 是空气中声波的波形曲线C ．水中质点振动频率较高，a 是水中声波的波形曲线D ．空气中质点振动频率较高，a 是空气中声波的波形曲线答案：A16.某科学家提出年轻热星体中核聚变的一种理论，其中的两个核反应方程为11H +126C →137N +1Q11H +157N →126C +X+2Q 方程式中Q 1、2Q 表示释放的能量，相关的原子核质量见下表：A X 是32He ，21Q Q > B. X 是42He ，21Q Q >C, X 是32He ，21Q Q < D. X 是42He ，21Q Q <答案：B17.据报道，“嫦娥一号”和“嫦娥二号”绕月飞行器的圆形轨道距月球表面分别约为200Km 和100Km ，运动速率分别为v 1和v 2，那么v 1和v 2的比值为（月球半径取1700Km ）A. 1918 D. 1819 答案：C18.某实物投影机有10个相同的强光灯L 1～L 10(24V/200W)和10个相同的指示灯X 1～X 10(220V/2W),将其连接在220V 交流电源上，电路见题18图，若工作一段时间后，L 2 灯丝烧断，则（ ）A. X 1的功率减小，L 1的功率增大B. X 1的功率增大，L 1的功率增大C, X 2功率增大，其它指示灯的功率减小D. X 2功率减小，其它指示灯的功率增大答案：C19.在题19图所示电路中，电池均相同，当电键S 分别置于a 、b 两处时，导线MM'与NN' ，之间的安培力的大小为 a f 、 b f ，判断这两段导线（ ）A.相互吸引，a f ＞b fB.相互排斥， a f ＞ b fC.相互吸引， a f ＜ b fD.相互排斥， a f ＜ b f答案：D20.题20图为一种早期发电机原理示意图，该发电机由固定的圆形线圈和一对用铁芯连接的圆柱形磁铁构成，两磁极相对于线圈平面对称，在磁极绕转轴匀速转动过程中，磁极中心在线圈平面上的投影沿圆弧 XOY 运动，（O 是线圈中心），则（ ） A.从X 到O,电流由E 经G 流向F ，先增大再减小B.从X 到O,电流由F 经G 流向E ，先减小再增大C.从O 到Y,电流由F 经G 流向E ，先减小再增大D. 从O 到Y ,电流由E 经G 流向F ，先增大再减小答案：D21.用a 、b 、c 、d 表示四种单色光，若①a 、b 从同种玻璃射向空气，a 的临界角小于b 的临界角；②用b 、c 和d 在相同条件下分别做双缝干涉实验，c 的条纹间距最大③用b 、d 照射某金属表面，只有b 能使其发射电子。

一绝密★启用前2009年普通高等学校招生全国统一考试（重庆卷）英语英语试题卷共16页。

满分150分。

考试时间120分钟。

一、听力（共三节，满分30分）做题时，请先将答案划在试题卷上。

录音内容结束后，你将有两分钟的时间将试题卷上的答案转涂或转填到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）请听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试题卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt？A. 19.15. B. 9.15.C. 9.18.答案是B。

1. Where is the woman from?A. Japan. B. England. C. Australia.2. How many children does the woman have?A. Two. B. Three. C. Five.3. What does the woman suggest?A. Going to town.B. Seeing a movie.C. Having a meal.4. What is the woman going to do?A. Stay for tea.B. Buy some fruits.C. Go back home.5. What is the conversation mainly about?A. The woman’s study.B. The woman’s friend.C. The woman’s trouble.【答案】CBCBA第二节（共12小题；每小题1.5分，满分18分）请听下面4段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试题卷的相应位置。

听每段对话或独白前，你将有时间阅读各小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。