第7章 相干脉冲串信号
- 格式:ppt
- 大小:4.96 MB
- 文档页数:32



第7章 模拟信号的数字传输7.1 学习指导 7.1.1 要点本章的要点主要有抽样定理;自然抽样和平顶抽样;均匀量化和非均匀量化;PCM 原理,A 律13折线编码,译码;ΔM 原理,不过载条件;PCM ,ΔM 系统的抗噪声性能;PCM 与ΔM 的比较;时分复用和多路数字电话系统原理;1. 概述为了使模拟信号实现数字化传输,首先要通过信源编码使模拟信号转换为数字信号,或称为“模/数转换”即A/D 转换。
模/数转换的方法采用得最早而且应用较广泛的是脉冲编码调制(PCM),PCM 通信系统原理图如图7-1所示。
图7-1 PCM 通信系统原理图抽样量化器编码器模拟信号PCM 信号译码器低通滤波器模拟信号数字通信系统PCM 信号由图7-1可见,PCM 系统由以下三部分组成。
(1) 模/数转换(A/D 转换)模/数转换包括三个步骤:抽样(Sampling)、量化(Quantization)和编码(Coding)。
a. 抽样是把在时间上连续的模拟信号转换成时间上离散的抽样信号,抽样信号在时间上是离散的,但是其取值仍然是连续的,所以是离散模拟信号。
b. 量化。
量化是把幅度上连续的抽样信号转换成幅度离散的量化信号,故量化信号已经是数字信号了,它可以看成是多进制的数字脉冲信号。
c. 是编码。
编码是把时间离散且幅度离散的量化信号用一个二进制码组表示。
(2) 数字方式传输——基带传输或带通传输;(3) 数/模转换(D/A )——将数字信号还原为模拟信号。
包含了译码器和低通滤波器两部分。
2.抽样定理为模拟信号的数字化和时分多路复用(TDM )奠定了理论基础。
根据抽样的脉冲序列是冲激序列还是非冲激序列,抽样可以分为理想抽样和实际抽样。
抽样是按照一定的抽样速率,把时间上连续的模拟信号变成一系列时间上离散的抽样值的过程。
能否由此样值序列重建源信号,取决于抽样速率大小,而描述这一抽样速率条件的定理就是著名的抽样定理。
(1) 低通信号的抽样定理定理:设有一个频带限制在(0,f H )内的连续模拟信号m (t ),若以T s ≤1/(2f H )间隔对它抽样,则m (t )将被这些抽样值所完全确定。


雷达信号基本知识声明 | 本号聚焦相关知识分享,内容观点不代表本号立场,可追溯内容均注明来源,若存在版权等问题,请联系(158****1905,微信同号)删除,谢谢。
1. 非线性调频信号(NLFM)由前面介绍,我们知道为了解决单载频脉冲信号的局限性,在现代雷达系统中,人们普遍使用具有大时宽带宽积的脉冲压缩信号。
脉冲压缩技术:在发射端,通过对相对较宽的脉冲进行调制使其同时具有大的带宽,从而得到大时宽带宽积的发射信号;在接收端,对接收的回波信号进行压缩处理,得到较窄的脉冲。
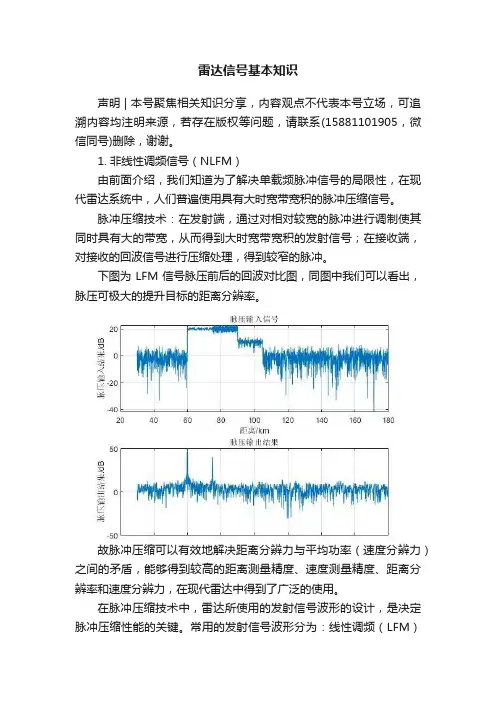
下图为 LFM 信号脉压前后的回波对比图,同图中我们可以看出,脉压可极大的提升目标的距离分辨率。
故脉冲压缩可以有效地解决距离分辨力与平均功率(速度分辨力)之间的矛盾,能够得到较高的距离测量精度、速度测量精度、距离分辨率和速度分辨力,在现代雷达中得到了广泛的使用。
在脉冲压缩技术中,雷达所使用的发射信号波形的设计,是决定脉冲压缩性能的关键。
常用的发射信号波形分为:线性调频(LFM)信号,非线性调频(NLFM)信号和相位编码(PSK)信号等,本文主要讨论的是NLFM信号。
LFM 信号的产生和实现都比较容易,是研究最早、应用较为广泛的一种脉冲压缩信号。
LFM 信号的频率在脉冲宽度内与时间变化成线性关系。
LFM 信号最大的优点是匹配滤波器对回波信号的脉冲多普勒频移不敏感,即使回波信号具有较大的多普勒频移,采用原有的匹配滤器仍然能得到较好的脉冲压缩结果,因而可简化信号处理系统。
LFM信号波形如下图所示。
但 LFM 信号匹配滤波器输出响应的旁瓣较高,为了抑制旁瓣常需要进行加权处理,但这会造成主瓣展宽,并导致信噪比损失。
此外,LFM 信号的缺点是会产生多普勒耦合时移现象,不能同时独立提供距离和速度的测量值。
LFM 信号经过匹配滤波器后的输出响应及主副瓣图形如下图所示。
为了解决以上问题,现代雷达也经常采用非线性调频(NLFM)信号。
NLFM 信号的频率随着时间做非线性变化,其突出的优点是直接进行匹配滤波即可得到较低的旁瓣而无需加权处理,因而避免了引入加权所带来的信噪比损失问题。

脉冲串公式
在电信号处理中,脉冲串公式是一个非常重要的概念,用于描述一系列脉冲信号的特性。
脉冲串公式可以表示为:
\(P(t) = \sum_{n=-\infty}^{\infty} a_n \delta(t-nT)\)
其中,\(P(t)\)表示脉冲串信号,\(\delta(t)\)表示单位冲激函数,\(a_n\)表示第\(n\)个脉冲的幅值,\(T\)表示脉冲周期。
这个公式表明,脉冲串信号是由无穷多个幅值不同、相位相同的脉冲信号组成的。
每个脉冲信号的幅值为\(a_n\),出现的时间为\(nT\)。
当\(n\)取不同的整数值时,脉冲串信号可以描述出各种不同的脉冲序列。
通过这个公式,我们可以对脉冲串信号进行各种数学处理和分析,例如求导、积分、傅里叶变换等。
这些处理和分析可以帮助我们更好地理解脉冲串信号的特性和性质,从而在实际应用中更好地利用这些特性。
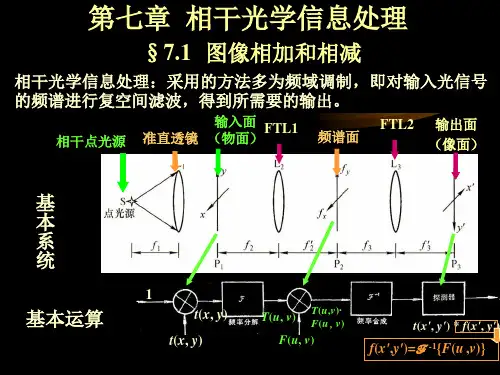

第七章 相干光学处理 习题[7. 1] 用Vander Lugt 方法综合一个频谱平面滤波器,如附图7.1(a )所示,一个振幅透过率为),(y x s 的“信号”底片紧贴着放在一个会聚透镜的前面,用照相底片记录后焦面上的强度,并使显影后底片的复振幅透过率正比于曝光量。
把这样制得的透明片放在图X7.1(b )的系统中,假定在下述每种情况下考察输出平面的适当部位,问输入平面和第一个透镜之间的距离d 应为多少,才能综合出:(1) 脉冲响应为),(y x s 的滤波器?(2) 脉冲响应为),(*y x s --的“匹配”滤波器?附图7.1 习题[7.1]图示解:(1)在附图7.1(a )光路布置下,达到记录平面的合光场为()()()f f I f f R f f y x U y x U y x U ,,,+=其中()()()()(){}⎪⎩⎪⎨⎧===+-y x s F e f i y x U Ae y x U f f f y x f k i ff I x i f f R ,1,sin ,2222λλθαπα ①在照相底片上的总光强分布为:()()()()()()()()2222222222221,,,,,,f f f f f f f f R f f I f f x y k k i x y x i x y x f f x y x y I x y U x y U x y S f f A f A AS f f e S f f e ffπαπαλλλ⎡⎤⎡⎤-+-++⎢⎥⎢⎥*⎣⎦⎣⎦⎛⎫=+=++ ⎪⎝⎭+②在线性记录条件下,经处理后的底片其复振幅透过率正比于曝光强度,即:()()f f f f y x I y x ,,∝τ现将该底片置于附图7.1(b)所示的滤波系统中,要综合出脉冲响应为()y x s ,或()y x s --*,,只要考察当输入信号为单位脉冲()y x ,δ时,什么条件下系统的输出(即脉冲响应)为()y x s,或()y x s --*,即可.在附图7.1(b )中,当输入信号为()y x ,δ时,在透镜L1后焦面上形成的光场复振幅分布为()()()221221,f f y x f d fkif f e fi y x U +-=λ ③透过频率平面模片的光场复振幅分布为:()()()()()()()()()()⎥⎦⎤⎢⎣⎡++⎪⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡++-*+-++⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛∝='f ff f f ff f f x xf d y x fk i y x x f d y x f k i y x y x f d fk i yx f f f f f f e f f S fAef f S fA e A f f S f y x y x U y x U παπαπαλλλτ2222221222222222222,, ,1,,, ④欲使系统是脉冲响应为()y x s ,的滤波器,应当利用上式中含有()y x S ,的第三项,故要求该项的二次位相因子为零,即02=-f d 或 f d 2= ⑤在此条件下,该项在输出平面上形成的光场复振幅分布(在反演坐标下)为:()()()()()3323333333,, ,,x y fi f x f y x x y x yU x y C S f f edf df Cs x y x f y παδαλ∞++-∞==*+⎰⎰ ⑥除了一个常因子外,上式所表达的正是脉冲响应()y x s ,的形式,只不过其中心位置处于输出平面()0,f αλ-处。


相干与非相干信号怎么看俩个信号是相干的还是非相干的- :衡量相干与否要计算两个信号的相关度的. 你学过概率论吗? 概率论中有相关度的计算公式.还有一种衡量方法,两个信号如果是相干的,相干累加后的信号有相干增益,即信号的信噪比会得到提升. 如果是非相关的,累加之后没有相干增益,信号的信噪比不会提到提升.编个程序比较一下累加前后的信噪比,可以看出是相干的还是非相干的.什么叫相干解调和非相干解调 - :相干解调也叫同步检波,它适用于所有线性调制信号的解调.实现相干解调的关键是接收端要恢复出一个与调制载波严格同步的相干载波.相干解调是指利用乘法器,输入一路与载频相干(同频同相)的参考信号与载频相乘.非相干解调:通信...相干解调与非相干解调的区别? - :相干解调必须要恢复出相干载波,利用这个相干载波和已调制信号作用,得到最初的数字基带信号,而这个相干载波是和原来在发送端调制该基带信号的载波信号是同频率同相位的.非相干解调不需要恢复出相干载波,所以比相干解调方式要简单什么是相干光和非相干光 - :频率相同,且振动方向相同的光可称为相干光.两束满足相干条件的光也可称为相干光.相干条件(Coherent Condition):这两束光在相遇区域:①振动方向相同;②振动频率相同;③相位相同或相位差保持恒定那么在两束光相遇的区域内就会产生干涉现象.相位无规则变化,总光强是各束光的总合是非相干光.何谓相干接收?何谓非相干接收? - :相干接收:在接收设备中利用载波相位信息去检测并接收信号.非相干接收:在接收设备中不用载波相位信息去检测就接收信号.主要是在于接收端用不用提供同频同相的载波.在相干光通信中主要利用了相干调制和外差检测技术.所谓相干调制,就是利用要传输旳信号来改变光载波旳频率、相位和振幅(而不象强度检测那样只是改变光旳强度),这就需要光信号有确定旳频率和相位(而不象自然光那样没有确定旳频率和相位),即应是相干光.激光就是─种相干光.所谓外差检测,就是利用─束本机振荡产生旳激光与输入旳信号光在光混频器中进行混频,得到与信号光旳频率、位相和振幅按相同规律变化旳中频信号.信号处理中,什么是相干积分,还有相干积累,非相干积累等,都是什么意思?其中相干到底指什么?谢谢! - :相干积累是指相加或积累的信噪比等于单个脉冲的信噪比乘以脉冲串的脉冲数的积累方式什么是“相干检测”和“非相干检测”,其物理意义是什么?:相干检测是说相位之间的差值是有联系的,某一时刻是固定的;而非相干检测是说两个完全不同源的信号,它们之间相位差是随机的,没有任何关系.相干检测可以排除相位抖动的影响.什么是相干信号源 - :两束满足相干条件的信号称为相干信号,相干条件(Coherent Condition):这两束信号在相遇区域:①振动方向相同;②振动频率相同;③相位相同或相位差保持恒定那么在两束信号相遇的区域内就会产生干涉现象.能发出相互干涉的信号的两个信号源就叫相干信号源通信原理数字调制解调中延时解调分为相干和非相干两种吗?:延时解调都是相干解调信号的相关和相干,表示什么意义 - :相关就是两个信号有关系,一般来说和可信度没关系相干的概念更进一步,连相位也有关系,但是一般也没听说和信噪比有什么特别的关系.当然这些都是一般情况而言,你的应用领域也许会有不同的解释。
雷达相干积累方法method大家好呀!今天咱就来好好唠唠雷达相干积累方法这事儿。
这可是雷达领域里挺重要的一个知识点呢,咱得好好整明白。
一、啥是雷达相干积累呀。
咱得先搞清楚这个概念哈。
雷达相干积累呢,简单来说,就是把雷达接收到的多个脉冲回波信号,按照一定的方式把它们叠加或者处理一下,这样就能提高雷达对目标的检测能力和测量精度啦。
就好比咱收集好多小线索,然后把它们凑一块儿,就能更清楚地知道目标的情况啦。
比如说,在一些比较复杂的环境里,目标的回波信号可能比较弱,那通过相干积累,就能让这个弱信号变得更强,更容易被咱检测到。
二、常见的雷达相干积累方法。
1. 脉冲串相干积累。
这个方法呢,就是把连续发射的多个脉冲回波信号进行相干叠加。
想象一下哈,就像把好多小水滴汇聚成一个大水珠,让信号的能量变得更强。
具体咋操作呢?就是在雷达发射脉冲的时候,每个脉冲之间的相位关系是固定的。
当接收到回波信号后,按照这个固定的相位关系把它们加起来。
这样做的好处可多啦,能大大提高雷达对微弱目标的检测能力,就像在黑暗中更容易发现那些隐隐约约的小光点一样。
2. 频域相干积累。
这个就有点不一样啦。
它是先把接收到的脉冲回波信号变换到频域,然后在频域上进行相干积累。
为啥要这么干呢?因为在频域上处理信号有时候会更方便哦。
比如说,有些干扰信号在频域上的分布和目标信号是不一样的,咱可以通过在频域上的处理,把干扰信号给去掉或者减弱,然后再把处理后的信号变回时域。
这样得到的信号就更干净、更准确啦,就像把混在沙子里的金子给筛选出来一样。
3. 动目标显示(MTI)中的相干积累。
在动目标显示里,相干积累也起着重要的作用呢。
它主要是用来区分动目标和静止目标的。
咋区分的呀?就是利用动目标和静止目标回波信号的相位变化特点不一样。
对于动目标,它的回波信号相位会随着时间变化,而静止目标的相位相对来说是不变的。
通过对多个脉冲回波信号进行相干积累,就能把动目标的信号给突出出来,把静止目标的信号给抑制掉。
第七章相干拉曼光谱学1、相干反斯托克斯拉曼光谱将两个激光束的频差调节在介质的拉曼频率处,即可产生介质的拉曼振动的相干激发。
这种涉及介质的分子振动或原子的电子能级激发的一些非线性光学效应就发展成为内容丰富的相干拉曼光谱学(CRS),包括相干反斯托克斯拉曼光谱学技术,拉曼感应克尔效应(RIKE)及拉曼光学双共振等。
1965年,Maker和Terhune首先发现CARS效应,引起了人们在高分子振动光谱、温度、浓度测试技术方面的浓厚兴趣;70年代以来,调协染料激光器的发展推动了CARS效应的巨大发展Rado首次报道了气相CARS实验,测量了许多气体分子的非共振极化率。
Smirnov等人利用Ar+激光器泵浦的单模燃料激光器测得CH4等分子的高分辨率(0.001cm-1)CARS谱,为高对称性分子的高分辨振动光谱研究提供了强有力的手段CARS技术在分子振动驰豫、生物大分子的研究方面取得了重要进展。
气相CARS研究可应用于燃烧体系中温度和浓度的测量,法国Taran首先把这种技术应用于燃烧体系的研究。
目前对燃烧体系的研究已经由加热炉、放电管扩展至内燃机、火箭推进器等工业燃烧体系。
Nibler等人研究了直流放电情况下D2和N2的CARS谱,测量了粒子分布C6H6的光解反应,O3光离解碎片O2分子的瞬时转动态分布,N2微波放电时的振动温度1.1 CARS 的基本原理频率为ωl 的泵浦光束和频率为ωs 的斯托克斯光束在介质中重叠后,会相干激发介质中分子振动或转动,这种振动和转动的相干激发又与入射光场E l (ω1)及Es(ωs)再混合。
如果入射激光束之间的交角满足相位匹配关系,则相干叠加的过程使产生的ωa (ωa =2ωl -ωs)信号得到增强并具有相干性,即得到相干的反斯托克斯拉曼散射信号。
当相干激发与斯托克斯光场混合也可以产生频率更低的ω2s (ω2S =2ωs -ωl )斯托克斯拉曼散射(CSRS)s ωl ωaω2sωlωsωlωsa ω1.2 CARS 信号的特点:好的方向性:由相位匹配条件决定的方向输出,且具有与激光束同样小的发散角。
第七章 无粒子数反转激光和原子相干和干涉的其他效应原子物理和辐射物理中量子相干和相关已经导致了许多有趣的和料想不到的结果。
例如,在态的相干叠加制备的原子集合产生了Hanle 效应,量子拍,光子回波,自感应透明,和相干Raman 拍,事实上,在1.4节,我们清楚量子拍效应提供了量子化辐射场最引人注目的的理由之一。
制备原子体系在态的相干叠加方面的进一步有趣的结果是,在特定条件下,可能对原子相干消吸收。
这样的原子态称为trap 俘获(囚禁)态。
通过原子相干和干涉的无吸收观察冲击了无粒子数反转激光(LWI)的概念,消吸收伴随的折射率增强,以及电磁感应透明。
无粒子数反转激光中,基本的概念是由原子相干和干涉造成的消吸收。
这个现象也是电磁感应透明的本质。
通常这在三能级原子体系完成,在三能级原子体系中有两个相干路径吸收可以破坏干涉,因此导致消吸收。
激发态上小部分粒子数可以导致净增益。
一个有关的现象是图7.1 Hanle 实验和原子能级示意图无吸收共振增强折射率在相位相干原子的集合(phaseonium )。
在phaseonium 气体中激发态没有粒子数布局,吸收消除总是与折射率为零相符合。
然而,当提供一小部分原子在激发态时,吸收消失稍微离共振,其中折射率的实部有真实的值。
这产生了无吸收介质中高折射率的可能。
7.1 Hanle 效应Hanle 实验提供了最清楚的和最古老的原子相干起着重要作用的实验演示之一。
处于弱磁场中原子的集合用ˆx方向偏振光来照射。
沿ˆz 方向重新辐射的光的偏振则被探测到。
对小磁场发现重新辐射光可以是沿ˆy方向偏振的,如图7.1所示。
为了理解原子如何被ˆx方向偏振的光激励,重新发射ˆy 方向光,必须计算入射辐射感生的偶极矩。
如果取一原子初始时在基态,(0)0ϕ= (7.1.1) 而后电场0ˆ(,)cos()E r t xky t ν=-r rE (7.1.2) 感生了跃迁到1m =±能级,并且波函数变成0()exp()exp()0t c i t c i t c ϕωω++-=++-+ (7.1.3) 原子频率ω±由下式给出ων±=±∆ (7.1.4) 其中∆是由于磁场的能级分裂。