§ 各配分函数的求法及其对热力学函数的贡献
- 格式:ppt
- 大小:548.00 KB
- 文档页数:33

第七章统计热力学基础教学目的与要求:通过本章的教学使学生初步了解统计热力学的基本研究方法,各种独立子系统的微观状态数的求法,不同系统的统计规律,系统的各热力学函数的表示式,配分函数的计算,固体的热容理论导出的基本思路。
重点与难点:统计热力学的基本研究方法,不同系统的微观状态数的计算,玻尔兹曼分布律的含义,系统的热力学函数的表示式,配分函数的计算,不同的固体热容理论的基本方法。
§7.1 概论统计热力学的研究任务和目的统计力学的研究对象是大量微观粒子所构成的宏观系统。
从这一点来说,统计热力学和热力学的研究对象都是一样的。
但热力学是根据从经验归纳得到的四条基本定律,通过演绎推理的方法,确定系统变化的方向和达到平衡时的状态。
由于热力学不管物质的微观结构和微观运动形态,因此只能得到联系各种宏观性质的一般规律,而不能给出微观性质与宏观性质之间的联系。
而统计热力学则是从物质的微观结构和基本运动特性出发,运用统计的方法,推导出系统的宏观性质,和变化的可能方向。
统计力学的研究方法是微观的方法,它根据统计单位(微粒)的力学性质如速度、动量、位置、振动、转动等,用统计的方法来推求系统的热力学性质,例如压力、热容、熵等热力学函数。
统计力学建立了体系的微观性质和宏观性质之间的联系。
从这个意义上,统计力学又可称为统计热力学。
相对于热力学,统计力学对系统的认识更深刻,它不但可以确定系统的性质,变化的方向和限度,而且还能确定系统的性质的微观根源,这一点要比热力学要深刻。
对于简单系统,应用统计热力学的方法进行处理,其结果是令人满意的。
当然统计热力学也有自身的局限性,由于统计力学要从微观粒子的基本运动特性出发,确定系统的状态,这就有一个对微观粒子的运动行为的认识问题。
由于人们对于物质结构的认识不断深化,不断地修改充实物质结构的模型,所对统计理论和统计方法也要随之修改,所以统计理论是一种不断发展和完善的。
同时模型本身也有近似性,所以由此得到的结论也有近似性。

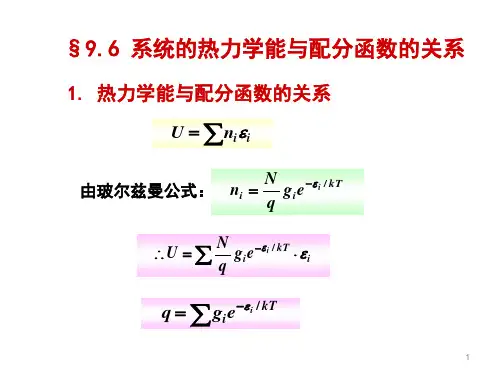


热力学配分函数热力学中,配分函数是一个非常重要的概念。
它是一种函数,用于描述一个系统处于不同的能量状态下的概率分布。
在统计物理学中,配分函数通常用于计算热力学量,如内能、熵和自由能等。
配分函数的定义与系统的哈密顿量有关。
对于一个具有N个粒子的系统,其哈密顿量可以表示为H = ∑i=1N hi其中,hi是每个粒子的能量。
假设系统总能量为E,那么系统的所有可能状态数可以用下面的式子计算:Ω(E) = ∫···∫d3Nq1···d3NqNδ(EH(q1,...,qN))其中,q1,...,qN是系统所有粒子的位置和动量,δ是狄拉克δ函数。
这个式子的意义是,系统总能量为E的所有可能状态数,等于所有粒子的位置和动量满足哈密顿量为E的状态数之和。
在统计物理学中,我们通常更关注系统的宏观性质,而不是具体的粒子位置和动量。
因此,我们需要将Ω(E)转化为一个更容易处理的函数。
这个函数就是配分函数Z,它定义为Z = ∫···∫d3Nq1···d3NqNeβH(q1,...,qN)其中,β=1/kBT,T是系统的温度,kB是玻尔兹曼常数。
配分函数的物理意义是,它描述了系统处于不同能量状态的概率分布。
具体来说,系统处于能量为E的状态的概率可以用下面的式子计算:P(E) = Ω(E) eβE / Z其中,Ω(E)是系统总能量为E的所有可能状态数。
配分函数的作用是将所有可能的状态数归一化,使得概率分布满足归一化条件。
配分函数不仅可以用来计算概率分布,还可以用来计算热力学量。
例如,系统的内能可以用下面的式子计算:U = lnZ/β系统的熵可以用下面的式子计算:S = kB lnZ + βU系统的自由能可以用下面的式子计算:F = U TS = kB T lnZ配分函数是热力学中非常重要的一个概念,它在理论物理、化学、材料学等领域都有广泛的应用。


物理化学电子教案第七章统计热力学基础物理化学教研室【基本概念·基本知识】1、统计热力学系统的分类:独立/非独立粒子系统、可别/不可别粒子系统2、独立粒子系统的分布、最可几分布、平衡态分布3、系统的微观状态4、粒子的配分函数5、转动特征温度,振动特征温度6、焓函数、吉布斯自由能函数7、统计熵、量热熵【基本定律与基本理论】1、等几率假设2、玻兹曼分布定律(推导和表达式的意义)3、Maxwall 速率分布的意义及与平动有关的各种统计平均值4、粒子配分函数与热力学函数的关系5、最低能级能量数值的选取对配分函数的影响6、双原子分子转动、振动、平动的能级公式7、波兹曼公式:ln S k =Ω8、热力学定律的统计解释【基本计算与基本方法】1、独立可别与不可别粒子系统Ω的计算2、用波兹曼分布定律计算简单系统的粒子分布3、单原子分子、双原子分子各种运动形式的配分函数4、单原子及双原子分子各种运动形式对热力学性质的贡献5、分别用配分函数和自由能函数计算简单理想气体反应的平衡常数第一讲:统计热力学概论·Boltzmann 统计一、统计热力学概论(一)、统计热力学的基本任务1、统计热力学的基本任务回 顾:A 、 经典热力学的任务:a )解决某一过程的能量衡算;b )过程的方向判断据; 基础:热力学三定律;优点:着眼与系统的状态而不依赖系统的微观结构,高度可靠; 缺点:无法描述系统的微观结构和微观运动规律B 、统计热力学的任务:用统计学的原理,从系统的微观结构和运动状态出发,揭示系统宏观性质的本质。
物质的宏观性质本质上是微观粒子不停地运动的客观反映,虽然每个粒子都遵守力学定律,但是无法用力学中的微分方程去描述整个系统的运动状态,所以必须用统计学的方法。
根据对物质结构的某些基本假定,以及实验所得的光谱数据,求得物质结构的一些基本常数,如核间距、键角、振动频率等。
利用这些数据可以计算分子配分函数,再根据配分函数求出物质的热力学性质,这就是统计热力学的基本任务。




南京理工大学研究生入学物理化学考试大纲绪论§ 0-1物理化学目的和内容§ 0-2物理化学的研究方法和学习方法§ 0-3气体概述第一章热力学第一定律及其应用§ 1-1 热力学概论①体系与环境;②体系的性质;③热力学平衡态和状态函数;④过程;⑤热和功。
§ 1-2 热力学第一定律①内能; ②热力学第一定律。
§ 1-3 准静态过程和可逆过程;①准静态过程;②可逆过程。
§ 1-4 焓§ 1-5 热容①热容;②恒压热容与恒容热容。
§1-6 热力学第一定律对理想气体的应用①盖·吕萨克一焦耳实验;②理想气体的内能与焓;③理想气体的Cp与Cv;④在物质的P、V、T变化、相变化、化学变化中计算Q、W、△U、△H值;⑤绝热过程方程式与绝热过程中Q、W、△U、△H计算;⑥等温过程中Q、W、△U、△H计算;⑦等压过程中Q、W、△U、△H计算;⑧等容过程中Q、W、△U、△H计算;⑨相变过程中Q、W、△U、△H 计算。
§ 1-7 实际气体①焦耳一汤姆逊效应;②实际气体的△H和△U。
§1-8 热化学①化学反应的热效应;②等压热效应和等容热效应;③反应进度;④热化学方程式。
§1-9 赫斯定律§1-10 几种热效应①化合物的标准生成焓;②燃烧焓;③离子生成焓;§ 1-11反应热和温度的关系---基尔霍夫定律①基尔霍夫公式。
§1-12 绝热反应一非等温反应①最高火焰温度的计算。
第二章热力学第二定律§ 2-1 自发变化共同特征一不可逆性①自发变化;②自发变化的共同特征。
§2-2 热力学第二定律①热力学第二定律的文字表述。
§2-3 卡诺定理①卡诺循环;②卡诺定理。
§ 2-4 熵的概念①熵§2-5 克劳修斯不等式与墒增加原理①克劳修斯不等式;②熵增加原理。
各配分函数的计算配分函数(partition function)是统计物理学中一个重要的概念,用于描述系统在不同能级上分布的概率。
根据系统的不同性质,配分函数可以分为经典配分函数和量子配分函数两种。
1.经典配分函数:经典配分函数描述的是经典力学体系中,粒子在不同能级上的分布情况。
对于一个具有N个粒子的经典体系,经典配分函数的表达式为:Z = Σexp(-βEi)其中,Z表示配分函数,β为热力学倒数,Ei为体系的不同能级。
Σ表示对所有能级求和。
经典配分函数的计算需要知道体系的能级和相应的能量。
对于简单的模型,如经典气体或固体的振动模型,能级和能量可以推算出来。
对于更复杂的体系,如相互作用粒子的分子力学模拟,需要借助计算方法,如动力学模拟、分子动力学方法等,获得能级和能量。
通过计算经典配分函数,可以得到系统的热力学性质,如内能、自由能、压强等,从而研究体系的宏观行为。
2.量子配分函数:量子配分函数描述的是量子力学体系中,粒子在不同能级上的分布情况。
由于量子力学的存在,不同能级之间存在着零点振动和波粒二象性效应。
量子配分函数的计算与经典配分函数略有不同。
一个具有N个粒子的量子体系的配分函数可记作:Z = Tr(exp(-βH))其中,Z为配分函数,β为热力学倒数,H为系统的哈密顿算符。
Tr表示对系统的所有态进行求和或求迹。
量子配分函数的计算在大多数情况下是非常困难的。
需要借助矩阵对角化或者数值方法,如矩阵迭代法、变分法等。
对于一些简单的系统,如理想玻色气体或费米气体,可以根据粒子的自旋来推导出精确的配分函数。
通过计算量子配分函数,可以得到量子体系的热力学性质,如内能、自由能、压强等。
通过对量子配分函数的研究,可以揭示出量子效应对系统性质的影响,如玻色-爱因斯坦凝聚、费米-狄拉克凝聚等。
总之,配分函数是描述统计物理体系中粒子分布情况的重要工具。
通过计算配分函数,可以得到体系的热力学性质,并进一步了解体系的宏观行为。