当前位置：文档之家 › 热力学函数间的关系

热力学函数间的关系

  • 格式：ppt
  • 大小：794.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

热力学函数的基本关系式

热力学函数的基本关系式

dU = TdS－ pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = －SdT－ pdV
(1-110)
dG = －SdT + Vdp
(1-111)
式(1-108)，(1-109)，(1-110)，(1-111)称为热力学基本方程
dU = TdS－ pdV dH = TdS + Vdp dA = －SdT－ pdV dG = －SdT + Vdp
常用的是式(1-120)及式(1-121)，这两等式右边的变化率是可以由 实验直接测定的，而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU＝TdS－pdV
定温下， dUT＝TdST－pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为：
即


(G / T )
T p


H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
（эG/эP）T，n=V
（э△G/эP）T，n=△V 此即G---V关系式
只要知道△V--p关系式，在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得： （△G）2/ T2- （△G）1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而： △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。

热力学函数的基本关系式

热力学函数的基本关系式

dG = －SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 ：表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法：
T p
S
V S
p
① 对角乘积永远是pV，TS；
② 等式两边分母与外角标互换；
S p
T
V T
4
由四个热力学基本方程，分别加上相应的条件，可得到
8个派生公式：
dU = TdS－ pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = －SdT－ pdV
A T
V
S
A V
T
p
dG = －SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习：由热力学基本方程出发证明，
H p
T
T
V T
p
V
证明：
dH＝TdS＋Vdp
定温下，等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程

热力学函数间关系及其相互变换

热力学函数间关系及其相互变换
证明： 先去掉U dU =TdS−pdV
恒压下，两边同时对S 求偏导
18
1.3 例证
或
19
1.3 例证
证明：
20
1.3 例证
任意绝热可逆过程膨胀后压力必降低。
21
中科院考研题
理想气体绝热膨胀时并不恒容，为什么仍可使用公式 dW=CvdT
dU U U U 答：dU dT dV 。 对理想气体 =0 ，故 dT T V V T V T U 或dU CV dT。因此在本例中dU d W CV dT 完全适用。 T V
热力学函数间关系及其相互变换
1
热力学函数间关系及其相互变换
两种情况:
一、U、H、S、F、G 等热力学量不能确定绝对值、 且不能通过设计实验直接测定，而p、V 、T、Cp 、 CV 、α、β、κ 等是可设计实验测定。而在研究U、H、 S、F、G 等变化规律时希望在不可测量与可测量的热 力学间建立起某些关系，从而取得某种规律性的认识
3
1.1 函数关系
三、定义式
四、Maxwell 关系
4 记忆口诀：“S−p、V−T，排成口字齐；平行求偏导，侧转找下 标”。
1.1 函数关系
◆ Maxwell 关系
5
1.1 函数关系
五、数学公式
Euler 关系
链关系：
倒易关系：
循环关系：
6
1.2 熵变换是函数变换之关键
（不含U、H、F、G）
24
25
二、科研和解决实际问题提出的许多命题要论证。
2
1.1 函数关系
一、基本方程
H = U+PV、 F=U-TS、 G = H-TS dU=TdS-pdV dF=-SdT-pdV dH=TdS+Vdp dG=-SdT+Vdp pV=nRT

3.7 热力学基本方程及Maxwell关系式

3.7 热力学基本方程及Maxwell关系式

恒T、p、W= 0： G 0
自发 平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明： 1. 等式右边只有四个物理量T，S， p，V
2. 十字交叉法：
对U来说，S，V分别表示dS和dV； dS对角线 对应T，dV对角线对应p；箭头方向表示正负，指向 为负，则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明：
1. 关系式中只有四个物理量T， S， p，V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量，而T和p为强 度量。同种性质的状态函数 的分式，不取负号。
分析：利用克拉佩龙方程 dT T βαVm
dp 解：由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分，得 lnT2
T1

热力学函数间的关系

热力学函数间的关系
T2 G2 G1 H = ∫ 2 dT T1 T2 T1 T rGm 2 rGm1 1 1 = rHm( ) T2 T1 T2 T1
r Gm ,2
1.400 × 105 1 1 5 ) = 1.966 × 10 ( 873 298 873 298
r Gm ,2 = 30820J mol -1
吉布斯－ 吉布斯－亥姆赫兹方程式
G T = H T2 T P
（微分形式）
应用：在等压下若已知反应在 应用：在等压下若已知反应在T1的rGm(T1)，则可求得该反 应在T 时的 应在 2时的rGm(T2)。 积分形式
∫
T2
T1
T2 G H ( ) = ∫ 2 dT T1 T T
( V V ) p dT = ( )T dp T p
1mol理想气体， PV = RT 理想气体， 理想气体 p T ( )p = , R V V V ( )T = , p p R p ( )V = V T 则 ( T ) p ( V )T ( p )V = 1
V p T
可写成
T V p ( )p( )T ( )V = 1 V p T
2010-8-2
三、Maxwell 关系式
证明： 例3证明：(
T V p )p( )T ( )V = 1 并以理想气体验证上式的正确。 并以理想气体验证上式的正确。 V p T
定量纯气体， 证： 定量纯气体， V = f (p,T)
dV = ( V V ) p dT + ( )T dp T p
当V恒定，dV = 0，则 恒定， ， 恒定
dU = Td S pdV
U S 等温对V求偏微分 等温对 求偏微分 ( )T = T ( )T p V V
S p S 不易测定，根据Maxwell关系式 ( )T = ( ) V 关系式 ( )T 不易测定，根据 V T V

热力学函数间的普遍关系式

热力学函数间的普遍关系式

不可逆过程 可逆过程 不可能过程
此式热力学第二定律的数学表达式之一，其中δQ为微循环中系 统从外界吸收的热量，T为吸热时热源的温度。
孤立系统的熵增原理：
孤立系统所进行的一切实际过程都朝着系统熵增 加的方向进行，在有限的情况下，系统的熵维持 不变，任何使系统熵减小的过程都是不可逆的。
S iso
0 0 0
U P V S H V p S A P V T G V p T
下变量N常常省略
A S T V G S T
因为U、H、A和G为热力学函数，因此他们的微分式是全 微分，因全微分的二阶偏导数与求导次序无关，从而得 到下列麦克斯韦关系式：
U U (S ,V ) H H ( S , p) A A(T ,V ) G G(T , p)
上述热力学基本关系式仅适用于摩尔数不变的均匀 系，如果考虑单组元系统摩尔数的变化，系统的广 延参数将取决于其摩尔数，这样上式就可扩展为：
U U ( S ,V , N ) H H ( S , p, N ) A A(T ,V , N ) G G (T , p, N )
V , S p, T V , T V , T p, S p, T
S T T V S V pT
p
由于热熔：
CV T S
并有：

T
V
C p T S
dH d (U pV ) TdS Vdp
dG SdT Vdp
dA SdT pdV
这四个式子，是组成固定物质的热力学基本微分关系式。

第二章 热力学函数及关系

第二章 热力学函数及关系
将上式改写为
d (U 0HM ) TdS pdV 0MdH 定义包括了磁介质在磁场中势能的内能：U * U 0HM ,则
dU * TdS pdV 0MdH
24
定义磁介质系统的吉布斯函数：G U * TS pV ,那么
dG SdT Vdp 0MdH
因为G是一个态函数，存在全微分，即在数学上
21
它常决定物体的性质，可看成是一个热力学系统， 状态参量：温度T、表面张力σ、表面积ξ。 物态方程：f (T,σ,ξ)=C, 外界对系统所做的功为
A d
dF SdT d
S F , T
F
T
注意：表面积扩大系外界对系统做功的结果，因此对于非气体 系统的广义位型变化前加一个负号。
22
下面这个图是解释表面张力的一个理想试验。一个光滑的金属 框，有一边是可以自由滑动的。把这个框在水里浸一下，框里 就形成一层水膜。水膜有上下两个表面。表面上的水分子有使 表面减小的倾向，所以必须施加一定的力F才能对抗这个力从 而保持住水膜面积。很显然，这个力F的大小与那个边的长度l 成正比。而这个比例是水的一种基本性质，与力F 和边l无关。 在界面科学里，这个比例被定义为表面张力，它的单位是力除 以长度，牛顿/米。
dG
G T
p,H
dT
G p
T
,H
dp
G H
T
,
p
dH
比较以上两个等式的右边对应项，可得
0M
G H
, T , p
V
G p
T ,H
对两者求混合偏导，有
0M
p
T
,
H
V H
T , p
此式将压缩效应（左边）与磁致伸缩效应（右边）

热力学函数的基本关系式

热力学函数的基本关系式
△S=QR/T; T △S= QR 故△G= △H- T △S=0- T △S= QR= WR=-RTlnP1/P2=5744Jmol-1 解法二： △G=∫ p1 p2Vdp = RTlnP2/P1=5744Jmol-1.
⑵等温等压相变△G 对于等温等压的可逆相变，直接可得（△G）T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G，可以通过设计可 逆过程进行计算，也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV，A =U-TS，G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′＝0时，则δWr＝－pdV，于是
一微小可逆过程
dU=δQr+δWr，
dS δ Qr T
δWr ′ ＝0时，则δWr＝－pdV，于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理，298K，1atm水不能经等温等压过程转变 为同温 同压的水蒸气，但其逆过程则是可以的。因此在298K， 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程：｛э（△G/T）/эT｝P=- △H/T2
△S=0，△T=0，△H=0，
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量，Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度，压力都不相等，根据G的定义：

第一章 热力学函数及其相互关系(1)

第一章 热力学函数及其相互关系(1)

第一章热力学函数及其相互关系（1）：热力学状态与气体方程系统与环境、平衡状态、非平衡状态、稳定状态、可逆过程与不可逆过程、局部平衡、部分平衡与介稳平衡、温标的发展、热力学温标、理想气体定律、van der Waals状态方程、virial方程、Redlich-Kwong方程、实际气体的液化与临界现象、对应态理论1.1系统、环境、热力学状态1.1.1 系统与系统的环境热力学把相互联系的客观真实世界区分为系统与系统的环境两部分。

系统(system)是我们要研究的那部分真实世界，即我们要研究的那部分物质或空间。

假如要研究一台运行着的热机汽缸内气体性质的变化，或者要研究一反应器中的全部物质，就分别是两种不同情况下的系统。

又如一氧气缸瓶在不断地向外喷射氧气，我们要研究喷射过程到某阶段时钢瓶中剩余氧气的性质，则该瞬间瓶中残留的氧应当是系统。

以往的书刊中曾用过一些系统的同义词，例如“物系”、“体系”等等。

系统的环境(surroundings)是系统以外与之相联系的真实世界，可以简单称为环境或外界。

需要指出，系统与环境之间可以有实际存在的边界隔开，例如上述汽缸、反应器壁等；也可能在系统与环境间只有假象的边界隔开，例如上述氧气瓶中作为系统的残留氧气与喷射出去的那些氧气本来是存在于同一钢瓶中，它们之间没有任何间隔，而喷射出去的那些氧气实际是环境的一部分。

系统与环境之间的联系包括有能量交换与物质交换两类。

针对二者之间联系情况的差别，可以把系统分成以下三种：(1) 隔离系统（孤立系统, isolated system）隔离系统（孤立系统）与环境之间既无能量交换，又无物质交换，所以环境对隔离系统中发生的任何变化不会有任何影响。

在热力学中，有时我们把所研究的系统及该系统的环境作为一个整体来看待，这个整体就应当是隔离系统。

(2)封闭系统(closed system)封闭系统与环境之间只有能量交换而无物质交换。

在前面提到的几个系统中，物质均被封闭于实有的容器间壁内或假象的边界内，使系统仅能通过界面与环境有热、功等形式的能量交换，故应当属于封闭系统。

热力学第二定律基本公式

热力学第二定律基本公式

（2）dH TdS Vdp
H T S V p T p T
谢谢观看
THANKS FOR WATCHING !
dS
H p
S
dp
dA = –SdT – pdV A dT A dV
T V
V T
dG = –SdT+Vdp
G T
dT
p
G p
T
dp
U H T S V S p
A G S T V T p U A p V S V T
H p
(4) U、H分别以S, V 和 S, p为变量， d前系数只能分别是T, p 和 T, V；
(5) “H最大”，所以都是“+”项；A最
小，都是“–”项 。
4.由基本公式导出的关系式
dU = TdS pdV U dS U dV
S V V S
dH = TdS + Vdp
H S
p
2.四个基本方程
由 A U TS 可得：
dA dU TS dU TdS SdT
将 dU TdS pdV 带入上式： dA SdT pdV
（3）
2.四个基本方程
由 G H TS 可得：
dG dH TS dH TdS SdT
将 dH TdS Vdp 带入上式： dG SdT Vdp
只有两个变量，但要保持系统组成不变。
若系统内发生相变或化学变化，就要增加组成变量， 所以这公式只适用于内部平衡的、只有体积功的封 闭系统。
2.四个基本方程
由 H U pV 可得：
dH dU pV dU pdV Vdp
将 dU TdS pdV 带入上式： dH TdS Vdp
（2）
热力学基本方程

热力学基本关系式

热力学基本关系式

至今讨论中常应用的八个热力学函数--p、V、T、U、H、S、A、G。

其中 U 和 S 分别由热力学第一定律和第二定律导出；H、A、G 则由定义得来。

而 U、H、A、G 为具有能量量纲的函数。

这些热力学函数间通过一定关系式相互联系着。

基本热力学关系式共有十一个（以下分别用公式左边括弧中的数字标明）。

从这十一个基本关系式出发，可以导出许多其它衍生关系式，它们表示出各不同物理量间的相互关系，利用它们可以帮助我们由易于直接测量的物理量出发以计算难于直接测量的物理量的数值。

由定义可得如下三个关系式：(1) (3-136)(2) (3-137)(3) (3-138)又由热力学第一定律、第二定律联合公式，在无非膨胀功条件下：将它和式(3-136)、(3-137)、(3-138)联系起来：即可得以下四个一组被称为恒组成均相封闭系统的热力学基本方程。

又称 Gibbs 方程。

(4) (3-139)(5) (3-140)(6) (3-141)(7) (3-142)这四个基本方程均不受可逆过程的限制，因为 U、H、A、G 等随着相应两个独立的状态函数变化而变化，因而与变化的具体途径（可逆或不可逆）无关，自然亦可用于不可逆过程。

公式虽然是四个，但式(5)、(6)、(7)实际上是基本公式(4)在不同条件下的表示形式。

根据全微分定义可有如下关系：(3-143)(3-144)(3-145)(3-146)式(3-139)与式(3-143)对比、式(3-140)与式(3-144)对比、式(3-141)与式(3-145)对比、式(3-142)与式(3-146)对比，可得如下关系(或称"对应系数式")：(3-147)(3-148)(3-149)和 (3-150)如分别将尤拉(Euler)定则：应用于热力学基本方程(4)、(5)、(6)、(7)可得如下四式：(8) (3-151)(9) (3-152)(10) (3-153)(11) (3-154)这四式常称为"麦克斯威关系式"。

热力学一般关系(热学-高等数学-偏微分)

热力学一般关系(热学-高等数学-偏微分)

热力学一般关系(热学-高等数学-偏微分)第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数（如内能U、熵S）及其为某一研究方便而设的组合函数（如焓H、自由能F、自由焓G等）许多都是不可测量，必须将它们与可测量（如压力p、体积V、温度T等）联系起来，否则我们将得不到实际的结果，解决不了诸如上一章讲的最大功计算等一些具体的问题。

这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。

热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数，当我们强调它们与独立变量的函数关系时，常称它们为状态函数。

从数学上说，状态函数必定具有全微分性质。

这一数学特性十分重要，利用它可导出一系列很有实用价值的热力学关系式。

下面我们扼要介绍全微分的一些基本定理。

设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂= （6-1） 则必然有（1） 互易关系令式（6-1）中),(y x M x z y=⎪⎪⎭⎫⎝⎛∂∂，),(y x N y z x=⎪⎪⎭⎫⎝⎛∂∂ 则 y xx N yM ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫⎝⎛∂∂ （6-2）互易关系与⎰=0dz 等价。

它不仅是全微分的必要条件，而且是充分条件。

因此，可反过来检验某一物理量是否具有全微分。

（2） 循环关系当保持z 不变，即0=dz 时，由式（6-1），得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂z xz y dy y z dx x z则 xy zy z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂yz x z x x y y z （6-3）此式的功能是：若能直接求得两个偏导数，便可确定第三个偏导数。

结果也很容易记忆，只需将三个变量依上、下、外次序，即))()((xzy yxz zyx 循环就行了。

物理化学：2.13热力学函数间的重要关系式

物理化学：2.13热力学函数间的重要关系式
即： (Wr ) T = dF
② 恒温恒容可逆：
dF = SdT PdV Wr, f = Wr, f
即： (Wr, f ) T, V = dF
③ 恒温恒压可逆：
dG = SdT + VdP Wr, f = Wr, f 即： (Wr, f ) T, P = dG
上述结论与前面讨论的结果一样。
U、T、S、P、V、T、 H、F、G
均与相同始、终态的可逆过程的改变 量相同。
2）涉及不可逆变化时，过程曲线不在状 态空间内，无法在始、终态范围内直 接对过程曲线积分求状态函数变化值；
但始、终态间状态函数变化值与经可 逆过程的变化值是一样的；
所以可设计有相同始、终态的可逆过 程，对上述公式积分，得到任意变化 过程的U、G、… 等。
二、热力学第一、第二定律基本公式
第一定律：dU = Q W = Q P环 dV Wf …①
第二定律：dS = Qr / T Qr = TdS （可逆） …②
②代入①：dU = TdS PdV Wf …③ （可逆过程： Q = Qr，P = P环）
dU = TdS PdV Wf …③
3）对上述公式直接积分计算时，仅适合 于体系组成不变，或仅发生可逆相变、 可逆化学反应的过程。
否则，需设计相同始态及最终态的可 逆过程、可逆相变等来分段计算并加 和（有例题）。
结论：
上述基本公式可用于封闭、无非体积 功 ( Wf = 0 )、组成平衡 ( 组成不变或 仅发生可逆变化 ) 的体系；
§2.13 热力学函数间的重要关系式
一、热力学函数之间的关系 • 在热力学第一、第二定律中，共涉及
五个热力学函数：U、H、S、F、G：
H U + PV F U TS G H TS F + PV

用特性函数G与特征变量p,T求所有热力学函数的表达式

用特性函数G与特征变量p,T求所有热力学函数的表达式

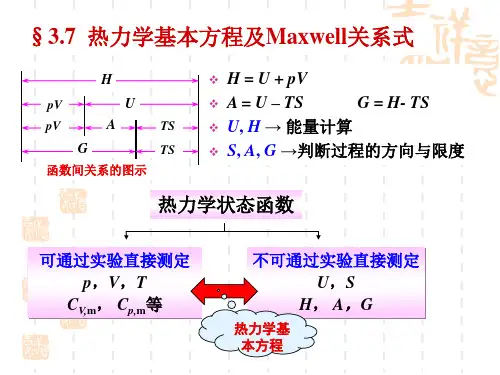
用特性函数G与特征变量p,T求所有热力学函数的表达式1.热力学函数间的关系(1) H=U+pV(2) A=U-TS(3) G=H-TS(4) G=A+pV根据定义，五个热力学函数有如下关系。

这些关系一方面反映了体系的热力学函数之间的联系，另一方面可以利用这种关系从已知函数值求未知函数值。

它们的关系用图示的方法可看得更清楚。

(1) 这是焓的定义式，因为在等压，不作非膨胀功的条件下，焓变等于等压热效应。

等压热效应容易测定，所以定义了焓。

(2) 这是亥姆霍兹自由能的定义式。

在等温可逆条件下，亥氏自由能的降低等于对外所作的最大功，可以衡量体系的作功能力，所以又称功函。

(3) 这是吉布斯自由能的定义式。

在等温等压可逆条件下，吉布斯自由能的下降等于对外所作的最大非膨胀功。

(4) 从上面三个公式可导出G与A之间的关系式，该式也可看作吉布斯自由能的定义式.2. 用特性函数G与特征变量p,T求所有热力学函数的表达式。

用特性函数及其特征变量可以求出所有热力学函数的表达式。

现以吉布斯自由能G为特性函数，其特征变量为T，p，从而求出热力学能，焓，熵，亥氏自由能和体积的表达式。

之所以可以这样做是因为U，H，S，A，G，T，p，V这8个量之间只有两个变量是独立的，其它都是这两个变量的函数。

所有根据两个变量热力学函数之间的关系可以写出其它热力学量的表达式。

画面中间是G与特征变量T，p之间的关系式。

(1) 保持p不变，对T求偏导，得到熵的表达式(2) 保持T不变，对p求偏导，得到体积V 的表达式(3) 根据焓的定义式代入熵的表达式，得到焓的表达式(4) 根据亥氏自由能的定义式，代入体积的表达式，得到亥氏自由能的表达式(5) 根据焓的定义式，代入焓和体积的表达式，就得到热力学能的表达式。

热力学中的热力学平衡与热力学势函数

热力学中的热力学平衡与热力学势函数

热力学中的热力学平衡与热力学势函数热力学是研究能量转化和传递的科学领域，而热力学平衡和热力学势函数则是热力学理论中的重要概念。

本文将着重讨论热力学平衡与热力学势函数的内涵、应用及其相互关系。

一、热力学平衡的概念与条件热力学平衡指的是在封闭系统中，系统各部分之间达到一种稳定状态，不再发生宏观可视化变化的状态。

在热力学平衡状态下，系统各部分之间的各项物理量呈现均衡状态，包括温度、压力、浓度等。

而要使系统达到热力学平衡，需要满足热力学平衡条件。

热力学平衡条件主要有三个方面。

首先是热力学平衡的力学条件，即系统各处物体的压力要相等。

其次是热力学平衡的热力学条件，即系统各处温度要相等。

最后是热力学平衡的物质平衡条件，即系统内各种组分的浓度要达到稳定状态。

二、热力学势函数的定义与特点热力学势函数是热力学系统的特性函数，它描述了系统在不同平衡态下的性质，并通过热力学势函数的变化来判断系统的稳定状态。

常见的热力学势函数包括内能、焓、自由能和吉布斯自由能等。

1. 内能（U）是描述系统内部能量的函数，它包括了系统的热能和势能。

内能的变化与系统的热交换和功交换有关，通过内能的变化可以判断系统的热力学状态。

2. 焓（H）是内能和系统对外界做功之和，它常用于描述恒压过程中的能量变化。

焓的变化可以提供系统在常压条件下的稳定性信息。

3. 自由能（F）是描述系统在恒温恒压条件下的稳定性的函数。

自由能分为哈密顿函数和亥姆霍兹函数，它们与系统的熵和能量有关。

通过自由能的变化可以判断系统的热力学稳定性。

4. 吉布斯自由能（G）是描述系统在恒温恒压条件下的稳定性和平衡的函数。

吉布斯自由能与自由能类似，但它是在恒压条件下选择的理想势函数，广泛应用于化学反应和相平衡的研究。

三、热力学平衡与热力学势函数的关系热力学平衡与热力学势函数有着密切的关系。

热力学平衡的达成正是通过热力学势函数的最小值原理来实现的。

对于一个封闭系统，当系统处于热力学平衡时，它的热力学势函数将达到最小值。

几个热力学函数间的关系

几个热力学函数间的关系

化学与环境科学学院
对于U，H，S，A，G 等热力学函数，只 要其独立变量选择适当，就可以从一个已知 的热力学函数求得所有其它热力学函数，从 而可以把一个热力学系统的平衡性质完全确
定下来。
这个已知函数就称为特性函数，所选择的 独立变量就称为该特性函数的特征变量。
Physical Chemistry
化学与环境科学学院
化学与环境科学学院
一、几个函数的定义式
Physical Chemistry
化学与环境科学学院
在热力学第一、第二定律中，共涉及五个热力学
函数：U、H、S、A、G，可通过定义式将它们相关 联。定义式适用于任何热力学平衡态系统，只是在特 定的条件下才有明确的物理意义。 (1) 焓的定义式
H U pV
Physical Chemistry
化学与环境科学学院
(2)
dH TdS Vdp
因为
H U pV
dH dU pdV Vdp
dU TdS pdV
所以
dH TdS Vdp
Physical Chemistry
化学与环境科学学院
(3)
dA SdT pdV
说明：
上述四个基本公式导出时，以 TdS 代 替 QR，以 pdV 代替 We，即在可逆过程条件下推得的。所以基 本公式对可逆过程、Wf = 0、组成平衡 ( 组成不变或 仅发生可逆相变、可逆化学反应的过程) 的封闭体系严 格成立。 但基本公式最终表达式中的每一热力学量（U、T 、S、P、V、T、H、F、G）都是体系的状态函数； 因此，其积分结果适用于任何始、终态相同的可逆或 不可逆过程。
Physical Chemistry
化学与环境科学学院

物理化学1.15-1 热力学函数的基本关系式

物理化学1.15-1 热力学函数的基本关系式
§1.15 热力学函数的基本关系式
8个热力学函数： 可直接测定
p、V、T、U 、H 、S、A、G
定 H ＝U＋pV 义 式 A ＝U－TS
可求得
G ＝H－TS＝A＋pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr －pdV ＋ δWr′
δQr =TdS
dU = TdS －pdV ＋ δWr' δWr'＝0：
dA = －SdT－ pdV dG = －SdT + Vdp
G S T p

G p
T
V
证明：无相变和化学变化的封 闭系统，在定温下其吉布斯自 由能随压力的改变恒为正值。
证明：
dG = －SdT + Vdp
G ( p )T
V
>0
解： dG = －SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系：体逆统积过，功程，。
可用于: (i)定量，定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式： dU = TdS－ pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS －pdV
dU=TdS－pdV
H=U+pV dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则T = 1000 K， rG1000 = 61900 Jmol-1>0
计算结果说明，在给定条件下，298K时，合成氨反应可 以进行；而在1000K时，反应不能自发进行
再见！
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大，△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃，反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯－亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯－亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
（微分形式）
应用：在等压下若已知反应在T1的rGm(T1)，则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x，y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数，数学上具有全微分性质，将上述
关系式用到四个基本公式中， 就得到Maxwell关系式：
M N ( y )x ( x )y
G r m,2 30820J mol-1
四、G与温度的关系—吉布斯-亥姆霍兹公式
(2) 若温度变化范围大，△H随温度变化而改变
Cp写成温度的函数 Cp = a bT cT2 …… 产物与反应物恒压热容之差为
rCp = a bT cT2 ……
则
r H
= H0
+
T
0 rC pdT
H0
三、Maxwell 关系式
例1 证明理想气体的热力学能只是温度的函数。
解：对理想气体， pV nRT
p nRT /V
(
p T
)V
nR V
(UV )T T(Tp )V p
T
nR V
p
0
所以，理想气体的热力学能只是温度的函数。
三、Maxwell 关系式
（2）求等温条件下，H 随 p 的变化关系
例2 证明理想气体的焓只是温度的函数。
解：对理想气体， pV nRT
p nRT /V
V nR
( T
)p
p
H ( p )T
V
T ( V T
)p V
T
nR p
0
所以，理想气体的焓只是温度的函数。
三、Maxwell 关系式
例3证明：( T
V
V ) p ( p
p )T ( T )V
1
并以理想气体验证上式的正确。
第十一节 热力学函数间的关系
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
函数间关系的图示
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
一、热力学基本关系式
得 dF SdT pdV
一、热力学基本关系式
(4) dG SdT Vdp 根据定义式 G H TS
取全微分：
dG dH TdS SdT 将 dH TdS Vdp 代入
得dG SdT Vdp
总结：热力学四个基本关系式
(1) dU TdS pdV
(2) dH TdS Vdp
(3) dF SdT pdV
( S
)p
p
( U V
)S
( F V
)T
从公式(2)，(4)导出 从公式(3)，(4)导出
H G V ( p )S ( p )T
F
G
S
( T
)V
( T
)P
三、Maxwell 关系式
全微分的性质
设函数Z的独立变量为x，y， Z具有全微分性质
z z(x, y)
Z
Z
dZ ( x )y dx ( y )x dy Mdx Ndy
R V
则
T V p ( V ) p ( p )T ( T )V
1
四、G与温度的关系—吉布斯-亥姆霍兹公式
对于一个化学反应：自一个温度反应的rG1求另一温度的rG2
dG SdT Vdp
G T
P
S
在温度T时 G H TS
因此
G T
P
G H T
两边同时除以T
1 T
G T
P
G T2
rHm不随温度而变化试求上述反应在600℃进行时的rGm
解：由于温度变化不大，可将rHm视为常数，由公式：
G2 G1
T2
T1
T2 T1
H T2
dT
rGm2 T2
rGm1 T1
1 r H m (T2
1 )
T1
rGm,2 1.400105 1.966105( 1 1 )
873
298
873 298
（1）求在等温条件下U随V的变化关系
已知基本公式 dU TdS pdV
等温对V求偏微分
U ( V )T
S
T( V
)T
p
S ( V )T
不易测定，根据Maxwell关系式
S
p
( V
)T
( T )V
求得
U
p
( V
)T
T( T
)V
p
只要知道气体的状态方程，就可得到
(
U V
)T
值，即等温时热
力学能随体积的变化值。
对于定组成只作体积功的封闭系统 存在 dU Q pdV
若系统经历可逆过程 dS Q T
代入上式即得 dU TdS pdV
(1)
这是热力学第一与第二定律的联合公式，适用于组成恒定、 不作非体积功的封闭系统。
注意理解： 在推导中引用了可逆过程的条件，但导出的关系式中所有的
物理量均为状态函数，在始终态一定时，其变量为定值，热力学 关系式与过程是否可逆无关。
3
2 N 2 (g) 2 H 2 (g) NH 3 (g)
已知，在298K各种气体均处于100kPa时，rH298 = －46.11kJ，
rG298 = 16.45kJ，试求1000K时的rGm值
解答：查表可知 Cp = 25.46 18.33 103T 2.05 10-7T2
则
r Hm
H0
(1) dU TdS pdV
( T V
)S
(
p S
)V
(2) dH TdS Vdp
(
T p
)S
( V S
)p
(3) dF SdT pdV
S
p
( V
)T
( T )V
(4) dG SdT Vdp
(
S p
)T
(
V T
)p
利用该关系式可将实验可测偏微商来代替那些不易直接测定的 偏微商。
三、Maxwell 关系式
一、热力学基本关系式
(2) dH TdS Vdp
根据定义式 H U pV
取全微分：
dH dU pdV Vdp
将 dU TdS pdV 代入
得 dH TdS Vdp
(3) dF SdT pdV
根据定义式 F U TS
取全微分：
dF dU TdS SdT 将 dU TdS pdV 代入
aT
1 2
bT
2
1 3
cT
3
......
式中H0是积分常数，代入吉布斯－亥姆霍兹公式得：
( G T
T
)
H0
aT
1 2
bT 2 T2
1 3
cT 3
p
积分得：
r
GO m ,T
H0
aT
ln T
b T 2 2
c T 3 6
IT
四、G与温度的关系—吉布斯-亥姆霍兹公式
氨的合成
1
25.46T
1 2
18
33
103T
2
1 3
2
05
107 T
3
将T = 298 K， rH298 = －46.11kJ代入得： H0 = 39340
rGmO,T 39340 25.46T lnT 9.17103T 2 0.35107T 3 IT
将T = 298 K， rG298 = 16.45kJ代入得：I= 65.5
(4) dG SdT Vdp
适用条件：组成恒定、不 作非体积功的封闭系统的 任何过程。
二、对应系数关系式
(1) dU TdS pdV (2) dH TdS Vdp
(3) dF SdT pdV (4) dG SdT Vdp
从公式(1)，(2)导出 从公式(1)，(3)导出
U
H
T
( S
)V
证： 定量纯气体， V = f (p,T)
V
V
dV
( T
) p dT
(
p
)T dp