2019年河北中考数学复习 第3讲 分式-2019年教学文档
- 格式:doc
- 大小:148.01 KB
- 文档页数:8





2019-2020年中考数学一轮复习第二章方程与不等式第3节分式方程及其应用试题课堂呈现指引方向了解分式和最简分式的概念,能利用分式的基本性质进行约分和通分:能进行简单的分式加、减、乘、除运算.能解可化为一元一次方程的分式方程.考点梳理夯实基础1.分母中含有的方程叫分式方程.2.解分式方程的一般步骤:(1)去分母,将分式方程转化为整式方程;(2)解整式方程:(3)验根:把整式方程的根代入,看结果是否为零,使分母为零的根是原方程的增根,必须舍去.【答案】1.未知数 2.(3)最简公分母考点一解分式方程【例1】解分式方程:(1)(xx乐山)解方程:.(2)(xx上海)解方程:解题点拨:此题考查了解分式方程的知识,将分式方程先化为整式方程求解,求得结果后一定要检验.解:(1)1—3(x一2)= -(x-l),1—3x+6= -x+l.-2x= -6x=3.经检验.x=3是原方程的解∴原方程的解是x=3.(2)x+2-4=x2-4x2-x-2=0x=2,x2 =-1,1经检验x=2是增根,舍去;x=-1是原方程的根,∴原方程的根是x=-1.考点二含参分式方程【例2】(1)若关于x的分式方程有增根,则m的值是()A.m= -1 B.m=0 C.m=3 D.m=0或m=3【答案】A(2)若关于x的方程的解为正数,则m的取值范围是()A.m<6B.m>6 C.m<6且m≠0 D.m>6且m≠8【答案】C(3)已知关于戈的方程无解,求a的值.解:2(x+2)+ax=3(x-2)(a-l)x=-10①当a-l=0,即a=l时,0.x=-10,整式方程无解;②当a-l≠0,即a≠1时,要原方程无解,则整式方程的根为增根若x=2时,则a=-4;若x= -2时,则a=6;所以,a=l或-4或6.解题点拨:含参分式方程主要三种类型,一是分式方程有增根,二是分式方程无解,三是分式方程解有条件,总的原则都是将分式方程转化成整式方程,再根据条件讨论求解.考点三分式方程应用【例3】某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.(1)求原计划每天生产的零件个数和规定的天数;(2)为了提前完成生产任务,T厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的霉件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.解题点拨:分式方程应用题等量关系比较清晰,难度不大,特别注意不要忘记对根的检验.解:(1)设原计划每天生产的零件x个,由题意得,,解得,x= 2400.经检验,x= 2400是原方程的根,且符合题意.∴规定的天数为24000÷2400 =10(天).答:原计划每天生产的零件2400个,规定的天数为10天.(2)设原计划安排的工人人数为y人,由题意得[5×20×(1+20%)×+2400] ×(10-2)= 24000解得,y= 480.经检验,y=480是原方程的根,且符合题意.答:原计划安排的工人人数为480人.课堂训练当堂检测1.(xx深圳)施T队要铺设一段全长xx米的管道,因在中考期间需停T两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是()A.B.C.D.【答案】A2.(xx凉山)关于戈的方程无解,则m的值为()A.-5 B.-8 C.一2 D.5【答案】A3.(xx贺州)若关于戈的分式方程的解为非负数,则a的取值范围是 .【答案】a≥1且a≠44.解分式方程(1)解:2+3x-6 =x-l2x=3x= 1.5.经检验.x= 1.5是原方程的解.∴原方程的解是x= 1.5.(2)解:x(x+1)一(2x-l)= x2—1x2+x-2x+l=x2-1-x= -2x=2.经检验.x=2是原方程的解∴原方程的解是x=2.中考达标模拟自测A组基础训练一、选择题1.(xx成都)分式方程的解为()A.x= -2B.x= -3C.x=2D.x=3【答案】B2.(xx潍坊)若关于戈的方程的解为正数,则m的取值范围是()A.m< B.m<且m≠C.m> D.m>且m≠【答案】B3.(xx山西)甲、乙两个搬运T搬运某种货物,已知乙比甲每小时多搬运600kg,甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等,求甲、乙两人每小时分别搬运多少千克货物.设甲每小时搬运xkg货物,则可列方程为(B)A. B.C.D.【答案】B4.(xx十堰)用换元法解方程,设,则原方程可化为()A.B.C.D.【答案】B二、填空题5.若分式方程有增根,则这个增根是.【答案】x=16.已知关于戈的分式方程的解为负数,则k的取值范围是.【答案】k>且k≠17.已知点P(l-2a,a-2)关干原点的对称点在第一象限内,且a为整数,则关于x的分式方程的解是.【答案】x=3三、解答题8.解分式方程:(1).解:x=2(3x-l)+1x= 6x-2+1x=经检验,x=是原方程的解∴原方程的解是x=(2)解:x2-5x+6-3x-9 =x2-9解得经检验,是分式方程的解∴原方程的解是.(3)解:2-x-l=x-3x=2经检验:x =2是原方程的解.∴原方程的解是x=2.(4)解:去分母得:(x+l)2-2 =x-l,整理得:x2+x=0,即x(x+1)=0,解得:x=0或x= -1,经检验x= -1是增根.∴原方程的解是x=0.9.(xx聊城)为加快城市群的建设与发展,在A,B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km.城际铁路的设计平均时速要比现行的平均时速快llOkm.运行时间仅是现行时间的,求建成后的城际铁路在A,B两地的运行时间.解:设城际铁路现行速度是xkm/h.由题意得:解这个方程得:x= 80.经检验:x= 80是原方程的根,且符合题意.则现行时间:120÷80×=0.6(小时)答:建成后的城际铁路在A,B两地的运行时间是0.6小时.B组提高练习10.(xx梅州)对于实数以、6,定义一种新运算“”为:,这里等式右边是实数运算.例如:13=,则方程的解是()A.x=4 B.x=5 C.x=6 D.x=7【答案】B(提示:依题意,得:,所以,原方程化为:,即:,解得:x=5.)11.(xx凉山)若实数x满足,则= .【答案】 10(提示:根据,可以求得的值,从而可以得到的值,∵,∴,∴,即,∴,故答案为:10)12.宁波火车站北广场将于xx年底投入使用,计划在广场内种植4、B两种花木共6600棵,若4花木数量是B花木数量的2倍少600棵.(1)A、B两种花木的数量分别是多少棵?(2)如果园林处安排26人同时种植这两种花木,每人每天能种植4花木60棵或B花木40棵,应分别安排多少人种植4花木和B花木,才能确保同时完成各白的任务?解:(1)设曰种花木的数量是x棵,则A种花木的数量是(2x-600)棵.根据题意,得x+( 2x-600)= 6600,解得x=2400,2x-600=4200.答:A种花木的数量是4200棵,口种花木的数量是2400棵.(2)设安排y人种植A种花木,则安排(26-y)人种植曰种花木.根据题意,得,解得y=14.经检验,y=14是原方程的根,且符合题意.26-y=12.答:安排14人种植A种花木,安排12人种植B种花木,才能确保同时完成各自的任务.$p20079 4E6F 乯20887 5197 冗32412 7E9C 纜24906 614A 慊 dFO BZ34560 8700 蜀。
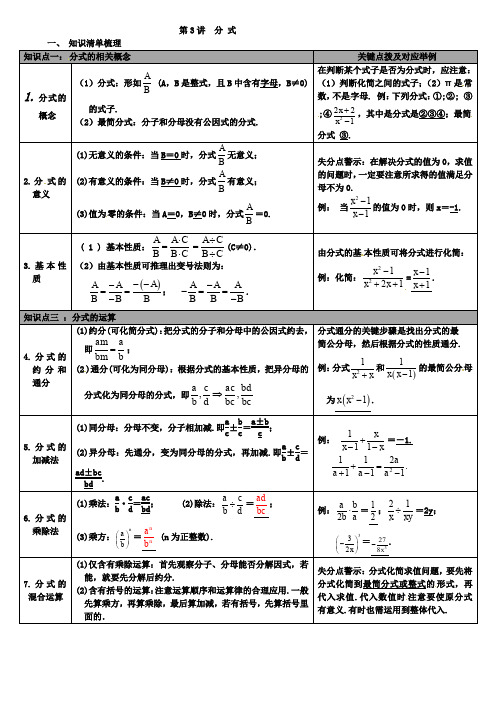
第3讲分式知识点一:分式的相关概念常不是字母;零的条件:当由分式的基本性质可将分式进行化简:)分式通分的关键步骤是找出分式的最的最简公分母2019-2020学年数学中考模拟试卷一、选择题1.如图,AB ∥CD ,BP 和CP 分别平分∠ABC 和∠DCB ,AD 过点P ,且与AB 垂直.若AD =8,则点P 到BC 的距离是( )A .8B .6C .4D .22.若关于x 的一元二次方程x 2﹣2x+m =0有两个不相等的实数根,则m 的值可以是( ) A .﹣1B .1C .3D .53.某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额超过30元的概率为( ) A.12B.13C.23D.144.统计数据显示,2018年绍兴市进出口贸易总额达2200亿元,其中2200亿元用科学记数法表示为( ) A .2.2×103元 B .22×108元 C .2.2×1011元D .0.22×1012元5.如图,已知点A 、B 、C 、D 均在已知圆上,AD ∥BC ,AC 平分∠BCD ,∠ADC =120°,四边形ABCD 的周长为10cm .图中阴影部分的面积为()A .13π﹣2B .13πC .23π﹣2D .23π6.若关于x 的不等式组27412x x x k ++⎧⎨-⎩<<的解集为x <3,则k 的取值范围为( )A.k >1B.k <1C.k≥1D.k≤17.如图,在O 中,AB 是直径,CD 是弦,AB CD ⊥,垂足为点E ,连接CO ,AD ,若30BOC ∠=︒,则BAD ∠的度数是( )A .30°B .25︒C .20︒D .15︒8.如图,□DEFG 内接于ABC ∆,已知ADE ∆、EFC ∆、DBG ∆的面积为1、3、1,那么□DEFG 的面积为( )A .4B .C .3D .29.中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识。
课时课题:分式授课教师:金鑫课型:复习课授课时间:2015 年 3月教学目标:1、理解分式的有关概念,能判断分式在什么情况下有意义、无意义、值为零。
2、掌握并灵活运用分式的基本性质,能熟练地进行分式的通分和约分,能正确地进行分式的混合运算。
教学重点难点:重点:判断分式在什么情况下有意义、无意义、值为零,熟练地进行分式的通分和约分,能正确地进行分式的混合运算。
难点:熟练且正确地进行分式的混合运算。
中考考点和题型分析中考考点:分式有无意义,值为0,分式化简和运算,题型:常以选择、填空、或计算题出现,分值在2-8分教法与学法:采用知识回顾-----题组训练-----诱导反思-----课堂检测----布置作业的课堂教学模式。
即以学案为载体,利用本章的知识结构框架,以问题串的方式帮助学生回顾本章的知识点;通过题组练习让学生在做中进一步理解掌握知识点,在错中纠正易错点,巩固本章知识;借助知识树诱导反思,谈收获,说困惑;然后分层检测达标;最后分层布置巩固作业。
课前准备:精心备课,编写学案,制作课件教学过程:一、知识回顾,扫清障碍知识在复习中升华,能力在训练中提升。
本节课让我们共同对分式的有关知识进行复习,争取人人达标过关。
请大家研读知识框架和复习目标。
同学们知道了今天我们要复习的内容和要达到目标,下面请小组合作完成复习知识要点回顾。
流噢!(3)约分:把一个分式的分子与分母的约分的主要步骤是:把分式的分子与分母(4)通分:把几个异分母的分式分别化成与分式的通分。
通分的关键是确定几个分式的(5)最简公分母:通常取各分母所有因式的最【活动形式】:先小组合作交流,再小组汇报,生生互动、师生互动,纠错完善,让学生适当举例说明,加强对知识的理解,为题组训练奠定基石。
二、题组训练,巩固提高我们回顾了分式的知识要点,在学业考试中怎样考查呢?让我们共同完成复习学案四:题组训练,比一比,赛一赛,看哪些同学思维敏捷,运算迅速正确。
第3讲 分 式1. (2019,河北)若a =2b ≠0,则a 2-b 2a 2-ab 的值为( 32 ).【解析】 ∵a =2b ≠0,∴原式=4b 2-b 24b 2-2b 2=32.2. (2019,河北)若3-2x x -1=( )+1x -1,则( )中的数是(B)A. -1B. -2C. -3D. 任意实数【解析】 3-2x x -1-1x -1=2-2x x -1=-2.3. (2019,河北)老师设计了接力游戏,用合作的方式完成分式化简.规则是每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示.第3题图接力中,自己负责的一步出现错误的是(D) A. 只有乙 B. 甲和丁 C. 乙和丙 D. 乙和丁【解析】 x 2-2xx -1÷x 21-x =x 2-2x x -1·1-x x 2=x 2-2x x -1·-(x -1)x 2,乙错误.x 2-2x x -1·x -1x 2=x (x -2)x -1·x -1x 2=x -2x ,丁错误.分式的概念例1 (2019,唐山路北区二模)若分式x 2-1x -1的值为0,则x 的值为(C)A. 0B. 1C. -1D. ±1【解析】 分式值为0的条件是x 2-1=0且x -1≠0.解得x =-1. 针对训练1 (2019,石家庄质检)若分式1x -1有意义,则x 的取值范围是(B)A. x =1B. x ≠1C. x =0D. x ≠0【解析】 分式有意义的条件是分母不等于0,即x -1≠0,∴x ≠1. 针对训练2 (2019,定西)若分式x 2-4x 的值为0,则x 的值是(A)A. 2或-2B. 2C. -2D. 0【解析】 由题意,得x 2-4=0且x ≠0.解得x =2或-2.分式的基本性质、通分与约分例2 (2019,合肥模拟)若x ,y 的值均扩大为原来的2倍,则下列分式的值保持不变的是(A) A. 3x 2yB. 3x 2y2C. 3x 22yD. 3x 32y2【解析】 根据分式的基本性质,可知若x ,y 的值均扩大为原来的2倍,A. 6x 4y =3x 2y .B. 6x 8y2=3x 4y 2≠3x 2y 2.C. 12x 24y =3x 2y ≠3x 22y .D. 24x 38y 2=3x 3y 2≠3x 32y2. 例3 (2019,邵阳模拟)下列分式中,是最简分式的是(C) A. a -b b -aB. a 3+a 4a 2C. a 2+b 2a +bD.1-a-a 2+2a -1【解析】 ∵a -b b -a =-1,∴选项A 不符合要求.∵a 3+a 4a 2=a 2+14a ,∴选项B 不符合要求.∵a 2+b 2a +b不能化简,是最简分式,∴选项C 符合要求.∵1-a -a 2+2a -1=-(a -1)-(a 2-2a +1)=a -1(a -1)2=1a -1,∴选项D 不符合要求.针对训练3(导学号5892921)若x ,y 的值均扩大为原来的3倍,则下列分式的值保持不变的是(D)A. 2+x x -yB. 2y x2C. 2y 33x2 D. 2y 2(x -y )2【解析】 根据分式的基本性质,可知若x ,y 的值均扩大为原来的3倍,A. 2+3x 3x -3y ≠2+xx -y .B.6y 9x 2≠2y x 2.C. 54y 327x 2≠2y 33x 2.D. 18y 29(x -y )2=2y 2(x -y )2.分式的运算例4 (2019,安顺)先化简,再求值:8x 2-4x +4÷⎝⎛⎭⎫x 2x -2-x -2,其中|x |=2.【思路分析】 先化简括号内的式子,再根据分式的除法进行计算即可化简原式,然后将x =-2代入化简后的式子即可解答本题.解:原式=8(x -2)2÷⎣⎢⎡⎦⎥⎤x 2x -2-(x +2)(x -2)x -2 =8(x -2)2÷x 2-x 2+4x -2 =8(x -2)2·x -24=2x -2. ∵||x =2,∴x =±2.当x =2时,原式没有意义. 当x =-2时,原式=2-2-2=-12.针对训练4 (2019,石家庄43中模拟)如图,请你阅读小明和小红两名同学的解题过程.训练4题图下列叙述正确的是(D) A. 只有小明的正确 B. 只有小红的正确C. 小明、小红都正确D. 小明、小红都不正确【解析】 小明错在第二步,分子做减法时,最后一项符号错;小红错在第二步,丢了分母.针对训练5 (2019,武威)计算:ba 2-b 2÷⎝⎛⎭⎫a a -b -1.【思路分析】 先把小括号内的分式通分,再按照分式的减法和分式除法法则进行化简即可.解:原式=b(a +b )(a -b )÷a -a +b a -b=b(a +b )(a -b )·a -b b=1a +b. 一、 选择题1. (2019,武汉)若分式1x +2在实数范围内有意义,则实数x 的取值范围是(D)A. x >-2B. x <-2C. x =-2D. x ≠-2【解析】 由题意,得x +2≠0.解得x ≠-2. 2. (2019,唐山丰南区一模)要使式子5xx +2有意义,则x 的取值范围是(B) A. x ≠2B. x >-2C. x <-2D. x ≠-2【解析】 由题意,得⎩⎪⎨⎪⎧x +2≠0,x +2≥0.解得x >-2.3. (2019,廊坊安次区一模)若分式x -2x -1的值为0,则x 的值为(B)A. 1或2B. 2C. 1D. 0【解析】 由题意,得⎩⎪⎨⎪⎧x -2=0,x -1≠0.解得x =2.4. (2019,唐山路南区二模)若分式2aba +b 中的a ,b 的值同时扩大为原来的3倍,则分式的值(B)A. 不变B. 扩大为原来的3倍C. 扩大为原来的6倍D. 扩大为原来的9倍【解析】 2·3a ·3b 3a +3b =18ab 3(a +b )=3·2aba +b.5. (2019,威海)化简(a -1)÷⎝⎛⎭⎫1a -1·a 的结果是(A) A. -a 2B. 1C. a 2D. -1【解析】 (a -1)÷⎝⎛⎭⎫1a -1·a =(a -1)·a 1-a·a =-a 2. 6. (2019,廊坊安次区一模)若分式x 2x -1 xx -1的运算结果为x ,则在“ ”中添加的运算符号为(D)A. +B. -C. +或×D. -或÷【解析】 x 2x -1-xx -1=x 2-x x -1=x (x -1)x -1=x .x 2x -1÷x x -1=x 2x -1·x -1x =x .7. (2019,石家庄40中二模)若⎝⎛⎭⎫4a 2-4+12-a ·w =1,则w 等于(D)A. a +2(a ≠-2)B. -a +2(a ≠2)C. a -2(a ≠2)D. -a -2(a ≠±2) 【解析】 ∵4a 2-4+12-a =-1a +2,∴w =1÷⎝ ⎛⎭⎪⎫-1a +2=-a -2(a ≠±2). 8. (2019,石家庄长安区一模)计算⎝⎛⎭⎫b a -a b ÷a +ba 的结果为(D) A. 1bB.a +bbC. bD. -a -b b【解析】 原式=b 2-a 2ab ·a a +b =b -a b =-a -bb.9. (2019,石家庄桥西区一模)下列运算结果是x +1的是(D)A. x 2+1x +1B. 1-x 2x +1C. x -1x 2-1D. x 2x -1+11-x【解析】 x 2+1x +1是最简分式.1-x 2x +1=1-x .x -1x 2-1=1x +1.x 2x -1+11-x =x 2-1x -1=x +1.10. (2019,南充,导学号5892921)已知1x -1y =3,则代数式2x +3xy -2y x -xy -y 的值是(D)A. -72B. -112C. 92D. 34【解析】 已知条件转化为y -x =3xy ,则原式=2(x -y )+3xy x -y -xy =-6xy +3xy -3xy -xy =-3xy -4xy =34.二、 填空题11. (2019,咸宁)如果分式1x -2有意义,那么实数x 的取值范围是 x ≠2 . 【解析】 由题意,得x -2≠0.∴x ≠2.12. 分式12ab ,2ab a 2-b 2,3ab -a的最简公分母是 2ab (a +b )(a -b ) . 【解析】 三个分母分别是2ab ,a 2-b 2=(a -b )(a +b ),b -a =-(a -b ),所以最简公分母是2ab (a +b )(a -b ).13. (2019,沈阳)化简:2a a 2-4-1a -2=( 1a +2 ).【解析】2aa 2-4-1a -2=2a -(a +2)(a +2)(a -2)=1a +2. 三、 解答题14. (2019,唐山路北区一模)先化简,再求值:⎝⎛⎭⎫x +1-3x -1÷x 2-4x +4x -1,其中x 满足方程x 2+x -6=0.【思路分析】 整式与分式的加减法,把整式看作分母为1,与分式通分即可;x 的取值要满足原分式有意义的条件.解:原式= (x +1)(x -1)-3x -1÷(x -2)2x -1=(x +2)(x -2)x -1·x -1(x -2)2=x +2x -2. 解方程x 2+x -6=0, 得x 1=2,x 2=-3.当x =2时,原式的分母为0,原式没有意义.当x =-3时,原式=-3+2-3-2=15.15. (2019,石家庄43中三模)如图,书上有这样一道题:第15题图 减号后面的分式被墨迹污损了,查答案得知化简结果为1x +2.(1)求被墨迹污损的分式;(2)若x =2-1,求被墨迹污损的分式的值.【思路分析】 (1)根据逆运算求污损部分.(2)代入求值. 解:(1)设被墨迹污损的分式为X . 根据题意,得X =x 2-2x +1x 2-1÷x 2-x x +1-1x +2=(x -1)2(x +1)(x -1)·x +1x (x -1)-1x +2 =1x -1x +2 =2x (x +2).(2)当x =2-1时,原式=2(2-1)(2+1)=2.1. 若a 2-ab =0(b ≠0),则aa +b 的值为(C)A. 0B. 12C. 0或12D. 1或2【解析】 由已知得a (a -b )=0,∴a =0或a =b ,代入aa +b 可得. 2. 已知ab =-1,a +b =2,则b a +ab= -6 .【解析】 b a +a b =b 2+a 2ab =(a +b )2-2abab,将已知条件代入可得.3. (2019,黄冈)若a -1a =6,则a 2+1a2的值为 8 .【解析】 把已知条件代入式子⎝⎛⎭⎫a -1a 2=a 2+1a 2-2,可以求得a 2+1a 2=8. 4. (导学号5892921)【探索】 (1)若3x +4x +1=3+mx +1,则m = 1 ; (2)若5x -3x +2=5+mx +2,则m = -13 .若ax +b x +c =a +mx +c(其中a ,b ,c 为常数),则m = b -ac . 【应用】利用上述结论解决:若代数式4x -3x -1的值为整数,求满足条件的整数x 的值.【思路分析】 【探索】和【总结】将等式右边通分并利用同分母分式的加法法则计算,再利用分式相等的条件确定出m 的值即可.【应用】根据得到的结论确定出整数x 的值即可.解:【探索】(1)1 (2)-13【总结】b -ac【应用】4x -3x -1=4+1x -1.∵x 为整数且4x -3x -1为整数,∴x -1=±1. ∴x =2或x =0.5. (导学号5892921)已知A =a +1a +2,B =a +3a +4. (1)若A =1-ma +2,求m 的值;(2)当a 取哪些整数时,分式B 的值为整数? (3)若a >0,比较A 与B 的大小关系.【思路分析】 (1)根据分式的值相等,可得关于m 的方程,解方程可得答案.(2)根据拆项法,可得a +3a +4=1-1a +4.根据1a +4是整数,可得a 的值.(3)根据作差法,可得答案.解:(1)由A =1-m a +2,得a +1a +2=1-ma +2=a +2-m a +2. ∴2-m =1. 解得m =1.(2)∵B =a +4-1a +4=1-1a +4,∴当a +4=±1时,B 为整数.∴a =-3或a =-5. (3)A -B =(a +1)(a +4)(a +2)(a +4)-(a +2)(a +3)(a +2)(a +4)=a 2+5a +4(a +2)(a +4)-a 2+5a +6(a +2)(a +4) =-2(a +2)(a +4).∵a >0, ∴A -B <0.。