高一学案第二章第三章学案及 答案
- 格式:doc
- 大小:40.00 KB
- 文档页数:6

第 3章 第1节DNA 是主要的遗传物质(第1课时) 学案学习目标核心素养 1.亲代传递给子代的遗传信息主要编码在DNA 分子上;2.概述多数生物的基因是DNA 分子的功能片段,有些病毒的基因在RNA分子上。
生命观念:从分子水平上,利用结构与功能观,分析DNA 适合作为遗传物质应具备的特点; 科学思维:运用归纳与概括的方法,分析肺炎链球菌的转化实验、噬菌体侵染大肠杆菌实验和烟草花叶病毒重组实验,归纳出其在实验思路上的共同点,并概括DNA 是主要的遗传物质; 科学探究:分析人类对遗传物质探索的实验设计思路。
基础知识梳理:(阅读教材,完成下列填空,在教材相应位置进行标注后,识记相关内容)一、肺炎链球菌的转化实验1.对遗传物质的早期推测(1)20世纪20年代,大多数科学家认为__蛋白质__是生物体的遗传物质。
(2)20世纪30年代,人们认识到____的重要性,但是认为__蛋白质__是遗传物质的观点仍占主导地位。
2.两种肺炎链球菌的比较细菌类型 菌体 菌落特点 有无荚膜 有无致病性S 型细菌有荚膜 R 型细菌表面 __粗糙__ 无荚膜 无3.格里菲思的肺炎链球菌体内转化实验实验结论:加热致死的S 型细菌内含有 ,促使R 型活细菌转化为S 型活细菌。
4.艾弗里的肺炎链球菌体外转化实验(1)实验过程及结果(2)实验分析:去除多糖、蛋白质、RNA 、脂质后,细胞提取物仍然具有转化活性,去除DNA 后细胞提取物失去转化活性。
(3)实验结论:__ 才是使R 型细菌产生稳定遗传变化的物质。
学习目标一:人们对遗传物质的早期推测有哪些?学习目标二:肺炎链球菌的体内转化实验原理、科学家、实验过程、结论是什么?学习目标三:肺炎链球菌的体外转化实验科学家、实验过程、结论是什么?学习目标四:如何理解自变量控制中的“加法原理”与“减法原理”?(教师)学习目标五:自学检测:1到10题为单选题,11到14题为不定项选择题,选全得5分,选对但不全的3分,每小题5分,共70分1.肺炎链球菌的转化实验中,发生转化的细菌和作为转化因子的物质分别是()A.R型细菌和蛋白质B.S型细菌和多糖荚膜C.R型细菌和DNA D.S型细菌和RNA2.艾弗里等人通过实验得出结论:使R型细菌产生稳定遗传变化的物质是()A.DNA B.蛋白质C.RNA D.糖类3.在培养R型细菌的培养基中加入某种物质后可能产生S型细菌,该物质是()A.S型细菌的多糖类物质B.S型细菌的DNA完全水解产物C.S型细菌的DNA D.S型细菌的蛋白质4.在生命科学发展过程中,证明DNA是遗传物质的实验是()①孟德尔的豌豆杂交实验②摩尔根的果蝇杂交实验③肺炎链球菌的转化实验④噬菌体侵染细菌的实验⑤DNA的X光衍射实验A.①② B.②③C.③④ D.④⑤5.下列关于遗传学发展史上4个经典实验的叙述,不正确的是()A.在艾弗里肺炎链球菌的转化实验中利用了自变量控制中的减法原理B.在噬菌体侵染细菌的实验中需经过短时间保温后,进行搅拌、离心C.T2噬菌体侵染细菌实验证明了DNA是大肠杆菌的遗传物质D.肺炎链球菌的转化实验证明了DNA是肺炎链球菌的遗传物质6.艾弗里实验证明了能使R型细菌转化为S型细菌的“转化因子”是()A.蛋白质B.DNAC.荚膜多糖D.脂肪7.美国科学家艾弗里的体外转化实验证明了()A.RNA是遗传物质B.蛋白质是遗传物质C.DNA是遗传物质D.DNA是主要的遗传物质8.下图表示艾弗里通过肺炎链球菌转化实验探究转化因子的实验过程。

第2课时热力环流与大气水平运动播放两幅图片,或者是微视频。
内容是火锅上空的水汽往上走;从冰箱里拿出来的冰块,放在桌面上,水汽往桌下沉。
通过对比,引导学生说出空气受热,气体膨胀上升;空气遇冷,气体收缩下沉。
进而引出本节课的内容——热力环流。
1.理解热力环流的形成原理和大气运动的根本原因。
2.运用各种示意图,说明大气运动状况。
理解大气水平气压梯度力、地转偏向力、近地面摩擦力对大气水平运动的影响。
一、热力环流(最基本的运动形式)1.概念:由于地面①而形成的空气环流。
2.气温与气压关系(近地面):气温高→气压②,气温低→气压③。
(高空与近地面气压状况相反)3.空气的垂直运动:温度高的地方气流④,温度低的地方气流⑤。
空气的垂直运动导致⑥上的气压差。
4.空气的水平运动:同一水平面上,大气由⑦的地方流向⑧的地方。
5.常见的热力环流(1)小尺度:城市风、海陆风、山谷风。
(2)大尺度:季风环流,赤道低压带、极地高压带的形成。
二、大气运动的基本原理⑨→空气的垂直运动→⑩→水平气压梯度力(原动力)→空气的→风。
三、大气的水平运动——风1.水平气压梯度力:形成风的原因,大小与气压梯度成,方向等压线,由高压区指向低压区。
2.地转偏向力:方向与物体的运动方向,北半球向右偏,南半球向左偏。
3.摩擦力:方向与风向,大小与距离地面高度成,高空可忽略不计。
4.风向(1)赤道:受水平气压梯度力(近地面有摩擦力)作用→风向等压线。
(2)其他纬度高空:受水平气压梯度力和地转偏向力作用→风向平行于等压线。
近地面:受水平气压梯度力、地转偏向力和摩擦力作用→风向与等压线斜交。
【答案】①冷热不均②低③高④上升⑤下沉⑥同一水平面⑦气压高⑧气压低⑨冷热不均⑩同一水平面上的气压差水平运动直接正比垂直于垂直相反反比垂直于1.大气运动的能量来源是什么?请简述大气运动的最简单形式。
【提示】大气运动的能量来源于太阳辐射。
大气运动的最简单形式是热力环流,是由于地面冷热不均而形成的空气环流。

第二章第7节 直线与平面垂直的判定高一( )班 姓名: 学号学习目标:(1)掌握直线和平面垂直的定义及判定定理; (2)掌握判定直线和平面垂直的方法;(3)培养几何直观能力,在直观感知,操作确认的基础上学会归纳、概括结论。
学习重点:直线和平面垂直的定义及判定定理;学习难点:直线和平面垂直的定义及判定定理及其应用。
学习过程:一、 预习﹒交流﹒回顾1、什么是直线与直线垂直?直线与直线垂直有几种情况?2、在现实生活中,我们经常看到一些直线与平面垂直的现象,例如:“旗杆与地面,大桥的桥柱和水面等的位置关系”,请你例举出一些类似的例子。
3、思考:从上面的例子中归纳,直线与平面到底什么时候就垂直呢? 二、新知﹒巩固﹒展示 探究一:直线与平面垂直的定义:如果直线l 与平面α内的 都垂直,就说直线l 与平面α互相垂直。
其中,直线l 叫做平面α的 ;平面α叫做直线l 的 ; 直线l 与平面α的公共点叫做 。
符号表示: 图形表示:探究二:请同学们准备一块三角形的纸片,我们一起来做如图2.3-2试验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,将翻折后的纸片竖起放置在桌面上(BD 、DC 与桌面接触),问如何翻折才能保证折痕AD 与桌面所在平面垂直?为什么?归纳得到:直线与平面垂直的判定定理:一条直线与一个平面内的直线都垂直,则该直线与此平面垂直。
图形表示: 数学符号表示:该定理的应用:线线垂直探究二:DCBA1、平面的斜线的定义:2、直线与平面所成的角的定义:特别的,(1)若直线与平面垂直,就说直线与平面所成的角为 。
(2)若直线与平面平行,就说直线与平面所成的角为 。
三、训练﹒拓展﹒提高例1如图,已知//,b a αα⊥,求证:b α⊥例2。
如图,在正方体1111ABCD A BC D -中,求直线A1、直线l 与平面α垂直指 ( ).A 直线l 与平面α内有无数条直线垂直;.B 直线l 与平面α内一组平行线垂直; .C直线l 与平面α内两条直线垂直; .D 直线l 与平面α内任意一条直线都垂直例3.(2005全国高考)如图,四棱锥P ABCD -中,底面,,AD PD E F =分别为,CD PB 的中点。
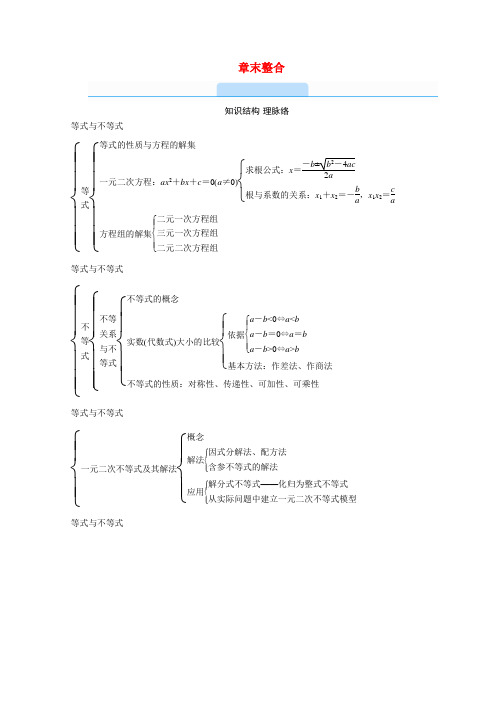
章末整合知识结构·理脉络等式与不等式⎩⎪⎪⎨⎪⎪⎧等式⎩⎪⎪⎨⎪⎪⎧等式的性质与方程的解集一元二次方程:ax 2+bx +c =0(a ≠0)⎩⎨⎧求根公式:x =-b ±b 2-4ac2a 根与系数的关系:x 1+x 2=-b a ,x 1x 2=ca 方程组的解集⎩⎪⎨⎪⎧二元一次方程组三元一次方程组二元二次方程组等式与不等式⎩⎪⎪⎨⎪⎪⎧不等式⎩⎪⎪⎨⎪⎪⎧不等关系与不等式⎩⎪⎨⎪⎧不等式的概念实数(代数式)大小的比较⎩⎪⎨⎪⎧ 依据⎩⎪⎨⎪⎧a -b <0⇔a <b a -b =0⇔a =ba -b >0⇔a >b基本方法:作差法、作商法不等式的性质:对称性、传递性、可加性、可乘性等式与不等式⎩⎪⎨⎪⎧一元二次不等式及其解法⎩⎪⎨⎪⎧概念解法⎩⎪⎨⎪⎧ 因式分解法、配方法含参不等式的解法应用⎩⎪⎨⎪⎧ 解分式不等式——化归为整式不等式从实际问题中建立一元二次不等式模型等式与不等式⎩⎪⎪⎪⎨⎪⎪⎪⎧均值不等式⎩⎪⎪⎨⎪⎪⎧内容:a +b2≥ab (a >0,b >0),当且仅当a =b 时,等号成立证明⎩⎪⎨⎪⎧ 几何证明代数证明应用⎩⎪⎨⎪⎧比较大小证明不等式求最值⎩⎪⎨⎪⎧⎦⎥⎤积定和最小和定积最大具备条件一正、二定、三相等解决实际问题要点梳理·晰精华1.不等式基本性质中注意问题(1)不等式的基本性质中性质4、6要注意符号,另外还有一些常用的结论,同学们也要掌握.如:“a >b 且ab >0,则1a <1b ”,“a >b ,c <d ,则a -c >b -d ”,“a >b >0,c >d >0,则a d >bc ”.在使用这些性质时,要注意上述各不等式成立的条件.(2)不等式的基本性质中,对表达不等式性质的各不等式要注意“箭头”是单向的还是双向的,也就是说,每条性质是否具有可逆性.运用不等式的基本性质解答不等式问题时,要注意不等式成立的条件,否则将会出现一些错误.2.一元二次不等式的解法 判别式Δ=b 2-4ac Δ>0Δ=0Δ<0二次函数y =ax 2+bx +c (a >0)的图像一元二次方程ax 2+bx +c =0(a >0)的根有两相异实数根x 1=-b -Δ2a ,x 2=-b +Δ2a(x 1<x 2) 有两相等实数根x 1=x 2=-b2a没有实数根ax 2+bx +c >0(a >0)的解集{x |x <x 1,或x >x 2} {x |x ∈R ,x ≠-b2a}R ax 2+bx +c <0(a >0)的{x |x 1<x <x 2}∅∅解集3.一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1,x 2,则x 1+x 2=-b a ,x 1+x 2=ca ,若bc=0时,关系式仍然成立.4.不等式组、简单分式不等式、绝对值不等式的解法(1)不等式组的解集等于组成该不等式组的每个不等式解集的交集. (2)解简单分式不等式应等价转化为整式不等式(整式不等式组)求解.(3)解绝对值不等式可根据绝对值的几何意义求解,也可按零点分段法逐段脱去绝对值号求解.5.均值不等式及有关结论(1)均值不等式:如果a >0,b >0,那么a +b2≥ab ,当且仅当a =b 时,等号成立,即正数a 与b 的算术平均数不小于它们的几何平均数.(2)几个常用的重要结论:①b a +ab≥2(a 与b 同号,当且仅当a =b 时取等号). ②a +1a ≥2(a >0,当且仅当a =1时取等号),a +1a ≤-2(a <0,当且仅当a =-1时取等号).③ab ≤(a +b 2)2(a ,b ∈R ,当且仅当a =b 时取等号).(3)利用均值不等式求最值 已知x >0,y >0,则①如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值2p (简记:积定和最小). ②如果x +y 是定值s ,那么当且仅当x =y 时,xy 有最大值s 24(简记:和定积最大).素养突破·提技能类型 特殊不等式的解法 ┃┃典例剖析__■ 1.一元高次不等式的解法典例1 解不等式:(x +2)(x 2-x -12)>0.思路探究:可转化为不等式组或用数轴标根法两种方法求解.解析:方法一:原不等式可化为⎩⎪⎨⎪⎧x +2>0,x 2-x -12>0或⎩⎪⎨⎪⎧ x +2<0,x 2-x -12<0,即⎩⎪⎨⎪⎧ x >-2,x <-3或x >4或⎩⎪⎨⎪⎧x <-2,-3<x <4.解得x >4或-3<x <-2.所以原不等式的解集为{x |-3<x <-2或x >4}. 方法二:令(x +2)(x 2-x -12)=0, 得x 1=-3,x 2=-2,x 3=4. 将-3,-2,4标在数轴上,如图.由图可知原不等式的解集为{x |-3<x <-2或x >4}.归纳提升:解简单的一元高次不等式,主要通过数轴标根法来求解,其步骤是 (1)将f (x )最高次项系数化为正数.(2)将f (x )分解为若干个一次因式或二次不可分解的因式的积,然后求出f (x )=0的解,并在数轴上标出.(3)自数轴正方向起,用曲线从右至左、自上而下依次从各解穿过数轴. (4)记数轴上方为正,下方为负,根据不等式写出解集.在用数轴标根法求解高次不等式的过程中要注意:①区间端点能否取到;②各因式中最高次项的系数要全为正数;③奇数个等根,穿过,偶数个等根,穿而不过.2.分式不等式的解法典例2 解不等式:x 2+2x -3-x 2+x +6<0.思路探究:一般地,解分式不等式的基本思想是化分式不等式为整式不等式或整式不等式组.解析:原不等式可变形为x 2+2x -3x 2-x -6>0,故原不等式的解集由下面两个不等式组的解集的并集构成:①⎩⎪⎨⎪⎧x 2+2x -3>0,x 2-x -6>0;②⎩⎪⎨⎪⎧x 2+2x -3<0,x 2-x -6<0.解①得x <-3或x >3;解②得-2<x <1.综上可得,原不等式的解集是{x |x <-3或-2<x <1或x >3}.归纳提升:分式不等式的求解在高考中比较常见,解分式不等式的过程就是转化的过程,通过不等式的性质和符号运算规律将其转化为整式不等式问题,注意不等式的等价变形.类型 含参不等式恒成立问题的求解策略 ┃┃典例剖析__■不等式恒成立问题是高考中的热点内容,它以多种形式出现在高中数学的各个分支中,扮演着重要的角色.求解含参不等式的恒成立问题的关键是转化与化归思想.一般而言,针对不等式的表现形式,有如下两种策略.1.判别式法典例3 对于x ∈R ,不等式x 2-2x +3-m ≥0恒成立,求实数m 的取值范围.思路探究:不等式x 2-2x +3-m ≥0恒成立,可转化为函数y =x 2-2x +3-m 图像恒在x 轴及其上方,即Δ≤0.解析:不妨设y =x 2-2x +3-m ,其函数图像是开口向上的抛物线,为了使y ≥0(x ∈R )恒成立,只需对应方程的Δ≤0,即(-2)2-4(3-m )≤0,解得m ≤2.故实数m 的取值范围为(-∞,2].归纳提升:有关含有参数的一元二次不等式问题,若能把不等式转化为二次函数或一元二次方程,通过根的判别式或数形结合思想,可使问题得到顺利解决.2.分离变量法典例4 若关于x 的不等式ax 2-2x +2>0对于满足1<x <4的一切实数x 恒成立.求实数a 的取值范围.思路探究:可先将参数的a 分离出来即a >2x -2x 2,然后再求2x -2x 2的最值.解析:∵1<x <4,∴不等式ax 2-2x +2>0可转化为a >2x -2x 2,令y =2x -2x 2=-2(1x -12)2+12≤12.∵14<1x<1, ∴当1x =12,即x =2时,函数取得最大值12,∴a >12,即实数a 的取值范围为(12,+∞).归纳提升:如果能够将参数分离出来,建立明确的参数和变量x 的关系,那么可以利用函数的最值求解.a >y 恒成立⇔a >y max ,a <y 恒成立⇔a <y min .类型 均值不等式的变形技巧 ┃┃典例剖析__■ 1.技巧一:添项典例5 求函数y =3x 2+162+x 2的最小值.思路探究:当求和的最小值时,尽可能凑定积,本题需添6,减6. 解析:易知2+x 2>0, 所以y =3(2+x 2)+162+x 2-6≥23(2+x 2)·162+x 2-6=83-6,当且仅当3(2+x 2)=162+x 2,即x =±433-2时,等号成立,此时y min =83-6. 2.技巧二:放入根号内或两边平方典例6 求函数y =x 1-x 2(0<x <1)的最大值.思路探究:求积的最值(因式中含根号),把变量都放在同一条件下的根号里或者将两边平方去根号,整合结构形式,凑成定和,是解决本题的关键所在.解析:由0<x <1,可得y =x 1-x 2=x 2(1-x 2)≤x 2+1-x 22=12,当且仅当x 2=1-x 2,即x =22时,等号成立,此时y max =12. 3.技巧三:分子常数化典例7 设x ∈(0,+∞),求函数y =2xx 2+4的最大值.思路探究:当分子的变量因子次数比分母的小且变量因子不为零时,都可同时除以分子所含变量因子使分子变量常数化,以实现变量形式的统一,从而使问题得以解决.解析:由题意知,y =2x x 2+4=2x +4x .∵x ∈(0,+∞),∴x +4x ≥2x ·4x=4, 当且仅当x 2=4, 即x =2时,等号成立, 此时,y max =12.归纳提升:运用均值不等式求解函数最值的关键是在求解过程中充分重视运用“一正、二定、三相等”这三个条件的基础上,观察结果,合理变形.其中,成功实现变形是关键.。

第三节细胞质是多项生命活动的场所课程目标第1课时内质网、核糖体、高尔基体、溶酶体、线粒体和叶绿体知识点一细胞质细胞质是细胞进行生命活动的主要场所,正常状态下为透明的胶状物,内含细胞__新陈代谢__所需的多种营养物质。
细胞质包含多种__细胞器__和__细胞溶胶__。
知识点二内质网和核糖体1.内质网(1)结构:由一系列片状的__膜囊__和管状的__腔__组成。
(2)类型:__粗面__内质网(多呈扁囊状,表面附着有__核糖体__)和__光面__内质网(常为管状)。
(3)功能:①光面内质网是__运输蛋白质__和__合成脂质__的重要场所。
肝细胞的光面内质网有__解毒__功能,一些内分泌细胞的光面内质网可以合成__类固醇激素__。
②粗面内质网进一步加工和运输__蛋白质__。
(4)特点:向内连接__细胞核的核膜__,向外连接__细胞膜__,并与__高尔基体__相互联系,构成了细胞内庞大的__物质运输__通道。
2.核糖体(1)形态:颗粒状。
(2)组成:由__RNA__和__蛋白质__组成,外表面没有__膜__包裹。
(3)类型:一部分游离在__细胞溶胶__中,一部分附着在__粗面内质网__等结构上。
(4)功能:合成__蛋白质__的场所,不同类型的核糖体合成的蛋白质功能有所不同。
①游离型核糖体合成的蛋白质,通常用于__细胞自身__或__构成自身结构__,如红细胞中的__血红蛋白__、肌细胞中的__肌纤维蛋白__等。
②附着型核糖体合成的蛋白质被运输至__胞外__或细胞的其他部位。
③核糖体在细胞中的位置并不是固定不变的,两种存在形式可以__相互转化__。
知识点三高尔基体1.存在:真核细胞中。
2.结构:由一系列__扁平膜囊__和大小不一的__囊泡__构成。
3.功能:(1)主要对由__内质网__运入的蛋白质进行__加工__、__分类__、__包装__和__运输__;(2)在植物细胞中合成__果胶物质__,参与__细胞壁__的构建。
第三节化学反应的速率和限度一、化学反应的速率1.速率定义:_____________________________________________________________ 2.速率公式:__________________________________,速率比等于_______________________________。
〔讨论〕1、在2 L容积不变的容器中,发生N2+3H22NH3的反应。
现通入0.8 mol H2和0.4 mol N2 ,2 min后生成了0.12 mol NH3,求V (H2)、V (N2) 、V (NH3)。
2、反应A(g) + 3B(g)=2C(g)在2L密闭容器中反应,0.5min内C的物质的量增加了0.6mol,有关反应速率正确的是()A、V(A)=0.005mol/(L·s)B、V(C)=0.002mol/(L·s)C、V(B)=V(A)/3D、V(A)=0.001mol/(L·s)结论:应用化学反应速率需注意以下问题:(1)化学反应速率是标量,只有而没有;(2)一般计算出来的化学反应速率是一段时间内的速率,不同时刻的化学反应速率是不相同的;(3)固体或气体反应中的液体物质,反应在其表面进行,它们的“浓度”是变的,因此一般用固体、纯液体表示化学反应速率;(4)对于同一化学反应,用不同的物质表示其化学反应速率可能相同,但其化学意义是一样的〔练习〕1、在2 L容积不变的容器中,发生N2 + 3H2 == 2NH3的反应。
现通入4 mol H2和4 mol N2 , 用H2表示的反应速率为0.12 mol/(L·s) ,则10 s后容器中N2的物质的量是()A. 1.6molB. 2.8molC. 3.2molD. 3.6mol2、在四个不同的容器中,在不同的条件下进行合成氨N2 + 3H2 == 2NH3的反应,测得的速率如下,其中生成氨的速率最快的是()A、v ( H2 )= 0.45 mol/ (L·min)B、v ( N2 )= 0.1 mol/ (L·min)C、v ( N2 )= 0.2mol/ (L·min)D、v ( NH3 )=0.3mol/ (L·min)3、合成氨的反应为:3H2+ N22NH3,其反应的速率可分别表示为v(H2)、v(N2)、v(NH3)(单位为mol·L-1·s-1),则下列关系正确的是:()A、v(H2)=v(N2)= v(NH3)B、v(H2)=3 v(N2)C、v(N2)=2 v(NH3)D、v(NH3)=3/2v(H2)4、反应N2+3H2=2NH3在2L的密闭容器中发生反应,5min内NH3的质量增加了1.7g,求ν(NH3)、ν(N2)、ν(H2)。
物理必修一全册学案第一章运动的描述1.1 质点、参考系和坐标系【学习目标】1.掌握质点的概念,能够判断什么样的物体可视为质点。
2.知道参考系的概念,并能判断物体在不同参考系下的运动情况。
3.认识坐标系,并能建立坐标系来确定物体的位置及位置变化。
【课前预习】1.机械运动物体相对于其他物体的变化,也就是物体的随时间的变化,是自然界中最、最的运动形态,称为机械运动。
是绝对的,是相对的。
2.质点我们在研究物体的运动时,在某些特定情况下,可以不考虑物体的和,把它简化为一个,称为质点,质点是一个的物理模型。
3.参考系在描述物体的运动时,要选定某个其他物体做参考,观察物体相对于它的位置是否随变化,以及怎样变化,这种用来做的物体称为参考系。
为了定量地描述物体的位置及位置变化,需要在参考系上建立适当的。
【课堂练习】1.敦煌曲子词中有这样的诗句:“满眼风波多闪烁,看山恰似走来迎,仔细看山山不动,是船行。
”其中“看山恰似走来迎”和“是船行”所选的参考系分别是()A.船和山B.山和船C.地面和山D.河岸和流水2.下列关于质点的说法中,正确的是()A.质点就是质量很小的物体B.质点就是体积很小的物体C.质点是一种理想化模型,实际上并不存在D.如果物体的大小和形状对所研究的问题是无关紧要的因素时,即可把物体看成质点3.关于坐标系,下列说法正确的是()A.建立坐标系是为了定量描写物体的位置和位置变化B.坐标系都是建立在参考系上的C.坐标系的建立与参考系无关D.物体在平面内做曲线运动,需要用平面直角坐标系才能确定其位置4.在以下的哪些情况中可将物体看成质点()A.研究某学生骑车由学校回家的速度B.对这名学生骑车姿势进行生理学分析C.研究火星探测器从地球到火星的飞行轨迹D.研究火星探测器降落火星后如何探测火星的表面【课后练习】5.在下述问题中,能够把研究对象当作质点的是()A.研究地球绕太阳公转一周所需时间的多少B.研究地球绕太阳公转一周地球上不同区域季节的变化、昼夜长短的变化C.一枚硬币用力上抛,猜测它落地时正面朝上还是反面朝上D.正在进行花样溜冰的运动员6.坐在美丽的校园里学习毛泽东的诗句“坐地日行八万里,巡天遥看一千河”时,我们感觉是静止不动的,这是因为选取作为参考系的缘故,而“坐地日行八万里”是选取作为参考系的。
第二章等式与不等式本章小结学习目标能够从函数的观点认识方程和不等式,感悟函数和方程、不等式之间的联系,认识函数的重要性.掌握等式与不等式的性质.重点提升数学抽象、逻辑推理和数学运算素养.自主预习{等式式与不等关系实数大小的比较依据——次不等式及其解法{{课堂探究任务一:不等式的基本性质的应用例1下列结论中正确的是()①a>b>0,d>c>0⇒ac>bd;②a>b,c>d⇒a-c>b-d;③ac2>bc2⇒a>b;④a>b⇒a n>b n(n∈N,n>1).A.①②③B.①③C.②③④D.①③④任务二:一元二次不等式的解法及其应用例2解下列不等式:(1)x-1x≥2;(2)2x3+x2-5x+2>0.例3解关于x的不等式(x-2)(ax-2)>0.解一元二次不等式的步骤:任务三:二次函数、一元二次方程、一元二次不等式之间的关系例4当实数m取何范围的值时,方程x2+(m-3)x+m=0的两根满足:(1)都是正根;(2)都在(0,2)内?思考:根的分布问题应该从哪几个方面考虑?例5已知一元二次不等式ax2+bx+1>0的解集为{x|-2<x<1},则a= ,b= .任务四:基本不等式的应用例6已知3a2+2b2=5,试求y=(2a2+1)(b2+2)的最大值.例7如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米.(1)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?(2)当DN 的长为多少时,矩形花坛AMPN 的面积最小?并求出最小值.课堂练习1.若a ∈R 且a ≠0,比较a 与1a 的大小.2.求函数y=x 4+3x 2+3x 2+1的最小值.核心素养专练对任意x ∈[1,2],不等式1-mx ≤√1+x≤1-nx 恒成立,试求n 的最大值与m 的最小值.参考答案自主预习略 课堂探究例1 思路分析:判断不等关系的真假,要紧扣不等式的性质,应注意条件与结论之间的联系. 【解析】∵d>c>0⇒1c >1d>0,又a>b>0,∴a c >bd,∴①对;∵a>b ,-c<-d 不同向,不等式不可加,∴②错; ∵ac 2>bc 2,c 2>0,∴a>b ,∴③对;只有当a>b>0时,才有a n >b n ,∴④错,故选B .答案:B例2 【思路分析】对于(1),要先移项、通分化为f(x)g(x)≥0(或f(x)g(x)≤0)的形式,再化为整式不等式,转化必须保持等价;对于(2),要因式分解后借助穿根法处理.【解】(1)原不等式可化为x -1x -2≥0,∴-x -1x>0,∴{x(x +1)≤0,x ≠0,∴-1≤x<0.∴原不等式的解集为{x|-1≤x<0}.(2)原不等式可化为(x-1)(x+2)(2x-1)>0. 利用数轴标根法或穿根法(如图所示),∴-2<x<12或x>1.∴不等式的解集为{x |-2<x <12或x >1}.例3 【思路分析】不等式中含有参数a ,因此需要先判断参数a 对方程(x-2)(ax-2)=0的解的影响,然后求解.【解】(1)当a=0时,原不等式化为x-2<0,∴x<2,∴原不等式的解集为{x|x<2}.(2)当a<0时,原不等式化为(x-2)(x -2a )<0.方程(x-2)(x -2a )=0的两根为2,2a ,又2>2a,∴原不等式的解集为{x |2a<x <2}.(3)当a>0时,原不等式化为(x-2)(x -2a )>0.方程(x-2)(x -2a )=0的两根为2,2a .当0<a<1时,2a >2,原不等式的解集为{x |x >2a 或x <2}. 当a=1时,原不等式化为(x-2)2>0,解集为{x ∈R |x ≠2}. 当a>1时,2>2a >0,原不等式的解集为{x |x >2或x <2a }. 综上所述,不等式解集为当a=0时,{x ∈R |x<2};当a=1时,{x ∈R |x ≠2};当a<0时,{x |2a<x <2};当0<a<1时,{x |x >2a 或x <2};当a>1时,{x |x >2或x <2a }.解一元二次不等式的步骤: 1.若能因式分解,则用数轴穿根法; 2.若不能因式分解,则用配方法. 配方法的步骤:(1)把一元二次不等式的二次项系数化为1;(2)一元二次不等式通过配方变为(x-h )2>k 或(x-h )2<k 的形式; (3)根据k 值情况确定不等式的解集.例4 【思路分析】对于(1),可利用判别式及根与系数的关系求解;对于(2),可构造二次函数,结合二次函数的图像求解.【解】(1)设方程的两根为x 1,x 2.则由题意可得{Δ=m 2-10m +9≥0,x 1+x 2=3-m >0,x 1x 2=m >0.解得m 的取值范围是(0,1]. (2)(由对应的函数几何意义求解) 设f (x )=x 2+(m-3)x+m ,由题意得{Δ=m 2-10m +9≥0,f(0)=m >0,0<3-m2<2,f(2)=3m -2>0.解得23<m ≤1. 思考:根的分布问题应该从哪几个方面考虑? 1.开口方向; 2.判别式Δ; 3.对称轴;4.区间端点函数值的正负.例5 【思路分析】由于一元二次不等式解集的分界点是相应一元二次方程的两根,所以解答就从这个关系入手.【解析】由于ax 2+bx+1>0的解集为{x|-2<x<1},所以-2和1是方程ax 2+bx+1=0(a ≠0)的两根. 由根与系数的关系,得 {-2+1=-ba ,-2×1=1a ,解得a=b=-12. 答案:-12-12例6 【思路分析】要求积的最大值,关键是结合条件配凑出和为定值,然后利用基本不等式求解. 【解】∵2a 2+1>0,b 2+2>0,y=(2a 2+1)(b 2+2),∴√12y =√3(2a 2+1)·4(b 2+2)≤6a 2+3+4b 2+82.∵3a 2+2b 2=5,∴6a 2+4b 2=10. ∴√12y ≤212,可得√y ≤7√34.∴y 的最大值为14716.例7 【思路分析】对于(1),首先建立矩形AMPN 的面积y 与DN 的长x 的函数关系式,然后利用不等式求解;对于(2),根据(1)中建立的函数关系式结合基本不等式求解.【解】(1)设DN 的长为x (x>0)米,则AN 的长为(x+2)米,如图所示.∵DN AN =DC AM ,∴AM=3(x+2)x.∴矩形花坛AMPN 的面积y=AN ·AM=3(x+2)2x.由y>32,得3(x+2)2x>32.∵x>0,∴3x 2-20x+12>0.解得0<x<23或x>6,即DN 长的取值范围是(0,23)∪(6,+∞). (2)由(1)知矩形花坛AMPN 的面积为y=3(x+2)2x=3x 2+12x+12x=3x+12x +12≥2√3x ·12x +12=24.当且仅当3x=12x,即x=2时,矩形花坛AMPN 的面积取得最小值24平方米.故DN 的长为2米时,矩形AMPN 的面积最小,最小值为24平方米. 课堂练习1.【思路分析】可以利用作差比较法比较两个代数式的大小. 【解】a-1a =(a -1)(a+1)a.当a=±1时,(a -1)(a+1)a=0,则a=1a ;当-1<a<0或a>1时,(a -1)(a+1)a>0,则a>1a . 当a<-1或0<a<1时,(a -1)(a+1)a<0,则a<1a .2.【思路分析】从函数解析式结构上看,它与基本不等式结构相差太大,而且利用前面求最值的方法不易求解,怎么办呢?事实上,我们可以把分母视为一个整体,用它来表示分子,原式即可展开.【解】令t=x 2+1,则t ≥1,且x 2=t-1.∴y=x 4+3x 2+3x 2+1=(t -1)2+3(t -1)+3t =t 2+t+1t=t+1t +1.∵t ≥1,∴t+1t ≥2√t ·1t =2,当且仅当t=1t ,即t=1时,等号成立.∴当x=0时,函数取得最小值3.核心素养专练【思路分析】对任意x ∈[1,2],不等式恒成立,且m 与n 都是一次的,因此可考虑分离参数m 和n. 【解】∵1-mx ≤√1+x≤1-nx 恒成立,∴-mx ≤√1+x -1≤-nx ,∴-mx ≤√1+x√1+x ≤-nx ,∴-mx ≤√1+x(1+√1+x)≤-nx.又∵x ∈[1,2],∴n ≤(√1+x)2+√1+x≤m 恒成立. 设y=(√1+x)2+√1+x,x ∈[1,2],令√1+x =t ,则t ∈[√2,√3],y=1t 2+t . 可求得y min =3-√36,y max =2-√22,∴m=2-√22,n=3-√36.故所求n 的最大值为3-√36,m 的最小值为2-√22.学习目标1.梳理等式的性质,理解不等式的概念,掌握不等式的性质,通过类比理解等式与不等式的共性与差异;2.会解常见的方程和不等式及不等式组,如一元二次方程、一元二次不等式、绝对值不等式、二元及三元方程组等;3.掌握基本不等式,结合具体实例,能用基本不等式解决简单的最大值和最小值问题. 本章重点:绝对值不等式的解法、一元二次不等式的解法、均值不等式的应用.本章难点:均值不等式的灵活应用及不等式的证明.重点提升数学抽象、逻辑推理和数学运算素养.培养学生类比思想、分类讨论思想和数形结合的数学思想等.知识点梳理课堂探究●不等式性质的应用例1(1)(多选)下列命题正确的有()A.若a>1,则1a<1B.若a+c>b,则1a <1 bC.对任意实数a,都有a2≥aD.若ac2>bc2,则a>b(2)已知2<a<3,-2<b<-1,求ab,b2a的取值范围.◎跟踪训练1(多选)已知a,b,c∈R,那么下列命题中错误的是() A.若a>b,则ac2>bc2B.若ac >bc,则a>bC.若a3>b3且ab<0,则1a >1 bD .若a 2>b 2且ab>0,则1a <1b●不等式组的解法 例21.解不等式组:{5x-1<3(x +1),2x-13-1≤5x +12.2.已知关于x 的不等式组{x +a ≤0,3+2x >5的整数解只有3个,求a 的取值范围.3.解下列关于x 的不等式. (1)-1<x 2+2x-1≤2; (2)m 2x 2+2mx-3<0.◎跟踪训练2 解下列不等式. (1)x -1x+2≤0; (2)-3x 2-2x+8≥0; (3)ax 2-(a+1)x+1<0.●绝对值不等式的解法 例3 解下列不等式. (1)|2x-5|>3; (2)|2x-1|+|2x+1|≤6.◎跟踪训练3解下列不等式.(1)|2x+1|-2|x-1|>0;(2)|x+3|-|2x-1|<x2+1.●均值不等式例4若x>0,y>0,且x+2y=5,求9x +2y的最小值,并求出取得最小值时x,y的值.◎跟踪训练41.函数y=x(3-2x)(0≤x≤1)的最大值是.2.当x>1时,不等式x+1x-1≥a恒成立,当x= 时等号成立,实数a的取值范围是.●等式与不等式的应用例5某单位用2 160万元购得一块空地,计划在该空上建造一栋至少10层,每层2 000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用建筑总面积.课堂练习1.已知集合M={x|-4≤x ≤7},N={x|x 2-x-12>0},则M ∩N=( ) A.{x|-4≤x<-3或4<x ≤7} B.{x|-4<x ≤-3或4≤x<7} C.{x|x ≤-3或x>4} D.{x|x<-3或x ≥4}2.(多选)已知a>b>0,下列不等式不成立的是( ) A.a+1b >b+1aB.a+1a ≥b+1bC.b a >b+1a+1D.b-1b>a-1a3.不等式|x+1|-|x-2|≥1的解集是 .4.已知x>0,y>0,且满足8x +1y=1,xy= 时,x+2y 的最小值为 .核心素养专练[A 基础达标]1.(多选)如果a ,b ,c 满足c<b<a ,且ac<0,那么下列不等式中一定成立的是( ) A .ab>ac B .c (b-a )>0 C .cb 2<ab 2 D .ac (a-c )<02.若a>0,b>0,且a 2+3b 2=6,则ab 的最大值为( ) A .1B .√2C .√3D .23.设m>1,P=m+4m -1,Q=5,则P ,Q 的大小关系为( ) A .P<QB .P=QC .P ≥QD .P ≤Q4.不等式1+x>11-x 的解集为( ) A .{x|x>0} B .{x|x ≥1} C .{x|x>1} D .{x|x>1或x=0} 5.设a ,b 是不相等的正数,x=√a+√b2,y=√a+b 2,则x ,y 的大小关系是 (用“>”“<”或“=”连接).6.设m+n>0,则关于x 的不等式(m-x )(n+x )>0的解集是 .7.已知0<x<12,则y=12x (1-2x )的最大值为 ,此时x= . 8.解下列不等式: (1)0<|x-2|≤|4x+2|; (2)2x+1x -5≥-1.9.已知x ,y 都是正数.(1)若3x+2y=12,求xy 的最大值;(2)若x+2y=3,求1x +1y 的最小值.[B 能力提升]10.不等式4x -2≤x-2的解集是( )A .(-∞,0]∪(2,4]B .[0,2)∪[4,+∞)C .[2,4)D .(-∞,2]∪(4,+∞)11.已知实数x ,y ,若x ≥0,y ≥0且x+y=3,则x+1x+2+y y+1的最大值为 ,此时xy= . 12.解不等式3x -7x 2+2x -3≥2.13.解关于x 的不等式ax 2+(1-a )x-1>0(a<0).14.志愿者团队要设计一个如图所示的矩形队徽ABCD ,已知点E 在边CD 上,AE=CE ,AB>AD ,矩形的周长为8 cm .(1)设AB=x cm,试用x 表示出图中DE 的长度,并求出x 的取值范围;(2)计划在△ADE 区域涂上蓝色代表星空,如果要使△ADE 的面积最大,那么应怎样设计队徽的长和宽?参考答案课堂探究例1 (1)AD (2)-6<ab<-213<b 2a <2跟踪训练1 ABD例2 1.解集为[-1,2) 2.(-5,-4]3.解:(1){x 2+2x -1≤2,x 2+2x -1>-1⇒{x 2+2x -3≤0,x 2+2x >0⇒{-3≤x ≤1,x >0或x <-2,不等式的解集为{x|-3≤x<-2或0<x ≤1}.(2)当m=0时,-3<0恒成立,解集为R .当m ≠0时,二次项系数m 2>0,Δ=16m 2>0.不等式化为(mx+3)(mx-1)<0.当m>0时,解集为{x |-3m <x <1m }; 当m<0时,解集为{x |1m <x <-3m }.跟踪训练2 (1)(-2,1](2)[-2,43] (3)解:当a=0时,x>1,解集为(1,+∞);当a ≠0时,方程化简为(ax-1)(x-1)<0.当a<0时,方程整理为(x -1a )(x-1)>0,(1a <0), ∴x>1或x<1a ,解集为(-∞,1a )∪(1,+∞);当a>0时,方程整理为(x -1a )(x-1)<0,(1a>0), 当0<a<1时,1a >1,∴1<x<1a ,解集为(1,1a); 当a=1时,1a =1,∴方程无解,解集为空集;当a>1时,1a <1,∴1a <x<1,解集为(1a ,1). 例3 (1)(-∞,-1)∪(4,+∞)(2)[-32,32]跟踪训练3(1)不等式的解集为{x |x >14}.(2)不等式的解集为{x |x <-25或x >2}.例4 解:因为x>0,y>0,且x+2y=5, 所以9x +2y =15(x+2y )(9x +2y ) =15(13+18y x +2x y ) ≥15(13+2√18y x ·2x y )=5,当且仅当{x +2y =5,18y x =2x y,即{x =3,y =1时等号成立. 所以9x +2y 的最小值为5,此时x=3,y=1. 跟踪训练41.982.2 a ≤3例5 解:设将楼房建为x 层,平均综合费用设为y 元. 则每平方米的平均购地费用为2 160×1042 000x =10 800x .∴每平方米的平均综合费用y=560+48x+10 800x =560+48(x +225x ). 当x+225x取最小值时,y 有最小值. ∵x>0,∴x+225x ≥2√x ·225x =30. 当且仅当x=225x ,即x=15时,上式等号成立.∴当x=15时,y 有最小值2 000元.因此该楼房建为15层时,每平方米的平均综合费用最少. 课堂练习1.A2.BCD3.[1,+∞)4.36 18 核心素养专练A 基础达标1.ABD2.C3.C4.C5.x<y6.(-n ,m )7.116 148.(1){x |x ≤-43或x ≥0且x ≠2} (2){x |x >5或x ≤43}9.(1)6 (2)1+23√2B 能力提升10.B11.43 212.(-3,1)13.当-1<a<0时,解集为{x |1<x <-1a } 当a=-1时,解集为⌀ 当a<-1时,解集为{x |-1a <x <1} 14.解: (1)设DE=y cm,则AE=CE=(x-y )cm, 由矩形周长为8 cm,可得AD=(4-x )cm . 在三角形ADE 中,由勾股定理可得(4-x )2+y 2=(x-y )2, 整理得y=4-8x ,由AB>AD 可得x>2,由周长为8可得x<4, 综上DE 长度为(4-8x )cm,2<x<4. (2)S=12(4-x )×y ,由y=4-8x 可得S=12(4-x )·(4-8x )=2(4-x )(1-2x )=2(6-x -8x), 由2<x<4可得x+8x ≥2√8=4√2,当且仅当x=2√2时取到等号, 因此S max =2(6-4√2)=12-8√2,此时队徽的长为2√2 cm,宽为(4-2√2)cm .。
学案 第二章 强身健体一、学习目标:1、明确体能的构成。
2、获得健康体能和运动体能方面的基本知识。
3、了解有氧运动和无氧运动,并能正确划分。
二、课前重点知识阅读学习 1、体能的构成体能健康体能运动体能成分1、 心肺耐力2、 肌肉力量和肌肉耐力3、 柔韧性4、 身体成分 1、速度 2、爆发力 3、灵敏性 4、平衡性5、协调性6、反应时目的 1、 保持身体健康2、 提高生活质量1、 提高运动技能水平2、 增大比赛中获胜的几率2、与健康有关的体能心肺耐力指呼吸及循环系统在活动时提供氧气及营养,以满足长时间身体活动身体所需要的能力,是评定人体健康体能的重要指标之一。
有氧运动是指人体在氧气充分供应的情况下进行的体育锻炼。
即在运动过程中,人体吸入的氧气与需求相等,达到生理上的平衡状态。
简单来说,有氧运动是指任何富韵律性的运动,其运动时间较长(约15分钟或以上),运动强度在中等或中上的程度(最大心率之75%至85%)。
有氧运动时葡萄糖代谢后生成水和二氧化碳,可以通过呼吸很容易被排出体外,对人体无害。
心率保持在150次/分钟的运动量为有氧运动,因为此时血液可以供给心肌足够的氧气; 因此,它的特点是强度低,有节奏,持续时间较长。
要求每次锻炼的时间不少于1小时,每周坚持3到5次。
这种锻炼,氧气能充分酵解体内的糖分,还可消耗体内脂肪,增强和改善心肺功能,预防骨质疏松,调节心理和精神状态,是健身的主要运动方式。
常见的有氧运动项目有:步行、快走、慢跑、竞走、滑冰、长距离游泳、骑自行车、打太极拳、跳健身舞、跳绳/做韵律操、球类运动如篮球、足球等等。
有氧运动特点是强度低、有节奏、不中断和持续时间长。
同举重、赛跑、跳高、跳远、投掷等具有爆发性的非有氧运动相比较,有氧运动是一种恒常运动,是持续5分钟以上还有余力的运动。
有氧运动的目的在于增强心肺耐力。
在运动时,由于肌肉收缩而需要大量养分和氧气,心脏的收缩次数便增加,而且每次压送出的血液量也较平常为多,同时,氧气的需求量亦增加,呼吸次数比正常为多,肺部的收张程度也较大。
所以当运动持续,肌肉长时间收缩,心肺就必须努力地供应氧气分给肌肉,以及运走肌肉中的废物。
而这持续性的需求,可提高心肺的耐力。
当心肺耐力增加了,身体就可从事更长时间或更高强度的运动,而且较不易疲劳。
无氧运动是指肌肉在“缺氧”的状态下高速剧烈的运动。
无氧运动大部分是负荷强度高、瞬间性强的运动,所以很难持续长时间,而且疲劳消除的时间也慢。
无氧运动是相对有氧运动而言的。
在运动过程中,身体的新陈代谢是加速的,加速的代谢需要消耗更多的能量。
人体的能量是通过身体内的糖、蛋白质和脂肪分解代谢得来的。
在运动量不大时,比如慢跑、打羽毛球、跳舞等情况下,机体能量的供应主要来源于脂肪的有氧代谢。
以脂肪的有氧代谢为主要供应能量的运动就是我们说的有氧运动。
当我们从事的运动非常剧烈,或者是急速爆发的,例如举重、百米冲刺、摔跤等,此时机体在瞬间需要大量的能量,而在正常情况下,有氧代谢是不能满足身体此时的需求的,于是糖就进行无氧代谢,以迅速产生大量能量。
这种状态下的运动就是无氧运动。
无氧运动能量来自无氧酵解,在酵解时产生大量乳酸等中间代谢产物,不能通过呼吸排除。
这呼吸、心跳加快和心律失常,严重时会出现酸中毒和增加肝肾负担。
所以无氧运动后,人总会疲惫不堪,肌肉酸痛要持续几天才能消失。
常见的无氧运动项目有:短跑、举重、投掷、跳高、跳远、拔河、俯卧撑、潜水、肌力训练(长时间的肌肉收缩)等。
三、课中问题探讨1、坚持有氧运动可以增强人们的心肺耐力,促进人的身体健康,下列属于有氧练习的是()①拳击②慢跑③跳高④举重⑤游泳⑥跳绳⑦骑自行车A. ①②④⑦B. ②③⑤⑥C. ②⑤⑥⑦D. ①④⑤⑥2、影响跑速的因素有很多种,下列不是影响跑速的因素是()A. 柔韧性B.腿长C. 运动技能巩固程度D. 身体成分3、投掷项目的用力顺序是()A. 自上而下B.自下而上C. 有中间的两端D. 同时发力4、下面哪种田径项目是集速度、爆发力、灵敏性、协调性、平衡性等于一身的运动形式()A. 长跑B. 跳高C. 跨栏D. 撑杆跳高5、在减肥和预防肥胖的方法中,正确的是()①加强体育锻炼,养成体育锻炼的习惯。
②改变不良的生活方式。
③减少油腻食物的摄入量,大量进食谷物和蛋白质。
④在医生的指导下服用减肥药物。
A. ①②③B. ①③④C. ①②④D. ②③④6、有些同学一打篮球就会忘掉一切,搞得筋疲力尽方肯罢休,这样的“发泄,忘我式”的锻炼很容易造成运动过度,不利于身体健康。
下列哪种情况不是运动过度的征兆()A、第二天醒来,仍然感到疲劳、沉重B、运动后5分钟检测脉率低于100次/分C、上课总想打瞌睡,做作业总出差错D、早晨醒来时的脉搏比平时高出10%以上7、运动强度范围在()最大吸氧量时,对增强心肺耐力最有意义。
A、50-85%B、10-30%C、50-75%D、65-85%8、某同学在参加《国家学生体质健康标准》测试中,测试了800米跑等多个项目,其中一个项目的测试方法是:受试者两腿伸直,两脚平蹬测试纵板坐在平地上,两脚分开10-15厘米,上体前屈,两臂伸直向前,用两手中指指尖逐渐向前推动游标,指导不能前推为止。
据此推断该测试项目的名称及该同学的性别分别是()A、仰卧起坐,男B、仰卧起坐,女C、坐位体前屈,男D、坐位体前屈,女四、课后思考:1、如何制定个人的体能发展计划?3、简述步频和步幅与跑的关系。
答案:三、1、C 2、B 3、A4、C 5、A 6、B 7、D 8、D四、1、提示:内容包括:发展目标、选择项目、锻炼频率、锻炼时间、运动强度2、提示:步幅与步频是一对矛盾,片面追求哪一个,都不会有效地提高跑的成绩。
学案第三章健身益心一、学习目标:1、了解体育锻炼怎样增强自我价值。
2明确不同的体育锻炼能培养人不同的意志品质。
二、课前重点知识阅读学习有规律的体育活动可以增强人的体质,促进身体的健康,预防和治疗心血管疾病、糖尿病、关节炎和骨质疏松等生理疾病。
同时,体育活动还有助于增进心理健康,如体育活动可以改善情绪状态,完善个性心理品质,帮助确立良好的自我概念,改善认知方式,还可以作为心理治疗的一种手段等。
因此,认识体育锻炼对人们健康的重要作用,可以养成长期锻炼习惯以及促进全面发展奠定基础。
古人云:喜伤心、怒伤肝、思伤脾、忧伤肺、恐伤肾。
当你突发震惊、恐惧、极度愤怒或过分激动时,可以选择自己喜欢或擅长的体育运动,因为身体的大幅度活动可以使高涨的心理压力排出体外,体内由不良情绪亢奋引起的能量也就释放出来了,从而有效地缓解不良情绪。
坚强的意志品质既是克服困难的过程中表现出来的,又是在此过程中培养起来的,具体包括目的性、独立性、果敢性、坚韧性和自制性等意志品质。
三、课中思考1、如果你发现自己遇事容易急躁、冲动,可以选择下列哪种运动项目()A、乒乓球B、围棋C、扑克D、跳绳2、你在学校学习和社会生活中可能会遇到许多困难和挫折,也许会给你的心理造成很大的压力,由此可能产生一些心理困惑或心理障碍。
有许多方法可以缓解和消除这些不良心理,下列说法不正确的是()A、经常参加接力跑、拔河等集体项目和游戏,可以消除某些心理困惑或心理障碍,建立和谐的人际关系。
B、长期中低强度的身体锻炼,对焦虑、抑郁等症状具有长期稳定的缓解和治疗作用。
C、《金蛇狂舞》、《步步高》等乐曲可以帮助你振奋精神。
D、倘若你发现自己遇事容易急躁、冲动,那你就应该多参加短跑、跳远等田径项目的锻炼。
3、悉尼奥运会柔道冠军唐琳,参赛前两年得了严重的腰椎病,当时几乎瘫痪。
在大家的帮助下,靠她坚定的信念,通过刻苦训练,终于夺得了金牌,此事体现了唐琳的意志品质是()A、坚韧性B、果敢性C、自制性D、目的性4、在体育运动中可以锻炼人坚强的意志品质,如乒乓球比赛中,参与者会随着场上出现的复杂战况而产生不同的心理状态,这时就需要有较强的()来调节、控制不良情绪的产生。
A、坚韧性B、果敢性C、自制性D、目的性A、和平、友谊、进步 B 、公平、公正、正义C、更高、更快、更强D 、光明、团结、进步6、下列不属于健康的四个纬度是:()A、身体健康B、心理健康C、社会适应D、体育锻炼7、在体育运动中具有和谐的人际关系和彼此默契的交流,不但会给比赛带来精彩绝伦的场面,而且还会增加团队的凝聚力。
下列体育比赛交流中属于默契配合的是()①空中接力扣篮②排球比赛中的“单脚背飞”进攻③乒乓球双打中通过手势发球抢攻④姚明大帽回敬小奥尼尔⑤篮球比赛中的侧掩护⑥足球比赛中扑出点球A.①②④ B.①②③⑤ C.②④⑥ D.以上全是8、下列对体育道德内涵叙述正确的是()A.体育道德是个体品德在体育活动中的反映,只是个体的行为反映,不良的体育道德不会对社会道德产生影响。
B.体育比赛中设立的“精神文明奖”,只是对成绩较差的运动队弥补一个心理平衡,与运动员的道德表现没有直接关系。
C.体育道德既是一种约束运动员、教练员、裁判员的职业道德,也能起到对全社会起教化作用的社会公德的作用。
D.某些观众在观看体育比赛时经常出言不逊,辱骂裁判和运动员,甚至向赛场内投掷杂物,这种行为只是个人情绪的变化,与体育道德范畴无关。
9、根据以下历史人物性格类型,太极拳适合于()帮助发展情绪调控的能力。
A.林黛玉B. 张飞C.哈姆雷特D.葛朗台10、体育锻炼对智力发展的效应可以表现为()A .体育锻炼可以治疗记忆力减退B .体育锻炼加速脑细胞疲劳,抑制大脑兴奋,造成记忆减退C .体育锻炼可以调节和延长大脑的适度兴奋,提高学习效率。
D .体育锻炼对扩大智力容量几乎没有作用。
11、在比赛中,运动员甲发现落后太远,名次无望,偷偷的退出了比赛;运动员乙尽管一直落后,却努力坚持到终点。
对两位运动员的表现说法正确的是()A.运动员甲很聪明,知道再跑也得不到名次,还不如趁早退出B.运动员乙很傻,明知道名次无望,还消耗体力,反而是在拖延时间,影响比赛C.运动员甲比乙的意志薄弱D.运动员乙比甲果断12、下列体育项目对培养学生主要意志品质对应正确的一组是( )A.长跑---坚韧性 B.射击---独立性 C.跳水---坚韧性 D.球类---自制性四、课后思考自制性是指能够自觉而灵活地控制自己情绪和活动方式的意志品质,如你想增强自我的控制能力,你应该选择那些运动项目?(至少举三项)答案:1、B2、D3、D4、C5、C6、D7、B8、C9、A 10、C 11、C 12、A 课后思考:棋类太极拳钓鱼射击射箭飞镖。