当前位置：文档之家 › 第七弹性力学平面问题的极坐标系解答

第七弹性力学平面问题的极坐标系解答

  • 格式：doc
  • 大小：579.00 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

《弹塑性力学》第七章 弹性力学平面问题的极坐标系解答.ppt

《弹塑性力学》第七章 弹性力学平面问题的极坐标系解答.ppt

x
应力：r, ,r= r 应变：r, ,r= r
P
y
位移：u r , u
2020/10/9
3
§7-1平面极坐标下的基本公式
直角坐标与极坐标之间关系:
x=rcos, y=rsin
r cos sin
x r x x
r r
r sin cos
y r y y
r
r
2 r
r )( f r
r
f 1
r
fr 0 0 f
fr ) r
2＝ 2 1 1 2
r 2 r r r 2 2
力的边界条件如前所列。
2020/10/9
14
§7-1平面极坐标下的基本公式
1.8 应力函数解法
当体力为零 fr=f=0时, 应力法基本方程中的应
力分量可以转为一个待求的未知函数 ( r, ) 表示,而应力函数 ( r, ) 所满足方程为
16
§7-2 轴对称问题
2.1 轴对称问题的特点
1.截面的几何形状为圆环、圆盘。
2.受力和约束对称于中心轴,因此，可知体 积力分量 f=0 ； 在边界上 r=r0 ：F 0， u （0 沿环向的受力和约束为零） 。
3.导致物体应力、应变和位移分布也是轴 对称的：
2020/10/9
17
§7-2 轴对称问题
上式代入平衡微分方程可得到用位移表 示的平衡微分方程,即位移法的基本方程。
r
r
1 r r
( r
r
)
Kr
0
r
r
1 r
2 r
r
K
0
力的边界条件也同样可以用位移表示。
2020/10/9

弹塑性力学 第07章平面问题的极坐标解答

弹塑性力学 第07章平面问题的极坐标解答

ϕ 改变，即与 ϕ 无关。由此可见，凡是轴
对称问题，总是使自变称的 物理量不能存在。
考擦应力函数 U 与 ϕ 无关的一种特殊情况，即轴对称， 此时极坐标形式的双调和方程变成常微分方程 ⎛ ∂2 1 ∂ 1 ∂ 2 ⎞⎛ ∂ 2U 1 ∂U 1 ∂ 2U ⎞ ⎜ ⎜ ∂ρ 2 + ρ ∂ρ + ρ 2 ∂ϕ 2 ⎟ ⎟⎜ ⎜ ∂ρ 2 + ρ ∂ρ + ρ 2 ∂ϕ 2 ⎟ ⎟=0 ⎝ ⎠⎝ ⎠ ⎛ d2 1 d ⎞⎛ d 2U 1 dU ⎞ ⎜ ⎜ d ρ 2 + ρ dρ ⎟ ⎟⎜ ⎜ dρ 2 + ρ dρ ⎟ ⎟=0 ⎝ ⎠⎝ ⎠
τ ρϕ = τ ϕρ
∂ ⎛ 1 ∂U ⎞ 1 ∂ 2U 1 ∂U ⎜ ⎟ =− + 2 =− ⎜ ∂ρ ⎝ ρ ∂ϕ ⎟ ρ ∂ρ∂ϕ ρ ∂ϕ ⎠
¾极坐标系中边界条件的处理： ①、对于由径向线和环向线所围成的弹性体，其边界面通常 均为坐标面，即ρ 面（ρ 为常数）和 ϕ 面（ϕ 为常数），使 边界的表示变得十分简单，所以边界条件也十分简单。 ②、对于应力边界条件，通常给定径向和切向面力值，可直 接与对应的应力分量建立等式（注意符号规定） 应力边界条件：
¾平面问题极坐标形式的几何方程
ερ =
∂u ρ
∂ρ u ρ 1 ∂uϕ εϕ = + ρ ρ ∂ϕ 1 ∂u ρ ∂uϕ uϕ + − γ ρϕ = ρ ∂ϕ ∂ρ ρ
平 面 应 变 问 题
⎧ 1 ⎪ε ρ = (σ ρ −ν 1σ ϕ ) E1 ⎪ ⎪ 1 ⎨ε ϕ = (σ ϕ −ν 1σ ρ ) E1 ⎪ ⎪ 2(1 +ν 1 ) γ τ ρϕ = ⎪ ρϕ E1 ⎩
¾平面问题极坐标形式的物理方程 平 面 应 力 问 题

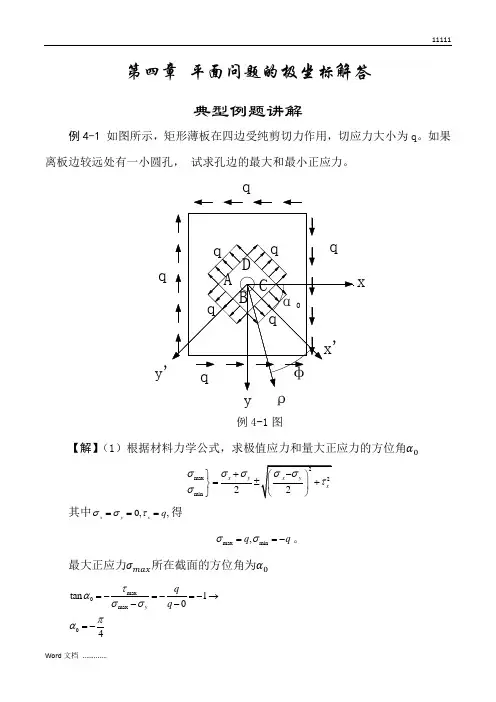
弹性力学简明教程-第四章-平面问题的极坐标解答习题详解

弹性力学简明教程-第四章-平面问题的极坐标解答习题详解

第四章 平面问题的极坐标解答典型例题讲解例4-1 如图所示，矩形薄板在四边受纯剪切力作用，切应力大小为q 。

如果离板边较远处有一小圆孔， 试求孔边的最大和最小正应力。

例4-1图【解】（1）根据材料力学公式，求极值应力和量大正应力的方位角max min 2x y σσσσ+⎫=⎬⎭ 其中0,,x y x q σστ===得max min ,q q σσ==-。

最大正应力 所在截面的方位角为max 0max 0tan 104yqq τασσπα=-=-=-→--=-qqx若在该纯剪切的矩形薄板中，沿与板边成方向截取矩形ABCD ，则在其边界上便承受集度为q 的拉力和压力，如图所示。

这样就把受纯剪切作用的板看作与一对边受拉，另一对边受压的板等效。

（2）取极坐标系如图。

由2222442222cos 2(1)(13),cos 2(13),(4-18)sin 2(1)(13).ρφρφr r σq φρρr σq φρr r τq φρρ⎫=--⎪⎪⎪⎪=-+⎬⎪⎪=--+⎪⎪⎭得矩形薄板ABCD 内的应力分量为()()()2222442222cos 2(1)(13)cos 2(13)sin 2(1)(13)ρφρφa a σq φa ρρa σq φb ρa a τq φc ρρ=--=-+=--+ 其中 为小孔的半径，而孔边最大与最小正应力由式（b ），在 处得到44cos 2(13)4cos 2,φa σq φaϕ=-+=-当 ， 时，孔边最小正应力为，当时，孔边最大正应力为。

分析：矩形板ABCD 边界上各点的应力状态与板内无孔时的应力状态相同。

也可以应用叠加法，求解薄板的各种较复杂的平面应力（应变）问题。

习题全解4-1试比较极坐标和直角坐标中的平衡微分方程、几何方程和物理方程，指出哪些项是相似的，哪些项是极坐标中特有的？并说明产生这些项的原因。

【解】 （1）极坐标，直角坐标中的平衡微分方程10210f f ρρϕρϕρρϕϕρϕϕστσσρρϕρτστρρϕρ∂∂-⎧+++=⎪∂∂⎪⎨∂∂⎪+++=⎪∂∂⎩ 00yxx x y xy yf xy f y x τσστ∂⎧∂++=⎪∂∂⎪⎨∂⎪++=⎪∂∂⎩将极坐标中的平衡微分方程与直角坐标中的平衡微分方程相比较，第一式中，前两项与直角坐标相似；而项是由于正 面上的面积大于负 面上的面积而产生的，是由于正负 面上的正应力 在通过微分体中心的 方向有投影而引起的。

弹性力学平面问题极坐标

弹性力学平面问题极坐标

r
r
2 2 2 x2 y2
sin cos
r
r
cos2 sin2
r2
sin cos
r2
2
2
2 r 2
1 r
r
1 r2
2 r 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
（1）极坐标系下的应力分量和体力分量
O
如图，根据应力状态的定义，过P
点分别以 r 方向和 方向为法线的截面
由半圆上的应力和外力的平衡关系，有
M
O
x
a
r r r
y
Fx 0
Fy 0 Mz 0
0
r
r
a
cos
ad
0
r
r a
sin
ad
0
0
r
ra
cos
r
ra
sin
d
0
0
r
ra
sin
r
ra
cos
d
0
a 0 a 0
0
r
ra
a ad
M
0
0
r
a2d M
ra
a 0
0
r
1 r
2 r
r
Fb
0
三. 极坐标系下的几何方程
1. 直角坐标与极坐标系下的位移分量关系
类似体力分量的投影关系 2. 极坐标系下的应变分量
O
x
r
Pu
u
ur
v
r
y
将P点分别沿 r 和 方向（相互垂直）两线元的线应变 r、 及其切应变 r ， 作为P点的应变分量。
3. 极坐标系下的几何方程

弹性力学第七章平面问题的极坐标解

弹性力学第七章平面问题的极坐标解

第七章 平面问题的极坐标解知识点极坐标下的应力分量 极坐标下的应变分量 极坐标系的 Laplace 算符 轴对称应力分量 轴对称位移和应力表达式 曲梁纯弯曲 纯弯曲位移与平面假设 带圆孔平板拉伸问题 楔形体问题的应力函数 楔形体应力 楔形体受集中力偶作用、内容介绍在弹性力学问题的处理时，坐标系的选择从本质上讲并不影响问题的求解， 但是坐标的选取直接影响边界条件的描述形式，从而关系到问题求解的难易程 度。

对于圆形，楔形，扇形等工程构件，采用极坐标系统求解将比直角坐标系统 要方便的多。

本章的任务就是推导极坐标表示的弹性力学平面问题基本方程， 且求解一些典型问题。

极坐标平衡微分方程 几何方程的极坐标表达 应力函数 轴对称位移 厚壁圆筒作用均匀压力 曲梁弯曲应力 曲梁作用径向集中力 孔口应力 楔形体边界条件 半无限平面作用集中力二、重点1、基本未知量和基本方程的极坐标形式；2、双调和方程的极坐标形式；3、轴对称应力与厚壁圆筒应力；4、曲梁纯弯曲、楔形体和圆孔等典型问题§7.1平面问题极坐标解的基本方程学习思路：选取极坐标系处理弹性力学平面问题，首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。

本节的主要工作是介绍基本物理量，包括位移、应力和应变的极坐标形式；并且将基本方程，包括平衡微分方程、几何方程和本构关系转化为极坐标形式。

由于仍然采用应力解法，因此应力函数的极坐标表达是必要的。

应该注意的是坐标系的选取与问题求解性质无关，因此弹性力学直角坐标解的基本概念仍然适用于极坐标。

学习要点:1、极坐标下的应力分量；2、极坐标平衡微分方程；3、极坐标下的应变分量；4、几何方程的极坐标表达；5、本构方程的极坐标表达；6极坐标系的LaPIaCe算符；7、应力函数。

1、极坐标下的应力分量为了表明极坐标系统中的应力分量，从考察的平面物体中分割出微分单元体ABCD ,其由两个相距茁的圆柱面和互成d「的两个径向面构成，如图所示在极坐标系中，用二表示径向正应力，用二表示环向正应力，「,和•二:分别表示圆柱面和径向面的切应力，根据切应力互等定理，.J=.二:。

弹性力学第4章-平面问题的极坐标解答

弹性力学第4章-平面问题的极坐标解答

两面不平行, d 夹角为 φ; 两
ρ 面面积不等,分别为 ρdφ, ( ρ + d ρ) dφ. ρ从原点出发为正, 从 x 轴向 y 轴方向转动为正.
微分体上的作用力有: 微分体上的作用力有
体力-- f ρ , f φ , 以坐标正向为正. -应力---
作用力
±ρ
面, φ 面分别表示应力及其增量. ±
第一节 第二节 第三节 第四节 第五节
极坐标中的平衡微分方程 极坐标中的几何方程及物理方程 极坐标中的应力函数与相容方程 应力分量的坐标变换式 轴对称应力和相应的位移
第六节 第七节 第八节 第九节 第十节 例题
圆环或圆筒受均布压力 压力隧洞 圆孔的孔口应力集中 半平面体在边界上受集中力 半平面体在边界上受分布力
基本方程的区别. 对于圆形,弧形,扇形及由径向线和环向围成的物 体,宜用极坐标求解.用极坐标表示边界简单,使边界条 件简化.
在A内任一点(ρ, )取出一个微分体,考虑其平 衡条件. 微分体:由夹 角为d φ的两 径向线和距离 为d ρ的两环 向线围成.
§4-1 极坐标中的平衡微分方程
注意: 注意:
即 Φ是通过中间变量 ρ,φ ,为 x, y 的复合函数. 有: Φ = Φ ρ + Φ φ, Φ=Φρ +Φφ. 而
ρ x φ x y ρ y φ y sin cos ρ ρ = , = sin; = cos, . = ρ x y ρ y x x
代入,即得一阶导数的变换公式,
Φ sin Φ sinφ Φ=cosφ =(cosφ )Φ x ρ ρ φ ρ ρ φ
u = uρ cos u sin, v = uρ sin + u cos.
(c) (d)

7第七讲、第二章 弹性力学平面问题(9~10)


ZS《Rock Mass Mechanics》
2020/8/12
6
ZS《Rock Mass Mechanics》
2020/8/12
ZS
1. 平衡微分方程
平面问题的基本方程
3. 物理方程
2. 几何方程
（2-2）
（2-15）
（2-9）
4. 边界条件 位移：
（平面应力问题） （2-17）
应力：
ZS《Rock Mass Mechanics》
注意：面力变换公式：
与坐标系的选取有关，
因此，适当选取坐标系，可使面力表达式简单。
2. 平面问题的基本方程： （1）平衡方程：
（3）物理方程：
（2）几何方程：
（2-2）
（2-15）
——平面应力问题 （2-9） （4）边界条件：
（1） ——位移边界条件
（2）
——应力边界条件
3. 平面问题一点的应力、应变分析 (a) 任意斜面上应力 或
（2） 然后将
代入式（2-26）求出应力分量：
(2-27)
(2-26)
(2-28)
（无体力情形）
（3） 再让
满足应力边界条件和位移单值条件（多连体问题）。
3. 应力函数 (x求, y解) 方法
3. 应力函数 (x求, y解) 方法
（1）逆解法
（1）根据问题的条件（几何形状、受力特点、边界条件等），
式(a)为非齐次方程，其解：
全解 = 齐次方程通解 +非齐次方程的特解。
的通解。
(2) 通解
式(a) 的齐次方程：
(d)
的通解。 将式(d)第一式改写为
由微分方程理论，必存在一函 数 A(x,y)，使得

弹性力学-平面问题的极坐标解答


l r
s
m
s
k
ur , u 为边界上已知位移， kr , k 为边界上已知的面力分量。
（位移单值条件）
r
r
r
0
r l
q0
r 0 0
0 r 0
r ra 0 r ra 0
r rb 0 r rb 0
b
a 0 dr 0
b
a r 0 dr 0
b
a 0 rdr M
d
r
P
ur
B
B
ur d
x
dr ur
A
P
A
1
(r ur )d
ur r
dr
径向线段PA的转角： 1 0
线段PB的相对伸长： 1
（b）
PB PB (r ur )d rd
PB
rd
ur （c） r
环向线段PB的转角：
tan 1 1
BB PP PB
(ur
ur
d )
ur
rd
1 ur
2
2 r 2
1 r
r
1 r2
2
2
极坐标下的相容方程为：
22
2 r 2
1 r
r
1 r2
2
2
2 r 2
1 r
r
1 r2
2
2
0
4
22
2 r 2
1 r
r
1 r2
2
2
2
0
说明： 方程（4－6）为常体力情形的相容方程。
（4－6）
结论： 弹性力学极坐标求解归结为
（1） 由问题的条件求出满足式（4－6）的应力函数 (r, )

第七章 平面问题的极坐标解答剖析


d
1
Fb
0
d
d
d
同理考虑与ρ垂直的 φ方向的平衡可得到:
1
2
Fb
0
第一节 平衡微分方程
最后得到ρ与 φ两个方向 的平衡方程:
1
Fb
0
1
2
Fb
0
这里应力分量仍然为三 个，平衡方程二个。
上述方程和直角坐 标系下的平衡方程有所 不同，直角坐标系中， 应力分量仅以偏导数的 形式出现，在极坐标系 中，由于微元体垂直于 半径的两面面积不等， 而且半径愈小差值愈大， 这些反映在方程里带下 划线的项中。
x x x
f f f sin f cos f
y y y
第三节 基本方程
2f cos2 2f 2 sin cos 2f
x 2
2
sin 2 f 2sin cos f
2
sin 2 2
2f 2
2f y 2
sin
2
2f 2
2sin cos
2f
cos2 f 2sin cos f
2
cos2 2f 2 2
2f xy
sin
c
os
2f 2
cos2 sin2
2f
sin cos
f
cos2 sin2 f sin cos 2f
2
2 2
第三节 基本方程
在φ=0时，极坐标的各分量和直角坐标各分量相同。
PB，变形后为P' B' 。
B'点φ方向的位移为:
v v d
因此PB正应变为
(v v d) v
BB PP PB
d
v
PB的方向用射线1表示， P'B'的 方向用射线2表示，PB的转角为 角POP'： （向角外转为负）

冯西桥弹性力学-07平面问题-B


平面应变
z 0
z



E
r


z r
z 0
11
Chapter 7.5
平面问题的极坐标解
基本方程
(4) 协调方程
2 r r2 2

2
r 2

2
rr

2 r rr

r r 2

r
rr
0
或
2 r r2 2


1 E
1

A r2
3
B
21
B ln
r

2 1

C

r 0
33
Chapter 7.6
轴对称问题
于是可得位移分量
ur

r
d
r

1 E
1

A/
r

1
3
Br

21 Br ln r 1 21 Cr f
r x y sin cos xy cos2 sin2
x r cos2 sin2 2 r sin cos y r sin2 cos2 2 r sin cos
x r x x
r
r
r sin cos 1
y r y y
r
r
2 x 2

cos2
2 r 2
2sin
cos
1 r
2
r
sin2
1 r
r
2 sin
cos
1 r2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.6按位移法求解
基本未知函数为位移u r , uθ，应变、应力均由位移导出。

1.截面的几何形状为圆环、圆盘。

2.受力和约束对称于中心轴,因此，可知体积力分量fθ=0；在边
2.2轴对称平面问题的基本公式
图示圆盘受力情况，得应力为σr=σθ=2C= -q
２．按位移法求解：
本节讨论楔形体分别受三种不同荷载作用时，其应力解答如何，并将其中某些解答推广到半无限体情况。

楔形体分别受三种不同荷载作用时，应力函数φ( r, θ)的选取考虑：（１）采用分离变量法φ( r, θ)=g(r)f(θ) ；
（２）考虑应力函数在楔形体边界上的变化规律，将φ( r, θ)中的g( r)的形式假设出来，然后利用∇4φ = 0求f( θ)的形
式；
首先应考虑边界条件来定，即θ = ±α /2 时，σθ= 0,τrθ= 0,自然满足。

可见仅靠力的边界条件不能确定所有待定系数，这是由于本问题的载荷是作用于一点的集中力，在顶点有奇点，待定系数需靠部分楔形体
2．当α =π时楔形体变为半无限体，受集中力作用：。