下载文档原格式
圆柱螺旋压缩弹簧计算首先，我们需要确定弹簧的基本参数，包括弹簧材料、弹簧直径、线径、圈数等。
这些参数直接影响弹簧的刚度和工作性能，因此需要仔细选择。
弹簧材料通常使用优质的弹簧钢，比如65Mn，其具有良好的弹性特性。
下面，我们将介绍弹簧设计中常用的基本公式和计算方法。
首先是弹簧的刚度计算。
圆柱螺旋压缩弹簧的刚度由以下公式给出：k=(Gd^4)/(8D^3n)其中，k表示弹簧的刚度，G表示弹簧的剪切模量，d表示线径，D表示弹簧直径，n表示圈数。
剪切模量可以根据弹簧材料的弹性模量和泊松比计算得到。
接下来，我们将介绍弹簧的最大压缩量计算。
在弹簧设计中，我们通常需要确定弹簧的最大压缩量，以确保在工作过程中不会发生过度压缩导致弹簧失效。
最大压缩量的计算公式为：δ=(Fn)/(k)其中，δ表示最大压缩量，F表示工作负荷，n表示圈数，k表示刚度。
此外，我们还需要计算弹簧的自由长度和变形高度。
自由长度是指弹簧在没有负荷作用下的长度，可以通过以下公式计算得到：L0 = np + d其中，L0表示自由长度，n表示圈数，p表示引伸量，d表示线径。
引伸量是指弹簧的初始压缩量。
变形高度是指弹簧在工作过程中的压缩量。
可以使用以下公式计算得到：H=L0-L其中，H表示变形高度，L0表示自由长度，L表示工作长度。
最后，我们需要进行弹性限制条件的计算，以确保弹簧工作时不会超过其弹性极限。
弹性极限可以通过材料的屈服强度进行估算。
一般来说，弹簧的工作负荷应该小于其屈服强度的一半。
综上所述，圆柱螺旋压缩弹簧的计算涉及到弹簧的刚度、最大压缩量、自由长度、变形高度和弹性限制条件等方面。
通过这些计算，我们可以合理地设计和制造弹簧，以满足特定的工作要求。
下面是一个具体的计算实例：假设我们需要设计一个圆柱螺旋压缩弹簧，用于承受1000N的工作负荷。
弹簧材料为65Mn，弹簧直径为20mm，线径为2mm，圈数为10。
首先，需要计算弹簧的剪切模量。
根据材料的弹性模量和泊松比，可以得到剪切模量为80GPa。
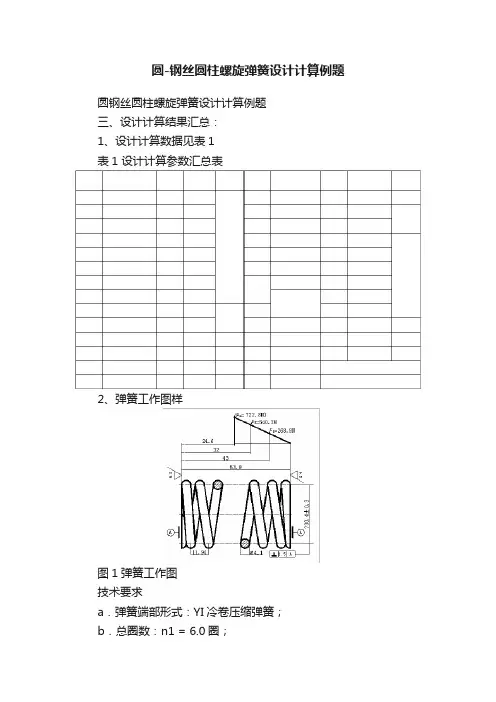
圆-钢丝圆柱螺旋弹簧设计计算例题圆钢丝圆柱螺旋弹簧设计计算例题三、设计计算结果汇总：1、设计计算数据见表1表1 设计计算参数汇总表2、弹簧工作图样图1弹簧工作图技术要求a．弹簧端部形式：YI冷卷压缩弹簧；b．总圈数：n1 = 6.0圈；c．有效圈数：n = 4.0圈；d．旋向：右旋；e．强化处理：喷丸和立定处理；f．喷丸强度0.3 A ～ 0.45A，表面覆盖率大于90%；g．表面处理：清洗上防锈油；h．制造技术条件：其余按GB/T 1239.2二级精度。
2) 圆钢丝圆柱螺旋拉伸弹簧设计计算例题例2 :设计一拉伸弹簧，循环次数N =1.0×105次。
工作负荷F =160N,工作负荷下变形量为22mm，采用LⅢ圆钩环，外径D2=21mm。
一、题解分析：a)此拉伸弹簧要求循环次数N = 1.0×107次，由此说明弹簧是按有限寿命设计；b)题设给出了最大工作负荷及对应变形量：c)端部结构采用LⅢ圆钩环，即为圆勾环扭中心；d)弹簧外径D2 = 21mm。
二、解题方法：由以上分析可知，本题中未给出自由高度，说明自由高度可在满足其它条件下按实际计算而定，显然，本题是按表1中第一个设计计算条件及要求给出的。
方法1：严格设计法1）材料选取，根据弹簧使用的疲劳寿命要求，我们可选重要用途的碳素弹簧钢丝E 组别的钢丝，根据弹簧手册P345表10-16查得材料抗拉强度d b ln 3582072-=σ即本讲公式（2）中的 a = 2072；b = -358 从分析可知本弹簧按有限寿命使用，即由表3查得试验切应力的强度系数为0.5×0.8 = 0.40即：b S στ4.0=；许用切应力系数36.08.045.0=?=κ即：b κστ=][ 2）把题中给定的D = 21mm;F = 160N 及以上所选取的材料所查找的有关强度许用应力系数a = 2072；b = -358; 及36.0=κ代入本讲公式（2）：0)2)(ln ()08.054.64(2322222≤-+-+-d d D d b a d d D D F πκ化简得：05644808.439486.25)ln 35.849897.49185()ln 37.80938.4684(234≤+-+---d d d d d d解得：d ＞2.43 mm 取：d = 2.5mm ；此时，材料抗拉强度)5.2ln(3582072-=b σ=1744Mpa 而查标准附录7—表7.1得b σ= 1680Mpa ；由此可见相对误差不到3.9%完全满足GB/5311标准的范围，因为标准给出的值按最低值给出。
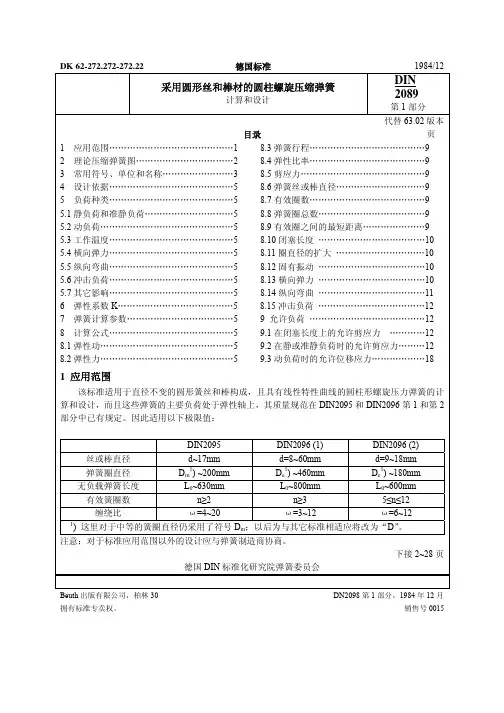
圆柱螺旋压缩弹簧计算示例圆柱螺旋压缩弹簧计算示例之一项目单位公式及数据原始条件最小工作载荷P1N P1=60最大工作载荷PnN Pn=240工作行程hmm h=36±1弹簧外径D2mm D2≤45弹簧类别N=103~106次端部结构端部并紧、磨平，支承圈数为1圈弹簧材料碳素弹簧钢丝C级参数计算初算弹簧刚度P/N/mm工作极限载荷PjN因是II类载荷：Pj≥1.25Pn顾Pj=1.25×210=300弹簧材料直径d及弹簧中径D与有关参数根据Pj与D条件从表11-2-19得：d D Pj fj Pd/3.5 38 306.97 11.37 27有效圈数n圈按照表11-2-10取标准值n=5.5总圈数n1圈n1=n+2=5.5+2=7.5弹簧刚度P/N /mm工作极限载荷下的变形量FjmmFj=nfj=5.5×11.37=14.95节距tm m自由高度H0mmH0=nt+1.5d=5.5×14.95+1.5×3.5=87.47取标准值H0=90弹簧外径D2mmD2=D+d=38+3.5=41.5弹簧内经D1mmD1=D-d=38-3.5=34.5螺旋角a（°）展开长度L mm最小载荷时高度H1m m最大载荷时高度Hnm m极限载荷时高度Hjm m实际工作行程hmmh=H1-Hn=77.76-41.02=36.74≈36±1工作区范围高度比bb＜2.6不必进行稳定性验算技术要求：1.总圈数n1=7.52.旋向为右旋3.展开长度L=902mm4.硬度HRC45~50。
圆柱螺旋压缩弹簧计算示例
1、圆柱螺旋压缩弹簧的基本参数
圆柱螺旋压缩弹簧是目前工业应用上最为常用的弹簧形式之一，其具有行程大、载荷大的特点，且计算简单、性能稳定、使用寿命长，在离合器、减震器等电器仪表中表现出色。
通常使用的圆柱螺旋弹簧参数有：外径Φd、内径ΦD、螺旋槽数N、槽宽t、槽深H、弹簧总长度n、起动拉力Fs、最大径向载荷Fa、作用位置系数X。
2、示例
a、弹簧的K值
弹簧的K值可以用下式计算
K=(8FH/πd3)X(1+X/n)
b、弹簧的弹性变形
弹性变形δ的计算公式为：
δ=(8F/Kπd3)X(1+X/n)
计算结果：δ=17.346mm
c、弹簧在拉伸时的变形量
弹簧在拉伸时的变形量是指当弹簧在外力作用下拉伸时，它的总长度变成多少。
一般情况下，弹簧的变形量的计算公式为：
ΔL=(8F/Kπd3)X(1+X/n)XL。
圆柱螺旋拉伸弹簧的设计计算首先，我们需要确定弹簧的使用条件和要求。
这包括弹簧所受的最大载荷、最小载荷、工作环境温度、可接受的变形范围等。
接下来，我们需要确定弹簧的材料。
选取合适的弹簧材料是确保弹簧性能和寿命的关键。
常用的弹簧材料有碳钢、不锈钢、合金钢等。
根据使用条件和要求，选择合适的材料。
然后，我们需要计算弹簧的刚度。
刚度是弹簧对受力的反应能力，用于计算弹簧的变形量。
刚度的计算可以通过胡克定律来实现，即应力与应变成正比。
刚度的计算公式为：k=Gd^4/(8D^3n)其中，k为弹簧的刚度，G为弹簧材料的剪切模量，d为弹簧线径，D 为弹簧的平均直径，n为弹簧的总匝数。
在计算刚度之后，我们可以进一步计算弹簧的自由长度。
自由长度是弹簧未施加载荷时的长度。
自由长度的计算公式为：Lf=L+F/k其中，Lf为弹簧的自由长度，L为弹簧未施加载荷时的实际长度，F 为弹簧施加的载荷，k为弹簧的刚度。
接下来，我们需要计算弹簧的最大变形量。
最大变形量是指弹簧从自由状态到最大受力状态时的变形量。
最大变形量的计算公式为：ΔL = (Fmax - Fmin) / k其中，ΔL为弹簧的最大变形量，Fmax为弹簧所受的最大载荷，Fmin 为弹簧所受的最小载荷，k为弹簧的刚度。
最后，我们需要检查弹簧的安全性。
在设计弹簧时，必须确保它能够承受所施加的载荷，并且不会发生破裂或变形。
为了确保弹簧的安全性，我们需要计算弹簧的应力，并与弹簧材料的抗拉强度进行比较。
如果应力超过了材料的强度，就需要重新设计弹簧或者更换更强的材料。
综上所述，圆柱螺旋拉伸弹簧的设计计算包括弹簧使用条件和要求的确定、弹簧材料的选择、刚度的计算、自由长度的计算、最大变形量的计算以及弹簧的安全性检查。
通过这些计算，我们能够设计出合适的圆柱螺旋拉伸弹簧，满足各种机械装置的要求。
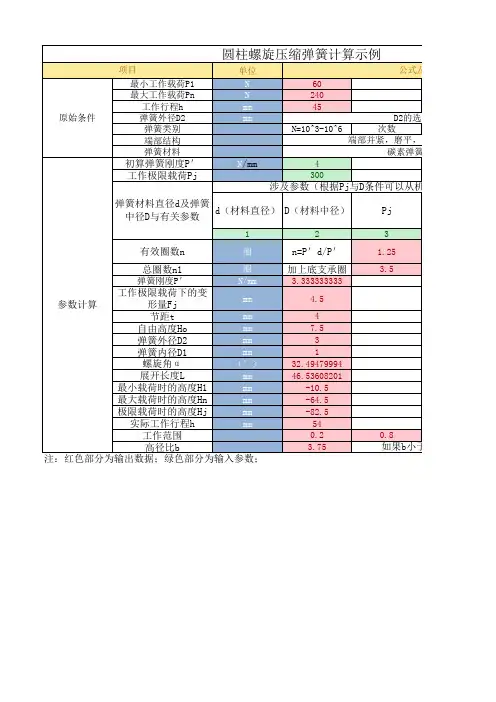
最大拉力Pn N 120最小拉力P1N 60工作行程hmm 60弹簧外径D2mm 20载荷作用次数10^6I类：10^6以上,II类：10^3至10^6,III类：弹簧材料琴钢丝-D级端部结构圆钩环压中心初算弹簧刚度P'N/mm 1I类≥ 1.5Pn II类≥ 1.25225d D Pj fj328264.57.258有效圈数n 圈36弹簧刚度P’N/mm 1.011111111最小载荷下的变形量F1mm 35.30769231最大载荷下的变形量Fnmm 94.64835165极限载荷下的变形量Fj mm 245.6504093弹簧外径D2mm 31弹簧内径D1mm 25自由长度H0mm 167最小工作载荷下的长度H1mm 202.3076923最大工作载荷下的长度Hn mm 261.6483516极限工作载荷下的长度Hjmm 412.6504093节距t=d3展开长度Lmm 3298.672286实际极限变形量mm 178.021978最大工作载荷Pn N 120实际极限载荷PjN246.6718232180因为是拉伸弹簧，所以Pj要乘以0.8（Pn/0.8） 选择的是弹性特性验算螺旋角α°arctan0.034091417查表选取原始条件工作极限载荷Pj N 材料直径d及弹簧中径Dmm 参数计算弹簧工作时最大长度185自由长度125类：10^3至10^6,III类：10^3。
Pn III类≥1Pn 180P'dP0δb G 36.424.3211079000择的是I类载荷，取Pj=由于弹簧材料是琴钢丝D级，所以其修正arctan（t/pi*D)Pj fj308.33988.529528。
圆柱螺旋压缩弹簧计算示例假设我们要设计一个圆柱螺旋压缩弹簧，用于悬挂汽车底盘的悬挂系统。
首先，我们需要确定弹簧的材料。
常用的弹簧材料有碳钢、合金钢、不锈钢等。
在这个示例中，我们选择使用碳钢材料，其具有良好的机械性能和耐磨性。
接下来，我们需要确定弹簧的几何尺寸和刚度。
弹簧的外径、内径、线径、圈数等参数都会影响其刚度和负载能力。
为了简化计算，我们假设弹簧材料为线弹簧，并且线径为0.5厘米，圈数为10。
在计算弹簧刚度时，我们可以使用胡克定律。
胡克定律表示弹簧的位移与受力之间的线性关系。
根据胡克定律，弹簧刚度（K）等于弹簧受力（F）与位移（x）之比。
在这个示例中，我们假设弹簧的刚度为100牛顿/米。
接下来，我们需要计算弹簧的自由长度。
弹簧的自由长度是指在未受外力作用时，弹簧处于松弛状态的长度。
我们可以使用公式Lf=(D+d)*n，其中Lf表示自由长度，D表示弹簧的外径，d表示弹簧的线径，n表示圈数。
在这个示例中，我们假设D为10厘米，d为0.5厘米，n为10，则弹簧的自由长度为100厘米。
接下来，我们需要计算弹簧的变形和负载能力。
弹簧的变形可以使用胡克定律来计算。
根据胡克定律，弹簧的变形等于外力除以刚度。
在这个示例中，我们假设外力为500牛顿，则弹簧的变形为500/100=5厘米。
最后，我们需要进行弹簧的可变速率计算。
可变速率是指弹簧在受力变化过程中的刚度变化程度。
为了简化计算，我们可以使用一个可变速率系数（Kv）来表示弹簧的可变速率。
在这个示例中，我们假设可变速率系数为1、则弹簧在受力变化过程中的刚度不变。
以上是一个圆柱螺旋压缩弹簧计算的示例。
实际应用中，需要考虑更多的因素，如材料的疲劳性能、应力分布等，以确保弹簧的安全可靠性。
圆钢丝圆柱螺旋弹簧设计计算例题
三、设计计算结果汇总：
1、设计计算数据见表1
表1 设计计算参数汇总表
2、弹簧工作图样
图1弹簧工作图
技术要求
a．弹簧端部形式：YI冷卷压缩弹簧；
b．总圈数：n1 = 6.0圈；
c．有效圈数：n = 4.0圈；
d．旋向：右旋；
e．强化处理：喷丸和立定处理；
f．喷丸强度0.3 A ～ 0.45A，表面覆盖率大于90%；
g．表面处理：清洗上防锈油；
h．制造技术条件：其余按GB/T 1239.2二级精度。
2) 圆钢丝圆柱螺旋拉伸弹簧设计计算例题
例2 :设计一拉伸弹簧，循环次数N =1.0×105次。
工作负荷F =160N,工作负荷下变形量为22mm，采用LⅢ圆钩环，外径D2=21mm。
一、题解分析：
a)此拉伸弹簧要求循环次数N = 1.0×107次，由此说明弹簧是按有限寿命设计；
b)题设给出了最大工作负荷及对应变形量：
c)端部结构采用LⅢ圆钩环，即为圆勾环扭中心；
d)弹簧外径D2 = 21mm。
二、解题方法：
由以上分析可知，本题中未给出自由高度，说明自由高度可在满足其它条件下按实际计算而定，显然，本题是按表1中第一个设计计算条件及要求给出的。
方法1：严格设计法
1）材料选取，根据弹簧使用的疲劳寿命要求，我们可选重要用途的碳素弹簧钢丝E 组别的钢丝，
根据弹簧手册P345表10-16查得材料抗拉强度d b ln 3582072-=σ即本讲公式（2）中的 a = 2072；b = -358 从分析可知本弹簧按有限寿命使用，即由表3查得试验切应力的强度系 数为0.5×0.8 = 0.40即：b S στ4.0=；许用切应力系数36.08.045.0=⨯=κ即：b κστ=][ 2） 把题中给定的D = 21mm;F = 160N 及以上所选取的材料所查找的有关强度许用应力系数
a = 2072；
b = -358; 及36.0=κ代入本讲公式（2）：
0)2)(ln ()08.054.64(232222
2≤-+-+-d d D d b a d d D D F πκ
化简得：
05644808.439486.25)ln 35.849897.49185()ln 37.80938.4684(234≤+-+---d d d d d d
解得：d ＞2.43 mm 取：d = 2.5mm ；
此时，材料抗拉强度)5.2ln(3582072-=b σ=1744Mpa 而查标准附录7—表7.1得b σ= 1680Mpa ； 由此可见相对误差不到3.9%完全满足GB/5311标准的范围，因为标准给出的值按最低值给出。
方法2：假设试算法（此方法同标准中介绍相同）
1) 材料选取同上即选重要用途碳素弹簧钢丝E 组；
2) 假设材料直径：d = 3mm ；从标准附录7表7.1查得b σ=1610；则：
许用切应力：[τ] = 0.36×1610 = 579Mpa; 弹簧中径：D = 21–3 = 18mm 旋绕比：C = 18/3 = 6；曲度系数：K = （4C-1）/（4C-4）+0.615/C = 1.253
3) 验算修正假设的d ：
mm 与假设基本符合；
1、取d = 2.5mm ；根据附录F 查得材料抗拉强度为R m = 1680 Mpa ；
根据表3选取计算试验切应力：τs = 0.50R m ×0.8 = 0.40×1680 = 670 Mpa ； 许用切应力为[τ] = 1680×0.36 = 604 Mpa 。
2、计算弹簧直径：
1) 弹簧外径: D 2 = 21mm ：
2）弹簧中径：D = D 2–d = 21–2.5 = 18.5mm ； 3）弹簧内径：D 1 = D –d = 18.5 - 2.5 = 16mm 。
3、弹簧旋绕比C ：
2.51580
14.318160253.18][833=⨯⨯⨯⨯=≥τπKFD d
4.75
.25.18===
d D C 4、曲度系数K ： 由公（7）得： 2.14
.7615
.044.7414.74615.04414=+-⨯-⨯=+--=C C C K
5、初拉力选取：
由标准图5查得初切应力：τ0 = 70 MPa ～130 MPa
则按公式 (37)计算初拉力为：
这里选取F 0 = 32N 6、计算弹簧刚度及有效圈数：
弹簧刚度按公式（34）计算：
mm N f F F F o /82.522
32
160'=-=-=
弹簧有效圈数按公式（4）推导计算：
10.482
.55.1885.2105.7883
4
334=⨯⨯⨯⨯='=F D Gd n 则弹簧有效圈数取n =10.5 圈。
7、弹簧刚度与初拉力核对与修正：
因n = 10.5圈，则弹簧的实际计算刚度，按公式（4）计算得：
67.55
.015.1885.2105.78834
334'
=⨯⨯⨯⨯==n D Gd F N/mm
初拉力按公式（34）计算：
F 0= F - '
F f =160-5.76×22=33.3N
F 0=33.3N 在23.2N ～43.1N 范围内
8、弹簧的试验负荷按公式(14)计算：
9、试验负荷下弹簧的变形量按公式(33)计算：
N ～～D
d F )1.432.23()13070(5
.1885.214.383
30
=⨯⨯⨯==τπN D d F S S 4.2216705.1885.214.383
3=⨯⨯⨯==τπ
mm 7.32)3.334.221(54
.2105.785.105.188)(833043=-⨯⨯⨯⨯⨯=-=F F Gd n D f S S
10、特性校核：
63.09
.3422
==
s
f f 满足0.2s f ≤f ≤0.8s f 的要求 11、强度校核
强度校核按公式（5）计算
τ＜[τ]，满足强度要求。
12、弹簧结构参数
1）自由长度按表13计算：
168.600.1625.2)15.01(2)1(10≈=⨯+⨯+=++=D d n H mm
选取自由长度为：H 0 = 61mm
2）工作长度： 38221601=+=+=f H H mm 3）试验长度： 7.937.3261s 0s =+=+=f H H mm 有初拉力要求，弹簧密绕。
4）弹簧的展开长度按公式（42）计算：
1.7265.1814.325.105.1814.3)(2=⨯⨯+⨯⨯=+≈钩环部分D Dn L ππ mm
5）弹簧质量按公式（29）计算：
13、自振频率：
由标准中公式（12）计算得： 247.7Hz 10
85.7105.7818.510.55.256.356.36
-3
22
=⨯⨯⨯⨯=
=ρG
nD d
f e
579.2Mpa 5.214.31605.1882.183
3=⨯⨯⨯⨯==d DF K πτkg 280.01085.71.7265.24
14
.34
622=⨯⨯⨯⨯=
=
-ρπ
L d m
三、设计结果汇总：
1、设计计算参数表：
表2 设计计算参数汇总表
2、弹簧工作图样
(F s=234.7N)
图2 拉伸弹簧工作图
技术要求
a.弹簧端部形式：LIII圆钩环扭中心拉伸弹簧；
b.圈数：n=10.5圈；
c.旋向：右旋；
d.表面处理：浸防锈油；
e.制造技术条件：其余按GB/T 1239.1二级精度。
