固体物理答案陆栋
- 格式:pdf
- 大小:834.40 KB
- 文档页数:40

固体物理试题分析及答案一、单项选择题(每题2分,共10分)1. 固体物理中,晶体的周期性结构是由哪种原子排列形成的?A. 金属原子B. 非金属原子C. 金属原子和非金属原子D. 任意原子答案:C解析:晶体的周期性结构是由金属原子和非金属原子按照一定的规律排列形成的,这种排列方式使得晶体具有长程有序性。
2. 哪种类型的晶体具有各向异性?A. 立方晶体B. 六角晶体C. 单斜晶体D. 等轴晶体答案:C解析:单斜晶体属于三斜晶系,其三个轴的长度和夹角均不相同,因此具有各向异性。
3. 固体物理中,电子的能带结构是由什么决定的?A. 原子核B. 电子C. 原子核和电子D. 晶格答案:C解析:电子的能带结构是由原子核和电子共同决定的,它们之间的相互作用导致了电子能级的分裂和能带的形成。
4. 哪种类型的晶体具有完整的布里渊区?A. 立方晶体B. 六角晶体C. 单斜晶体D. 等轴晶体答案:A解析:立方晶体具有完整的布里渊区,这是因为立方晶体的晶格常数相等,使得布里渊区的形状为正八面体。
5. 固体物理中,哪种类型的晶体具有最高的对称性?A. 立方晶体B. 六角晶体C. 单斜晶体D. 等轴晶体答案:A解析:立方晶体具有最高的对称性,这是因为立方晶体的晶格常数相等,且晶格中的原子排列具有高度的对称性。
二、填空题(每题2分,共10分)1. 晶体的周期性结构是由______和______共同决定的。
答案:原子核、电子解析:晶体的周期性结构是由原子核和电子共同决定的,原子核提供了晶格的框架,而电子则填充在晶格中,形成了晶体的周期性结构。
2. 晶体的对称性可以通过______来描述。
答案:空间群解析:晶体的对称性可以通过空间群来描述,空间群是描述晶体对称性的数学工具,它包含了晶体的所有对称操作。
3. 电子的能带结构是由______和______共同决定的。
答案:原子核、电子解析:电子的能带结构是由原子核和电子共同决定的,它们之间的相互作用导致了电子能级的分裂和能带的形成。

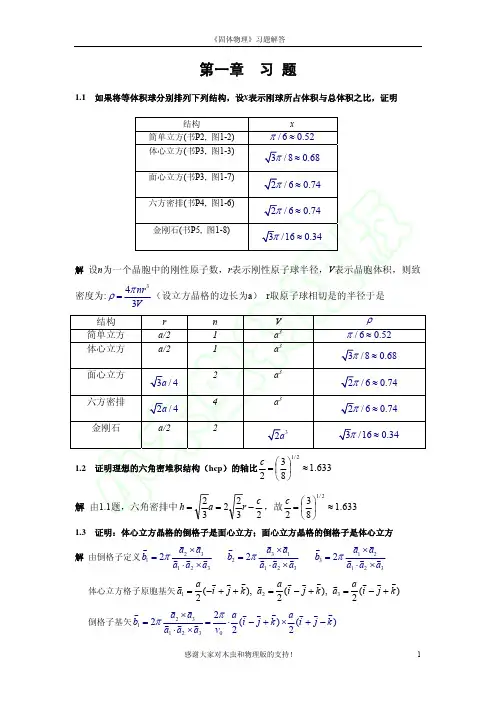
1.1 如果将等体积球分别排列成下列结构,设x 表示钢球所占体积与总体积之比,证明结构x简单立方π/ 6 ≈0.52 体心立方3π/ 8 ≈0.68 面心立方2π/ 6 ≈0.74六方密排2π/ 6 ≈0.74 金刚石3π/16 ≈0.34解:设钢球半径为r ,根据不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,分别为:简单立方:a = 2r金刚石:根据金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比,正是晶格常数为4π/ a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式上的,或者说是倒格子空间中的布拉菲格子。
根据定义,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:根据定义,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义,倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 满足其中a 为立方边长。
解:根据倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢互相正交,因此其大小为则带入前边的关系式,即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。

《固体物理》基础知识训练题及其参考答案说明:本内容是以黄昆原著、韩汝琦改编的《固体物理学》为蓝本,重点训练读者在固体物理方面的基础知识,具体以19次作业的形式展开训练。
第一章作业1:1.固体物理的研究对象有那些?答:(1)固体的结构;(2)组成固体的粒子之间的相互作用与运动规律;(3)固体的性能与用途。
2.晶体和非晶体原子排列各有什么特点?答:晶体中原子排列是周期性的,即晶体中的原子排列具有长程有序性。
非晶体中原子排列没有严格的周期性,即非晶体中的原子排列具有短程有序而长程无序的特性。
3.试说明体心立方晶格,面心立方晶格,六角密排晶格的原子排列各有何特点?试画图说明。
有那些单质晶体分别属于以上三类。
答:体心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体的体心位置还有一个原子。
常见的体心立方晶体有:Li,Na,K,Rb,Cs,Fe等。
面心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体每个表面的中心还都有1个原子。
常见的面心立方晶体有:Cu, Ag, Au, Al等。
六角密排晶格:以ABAB形式排列,第一层原子单元是在正六边形的每个角上分布1个原子,且在该正六边形的中心还有1个原子;第二层原子单元是由3个原子组成正三边形的角原子,且其中心在第一层原子平面上的投影位置在对应原子集合的最低凹陷处。
常见的六角密排晶体有:Be,Mg,Zn,Cd等。
4.试说明, NaCl,金刚石,CsCl, ZnS晶格的粒子排列规律。
答:NaCl:先将两套相同的面心立方晶格,并让它们重合,然后,将一套晶格沿另一套晶格的棱边滑行1/2个棱长,就组成Nacl晶格;金刚石:先将碳原子组成两套相同的面心立方体,并让它们重合,然后将一套晶格沿另一套晶格的空角对角线滑行1/4个对角线的长度,就组成金刚石晶格;Cscl::先将组成两套相同的简单立方,并让它们重合,然后将一套晶格沿另一套晶格的体对角线滑行1/2个体对角线的长度,就组成Cscl晶格。
![《固体物理学》答案[1]](https://uimg.taocdn.com/f8d34b12866fb84ae45c8da9.webp)

第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。

固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。


固体物理试题及答案一、选择题(每题2分,共10分)1. 固体物理中,晶体的周期性结构是通过哪种方式描述的?A. 电子云B. 原子轨道C. 布洛赫定理D. 费米面答案:C2. 以下哪种材料不属于半导体材料?A. 硅B. 锗C. 铜D. 砷化镓答案:C3. 在固体物理中,能带理论描述的是:A. 电子在固体中的自由运动B. 电子在固体中的局域化C. 电子在固体中的能级分布D. 电子在固体中的跃迁过程答案:C4. 固体中的声子是:A. 一种基本粒子B. 一种准粒子C. 一种实际存在的粒子D. 一种不存在的粒子答案:B5. 以下哪种效应与超导现象无关?A. 迈斯纳效应B. 约瑟夫森效应C. 霍尔效应D. 量子隧穿效应答案:C二、填空题(每题2分,共20分)1. 固体物理中,描述电子在周期性势场中的运动的定理是______。
答案:布洛赫定理2. 固体中的能带结构是由______决定的。
答案:电子波函数3. 在固体中,电子的费米能级是______。
答案:电子占据的最高能级4. 固体中的电子输运性质可以通过______来描述。
答案:电导率5. 固体中的晶格振动可以用______来描述。
答案:声子6. 固体中的电子-声子相互作用会导致______。
答案:电子散射7. 固体中的能隙是指______。
答案:价带顶部和导带底部之间的能量差8. 超导体的临界温度是指______。
答案:超导相变发生的温度9. 固体中的霍尔效应是由于______。
答案:电子在磁场中的偏转10. 固体中的磁阻效应是由于______。
答案:电子在磁场中的运动受到阻碍1. 简述固体物理中能带理论的基本思想。
答案:能带理论的基本思想是将固体中的电子视为在周期性势场中运动的量子粒子。
由于周期性势场的存在,电子的能级不再是离散的,而是形成了连续的能带。
这些能带决定了固体的电子结构和性质,如导电性、磁性和光学性质等。
2. 描述固体中的声子是如何产生的。
答案:固体中的声子是由于晶格振动的量子化而产生的准粒子。

第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。

材料力学教程单祖辉答案材料力学教程单祖辉答案【篇一:寒旱所考试科目参考书】s=txt>2006年招收硕士学位研究生考试科目参考书中国科学院寒区旱区环境与工程研究所2006年招收硕士学位研究生考试科目参考书【篇二:上海交大考博参考书目】txt>010船舶海洋与建筑工程学院2201流体力学《水动力学基础》,刘岳元等,上海交大出版社2202声学理论《声学基础理论》,何祚庸,国防工业出版社2203高等工程力学(理力、材力、流力、数学物理方法)(四部分任选二部分做)《理论力学》,刘延柱等,高等教育出版社;《材料力学》,单祖辉,北京航空航天大学出版社;《流体力学》,吴望一,北京大学出版社;《数学物理方法》,梁昆淼,高等教育出版社2204结构力学《结构力学教程》,龙驭球,高等教育出版社3301船舶原理《船舶静力学》,盛振邦,上海交大出版社;《船舶推进》,王国强等,上海交大出版社;《船舶耐波性》,陶尧森,上海交大出版社;《船舶阻力》,邵世明,上海交大出版社3302振动理论(i)《机械振动与噪声学》,赵玫等,科技出版社20043303海洋、河口、海岸动力学《河口海岸动力学》,赵公声等,人民交通出版社2000 3304高等流体力学《流体力学》,吴望一,北京大学出版社3305弹性力学《弹性力学》上、下册(第二版),徐芝纶,高等教育出版社3306振动理论(Ⅱ)《振动理论》,刘延柱等,高等教育出版社20023307钢筋混凝土结构《高等钢筋混凝土结构学》,赵国藩编,中国电力出版社3308地基基础《土工原理与计算》(第二版),钱家欢、殷宗泽,水利电力出版社020机械与动力工程学院2205计算方法《计算方法》,李信真,西北工业大学出版社2206核反应堆工程《核反应堆工程设计》,邬国伟3309工程热力学《工程热力学》(第三版),沈维道;《工程热力学学习辅导及习题解答》,童钧耕3310传热学《传热学》(第三版),杨世铭3311机械控制工程《现代控制理论》,刘豹;《现代控制理论》,于长官3312机械振动《机械振动》,季文美3313生产计划与控制《生产计划与控制》,潘尔顺,上海交通大学出版社3314机械制造技术基础《机械制造技术基础》,翁世修等,上海交通大学出版社1999;《现代制造技术导论》,蔡建国等,上海交通大学出版社20003315现代机械设计《高等机械原理》,高等教育出版社1990030电子信息与电气工程学院2207信号与系统《信号与系统》,胡光锐,上海交大出版社2208电子科学与技术概论《电子科学与技术导论》,李哲英,20062209信息处理与控制系统设计《线性系统理论》,郑大钟,清华大学出版社2002;或《数字图像处理》(第二版)《digital image processing》second edition (英文版),r. c. gonzalez, r. e. woods,电子工业出版社2002(从“线性系统理论”或“图像处理”中选考其一)2210计算机科学与技术方法论《数理逻辑与集合论》,石纯一,清华大学出版社2000;《图论与代数结构》,戴一奇,清华大学出版社1995;《组合数学》,richard a. brualdi著,卢开澄等译,机械工业出版社20012211数字信号处理(i)《数字信号处理(上)》,邹理和;《数字信号处理(下)》,吴兆熊,国防工业出版社2212电力系统分析与电力电子技术《电力电子技术基础》,金如麟,机械工业出版社,或《电力系统分析(上册)》,诸骏伟,中国电力出版社1995;《电力系统分析(下册)》,夏道止,中国电力出版社19953316网络与通信《数字通信》(第四版),proakis,电子出版社(必考,占30%):另按照专业加考70%:无线通信方向、信息安全方向,《数字通信》(第四版),proakis,电子出版社;或光通信方向,《光纤通信系统》(第3版), govind p.agrawal,国外大学优秀教材-通信系列(影印版);或数据通信网络方向,《computer networks》(fourth edition),pearson education andrews.tanenbaum,vrije universiteit,amsterdam,the netherlands,翻译版:潘爱民译,书号7302089779,清华大学出版社20043317信号与信息处理信号处理方向:《discrete-time signal processing》(second edition),alan v. oppenheim,prentice-hall,1998;《现代信号处理》(第二版),张贤达,清华大学出版社2002;或图像处理方向:《数字图像处理》,余松煜等,上海交通大学出版社20073319电路与系统《大规模集成电路设计》,陈贵灿,高等教育出版社3320最优控制《最优控制的理论与方法》(第二版),吴沧浦,国防工业出版社20003321模式识别《模式识别》(第二版),边肇祺等,清华大学出版社20003322微机控制与接口技术《微型计算机控制技术》(第三版),谢剑英,国防工业出版社2001 3354运筹学《运筹学》(修订版),运筹学编写组,清华大学出版社20033323计算机软件《程序语言语言编译原理(第3版)》,陈火旺等,国防工业出版社2000;《distributed systems: principles and paradigm》,tanenbaum and steen,prentice hall 2003(清华大学出版社影印出版)3324数据库系统原理《数据库系统概念》(第四版,中译本),silberschatz等著,杨冬青等译,机械工业出版社3325机器学习《机器学习》,曾华军、张银奎译,机械工业出版社20033326计算机网络与系统结构《computer network》(第四版),a. s. taneubaum, 清华大学出版社;《computer architecture: a quantitative approach》(3rd edition),patterson,d.and hennessy,j.,san mateo, california: morgan kaufman publishers2002,机械工业出版社影印出版3327现代控制理论《现代控制理论》,刘豹,机械工业出版社3328现代传感器技术《传感器技术》,贾伯平,东南大学出版社3329电力传动控制系统《电力拖动自动控制系统》,陈伯时,机械工业出版社3330电力网络规划与电压稳定《电力网络规划的方法与应用》,程浩忠、张焰,上海科学技术出版社;或《电力系统无功与电压稳定性》,程浩忠、吴浩,中国电力出版社3331电气绝缘在线监测技术《电力设备在线监测与故障诊断》,肖登明,上海交通大学出版社20043332电机理论《交流电机数学模型及调速系统》,陈坚,国防工业出版社;《交流电机及其系统的分析》(第二版),高景德等,清华大学出版社2005036信息安全学院2213信息安全数学基础《信息安全数学基础》,陈恭亮,清华大学出版社20043333密码学基础《密码学理论与实践》(第二版),d.r. stinson,电子工业出版社2003;《应用密码学》(第二版),bruce schneier,机械工业出版社2000050材料科学与工程学院2214材料科学基础及加工原理《材料科学基础》,胡赓祥等,上海交大出版社2006;《材料科学基础辅导与习题》,蔡珣、戎咏华,上海交大出版社2004;或《材料加工原理》,徐洲等,科学出版社2003;或《材料加工原理》,李言祥等,清华大学出版社2005(材料科学基础、材料加工原理各100分考题,考生任选其一)3334材料热力学与动力学《材料热力学》(第三版),徐祖耀、李麟,科学出版社2005;或《材料热力学与动力学》,徐瑞、荆天辅,哈尔滨工业大学出版社20033335材料微结构分析《分析电子显微学导论》第一、三章,第五章中5.1和5.2节,戎咏华,高等教育出版社2006;或《金属x射线学》,范雄,机械工业出版社19963336凝固或焊接《凝固过程》(中译本),m. c. flemings,冶金工业出版社1981;或《焊接过程现代控制技术》,陈善本等,哈尔滨工业大学出版社2001071数学系2215泛函分析《实变函数论与泛函分析》(第二版),夏道行等,高等教育出版社3337近世代数《代数学基础》(群.环.域.模等部分),孟道骥,南开大学出版社3338微分几何《微分流形初步》(第二版),陈维桓,高等教育出版社;《微分几何讲义》(第二版),陈省身、陈维桓,北京大学出版社072物理系2216量子力学《量子力学》卷i、卷ii (第三版),曾谨言2217物理光学《物理光学》,梁铨廷,机械工业出版社;或《物理光学与应用光学》,石顺祥等,西安电子科学技术大学出版社2000;或《物理光学》,范少卿等,1990;或《应用物理光学》,严瑛白,清华大学出版社19903339高等光学《光学原理》,m. born,世界图书出版公司3340固体物理学《固体物理学》(上、下册),方俊鑫、陆栋,上海科学技术出版社3341电动力学《电动力学》(第二版),郭硕鸿等,高等教育出版社3342半导体物理《半导体物理》,刘恩科等,国防工业出版社;或《半导体物理学》,刘恩科等,电子工业出版社3343工程光学《工程光学》,郁道银、谈恒英,机械工业出版社080生命科学技术学院2218生物化学(i)《生物化学》,沈同,高等教育出版社2219病理学《病理学》(七年制规划教材,临床医学专业用),李甘地,人卫版2240微机原理与微机接口《微型计算机原理与接口技术》,吴秀清,中国科技大学出版社3304高等流体力学《流体力学》,吴望一,北京大学出版社3375细胞生物学《细胞生物学》,翟中和,高等教育出版社3344分子生物学《现代遗传原理》,徐晋麟等,科学出版社3345微生物学(i)《微生物学》,沈萍,高等教育出版社20003346生理学《生理学》(七年制规划教材,临床医学专业用),姚泰,人卫版3347数字信号处理(Ⅱ)《数字信号处理》(上、下),吴兆雄,国防工业出版社090人文学院2220科学史导论《科学史》,w.c.丹皮尔,商务印书馆1979或广西师范大学出版社2001;《科学的历程》(第二版),吴国盛,北京大学出版社2002;《中国科学技术史稿》(上下册),杜石然等,科学出版社1982110化学化工学院2221聚合物材料结构与性能《高聚物的结构与性能》,马德柱等,科学出版社;《高分子物理》,何曼君,复旦大学出版社2222物理化学(含结构与波谱化学)《物理化学》(第四版),傅献彩等,高等教育出版社1990;《结构化学基础》(第三版),周公度,北京大学出版社2002;《有机化合物结构鉴定与有机波谱学》(第二版),宁永成,科学出版社20003349高分子合成化学《高分子化学》,潘祖仁,化学工业出版社;《高分子化学》,自然科学基金委,化学工业出版社3350高等无机化学《普通无机化学》,严宣生,王长富,北京大学出版社1999;《催化原理》,吴越,高等教育出版社20013351化学反应工程与催化《化学反应工程与催化》,李绍芬,化学工业出版社;《催化原理》,吴越,高等教育出版社20013352高等有机化学《高等有机化学》,f. a凯里、r. j 森德伯格,人民教育出版社3376仪器分析《仪器分析教程》,北京大学化学系仪器分析组,北京大学出版社;《仪器分析》(第三版),朱明华,高教出版社2000120安泰经济与管理学院3353统计学《概率论与数理统计教程》,魏宗舒,高等教育出版社1983;《概率论与数理统计》(第三版),盛骤等,高等教育出版社20013354运筹学《运筹学》(修订版),运筹学编写组,清华大学出版社20033355计量经济学《introductory econometrics:a modern approach 》,jeffrey m. wooldridge,south-western college publishing,清华大学出版社(影印本);《计量经济学3374战略管理《战略管理》,王方华、吕巍,机械工业出版社2004130国际与公共事务学院2225中国特色社会主义理论与实践《邓小平文选》(第二、三卷),人民出版社1993/1994;《“三个代表”重要思想概论》,中华人民共和国教育部,中国人民大学出版社20033357当代中国政治与政策《政府过程》,胡伟,浙江人民出版社1998/上海人民出版社2007;《理解公共政策》,托马斯?戴伊,华夏出版社2005140外国语学院1102日语(二外)《日语中级阅读》、《日语高级阅读》,日本语教育教师协会(jaltta),上海外语教育出版社1103法语(二外)《法语》(1—4册),马晓宏,外语教学与研究出版社1104德语(二外)《基础德语》,王志强等;《中级德语》,樊迪生,同济大学出版社2226语言学linguistics: an introduction,andrew radford,外语教学与研究出版社;course in general linguistics,f.de saussure ,外语教学与研究出版社;linguistic theory:the discourse of fundamental works,robert de beaugrande,外语教学与研究出版社3358英语写作不指定参考书目150农业与生物学院2227分子生物学原理《现代分子生物学》(第二版),朱玉贤、李毅,高等教育出版社2002;《基因工程原理》(第二版),吴乃虎,科学出版社20012228植物生物化学与分子生物学《植物生物化学与分子生物学》,b.b.布坎南等主编;瞿礼嘉等主译,科学出版社20042210计算机科学与技术方法论《数理逻辑与集合论》,石纯一,清华大学出版社2000;《图论与。
第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
固体物理第一章习题及参考答案1.题图1-1表示了一个由两种元素原子构成的二维晶体,请分析并找出其基元,画出其布喇菲格子,初基元胞和W -S 元胞,写出元胞基矢表达式。
解:基元为晶体中最小重复单元,其图形具有一定任意性(不唯一)其中一个选择为该图的正六边形。
把一个基元用一个几何点代表,例如用B 种原子处的几何点代表(格点)所形成的格子 即为布拉菲格子。
初基元胞为一个晶体及其空间点阵中最小周期性重复单元,其图形选择也不唯一。
其中一种选法如图所示。
W -S 也如图所示。
左图中的正六边形为惯用元胞。
2.画出下列晶体的惯用元胞和布拉菲格子,写出它们的初基元胞基矢表达式,指明各晶体的结构及两种元胞中的原子个数和配位数。
(1) 氯化钾 (2)氯化钛 (3)硅 (4)砷化镓 (5)碳化硅 (6)钽酸锂 (7)铍 (8)钼 (9)铂 解:基矢表示式参见教材(1-5)、(1-6)、(1-7)式。
11.对于六角密积结构,初基元胞基矢为→1a =→→+j i a 3(2 →→→+-=j i a a 3(22求其倒格子基矢,并判断倒格子也是六角的。
倒空间 ↑→ji i (B)由倒格基失的定义,可计算得Ω⨯=→→→3212a a b π=a π2)31(→→+j i →→→→→+-=Ω⨯=j i a a a b 31(22132ππ→→→→=Ω⨯=k ca ab ππ22213正空间二维元胞(初基)如图(A )所示,倒空间初基元胞如图(B )所示(1)由→→21b b 、组成的倒初基元胞构成倒空间点阵,具有C 6操作对称性,而C 6对称性是六角晶系的特征。
(2)由→→21a a 、构成的二维正初基元胞,与由→→21b b 、构成的倒初基元胞为相似平行四边形,故正空间为六角结构,倒空间也必为六角结构。
12.用倒格矢的性质证明,立方晶格的(hcl )晶向与晶面垂直。
证:由倒格矢的性质,倒格矢→→→→++=321b l b k b h G hkl 垂直于晶面(h 、k 、l )。
11级第一次(作业)请充分利用网络、本校及外校图书馆的相关资料,同时联系相关专业的老师,调查关于固体物理的简史、发展趋势以及当代的热门前沿课题(针对自己感兴趣的某个方面),形成一份报告,阐述自己的看法,要求2000字以上。
(已经在第一次课布置,11月1日前后上交)11级固体物理第2次习题和思考题1.在结晶学中,我们课堂上讲的单胞,也叫元胞,或者叫结晶学原胞,也叫晶胞,试回忆一下晶胞是按晶体的什么特性选取的?答:在结晶学中,晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性。
2.解释Bravais 点阵并画出氯化钠晶体的结点所构成的Bravais 点阵。
答:晶体的内部结构可以概括为由一些相同的结点构成的基元在空间有规则的作周期性的无限分布,这些结点构成点阵,如果基元只由一个结点构成,这种点阵称为Bravais 点阵。
氯化钠晶体的Bravais 点阵可参照书p8的图1-13,点阵的结点由钠离子和氯离子组成。
3.说明金刚石结构是复式点阵的原因。
答:金刚石结构可这样描述:面心立方的体心向顶角引8条对角线,在互不相邻的四条对角线中点,各有一个原子。
以金刚石为例,顶角和面心处的原子周围情况和对角线上的原子周围情况不相同,因而金刚石结构是复式晶格,可看作两套面心立方子晶格沿体对角线移开1/4体对角线长度而成。
Bravais 点阵包含两个原子。
4.体心立方点阵和面心立方点阵互为正、倒格子,试证明之。
答:面心立方的三个基矢为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(2)(2)(2321i k a a k j a a j i a a其体积为43a ,根据倒格矢的定义得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=⨯⋅⨯=++-=⨯⋅⨯=+-=⨯⋅⨯=)(2)(2)(2)(2)(2)(2321213321132321321k j i a a a a a a b k j i a a a a a a b k j i a a a a a a bππππππ 可见,除了系数不同之外,方向正好是体心立方的晶格基矢。
大学固体物理试题及答案一、选择题(每题2分,共20分)1. 固体物理中,晶格振动的量子化描述中,声子是()。
A. 电子的量子化B. 光子的量子化C. 晶格振动的量子化D. 磁场的量子化答案:C2. 能带理论中,价带和导带之间的区域称为()。
A. 能隙B. 能级C. 能带D. 能区答案:A3. 在固体中,电子的自由度不包括()。
A. 位置B. 动量C. 能量D. 质量答案:D4. 固体物理中,金属的自由电子模型是由哪位科学家提出的?()A. 薛定谔B. 泡利C. 德鲁德D. 海森堡答案:C5. 固体物理中,半导体的能带结构中,导带和价带之间的能隙称为()。
A. 能隙B. 能级C. 能带D. 能区答案:A6. 晶格常数是指()。
A. 晶格中原子间的平均距离B. 晶格中原子间的最大距离C. 晶格中原子间的最小距离D. 晶格中原子间的任意距离答案:A7. 固体物理中,费米能级是指()。
A. 最高占据能级的电子能量B. 最低未占据能级的电子能量C. 电子从导带跃迁到价带所需的能量D. 电子从价带跃迁到导带所需的能量答案:B8. 固体物理中,布拉格反射定律描述的是()。
A. X射线在晶体中的衍射现象B. 电子在晶体中的衍射现象C. 光在晶体中的反射现象D. 声波在晶体中的反射现象答案:A9. 固体物理中,超导现象是指()。
A. 材料在低温下电阻突然消失的现象B. 材料在高温下电阻突然消失的现象C. 材料在低温下电阻突然增加的现象D. 材料在高温下电阻突然增加的现象答案:A10. 固体物理中,霍尔效应是指()。
A. 电流通过导体时,导体两端产生电压的现象B. 电流通过导体时,导体两侧产生磁场的现象C. 电流通过导体时,导体内部产生电场的现象D. 电流通过导体时,导体内部产生磁场的现象答案:B二、填空题(每题2分,共20分)1. 固体物理中,晶格振动的量子化描述中,声子是晶格振动的_______。
答案:量子化2. 固体物理中,金属的自由电子模型中,电子被视为_______。