航天器控制大作业

《飞行控制系统》课程实验报告班级 0314102学号 ********* 姓名孙旭东成绩南京航空航天大学2017年4月（一）飞机纵向飞行控制系统的设计与仿真1、分析飞机纵向动力学模态，求飞机的长周期与短周期阻尼与自然频率。

在MATLAB环境下导入数据文件，输入damp(alon),得出结果：Eigenvalue Damping Freq. (rad/s)-2.29e+000 + 4.10e+000i 4.88e-001 4.69e+000-2.29e+000 - 4.10e+000i 4.88e-001 4.69e+000-3.16e-002 1.00e+000 3.16e-002-7.30e-003 + 3.35e-002i 2.13e-001 3.42e-002-7.30e-003 - 3.35e-002i 2.13e-001 3.42e-002长周期的根为 -7.30e-003 + 3.35e-002i 和 -7.30e-003 - 3.35e-002i阻尼为 2.13e-001自然频率为 3.42e-002(rad/s)短周期的根为 -2.29e+000 + 4.10e+000i 和 -2.29e+000 - 4.10e+000i阻尼为 4.88e-001自然频率为 4.69e+000(rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真，画出相应的状态曲线。

sys=ss(alon,blon,clon,dlon)[y,t]=step(sys,500)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Delta\alpha(deg)')200400600-10-505t(s)∆q (d e g /s )200400600-4-2024t(s)∆q (d e g /s )200400600-150-100-50050t(s)∆θ(d e g )0200400600-50050100t(s)∆θ(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-6-4-2t(s)∆α(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-2024t(s)∆α(d e g )subplot(221) plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\theta(deg)')subplot(121) plot(t,y(:,5,1)) xlabel('t(s)')ylabel('\Deltah(m)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)')ylabel('\Deltah(m)')2004006004t(s)∆h (m )200400600-2.5-2-1.5-1-0.54t(s)∆h (m )以上各图为升降舵及油门单位阶跃输入下的飞机自然特性行仿真，左边一列为升降舵的阶跃输入，右边一列为油门的阶跃输入。

航天器制导与控制课后题答案(西电)1.3 航天器的基本系统组成及各部分作用？航天器基本系统一般分为有效载荷和保障系统两大类。

有效载荷:用于直接完成特定的航天飞行任务的部件、仪器或分系统。

保障系统:用于保障航天器从火箭起飞到工作寿命终止, 星上所有分系统的正常工作。

1.4 航天器轨道和姿态控制的概念、内容和相互关系各是什么?概念：轨道控制：对航天器的质心施以外力, 以有目的地改变其运动轨迹的技术; 姿态控制：对航天器绕质心施加力矩, 以保持或按需要改变其在空间的定向的技术。

内容：轨道控制包括轨道确定和轨道控制两方面的内容。

轨道确定的任务是研究如何确定航天器的位置和速度, 有时也称为空间导航, 简称导航; 轨道控制是根据航天器现有位置、速度、飞行的最终目标, 对质心施以控制力, 以改变其运动轨迹的技术, 有时也称为制导。

姿态控制包括姿态确定和姿态控制两方面内容。

姿态确定是研究航天器相对于某个基准的确定姿态方法。

姿态控制是航天器在规定或预先确定的方向( 可称为参考方向)上定向的过程, 它包括姿态稳定和姿态机动。

姿态稳定是指使姿态保持在指定方向, 而姿态机动是指航天器从一个姿态过渡到另一个姿态的再定向过程。

关系：轨道控制与姿态控制密切相关。

为实现轨道控制, 航天器姿态必须符合要求。

也就是说, 当需要对航天器进行轨道控制时, 同时也要求进行姿态控制。

在某些具体情况或某些飞行过程中,可以把姿态控制和轨道控制分开来考虑。

某些应用任务对航天器的轨道没有严格要求, 而对航天器的姿态却有要求。

1.5 阐述姿态稳定的各种方式, 比较其异同。

姿态稳定是保持已有姿态的控制, 航天器姿态稳定方式按航天器姿态运动的形式可大致分为两类。

自旋稳定:卫星等航天器绕其一轴(自旋轴) 旋转, 依靠旋转动量矩保持自旋轴在惯性空间的指向。

自旋稳定常辅以主动姿态控制, 来修正自旋轴指向误差。

三轴稳定: 依靠主动姿态控制或利用环境力矩, 保持航天器本体三条正交轴线在某一参考空间的方向。

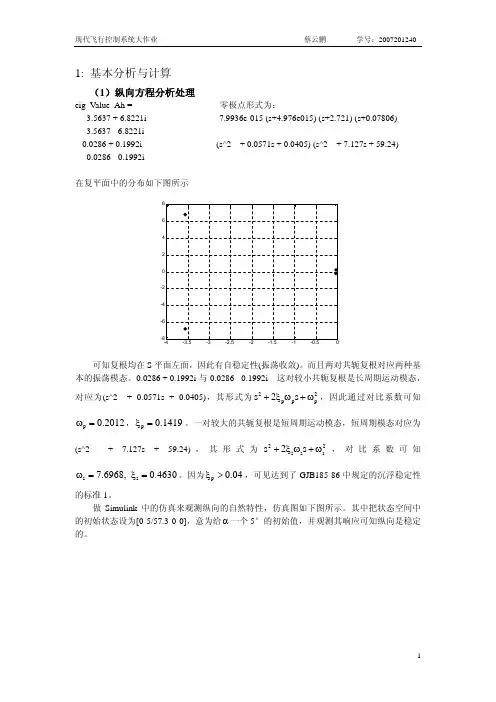
1: 基本分析与计算（1）纵向方程分析处理eig_Value_Ah = 零极点形式为： -3.5637 + 6.8221i -7.9936e-015 (s+4.976e015) (s+2.721) (s+0.07806) -3.5637 - 6.8221i ---------------------------------------------------------------------- -0.0286 + 0.1992i (s^2 + 0.0571s + 0.0405) (s^2 + 7.127s + 59.24) -0.0286 - 0.1992i在复平面中的分布如下图所示可知复根均在S 平面左面，因此有自稳定性(振荡收敛)。

而且两对共轭复根对应两种基本的振荡模态。

-0.0286 + 0.1992i 与-0.0286 - 0.1992i 这对较小共轭复根是长周期运动模态，对应为(s^2 + 0.0571s + 0.0405)，其形式为22p p s 2s p +ξω+ω，因此通过对比系数可知，。

一对较大的共轭复根是短周期运动模态，短周期模态对应为p 0.2012ω=p 0.1419ξ=(s^2 + 7.127s + 59.24)，其形式为2s s s s 2s 2+ξω+ω，对比系数可知。

因为s s 7.6968, 0.4630ω=ξ=p 0.04ξ>，可见达到了GJB185-86中规定的沉浮稳定性的标准1。

做Simulink 中的仿真来观测纵向的自然特性，仿真图如下图所示。

其中把状态空间中的初始状态设为[0 5/57.3 0 0]，意为给α一个5°的初始值，并观测其响应可知纵向是稳定的。

上图中右图是空速V 的响应，左图是迎角α的响应。

可以看出其纵向自然特性是随着时间而自稳定的。

在讨论纵向操纵性时，给定升降舵偏角一个幅值为5=°e δ，宽度为1秒的一个脉冲，其中脉冲可用signal builder 来构造，Simulink 框图和各状态变量的响应的输出如下图所示：Vαqθ可见,,,V q αθ在升降舵受到脉冲干扰后，其均随时间而收敛，其中空速V 和仰俯角θ的变换范围较大，其稳定所需时间较长。

航空航天工程师的工作中的航天器控制系统航空航天工程师是专门从事航空航天技术研发和应用的专业人员。

在他们的工作中，航天器控制系统扮演着至关重要的角色。

航天器控制系统是航天器的大脑，负责监测、控制和导航航天器的飞行和姿态，保证航天器在太空环境中的正常运行。

本文将介绍航空航天工程师的工作中航天器控制系统的相关内容。

一、航天器控制系统的组成航天器控制系统主要由以下几个部分组成：导航系统、制导系统、姿态控制系统和飞行控制系统。

1. 导航系统导航系统通过使用多种导航传感器（如星敏感器、陀螺仪、加速度计等）获取航天器的准确位置、速度和方向信息，以便为航天任务提供准确的导航支持。

2. 制导系统制导系统是基于导航系统提供的准确信息，通过对航天器的轨道、速度和方向进行精确控制，实现航天器的轨道调整、进入和离开轨道、转向等功能。

3. 姿态控制系统姿态控制系统是用于控制航天器在太空中的姿态的关键系统。

通过使用陀螺仪、反动力轮、推进器等设备，精确控制航天器的姿态，保持其在太空中的稳定飞行。

4. 飞行控制系统飞行控制系统是整个航天器控制系统的核心。

它负责将导航、制导和姿态控制系统的信息进行综合处理和判断，并生成相应的飞行指令。

飞行控制系统通常由控制计算机和执行机构组成。

二、航空航天工程师的任务航空航天工程师的工作是设计、开发和测试航天器控制系统，以确保航天器能够在各种极端条件下正常运行。

1. 系统设计航空航天工程师首先要进行航天器控制系统的整体设计。

他们需要根据航天任务的要求和目标，设计出满足需求的系统架构，并选择合适的硬件和软件组件。

2. 功能开发在系统设计的基础上，航空航天工程师负责开发控制系统的各个功能模块，包括导航、制导、姿态控制和飞行控制等。

他们需要编写相应的算法，并进行仿真和测试，确保系统具备稳定性和可靠性。

3. 硬件集成为了将航天器控制系统与其他航天器子系统（如动力系统、通信系统等）有效地集成起来，航空航天工程师需要进行硬件和软件的集成工作。

航天概论大作业航天技术概论大作业第二章1、大气层分几层？各层有什么特点?答：大气层共有对流层,平流层，中间层，热层与散逸层5个层次。

（1)对流层主要特点：气温随高度升高而降低;风向、风速经常变化;空气上下对流剧烈;有云、雨、雾、雪等天气现象.（2）平流层主要特点：空气沿铅垂方向得运动较弱,因而气流比较平稳，能见度较好。

（３)中间层主要特点:气温随高度升高而下降，且空气有相当强烈得铅垂方向得运动。

(４)热层主要特点：空气密度极小,温度随高度增高儿上升.(5）散逸层主要特点:空气极其稀薄，大气分子不断向星际空间逃逸。

2、什么就是国际标准大气？答：国际标准大气就是由国际性组织（如国际民用航空组织、国际标准化组织）颁布得一种“模式大气",它依据实测资料,用简化方程近似地表示大气温度、密度与压强等参数得平均铅垂分布,并排列成表,形成国际标准大气表.3、大气得状态参数有哪些？答：大气得状态参数就是指它得压强P、温度T、密度这三个参数。

对一定数量得气体，这三个参数就可以决定它得状态。

它们之间得关系，可用气体状态方程表示,如下4、什么就是大气得粘性?答：大气得粘性就是空气在流动过程中表现出得一种性质，主要就是由于气体分子作不规则运动得结果。

５、何谓声速与马赫？答：声速就是指声波在物体中传播得速度。

空气被压缩得程度与声速成反比，与飞机飞行速度成正比，要衡量空气被压缩程度得大小，就用马赫来表示，。

6、什么就是飞行相对原理？答：在实验研究与理论分析中，往往采用让飞机静止不动，而空气以相同得速度沿相反得方向流过飞机表面，此时在飞机上产生得空气动力效果与飞机以同样得速度在空气中飞行所产生得空气动力效果完全一样，这就就是飞行“相对运动原理”。

8、低速气流与超声速气流得流动特点有何不同？答:低速气流在流动得过程中，其密度变化不大,可认为就是不可压缩得，即密度就是常数；超声速气流在流动中，空气密度急剧变化引起空气动力发生很大变化,随着流速增大,管道截面面积必然增大。

航空航天工程师的航天器发射与控制航天工程包含了航天器的发射与控制，这是航空航天工程师所负责的重要任务。

航天器发射与控制涉及了许多关键技术和流程，必须在高度精确和协同的条件下进行。

本文将探讨航天器发射与控制的过程、所需技术和工程师的角色。

一、航天器发射过程航天器的发射过程可以分为多个阶段，其中包括准备、发射、分离和轨道控制。

首先是准备阶段，这包括航天器的组装、燃料充填以及系统检查。

确保所有系统都处于正常工作状态对于成功的发射至关重要。

接下来是发射阶段，这是航天器从地面升空进入太空的关键阶段。

在发射过程中，推进剂被点燃产生推力，驱动航天器脱离地球引力。

发射阶段需要高度的准确性和稳定性，以确保航天器能够按计划进入预定轨道。

当航天器进入太空后，分离阶段开始。

这包括分离发射器和航天器的所有部分，以及准备航天器进入目标轨道。

分离过程需要精确计时和金属零件的可靠工作，以确保航天器按计划顺利进入轨道。

最后是轨道控制阶段，这是航天器在轨道上的姿态和位置调整过程。

航天器需要进行精确的姿态控制，以实现轨道纠偏、轨道变换等任务。

这需要使用推进剂、控制系统和导航设备来实现。

二、航天器发射与控制所需技术在航天器发射与控制中，许多技术被应用于不同的阶段和任务。

以下是一些常见的技术：1. 推进系统技术：包括推进剂的选择和管理、发动机设计和燃烧控制等，以提供足够的推力和精确的控制能力。

2. 姿态控制技术：使用陀螺仪、推进器和飞行控制系统对航天器进行精确的姿态控制。

这是实现轨道调整和目标对接的关键技术。

3. 导航与定位技术：使用卫星导航系统和地面测量设备，对航天器的位置进行精确测量和定位，以实现轨道控制和导航任务。

4. 通信与数据传输技术：通过卫星链路和地面站，实现与航天器的通信和数据传输。

这对于航天器的遥测遥控以及指令下达至关重要。

5. 火箭发动机技术：设计和开发高效可靠的火箭发动机，确保航天器能够达到所需的速度和轨道。

以上技术是航天器发射与控制过程中不可或缺的关键技术，工程师们需要具备扎实的技术知识和实践经验来应对复杂的任务和挑战。

参考资料：【1】卫星轨道姿态动力学与控制，章仁为，北京航空航天大学出版社。

【2】航天器控制原理，周军，西北工业大学出版社。

第二章 作 业一、设刚体B 相对某参考坐标系的姿态可用方向余弦阵A 表示，角速度矢量为ω，试证明： (1) AA T =E (2) |A |=1 (3) dA/dt = -ω⨯A证明：设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211A A A A A A A A A A (1) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=332313322212312111333231232221131211A A A A A A A A A A A A A A A A A A AA T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++++++++++++++=233232231233322322131133312321131332332223121223222221132312221121331332123111231322122111213212211A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A AA T根据A 阵的性质，可知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100010001T AA (2) 由于方向余弦阵A 描述的坐标系皆为右手正交坐标系，由此可以验证（代入变换矩阵公式即可验证）A T = A *又由于A T = A -1因此，由A -1= A */|A |可以推知|A |=1(3) 令姿态相对参考坐标系的转速为ω，转轴为e ，则ω= ω e 。

如在t 时刻姿态矩阵为A (t ) ，在t +∆t 时刻为A (t +∆t )。

如用A '表示姿态的变化，则有A (t +∆t ) =A ' A (t )利用Euler 轴/角与姿态矩阵间的转换关系，可以写出cos (1cos )sin T A I ee e φφφ⨯'=⋅+--⋅当0t ∆→时，A I t ω⨯'=-∆因此，有A (t +∆t ) = A (t )-ω⨯ ∆t A (t )tt A t t A dt dA t ∆-∆+=→∆)()(lim/0= -ω⨯ A (t )二、试推导方向余弦阵与Euler 轴/角间的转换关系。

1. 控制系统任务的物理描述为了满足飞机品质的要求，飞机的纵向运动和横侧向运动都需要有能够连续工作的阻尼器，以用来调整飞机的飞行姿态，避免其出现不必要的俯仰和倾斜。

维持飞机纵向运动的阻尼器称为俯仰阻尼器，维持飞机横侧向运动的阻尼器称为偏航阻尼器。

本次课程大作业旨在通过运用Matlab 的经典控制系统设计工具对某型飞机偏航阻尼器进行控制系统的设计。

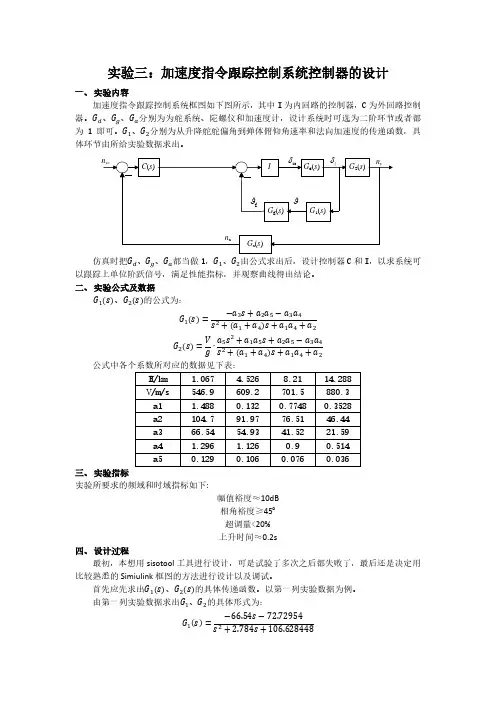
2. 控制系统对象的数学模型巡航状态下，某型飞机侧向运动的状态空间模型为：111121314111222122232421221313233343132234142434441424()1()()()()2()()()3()()4t x t a a a a b b t x t a a a a b b u t a a a a b b u t x t t a a a a b b x t t x x x x ••••⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 1111213141221222324234()()()()()()x t c c c c y t x t c c c c y t x t x t ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦式中： 1()x t ：侧滑角（单位为rad ）2()x t ：偏航角速度（单位为/rad s ）3()x t ：滚转角速度（单位为/rad s ）4()x t ：倾斜角（单位为rad ）输入向量及输出向量分别为：1()u t ：方向舵偏角（单位为rad ）2()u t ：副翼偏角（单位为rad ）1()y t ：偏航角速度（单位为/rad s ）2()y t ：倾斜角（单位为rad ）设飞机巡航飞行时的速度为0.8马赫，高度为40000英尺，此时模型的参数为：0.055800.99680.08020.04150.598000.11500.031803.050000.38800.4650000.0805 1.00000A --⎡⎤⎢⎥--⎢⎥=⎢⎥--⎢⎥⎣⎦ 0.007290.00000.475000.007750.15300.1430000B ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦0 1.000000 1.0C ⎡⎤=⎢⎥⎣⎦0000D ⎡⎤=⎢⎥⎣⎦首先输入飞机状态空间模型参数。

西北工业大学航天学院航天器控制原理实验报告（2013 ～ 2014 学年第一学期）实验人：实验班级：指导老师：周军刘莹莹黄河刘睿实验日期：1.实验目的（1）提高对航天器控制系统总体的了解，掌握航天器控制部件的工作原理和模式；（2）掌握航天器姿态控制系统建模、控制理论、实验动手及计算机仿真能力；（3）加深对航天器控制原理和控制工程的理解，提高理论与实验研究相综合的能力；2.实验内容（1）了解航天器控制全物理仿真系统的各部分工作原理；（2）航天器刚挠耦合动力学特性实验；（3）航天器控制系统工程非理想因素分析与简化；（4）推力器控制原理实验；（5）飞轮控制原理实验；（6）干扰和挠性振动条件下航天器姿态稳定控制实验；（7）航天器姿态大角度机动控制实验；（8）航天器多轴指向控制拓展演示实验；（9）实验分析、总结与报告；3.实验条件实验地点：西北工业大学航天学院航天器控制全物理仿真实验室主要设备：（1）单轴气浮台航天器控制全物理仿真实验平台；（2）计算机测控系统；（3）配套高压气源系统；4.实验原理（1）写出刚体航天器三轴姿态动力学方程，说明单通道仿真实验的合理性；根据你的理解，说明挠性部件对三轴航天器姿态的影响。

（2）写出带有飞轮的航天器姿态动力学方程，叙述飞轮控制的基本原理。

（3）画出一种推力器在航天器上的安装方式，叙述推力器姿态控制的基本原理。

5.实验现象与分析（1）航天器控制全物理仿真与数学仿真相比，有哪些不同？（2）根据你的理解，解释帆板振动实验现象。

（3）叙述实验中飞轮开环工作过程，解释实验现象。

（4）叙述实验中推力器开环工作过程，解释实验现象。

（5）叙述航天器姿态稳定控制实验过程，对实验现象进行分析解释。

（6）叙述航天器大角度姿态机动控制实验过程，对实验现象进行分析解释。

6.试验设计（1）结合全物理仿真实验系统，设计一种航天器姿态稳定控制算法。

假设姿态角度与角速度可测量，飞轮与推力器为执行机构。