当前位置：文档之家 › 塑性力学05-球对称与轴对称问题

塑性力学05-球对称与轴对称问题

  • 格式：ppt
  • 大小：594.00 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

河海大学05-06第二学期弹塑性力学考试试卷

河海大学05-06第二学期弹塑性力学考试试卷

2005-2006 学年第二学期《弹性力学及有限元》期末试卷一、选择题（20 分） 1、 弹性力学建立的基本方程多是偏微分方程，最后需结合（）求解这些微分方程，以求得具体问题的应力、应变、位移。

A．几何方程 B．边界条件 C．数值方法 D．附加假定2、 弹性力学平面问题的求解中，平面应力问题与平面应变问题的三类基本方程具有下列关系（ ）。

A．平衡方程、几何方程、物理方程完全相同B．平衡方程、几何方程相同，物理方程不同C．平衡方程、物理方程相同，几何方程不同3、 根据圣维南原理，作用在物体一小部分边界上的力系可以用下列（ ）的力系代替，则仅在近处应力分布有改变，而在远处所受的影响可以不计。

A．静力上等效 B．几何上等效 C．平衡 D．任意4、 三结点三角形单元中的位移分布为（ ）。

A．常数 B．线性分布 C．二次分布 D．三次分布二、简答题1、在什么条件下，平面应力问题的 的？（9 分）与平面应变问题的是相同2、若引用应力函数 求解平面问题，应力分量与应力函数的关系式、 推导出来的。

（5 分）、是根据弹性力学哪一类基本方程3、有限单元法中选取单元位移模式应满足什么条件? （9 分）三、计算题1、 试问 分量？（10 分）是否可能成为弹性力学问题中的应变2、圆环内半径和外半径为别为 a 和 b，内边界受均布法向压力 作用，外边界固 定。

已知平面轴对称问题的应力分量为，相应位移分量为 ，试求圆环的应力分量和位移分量。

（15 分）3、试用应力函数求解题 3 图所示的应力分量（设）。

（20 分）题3图 4、某结构的有限元计算网格如题 4 图（a）所示。

网格中两种类型单元按如题 4 图（b）所示的局部编号，它们单元劲度矩阵均为试求：（1）结点 2 的等效荷载列阵 。

（4 分） （2）整体劲度矩阵中的子矩阵 和 。

（8 分）（a）（b）。

《弹塑性力学》第九章空间轴对称问题

《弹塑性力学》第九章空间轴对称问题


80%
物理方程
描述了材料在不同应力状态下表 现出的物理性质。
塑性力学的基本方程
流动法则
描述了塑性应变与应力之间的 关系。
屈服准则
描述了材料屈服的条件，即应 力达到屈服点时的状态。
强化准则
描述了材料在塑性变形过程中 的应力增强机制。
空间轴对称问题的边界条件和初始条件
边界条件
描述了物体在边界上的受力状态和位 移约束。
如旋转机械、航空航天器等的 设计和分析。
土木工程
如桥梁、高层建筑等大型结构 的分析。
石油工程
如油藏模拟、油气管道设计等 。
核工程
如核反应堆、核废料处理设施 等安全评估。
02
空间轴对称问题的数学模型
弹性力学的基本方程
80%
平衡方程
描述了物体内部各点的受力平衡 状态。
100%
几何方程
描述了物体在受力后产生的形变 和位移。
近原问题的解。
在处理空间轴对称问题时，有限元法能 够将复杂的空间几何形状和边界条件简 化为易于处理和计算的离散模型，从而
提高求解效率。
有限元法在空间轴对称问题中广泛应用 于弹性力学、塑性力学等领域，能够得
到高精度的数值解。
有限差分法在空间轴对称问题中的应用
有限差分法是一种将偏微分方程离散化为差分方程的方法，通过求解差分方程来逼近原问题
目
CONTENCT
录
• 空间轴对称问题的基本概念 • 空间轴对称问题的数学模型 • 空间轴对称问题的解析解法 • 空间轴对称问题的数值解法 • 空间轴对称问题的实验研究
01
空间轴对称问题的基本概念
定义与特性
定义
空间轴对称问题是指物体在空间中关于某一直线或平面对称分布 的问题。
理论力学中的轴对称问题如何处理？

理论力学中的轴对称问题如何处理？

理论力学中的轴对称问题如何处理？在理论力学的广阔领域中，轴对称问题是一类具有重要意义和实际应用价值的研究对象。

轴对称问题常见于工程结构、机械设计以及许多物理现象的分析中。

理解和掌握如何处理这类问题，对于解决实际工程和科学中的力学难题至关重要。

首先，我们需要明确什么是轴对称问题。

简单来说，轴对称是指一个物体或系统绕着某一轴旋转一定角度后，与原来的形状完全重合。

在力学中，这意味着物体的几何形状、受力情况以及运动状态等在绕对称轴旋转时保持不变。

对于轴对称问题的处理，第一步通常是建立合适的坐标系。

由于轴对称的特性，选择柱坐标系往往是最为方便和直观的。

在柱坐标系中，我们有径向坐标 r、轴向坐标 z 和周向坐标φ 。

其中，周向坐标φ 在轴对称问题中通常不参与计算，因为物体在周向上的性质是相同的。

在确定了坐标系后，接下来就是对物体进行受力分析。

对于轴对称物体，其受力情况在绕对称轴旋转时也具有相应的对称性。

例如，如果受到的外力是集中力，那么这个力必然沿着对称轴或者在与对称轴垂直的平面内。

如果是分布力，比如压力、重力等，其分布规律也应该在轴对称的基础上进行考虑。

以一个简单的例子来说明，假设我们有一个轴对称的圆柱体，在其侧面受到均匀分布的压力。

在这种情况下，我们可以将这个分布压力等效为一个合力，这个合力的作用线必然通过圆柱体的轴线。

在处理轴对称问题时，运动学分析也是必不可少的环节。

对于旋转运动，我们需要考虑角速度、角加速度等参数。

由于轴对称的特点，角速度和角加速度在周向上的分量通常为零，只有轴向和径向的分量需要重点关注。

在动力学分析中，我们要运用牛顿第二定律来建立运动方程。

对于轴对称问题，由于受力和运动的对称性，方程往往会得到一定程度的简化。

例如，在考虑转动惯量时，由于轴对称性，只需要考虑轴向和径向的转动惯量分量。

材料力学性能在轴对称问题中也起着关键作用。

不同的材料在受力时的变形和应力分布规律不同。

对于常见的各向同性材料，其在轴对称条件下的应力应变关系可以通过相应的本构方程来描述。

弹性力学第四章 (5)轴对称问题

弹性力学第四章 (5)轴对称问题


u
1 A [(1 ) 2 (3 ) B 2(1 ) B ln 2(1 )C E
u
u u 1 u 0
（a ）
由（a）第一式积分： 1 A u (1 ) B[(1 3 ) 2(1 ) (ln 1)] E 2(1 )C f ( ) （b） 由（a）第二式，将（b）带入，整理：
A 2 BC (1 2 ln ) 2C A 2 B (3 2 ln ) 2C 0
（4—11）
三、位移分量：
（4-11） 代 （4-3） 代 （4-2）
1 1 A ( ) (1 ) 2 B[(1 3 ) E E
1 2 2 0
3）. 故应力函数，应力分量与 无关，仅是ρ 的函数。
不计体力时
( )
（4—9）变为
正应力与无关 剪应力为 0
2 . 平微方程：
1 f 0 由： 2 1 f 0
将 (h)、（f） 代入（c）式
位移分量： 1 A u [(1 ) 2(1 ) B (ln 1) (1 3 ) B E 2(1 )C ] I cos K sin （4—12）
4 B u H I sin K cos E
1??????不计体力时??49变为??022?????????????????正应力与?无关剪应力为0????????????????????????????????02?101?f??????f???????????由
弹塑性力学5极坐标解答1

弹塑性力学5极坐标解答1

x sin2 y cos2 2 xy cos sin. (c)
2、已知 σ ρ ,σφ，,τ求ρφ σ x ,σ y ,τ xy .
应用相似的方法，可得到
x cos2 sin 2 2 sincos, y sin 2 cos2 2 sincos, xy ( )sincos (cos2 sin 2).
(b)
考察多连体中的位移单值条件：
圆环或圆筒，是有两个连续边界的多连 体。而在位移解答中，
uφ
4B E
ρφ ,
(c)
是一个多值函数：对于ρ,φ和 ρ,2π是同φ
一点，但式(c)却得出两个位移值。由于 同一点的位移只能为单值，因此
B = 0。
由B=0 和边界条件 (b) ，便可得出拉梅解答，
σρ σφ
取出一个包含x面y(含 σ x ,σ y),和τ xy 面 ρ
（含 σ ρ ,τ ρφ）的三角形微分体，厚度为1，
如下图 A，考虑其平衡条件。
设bc ds,则ab ds cos, ac ds sin,由
F 0,
ds xds cos cos yds sin sin xyds cos sin yxds sin cos 0,
sin
K
cos。
其中
I，K—为x、y向的刚体平移，
H —为绕o点的刚体转动角度。
说明
（1）在轴对称应力条件下，式 (c),(d),(e) 为应力函数、应力和位移的通解，适用 于任何轴对称应力问题。
（2）在轴对称应力条件下，形变也是轴对称 的,但位移不是轴对称的。
（3）实现轴对称应力的条件是，物体形状、 体力和面力应为轴对称。
§5－1 极坐标中的平衡微分方程
微分体上的作用力有： 体力-- f ρ , fφ， 以坐标正向为正。 应力-- ρ面，φ面分别表示应力及其
弹塑性力学讲义 第九章空间轴对称问题

弹塑性力学讲义 第九章空间轴对称问题


的取值范围：由 0 1 的取值范围：0
r sin 1 a a sin

2
w
4(1 2 )q 2 2 a a 2 sin 2 0 E
a cos d a2 r 1 2 sin 2 r

4(1 2 )q a 2 cos 2 d E a2 r 1 2 sin 2 r
r R z z
当 R 时 R=(r +z ) ， 应力、位移 0； 当 R 0 时，应力奇异。 Boussinesq 采取 Love 函数求解，

x
y
(r,z)为重调和函数，由(r,z)的三次微分导出应力。
选
(r,z) 为 r 和 z 的正一次幂式: (r,z) = A1R+ A2[R - zln(R+z)] ——为双调和函数 (r,z) 自然满足 4=0 。代入位移、应力计算式
其中
2 1 2 2 r r z 2 r
2
7．按位移法解 a．基本未知函数： ur 和 w
基本方程两个：
( G )
u e G( 2 u r r ) f r 0 r r
( G )
e G 2 w f z 0 z
并考虑适当的边界条件。 b. 引入 Love（拉甫、勒夫）位移函数（当无体力作用时） 对于位移法的基本方程的解可由考虑体力的一个特解加上齐次 方程的通解。 轴对称问题齐次拉梅方程的通解可以引入一个 Love 位移函数
(1 ) P (1 2 ) P w 2Gr Er
圆面积均布荷载 q 对圆外 M 点竖向位移影响可取一个微面元， 距 M 点为 s，角度为 处，dA=sdds ，dA 上 q 对 M 点影响：
弹塑性力学 5_厚壁圆筒的分析

弹塑性力学 5_厚壁圆筒的分析

2
p
pl
厚壁圆筒内表 面处径向位移 与内压的关系
pe
o
ue
ul
u r a
圆筒端面条件的影响
工程中的圆筒，其端部通常为开口或闭口。 前面讨论中假设的平面应变状态，与实际情况的差别 对结果的有多大影响呢？ 弹性状态下的轴向应力
a2 z E z 2p 2 2 b a
z E z ( r )
应力组合 ( r ) 在r=a和r=b处 均有可能先达到临界值。
何处先达到与 b 和δ的选择有关 设内外筒体同时产生屈服 内筒：内表面处 p1 外表面处 q p ( r ) r b
p — 套装压力, ( r ) r b a (b c ) 2 2 p1 2 b (c a )
a 2 p1 (1 )b 2 u [ (1 )r ] 2 2 E (b a ) r

p1
+
-
r
p2
②厚壁圆筒仅受外压p2，即p1=0
b 2 p2 a2 b 2 p2 a2 r 2 2 (1 2 ), 2 2 (1 2 ) b a r b a r
当 p < pe 时，圆筒处于弹性状态；
当 p > pe 时，圆筒处于弹塑性状态。
①塑性区 a r rp
d r r 平衡方程： 0 dr r 屈服条件： r s d r s 0 dr r
q
a
rp
pp
塑性区
r s ln r C
基本方程
平衡方程： 几何方程： 物理方程：
（平面应力）
Hale Waihona Puke d r r 0 （平面应变） dr r 2 E E E ( 1 ) du u r , (1 ) dr r E 1 ( r ) r ( r ) r 2 1 E 1 E ( r ) ( r ) 2 E 1
轴对称问题

轴对称问题


(i , j , m )

由上式可见，单元内应变 εr、εz、γrz都是常量，但φi, φj, φm与各单元中各点的位置(r, z)有关，环向应变εθ不是常量； 当结构包含对称轴(r = 0)在内时，φi , φj , φm是奇异的， 这将给数值计算带来困难。
汽车工程系
结构分析与CAE研究室
- 16 -
z j
wj uj wi ui
单元结点力向量：
wm um
i m
{ f }e
⎧ fi ⎫ ⎪ ⎪ = ⎨fj ⎬ ⎪ ⎪ ⎩ f m ⎭ 6×1
r
汽车工程系
结构分析与CAE研究室
- 11 -
4.2 三结点三角形轴对称单元
4.2.2 单元位移模式 由于有三个结点，在r方向和z方向上各有三个结点条件， 因此设它的单元位移模式为
u ( r , z ) = α1 + α 2 r + α 3 z ⎫ ⎬ w(r , z ) = α 4 + α 5 r + α 6 z ⎭
该位移模式与平面问题三结点三角形单元完全相同。同样， 将结点坐标和结点位移代入上式可得到单元内部位移
⎧ ui ⎫ ⎪w ⎪ ⎪ i⎪ 0 ⎤ ⎪uj ⎪ e ⎪ ⎪ ⎨ ⎬ = [ N (r , z )]{δ } Nm ⎥ ⎪ wj ⎪ ⎦ ⎪ um ⎪ ⎪ ⎪ ⎪ wm ⎪ ⎩ ⎭
-5-
4.1 基本概念
4.1.2 基本方程 ①平衡方程
∂σ r ∂τ zr σ r −σ θ + + + br = 0 ∂r ∂z r ∂σ z ∂τ rz τ rz + + + bz = 0 ∂z ∂r r ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭
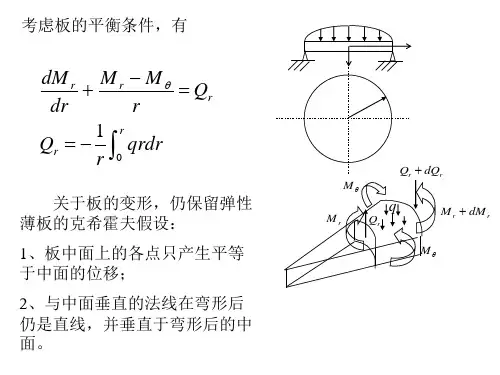
圆板的轴对称弯曲

圆板的轴对称弯曲

tg2 2 xy x y
如右图所示
2、滑移线
在平面应变状态下，其上每一点皆与最大剪应力面相切 的线叫滑移线。
由于剪应力成对且互相垂直，则过xoy平面内的每一点可 以作两条这样的线。所以在整个xoy平面内滑移线是两族正交 曲线，分别称为族和族。
规定：α、β的正方向成右手坐标系，并使τ在该坐标系内 成正方向。 α的切线与x轴的夹角用θ表示，由x轴的正方向按 逆时针算起。不难看出，最大主应力σ1的方向在α—β坐标系 的第一及第三象限，所以σ1方向顺时针转过π/4就是α方向， 逆时针转过π/4就是β方向。
M Ms
代入平衡方程，
M
B
A
s Ms
C
F
s Ms r Mr
D
E
dM r
dr
Mr M r
Qr
1 r
r qrdr 1 qr
0
2
r
dM r dr
Mr
1 qr2 2
Ms
积分得：
Mr Ms qr2 6 C r
由边界条件和限值条件
Mr
r0
Ms,Mr
ra
0
计算得：
C0
qp 6M s a2 6 sh2 a2
u z dw dr
而应变分量为
r
du dr
z
d 2w dr 2
u r
z r
dw dr
应变增量为
d du d 2 dw
dr dr z dr2
d
du r
z r
d
dw
dr
应变增量比值
dr d r
注意不记弹性变形及 z ，有
m 0,m r 3
则由刚塑性的利维-米塞斯流动法则
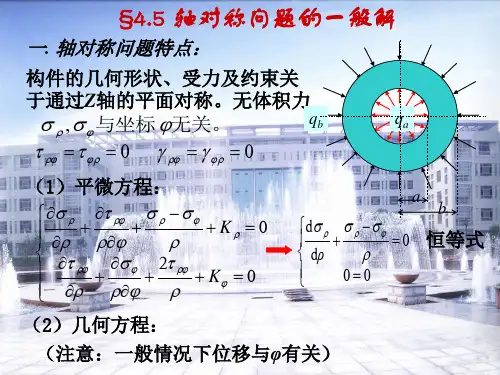
第四章轴对称.圆环(5,6)

第四章轴对称.圆环(5,6)


都是任意常数其中F 都是任意常数其中 式中： 式中：A、B、C、F、I、K都是任意常数其中 、I、K 一样代表刚体的位移(由位 和2-4节中的ω、u0、v0一样代表刚体的位移 由位 节中的 移边界确定) 移边界确定 E µ , 对于平面应变问题 E , µ 换成 2 1− µ 1− µ
[例1]：曲梁纯弯曲问题的弹力解答 例 ： 曲梁区域由两对圆弧坐标线和两条径线围成， 曲梁区域由两对圆弧坐标线和两条径线围成， 设厚度为单位1 设厚度为单位 由于是纯弯曲，各截面 相同 相同， 由于是纯弯曲，各截面M相同，因而应力分 量与φ无关 为轴对称问题。 无关， 量与 无关，为轴对称问题。 解: (1)应力分量 应力分量
四.位移分量： 位移分量：
1 A uρ = [−(1+ µ) + Cρ(1− µ)] ρ E uϕ = Fρ − I sinϕ + K cosϕ
qa
若适当给定约束条件， 若适当给定约束条件，无刚性位移
uϕ |ϕ =0 = 0, uϕ |ϕ =π / 2 = 0 → F = K = I = 0
讨论：位移分量确定： 讨论：位移分量确定：
得：N=0,K=0
1 A H = [(1 + µ ) − 2(1 − µ ) Bρ 0 ln ρ 0 E ρ0 + (1 + µ ) Bρ 0 − 2(1 − µ )Cρ 0 ]
代回位移表达式即得位移分量 本例可见，尽管位移分量中含多值函数项（ 项 本例可见，尽管位移分量中含多值函数项（φ项）， 但应用单值条件可得唯一解。 但应用单值条件可得唯一解。
a +b 须给出位移约束条件。 须给出位移约束条件。设 ρ = ρ0 = 2 和ϕ = 0处 ∂uϕ uρ = 0, uϕ = 0, =0 ∂ρ
塑性力学-简单弹塑性问题

塑性力学-简单弹塑性问题

ys
h2
理想弹塑性材料、矩形截面 b × h −σ s −
σ = Φ (ε ) = σ s
ys ys
其中：
⎤ ⎡ I (A ) M = σs ⎢ z e + Sp⎥ ⎦ ⎣ ys
2 3 I z ( Ae ) = b ⋅ y s 3
h2 2 S p = b( − y s ) 4
6
σs
+
M 3 1 y = − ( s )2 Me 2 2 h 2
+
ε=
y
+
σ
−
+
σs
σ
ρ
σ*
卸载前的应力、应变：σ 残余应力： σ * = σ − σ
ε
卸载过程应力改变量： σ = M y
I
10
2. 等截面梁的横向弯曲
•弯矩是变化的 M = M (x) •存在剪应力 忽略剪应力对屈服的影响
y ⎧ σs ⎪ σ ( x, y ) = ⎨ y s ( x ) ⎪Φ ( ε ) ⎩ 在 y ≤ ys ( x )时 在 y ≥ ys ( x )时
中性层曲率：
ρ
=
σs
Ey s
5
M = 2 ∫ σ ⋅ dA ⋅ y = 2 ∫ σ ⋅ dA ⋅ y + 2 ∫ σ ⋅ dA ⋅ y
0
h2
ys
h2
0
ys
= =
E
ρ σs
ys
I z ( Ae ) + 2 ∫ Φ (ε ) ⋅ dA ⋅ y
ys
h2
I z ( Ae ) + 2 ∫ Φ (ε ) ⋅ dA ⋅ y
z
该问题是球对称的。采用 球坐标 不为零的应力分量 σ θ σ ϕ σ r

弹塑性力学-05厚壁圆筒


σθ
r
r b2 p a2 1 + 2 σ s 1 + ln − 2 2 a b −a r = σ sρ 2 a 2 p b2 2b 2 − b 2 − a 2 1 + r 2

ρ ＝b
b p l = σ s ln a
r σ r = σ s ln b
σ θ = σ s 1 + ln
r b
p=
σs
ρ 1 − 2 + 2 ln 2 b a
ρ2
塑性极限压力
σθ
σs σr
p
a
b
12
讨论： 讨论：
Mises 条件 条件:
(σ r − σ θ )2 + (σ θ
14
四、残余应力
结构经历弹塑性变形历史后零外载对应的应力。 结构经历弹塑性变形历史后零外载对应的应力。 初次加载( 时的应力： 初次加载 p*>pe ) 时的应力：σij 卸除的应力： 卸除的应力：σij e 残余应力： 残余应力：σij r
σ ij = σ ij − σ
r
e ij
15
σr = −
2. 弹塑性分析
弹性区：ρ≤ r ≤ b 弹性区： σ r = C 1 + C 2 r −2 σ θ = C 1 − C 2 r −2
边界条件： σ 边界条件：
r r=b
ρ: 弹塑性分界面的半径。 弹塑性分界面的半径。 σs
σθ a b
σr
=0
p
屈服条件： 屈服条件： σθ – σr）r=ρ = σs （

a≤r≤ ρ
ρ ≤r≤b

李同林 弹塑性力学 第八章 空间轴对称问题


并采用拉普拉斯算符：
可得下列用位移表示的平衡微分方程，也称拉梅位移方程：
可缩记为：
G u jji Guijj Fi 0
可改写为：
187
缩记为：
G i G2ui Fi 0 1 2
2．位移解法的张量推导：
若以位移为基本未知量，必须将泛定方程改用位移 ui 来表示。现在来进行 推导： 将式几何方程（4—2）代入本构方程（4—6）得：
192
（6）
uv0
(1 )(1 2 ) p 2 2 w q ( h z ) 2 (h z ) (1 ) E
（8—7）
显然最大位移发生在边界上，由式（8—7）可知：
wmax ( w) z 0 (1 )(1 2 ) 1 2 qh ph (1 ) E 2
一、 位移法： 1．位移解法的一般推导：
为用位移作为基本未知量，必须将泛定方程改用位移 u、v 和 w 来表示。
186
为此，由本构方程，再利用几何方程可得：
再代入平衡微分方程得： 注意到：
x y z ，则：
2u 2v 2 w x x 2 xy xz
问题的特点假设一部分应力或位移为已知，然后在基本方程和边界条件中，求 解另一部分，这样便得到了全部未知量。在具体计算中对于简单问题经常先利 用材料力学中对同类型问题的初等解作为近似解，建立应力（或位移）函数再 代入弹性力学的基本方程中逐步修正得到精确解。
（3）迭代法：在塑性力学中使用全量理论并按位移求解问题时，还经常
F i (e ij 2Gij )l j e ijl j G(uij u ji )l j

塑性成形原理-33-平面问题和轴对称问题

1133平面问题和轴对称问题22331平面应力状态和轴对称应力状态一平面应力状态这个问题大家学了材料力学都懂请同学说一下什么是平面应力状态平面应力状态的关键特征
3.3 平面问题和轴对称问题
1
3.3.1 平面应力状态和轴对称应力状态 一、平面应力状态
这个问题大家学了材料力学都懂，请同学 说一下什么是平面应力状态，平面应力状态的 关键特征…
9
2、 应力平衡微分方程
r zr r 0 r z r rz z rz 0 z r r
怎么来的？
10
习题11： 证明：在柱坐标条件下，轴对称应力状态 的应力平衡微分方程为：
r zr r 0 r z r rz z rz 0 z r r
18
注意：环向应变公式怎么来的？
习题14： 轴对称物体子午面上某点的半径为 r，该 点的径向位移为 u。证明该点的环向应变为：
u r
(邓丽萍：…)
19
对于某些轴对称问题，例如均匀变形时的 单向拉伸、拉拔，以及平砧间圆柱体无摩擦压 缩等，其径向位移分量u与坐标r成线性关系， 于是：
u (c.r ) r c r r u c，故 ቤተ መጻሕፍቲ ባይዱ 且 r r
2
平面应力状态… 1、 特征 若在点的某个切面上全应力为 0（为叙述 方便设该面为Z面，则所有与坐标Z有关的应力 分量均为0)。 ↓ 即 Z面上全应力、正应力、剪应力均为0， Z面为主平面（主应力为零）。
3
● 不要思考，马上回答： 单向拉伸是否属于平面应力？
再想想：按照上面的说法，下面这个应力 状态肯定不是平面应力状态了吗？（请同学回 答）

塑性力学05-球对称与轴对称问题

解这个方程得到:
因为材料是理想弹塑性, 出口截面处的拉拔应力不能超过屈 服应力, 所以有 A1 A1 这样得到 s ln s e A2 A2 那么最大减缩率为
1 Rmax 1 0.63 e
5-3 理想弹塑性材料的厚壁圆筒 问题的描述: 分析内径为 a ,外径为 b 的厚壁圆筒,在其内表面受 内压为 q .假定是不可压缩的理想弹塑性材料, 并限定为平面应 变问题.取柱坐标,使 z 轴与筒轴线重合. 1)弹性状态 • 弹性应力解为(由于材料不可压缩 1/ 2 ): a 2 p1 b2 a 2 p1 b2 1 r 2 2 1 2 , 2 2 1 2 , z r b a r b a r 2 应力强度为 1 2 2 2 i 1 2 2 3 3 1 那么根据Mises屈 2 服条件得到弹性极 2 3 3b q 即 限压力为: i r 2 b 2 r2 2 s a 1 2 qe 1 2 a b 3 因此可见最大应力强度发生在内壁处.
这里常数B可以按照内壁的 半径条件 r r a q 来定.
2. 弹塑性状态 当压力 q qe 时,球壳内壁开始屈 服并向外扩展到半径 rs 处,如果材 料是理想弹塑性, 在塑性区应力仍 要满足平衡条件,此时考虑到屈服 条件 r s ,因此有 d r 2 s 0 dr r 积分得到 r 2 s ln r C 根据边界条件 r |r a q 得到积分常数 C q 2 s ln a 得到塑性区的应力为 r r 2 s ln q a r s 1 2ln q a
z

d
r

塑性力学05-球对称与轴对称问题

2 r s 1 ln b 3 2 r 1 z s ln b 3 2
r b2

4)残余应力的计算. 厚壁圆筒在进入塑性状态以后, 将内压 力全部卸载, 此时卸载的荷载变换为 q ,按弹性计算得到变化的 应力, 这样用卸载前的应力减去这个变换应力就得到残余应力. 用图来表示(残余应力只给出环向应力)为:
E r 1 r 2 1 1 2 E r 1 1 2
把它代入平衡方程得到用位移表示的平衡方程: d 2u 2 du 2u 2 0 2 dr r dr r • 解这个方程得 u Ar Br 2 利用边界条件得到
• 弹性区的应力,可以利用 弹性状态的解令 q qe , a rs
r 1 2 2 3b r r 2 1 3b r s rs2 z 3b 2
2 s s 2
s rs2 b 2
这是 q 和 rs 的关系式. 3) 上式令 rs b ,得到塑性极限 压力: 2 s b qp ln 3 a 此时塑性区应力为: 2 r r s ln b 3
这里常数B可以按照内壁的 半径条件 r r a q 来定.


r


r
r


r


弹性应力
b rs
弹塑性应力
塑性极限应力 残余应力
a
从残余应力图中看出,内壁有残余压应力, 这就是对厚壁圆筒施 加了预应力, 从而可以提高筒的压应力.这种利用预加塑性变形 来提高结果承载能力的技术在工程中被广泛使用.
5)变形计算. • 考虑平面应变和小变形, 建立位移方程并求解.因为 r 0 du u 又根据几何方程 du , u 就可以得到 0 r dr r dr r B u 解为 注意,这里推导没有涉及应力应变的关系. r 也就是这个解适用弹性区和塑性区.

轴对称问题读书笔记

轴对称问题读书笔记杨云 1049721301638定义：弹性体的几何形状、约束条件以及作用的载荷都对称于某一对称轴，在这种条件下的物体中的位移、应变和应力也对称于此轴。

这种问题称为轴对称问题。

基本概念：所有的应力、应变和位移都与θ方向无关，仅是坐标r 和z 的函数，任一点的位移只有两个方向的分量，即沿r 方向的径向位移u 和沿z 方向的轴向位移w 。

由于轴对称，θ方向的位移v 等于零，因此轴对称问题可作为二维问题处理。

{}[]Tmm j j i i e w u w u w u =δ{}[]TmmjjiieW U W U W U R =根据广义坐标选择的位移函数： ⎩⎨⎧++=++=zr w z r u 654321αααααα根据型函数选择的位移函数：⎩⎨⎧++=++=mm j j i i mm j j i i w N w N w N w u N u N u N u其中 ()),,(21循环m j i z c r b a AL N i i i i i ++==，面积mmjji iz r z r z r A 111=常数：),,(m j i r r c z z b z r z r a mj jm j i j m m j i ⎪⎩⎪⎨⎧+-=-=-=确定应力应变关系和应变位移关系：{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=m m j j i i m mjjii m j i m j im j i rz z r w u w u w u b c b c b c c c c f f f b b b A r w z u z w r u r u 00000000021γεεεεθ其中 ：),,(m j i rzc b r a f i i i i ++=应变r ε z ε rz γ 是常量, θε是单元中r 和z 的函数;{}[]{}[]{}em jieB B B B δδε==应变：{}[]{}[]{}em jieB B B B δδε==其中：[]),,(000m j i b c c f b B i i i ii i ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=应力： 应力向量： 导出单元刚度矩阵和方程根据虚功原理有：{}{}{}{}⎰⎰⎰=VT e eTz r r R θσεδd d d **{}[]{}[][]{}[]{}eeS B D D δδεσ==={}[]Trz z rτσσσσθ=则刚度矩阵为：[][][][][][][]⎰⎰⎰⎰⎰==VAT T e zr r B D B z r r B D B k d d π2d d d θ其分块矩阵形式为：[]emm mjmi jm jj ji im ij ii ek k k k k k k k k k ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=子矩阵：[][][][]zr r B D B k As T r rs d d π2⎰⎰=()()()),,,(2π22121213m j i s r b b A c c b b A f b c A b c A f b c A c c A b f f b A f f b b A A r s r s r sr s s r s r r r s sr s r s r s r s r c =⎥⎦⎤⎢⎣⎡+++++++++≈其中：μμ-=11A ，)1(2212μμ--=A ，)21)(1()1(3μμμ-+-=E A这个过程中虽能精确的导出单元刚度阵，但单元不大时，近似解已满足工程要求。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

那么最大减缩率为
Rmax
1
1 e
0.63
5-3 理想弹塑性材料的厚壁圆筒
问题的描述: 分析内径为 a ,外径为 b 的厚壁圆筒,在其内表面受 内压为 q .假定是不可压缩的理想弹塑性材料, 并限定为平面应
变问题.取柱坐标,使 z 轴与筒轴线重合.
1)弹性状态
• 弹性应力解为(由于材料不可压缩 1/ 2 ):
力强度
i
3 2
r 2
3 2
r
根据塑性区是理想弹塑性所以Mises屈服条件有 r
2 3
s
平面轴对称问题的平衡方程为
d r r 0
dr
r
这样由屈服条件和平衡方程得到 d r
2 3
s
dr r
积分得到
r
2 3
s
ln
r
C
再由边界条件 r |ra q 得积分常数C
• 这样得到塑性区的应力:
u r
这里 u 是径向位移.
它们应满足应变连续性方程 d r 0
dr r
边界条件为 r |ra q, r |rb 0
1. 弹性状态
• 首先建立位移表示的平衡方程.
球体处于弹性状态, 根据广义Hooke定律
r
r
2
E
,
r
E
然后用应变表示应力得到:
r
1
E
1 2
1
r
2
1
E
1
2
r
把它代入平衡方程得到用位移表示的平衡方程:
qe
2 s
b3 a3 3b3
从上式可以看出,当 b 时, qe 2 s / 3, 这说明如果使
球壳处于弹性工作状态, 那么无论壁厚增加多少也不能提
高它的承载能力.
2. 弹塑性状态
当压力 q qe 时,球壳内壁开始屈
服并向外扩展到半径 rs 处,如果材
料是理想弹塑性, 在塑性区应力仍
要满足平衡条件,此时考虑到屈服
a2 b2
s
3
2)弹塑性状态 令 rs是弹塑性交界面的半径. 首先我们分析一
下在塑性区的应力分量的关系. 因为材料的不可压缩, m 0 ,又 因为的平面应变 z 0,这样根据简单加载的全量理论有
z
m
2 i 3i
z
m
0
因此得到
z
1 2
r
另外根据筒的受力性质知道 是拉应力, r 是压应力,所以应
r q
2 3
s
ln
r a
q
2 3
s
1
ln
r a
z q
2 3
s
1 2
ln
r a
• 弹性区的应力,可以利用 弹性状态的解令 q qe, a rs
r
srs2
3b2
b2
r
2
1
r
srs2
3b2
b2 r2
1
z
srs2
3b2
• 交界面应力连续得到
q
2 s
3
ln
d 2u dr 2
2 r
du dr
2u r2
0
• 解这个方程得 u Ar Br2 利用边界条件得到
1 2 qa3
21 qa3b3
A
, B
E b3 a3
E b3 a3
最后得到位移解为:
u
q1 1 2 a3
E b3 a3
r3
1
2b3
1 2
可以得到应力分量
r r3
qp
2 s
ln
b a
此时塑性区的应力为
r
2 s
ln
r b
s
1
2
ln
r b
5-2 棒材的拉拔加工
1)问题说明见图
2)假定条件
• 理想弹塑性
•无摩擦,接触面 是主平面
A1
r1
2
A2 o
dr r
r2
• 塑性变形向o点径 向流动,并且稳定.
3)可以看成球壳的一部分,全部进入塑性状态,可以利用上面解 球壳的思路. 平衡方程不变.屈服条件的形式不同, 因为在拉拔ra2 p1 b2 源自a21 b2 r2
,
a2 p1 b2 a2
1
b2 r2
,
z
1 2
r
应力强度为
i
1 2
1 2 2 2 3 2 3 1 2 那么根据Mises屈
服条件得到弹性极
即
i
3 2
r
3b2 q
b2 a2
1 r2
因此可见最大应力强度发生在内壁处.
限压力为:
qe
1
塑性力学05
第五章 球对称和轴对称的弹塑性问题 z
5-1 理想弹塑性材料的厚壁球壳
• 问题的描述与分析
问题: 内径为 a ,外径为 b 球,受 内压力 q ,求弹塑性极限荷载.
r
分析:很显然它的应力和位移
场是球对称的, 采用球坐标.
d
y
应力场:
1 2 0, 3 r 0
d
应变为
情况, r 0, 0 , 屈服条件为 r s 代入平
衡方程得到
d r 2 s 0
dr r
解这个方程得到:
r 2 s ln r C
由进口截面处的边界条件 r |rr1 0 得积分常数为 C 2 s ln r1
解得应力分量为
r
2 s
ln
r1 r
,
s
2
ln
r1 r
1
解中的 a rs , q qe 即可
r
2 srs3
3b3r 3
r3 b3
srs3
3b3r 3
2r3 b3
考虑到在交界面处 r 要连续, 所以得到 q 和 rs 的关系式.
q
2
3
s
3ln
rs a
1
rs3 b3
3. 塑性极限状态. 极限压力为
上式令 rs b , 球壳全部进入塑性得到塑性
4)求解出口截面的拉拔应力为
r
|r r2
2
s
ln
r1 r2
s ln
A1 A2
那么拉拔力为
P
A2
A2
s
ln
A1 A2
5)定义截面减缩率为 R A1 A2 1 A2
A1
A1
可以求得拉拔时最 大减缩率.
因为材料是理想弹塑性, 出口截面处的拉拔应力不能超过屈
服应力,
所以有
s
ln
A1 A2
s
这样得到 A1 e A2
条件 r s ,因此有
d r 2 s 0
dr r
积分得到 r 2 s ln r C
根据边界条件 r |ra q
得到积分常数 C q 2 s ln a
得到塑性区的应力为
r
2 s
ln
r a
q
s 1 2ln
r a
q
弹塑性交界面
q a rs b
塑性区
弹性区
弹性区的应力把前面的弹性
x
1 2 0,3 r 0
显然 1
这就是说,在加载过程中 应力和应变主方向是重合的, 并保持 不变, 那么加载是简单加载, 适用全量理论.
• 球对称问题的平衡方程, 应变连续方程和边界条件
平衡方程为(不考虑体力): d r 2 r 0
dr
r
应变分量为
r
du , dr
qa3 b3 a3
r3 b3
2r3
qa3 b3 a3
2r3 b3
• 求弹性极限压力. 根据球壳的屈服条件(例2-3)即 r s
将上面的应力分量代入屈服条件得
r r3
a3q b3 a3
3b3 2
从上式可以看出在球壳内壁最先屈服, 令 r a 得到弹性
极限压力: