压缩弹簧压力计算公式

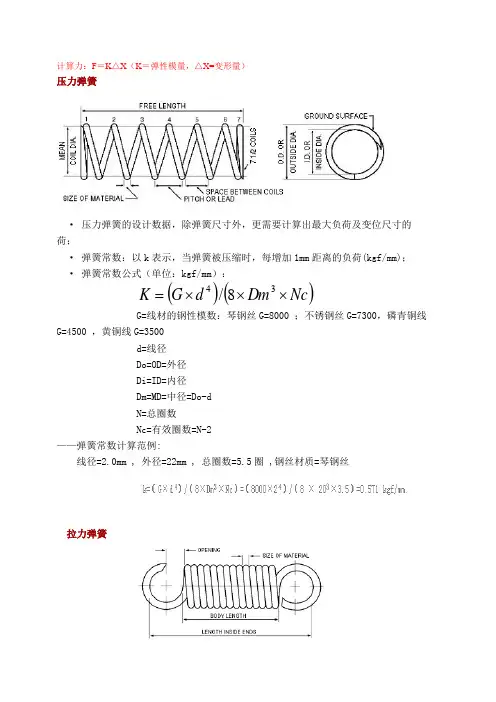
压簧、拉簧、扭簧弹力计算公式压力弹簧压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；·弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；·弹簧常数公式（单位：kgf/mm）：G=线材的钢性模数：琴钢丝G=8000，不锈钢丝G=7300，磷青铜线G=4500 ，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

·初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）·弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm).·弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200 ,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

计算力：F ＝K △X （K ＝弹性模量，△X=变形量）压力弹簧· 压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的荷；· 弹簧常数：以k 表示，当弹簧被压缩时，每增加1mm 距离的负荷(kgf/mm)； · 弹簧常数公式（单位：kgf/mm ）：()()Nc Dm d G K ⨯⨯⨯=348/G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300，磷青铜线G=4500 ，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2——弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

· 初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧· 弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm).· 弹簧常数公式（单位：kgf/mm）:()()R4⨯⨯/=1167⨯K⨯pN⨯DmdEE=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

压缩弹簧的压缩极限基本计算公式
压缩弹簧的压缩极限是指该弹簧所能够承受的最大压力。

超过这个压力弹簧就会变形（失效）可以通过设计计算来确定它的极限力。

或者根据已知的弹簧，来复核它所能够承受的极限压力。

它的计算方法是：
压缩弹簧的基本计算公式
（1）材料直径（mm）
（2）弹簧力（N）
（3）变形量
（mm）
（4）切应力
（Mpa）
（5）试验（极限）负荷（N）
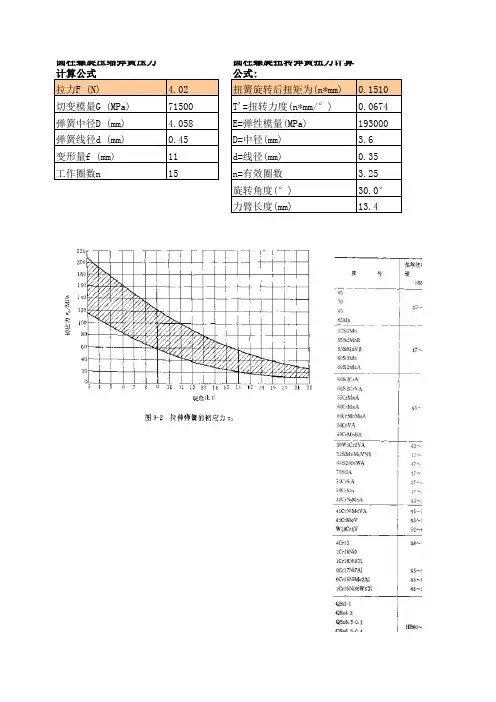
常用螺旋弹簧材料许用应力值[1] （Mpa）
以上信息由玖胜弹簧生产厂家（）整理发布，不排除有错误可能，仅供参考，请谨慎下载，谢谢！！。

压缩弹簧压力计算公式F=k*x其中，F表示弹力，k表示弹簧的弹性系数，x表示弹簧的形变量。

弹簧的弹性系数k是表示弹簧刚度的一个常数，其单位是N/m。

弹性系数的大小与弹簧的刚度成正比。

刚度越大，弹性系数就越大，弹簧变形越小；反之亦然。

形变量x是指弹簧的变形量。

当外力作用于弹簧时，弹簧会因而发生形变，形变量表示弹簧的压缩或伸展的程度。

形变量的单位通常是米。

1.弹簧受力平衡原理当外力作用于弹簧时，弹簧内部各点受到的应力和变形都保持平衡。

根据受力平衡原理，可以得到其中一截面上的外力与内力之间的关系式。

2.应力-应变关系根据胡克定律，应力与应变之间的关系式可以写为：σ=E*ε其中，σ表示应力，E表示弹簧的杨氏模量，ε表示应变。

应力是单位面积上的力，单位是帕斯卡（Pa），表示为N/m²。

杨氏模量是描述固体材料弹性性能的物理量，单位是帕斯卡（Pa）。

应变是单位长度上的变形量，是一个无量纲量。

3.弹簧变形与应变的关系由于弹簧在压缩过程中无法保持完全均匀形变，故无法应用长度不变原理。

我们可以假设弹簧的变形是线弹性的，且弹簧截面积保持不变。

这样，弹簧的应变与形变量之间可以表示为：ε=ΔL/L其中，ΔL表示弹簧的变形量，L表示弹簧的原始长度。

4.弹性系数k的计算根据弹性系数的定义，该值可以表示为应力与应变的比例系数。

由应力-应变关系式，我们可以得到：σ=E*εk*x/A=E*ΔL/Lk=E*A/L其中，A表示弹簧的截面积。

5.弹簧的压力计算将弹性系数k的计算结果代入弹簧的压力计算公式，可以得到：F=k*xF=E*A*ΔL/L以上就是压缩弹簧压力计算公式的推导过程。

根据此公式，我们可以通过测量弹簧的形变量和已知的材料参数，计算出弹簧所产生的压力。

这个公式在设计和选择弹簧系统时非常有用，可以帮助工程师确定所需的弹簧参数，以满足特定的压力需求。

弹簧力值：弹簧力值简单地说就是弹簧的弹力计算。

弹簧力值是指：发生弹性形变的弹簧，会对跟它接触的物体产生力的作用。

这种力叫弹簧弹力。

弹簧力值就是对弹簧弹力的计算。

压缩弹簧力值：它是是承受向压力的螺旋弹簧，它所用的材料截面多为圆形，也有用矩形和多股钢萦卷制的，弹簧一般为等节距的。

压缩弹簧的形状有：圆柱形、圆锥形、中凸形和中凹形以及少量的非圆形等，压缩弹簧的圈与圈之间有一定的间隙，当受到外载荷时弹簧收缩变形，储存变形能。

弹簧力值压缩弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；1.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；2.弹簧常数公式（单位：kgf/mm）：3.G=线材的钢性模数：琴钢丝G=8000；不锈钢丝G=7300，磷青铜线G=4500，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:比如：线径=2.0mm,外径=22mm,总圈数=5.5圈,钢丝材质=琴钢丝拉伸弹簧力值：拉力弹簧简称拉簧。

拉伸弹簧拉力弹簧的k值与压力弹簧的计算公式相同1.拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

2.初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧力值：扭力弹簧1.弹簧常数：以k表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).2.弹簧常数公式（单位：kgf/mm）:E=线材之钢性模数：琴钢丝E=21000,不锈钢丝E=19400,磷青铜线E=11200,黄铜线E=11200 d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

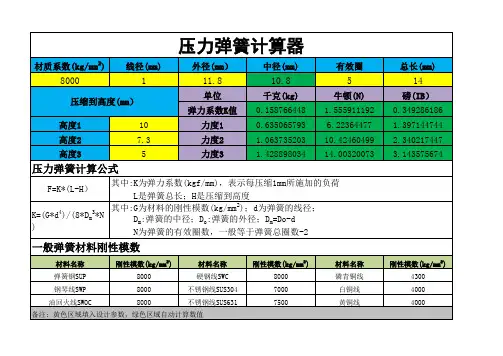
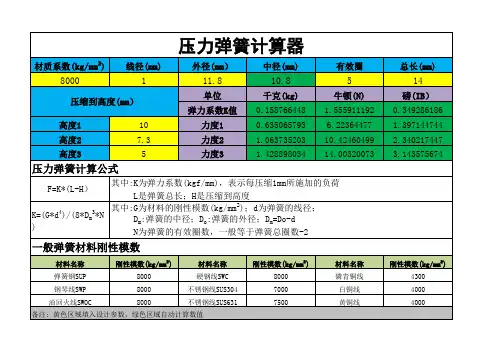
弹簧弹力计算公式标准化管理部编码-[99968T-6889628-J68568-1689N]弹力计算公式压力弹簧初拉力计算F0=〖｛π×d 3｝÷(8×D)〗×79mpaF0=｛×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=圈 ,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×=mm×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000 ，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=。

弹簧压力计算
压缩弹簧压力一般指压缩弹簧的弹力，其计算公式：k=Gd^4/8nD^3，压缩弹簧（压簧）是承受向压力的螺旋弹簧，它所用的材料截面多为圆形，也有用矩形和多股钢萦卷制的，弹簧一般为等节距的。

扩展资料
公式
弹簧常数：以k表示，当弹簧被压缩时，每增加一毫米距离的负荷（kgf/mm）；
弹簧常数公式：k=Gd^4/8nD^3。

进行弹簧压力测试的步骤
1.在对弹簧进行正式的检测之前，先将弹簧压缩一次到实验的荷重，当试验荷重比压并荷重大时，就可以进行压并荷重作为试验荷重，但是压并力最大不能超过定见压并荷重的1.5倍。

2.对荷重检测前的准备：用对应量程的三等规范测力计或者划一以上精度的砝码对荷重试验机进行勘正，确保试验机精密不要低于1%；同时用量块勘正荷重试验机的长度读数误差。

3.弹簧压到指定高度荷重的检测：将与指定高度相同的量块放置在荷重试验机压盘的中央，在量块上加载与图样名义值相近的荷重，然后锁紧定位螺钉或者定位稍，将量块放入待测弹簧，调解零位，去除弹簧自重，将弹簧压至指定高度，并读出相应的'荷重，最后根据标定的荷重试验机误差，对度数进行相应的修改。

4.将上压盘压制弹簧刚解除到的位置，荷重试验机预示值F0≈0.05F;记载荷重试验的初读数地F0以及长度数，然后继续加载，使长度预示的读数变化值达到划定的变形量。

压缩弹簧压力计算公式
压缩弹簧压力通常指弹簧力。

计算公式为k=gd^4/8nd^3。

压缩弹簧（压缩弹簧）是受压的螺旋弹簧。

使用的大多数材料是圆形的，也由矩形钢和多股钢制成。

弹簧通常是等距的。

压缩弹簧压力计算公式
压缩弹簧力公式
公式：k=gd^4/8nd^3
上述公式中的每一项是指：
G=剪切弹性模量[mpa]（G值：碳钢80000，不锈钢72000）
D=钢丝直径[mm，in]
N=有效圈数[-]
D=中心直径[mm，in]
K=弹簧常数[n/mm，lb/in]
该公式用于计算弹簧刚度。

刚度乘以工作行程等于弹簧的工作力。

由上式可知，压缩弹簧的参数必须由材料、线径、中心直径、有效圈数、弹簧总长度、工作高度和所需强度组成。

如果弹簧强度没有特殊要求，则无法提供工作高度和所需力的参数。

什么是灵活性
物体在力的作用下形状或体积的变化称为变形。

外力停止后，能恢复原状的变形称为弹性变形。

变形的物体必须对与其接触的物体施加力，因为它必须回到原来的状态。

这叫做弹性。

也就是说，在弹性极限内，物体所产生的使物体变形的力被称为弹性力。

日常生活中观察到的相互作用，无论是推、拉、举、拉火车、锻造工件、打球、射箭等，都只有在物体与物体接触时才会发生。

这种相互作用可以称为接触力。

接触力按其性质可分为弹性力和摩擦力。

它们基本上是由电磁力引起的。

弹性力就是接触力，弹性力只能存在于物体的接触部位，而相互接触的物体之间不存在弹性效应。

因为弹性不仅需要接触，还需要相互作用。

压力弹簧计算公式压力弹簧是一种用于储存弹性能量并提供稳定力的装置。

它由硬质材料制成，通常用于工业和机械应用中。

在设计和使用压力弹簧时，计算其弹性特性是非常重要的。

本文将介绍压力弹簧的计算公式及其相关概念。

接下来，我们可以利用胡克定律（Hooke's law）来计算压力弹簧的刚度。

根据胡克定律，弹簧恢复的力与其压缩或伸长的距离成正比。

通常用以下公式表示：F=K*x其中，F是弹簧恢复的力，K是弹簧的刚度，x是压缩或伸长的距离。

在计算压力弹簧的弹性特性时，我们通常会考虑材料的弹性模量（elastic modulus）和截面形状。

压力弹簧的截面形状可以是圆形、方形或其他形状，因此我们需要根据实际情况选择适当的公式。

在研究圆形截面的弹簧时，我们可以利用以下公式来计算刚度K：K=(G*d^4)/(8*D^3*n)其中，K是弹簧的刚度，G是材料的剪切模量，d是弹簧的线径，D是弹簧的外径，n是绕制圈数。

当研究方形截面的弹簧时，我们可以利用以下公式来计算刚度K：K=(G*b*h^3)/(12*L)其中，K是弹簧的刚度，G是材料的剪切模量，b是弹簧的边宽，h是弹簧的边高，L是弹簧的长度。

计算初始压缩量Lo时，我们可以利用以下公式：Lo=n*h其中，Lo是初始压缩量，n是绕制圈数，h是弹簧的边高。

需要注意的是，以上计算公式仅适用于理想的理论计算。

在实际应用中，还需要考虑材料的非线性特性、压缩或伸长的极限以及边界条件等因素。

综上所述，压力弹簧的计算公式涉及到刚度和初始压缩量的计算。

这些公式可以帮助工程师和设计师在设计和使用压力弹簧时更好地了解其弹性特性，并进行相应的优化和调整。

但需要注意的是，在实际应用中，还需考虑其他因素的影响，以确保弹簧的性能和可靠性。

胡克的弹性定律指出：在弹性限度内，弹簧的弹力f和弹簧的长度x成正比，即f=-kx，k是物质的弹性系数，它由材料的性质所决定，负号表示弹簧所产生的弹力与其伸长（或压缩）的方向相反。

压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；弹簧常数公式（单位：kgf/mm）：K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300；磷青铜线G=4500 ；黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝K=(G×ｄ４)／（８×Ｄｍ３×Ｎｃ）＝（８０００×２４）／（８×２０３×３．５）＝０．５７１ｋｇｆ／ｍｍ拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同。

拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).弹簧常数公式（单位：kgf/mm）: K=(Ｅ×ｄ４)／（１１６７×Ｄｍ×ｐ×Ｎ×Ｒ）E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

压缩弹簧压力通常指弹簧力。

计算公式为k=gd^4/8nd^3。

压缩弹簧（压缩弹簧）是受压的螺旋弹簧。

使用的大多数材料是圆形的，也由矩形钢和多股钢制成。

弹簧通常是等距的。

压缩弹簧压力计算公式
压缩弹簧力公式
公式：k=gd^4/8nd^3
上述公式中的每一项是指：
G=剪切弹性模量[mpa]（G值：碳钢80000，不锈钢72000）
D=钢丝直径[mm，in]
N=有效圈数[-]
D=中心直径[mm，in]
K=弹簧常数[n/mm，lb/in]
该公式用于计算弹簧刚度。

刚度乘以工作行程等于弹簧的工作力。

由上式可知，压缩弹簧的参数必须由材料、线径、中心直径、有效圈数、弹簧总长度、工作高度和所需强度组成。

如果弹簧强度没有特殊要求，则无法提供工作高度和所需力的参数。

什么是灵活性
物体在力的作用下形状或体积的变化称为变形。

外力停止后，能恢复原状的变形称为弹性变形。

变形的物体必须对与其接触的物体施加力，因为它必须回到原来的状态。

这叫做弹性。

也就是说，在弹性极限内，物体所产生的使物体变形的力被称为弹性力。

日常生活中观察到的相互作用，无论是推、拉、举、拉火车、锻造工件、打球、射箭等，都只有在物体与物体接触时才会发生。

这种相互作用可以称为接触力。

接触力按其性质可分为弹性力和摩擦力。

它们基本上是由电磁力引起的。

弹性力就是接触力，弹性力只能存在于物体的接触部位，而相互接触的物体之间不存在弹性效应。

因为弹性不仅需要接触，还需要相互作用。