曲线运动第二讲平抛运动

第二讲：平抛运动一、平抛运动1．定义：将物体以一定的初速度沿水平方向抛出，物体只在重力作用下的运动．2．性质：平抛运动是加速度为g 的匀变速曲线运动，运动轨迹是抛物线．3．研究方法：运动的合成与分解 (1)水平方向：匀速直线运动； (2)竖直方向：自由落体运动． 4.基本规律如图，以抛出点O 为坐标原点，以初速度v 0方向(水平方向)为x 轴正方向，竖直向下为y 轴正方向．(1)位移关系(2)速度关系(3)轨迹方程：h =g2v 02x 25.基本应用例题、如图所示，x 轴在水平地面上，y 轴在竖直方向．图中画出了从y 轴上沿x 轴正方向水平抛出的三个小球a 、b 和c 的运动轨迹．不计空气阻力，下列说法正确的是( )A ．a 和b 的初速度大小之比为2∶1B ．a 和b 在空中运动的时间之比为(1)飞行时间由t ＝2hg知，时间取决于下落高度h ，与初速度v 0无关．(2)水平射程x ＝v 0t ＝v 02hg，即水平射程由初速度v 0和下落高度h 共同决定，与其他因素无关． (3)落地速度v ＝v x 2＋v y 2＝v 02＋2gh ，以θ表示落地速度与水平正方向的夹角，有tan θ＝v y v x＝2ghv 0，落地速度与初速度v 0和下落高度h 有关． (4)速度改变量因为平抛运动的加速度为恒定的重力加速度g ，所以做平抛运动的物体在任意相等时间间隔Δt 内的速度改变量Δv ＝g Δt 是相同的，方向恒为竖直向下，如图所示．(5)两个重要推论①做平抛运动的物体在任意时刻的瞬时速度的反向延长线一例题、如图甲所示是网球发球机，某次室内训练时将发球机放在距地面一定的高度，然后向竖直墙面发射网球.假定网球均水平射出，某两次射出的网球碰到墙面时速度与水平方向夹角分别为30°和60°，若不考虑空气阻力，则( )A.两次发射的初速度大小之比为3∶1定通过此时水平位移的中点，如图所示，即x B ＝x A2.推导：⎭⎪⎬⎪⎫tan θ＝y Ax A －x Btan θ＝v yv 0＝2y Ax A→x B＝x A2①做平抛运动的物体在任意时刻任意位置处，有tan θ＝2tan α. 推导：⎭⎪⎬⎪⎫tan θ＝v y v 0＝gtv 0tan α＝y x ＝gt 2v 0→tan θ＝2tan α二、与斜面结合的平抛运动1．顺着斜面平抛(如图)方法：分解位移．x ＝v 0t ，y ＝12gt 2，tan θ＝y x，可求得t ＝2v 0tan θg.2．对着斜面平抛(垂直打到斜面，如图) 方法：分解速度．v x ＝v 0， v y ＝gt ，tan θ＝v x v y ＝v 0gt，可求得t ＝v 0g tan θ.三、斜抛运动1．定义：将物体以初速度v 0斜向上方或斜向下方抛出，物体只在重力作用下的运动．2．性质：斜抛运动是加速度为g 的匀变速曲线运动，运动轨迹是抛物线．3．研究方法：运动的合成与分解(1)水平方向：匀速直线运动；(2)竖直方向：匀变速直线运动．例题、某同学在练习投篮时将篮球从同一位置斜向上抛出，其中有两次篮球垂直撞在竖直放置的篮板上，运动轨迹如图所示，不计空气阻力，关于这两次篮球从抛出到撞击篮板的过程( )4.基本规律(以斜上抛运动为例，如图所示)(1)水平方向：v 0x ＝v 0cos θ，F 合x ＝0；做匀速直线运动，v 0x ＝v 0cos θ，x ＝v 0tcos θ. (2)竖直方向：v 0y ＝v 0sin θ，F 合y ＝mg .做竖直上抛运动，v 0y ＝v 0sin θ，y ＝v 0tsin θ－12gt2四、类平抛运动1．类平抛运动物体受到与初速度垂直的恒定的合外力作用时，其轨迹与平抛运动相似，称为类平抛运动．类平抛运动的受力特点是物体所受合力为恒力，且与初速度的方向垂直．2.类平抛运动问题的求解技巧(1)常规分解法：将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力方向)的匀加速直线运动，两分运动彼此独立，互不影响，且与合运动具有等时性．(2)特殊分解法：对于有些问题，可以过抛出点建立适当的直角坐标系，将加速度a 分解为a x 、a y ，初速度v 0分解为v x 、v y ，然后分别在x 、y 方向上列方程求解．针对训练题型1：平抛运动性质例题、如图所示的光滑斜面ABCD 是边长为l 的正方形，倾角为30°，一物块（视为质点）沿斜面左上方顶点A 以平行于AB 边的初速度v 0水平射入，到达底边CD 中点E ，则（ ）A ．初速度2glB ．初速度4glC ．物块由A 点运动到E 点所用的时间2lt g= D ．物块由A 点运动到E 点所用的时间lt g=1．关于平抛运动的性质，以下说法中正确的是（）A．变加速运动B．匀变速运动C．匀速率曲线运动D．不可能是两个直线运动的合运动2．人站在平台上平抛一小球，球离手时的速度为v1，落地时速度为v2，不计空气阻力，下列图中能表示出速度矢量的演变过程的是（）A．B．C．D．题型2：平抛运动规律3．如图所示，从A、B、C三个不同的位置向右分别以v A、v B、v C的水平初速度抛出三个小球A、B、C，其中A、B在同一竖直线上，B、C在同一水平线上，三个小球均同时落在地面上的D点，不计空气阻力。

第二讲 运动学(曲线运动)1、曲线运动的基本知识轨迹为曲线的运动叫曲线运动。

它一定是一个变速运动。

图2-3-1表示一质点作曲线运动，它经过P 点时，在P 点两旁的轨迹上取11b a 、两点，过11b P a 、、三点可作一圆，当这两点无限趋近于P 点时，则圆亦趋近于一个定圆，我们把这个圆叫P 点的曲率圆，曲率圆的半径叫P 点的曲率半径，曲率圆的圆心叫P 点的曲率中心，曲率半径的倒数叫P 点的曲率。

如图2-3-1，亦可做出Q 点的曲率圆。

曲率半径大，曲率小，表示曲线弯曲较缓，曲率半径小，曲率大，表示曲线弯曲厉害。

直线可认为是曲率半径为无穷大的曲线。

质点做曲线运动的瞬时速度的方向总是沿该点的切线方向。

如图2-3-2所示，质点在△t 时间内沿曲线由A 点运动到B 点，速度由V A 变化到V B ，则其速度增量V ∆为两者之矢量差，V ∆=V B ―V A ，这个速度增量又可分解成两个分量：在V B 上取一段AC 等于V A ，则△V 分解成△V 1和△V 2，其中△V 1表示质点由A运动到B 的速度方向上的增量，△V 2表示速度大小上的增量。

其方向指向A 点的曲率中心。

切向加速度τa 表示质点作曲线运动时速度大小改变的快慢，方向亦沿切线方向，其大小为:tV a t X ∆∆=→∆20lim法向加速度a n 表示质点作曲线运动时速度方向改变的快慢，其大小为在A 点的曲率圆的向心加速度：AA t n R V t V a 210lim =∆∆=→∆ 总加速度a 方法向加速度和切向加速度的矢量和。

2、抛物运动抛体运动是曲线运动。

由于质点在运动中加速度始终为方向竖直向下的重力加速度g ，因此，抛体运动是匀变速曲线运动。

又因为抛体运动中抛射物始终运动在初速度与重力加速度所决定的平面内，所以抛体运动是一个平面运动。

运动方程很容易由方程类似给出：其中r 0、v 0分别为质点在刚抛出(t ＝0)时的位矢和速度。

若把抛出点作为坐标原点，则r 0＝0。

第2讲平抛运动【教学目标】1．知道平抛运动的定义以及条件，知道其运动轨迹是抛物线；2．理解平抛运动是加速度为g的匀变速曲线运动；3．熟练掌握平抛运动的规律，学会用平抛运动的规律解决实际问题的方法；4．理解平抛运动可以看作水平方向的匀速直线运动与竖直方向的自由落体运动的合运动，并且这两个运动互不影响．【重、难点】1．平抛运动的特点和规律；2．对平抛运动的两个分运动的理解和运用．如图所示，沿水平方向扔出一块橡皮，或者将一个小球从水平桌面以一定的初速度推离边沿，可以看到它们做曲线运动的轨迹是相似的．本节课我们来学习这一类常见曲线运动的规律．知识点睛一、平抛运动1．定义：将物体以一定的初速度沿水平方向抛出，仅在重力作用下物体所做的运动称为平抛运动．2．由于平抛运动只受重力作用，加速度为g，故平抛运动是匀变速曲线运动．二、平抛运动的研究方法由于平抛运动是匀变速曲线运动，速度、位移的方向时刻发生变化，无法直接应用运动学公式，因此研究平抛运动问题时采用运动分解的方法．那么平抛运动可以看成哪两个分运动的合成呢？做平抛运动的物体，在水平方向上由于不受力，将做匀速直线运动；在竖直方向上物体的初速度为零，且只受到重力作用，物体做自由落体运动，加速度等于g．平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动．以上是从理论角度去分析得到的结论，我们能否通过实验来验证我们的结论呢？实验探究平抛运动的特点（1）研究平抛运动水平方向分运动的特点①使电磁铁C 和D 分别相对各自轨道出口水平线处于相同高度．把两个钢球分别吸在电磁铁C 、D 上．切断电源，使两个钢球以相同的初速度同时水平射出．②改变电磁铁C 、D 与各自轨道出口水平线的相对高度，并确保高度相等． ③多次重复以上步骤．观察实验现象，并分析平抛运动水平方向分运动的特点． （2）研究平抛运动竖直方向分运动的特点①把两个钢球分别吸在电磁铁C 、E 上，并确保电磁铁E 上的钢球与轨道A 出口处于同一高度，释放轨道A 的钢球．钢球在水平出口处碰撞开关S ，切断电磁铁E 的电源，使钢球从电磁铁E 处释放． ②改变电磁铁E 的位置，让其从N 向M 移动．③多次重复以上步骤．观察实验现象，并分析平抛运动竖直方向分运动的特点．（3）结论：平抛运动在水平方向的分运动是匀速直线运动，在竖直方向的分运动是自由落体运动． 三、平抛运动的规律如图所示，以抛出点O 为坐标原点，水平方向为x 轴（正方向与初速度v 0方向相同），以竖直方向为y 轴（正方向向下），经时间t 做平抛运动的质点到达P 位置，速度为v ．1．平抛运动的位置坐标与位移（1）位置坐标⎩⎪⎨⎪⎧x ＝v 0t y ＝12gt 2 （2）位移大小s ＝x 2＋y 2＝v 20t 2＋14g 2t 4（3）位移方向tan α＝y x ＝gt2v 0，其中α为位移与x 轴的夹角2．平抛运动的速度（1）水平分速度v x ＝v 0 （2）竖直分速度v y ＝gt （3）合速度大小v ＝v 20＋v 2y ＝v 20＋g 2t 2（4）合速度方向tan θ＝v y v x ＝gtv 0，其中θ为合速度与水平方向的夹角3．平抛运动的轨迹由x ＝v 0t 与y ＝12gt 2可得y ＝g2v 20x 2．因此，平抛运动的轨迹是一条抛物线．考点一 对平抛运动的理解1．物体做平抛运动的条件物体的初速度v 0沿水平方向，只受重力作用，两个条件缺一不可． 2．平抛运动的性质：加速度为g 的匀变速曲线运动． 3．平抛运动的三个特点（1）理想化特点：平抛运动是一种理想化的模型，即把物体看成质点，抛出后只考虑重力作用，忽略空气阻力．（2）匀变速特点：平抛运动的加速度恒定，即始终等于重力加速度．（3）速度变化特点：任意两个相等的时间间隔内速度的变化相同，Δv ＝g Δt ，方向竖直向下，如图所示．例1．（多选）在空气阻力可忽略的情况下，下列物体的运动可视为平抛运动的是（ ） A ．沿水平方向扣出的排球 B ．沿斜向上方投出的篮球 C ．沿水平方向抛出的小石子 D ．沿竖直方向向上抛出的橡皮 例2．（多选）关于平抛运动，下列说法中正确的是（ ） A ．平抛运动是一种非匀变速曲线运动 B ．平抛运动是一种匀变速曲线运动 C ．平抛运动的速度，加速度都在变化D ．平抛运动中某时刻的速度方向为轨迹切线方向例3．从高空水平方向匀速飞行的飞机上，每隔1分钟投一包货物，空气阻力忽略不计，则空中下落的许多包货物和飞机的连线是（ ） A ．倾斜直线 B ．竖直直线 C ．平滑曲线 D ．抛物线典例精析考点二 平抛运动中运动参量的决定因素 物体从离地高为h 处以初速度v 0水平抛出，则 1．由h ＝12gt 2，得落地时间t =2hg，故平抛运动的时间仅由下落高度h 决定，跟其他因素无关； 2．落地时的水平位移x= v 0t = v 02hg，故水平位移由初速度v 0和下落高度h 共同决定； 3．v y ＝gt =2gh ，落地时的速度v ＝v 20＋v 2y =v 20＋2gh ，故落地时的速度由初速度v 0和下落高度h共同决定．例4．（多选）如图所示，滑板运动员以速度v 0从离地高度为h 的平台末端水平飞出，落在水平地面上．忽略空气阻力，运动员和滑板可视为质点，下列表述正确的是（ ）A ．v 0越大，运动员在空中运动时间越长B ．v 0越大，运动员落地瞬间速度越大C ．运动员落地瞬间速度与高度h 有关D ．运动员落地位置与v 0大小无关变式1、做平抛运动的物体，在水平方向通过的最大距离取决于（ ） A ．物体的高度和受到的重力 B ．物体受到的重力和初速度 C ．物体受到的重力、高度和初速度 D ．物体的高度和初速度 考点三 平抛运动的规律应用例5．一架老式飞机在高出地面h =2km 的高度，以v 0=3.6×102km/h 的速度水平飞行，为了使飞机上投下的炸弹落在指定的目标上，应该在与轰炸目标的水平距离为多远的地方投弹？g 取10m/s 2，不计空气阻力．变式2、如图所示，飞机离地面高度为H＝500m，水平匀速飞行，速度为v1＝100m/s，追击一辆速度为v2＝20m/s同向行驶的汽车，欲使炸弹击中汽车，飞机应在距离汽车的水平距离多远处投弹？（飞机和汽车均视为质点，不计空气阻力，重力加速度g=10m/s2）变式3、如图所示，在距地面高为H＝45 m处，有一小球A以初速度v0＝10 m/s水平抛出．与此同时，在A的正下方有一物块B也以相同的初速度v0同方向滑出，B与地面间的动摩擦因数μ＝0.5，A、B均可看成质点，空气阻力不计．求：（1）A球从抛出到落地的时间；（2）A球从抛出到落地这段时间内的水平位移；（3）A球落地时，A、B之间的距离．例6．一小球水平抛出时的速度大小为10m/s，落地时的速度大小为20m/s，g取10m/s2．求：（1）在空中的飞行时间t；（2）小球抛出时的高度h；（3）水平位移x．变式4、（多选）以v0的速度水平抛出一个物体，当其竖直分位移与水平分位移相等时，则（）A．运动的时间为gv0B．竖直分速度等于水平分速度C．瞬时速度为5v0D．运动的位移是gv2222变式5、（多选）在距离水平地面高为h 处，将一物体以初速度v 0水平抛出（不计空气阻力），落地时速度为v 1，竖直分速度为v y ，落地点与抛出点的水平距离为s ，则能用来计算该物体在空中运动时间的式子有（ ）A ．v 21－v 2gB ．2h g C ．2hv y D ．sv 1例7．如图所示，斜面上a 、b 、c 三点等距，小球从a 点正上方O 点抛出，做初速度为v 0的平抛运动，恰好落在b 点．若小球初速度变为v ，其落点位于c ，则（）A ．v 0＜v ＜2v 0B ．v ＝2v 0C ．2v 0＜v ＜3v 0D ．v ＞3v 0例8．在水平地面上方某一高度处沿水平方向抛出一个小物体，抛出t 1＝1s 后物体的速度方向与水平方向的夹角为45°，落地时物体的速度方向与水平方向的夹角为60°，重力加速度g 取10 m/s 2．求： （1）物体平抛时的初速度v 0； （2）抛出点距离地面的竖直高度h ； （3）物体从抛出点到落地点的水平位移x ．变式6、如图所示，由倾角为θ的斜面顶端A 处水平抛出一钢球，落到斜面底端B 处，斜面长为L ，重力加速度为g ．求抛出时的初速度．研究平抛运动的一般思路1．把平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动；2．分别运用两个分运动的运动规律去求分速度、分位移等，再合成得到平抛运动的速度、位移等．这种处理问题的方法可以变曲线运动为直线运动，变复杂运动为简单运动，使问题的解决过程得到简化．考点四 两类与斜面结合的平抛运动 1．模型构建（1）物体从斜面上某一点水平抛出以后又重新落在斜面上，此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角；（2）做平抛运动的物体垂直打在斜面上，此时物体的合速度与竖直方向的夹角等于斜面的倾角．2．求解思路例9．如图所示，斜面倾角为θ=30°，小球从斜面上的P 点以初速度v 0水平抛出，恰好落到斜面上的Q 点．重力加速度为g ．求：（1）小球从P 到Q 运动的时间；（2）PQ 的长度．例10．如图所示，以10m/s 的水平速度抛出的物体，飞行一段时间后垂直撞在倾角为θ＝30°的斜面上，空气阻力不计，g 取10m/s 2，物体飞行的时间和物体撞在斜面上的速度的大小分别为（ ）A ．3s ，20 m/sB ．3s ，15 m/sC ．3s ，15 m/sD ．3s ，20 m/s变式7、一水平抛出的小球落到一倾角为θ的斜面上时，其速度方向与斜面垂直，运动轨迹如图中虚线所示．小球在竖直方向下落的距离与在水平方向通过的距离之比为（ ）A ．tan θB ．2tan θC ．1tan θD ．12tan θ考点五 多个物体的平抛问题例11．如图所示，在同一竖直面内，小球a 、b 从高度不同的两点，分别以初速度v a 和v b 沿水平方向抛出，经过时间t a 和t b 后落到与两抛出点水平距离相等的P 点．若不计空气阻力，下列关系式正确的是（ ）A ．t a >t b ，v a <v bB ．t a >t b ，v a >v bC ．t a <t b ，v a <v bD ．t a <t b ，v a >v b 变式8、（多选）如图所示，在同一竖直平面内，距地面不同高度的地方，以不同的水平速度同时抛出两个小球．则两球（ ）A ．一定不能在空中相遇B ．抛出到落地的水平距离有可能相等C ．落地时间可能相等D ．抛出到落地的水平距离一定不相等考点六 平抛运动的两个推论a1．推论一：某时刻速度、位移与初速度方向的夹角α、θ的关系为tan α＝2tan θ2．推论二：平抛运动的物体在任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点 例12．如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上，物体与斜面接触时速度与水平方向的夹角φ满足（ ）A ．tan φ＝sin θB ．tan φ＝cos θC ．tan φ＝tan θD ．tan φ＝2tan θ变式9、如图所示，从倾角为θ的足够长的斜面上的A 点，先后将同一小球以不同的初速度水平向右抛出．第一次初速度为v 1，球落到斜面上的瞬时速度方向与斜面夹角为α1，第二次初速度为v 2，球落到斜面上的瞬时速度方向与斜面夹角为α2，则（ ）A ．当v 1>v 2时，α1>α2B ．当v 1>v 2时，α1<α2C ．α1、α2的关系与斜面倾角θ有关D ．无论v 1、v 2关系如何，均有α1＝α2变式10、在一斜面顶端，将甲、乙两个小球分别以v 和v2的速度沿同一方向水平抛出，两球都落在该斜面上．甲球落至斜面时的速率是乙球落至斜面时速率的（ ） A ．2倍 B ．4倍 C ．6倍 D ．8倍 考点七 平抛运动中的临界极值问题 1．特点（1）若题目中有“刚好”“恰好”“正好”等字眼，表明题述过程中存在临界点；（2）若题目中有“最大”“最小”“至多”“至少”“取值范围”等字眼，表明题述的过程中存在着极值，这些极值点也往往是临界点． 2．求解思路（1）画出临界轨迹，找出临界状态对应的临界条件； （2）分解速度或位移； （3）列方程求解结果．例13．如图所示，水平屋顶高H＝5m，围墙高h＝3.2 m，围墙到房子的水平距离L＝3m，围墙外马路宽x＝10m，为使小球从屋顶水平飞出落在围墙外的马路上，求小球离开屋顶时的速度v的大小范围．（g取10 m/s2）变式11、一阶梯如图所示，其中每级台阶的高度和宽度都是0.4m．一小球以水平速度v飞出，g取10 m/s2，欲打在第四级台阶上，则v的取值范围是（）A． 6 m/s <v≤2 2 m/s B．2 2 m/s <v≤3.5 m/sC． 2 m/s<v< 6 m/s D．2 2 m/s<v< 6 m/s【能力展示】【小试牛刀】1．做平抛运动的物体，每秒的速度增量总是（）A．大小相等，方向相同B．大小不等，方向不同C．大小相等，方向不同D．大小不等，方向相同2．在空中将一个小球水平抛出，不计空气阻力作用，则下列说法正确的是（）A．不论抛出速度多大，抛出位置越高，飞得一定越远B．不论抛出速度多大，抛出位置越高，其飞行时间一定越长C．不论抛出位置多高，抛出速度越大的物体，其飞行时间一定越长D．不论抛出位置多高，抛出速度越大的物体，其水平位移一定越大3．从同一点O 抛出三个物体A 、B 、C ，做平抛运动的轨迹如图所示，则三个物体做平抛运动对应的初速度v A 、v B 、v C 的关系和三个物体做平抛运动对应的时间t A 、t B 、t C 的关系分别是（ ）A ．v A >vB >vC t A >t B >t C B ．v A =v B =v C t A =t B =t CC ．v A <v B <v C t A >t B >t CD ．v A >v B >v C t A <t B <t C4．（多选）在高度为h 的同一位置上向水平方向同时抛出两个小球甲和乙，若抛出时甲球的初速度大于乙球的初速度，则下列说法正确的是（ ）A ．甲球落地时间小于乙球落地时间B ．在空中飞行的任意时刻，甲球的速度总大于乙球的速度C ．在飞行过程中的任一段时间内，甲球的水平位移总是大于乙球的水平位移D ．若两球在飞行中遇到一堵竖直的墙，甲球击中墙的高度总是大于乙球击中墙的高度5．（多选）如图所示，在网球的网前截击练习中，若练习者在球网正上方距地面H 处，将球以初速度v 沿垂直球网的方向击出，球刚好落在底线上，已知底线到网的距离为L ，重力加速度取g ，将球的运动视作平抛运动，下列表述正确的是（ ）A ．球的初速度v 等于L g 2HB ．球从击出至落地所用时间为2H g C ．球从击球点至落地点的位移等于LD ．球从击球点至落地点的位移与球的质量有关6．一个物体从某一确定高度以v 0的初速度水平抛出，已知它落地时的速度为v ，那么它的运动时间是（ ）A ．v －v 0gB ．v ＋v 0gC ．v 2－v 20gD ．v 2＋v 20gA OBC7．物体做平抛运动时，它的速度方向和水平方向间的夹角θ的正切tan θ随时间t 变化的图象是图中的（ ）8．如图所示，斜面上有a 、b 、c 、d 四个点，ab =bc =cd ．从a 点正上方的O 点以速度v 水平抛出一个小球，它落在斜面上b 点．若小球从O 点以速度2v 水平抛出，不计空气阻力，则它落在斜面上的（ ）A ．c 点B ．b 与c 之间某一点C ．d 点D ．c 与d 之间某一点9．战斗机在某一高度匀速飞行，发现目标后在离目标水平距离为s 处投弹，可以准确命中目标，现战斗机飞行高度减半，速度大小减为原来的23，要仍能命中目标，则战斗机投弹时到目标的水平距离应为（不考虑空气阻力）（ ）A ．13sB ．23sC ．23sD ．223s 10．平抛物体的运动规律可以概括为两点：（1）水平方向做匀速运动；（2）竖直方向做自由落体运动．为了研究平抛物体的运动，可做下面的实验：如图所示，用小锤打击弹性金属片，A 球就水平飞出，同时B 球被松开，做自由落体运动，两球同时落到地面，这个实验 （ ）A ．只能说明上述规律中的第（1）条B ．只能说明上述规律中的第（2）条C ．不能说明上述规律中的任何一条D ．能同时说明上述两条规律tA B tC tD t11．如图所示，以v0＝10 m/s 的水平初速度抛出的物体，飞行一段时间后，垂直地撞在倾角θ为45°的斜面上(g取10 m/s2)，可知物体完成这段飞行的时间是（）3s B． 3 s C．1 s D．2 s 12．（多选）刀削面是同学们喜欢的面食之一，因其风味独特，驰名中外．刀削面全凭刀削，因此得名．如图所示，将一锅水烧开，拿一块面团放在锅旁边较高处，用一刀片飞快地削下一片片很薄的面片儿，面片便飞向锅里，若面团到锅的上沿的竖直距离为0.8 m，最近的水平距离为0.5 m，锅的半径为0.5 m．要想使削出的面片落入锅中，则面片的水平速度可以是下列选项中的（g＝10 m/s2）（）A．1 m/s B．2 m/s C．3 m/s D．4 m/s 【大显身手】13．（多选）甲、乙、丙三个小球分别位于如图所示的竖直平面内，甲、乙在同一条竖直线上，甲、丙在同一条水平线上，水平面上的P点在丙的正下方，在同一时刻甲、乙、丙开始运动，甲以初速度v0做平抛运动，乙以水平速度v0沿光滑水平面向右做匀速直线运动，丙做自由落体运动，则（）A．若甲、乙、丙三球同时相遇，则一定发生在P点B．若甲、丙两球在空中相遇，此时乙球一定在P点C．若只有甲、乙两球在水平面上相遇，此时丙球还未着地D．无论初速度v0大小如何，甲、乙、丙三球一定会同时在P点相遇14．（多选）枪管AB对准小球C，A、B、C在同一水平面上，如图所示，枪管和小球距地面的高度为45m．已知BC＝100m，当子弹射出枪口时，C球开始自由下落，若子弹射出枪口时的速度v0＝50 m/s，子弹恰好能在C下落20m时击中它．现其他条件不变，只改变子弹射出枪口时的速度v0，不计空气阻力，g取10 m/s2．则（）A．v0＝60 m/s时，子弹能击中小球B．v0＝40 m/s时，子弹能击中小球C．v0＝30 m/s时，子弹能击中小球D．以上的三个v0值，子弹可能都不能击中小球15．如图所示，一架在2 000 m高空以200 m/s的速度水平匀速飞行的轰炸机，要用两枚炸弹分别炸山脚和山顶的目标点A、B．已知山高720 m，山脚与山顶的水平距离为1 000 m，若不计空气阻力，g取10 m/s2，则投弹的时间间隔应为（）A．4 s B．5 s C．9 s D．16 s 16．如图所示，相对的两个斜面，倾角分别为37°和53°，在顶点把两个小球A、B以同样大小的初速度分别向左、向右水平抛出，两个小球最终都落在斜面上．若不计空气阻力，sin 37°＝0.6，cos 37°＝0.8，sin 53°＝0.8，cos 53°＝0.6，则该过程中A、B两个小球运动时间之比为（）A．1∶1 B．4∶3 C．16∶9 D．9∶16 17．如图所示，在距地面2l高空A处以水平初速度v0＝gl投掷飞镖，在与A点水平距离为l的水平地面上的B点有一个气球，选择适当时机让气球以速度v0＝gl匀速上升，在升空过程中被飞镖击中．飞镖在飞行过程中受到的空气阻力不计，在计算过程中可将飞镖和气球视为质点，已知重力加速度为g．试求：（1）飞镖是以多大的速度击中气球的？（2）掷飞镖和放气球两个动作之间的时间间隔Δt应为多少？18．如图所示，女排比赛时，排球场总长为18 m，设球网高为2 m，运动员站在网前3 m处正对球网跳起将球水平击出．若击球的高度为2.5 m，为使球既不触网又不越界，求球的速度范围．（不计空气阻力，g取10 m/s2）第2讲 平抛运动答案例1．AC 例2．BD 例3．B 例4．BC 变式1、D例5．2000m 变式2、800m 变式3、（1）3 s （2）30 m （3）20 m 例6．（1） 3 s （2）15m （3）10 3 m 变式4、CD 变式5、ABC例7．A 例8．（1）10 m/s 2）15 m 3）10 3 m 变式6、cos θgL 2sin θ例9．（1）gv 3320（2）g v 3420 例10．A 变式7、D 例11．A 变式8、AB 例12．D 变式9、D 变式10、A 例13．5 m/s≤v ≤13 m/s 变式11、A【能力展示】1．A 2．B 3．C 4．BCD 5．AB 6．C 7．C 8．B 9．C 10．B11．C 12．BC 13．AB 14．AB 15．C 16．D17．答案：（1）2gl （2）12l g解析：（1）飞镖A 被投掷后做平抛运动．从掷出飞镖到击中气球，经过时间t 1＝l v 0＝l g 此时飞镖在竖直方向上的分速度v y ＝gt 1＝gl故此时飞镖的速度大小v ＝v 20＋v 2y ＝2gl （2）飞镖从掷出到击中气球过程中下降的高度h 1＝12gt 21＝l 2气球从被释放到被击中过程中上升的高度h 2＝2l －h 1＝3l 2气球的上升时间t 2＝h 2v 0＝3l 2v 0＝32l g可见，t 2>t 1，所以应先释放气球．释放气球与掷飞镖之间的时间间隔Δt ＝t 2－t 1＝12l g18．310 m/s<v 0≤122m/s。

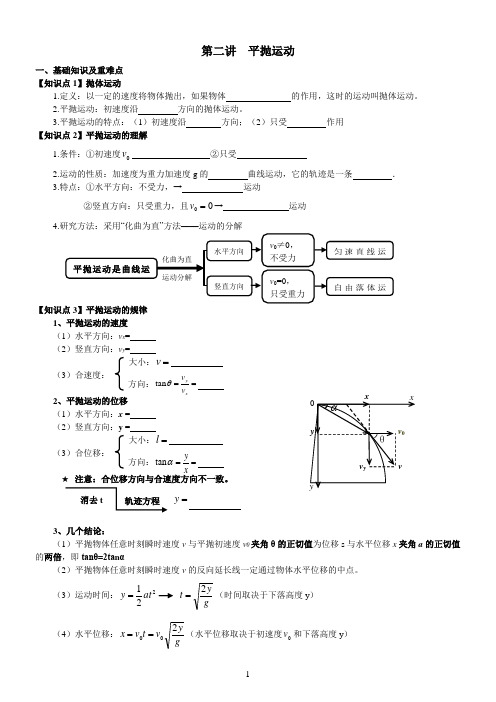
第二讲 平抛运动一、基础知识及重难点 【知识点1】抛体运动1.定义：以一定的速度将物体抛出，如果物体 的作用，这时的运动叫抛体运动。

2.平抛运动：初速度沿 方向的抛体运动。

3.平抛运动的特点：（1）初速度沿 方向；（2）只受 作用 【知识点2】平抛运动的理解1.条件：①初速度0v ②只受2.运动的性质：加速度为重力加速度g 的 曲线运动，它的轨迹是一条 ．3.特点：①水平方向：不受力，→ 运动②竖直方向：只受重力，且00=v → 运动 4.研究方法：采用“化曲为直”方法——运动的分解【知识点3】平抛运动的规律1、平抛运动的速度（1）水平方向：v x = （2）竖直方向：v y = （3）合速度： 2、平抛运动的位移（1）水平方向：x = （2）竖直方向：y = （3）合位移： ★ 注意：合位移方向与合速度方向不一致。

3、几个结论：（1）平抛物体任意时刻瞬时速度v 与平抛初速度v 0夹角θ的正切值为位移s 与水平位移x 夹角a 的正切值的两倍，即tanθ=2ta n α（2）平抛物体任意时刻瞬时速度v 的反向延长线一定通过物体水平位移的中点。

（3）运动时间：221at y =gy t 2=（时间取决于下落高度y ） （4）水平位移：gyv t v x 200==（水平位移取决于初速度0v 和下落高度y ） 大小：=v 方向： ==xyv v θtan 大小：=l 方向： ==xyαtan 消去t 轨迹方程 =y（5）落地速度：gy v v v v y 220220+=+=（取决于初速度0v 和下落高度y ）【知识点4】平抛运动的特点1、理想化特点:物理上提出的平抛运动是一种理想化模型，即把物体看出质点，抛出后只考虑重力作用，忽略空气阻力。

2、匀变速特点：平抛运动的加速度恒定，始终为重力加速度g 所以平抛运动是一种 运动。

3、速度变化特点：平抛运动中，任意一段时间内速度的变化量Δv ＝g Δt ，方向恒为竖直向下（与g 同向），即任意两个相等的时间间隔内速度的变化相同，如右图所示。

高二物理的平抛运动公式详解物理在绝大多数的省份既是会考科目又是高考科目，在高中的学习中占有重要地位。

下面店铺的小编将为大家带来高二的物理公式介绍，希望能够帮助到大家。

高二物理的平抛运动公式1.水平方向速度：Vx=V02.竖直方向速度：Vy=gt3.水平方向位移：x=V0t4.竖直方向位移：y=gt2/25.运动时间t=(2y/g)1/2(通常又表示为(2h/g)1/2)6.合速度Vt=(Vx2+Vy2)1/2=[V02+(gt)2]1/2，合速度方向与水平夹角β:tgβ=Vy/Vx=gt/V07.合位移：s=(x2+y2)1/2,位移方向与水平夹角α:tgα=y/x=gt/2Vo8.水平方向加速度：ax=0;竖直方向加速度：ay=g强调：(1)平抛运动是匀变速曲线运动，加速度为g，通常可看作是水平方向的匀速直线运与竖直方向的自由落体运动的合成;(2)运动时间由下落高度h(y)决定与水平抛出速度无关;(3)θ与β的关系为tgβ=2tgα; (4)在平抛运动中时间t是解题关键;(5)做曲线运动的物体必有加速度，当速度方向与所受合力(加速度)方向不在同一直线上时，物体做曲线运动。

高二的物理直线运动公式介绍1)匀变速直线运动1.平均速度V平=s/t(定义式)2.有用推论Vt2-Vo2=2as3.中间时刻速度Vt/2=V平=(Vt+Vo)/24.末速度Vt=Vo+at5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/26.位移s=V平t=Vot+at2/2=Vt/2t7.加速度a=(Vt-Vo)/t{以Vo为正方向，a与Vo同向(加速)a>0;反向则a<0｝8.实验用推论Δs=aT2{Δs为连续相邻相等时间(T)内位移之差｝9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算：1m/s=3.6km/h。