当前位置：文档之家 › 修正的MUSIC算法在智能天线中的应用

修正的MUSIC算法在智能天线中的应用

  • 格式：pdf
  • 大小：244.32 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

MUSIC声源定位算法的改进及其矩阵分析

MUSIC声源定位算法的改进及其矩阵分析

摘 要 : 对 传 统 的 M USI C 算 法 时 域 特 征 分 析 方 法 改 进 到 频 域 ， 并 将 其 在 G SM M A 麦 克 风 阵 列 模 型 上 进 行 声
源定 位仿真 计算 ，获得 了良 好的定 位效 果，同 时对 改进算 法进 行了矩 阵理 论分析 。
关 键 字 : 声 源 定 位 ； GS M MA ； M US IC 改 进 算 法 ； 矩 阵 分 析 。
r e s
j
Ms
c
rJ 1
2 πf j
(rJ
1,M
rJ 1 )
e
c
.. .
rM
rJ 1, M
.
rJ K e rJK , M
j 2 πf ( rJ K ,M c
rJK )
以上(1-1)~(1-4)式就是 GSMMA 麦克风阵列数学模型， 它对远场和 近场声源 程序都兼 容且适用于 任意拓扑 结构的 麦克风阵列，因此，我们将此模型用于声源定位的场合。 1.2 MUSIC 算 法的改进
r
c
, . . ., s e
rM
j 2 π f (rM c
rs )
]T
的声源频率分量对应的方向矢量为 (1-3) 。同理，得出 K 个干扰源的方向矢量为 aJK(ΘJK , f ) ，传输矩阵为：
A( f ) = [a s (Θs , f ), aJ 1( ΘJ 1, f ),..., aJ K (ΘJ K, f )]
Байду номын сангаас
量，是阵列信号处理的新方向。收集语音信号的麦克风阵列
不同算法应用的矩阵模型也会有所不同，下面采用任意拓扑
结构的麦克风阵列模型[1]（GSMMA）进行声源定位算法学

MUSIC及其改进算法的研究与实现

MUSIC及其改进算法的研究与实现

MUSIC及其改进算法的研究与实现黄丽薇;陈慧琴;陈玉林【摘要】研究了用于阵列信号处理领域的重要分支,即信号到达角估计的几种MUSIC算法.阐述了经典MUSIC算法、前后向空间平滑MUSIC算法、改进MUSIC算法的原理.采用Matlab进行的仿真表明,经典MUSIC算法对于非相干信源的到达角估计具有良好的性能,但不能用于相干信源的到达角估计;前后向空间平滑MUSIC算法使可估计信源数减小、计算复杂度较高;改进MUSIC算法性能最好,不影响非相关信源的估计,也无明显计算量增加.几种算法在到达角估计中有各自的优缺点.【期刊名称】《电子科技》【年(卷),期】2015(028)003【总页数】4页(P55-57,75)【关键词】MUSIC;空间平滑MUSIC;改进MUSIC;到达角估计【作者】黄丽薇;陈慧琴;陈玉林【作者单位】东南大学成贤学院,江苏南京 210088;东南大学成贤学院,江苏南京210088;东南大学成贤学院,江苏南京 210088【正文语种】中文【中图分类】TN957阵列信号处理是信号处理的重要分支，信号到达角(DOA)估计是阵列信号的重要部分［1－2］。

经典MUSIC算法［3］基于接收信号的协方差矩阵分解，对于非相干信源的到达角估计具有良好的性能。

前/后向空间平滑算法［4］和改进MUSIC(MMUSIC)算法［5］可以实现相干信源的到达角估计。

1 经典MUSIC算法1.1 经典MUSIC原理考虑M元均匀线阵，有N个窄带信源平面波入射，信源方向为θ1，θ2，…，θN。

S(k)=［s1(k)，…，sN(k)］T，si(k)为第i个信源的复振幅。

阵列的导向矢量a(θi)=［1，e－jωi，…，e－j(M－1)ωi］T，i=1，…，N，A=，d 为阵元间距，λ 为载波波长。

n(k)=［n1(k)，…，nM(k)］T，ni(k)为零均值、方差σ2的白噪声，与信源不相关。

第k次快拍，得到的数据为X(k)=AS(k)+n(k)，k=1，2，…，K，K 为快拍次数。

基于MUSIC和LMS算法的智能天线设计

基于MUSIC和LMS算法的智能天线设计

基于MUSIC和LMS算法的智能天线设计
作为当今三大主流标准之一的TD―SCDMA是由中国自主提出使用时分双工方式的第三代移动通信系统标准。

TD―SCDMA的核心技术之一是智能天线
技术。

在TD―SCDMA系统中使用智能天线技术，基站可以利用上行信号信息对下行信号进行波束成形，从而降低对其他移动台的干扰，同时提高接收灵敏度，增加覆盖距离和范围，改善整个通信系统的性能。

传统的切换波束方式只是把空间分成几个固定扇区，当移动台进入扇区时，切换波束系统选择一个收到最强信号的波束用于该用户。

由于用户信号并不一定在固定波束的中心处，当用户信号位于波束边缘，干扰信号位于波束中央时，接受效果差，同时也不能实现自适应干扰置零，抑制干扰差。

而智能天线通过自适应阵列天线跟踪并提取各用户的空间信息，利用用户位置的不同，使在同一信道中发送和接收各用户的信号不发生相互干扰。

智能天线能够根据信号环境情况自动形成最佳阵列波束，通过在天线中引入自适应信号处理，实现噪声抵消，在干扰入射方向上产生零陷以及主波束跟踪有用信号，从而使天线阵具有智能接收的能力，以解决切换波束方式的不足。

文中正是结合多重信号分类算法和最小均方误差的自适应算法来实现智能天线系统。

1 阵列天线信号模型在基站天线的远场区域，可以认为电磁波以球面波的形式向外辐射，如果接收天线离辐射源足够远，在接收的局部区域可近似为平面波。

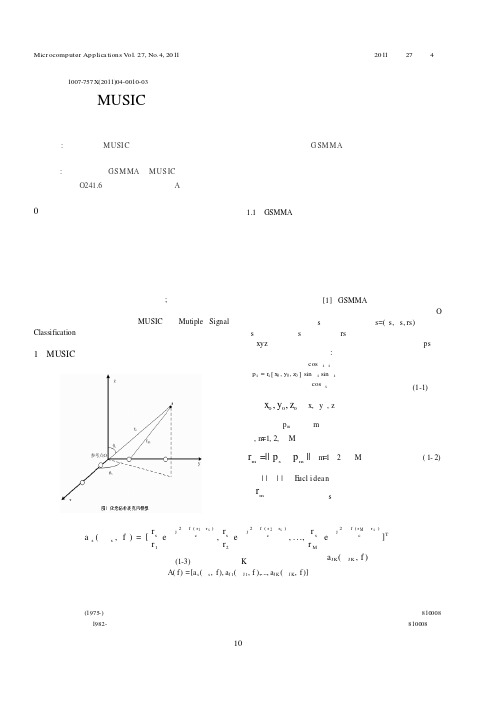
图1 所示为等距线阵，由M 个阵元组成，设阵元间距为△x，入射信号s(t)的入射角为θ，即s(t)的波达方向，以原点为信号的参考点，则等距直线阵的方向向量为
其中λ为信号波长。

对于来自d 个方向的信号入射到阵列天线的M 个阵元上，则接收信号写成矩阵形式为。

一种改进MUSIC算法的FPGA实现

一种改进MUSIC算法的FPGA实现
MUSIC 算法的基本思想是将阵列输出数据的协 方差矩阵进行特征分解 ,从而得到与信号分量相对 应的信号子空间和与信号分量相正交的噪声子空 间 ,利用 2 个子空间的正交特性构造出“针状”空间 谱峰来估计信号的 DOA 。该算法具有高分辨特性 及较小的估计方差 ,但采样协方差矩阵的特征分解 涉及大量不规则矩阵运算 ,需要利用 DSP 实现 ,在 实时性要求高的场合性能难以满足要求 。因此大量 文献致力于降低该算法复杂度 。文献 [ 4 ]提出了一 种改进的 MUSIC 算法 ,该方法利用采样协方差矩阵 的子矩阵构造信号子空间 ,无需特征分解 ,从而大大
图 1 估计成功概率与信噪比关系
图 2 估计方差与信噪比关系
2 改进算法的 FPGA 实现
改进算法可以分 3 步实现 :计算采样协方差矩 阵的子阵 Rsub 、对 Rsub的列矢量进行施密特正交化 得到信号子空间 、谱峰搜索 。实现框图如图 3 和 图 4所示 。本文选用的 FPGA 是 ALTERA 公司的大 容量高速处理芯片 2C70 , 对于阵元为 4 的均匀线 阵 ,1 个入射信号 ,在估计精度要求为的情况下 ,通 过 MATLAB 仿真确定 ,14 位以下字长难以满足精度 要求 ,而 16 位字长能较好地完成设计 。
一种改进 MUSIC 算法的 FPGA 实现
宋树田 , 秦建存
( 中国电子科技集团公司第五十四研究所 , 河北 石家庄 050081)
摘 要 MUSIC[1] 算法具有很高的分辨力 、估计精度及稳定性 , 但是由于需要对 采 样 协 方 差 矩 阵 进 行 特 征 分 解 , 运算量巨大 , 难以利用 FPGA 实时实现 。通过对等距线阵 特 点 及 MUSIC 算 法 的 研 究 , 发 现 可 以 利 用 局 部 协 方 差 矩 阵 构造信号子空间 , 进一步得到噪声子空间进行谱峰搜索 , 从而大大降低了算法的复杂度 , 计算机仿真验证了该算法 的有效性 。利用 FPGA 对该算法进行了硬件实现 , 测试的估计精度和实时性良好 , 对工程应用具有重要的指导意义 。

基于修正MUSIC算法的信号DOA估计的开题报告

基于修正MUSIC算法的信号DOA估计的开题报告

基于修正MUSIC算法的信号DOA估计的开题报告一、研究背景在无线通信中，多个发射机向一个接收机发送信号，需要准确地知道信号到达的方向，这个问题就被称为信号的方向（DOA）估计问题。

信号DOA估计在雷达定位、无线通信等领域普遍存在。

传统的信号DOA估计算法包括MUSIC、ESPRIT、ROOT-MUSIC等，但这些算法都存在着一定的局限性，例如对信号频率的限制、基于阵列空间采样的器件复杂和精度低等问题。

为了克服这些局限性，修正MUSIC算法应运而生。

修正MUSIC算法是基于自相关函数的高分辨率频谱分析技术，在信号DOA估计中具有较高的精度和抗噪声能力。

该算法在阵列信号处理领域得到广泛应用，并在实际应用中取得了良好的效果。

二、研究内容本研究将基于修正MUSIC算法，研究信号DOA估计的问题。

研究内容包括以下几个方面：1. 修正MUSIC算法的理论研究：探究修正MUSIC算法的理论基础、分析算法的优缺点，为后续的实验研究提供理论依据。

2. 信号DOA估计的算法设计：根据修正MUSIC算法的原理，设计可靠高效的信号DOA估计算法。

3. 仿真实验的设计与实现：通过对不同条件下的仿真实验，验证所设计的算法的准确性和鲁棒性，在实验中验证算法的可靠性和实用性。

4. 实际测试的验证：基于硬件平台，对所设计的信号DOA估计算法进行实际测试验证。

三、研究意义本研究将基于修正MUSIC算法，研究信号DOA估计的问题，将会具有以下的研究意义：1. 提高信号DOA估计的准确性和鲁棒性，满足实际应用中对信号DOA估计的实时性和高精度的需求。

2. 对修正MUSIC算法和信号DOA估计问题进行深入的研究，提高学术研究水平和阵列信号处理领域技术水平。

3. 为实际应用场景中对信号DOA估计的要求提供解决方案，提升我国在阵列信号处理领域的研究和应用水平。

四、研究方法本研究将采用以下研究方法：1. 文献调研方法：对修正MUSIC算法和信号DOA估计问题进行深入的文献调研，为后续的研究提供理论基础。

基于MUSIC算法的测向性能分析

基于MUSIC算法的测向性能分析

基于MUSIC算法的测向性能仿真2013 年 1 月 16 日摘要随着移动通信技术的飞速发展，智能天线技术研究的不断深入，来波方向(DOA)估计技术逐渐成为研究的热点之一，而MUSIC算法是智能天线技术的典型算法。

本文在对MUSIC算法进行分析的基础上，设计了MUSIC算法的仿真程序，对不同情况下该算法的性能进行了仿真分析。

仿真结果表明该算法在不同阵列结构、信号入射角度时具有不同的性能。

关键词：智能天线；DOA；MUSIC；阵元目录摘要 (I)引言 (1)一、MUSIC算法介绍 (1)1.1 MUSIC算法的提出 (1)1.2波达方向估计问题中的阵列信号数学模型 (2)1.3阵列协方差矩阵的特征分解 (4)1.4 MUSIC算法的原理及实现 (6)1.5 MUSIC算法的实现步骤： (8)二、MUSIC算法的DOA估计仿真 (8)2.1MUSIC算法的基本仿真 (8)2.2 MUSIC算法DOA估计与阵元数的关系 (9)2.3 MUSIC算法DOA估计与阵元间距的关系 (10)2.4 MUSIC算法DOA估计与快拍数的关系 (11)2.5 MUSIC算法DOA估计与信噪比的关系 (12)2.6 MUSIC算法DOA估计与信号入射角度差的关系 (13)三、MUSIC算法性能分析小结 (15)参考文献 (15)附录 (16)附录一：MUSIC算法的基本仿真源代码 (16)附录二：MUSIC算法DOA估计与不同阵元数关系仿真源代码 (17)附录三：MUSIC算法DOA估计与阵元间距的关系仿真源代码 (18)附录四：MUSIC算法DOA估计与快拍数的关系仿真源代码 (21)附录五：MUSIC算法DOA估计与信噪比的关系仿真源代码 (22)附录六：MUSIC算法DOA估计与信号入射角度差的关系仿真源代码 (24)图目录图1-1等距线阵与远场信号 (2)图2-1MUSIC算法的DOA估计谱 (9)图2-2阵元数不同时MUSIC算法的DOA估计谱 (10)图2-3阵元间距不同时MUSIC算法的DOA估计谱 (11)图2-4快拍数不同时MUSIC算法的DOA估计谱 (12)图2-5信噪比不同时MUSIC算法的DOA估计谱 (13)图2-6角度间隔不同时MUSIC算法的DOA估计谱 (14)引言智能天线技术是当前无线移动通信领域颇为关注和研究的热点领域之一，可将无线电的信号导向到具体的方向上，产生空间定向波束，使天线主波束对准用户信号到达方向，旁瓣或零陷对准干扰信号的到达方向，起到充分高效利用移动用户信号并删除或抑制干扰信号的目的。

基于MUSIC和LMS算法的智能天线设计

基于MUSIC和LMS算法的智能天线设计
刘档;李莉;张静
【期刊名称】《电子科技》
【年(卷),期】2009(22)1
【摘要】基于来渡方向估计和自适应波束成形的智能天线系统,用多重信号分类(MUSIC)算法实现来波方向估计,辨识天线阵列上接收信号的各个方向,使用最小均方误差(LUS)的自适应算法控制天线的主辩方向,实现对期望信号的跟踪,同时实现对干扰信号的零陷处理.文中使用Matlab编程进行计算机仿真,通过仿真结果,MUSIC 算法可以识别天线接收端的信号的入射方向,LMS算法可以实现对干扰信号的抑制.【总页数】4页(P5-8)
【作者】刘档;李莉;张静
【作者单位】上海师范大学,数理信息学院,上海,200234;上海师范大学,数理信息学院,上海,200234;上海师范大学,数理信息学院,上海,200234
【正文语种】中文
【中图分类】TN821+.91
【相关文献】
1.基于LMS算法的智能天线波束形成技术的研究 [J], 陈晓军;崔唯佳;李晓雷;李红亮;赵晓霞
2.基于LMS算法的智能天线的MATLAB仿真 [J], 汪睿;曾庆栋
3.基于LMS算法的智能天线波束方向图仿真 [J], 杨尚贤;王明皓
4.基于LMS算法的智能天线自适应波束形成研究 [J], 冉光福;周围;邓琦新
5.基于智能天线的LMS算法的研究 [J], 王兵
因版权原因，仅展示原文概要，查看原文内容请购买。

MUSIC算法在GPS干扰检测及抵消中的应用

MUSIC算法在GPS干扰检测及抵消中的应用
向乐乐;卢艳娥
【期刊名称】《弹箭与制导学报》
【年(卷),期】2011(031)002
【摘要】由于GPS信号的低能级特性,在有些应用场合GPS接收机需采取抗干扰措施.在均匀线性天线阵条件下,文中采用MUSIC算法对于扰进行了抵消,并进行GPS信号捕获的仿真.仿真实验表明,多重信号分类法(MUSIC)对于大干扰噪声比(J/N)的干扰具有较高的到达角度(DOA)估计精度和信号噪声分离度.当GPS信号和干扰信号的DOA相差一定角度时MUSIC算法能够提高GPS接收机的抗干扰性能.【总页数】3页(P205-206,210)
【作者】向乐乐;卢艳娥
【作者单位】空军工程大学电讯工程学院,西安,710077;空军工程大学电讯工程学院,西安,710077
【正文语种】中文
【中图分类】TN972;P228.4
【相关文献】
1.空域MUSIC算法在GPS抗干扰中的应用 [J], 王顿;卢艳娥;裴文林;庞春雷
2.干扰检测技术在某雷达接收机中的应用 [J], 孙健
3.干扰检测在抗干扰算法中的应用 [J], 邹瑜
4.MUSIC算法在国产多波束测深仪中的应用研究 [J], 姜彦宇;罗宇
5.多处理器技术在30中回波抵消器中的应用 [J], 薛勇强;费元元
因版权原因，仅展示原文概要，查看原文内容请购买。

MUSIC算法的性能比较


ｒ ｉ ｔ ｈ ｍｓ ｅ ｎ ｈ ａ ｎ ｃ ｅ ｔ ｈ ｅ ａ ｄ ｖ ａ ｎ ｔ ａ ｇ ｅ ｓ ｉ ｎ ｈ ｉ ｇ ｈ ｒ ｅ ｓ ｏ ｌ ｕ ｔ ｉ ｏ ｎ ｆ ｏ ｒ ａ ｐ ｐ ｌ ｉ ｃ ａ ｔ ｉ ｏ ｎ ｓ ｉ ｎ ｓ ｍａ ｒ ｔ ａ ｎ ｔ ｅ ｎ ｎ ａ ｓ ． Ｋｅ ｙ ｗｏ ｒ ｄ ｓ Ｄ ＯＡ ；Ｒｏ ｏ ｔ — ＭＵＳ Ｉ Ｃ； ｓ ｐ ａ ｔ ｉ ｌ ａ ｓ ｍｏ ｏ ｔ ｈ ｉ ｎ ｇ ｔ ｅ ｃ ｈ ｎ ｏ ｌ ｏ ｇ ｙ ；ｉ ｍｐ ｏｖ ｒ ｅ ｄ Ｕ Ｓ Ｍ Ｉ Ｃ； ｍｏ ｄ ｉ ｉ ｆ ｄ ｅ Ｕ Ｓ Ｍ Ｉ Ｃ； ｓ ｍａ ｒ ｔ ａ ｎ ｔ ｅ ｎ ｎ ａ
且 有利于其在智能天线方 面的应用 。
关键词 Ｄ Ｏ Ａ；求根 ＭＵ Ｓ Ｉ Ｃ；空间平 滑技术 ；改进 Ｍ Ｕ Ｓ Ｉ Ｃ算法 ；修 正 ＭＵ Ｓ Ｉ Ｃ算法 ；智能天线 Ｔ Ｎ ８ ２ １ ． ９ １ ；Ｔ Ｐ ３ ０ １ ． ６ 文献标识码 Ａ 文章编 号 １ ０ ０ ７— ７ ８ ２ ０ （ ２ ０ １ ４ ） ０ ７— ０ １ ９— ０ ４ 中图分 类号
ｏ ｎ ｔ ｈ ｅ ｒ ｅ ｓ ｏ ｌ ｕ ｔ ｉ ｏ ｎ ｏ ｆ ｔ ｈ ｅ ｉ ｍｐ ｒ ｏ ｖ ｅ ｄ ＭＵＳ Ｉ Ｃ ｌｇ ａ ｏ ｒ ｉ ｔ ｈ ｍ ｉ ｓ ａ ｎ ａ ｌ ｙ ｚ ｅ ｄ ｂ ｙ ｓ ｉ ｍｕ ｌ ａ ｔ ｉ ｏ ｎ． Ｔｈ ｅ ｐ ｒ ｏ ｐ ｏ ｓ ｅ ｄ ｉ ｍｐ ｒ ｏ ｖ ｅ ｄ Ｍ ＵＳ Ｉ Ｃ ｌｇ ａ ｏ －
ｃ ａ ｎ ｃ ｅ ｉ ｎ ｗｉ ｒ ｅ ｌ ｅ ｓ ｓ ｃ ｏ ｍｍｕ ｎ ｉ ｃ ａ ｔ ｉ ｏ ｎ ｓ ． Ｍ ＵＳ Ｉ Ｃ ａ ｌ ｇ ｏ ｉｔ ｒ ｈ ｍ ｉ ｓ ａ ｃ ｌ ａ ｓ ｓ ｉ ｃ ＤＯＡ ｅ ｓ ｔ ｉ ｍａ ｔ ｉ ｏ ｎ ａ ｌ ｇ ｏ ｒ ｉ ｔ ｈ ｍ ， ｗｈ ｉ ｃ ｈ ｈ ａ ｓ ｌ ａ ｒ ｇ ｅ ａ ｍｏ ｕ ｎ ｔ

提高阵列天线DOA估计的改进MUSIC算法

第２卷 第ｌ期 ５ ０
文章 编 号 ：０ ６— ３８ ２０ ） ０— ３ ０一ｏ １０ ９ ４ （０ ８ １ ０ ４ ４
计
算

机
仿
真
２８ ０ ０ 年１月 ０
提 高 阵列天 线 Ｄ ＯＡ估 计 的改进 ＭＵＳＣ算 法 Ｉ
袁 峰 ， 张 捷
（ ．西北工业大学电子信息学院， １ 陕西 西安 ７０ ７ ； １０ ２ ２ ．中国人 民解放军 ９ ９０部队 ７ 分 队， １６ １ 广东 汕头 ５ ５ ７ １０４）
ｒｔ ｍ ． ｉｈ
ＫＥ ＹＷ ＯＲＤＳ： ｏ ｅ ｎ ｅ ｍｕ ｔ —ｐ ｔ ＤＯＡ ｅ ｔ ｔ ｎ； ａ ａ ｃ ｖ ｒ ｎ ｅ ｐ ｃｒ ｍ ｅ ｏ ｖｎ ｏ ｒ Ｃ ｈ ｒ ｃ ｌ ｅ ｉ ａ ｈ； ｓ ｍａｉ Ｄ ｔ ｏ ａ ｉ ｃ ；Ｓ ｅ ｔ ｉ ｏ ａ ｕ ｒ ｓ ｌｉ ｇ ｐ ｗｅ
征 向量发散到噪声子空间去。因此 ， Ｕ Ｉ 间谱 也就无法 Ｍ ＳＣ空
１ 引 言
阵列信号处理广泛的应用 于声 纳 ， 雷达 、 通信 、 生物 医学 等领域 ， 需要准确 的估 计空 间信号 源的方 向与分 布 ， 波达方 向（ Ｏ 估计是阵列信 号空 间谱 估计研究 的主要 内容 。在 Ｄ Ａ） 众 多的 Ｄ Ａ估计算法 中 ， 于接 收信号相 关矩 阵特征 分解 Ｏ 基 的 ＭＵ Ｉ ＳＣ算法 ， 具有 良好 的 Ｄ Ａ估计性 能。它是利用 信号 Ｏ 子空 间和噪声子空间 的正交性 ， 造空 间谱 函数 ， 构 通过 谱峰 搜索来检测信号的 Ｄ Ａ。但是 ， Ｏ 由于多径传输 以及人为干扰
ＹＵＡＮ Ｆ ｎ ， ＨＡＮＧ Ｊｅ ｅ ｇ Ｚ ｉ
（ ． ｏ ｅｅｏ Ｅｅｔ ｎ ｓａｄＩｆｒ ａ ｏ ，Ｎ ｒ ｗ ｓ ｒ ｏ ｔ ｈ ｉ ｌ ｎｖｒｉ ， ｉｎＳ ａｘ ７ ０７ ， ｈｎ ； １ Ｃ ｌ ｇ ｆ ｌ ｒ ｉ ｎ ｏｍ ｔ ｎ ｏｔ ｅｔ ｎＰ ｌｅ ｎｃ ｉ ｓｙ Ｘ’ ｈｎｉ １０ ２ Ｃ ｉ ｌ ｃｏｃ ｎ ｉ ｈ ｅ ｙ ｃ ａＵ ｅ ｔ ａ ａ ２ １Ｕ ｉｏ １６ ｒ ｙｏ ｅｐｅ ｉｅａｏ ｒ ｙｏ Ｃ ｉａ ｈｎｏ ｕｎ ｄｎ １０ ４ Ｃ ｉａ ．７ ｎｔ ｆ ９０Ａ ｆ ｏｌ’Ｌｂ ｒ ｉ Ａｍ ｆ ｈｎ ，Ｓａ ｔ Ｇ ａｇ ｏｇ ５ ７ ， ｈ ） ９ ｍ Ｐ Ｓ ｔｎ ｕ ５ ｎ
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

修正的MUSIC算法在智能天线中的应用李旭健孙绪宝（山东科技大学，山东青岛 266510）摘要: 本文提出了修正的MUSIC算法用于智能天线中的方向估计,详细描述了该方法的操作原理,并得到了较好的DOA估计.模拟仿真表明,该方法不仅在DOA估计上优于MUSIC算法,而且由此可以获得较好性能的波束形成,几个模拟结果证明了本文提出的方案.关键词: MUSIC算法；智能天线；到达方向Application of MMUSIC Algorithm In a Smart AntennaLI Xu-jian SUN Xu-bao(Shandong University of Science & Technology, Tsingtao, Shandong 266510, China) Abstract：In this paper, the Modified Multiple Signal Classification (MMUSIC) algorithm for the DOA estimation in smart antenna has been presented. The operation principles of this algorithm are described in detail and can make the DOA estimation better. Finally, some simulating results to verify the theoretical analyses are presented. The performances of MMUSIC algorithm are better than that MUSIC algorithm not only in the estimation of DOA but also in the satisfactory results have been obtained on the Simulation of a beamforming.Key words：MUSIC algorithm; smart antennas ;Direction of arrival (DOA)０ 引言移动通信中的智能天线]1[近期主要是用于无线蜂窝系统的基站. 是进一步增加系统容量实现空分多址(SDMA)的关键技术之一. 智能天线的功能主要是表现在它能够自适应的判断信号方向和数量,并跟踪期望信号.然后通过下行链路进行波束赋形,将在期望信号方向产生最大增益,并使干扰方向增益最小,从而抑制了干扰信号.近年来,信号到达方向(DOA)的估计及跟踪方面的研究已有很多报道]3,2[.主要的DOA算法大致有最大似然法、传播算子法、ESPRIT算法]4[和 MUSIC算法]5[等.在进行信号DOA估计的实际工程应用中,由于事先并不知被估信号源的是否相关.为此,本文提出在不影响算法对非相关源DOA正常估计的前提下,可提高对相关信号源DOA估计的性能,相当于可减少相关信号源间的相关系数,这种方法在文献[6]中被称为修正MUSIC(MMUSIC)算法. 本文采用该方法用于智能天线的自适应处理,获得了优于传统的MUSIC 方向估计精度,进而获得了更为准确的下行链路的波束形成。

１ 智能天线模型如图(1)所示,M个天线单元等间距d构成直线天线阵.通过预处理,将天线接收到的信号转化为数字信号,再进行自适应处理,自适应部分主要包括两方面的内容,一方面是估计源信号到达方向(DOA)并能跟踪信号.另一方面,将获得的信源信息进行自适应地波束赋形. 从而实现抑制干扰,增强期望信号的目的.user1user21θ2θ)(1k x )(2k x )(k x M ...Adaptive processingoutput图1 智能天线结构图假设空间有K(K<M)个信号,天线接收到的信号为:)()()()(t n e t st x K k m m j k m k ∑=−−+=11β，m=1,2,…M ; (1)其中 k k cd θωβsin 0=.k S 及k θ分别是第k 个入射信号及其波达角, 0ω为中心频率, c 为波速.)(t n m 是第m 阵元的噪声. 也可将(1)式表示成矩阵形式:)()()(t t t N AS X += (2)其中T M t x t x t x )](,),(),([Λ21=(t)X (3a)T M t n t n t n t )](,),(),([)(Λ21=N (3b)T K t s t s t s t )](,),(),([)(Λ21=S (3c))](,),(),([K θθθa a a A Λ21= (3d)],,,,[)()(Kk k M j j j k e e e βββθ121−−−−=Λa (3e) 式中T 表示转置. 处理接收信号时,首先需要计算接收信号的相关阵:M H H t t I AQA X X R 2σ+==})()({E (4))]()([(k k H S S Q E = 为源信号相关矩阵,M I 为M 阶单位矩阵. H )(⋅表示共轭转置.传统的MUSIC算法是对相关阵R 进行特征值分解,获得噪声子空间矩阵U .利用如下(5)式空间谱给出波达方向的估计]7[:)()()()()(θθθθθa UU a a a P H H H MUSIC = (5) ２ 修正的MUSIC 算法本文采用文献[6]方法对MUSIC 算法进行修正.首先,令)()(k k M ∗=X J Y ∗⋅)(表示复共轭.M J 是M 阶交换矩阵,除副对角线上元素为1外,其余元素均为零.且有性质M M M I J J =,由此可得)(k Y 的相关矩阵: M M M M H M H k k J R J I J AQA J Y Y R ∗∗=+==21σ)()]()([E (6)定义矩阵:],,,[)()()(KM j M j M j e e e diag βββ11121−−−−−−=ΛD (7) 则有如下关系∗∗=AD A J M (8)对非相关源,矩阵Q 应为实矩阵,将(8)代入(6),并利用对角阵乘积可交换顺序及M I D D =∗可以得出R AQA R =+=M H I 21σ (9)由此可以获得修正后的相关阵M RM M M J R J R R R R ∗+=+=1 (10)显然,对R 、1R 或M R 进行特征分解，且用MUSIC 算法进行信号DOA 估计，会得出同样的结果。

但快拍数较少时，由于R 、1R 是用有限次快拍的数据进行估计的，存在估计误差，而用M R 进行信号DOA 估计，具有平均意义，可以提高信号DOA 估计的性能.分解修正后的相关阵M R ,用MUSIC 算法获得新的噪声子空间矩阵,根据(5)式获得更为精确的信号源的方向信息.从而获得天线下行链路的准确波束赋形.３ 仿真结果图2 信号源的波达向 图3 阵波束方向图 采用元距离d=λ/2（λ为真空中波长）的8元均匀线阵天线,假设有两个信号源, 入射方向为ο30和ο45,分别为期望信号和干扰信号,信噪比均为10dB.智能天线能够由上行链路对接收到的信号进行方向估计,如图2所示, 是采用两种算法(MUSIC 及MMUSIC)对波达方向估计的对比.显然,本文采用的算法精度要高于常用的MUSIC 算法. 然后,将获得的信号方向信息,由下行链路对天线进行波束赋形.本文采用的是线性约束最小方差波束形成法(LCMV)进行自适应赋形, 能够在期望信号方向上产生最大增益.而在干扰方向上产生零陷.从而抑制干扰.如图3所示, 两种算法仿真结果看出, 在ο30的期望信号方向上, 传统的MUSIC 算法还能够产生与本文的算法产生同样的理想的增益. 但由于方向估计精度的差别, 在ο45的干扰信号方向上, 本文采用的算法抑制效果较为显著. ４ 结论本文将修正的MUSIC 算法用于智能天线自适应处理部分, 并与传统的MUSIC 算法处理比较, 获得较为理想的结果. 多次仿真对比, 说明了该方案的有效性.该方法在信噪偏底,快拍数较少的情况下,同样有较好的性能,在相同快拍条件下,比原MUSIC 算法进行DOA 估计的精度要高,为智能天线的准确赋形提供了保证,因此,MMUSIC 算法为设计智能天线提供了一条新途径.参考文献[1] Salvatore Bellofiore,Constantine A.Balanis,Jeffrey Foutz, and Anddreas S.Spanias. Smart-antenna systems for mobile communication networks part 1[J]. IEEE Antennas and Propagation Magazine, 2002,June，44(3).[2] Josef Johannes Blanz and Apostolos Papathanassiou .Smart Antennas for Combined DOA and Joint Channel Estimation in Time-Slotted CDMA Mobile Radio Systems with Joint Detection[J]. IEEE Transactions on Vehicular Technology, 2000, March, 49(2).[3] R.Weber and J.A.Nossek. Efficient DOA tracking for TDMA-based SDMA mobile communications[C]. In Proceeding of the IEEE Vehicular Technology Conference, 1999,2099-2103.[4] R,Roy and T.Kailath. ESPRIT-Estimation of Signal Parameters Via Rotational Invariance Techniques[J].IEEE Trans.on Acoustic, Speech, and Signal Processing, 1989, July. 37:984~995. [5] Stoica P and Nehorai A.MUSIC,maximum likelihood and cramer-raobound[J]. IEEE Trans. ASSP,1989:37(5);720—741.[6]KUNDU D.Modified MUSIC algorithm for estimating DOA of signals [J].Signal Processing,1996,(48):85-89.[7]张贤达.通信信号处理. 国防工业出版社[M] p326~330.。