不等式与逻辑综合练习答案

集合、逻辑用语，不等式基础练习1.若A、B是全集I的真子集，则下列四个命题：①A∩B=A； ②A∪B=A; ③A∩(∁IB)=⌀; ④A∩B=I⑤x∈B是x∈A的必要不充分条件.其中与命题A⊆B等价的有( )A. 1个B. 2个C. 3个D. 4个2.有下列关系式：①{a,b}={b,a}；②{a,b}⊆{b,a}；③⌀={⌀}；④{0}=⌀；⑤⌀⫋{0}；⑥0∈{0}.其中不正确的是()A. ①③B. ②④⑤C. ①②⑤⑥D. ③④3.已知集合A={−1,2}，B={x|ax+2=0}，若A∪B=A，则实数a的取值所组成的集合是()A. {−1,2}B. {−1,1}C. {−2,0，1}D. {−1,0，2}4.若全集U=R，集合A={0,1，2，3，4，5}，B={x|x<3}，则图中阴影部分表示的集合为()A. {0,1，2，3}B. {0,1，2}C. {3,4，5}D. {4,5}5.已知全集U=R，集合A={x|x≤0}，B={x|x≥1}，则集合∁U(A∪B)=()A. {x|x≥0}B. {x|x≤1}C. {x|0≤x≤1}D. {x|0<x<1}6.设x∈R，则x>2的一个必要条件是()A. x>1B. x<1C. x>3D. x<37.若不等式|x−1|<a成立的充分条件为0<x<4，则实数a的取值范围是()A. {a|a≥3}B. {a|a≥1}C. {a|a≤3}D. {a|a≤1}8.设命题甲为“0<x<3”，命题乙为“|x−1|<2“，那么甲是乙的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件9.已知p:x2−x<0，那么命题p的一个必要条件是()A. 0<x<1B. −1<x<1C. 12<x<23D. 12<x<210.已知命题p：∃x0∈R，x02−x0+14≤0，则¬p为()A. ∃x0∈R，x02−x0+14>0 B. ∃x0∈R，x02−x0+14<0C. ∀x∈R，x2−x+14≤0 D. ∀x∈R，x2−x+14>011.已知命题“∃x∈R，使4x2+(a−2)x+14≤0”是假命题，则实数a的取值范围是()A. a<0B. 0≤a≤4C. a≥4D. 0<a<412.已知a，b，c∈R，那么下列命题中正确的是()A. 若ac2>bc2，则a>bB. 若ac >bc，则a>bC. 若a3>b3，且ab<0，则1a <1bD. 若a2>b2，且ab>0则1a<1b13.设t=a+2b，s=a+b2+1，则t与s的大小关系是()A. s≥tB. s>tC. s≤tD. s<t14.若a>0，则a+4a的最小值为()A. 2B. 4C. 8D. 1615.若f(x)=x+1x−2(x>2)在x=n处取得最小值，则n=()A. 52B. 3 C. 72D. 416.设x,y均为正数，且x+4y=4，则xy的最大值为()A. 1B. 2C. 4D. 1617.若正数m，n满足2m+n=1，则1m +1n的最小值为()A. 3+2√2B. 3+√2C. 2+2√2D. 318.下列函数中，最小值为2的函数是()A. y=√x2+2√x2+2B. y=x2+1xC. y=x(2√2−x),(0<x<2√2)D. y=2√x2+119.不等式x(2−x)>3的解集是()A. {x|−1<x<3}B. {x|−1<x<1}C. {x|x<−3或x>1}D. ⌀20.已知不等式x2+ax+b<0的解集是{x|−1<x<2}，则a+b等于()A. −3B. 1C. −1D. 321.不等式(m+1)x2−mx+m−1<0的解集为⌀，则m的取值范围是()A. m<−1B. m≥2√33C. m≤−2√33D. m≥2√33或m≤−2√33答案和解析1.【答案】B【解答】解：由A⊆B得Venn图，①A∩B=A⇔A⊆B;②A∪B=A⇔B⊆A;③A∩(∁I B)=⌀⇔A⊆B;④{A∩B=IA⊆IB⊆I⇔A=B=I⇒A⊆B,但A⊆B不一定能得出A=B=I，故A∩B=I与A⊆B不等价;⑤x∈B是x∈A的必要不充分条件，则A⊆B，但A⊆B不一定能得x∈B是x∈A的必要不充分条件，所以不等价．故和命题A⊆B等价的有①③，故选B．2.【答案】D【解答】对①：因为集合元素具有无序性，显然①正确；对②：因为集合{a,b}={b,a}，故{a,b}⊆{b,a}正确，即②正确；对③：空集⌀是一个集合，而集合{⌀}是以空集为元素的一个集合，因此⌀={⌀}不正确；对④：{0}是一个集合，仅有一个元素0，但是空集不含任何元素，于是{0}≠⌀，故④不正确；对⑤：由④可知，{0}非空，于是有⌀⫋{0}，因此⑤正确；对⑥：显然0∈{0}成立，因此⑥正确．综上，本题不正确的有③④，于是本题选项为D．故选D．3.【答案】D【解答】解：∵A∪B=A，∴B⊆A．当a=0时，B=⌀，满足条件．当a≠0时，−a+2=0或2a+2=0，解得a=2或a=−1．综上可得，实数a的取值所组成的集合是{0,2，−1}．故选D．4.【答案】C【解答】解：由韦恩图可知，阴影部分表示的集合为A∩(∁U B)，∵全集U=R，集合A={0,1，2，3，4，5}，B={x|x<3}，∴∁U B={x|≥3}，∴A∩(∁U B)={3,4，5}，故选：C．5.【答案】D【解答】解：由已知，得A∪B={x|x≤0或x≥1}，故∁U(A∪B)={x|0<x<1}．故选D．6.【答案】A【解答】解：由x>2成立可得x>1也成立，但是x>1成立，x>2不一定成立，所以x>2的一个必要条件为x>1．故选A．7.【答案】A解：∵不等式|x−1|<a成立的充分条件是0<x<4，设不等式的解集为A，则{x|0<x<4}⊆A，当a≤0时，A=⌀，不满足要求；当a>0时，A={x|1−a<x<1+a}，若{x|0<x <4}⊆A ，则{1−a ⩽01+a ⩾4,解得a ≥3． 故选A ．8.【答案】A【解答】解：命题乙为“|x −1|<2“，解得：−1<x <3． 又命题甲为“0<x <3”，那么甲是乙的充分不必要条件．故选A ．9.【答案】B【解答】解：x 2−x <0⇔0<x <1，根据充分条件必要条件的定义可知： A 中0<x <1是p 的充要条件;B 中−1<x <1是p 的必要条件;C 中12<x <23是p 的充分不必要条件;D 中12<x <2是p 的既不充分也不必要条件．故选B ． 10.【答案】D【解答】解：存在量词命题的否定是全称量词命题得命题p ：∃x 0∈R ，x 02−x 0+14≤0的否定 ¬p ：∀x ∈R ，均有x 2−x +14>0，故选：D ． 11.【答案】D【解答】解：因为命题“∃x ∈R,4x 2+(a −2)x +14⩽0”是假命题， 所以否定为“”是真命题， 则，解得0<a <4， 故选D ．12.【答案】A【解答】解：A.若ac 2>bc 2，则a >b ，A 正确；B .a c >b c，若c <0，则a <b ，B 不正确； C .若a 3>b 3且ab <0，则{a >0b <0,1a >1b,C 不正确． D .a 2>b 2且ab >0，若a <b <0，则1a >1b，D 不正确． 故选A ． 13.【答案】A【解答】解：∵b 2+1−2b =(b −1)2≥0，∴b 2+1≥2b ， ∴a +2b ≤a +b 2+1，即t ≤s ．故选A ．14.【答案】B【解答】解：∵a >0，∴a +4a ≥2·√a ·4a =4， 当且仅当a =4a ，即a =2时取等号，∴a +4a 的最小值为4， 故选B ． 15.【答案】B【解答】解：∵x >2，x −2>0，∴f(x)=x +1x−2=(x −2)+1x−2+2≥2√(x −2)⋅1x−2+2=4， 当且仅当x =3时取等号．∴n =3．故选B ． 16.【答案】A【解答】解：由基本不等式可得4=x +4y ≥2√4xy =4√xy ， 于是4√xy ≤4，xy ≤1，当且仅当x =2,y =12时取等号，故xy 的最大值为1； 故选A ． 17.【答案】A【解析】解：∵2m +n =1，m >0,n >0则1m +1n =(1m +1n )(2m +n)=3+2m n +n m ≥3+2√2， 当且仅当2m n =n m ，即n =√2m 时取等号，此时m =2−√22,n =√2−1，满足题意．即最小值3+2√2， 故选：A ．18.【答案】D【解析】解：选项A ，令√x 2+2=t ≥√2，则y =t +1t ，t ≥√2，函数y =t +1t 在[√2,+∞)上单调递增，则最小值为√2+√22=3√22，故选项A 不满足； 选项B ，y =x 2+1x 中取x =−1，则y =−2，故B 不满足；选项C ，y =x(2√2−x)≤ (x+2√2−x 2)2 =2，当且仅当x =√2时取等号，故C 不满足； 选项D ，y =2√x 2+1=√x 2+1√x 2+1≥2，当且仅当x =0取等号，故最小值为2正确；故选D ． 本题主要考查了基本不等式，属于基础题．根据基本不等式逐一分析判断即可，注意等号成立的条件． 19.【答案】D【解答】解：不等式x(2−x)>3化为x 2−2x +3<0，因为该不等式的相应方程x 2−2x +3=0的根的判别式Δ=−8<0， 所以不等式x(2−x)>3的解集为⌀，故选：D ．20.【答案】A【解答】解：不等式x 2+ax +b <0的解集是{x|−1<x <2}，∴方程x 2+ax +b =0的实数根是−1和2，由韦达定理可知{−1+2=−a1(−1)×2=b 1,解得：{a =−1b =−2, ∴a +b =−1−2=−3．故选：A ．21.【答案】B【解答】解：∵关于x的不等式(m+1)x2−mx+m−1<0的解集为⌀，∴不等式(m+1)x2−mx+m−1≥0恒成立，①当m+1=0，即m=−1时，不等式化为x−2≥0，解得x≥2，不是对任意x∈R恒成立，②当m+1≠0时，即m≠−1时，∀x∈R，使(m+1)x2−mx+m−1≥0，即m+1>0且△=(−m)2−4(m+1)(m−1)≤0，解得m≥2√3，3．综上，实数m的取值范围是m≥2√33故选B．。

第2讲集合、不等式、常用逻辑用语一、选择题1．(2019·高考全国卷Ⅱ)设集合A＝｛x|x2－5x＋6>0}，B＝｛x｜x－1<0｝，则A∩B＝（)A．(－∞，1) B．（－2,1）C．(－3，－1) D．(3，＋∞)解析：选A.A∩B＝｛x|x2－5x＋6>0}∩{x|x－1〈0}＝｛x|x<2或x〉3}∩{x|x<1}＝｛x|x<1｝．故选A。

2．命题“∀x〉0，ln x≥1－错误!”的否定是( )A．∃x0≤0,ln x0≥1－错误!B．∃x0≤0,ln x0〈1－1 x0C．∃x0>0，ln x0≥1－错误!D．∃x0〉0，ln x0〈1－错误!解析：选D.若命题为∀x∈M，p（x)，则其否定为∃x0∈M，綈p(x0）．所以“∀x>0，ln x≥1－错误!”的否定是∃x0〉0，ln x0<1－错误!，故选D.3.(2019·沈阳市质量监测（一）)已知全集U＝｛1，3，5，7｝，集合A＝｛1,3}，B＝｛3，5}，则如图所示阴影区域表示的集合为（)A．{3} B．｛7}C．｛3，7} D．{1，3,5}解析:选B。

由图可知，阴影区域为∁U(A∪B）,由并集的概念知，A∪B＝{1，3,5｝，又U＝{1，3,5，7｝,于是∁U(A∪B）＝｛7｝,故选B。

4．（2019·广西钦州期末）已知a，b∈R，a2＋b2＝15－ab，则ab的最大值是（）A．15 B．12C．5 D．3解析：选C。

因为a2＋b2＝15－ab≥2ab，所以3ab≤15，即ab≤5，当且仅当a＝b＝±错误!时等号成立．所以ab的最大值为5.故选C.5．已知a＞0＞b,则下列不等式一定成立的是（)A．a2＜－ab B．|a｜＜|b｜C．错误!＞错误!D．错误!错误!＞错误!错误!解析：选C。

通解：当a＝1,b＝－1时，满足a＞0＞b，此时a2＝－ab，｜a｜＝｜b|，错误!错误!＜错误!错误!，所以A，B，D不一定成立．因为a＞0＞b，所以b－a＜0,ab＜0，所以错误!－错误!＝错误!＞0，所以错误!＞错误!一定成立，故选C.优解：因为a＞0＞b，所以错误!＞0＞错误!，所以错误!＞错误!一定成立，故选C.6．（2019·高考北京卷)设函数f(x)＝cos x＋b sin x（b为常数），则“b＝0"是“f（x）为偶函数”的( ）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件解析:选C.因为f（x)＝cos x＋b sin x为偶函数，所以对任意的x∈R 都有f(－x)＝f(x)，即cos（－x)＋b sin（－x)＝cos x＋b sin x,所以2b sin x＝0。

集合、逻辑用语、不等式小题强化训练一、单选题1．已知集合,M N ，则“M N M ⋂=”是“M N N ⋃=”的（ ）条件． A ．充分不必要 B ．必要不充分 C ．充要 D ．既不充分又不必要【答案】C【详解】因为M N M ⋂=，所以M N ⊆， 因为M N N ⋃=，所以M N ⊆，所以“”M N M ⋂=是“”M N N ⋃=的充要条件, 故选：C.2．已知a b c >>，若11ma b b c a c+=−−−成立，则实数m 的最小值为（ ） A ．2 B ．3C ．4D ．5【答案】C【详解】令x a b =−，y b c =−，则x y a c +=−， 因为a b c >>，所以0,0x y >>， 因为11m a b b c a c +=−−−，所以()11a c m a b b c ⎛⎫+−= ⎪−−⎝⎭，则()11224y x m x y x y x y ⎛⎫=++=++≥= ⎪⎝⎭， 当且仅当x y =时取等号，所以m 的最小值为4. 故选：C.3．设全集U =R ，集合{}2M x x =<，{}23N x x =−<<，则{}3x x ≥=（ ） A ．()U MN ðB ．()U N M ðC ．()U M N ⋂ðD ．()U M N ⋃ð【答案】A【详解】对于A ，由题意得{}3M N x x ⋃=<，所以(){}3U M N x x ⋃=≥ð．故A 正确； 对于B ，U M ð{}2x x =≥，{}23N x x =−<<，所以N ⋃()U M ð{}2x x =>−，故B 错误； 对于C ，}{22M N x x ⋂=−<<，U ð(){2M N x x ⋂=≤−或}2x ≥，故C 错误； 对于D ，U N ð{2x x =≤−或}3x ≥，M ()U N ð{2x x =<或}3x ≥，故D 错误.故选：A.4．已知2:230p x x +−<，2:20q x x +−<，则p 是q 的（ ）条件 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分又不必要条件【答案】B【详解】由2:230p x x +−<得31x −<<， 由2:20q x x +−<得21x −<<， 则p 是q 的必要不充分条件. 故选：B.5．已知集合{}0A x x a =−<，{}B x x b x b =−=−，若[)1,2A B =，则a b −=（ ） A ．-3 B ．-1C ．1D ．3【答案】C【详解】{}{}0A x x a x x a =−<=<，{}{}B x x b x b x x b =−=−=≥， 若[)1,2A B =， 则1b =，2a =， 故1a b −=． 故选：C.6．已知0,0a b >>，则下列选项中，能使4a b +取得最小值25的为（ ） A ．36ab = B ．9ab a b =+C ．221a b +=D ．2216625a b +=【答案】B【详解】A 选项，424a b +≥=， 当且仅当4a b =，即3,12a b ==时，等号成立，A 错误；B 选项，因为9ab a b =+，所以911b a+=，故()913644491325a b a b a b b a b a ⎛⎫+=++=+++≥+= ⎪⎝⎭， 当且仅当36a b b a =，即515,2b a ==时，等号成立，B 正确； C 选项，当4,5a b ==时，满足221a b +=，此时41652125a b +=+=<，C 错误；D 选项，0,0a b >>，设25cos ,25sin 4a b θθ==，其中π0,2θ⎛⎫∈ ⎪⎝⎭，则π425cos 25sin 4a b θθθ⎛⎫+=+=− ⎪⎝⎭，因为π0,2θ⎛⎫∈ ⎪⎝⎭，所以πππ,444θ⎛⎫−∈− ⎪⎝⎭，故(π425,4a b θ⎛⎫+=−∈ ⎪⎝⎭， 显然4a b +取不到最小值25，D 错误. 故选：B7．已知集合{}{}20,,1,1,1A a B a a ==+−，则“1a =”是“A B ⊆”的（ ）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件【答案】B【详解】当1a =时，{0,1},{0,1,2}==A B ，则A B ⊆； 反之，当A B ⊆时，10a +=或10a −=，解得1a =−或1a =，若1a =−，{0,1},{0,1,2}A B ==−，满足A B ⊆，若1a =，显然满足A B ⊆， 因此1a =−或1a =，所以“1a =”是“A B ⊆”的充分不必要条件. 故选：B8．已知集合{}N 5A x x =∈≤，集合{}2430B x x x =−+>，则A B =（ ）A ．{}2B ．{}0,1,3,4,5C ．{}0,4,5D ．{}4,5【答案】C【详解】由题意可得{}{}N 50,1,2,3,4,5A x x =∈≤=，由()()243310x x x x −+=−−>，解得3x >或1x <，所以{1B x x =<或}3x >，所以{}0,4,5A B ⋂=， 故选：C9．已知a ，b 均为正实数，则“11a b>”是“2223a b ab +>”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【详解】a ，b 均为正实数，11a b>，故b a >， ()()22222332020a b ab a ab b a b a b +>⇒−+>⇒−−>，充分性，b a >，2b a >，故()()20a b a b −−>，充分性成立，必要性，()()20a b a b −−>，不妨设1,2a b ==，满足()()20a b a b −−>， 但不满足b a >，必要性不成立， 则“11a b>”是“2223a b ab +>”的充分不必要条件. 故选：A10．下列命题中假命题的是（ ） A ．0x ∃∈R ，0ln 0x < B ．(),0x ∀∈−∞，e 0x > C ．0x ∃∈R ，00sin x x > D ．()0,x ∀∈+∞，22x x >【答案】D【详解】由题意，对于A 中，例如：当01x e=时，此时01ln ln 10x e ==−<，所以A 为真命题；对于B 中，对任意(),0x ∈−∞，根据指数函数的性质，可得e 0x >成立，所以B 为真命题； 对于C 中，例如：当02x π=−时，此时0sin 1x =−，满足12π−>−，所以C 为真命题；对于D 中，例如：当2x =时，此时22x x =，所以D 为假命题. 故选：D .【点睛】本题主要考查了全称命题与存在性命题的真假判定，其中解答中熟记全称命题和存在性命题的真假判定方法，以及合理利用反例进行判定是解答的关键.11．已知集合{}{}20,320A x x m B x x x =<<=−+>，若R B A ⊆ð，则实数m 的取值范围为（ ）A ．(,2]−∞B ．(1,2]C ．[2,)+∞D ．(2,)+∞【答案】D【详解】因为23202x x x −+>⇒>或1x <， 所以{2,B x x =>或}1x <， 所以{}R |12B x x =££ð，又R B A ⊆ð，且{}0A x x m =<<， 所以m>2，所以实数m 的取值范围为(2,)+∞， 故选：D.12．下列命题为真命题的是（ ） A ．若a b >，则b c ba c a+>+ B ．若a b >，c d >，则a d b c −>− C ．若0a b <<，则22a ab b << D ．若a b >，则11a b a>− 【答案】B【详解】对于A ，可以取2a =，1b =，1c =−，此时b c ba c a+<+，所以A 错误. 对于B ：∵c d >，∴d c −>−，因为a b >，所以a d b c −>−，故B 正确；对于C ：取2a =−，1b =-时，则24a =，2ab =，21b =，则22a ab b >>，故C 错误； 对于D ：当1a =，1b =-时，112a b =−，11a=，则11a b a <−，故D 错误；故选：B.13．若命题“[]1,3a ∃∈,()2220ax a x +−−>”是假命题，则x 不能等于（ ）A ．1−B ．0C ．1D ．23【答案】C【详解】根据题意，知原命题的否定“[]1,3a ∀∈,()2220ax a x +−−≤”为真命题.令2()()22f a x x a x =+−−,{22(1)20(3)320f x x f x x =−−≤=+−≤,解得213x −≤≤. 故选:C.14．下列四个命题中，是假命题的是（ ） A ．x ∀∈R ，且10,2x x x≠+≥ B ．x ∃∈R ，使得212x x +≤C ．若x ＞0，y ＞02xyx y≥+ D ．若52x ≥，则24524x x x −+−的最小值为1【答案】A【详解】解析：选A.对于A ，x ∀∈R ，且10,2x x x≠+≥对x ＜0时不成立； 对于B ，当x ＝1时，x 2＋1＝2，2x ＝2，212x x +≤成立，正确；对于C ，若x ＞0，y ＞0，则()22222()248x y x y xy xy x y ++≥⋅=，2xyx y+，当且仅当0x y =>时取等号，C 正确；对于D ，2245(2)111(2)242(2)22x x x y x x x x −+−+⎡⎤===−+⎢⎥−−−⎣⎦，因为52x ≥，所以-20x >，所以111(2)1222x x ⎡⎤−+≥⨯=⎢⎥−⎣⎦，当且仅当122x x −=−，即3x =时取等号.故y 的最小值为1，D 正确. 故选：A15．已知全集U =R ，集合(){}223|log 11|14x A x x B x y ⎧⎫=−<=+=⎨⎬⎩⎭，，则能表示A B U ，，关系的图是（ ）A ．B ．C ．D ．【答案】B【详解】因为(){}{}3|log 11|14A x x x x =−<=<<，{}22|1|224x B x y x x ⎧⎫=+==−≤≤⎨⎬⎩⎭，所以{}|12A B x x ⋂=<≤， 对于A ，A B B =，错误； 对于C ，A B ⋂=∅，错误；对于D ，A B A =错误；B 选项符合题意， 故选：B.16．设实数a ，b ，c 满足，221a b c +≤≤则a b c ++的最小值为（ ）A 1B ．12−C ．D ．1−【答案】B【详解】由221a b c +≤≤可得：22221111()()2222a b c a b a b a b ++≥+++=+++−≥−，当12a b ==−时取等号，所以a b c ++的最小值为12−.故选：B17．记{}123max ,,x x x 表示123,,x x x 这3个数中最大的数．已知a ，b ，c 都是正实数，12max ,,b c M a a c b ⎧⎫=+⎨⎬⎩⎭，则M 的最小值为（ ）AB C ．D ．【答案】A【详解】因为12max ,,b c M a a c b ⎧⎫=+⎨⎬⎩⎭，所以a M ≤，c M b ≤，所以1212b M M M a c +≤+≤，所以3MM ≤，即M ≥ca b==M 故选：A18．已知集合{}{}32,1,0,1,2,3,4,0,Z ,22x U A xx B x −⎧⎫=−−=≥∈=⎨⎬+⎩⎭，则()U AB =ð（ ）A ．{}2−B ．{}3,4C ．{}2,3,4−D ．{}2,0,3,4−【答案】C【详解】由题意知{}{}(3)(2)0,20,Z 1,0,1,2,3A x x x x x =−+≥+≠∈=−，{}13B x x =−≤<， 则{}1,0,1,2A B ⋂=−，所以(){2,3,4}U AB =−ð． 故选：C ． 二、多选题19．设a ，b ，c ，d 为实数，且0a b c d >>>>，则下列不等式正确的有（ ） A ．2c cd < B ．a c b d −<− C ．ac bd < D ．0c da b−> 【答案】AD【详解】对于A ，由0c d >>和不等式性质可得2c cd <，故A 正确； 对于B ，因0a b c d >>>>，若取2a =，1b =，1c =−，2d =−， 则3a c −=，3b d −=，所以a c b d −=−，故B 错误；对于C ，因0a b c d >>>>，若取2a =，1b =，1c =−，2d =−， 则2ac =−，2bd =−，所以ac bd =，故C 错误； 对于D ，因为0a b >>，则110a b<<，又因0c d >>则0c d <−<−， 由不等式的同向皆正可乘性得，c d a b −<−，故0c da b−>，故D 正确． 故选：AD ．20．已知实数,a b 满足,1a b a b >+=，则（ ） A ．2a ab ＞ B ．2ab b > C ．14ab ≤D ．221a b +≥【答案】AC【详解】因为,10a b a b >+=>， 所以0,a b >的符号不确定， 由不等式的性质知2a ab ＞成立，但2ab b >不一定成立，故A 正确，B 错误；因()21111244ab a a a ⎛⎫=−=−−+≤ ⎪⎝⎭，故C 正确；因为a b >，所以222a b ab +>，所以222()122a b a b ++>=，故D 错误.故选：AC.21．已知全集{}2230U x x x =∈+−≤Z ∣，集合{}210B x x =−=∣，若U A ð有4个子集，且A B ⋂=∅，则（ ） A ．1A ∉ B ．集合A 有3个真子集 C ．3A −∈ D ．A B U ⋃=【答案】ACD【详解】依题意，()(){}{}{}{}130313,2,1,0,1,1,1U x x x x x B =∈−+≤=∈−≤≤=−−−=−ZZ ∣∣， 而U A ð有4个子集，A B ⋂=∅，故{}3,2,0A =−−，故集合A 有7个真子集，B 错误，1A ∉，3A −∈，A B U ⋃=，ACD 均正确.故选：ACD.22．已知集合{2,3,5,7,11,13,17},{2,5,7,13},{3,7,13,17},{7,13}U A B C ====，则下列关系正确的是（ ） A ．()()()⋂=⋃U U U A B A B ððð B ．()()U U U U A B =ðððð C ．A C B C ⋂=⋂ D ．()U U A B C =ðð【答案】ACD【详解】因为集合{2,3,5,7,11,13,17},{2,5,7,13},{3,7,13,17},{7,13}U A B C ====，可得{2,3,5,7,13,17}A B =，{7,13}A B =，{3,11,17},{2,5,11}U U A B ==ðð且()(),U U U U A A B B ==ðððð，对于A 中，由()(){11}U UA B =ðð，(){11}U AB =ð，可得()()()⋂=⋃U U U A B A B ððð，所以A 正确；对于B 中，由()(),U U U U A A B B ==ðððð，可得()()U U U U A B ≠ðððð，所以B 不正确； 对于C 中，由{7,13},{7,13}A C B C ==，可得A C B C ⋂=⋂，所以C 正确；对于D 中， 由(){2,3,5,11,17}U A B =ð，{2,3,5,11,17}U C =ð，所以()U U A B C =ðð，所以D 正确. 故选：ACD.23．对于R 的两个非空子集,A B ，定义运算(){},,A B x y x A y B ⨯=∈∈，则（ ） A ．A B B A ⨯=⨯ B ．()()()A B C A B A C ⨯=⨯⨯C ．若A C ⊆，则()()A B C B ⨯⊆⨯D ．A A ⨯表示一个正方形区域 【答案】BC【详解】由题意知，(){},,A B x y x A y B ⨯=∈∈表示以数集A 中的数为横坐标，数集B 中的数为纵坐标的点的集合，故A B B A ⨯≠⨯，故A 错误； 因为()()(){},,A B C x y x A y B C ⨯⋂=∈∈⋂，又()()(){}(){},,,,A B A C x y x A y B x y x A y C ⨯⋂⨯=∈∈⋂∈∈， 所以()()()A B C A B A C ⨯=⨯⨯，则B 正确；若A C ⊆，则()()A B C B ⨯⊆⨯，故C 正确；若{}1A =，集合A A ⨯只包含一个点，故D 错误． 故选：BC ．24．已知正数,a b 满足()()111a b −−=，则下列选项正确的是（ ） A ．111a b+= B ．25ab b+³ C ．4a b +≥ D ．228a b +≥【答案】ACD【详解】对于A ，由题可得ab a b =+，即111a b+=，故A 正确；对于()1B,221221a b b b b +=+-+³-，当且仅当1b =+B 不正确；对于C ，()112224b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当2a b ==时，等号成立，故C 正确；对于D ，2222()4822a b a b ++³³=，当且仅当2a b ==时，等号成立，故D 正确.故选：ACD.25．已知命题p ：0x ∃∈R ，20440ax x −−=，若p 为真命题，则a 的值可以为（ ） A ．2− B ．1− C ．0 D ．3【答案】BCD 【详解】命题p ：0x ∃∈R ，200440ax x −−=，p 为真命题，即2440ax x −−=有根， 当0a =时，=1x −成立，当0a ≠时，需满足2(4)4(4)0a ∆=−−⨯⋅−≥，解得1a ≥−且0a ≠，a ∴的取值范围为[1,)−+∞，故选：BCD ．26．已知22421a b ab ++=，则（ ）A ．ab 的最大值为16B ．224a b +的最小值为57C ．224a b +的最大值为2D ．ab 的最小值为13−【答案】AC【详解】对A ：由22a 4b 4ab +≥，得22426a b ab ab ++≥，所以16ab ≤， 当且仅当2a b =时取等号，故A 正确；对B ：由224222a b ab a b +=⋅≤，得()222234422a b a b ab +++≤，所以22243a b +≥，当且仅当2a b =时取等号，故B 错误； 对C ：由224222a b ab a b +=⋅≥−，得22224422a b a b ab +++≥，所以2242a b +≤，当且仅当2a b =−时取等号，故C 正确； 对D ：由2244a b ab +≥−，得22422a b ab ab ++≥−，所以12ab ≥−，当且仅当2a b =−时取等号，故D 错误.故选：AC.27．若表示集合M 和N 关系的Venn 图如图所示，则M ，N 可能是（ ）A ．{}{}0,2,4,6,4M N ==B ．{}{}2|1,1M x x N x x =<=−C ．{}1|log ,|e e xx M x y x N y y ⎧⎫====+⎨⎬⎩⎭D ．(){}(){}22,|,,|}M x y x y N x y y x ====【答案】ACD【详解】由题意可知：集合N 是集合M 的真子集， 对于选项A ：可知集合N 是集合M 的真子集，故A 正确；对于选项B ：因为{}{}2|1|11M x x x x =<=−<<，可知集合M 是集合N 的真子集，故B 错误；对于选项C ：因为{}{}|log |0M x y x x x ===>，且e 0x >，则1e 2e x x y =+≥，当且仅当1e e x x =，即0x =时，等号成立， 可得{}1|e |2e xx N y y y y ⎧⎫==+=≥⎨⎬⎩⎭，可知集合N 是集合M 的真子集，故C 正确；对于选项D ：因为(){}(){}(){}22,|,|},|}M x y x y x y y x x y y x =====−U ，可知集合N 是集合M 的真子集，故D 正确； 故选：ACD.28．以下说法正确的有（ ）A ．“24−<<x ”是“22150x x −−<”的必要不充分条件B ．命题“01x ∃>，()0ln 10x −≥”的否定是“1x ∀≤，()ln 10x −<”C ．“ln ln a b >”是“22a b >”的充分不必要条件D ．设a ，R b ∈，则“0a ≠”是“0ab ≠”的必要不充分条件 【答案】CD【详解】A 选项，()()2215530x x x x −−=−+<，解得35x −<<，所以“24−<<x ”是“22150x x −−<”的充分不必要条件，A 选项错误. B 选项，因为由()ln 10x −≥，得1x −≥，即2x ≥，命题“01x ∃>，()0ln 10x −≥”的否定是“1x ∀>，2x <”，所以B 选项错误. C 选项，ln ln 0a b a b >⇔>>；所以2222ln ln a b a b a b >⇒>>⇒ln ln a b⎧⎨>⎩，所以“ln ln a b >”是“22a b >”的充分不必要条件， 所以C 选项正确.D 选项，由于0a ≠⇒000ab ab a ⎧≠⎪⎨≠⇒≠⎪⎩，所以“0a ≠”是“0ab ≠”的必要不充分条件，所以D 选项正确. 故选：CD29．下列命题是真命题的是（ ）A ．若a b >，则ac bc >B ．若0a b >>，则33a b >C ．若ln ln a b >，则11a b <D ．若22a b +=，则244a b +≥【答案】BCD【详解】对于A ，当0c ≤时，ac bc >不成立，故A 错误；对于B ，由0a b >>，得()()33220a b a b a ab b −=−⋅++>，所以33a b >，故B 正确；对于C ，由ln ln a b >，得0a b >>，所以110a b<<，故C 正确；对于D ，因为22a b +=，所以244a b +≥===，当且仅当24a b =，即11,2a b ==时，等号成立， 故D 正确． 故选：BCD. 三、填空题30．已知集合{}230,{22},{}A xx x B x x C x x a =−<=−<<=<∣∣∣，且()A B C ⊆，则实数a 的取值范围是 . 【答案】[)2,+∞【详解】依题意，{}230{03}A xx x x x =−<=<<∣∣，则{02}A B x x =<<∣， 由()A B C ⊆，得2a ≥，所以a 的取值范围是[)2,+∞. 故答案为：[)2,+∞31．已知实数x 、y 满足223x y −≤+≤，220x y −≤−≤，则34x y −的取值范围为 ． 【答案】[7,2]−【详解】解：设34(2)(2)x y m x y n x y −=++−，则2324m n m n +=⎧⎨−=−⎩，解得12m n =−⎧⎨=⎩，所以34(2)x y x y −=−++2(2)x y −， 因为223x y −≤+≤，220x y −≤−≤， 所以3(2)2x y −≤−+≤，42(2)0x y −≤−≤， 所以7342x y −≤−≤， 故答案为：[7,2]−.32．已知集合{1,2,4}A =，{(,),,}B x y x A y A x y A =∈∈−∈∣，则集合B 的元素个数为 ． 【答案】2【详解】当1x =时，1y =，2，4，x y −分别为0,1,3−−,均不能满足x y A −∈， 当2x =时，1y =时可满足1x y A −=∈，2x =时，2,=0y x y =−，2x =时，4,=2y x y =−−均不满足x y A −∈，当4x =时，2y =可满足2x y A −=∈，4x =时，1,=3y x y =−，4x =时，4,=3y x y =−均不满足x y A −∈， 所以()(){}2142B =，，，，故集合B 的元素有2个， 故答案为：233．能够说明“设,,a b c 是任意实数，若a b c <<，则ac bc <”是假命题的一组整数,,a b c 的值依次为 . 【答案】2,1,0−−（答案不唯一） 【详解】若a b <，当0c >时，ac bc <； 当0c =时，ac bc =； 当0c <时，ac bc >；“设,,a b c 是任意实数，若a b c <<，则ac bc <”是假命题的一组整数,,a b c 的值依次为2,1,0−−， 故答案为：2,1,0−−（答案不唯一） 34．已知集合21{|0}1x A x x −=≤+，全集R U =，则U A =ð ． 【答案】(]1,1,2∞∞⎛⎫−−⋃+ ⎪⎝⎭【详解】解：集合21{|0}1x A x x −=≤+1|12x x ⎧⎫=−<≤⎨⎬⎩⎭，全集R U =，所以UA =ð(]1,1,2∞∞⎛⎫−−⋃+ ⎪⎝⎭， 故答案为：(]1,1,2∞∞⎛⎫−−⋃+ ⎪⎝⎭35．已知集合{}2|20A x x x a =−−+>，R B =，若A B ⋂=∅，则a 的取值范围是 ．【答案】1a ≤−【详解】因为R B =，A B ⋂=∅， 所以A =∅，则不等式220x x a −−+>无解， 所以440a ∆=+≤，解得1a ≤−. 故答案为：1a ≤−.36．已知集合{}220A x x x =∈−−≤N∣，集合(){}22210B x x a x a a =−+++=∣，若B A ⊆，则=a . 【答案】0或1【详解】由题意可知：{}{}{}220120,1,2A x x x x x =∈−−≤=∈−≤≤=NN ∣∣， (){}{}22210,1B x x a x a a a a =−+++==+∣，因为B A ⊆，可知{}0,1B =或{}1,2B =，可得0a =或1a =. 故答案为：0或1.37．如图，某人沿围墙CD 修建一个直角梯形花坛ABCD ，设直角边AD x =米，2BC x =米，若12AD AB BC ++=米，问当x = 米时，直角梯形花坛ABCD 的面积最大．【答案】2【详解】由题意123AB x =−米， 则直角梯形花坛ABCD 的面积()()(()23123212311312182224x x x x x S x x +−⎡⎤+−⎣⎦==⨯−≤⨯=， 当且仅当3123x x =−，即2x =时，等号成立， 所以当2x =米时，直角梯形花坛ABCD 的面积最大． 故答案为：2.38．已知集合12|log (2)0A x x ⎧⎫=+<⎨⎬⎩⎭，集合()(){}|0B x x a x b =−−<，若“ 3a =− ”是“A B ⋂≠∅”的充分条件，则实数b 的取值范围是 ． 【答案】1b >−【详解】解：12{|log (2)0}{|1}A x x x x =+<=>−， 3a =−(){|()()0}3,B x x a x b b ∴=−−<=−或(,3)b −，由“A B ⋂≠∅”，得1b >−， 故答案为：1b >−．【点睛】本题考查了充分必要条件，考查对数函数以及解不等式问题，考查集合的关系，是一道基础题．39．若命题：“0x ∃∈R ，使220(1)(1)10m x m x −−++≤”是假命题，则实数m 的取值范围为 ． 【答案】1m ≤−或53m >【详解】由题意得，“0x ∀∈R ，使2200(1)(1)10m x m x −−++>”是真命题，当2101m m −=⇒=±时，易得1m =−时命题成立；当()2101,1m m −<⇒∈−时，由抛物线开口向下，命题不成立；当()()210,11,m m −>⇒∈−∞−+∞时，则命题等价于()()2221413250m m m m ∆=+−−=−++<，即()()35101m m m −+>⇒<−或53m >故答案为：1m ≤−或53m >40．已知函数()2f x ax =+()0a >，()21g x x =−，若[]11,2x ∃∈−，[]22,3x ∀∈，使()()12f x g x =成立，则实数a 的取值范围是 . 【答案】[1,)+∞【详解】由题意，函数()21g x x =−在[]2,3为单调递减函数，可得 ()12g x ≤≤， 即函数()g x 的值域构成集合[1,2]B =，又由函数()2(0)f x ax a =+>在区间 []1,2−上单调递增，可得()222a f x a −+≤≤+， 即函数()f x 的值域构成集合[2,22]A a a =−++，又由[]11,2x ∃∈−， []22,3x ∀∈，使()()12f x g x =成立，即 B A ⊆,则满足21222a a −+≤⎧⎨+≥⎩，解得 1a ≥，即实数a 的取值范围是[1,)+∞. 故答案为：[1,)+∞.【点睛】结论点睛：本题考查不等式的恒成立与有解问题，可按如下规则转化：一般地，已知函数()[],,y f x x a b =∈， ()[],,y g x x c d =∈（1）若[]1,x a b ∀∈，[]2,x c d ∀∈，总有 ()()12f x g x <成立，故()()max min f x g x <； （2）若[]1,x a b ∀∈，[]2,x c d ∃∈，有 ()()12f x g x <成立，故()()max max f x g x <； （3）若[]1,x a b ∃∈， []2,x c d ∃∈，有()()12f x g x <成立，故 ()()min max f x g x <；（4）若[]1,x a b ∀∈， []2,x c d ∃∈，有()()12f x g x =，则 ()f x 的值域是()g x 值域的子集 ． 41．命题“任意(1,3)x ∈，4≥+a x x”为假命题，则实数a 的取值范围是 ． 【答案】(,5)−∞【详解】若命题“任意(1,3)x ∈，4≥+a x x ”为真命题，则max 4a x x ⎛⎫≥+ ⎪⎝⎭，设4y x x =+，(1,3)x ∈，44x x +≥=，当2x =时，等号成立， 由对勾函数的性质可知，当()1,2x ∈时，函数单调递减，当()2,3x ∈单调递增，()15f =，()43353f =+<，所以445x x ≤+<，即5a ≥，所以命题“任意(1,3)x ∈，4≥+a x x”为假命题，则a 的取值范围为(),5−∞. 故答案为：(),5−∞42．设条件p ：231x +<；条件q ：()()22220x a x a a −+++…，若q 是p 的必要不充分条件，则实数a 的取值范围是 . 【答案】[]3,2−−【详解】∵q 是p 的必要不充分条件，∴p q ⇒，且q p ⇒/. 记p ：{}{}|2312|1=+<=−<<−A x x x x ，q ：()(){}2220|2B x x a x a a =−+++≤={|x a x ≤≤}2a +，则A 是B 的真子集，从而221a a ≤−⎧⎨+≥−⎩解得32a −−≤≤.故实数a 的取值范围是[]3,2−− 故答案为：[]3,2−−【点睛】本题考查了含有绝对值不等式和一元二次不等式的解法，充分必要条件，集合之间的关系等基本数学知识，考查了运算求解能力和逻辑推理能力，属于基础题目.43．由命题“存在x ∈R ，使220x x m ++≤”是假命题，求得m 的取值范围是(,)a +∞，则实数a 的值是 . 【答案】1【详解】因为命题“存在x ∈R ，使220x x m ++≤”是假命题， 所以命题“R x ∀∈，220x x m ++>”是真命题， 故2240m ∆=−<，即1m >，故1a =. 故答案为：1。

集合与常用逻辑用语、不等式试题一、选择1．设集合{}{}2|lg(3),|540A x y x B x x x ==-=-+<，则AB =（ B ）A ．∅B ．()3,4C ．()2,1-D ．()4.+∞2．集合{}0,2,A a =,{}21,B a =,若{}0,1,2,4,16AB =,则a 的值为( D ) A.0 B.1 C.2 D.43．已知集合{}6,5,4=P ，{}3,2,1=Q ，定义{}Q q P p q p x x Q P ∈∈-==⊕,,|，则集合Q P ⊕的所有真子集的个数为（ B ）A ．32B ．31C ．30D ．以上都不对4．已知)(,13)(R x x x f ∈+=，若a x f <-|4)(|的充分条件是b x <-|1|，)0,(>b a ，则b a ,之间的关系是 （ B ） A ．3ba ≤B ． 3a b ≤C ．3a b >D ．3b a >5．下列说法错误的是 （ C ） A ．命题“若x 2 — 3x +2＝0，则x =1”的逆否命题为：“若x ≠1，则x 2—3x +2≠0” B ．“x ＞1”，是“|x |>1”的充分不必要条件 C ．若p ∧q 为假命题，则p 、q 均为假命题 D ．若命题p ：“∃x ∈R ，使得x 2+x +1＜0”,则⌝p ：“∀x ∈R ，均有x 2+x +1≥0” 6．集合{1,0,1}A =-,A 的子集中,含有元素0的子集共有 ( B ) A.2个 B.4个 C.6个 D.8个7．设集合A={x|1≤x ≤2},B={x|x ≥a }.若A ⊆B 则a 的范围是( B )A. a <1B. a ≤1C. a <2D. a ≤2 8．已知集合{}{}4),(,2),(=-==+=y x y x B y x y x A ，那么集合A B 为(D)A ．1,3-==y xB ．)1,3(-C ．{}1,3-D ．{})1,3(-9．命题“所有能被2整除的数都是偶数”的否定．．是( D ) A.所有不能被2整除的数都是偶数 B.所有能被2整除的数都不是偶数 C.存在一个不能被2整除的数是偶数 D.存在一个能被2整除的数不是偶数 10．设,x y ∈R ，那么“0x y <<”是“1xy>”的（ B ） A ．必要不充分条件 B ．充分不必要条件C ．充要条件D ．既不充分又不必要条件11．已知直线22x y +=与x 轴，y 轴分别交于,A B 两点，若动点(,)P a b 在线段AB 上，则ab 的最大值为（ A ）A ．12B ．2C ．3D ．31 12．已知f (x )为R 上的减函数，则满足f )1(x>f (1)的实数x 的取值范围是 （ D ）A ．(－∞,1)B ．(1,+∞)C ．(－∞,0)∪(0,1)D ．(－∞,0)∪(1,+ ∞) 13．下列结论正确的是（ B ） A ．当101,lg 2lg x x x x >≠+≥且时B．02x >≥当时C ．x x x 1,2+≥时当的最小值为2 D ．当102,x x x<≤-时无最大值 14．已知正数x 、y 满足⎩⎨⎧≥+-≤-05302y x y x ，则yx z +=22的最大值为（ B ）A ．8B ．16C ．32D ．64 15． 下列三个不等式中，恒成立的个数有( B ) ①12(0)x x x+≥≠; ②(0)c c a b c a b <>>>;③(,,0,)a m a a b m a b b m b+>><+。

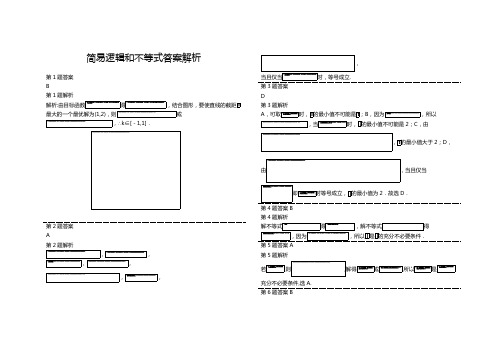
简易逻辑和不等式答案解析第1题答案B第1题解析解析:由目标函数得，结合图形，要使直线的截距最大的一个最优解为(1,2)，则或，∴k ∈[－1,1]．第2题答案A第2题解析，，，，，，，当且仅当时，等号成立.第3题答案D第3题解析A，可取时，的最小值不可能是；B，因为，所以，当时，的最小值不可能是2；C，由，的最小值大于2；D，由，当且仅当即时等号成立，的最小值为2．故选D．第4题答案B第4题解析解不等式得，解不等式得，因为，所以是的充分不必要条件．第5题答案A第5题解析若,则,解得或.所以是充分不必要条件,选A.第6题答案B第6题解析原命题的否定为任意，，由题意知，其为真命题，有，则，则.故选B.第7题答案B第7题解析令，则，做出可行域，平移直线，由图象知当直线经过点时，最小，当经过点时，最大，所以，所以，即的值域是，选B.第8题答案B 第8题解析①若，显然不成立；②若，显然不成立；③若，则，∴成立，④若，不成立，故选B.第9题答案B第9题解析因为是与的等比中项，则，，，因为a＞0，b＞0，所以，所以，所以.第10题答案A第10题解析依题意知，均为假命题，当是假命题时，恒成立，则有；当是真命题时，则有，.由，均为假命题得，即.故选A.第11题答案第11题解析设命题对应的集合分别为,由可得，集合，同理，命题对应的集合或．∴非对应的集合或，由题非是的充分不必要条件，∴解得. 故的取值范围为．第12题答案第12题解析(1)不等式恒成立，即函数图象全部在轴下方.（i) 当时，不恒成立；（ii) 当时，函数为二次函数，需满足图象开口向下且方程无解，即则无解.综上所述，不存在这样的，使不等式恒成立.（2）构造函数，①当时，即，检验得是符合题意。

②当时，此时函数是自变量为的一次函数，其图像是一条直线，由题意知直线当时的线段在下方，，即解出不等式组得：，且综上所述：的取值范围是：。

2023届高考数学复习：精选好题专项(不等式与逻辑用语多选题)练习题型一 不等式的性质1、（2022年湖南磁力一中高三月考试卷）下列四个条件中，能成为x y >的充分不必要条件的是（ ） A. 22xc yc >B. 22x y >C. x y >D. ln ln x y >2、（2022年江苏镇江市高三月考试卷）已知a ，b ，c ，d ∈R ，下列命题正确的是（ ） A. 若a <b <0，则a 2<ab <b 2B. 若a >b ，则ac 2≥bc 2C. 不等式e e 2a a -+≥恒成立D. 若a b >，且c d >，则()()ln ln ac bd >3、（2022ꞏ江苏无锡ꞏ高三期末）已知e e 1b a <<，则下列结论正确的是（ ） A ．22a b < B ．2b aa b+>C ．2ab b >D ．2lg lg()a ab <4、（2022ꞏ广东汕尾ꞏ高三期末）已知a ，b 都是不等于1的正实数，且a >b ，0<c <1，则下列不等式一定成立的是（ ） A ．a b c c > B ．c c a b >C ．log log c c a b >D ．11()()4a b a b++>5、（2022ꞏ山东济南ꞏ高三期末）已知实数a ，b ，c 满足0a b c >>>，则下列说法正确的是（ ） A ．()()11a c abc a <--B ．b bc a a c+<+ C ．2ab c ac bc +>+D ．()11a b a b ⎛⎫++ ⎪⎝⎭的最小值为46、（2022ꞏ山东泰安ꞏ高三期末）若,,0a b R a b ∈<<，则下列不等式中，一定成立的是（ ） A ．11a b a>- B ．11a b > C ．2a bb a+>D ．a b >7、（华南师范大学附属中学高三期末试题）已知0a b >>，则下列说法正确的是（ ） A.33b b a a +>+ B.3223a b aa b b+<+C. <D. lg lg lg 22a b a b++> 题型二 简单不等式1、(2022·江苏苏州期中)已知不等式x 2＋2ax ＋b －1＞0的解集是{x |x ≠d }，则b 的值可能是A ．－1B ．3C ．2D ．02、(2022·江苏常州期中)已知关于x 的不等式a e x ＋bx ＋c ＞0的解集为(－1，2)，则A ．a ＞0B ．b ＞0C ．c ＞0D ．a ＋b ＋c ＞03、（2022年湖南湘阴县知源高级中学高三月考试卷）已知关于x 的不等式20ax bx c ++>的解集为(,2)(3,)-∞-⋃+∞，则（ ）A. 0a >B. 不等式0bx c +>的解集是{}|6x x <-C. 0a b c ++>D. 不等式20cx bx a -+<的解集为11(,(,)32-∞-⋃+∞4、（2022年江苏盐城市高三月考试卷）若“2340x x +-<”是“222()330x k x k k -+++≥”的充分不必要条件，则实数k 可以是（ ）A. 8-B. 5-C. 1D. 45、（2022年重庆市北山中学高三月考试卷）. 下列叙述不正确的是（ ） A.12x<的解是12x >B. “04m ≤≤”是“210mx mx ++≥”的充要条件C. 已知x ∈R ，则“0x >”是“11x -<”的必要不充分条件D. 函数()2232f x x x =++的最小值是2- 题型三 基本不等式1、（2022年辽宁葫芦岛市中学高三月考试卷）已知0a >，0b >，4165log 2log 16a b +=，则下列结论正确的是（ ）A. 45a b +=B. 542a b +=C. ab 的最大值为2564D.11a b+的最小值为1852、 （2022年湖南邵阳市高三月考试卷）已知实数a ，b ，c 满足0a b c <<<，则下列说法正确的是（ ）A.()()11a c abc a >-- B.b bc a a c+>+ C. 2ab c ac bc +>+D. 11()()a b a b++的最小值为43、（2022ꞏ广东ꞏ铁一中学高三期末）若0,0a b >>．且4a b +=，则下列不等式恒成立的是（ ）A ．1104ab <≤ B 2 C ．111a b+≥D ．22118a b ≤+ 4、（2022ꞏ重庆ꞏ模拟预测）（多选题）已知正数a ，b 满足22a b ab +=，则下列说法一定正确的是（ ） A ．24a b +≥ B ．4a b +≥ C ．8ab ≥D ．2248a b +≥5、（2022ꞏ湖南常德ꞏ高三期末）若0a >，0b >，111a b+=，则（ ）A ．4ab ≤B ．4a b +≥C ．228a b +≤D ．22log log 2a b +≥6、（2022ꞏ湖北襄阳ꞏ高三期末）已知()lg f x x =，当a b <时，()()f a f b =，则（ ） A ．01a <<，1b >B ．10ab =C ．2114b a -<D ．224a b +>7、（2022ꞏ山东德州ꞏ高三期末）已知0a >，0b >，2a b ab +=，则下列结论正确的是（ ）A ．a b +的最小值为3+B ．22a b +的最小值为16CD ．lg lg a b +的最小值为3lg 28、（2022ꞏ山东烟台ꞏ高三期末）已知0a >，0b >，则下列命题成立的有（ ） A ．若1ab =，则222a b +≥ B ．若1ab =，则112a b +≥C ．若1a b +=，则2212a b +≤D ．若1a b +=，则114a b+≥9、（2022ꞏ湖北ꞏ蕲春县第一高级中学模拟预测）（多选题）若0,0a b >>，且4a b +=，则下列不等式恒成立的是（ ）A ．1104ab <≤ B ．111a b+≥C ．22log log 2a b +<D ．22118a b ≤+10、（2022ꞏ辽宁辽阳ꞏ二模）（多选题）已知0a >，0b >，且24a b +=，则（ ） A ．124a b ->B ．22log log 1a b +≤C ≥D ．412528a b +≥11、（2022ꞏ福建莆田ꞏ模拟预测）（多选题）已知直线l ：()100,0ax by a b ++=>>与圆C ：221x y +=相切，则下列说法正确的是（ ）A ．12ab ≥B ．22114a b+≥C ．2122a b +⎛⎫≤ ⎪⎝⎭D ．11a b+≤12、（2022ꞏ江苏ꞏ扬中市第二高级中学模拟预测）（多选题）已知0a >，0b >，且2a b ab +=，则（ ）A ．8ab ≥B ．3a b +≤+C ．24b >D ．()()221log 1log 24a b -⋅-≤13、（2022ꞏ湖南衡阳ꞏ三模）（多选题）已知实数0a >，0b >，1a b +=．则下列不等式正确的是（ ）A ．22a b +≥ BC ．112216a b ⎛⎫⎛⎫++≤ ⎪⎪⎝⎭⎝⎭D ．222a b a b b a +≤++14、（2022ꞏ辽宁葫芦岛ꞏ二模）（多选题）已知0a b >>，115a b a b+++=，则下列不等式成立的是（ ）A ．14a b <+<B ．114b a a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭C ．2211b a a b ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭D ．2211a b a b ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭15、（2022ꞏ河北ꞏ模拟预测）（多选题）已知220,0,2a b a b >>+=，则以下不等式成立的是（ ） A ．2a b +>B ．332a b +≥C ．114a b b a ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭ D ．112a b +≥参考答案题型一 不等式的性质1、（2022年湖南磁力一中高三月考试卷）下列四个条件中，能成为x y >的充分不必要条件的是（ ） A. 22xc yc > B. 22x y >C. x y >D. ln ln x y >【答案】AD 【答案解析】【要点分析】由充分必要条件的概念与不等式性质对选项逐一判断， 【过程详解】对于A ，若22xc yc >，则20c >，x y >，而当0c =，x y >时，22xc yc =，故22xc yc >是x y >的充分不必要条件，故A 正确， 对于B ，若22x y >，则x y >，若x y >，则22x y >， 故22x y >是x y >的充要条件，故B 错误，对于C ，当2,1x y =-=时，x y >，而x y <，故C 错误，对于D ，若ln ln x y >，则0x y >>，当x y >，0y <时，ln y 无意义， 故ln ln x y >是x y >的充分不必要条件，故D 正确， 故选：AD2、（2022年江苏镇江市高三月考试卷）已知a ，b ，c ，d ∈R ，下列命题正确的是（ ） A. 若a <b <0，则a 2<ab <b 2B. 若a >b ，则ac 2≥bc 2C. 不等式e e 2a a -+≥恒成立D. 若a b >，且c d >，则()()ln ln ac bd >【答案】BC 【答案解析】【要点分析】对于AD ，举反例即可排除； 对于B ，利用不等式的性质即可判断； 对于C ，利用基本不等式即可判断.【过程详解】对于A ，令2,1a b =-=-，则0a b <<，但2222(2)(1)a b =->-=，故A 错误； 对于B ，因为a b >，2c ≥0，所以22ac bc ≥，当0c =时取“"=，故B 正确；对于C ，因为e e 2a a -+≥=，当且仅当e e a a -=，即0a =时，等号成立，所以e e 2a a -+≥恒成立，故C 正确；对于D ，令1,2,3,4a b c d =-=-=-=-，则a b >，c d >，且3,8ac bd ==，所以由ln y x =的单调性可知()()ln ln ac bd <，故D 错误. 故选：BC.3、（2022ꞏ江苏无锡ꞏ高三期末）已知e e 1b a <<，则下列结论正确的是（ ） A ．22a b < B ．2b aa b+>C ．2ab b >D ．2lg lg()a ab <【答案】ABD 【要点分析】先根据函数单调性，得到0b a <<，AC 选项用作差法比较大小；B 选项用基本不等式求取值范围；D 选项，先用作差法，再结合函数单调性比大小. 【过程详解】e e 1b a <<，则0b a <<，因为22()()0a b a b a b -=-+<，所以22a b <，A 选项正确；因为0b a <<，所以0,0b a a b >>，由基本不等式得：2a b b a +>=，B 选项正确；2()0ab b b a b -=-<，2ab b ∴<，C 选项错误；2()0a ab a a b -=-<，2a ab ∴<，2lg lg a ab ∴<，D 选项正确，故选：ABD4、（2022ꞏ广东汕尾ꞏ高三期末）已知a ，b 都是不等于1的正实数，且a >b ，0<c <1，则下列不等式一定成立的是（ ）A ．a b c c >B ．c c a b >C ．log log c c a b >D ．11()()4a b ab++>【答案】BD 【要点分析】根据指数函数，对数函数，幂函数的单调性，结合题意，可判断A 、B 、C 的正误，根据基本不等式，可判断D 的正误，即可得答案.【过程详解】函数x y c =，因为01c <<，所以x y c =是减函数， 因为a >b ，所以a b c c <，故A 错．函数c y x =，因为01c <<，所以c y x =在(0,)+∞是增函数， 因为a >b ，所以c c a b >，故B 正确．函数log c y x =，因为01c <<，所以log c y x =在(0,)+∞是减函数， 因为a >b ，所以log log c c a b <，故C 错．11()1124a b a b a b b a ⎛⎫++=+++≥+= ⎪⎝⎭，当且仅当a b =时取等号， 又a b >，所以11()4a b a b ⎛⎫++> ⎪⎝⎭，故D 正确．故选：BD5、（2022ꞏ山东济南ꞏ高三期末）已知实数a ，b ，c 满足0a b c >>>，则下列说法正确的是（ ）A ．()()11a c abc a <--B ．b bc a a c+<+ C ．2ab c ac bc +>+ D ．()11a b a b ⎛⎫++ ⎪⎝⎭的最小值为4【答案】BC 【要点分析】对于A ，利用不等式的性质判断，对于BC ，作差判断即可，对于D ，利用基本不等式判断 【过程详解】对于A ，因为0a b c >>>，所以11a b <，10c a<-，所以()()11a c a b c a >--，所以A 错误， 对于B ，因为0a b c >>>，所以()0,()0c a b a a c ->+>， 所以()()()0()()()b c b a b c b a c ab ac ab bc c a b a c a a a c a a c a a c ++-++----===>++++，所以b b ca a c+<+，所以B 正确， 对于C ，因为0a b c >>>，所以0,0a c b c ->->，所以2()()()()()0ab c ac bc a b c c b c a c b c +-+=---=-->，所以2ab c ac bc +>+，所以C 正确，对于D ，因为0,0a b >>，所以()11224b a a b a b a b ⎛⎫++=++≥+= ⎪⎝⎭，当且仅当b a a b =即a b =时取等号，因为a b >，所以取不到等号，所以()11a b a b ⎛⎫++ ⎪⎝⎭的最小值不为4，所以D 错误，故选：BC6、（2022ꞏ山东泰安ꞏ高三期末）若,,0a b R a b ∈<<，则下列不等式中，一定成立的是（ ）A ．11a b a>- B ．11a b > C ．2a bb a+>D ．a b >【答案】BCD 【要点分析】以求差法判断选项AB ；以均值定理判断选项C ；以绝对值的几何意义判断选项D. 【过程详解】 选项A ：()()11()a a b b a b a a b a a b a---==---，由0a b <<，可知0a <，0b <，0a b -<， 则()0ba b a <-，即11a b a<-.选项A 判断错误；选项B ：11b aa b ab --=，由0a b <<，可知0a <，0b <，0b a ->，则0b a ab ->，即11a b>.选项B 判断正确； 选项C ：当0a b <<时，2a b b a +>=.选项C 判断正确； 选项D ：当0a b <<时，a b >.选项D 判断正确. 故选：BCD7、（华南师范大学附属中学高三期末试题）已知0a b >>，则下列说法正确的是（ ） A.33b b a a +>+ B.3223a b aa b b+<+C. <D. lg lg lg 22a b a b++> 【答案】BD 【答案解析】【过程详解】对于A ，因为()()330,033b a b b a b a a a a -+>>-=<++，所以33b b a a +<+，故A 错误； 对于B ，因为0a b >>，所以22a b >，所以()()()()()2223223320232323b aa b b a a b a b a a b b a b b a b b-+-++-==<+++，即3223a b a a b b +<+，故B 正确； 对于C ，因为0a b >>>>，所以>，故C 错误；对于D ，因为0a b >>，所以lg lg lg 22a b a b++>=，故D 正确. 故选：BD.题型二 简单不等式1、(2022·江苏苏州期中)已知不等式x 2＋2ax ＋b －1＞0的解集是{x |x ≠d }，则b 的值可能是A ．－1B ．3C ．2D ．0 【答案】BC【答案解析】由题意可知，方程x 2＋2ax ＋b －1＝0的根为d ，则∆＝4a 2－4(b －1)＝0，则b －1＝a 2≥0，所以b ≥1，则选项B 、C 正确；选项A 、D 错误；综上，答案选BC ．2、(2022·江苏常州期中)已知关于x 的不等式a e x ＋bx ＋c ＞0的解集为(－1，2)，则A ．a ＞0B ．b ＞0C ．c ＞0D ．a ＋b ＋c ＞0 【答案】BCD【答案解析】由题意可知，当a ＝0时，不等式不成立；当a ≠0时，－1，2是方程a e x ＋bx ＋c ＝0的两个根，则有⎩⎪⎨⎪⎧a e －1－b ＋c ＝0a e 2＋2b ＋c ＝0，所以⎩⎨⎧b ＝－a3()e 2－e －1＞0c ＝－a 3()e 2＋2e －1＞0，故选项B 正确；选项C 正确；对于选项D ，a ＋b ＋c ＝a －a 3(e 2－e －1)－a 3(e 2－2e －1)＝a [1－13(e 2－e －1)－13(e 2－2e －1)]＝a (1－e 23＋13e －e 23－23e )＝a (1－2e 23－13e )＞0，故选项D 正确；综上，答案选BCD ．3、（2022年湖南湘阴县知源高级中学高三月考试卷）已知关于x 的不等式20ax bx c ++>的解集为(,2)(3,)-∞-⋃+∞，则（ ）A. 0a >B. 不等式0bx c +>的解集是{}|6x x <-C. 0a b c ++>D. 不等式20cx bx a -+<的解集为11(,(,)32-∞-⋃+∞ 【答案】ABD 【答案解析】【过程详解】关于x 的不等式20ax bx c ++>的解集为()(),23,,0,A a ∞∞--⋃+∴>选项正确；且－2和3是关于x 的方程20ax bx c ++=的两根，由韦达定理得2323b a c a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，则,6b a c a =-=-，则60a b c a ++=-<，C 选项错误；不等式0bx c +>即为60ax a -->，解得6,B x <-选项正确；不等式20cx bx a -+<即为260ax ax a -++<，即2610x x -->，解得13x <-或1,D 2x >选项正确.故选：ABD .4、（2022年江苏盐城市高三月考试卷）若“2340x x +-<”是“222()330x k x k k -+++≥”的充分不必要条件，则实数k 可以是（ ）A. 8-B. 5-C. 1D. 4【答案】ACD 【答案解析】【过程详解】2340x x +-<，解得41x -<<，222()330x k x k k -+++≥即[]()(3)0x k x k --+≥，解得x k ≤或3x k ≥+，由题意知(4,1)-是(][),3,k k -∞⋃++∞的真子集， 所以1k ≥或34k +≤-， 所以1k ≥或7k ≤-，即(,7][1,)k ∈-∞-⋃+∞. 故选：ACD5、（2022年重庆市北山中学高三月考试卷）. 下列叙述不正确的是（ ） A.12x<的解是12x >B. “04m ≤≤”是“210mx mx ++≥”的充要条件C. 已知x ∈R ，则“0x >”是“11x -<”的必要不充分条件D. 函数()2232f x x x =++的最小值是2- 【答案】AD 【答案解析】 【过程详解】选项A ：12x<的解是12x >或0x <，故A 不正确；选项B ：由21y mx mx =++得24m m ∆=-，210mx mx ++≥恒成立则240m m m >⎧⎨-≤⎩或0m =，解得 04m ≤≤，所以“04m ≤≤”是“210mx mx ++≥”的充要条件，故B 正确；选项C ：由11x -<得111x -<-<，解得02x <<，所以“0x >”是“11x -<”的必要不充分条件，故C 正确；选项D ：由均值不等式得22322x x ++≥=+，当且仅当22322x x +=+时等号成立，此时x 无实数解，所以()2232f x x x =++的最小值大于2-，故D 不正确； 故选：AD题型三 基本不等式1、（2022年辽宁葫芦岛市中学高三月考试卷）已知0a >，0b >，4165log 2log 16a b +=，则下列结论正确的是（ ）A. 45a b +=B. 542a b +=C. ab 的最大值为2564D.11a b+的最小值为185【答案】BCD【答案解析】【过程详解】由4165log 2log 16a b +=可得，52816a b +=，即542a b +=．所以A 错误，B 正确；因为5254264a b ab =+≥⇒≤，当且仅当55,164a b ==时取等号，所以ab 的最大值为2564，C 正确；因为()11211244555b a a b a b a b a b ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭(218555≥+=，当且仅当55,126a b ==时取等号，所以11a b+的最小值为185，D 正确．故选：BCD ．2、 （2022年湖南邵阳市高三月考试卷）已知实数a ，b ，c 满足0a b c <<<，则下列说法正确的是（ ）A.()()11a c abc a >--B.b bc a a c+>+ C. 2ab c ac bc +>+ D. 11()()a b a b++的最小值为4 【答案】ABC 【答案解析】【过程详解】由题0a b c <<<，所以有()()1111b a ac a b c a a b>⇒>⇒>--，故A 正确；()()b b c b a c a b c bc ac b a a a c+>⇒+>+⇒>⇒>+，故B 正确； ()()()()200ab c ac bc c c b a c b c a c b +>+⇒--->⇒-->，故C 正确；11()(224b a a b a b a b ++=++≥+=，当且仅当a b b a =即a b =时取等，又因为0a b <<，所以11()(4a b a b++>，即11()(a b a b++无最小值，故D 错误. 故选：ABC.3、（2022ꞏ广东ꞏ铁一中学高三期末）若0,0a b >>．且4a b +=，则下列不等式恒成立的是（ ）A ．1104ab <≤ B 2C ．111a b+≥D ．22118a b ≤+ 【答案】CD 【要点分析】结合基本不等式对选项进行要点分析，由此确定正确选项. 【过程详解】22222a b a b ab ++⎛⎫≤≤⎪⎝⎭，当且仅当2a b ==时等号成立， 则2442ab ⎛⎫≤= ⎪⎝⎭或222422a b +⎛⎫≤ ⎪⎝⎭，则222211112,8,48a b ab a b ≥≤+≥≤+， 即AB 错误，D 正确.对于C 选项，1141414a b a ab ab b ++==≥⨯=，C 选项正确. 故选：CD4、（2022ꞏ重庆ꞏ模拟预测）（多选题）已知正数a ，b 满足22a b ab +=，则下列说法一定正确的是（ ） A ．24a b +≥ B ．4a b +≥ C ．8ab ≥ D ．2248a b +≥【答案】AD 【要点分析】由基本不等式判断AD ，取1,2b a ==判断BC. 【过程详解】 由题意可知1112b a +=，1122(2)2422a b a b a b b a b a ⎛⎫+=++=++ ⎪⎝⎭…（当且仅当22a b ==时取等号），故A 正确；取1,2b a ==，则3,2a b ab +==，故BC 错误；因为22a b ab +=≥所以2ab …（当且仅当22a b ==时取等号），则22448a b ab +厖（当且仅当22a b ==时取等号），故D 正确； 故选：AD5、（2022ꞏ湖南常德ꞏ高三期末）若0a >，0b >，111a b+=，则（ ）A ．4ab ≤B ．4a b +≥C ．228a b +≤D ．22log log 2a b +≥【答案】BD 【要点分析】利用基本不等式及指对数函数的性质逐项要点分析即得. 【过程详解】∵0a >，0b >，111a b +=≥ ∴4ab ≥，当且仅当2a b ==时取等号，故A 错误；由()1124b a a b a b a b a b ⎛⎫+=++=++≥ ⎪⎝⎭，当且仅当b a a b =，即2a b ==时取等号，故B 正确；因为228a b ≥≥=+，当且仅当2a b ==时取等号，故C 错误； 因为()2222log log log log 42a b ab +=≥=，当且仅当2a b ==时取等号，故D 正确.故选：BD.6、（2022ꞏ湖北襄阳ꞏ高三期末）已知()lg f x x =，当a b <时，()()f a f b =，则（ ） A ．01a <<，1b >B ．10ab =C ．2114b a -<D ．224a b +>【答案】ACD 【要点分析】利用()()f a f b =，可得lg lg a b -=，从而得到1ab =，再对每一个选项进行要点分析即可. 【过程详解】因为()()f a f b =，且a b <，可得lg lg lg lg 0a b a b -=⇒+=，从而得到1ab =， 因为0a b <<，所以01a b <<<，所以2221111()244b b b b a -=-+=--+<，而12a b b b +=+>=，（1b >，等号不成立）所以422ab>==>=+.从而可知选项ACD 正确. 故选：ACD7、（2022ꞏ山东德州ꞏ高三期末）已知0a >，0b >，2a b ab +=，则下列结论正确的是（ ）A ．a b +的最小值为3+B ．22a b +的最小值为16CD ．lg lg a b +的最小值为3lg 2【答案】ACD 【要点分析】利用“1”的代换结合基本不等式判断AD +C ，由对数的运算结合基本不等式判断B. 【过程详解】由2a b ab +=可得，211b a +=，212()33a b a b a b b a b a ⎛⎫+=++=+++ ⎪⎝⎭…2b ==等号），故A 正确；214(2)448a b ab a b b a b a ⎛⎫=++=+++= ⎪⎝⎭…（当且仅当24b a ==时，取等号），即lg lg lg lg83lg 2a b ab +=≥=，故D 正确；222a b ab +≥（当且仅当3b a ==时，取等号），8ab …（当且仅当24b a ==时，取等号），即2216a b +>，故B 错误；212112a b =+++=≤（当且仅当1212a b ==时，取等号），故C 正确； 故选：ACD8、（2022ꞏ山东烟台ꞏ高三期末）已知0a >，0b >，则下列命题成立的有（ ） A ．若1ab =，则222a b +≥ B ．若1ab =，则112a b +≥C ．若1a b +=，则2212a b +≤ D ．若1a b +=，则114a b+≥【答案】ABD 【要点分析】利用基本不等式逐项判断. 【过程详解】A.若1ab =，则2222a b ab +≥=，当且仅当1a b ==时，等号成立，故正确；B.若1ab =，则112a b +≥=当且仅当1a b ==时，等号成立，故正确；C.若1a b +=，则()2221122=+≥+a b a b ，当且仅当1a b ==时，等号成立，故错误； D.若1a b +=，则2111421a b ab a b ab a b +==≥++⎛⎫ ⎪⎝⎭=，当且仅当1a b ==时，等号成立，故正确；故选：ABD9、（2022ꞏ湖北ꞏ蕲春县第一高级中学模拟预测）（多选题）若0,0a b >>，且4a b +=，则下列不等式恒成立的是（ ）A ．1104ab <≤ B ．111a b +≥C ．22log log 2a b +<D ．22118a b ≤+【答案】BD 【要点分析】由基本不等式对选项逐一判断【过程详解】因为0,0a b >>，22222a b a b ab ++⎛⎫≤≤⎪⎝⎭，当且仅当2a b ==时等号成立， 则2442ab ⎛⎫≤= ⎪⎝⎭或222422a b +⎛⎫≤ ⎪⎝⎭，当且仅当2a b ==时等号成立，则222211112,8,48a b ab a b ≥≤+≥≤+， 当且仅当2a b ==时等号成立，则22222log log log log 22a b ab +=≤≤，当且仅当2a b ==时等号成立，故AC 错误，D 正确. 对于B 选项，1141414a b a ab ab b ++==≥⨯=， 当且仅当2a b ==时等号成立，故B 正确. 故选：BD10、（2022ꞏ辽宁辽阳ꞏ二模）（多选题）已知0a >，0b >，且24a b +=，则（ ） A ．124a b ->B ．22log log 1a b +≤C ≥D ．412528a b +≥ 【答案】BD【要点分析】由不等式的性质与基本不等式对选项逐一判断 【过程详解】对于A ，02a <<，()()42344,2a b a a a -=--=-∈-，所以12416a b -<<，故A 错误，对于B ，420a b =+≥>，即0<≤02ab <?，()222log log log 1a b ab +=≤，故B 正确，对于C ，228a b =++≤≤C 错误，对于D ，4122171725288488a b a b b a a b a b a b ++⎛⎫+=+=++≥+= ⎪⎝⎭，当且仅当825a b ==时，等号成立，故D 正确． 故选：BD11、（2022ꞏ福建莆田ꞏ模拟预测）（多选题）已知直线l ：()100,0ax by a b ++=>>与圆C ：221x y +=相切，则下列说法正确的是（ ）A ．12ab ≥B ．22114a b+≥C ．2122a b +⎛⎫≤ ⎪⎝⎭D ．11a b+≤【答案】BC 【要点分析】先根据直线和圆相切得到221a b +=，再利用基本不等式判定选项A 错误、选项B 、C 正确，利用反例得到选项D 错误. 【过程详解】因为直线l ：10ax by ++=与圆C ：221x y +=相切， 所以圆心(0,0)C 到直线l 的距离等于1，1=，即221a b +=，且0a >，0b >；对于A ：因为222a b ab +≥且221a b +=，所以22122a b ab +=≤，即选项A 错误；对于B ：因为221a b +=，所以222222222222112a b a b b a a b a b a b+++=+=++24≥+=（当且仅当2222b a a b =，即a b =时取等号）， 即选项B 正确；对于C ：因为222a b ab +≥且221a b +=， 所以222222224412()a b ab a a b b +++⎛⎫+⎭≤ ⎝=⎪=（当且仅当a b =时取等号）， 即选项C 正确；对于D ：当219a =且289b =时，1134a b +=+>即选项D 错误. 故选：BC.12、（2022ꞏ江苏ꞏ扬中市第二高级中学模拟预测）（多选题）已知0a >，0b >，且2a b ab +=，则（ ） A．8ab ≥B ．3a b +≤+C ．24b >D ．()()221log 1log 24a b -⋅-≤【答案】ACD 【要点分析】利用基本不等式判断AB ，由不等式性质和指数函数性质判断C ．由基本不等式结合对数运算法则判断D ． 【过程详解】对于A，2a b ab +=≥8ab ≥，当且仅当2a =，4b =时，等号成立．对于B ，2a b ab +=变形得211b a +=，所以()212213ab a b a b b a b a ⎛⎫+=++=+++≥+ ⎪⎝⎭当且仅当2a b b a =，即2b ==时，等号成立，故B 错误． 对于C ，因为211ba+=，所以201b<<，即2b >，则24b >． 对于D ，由2a b ab +=可得()()122a b --=，()()222log [(1)(2)]1log 1log 2a a b b -+---==，()()()()22222log 1log 2log 1log 22a b a b -+-⎡⎤-⋅-≤⎢⎥⎣⎦14=，当且仅当12a b -=-，即1a =，2b =+时等号成立． 故选：ACD ．13、（2022ꞏ湖南衡阳ꞏ三模）（多选题）已知实数0a >，0b >，1a b +=．则下列不等式正确的是（ ） A．22a b +≥ BC ．112216a b ⎛⎫⎛⎫++≤ ⎪⎪⎝⎭⎝⎭D．222a b a b b a+≤++【答案】ABD 【要点分析】对于A 、D 利用1b a =-换元整理，22222abaa +=+，222211313a b a a b b a a a t t++==++-++-，再结合基本不等式；对于B 根据()2222a b a b ++≥，代入整理；对于C 113224a b ab ⎛⎫⎛⎫++=+ ⎪⎪⎝⎭⎝⎭，结合()24a b ab +≤计算处理． 【过程详解】∵1a b +=，则1b a =-∴12222222a b a a a a-+=+≥=+222aa =即12ab ==时等号成立A 正确；()222222211111a b a a a a b b a a a a a a a -++=+=+++--+-+令()11,2t a =+∈，则1a t =-221131333a t a a t t t t +==≤-+-++-3t t=即t 时等号成立 D 正确；∵22a b +≥，即212≥≤，当且仅当12a b ==时等号成立，B 正确； ∵()2144a b ab +≤=，当且仅当12a b ==时等号成立 ()421112121322416ab a b a b a b a b ab ab +++++⎛⎫⎛⎫++=⨯==+≥ ⎪⎪⎝⎭⎝⎭，C 不正确； 故选：ABD ．14、（2022ꞏ辽宁葫芦岛ꞏ二模）（多选题）已知0a b >>，115a b a b+++=，则下列不等式成立的是（ ） A ．14a b <+<B ．114b a a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭C ．2211b a a b ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭D ．2211a b a b ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭【答案】AB 【要点分析】AB 选项，利用基本不等式进行求解；CD 选项，利用作差法比较大小. 【过程详解】 115a b a b +++=，即5a b a b ab+++=，所以()5a b ab a b +=-+，因为0a b >>，所以由基本不等式得：()24a b ab +<，所以()()254a b a ba b ++<-+，解得：14a b <+<，A 正确；111224b a ab a b ab ⎛⎫⎛⎫++=++≥≥ ⎪⎪⎝⎭⎝⎭，当且仅当1ab ab =时等号成立，故B 正确； ()221111111111b a b a b a b a b a a b a b a b a b ab ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+=++++--=++++- ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，因为0a b >>，所以()11110b a b a a b ab ⎛⎫⎛⎫++++-< ⎪⎪⎝⎭⎝⎭，所以2211b a a b ⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭，C 错误；()221111111111a b a b a b a b b a a b a b a b a b ab ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+=++++--=+++-- ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，因为0a b >>，而1ab 可能比1大，可能比1小，所以()1111a b b a a b ab ⎛⎫⎛⎫+++-- ⎪⎪⎝⎭⎝⎭符号不确定，所以D 错误， 故选：AB15、（2022ꞏ河北ꞏ模拟预测）（多选题）已知220,0,2a b a b >>+=，则以下不等式成立的是（ ） A ．2a b +> B ．332a b +≥C ．114a b b a ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭ D ．112a b +≥【答案】BCD 【要点分析】直接利用基本不等式即可判断ACD ，由2a b +≤，可得()()()33332a b a b a b +≥++，整理即可判断B.【过程详解】解：对于A ，因为220,0,2a b a b >>+=，所以()()22224a b a b +≤+=，所以2a b +≤，当且仅当1a b ==时取等号，故A 错误；对于B ，()()()33332a b a b a b +≥++4334a ab a b b =+++()()22222222=+-++a b a b ab a b ()()222222a b ab a b ab ab =+++-⋅ ()()222222a b ab a b ab =+++- ()()22224a b ab a b =++-≥，当且仅当1a b ==时取等号，所以()3324a b +≥，即332a b +≥，故B 正确；对于C ，111224a b ab b a ab ⎛⎫⎛⎫++=++= ⎪⎪⎝⎭⎝⎭≥，当且仅当1abab=，即1ab=时取等号，故C正确；对于D，112a b+≥≥=，当且仅当11a b=且a b=，即1a b==时取等号，故D正确.故选：BCD.。

一元二次方程、不等式考试要求 1.会从实际情景中抽象出一元二次不等式.2.结合二次函数图象，会判断一元二次方程的根的个数，以及解一元二次不等式.3.了解简单的分式、绝对值不等式的解法．知识梳理1．二次函数与一元二次方程、不等式的解的对应关系判别式Δ＝b 2－4acΔ>0 Δ＝0 Δ<0二次函数y ＝ax 2＋bx ＋c (a >0)的图象方程ax 2＋bx ＋c ＝0(a >0)的根有两个不相等的实数根x 1，x 2(x 1<x 2)有两个相等的实数根x 1＝x 2＝－b2a没有实数根ax 2＋bx ＋c >0(a >0)的解集{x |x <x 1，或x >x 2}错误!Rax 2＋bx ＋c <0(a >0)的解集{x |x 1<x <x 2}∅ ∅2.分式不等式与整式不等式 (1)f xg x>0(<0)⇔f (x )g (x )>0(<0)；(2)f xg x≥0(≤0)⇔f (x )g (x )≥0(≤0)且g (x )≠0.3．简单的绝对值不等式|x |>a (a >0)的解集为(－∞，－a )∪(a ，＋∞)，|x |<a (a >0)的解集为(－a ，a )． 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若方程ax 2＋bx ＋c ＝0无实数根，则不等式ax 2＋bx ＋c >0的解集为R .( × ) (2)若不等式ax 2＋bx ＋c >0的解集为(x 1，x 2)，则a <0.( √ ) (3)若ax 2＋bx ＋c >0恒成立，则a >0且Δ<0.( × )(4)不等式x －ax －b≥0等价于(x －a )(x －b )≥0.( × ) 教材改编题1．若集合A ＝{x |x 2－9x >0}，B ＝{x |x 2－2x －3<0}，则A ∪B 等于( ) A ．R B ．{x |x >－1} C ．{x |x <3或x >9} D ．{x |x <－1或x >3} 答案 C解析 A ＝{x |x >9或x <0}，B ＝{x |－1<x <3}， ∴A ∪B ＝{x |x <3或x >9}．2．若关于x 的不等式ax 2＋bx ＋2>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <13，则a ＋b ＝________. 答案 －14解析 依题意知⎩⎪⎨⎪⎧－b a ＝－12＋13，2a ＝⎝ ⎛⎭⎪⎫－12×13，解得⎩⎪⎨⎪⎧a ＝－12，b ＝－2，∴a ＋b ＝－14.3．一元二次不等式ax 2＋ax －1<0对一切x ∈R 恒成立，则实数a 的取值范围是________． 答案 (－4,0)解析 依题意知⎩⎪⎨⎪⎧a <0，Δ<0，即⎩⎪⎨⎪⎧a <0，a 2＋4a <0，∴－4<a <0.题型一 一元二次不等式的解法 命题点1 不含参的不等式例1 (1)不等式－2x 2＋x ＋3<0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1<x <32 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－32<x <1C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x <－1或x >32 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－32或x >1答案 C解析 －2x 2＋x ＋3<0可化为2x 2－x －3>0， 即(x ＋1)(2x －3)>0， ∴x <－1或x >32.(2)(多选)已知集合M ＝{}x ||x －1|≤2，x ∈R ，集合N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪5x ＋1≥1，x ∈R ，则( ) A ．M ＝{}x |－1≤x ≤3 B ．N ＝{}x |－1≤x ≤4 C ．M ∪N ＝{}x |－1≤x ≤4 D ．M ∩N ＝{}x |－1<x ≤3 答案 ACD解析 由题设可得M ＝[－1,3]，N ＝(－1,4]， 故A 正确，B 错误；M ∪N ＝{x |－1≤x ≤4}，故C 正确；而M ∩N ＝{x |－1<x ≤3}，故D 正确． 命题点2 含参的不等式例2 解关于x 的不等式ax 2－(a ＋1)x ＋1<0(a >0)． 解 原不等式变为(ax －1)(x －1)<0，因为a >0，所以⎝⎛⎭⎪⎫x －1a (x －1)<0.所以当a >1时，解得1a<x <1； 当a ＝1时，解集为∅； 当0<a <1时，解得1<x <1a.综上，当0<a <1时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1<x <1a ； 当a ＝1时，不等式的解集为∅；当a >1时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1a<x <1.延伸探究 在本例中，把a >0改成a ∈R ，解不等式． 解 当a >0时，同例2，当a ＝0时， 原不等式等价于－x ＋1<0，即x >1， 当a <0时，1a<1，原不等式可化为⎝⎛⎭⎪⎫x －1a (x －1)>0，解得x >1或x <1a.综上，当0<a <1时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1<x <1a ， 当a ＝1时，不等式的解集为∅，当a >1时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1a<x <1， 当a ＝0时，不等式的解集为{x |x >1}，当a <0时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <1a或x >1. 教师备选解关于x 的不等式x 2－ax ＋1≤0. 解 由题意知，Δ＝a 2－4，①当a 2－4>0，即a >2或a <－2时，方程x 2－ax ＋1＝0的两根为x ＝a ±a 2－42，∴原不等式的解为a －a 2－42≤x ≤a ＋a 2－42.②若Δ＝a 2－4＝0，则a ＝±2.当a ＝2时，原不等式可化为x 2－2x ＋1≤0， 即(x －1)2≤0，∴x ＝1；当a ＝－2时，原不等式可化为x 2＋2x ＋1≤0， 即(x ＋1)2≤0，∴x ＝－1. ③当Δ＝a 2－4<0，即－2<a <2时， 原不等式的解集为∅.综上，当a >2或a <－2时，原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a －a 2－42≤x ≤a ＋a 2－42； 当a ＝2时，原不等式的解集为{1}； 当a ＝－2时，原不等式的解集为{－1}；当－2<a <2时，原不等式的解集为∅.思维升华 对含参的不等式，应对参数进行分类讨论，常见的分类有 (1)根据二次项系数为正、负及零进行分类． (2)根据判别式Δ与0的关系判断根的个数． (3)有两个根时，有时还需根据两根的大小进行讨论．跟踪训练1 (1)(多选)已知关于x 的不等式ax 2＋bx ＋c ≥0的解集为{x |x ≤－3或x ≥4}，则下列说法正确的是( ) A ．a >0B ．不等式bx ＋c >0的解集为{x |x <－4}C ．不等式cx2－bx ＋a <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－14或x >13 D ．a ＋b ＋c >0 答案 AC解析 关于x 的不等式ax 2＋bx ＋c ≥0的解集为(－∞，－3]∪[4，＋∞)， 所以二次函数y ＝ax 2＋bx ＋c 的开口方向向上，即a >0，故A 正确； 对于B ，方程ax 2＋bx ＋c ＝0的两根分别为－3,4，由根与系数的关系得⎩⎪⎨⎪⎧－ba＝－3＋4，ca ＝－3×4，解得⎩⎪⎨⎪⎧b ＝－a ，c ＝－12a .bx ＋c >0⇔－ax －12a >0，由于a >0，所以x <－12，所以不等式bx ＋c >0的解集为{}x |x <－12， 故B 不正确；对于C ，由B 的分析过程可知⎩⎪⎨⎪⎧b ＝－a ，c ＝－12a ，所以cx 2－bx ＋a <0⇔－12ax 2＋ax ＋a <0⇔12x 2－x －1>0⇔x <－14或x >13，所以不等式cx 2－bx ＋a <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <－14或x >13，故C 正确； 对于D ，a ＋b ＋c ＝a －a －12a ＝－12a <0，故D 不正确． (2)解关于x 的不等式(x －1)(ax －a ＋1)>0.解 ①当a ＝0时，原不等式可化为x －1>0，即x >1； 当a ≠0时，(x －1)(ax －a ＋1)＝0的两根分别为1,1－1a.②当a >0时，1－1a<1，∴原不等式的解为x >1或x <1－1a.③当a <0时，1－1a>1，∴原不等式的解为1<x <1－1a.综上，当a ＝0时，原不等式的解集为{x |x >1}；当a >0时，原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >1或x <1－1a ； 当a <0时，原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1<x <1－1a . 题型二 一元二次不等式恒(能)成立问题 命题点1 在R 上恒成立问题例3 (2022·漳州模拟)对∀x ∈R ，不等式(a －2)x 2＋2(a －2)x －4<0恒成立，则a 的取值范围是( ) A ．－2<a ≤2 B ．－2≤a ≤2 C ．a <－2或a ≥2 D ．a ≤－2或a ≥2答案 A解析 不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立，当a －2＝0，即a ＝2时，－4<0恒成立，满足题意；当a －2≠0时，要使不等式恒成立，需⎩⎪⎨⎪⎧a －2<0，Δ<0，即有⎩⎪⎨⎪⎧a <2，4a －22＋16a －2<0，解得－2<a <2.综上可得，a 的取值范围为(－2,2]． 命题点2 在给定区间上恒成立问题例4 已知函数f (x )＝mx 2－mx －1.若对于x ∈[1,3]，f (x )<5－m 恒成立，则实数m 的取值范围为________． 答案 ⎝⎛⎭⎪⎫－∞，67 解析 要使f (x )<－m ＋5在x ∈[1,3]上恒成立，即m ⎝ ⎛⎭⎪⎫x －122＋34m －6<0在x ∈[1,3]上恒成立．有以下两种方法：方法一 令g (x )＝m ⎝ ⎛⎭⎪⎫x －122＋34m －6，x ∈[1,3]．当m >0时，g (x )在[1,3]上单调递增， 所以g (x )max ＝g (3)，即7m －6<0， 所以m <67，所以0<m <67；当m ＝0时，－6<0恒成立；当m <0时，g (x )在[1,3]上单调递减， 所以g (x )max ＝g (1)，即m －6<0， 所以m <6，所以m <0.综上所述，m 的取值范围是⎝⎛⎭⎪⎫－∞，67.方法二 因为x 2－x ＋1＝⎝ ⎛⎭⎪⎫x －122＋34>0，又因为m (x 2－x ＋1)－6<0在x ∈[1,3]上恒成立， 所以m <6x 2－x ＋1在x ∈[1,3]上恒成立．令y ＝6x 2－x ＋1，因为函数y ＝6x 2－x ＋1＝6⎝ ⎛⎭⎪⎫x －122＋34在[1,3]上的最小值为67，所以只需m <67即可． 所以m 的取值范围是⎝ ⎛⎭⎪⎫－∞，67.命题点3 给定参数范围的恒成立问题例5 (2022·宿迁模拟)若不等式x 2＋px >4x ＋p －3，当0≤p ≤4时恒成立，则x 的取值范围是( ) A ．[－1,3] B ．(－∞，－1] C ．[3，＋∞)D ．(－∞，－1)∪(3，＋∞) 答案 D解析 不等式x 2＋px >4x ＋p －3 可化为(x －1)p ＋x 2－4x ＋3>0，由已知可得[(x －1)p ＋x 2－4x ＋3]min >0(0≤p ≤4)， 令f (p )＝(x －1)p ＋x 2－4x ＋3(0≤p ≤4)，可得⎩⎪⎨⎪⎧f 0＝x 2－4x ＋3>0，f4＝4x －1＋x 2－4x ＋3>0，∴x <－1或x >3.教师备选函数f (x )＝x 2＋ax ＋3.若当x ∈[－2,2]时，f (x )≥a 恒成立，则实数a 的取值范围是________． 若当a ∈[4,6]时，f (x )≥0恒成立，则实数x 的取值范围是________________． 答案 [－7,2](－∞，－3－6]∪[－3＋6，＋∞)解析 若x 2＋ax ＋3－a ≥0在x ∈[－2,2]上恒成立， 令g (x )＝x 2＋ax ＋3－a ，则有①Δ≤0或②⎩⎪⎨⎪⎧Δ>0，－a2<－2，g －2＝7－3a ≥0.或③⎩⎪⎨⎪⎧Δ>0，－a 2>2，g 2＝7＋a ≥0，解①得－6≤a ≤2，解②得a ∈∅， 解③得－7≤a <－6.综上可得，满足条件的实数a 的取值范围是[－7,2]． 令h (a )＝xa ＋x 2＋3.当a ∈[4,6]时，h (a )≥0恒成立．只需⎩⎪⎨⎪⎧h 4≥0，h 6≥0，即⎩⎪⎨⎪⎧x 2＋4x ＋3≥0，x 2＋6x ＋3≥0，解得x ≤－3－6或x ≥－3＋ 6.∴实数x 的取值范围是(－∞，－3－6]∪[－3＋6，＋∞)． 思维升华 恒成立问题求参数的范围的解题策略(1)弄清楚自变量、参数．一般情况下，求谁的范围，谁就是参数．(2)一元二次不等式在R 上恒成立，可用判别式Δ，一元二次不等式在给定区间上恒成立，不能用判别式Δ，一般分离参数求最值或分类讨论．跟踪训练2 (1)已知关于x 的不等式－x 2＋4x ≥a 2－3a 在R 上有解，则实数a 的取值范围是( )A ．{a |－1≤a ≤4}B ．{a |－1<a <4}C ．{a |a ≥4或a ≤－1}D ．{a |－4≤a ≤1}答案 A解析 因为关于x 的不等式－x 2＋4x ≥a 2－3a 在R 上有解， 即x 2－4x ＋a 2－3a ≤0在R 上有解，只需y ＝x 2－4x ＋a 2－3a 的图象与x 轴有公共点， 所以Δ＝(－4)2－4×(a 2－3a )≥0， 即a 2－3a －4≤0，所以(a －4)(a ＋1)≤0， 解得－1≤a ≤4，所以实数a 的取值范围是{a |－1≤a ≤4}．(2)当x ∈(1,2)时，不等式x 2＋mx ＋4<0恒成立，则m 的取值范围是( ) A ．(－∞，4] B ．(－∞，－5) C ．(－∞，－5] D ．(－5，－4)答案 C解析 令f (x )＝x 2＋mx ＋4， ∴当x ∈(1,2)时，f (x )<0恒成立， ∴⎩⎪⎨⎪⎧f 1≤0，f2≤0，即⎩⎪⎨⎪⎧1＋m ＋4≤0，4＋2m ＋4≤0，解得m ≤－5.课时精练1．不等式9－12x ≤－4x 2的解集为( ) A ．RB ．∅C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝32 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠32 答案 C解析 原不等式可化为4x 2－12x ＋9≤0，即(2x －3)2≤0， ∴2x －3＝0，∴x ＝32，∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝32. 2．(2022·揭阳质检)已知p ：|2x －3|<1，q ：x (x －3)<0，则p 是q 的( ) A ．充要条件 B ．充分不必要条件 C ．既不充分也不必要条件 D ．必要不充分条件 答案 B解析 ∵p ：|2x －3|<1，则－1<2x －3<1， 可得p ：1<x <2，又∵q ：x (x －3)<0，由x (x －3)<0，可得q ：0<x <3， 可得p 是q 的充分不必要条件．3．(2022·南通模拟)不等式(m ＋1)x 2－mx ＋m －1<0的解集为∅，则m 的取值范围是( ) A ．m <－1 B ．m ≥233C ．m ≤－233D ．m ≥233或m ≤－233答案 B解析 ∵不等式(m ＋1)x 2－mx ＋m －1<0的解集为∅， ∴不等式(m ＋1)x 2－mx ＋m －1≥0恒成立．①当m ＋1＝0，即m ＝－1时，不等式化为x －2≥0， 解得x ≥2，不是对任意x ∈R 恒成立，舍去； ②当m ＋1≠0，即m ≠－1时，对任意x ∈R ， 要使(m ＋1)x 2－mx ＋m －1≥0，只需m ＋1>0且Δ＝(－m )2－4(m ＋1)(m －1)≤0， 解得m ≥233.综上，实数m 的取值范围是m ≥233.4．(2022·合肥模拟)不等式x 2＋ax ＋4≥0对一切x ∈[1,3]恒成立，则a 的最小值是( ) A ．－5B ．－133C ．－4D ．－3答案 C解析 ∵x ∈[1,3]时，x 2＋ax ＋4≥0恒成立，则a ≥－⎝⎛⎭⎪⎫x ＋4x 恒成立，又x ∈[1,3]时，x ＋4x≥24＝4，当且仅当x ＝2时取等号．∴－⎝⎛⎭⎪⎫x ＋4x ≤－4，∴a ≥－4.故a 的最小值为－4.5．(多选)满足关于x 的不等式(ax －b )(x －2)>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <2，则满足条件的一组有序实数对(a ，b )的值可以是( ) A ．(－2，－1) B ．(－3，－6) C ．(2,4) D.⎝⎛⎭⎪⎫－3，－32答案 AD解析 不等式(ax －b )(x －2)>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <2， ∴方程(ax －b )(x －2)＝0的实数根为12和2，且⎩⎪⎨⎪⎧a <0，b a ＝12，即a ＝2b <0，故选AD.6．(多选)(2022·湖南长郡中学月考)已知不等式x 2＋ax ＋b >0(a >0)的解集是{x |x ≠d }，则下列四个结论中正确的是( ) A ．a 2＝4b B ．a 2＋1b≥4C ．若不等式x 2＋ax －b <0的解集为(x 1，x 2)，则x 1x 2>0D ．若不等式x 2＋ax ＋b <c 的解集为(x 1，x 2)，且|x 1－x 2|＝4，则c ＝4 答案 ABD解析 由题意，知Δ＝a 2－4b ＝0， 所以a 2＝4b ，所以A 正确； 对于B ，a 2＋1b ＝a 2＋4a2≥2a 2·4a 2＝4，当且仅当a 2＝4a2，即a ＝2时等号成立，所以B 正确；对于C ，由根与系数的关系， 知x 1x 2＝－b ＝－a 24<0，所以C 错误；对于D ，由根与系数的关系，知x 1＋x 2＝－a ，x 1x 2＝b －c ＝a 24－c ，则|x 1－x 2|＝x 1＋x 22－4x 1x 2＝a 2－4⎝ ⎛⎭⎪⎫a 24－c ＝2c ＝4， 解得c ＝4，所以D 正确． 7．不等式3x －1>1的解集为________． 答案 (1,4) 解析 ∵3x －1>1， ∴3x －1－1>0，即4－x x －1>0， 即1<x <4.∴原不等式的解集为(1,4)．8．一元二次方程kx 2－kx ＋1＝0有一正一负根，则实数k 的取值范围是________． 答案 (－∞，0)解析 kx 2－kx ＋1＝0有一正一负根，∴⎩⎪⎨⎪⎧Δ＝k 2－4k >0，1k<0，解得k <0.9．已知关于x 的不等式－x 2＋ax ＋b >0.(1)若该不等式的解集为(－4,2)，求a ，b 的值； (2)若b ＝a ＋1，求此不等式的解集．解 (1)根据题意得⎩⎪⎨⎪⎧2－4＝a ，2×－4＝－b ，解得a ＝－2，b ＝8.(2)当b ＝a ＋1时，－x 2＋ax ＋b >0⇔x 2－ax －(a ＋1)<0， 即[x －(a ＋1)](x ＋1)<0. 当a ＋1＝－1，即a ＝－2时， 原不等式的解集为∅； 当a ＋1<－1，即a <－2时， 原不等式的解集为(a ＋1，－1)；当a ＋1>－1，即a >－2时， 原不等式的解集为(－1，a ＋1)．综上，当a <－2时，不等式的解集为(a ＋1，－1)；当a ＝－2时，不等式的解集为∅； 当a >－2时，不等式的解集为(－1，a ＋1)．10．若二次函数f (x )＝ax 2＋bx ＋c (a ≠0)，满足f (x ＋2)－f (x )＝16x 且f (0)＝2. (1)求函数f (x )的解析式；(2)若存在x ∈[1,2]，使不等式f (x )>2x ＋m 成立，求实数m 的取值范围． 解 (1)由f (0)＝2，得c ＝2， 所以f (x )＝ax 2＋bx ＋2(a ≠0)，由f (x ＋2)－f (x )＝[a (x ＋2)2＋b (x ＋2)＋2]－(ax 2＋bx ＋2)＝4ax ＋4a ＋2b ， 又f (x ＋2)－f (x )＝16x ， 得4ax ＋4a ＋2b ＝16x ，所以⎩⎪⎨⎪⎧4a ＝16，4a ＋2b ＝0，故a ＝4，b ＝－8，所以f (x )＝4x 2－8x ＋2. (2)因为存在x ∈[1,2]， 使不等式f (x )>2x ＋m 成立，即存在x ∈[1,2]，使不等式m <4x 2－10x ＋2成立， 令g (x )＝4x 2－10x ＋2，x ∈[1,2]， 故g (x )max ＝g (2)＝－2，所以m <－2， 即m 的取值范围为(－∞，－2)．11．(多选)已知函数f (x )＝4ax 2＋4x －1，∀x ∈(－1,1)，f (x )<0恒成立，则实数a 的取值可能是( )A ．0B ．－1C ．－2D ．－3 答案 CD解析 因为f (x )＝4ax 2＋4x －1， 所以f (0)＝－1<0成立．当x ∈(－1,0)∪(0,1)时，由f (x )<0可得4ax 2<－4x ＋1，所以4a <⎝⎛⎭⎪⎫1x 2－4xmin ，当x ∈(－1,0)∪(0,1)时， 1x∈(－∞，－1)∪(1，＋∞)，所以1x2－4x ＝⎝ ⎛⎭⎪⎫1x －22－4≥－4，当且仅当x ＝12时，等号成立，所以4a <－4，解得a <－1.12．(2022·南京质检)函数y ＝lg(c ＋2x －x 2)的定义域是(m ，m ＋4)，则实数c 的值为________． 答案 3解析 依题意得，一元二次不等式－x 2＋2x ＋c >0，即x 2－2x －c <0的解集为(m ，m ＋4)，所以m ，m ＋4是方程x 2－2x －c ＝0的两个根，所以⎩⎪⎨⎪⎧m ＋m ＋4＝2，m m ＋4＝－c ，解得m ＝－1，c ＝3.13．若不等式x 2－(a ＋1)x ＋a ≤0的解集是[－4,3]的子集，则a 的取值范围是________． 答案 [－4,3]解析 原不等式为(x －a )(x －1)≤0，当a <1时，不等式的解集为[a,1]，此时只要a ≥－4即可，即－4≤a <1；当a ＝1时，不等式的解为x ＝1，此时符合要求；当a >1时，不等式的解集为[1，a ]，此时只要a ≤3即可，即1<a ≤3，综上可得－4≤a ≤3. 14．若不等式x 2＋ax －2>0在[1,5]上有解，则a 的取值范围是________．答案 ⎝⎛⎭⎪⎫－235，＋∞解析 对于方程x 2＋ax －2＝0， ∵Δ＝a 2＋8>0，∴方程x 2＋ax －2＝0有两个不相等的实数根， 又∵两根之积为负， ∴必有一正根一负根， 设f (x )＝x 2＋ax －2，于是不等式x 2＋ax －2>0在[1,5]上有解的充要条件是f (5)>0， 即5a ＋23>0， 解得a >－235.故a 的取值范围是⎝ ⎛⎭⎪⎫－235，＋∞.15．(2022·湖南多校联考)若关于x 的不等式x 2－(2a ＋1)x ＋2a <0恰有两个整数解，则a 的取值范围是( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪32<a ≤2 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪－1<a ≤－12 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪－1<a ≤－12或32≤a <2D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪－1≤a <－12或32<a ≤2答案 D解析 令x 2－(2a ＋1)x ＋2a ＝0，解得x ＝1或x ＝2a . 当2a >1，即a >12时，不等式x 2－(2a ＋1)x ＋2a <0的解集为{x |1<x <2a }， 则3<2a ≤4， 解得32<a ≤2；当2a ＝1，即a ＝12时，不等式x 2－(2a ＋1)x ＋2a <0无解， 所以a ＝12不符合题意；当2a <1，即a <12时，不等式x 2－(2a ＋1)x ＋2a <0的解集为{x |2a <x <1}，则－2≤2a <－1，解得－1≤a <－12.综上，a 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪－1≤a <－12或32<a ≤2. 16．已知f (x )＝2x 2＋bx ＋c ，不等式f (x )<0的解集是(0,5)．(1)若不等式组⎩⎪⎨⎪⎧fx >0，f x ＋k <0的正整数解只有一个，求实数k 的取值范围；(2)若对于任意x ∈[－1,1]，不等式t ·f (x )≤2恒成立，求t 的取值范围． 解 (1)因为不等式f (x )<0的解集是(0,5)，所以0,5是一元二次方程2x 2＋bx ＋c ＝0的两个实数根，可得⎩⎪⎨⎪⎧0＋5＝－b2，0×5＝c2，解得⎩⎪⎨⎪⎧b ＝－10，c ＝0.所以f (x )＝2x 2－10x .不等式组⎩⎪⎨⎪⎧f x >0，f x ＋k <0，即⎩⎪⎨⎪⎧2x 2－10x >0，2x 2＋2kx ＋k 2－10x ＋k <0，解得⎩⎪⎨⎪⎧x <0或x >5，－k <x <5－k ，因为不等式组的正整数解只有一个， 可得该正整数解为6， 可得6<5－k ≤7， 解得－2≤k <－1，所以k 的取值范围是[－2，－1)． (2)tf (x )≤2，即t (2x 2－10x )≤2， 即tx 2－5tx －1≤0， 当t ＝0时显然成立，当t >0时，有⎩⎪⎨⎪⎧t ·1－5t ·－1－1≤0，t ·1－5t ·1－1≤0，即⎩⎪⎨⎪⎧t ＋5t －1≤0，t －5t －1≤0，解得－14≤t ≤16，所以0<t ≤16；当t <0时，函数y ＝tx 2－5tx －1在[－1,1]上单调递增， 所以只要其最大值满足条件即可， 所以t －5t －1≤0， 解得t ≥－14，即－14≤t <0，综上，t 的取值范围是⎣⎢⎡⎦⎥⎤－14，16.。

合用优选文件资料分享高三数学不等式、推理与明(含答案)2013 届高三数学章末合（11）不等式、推理与明一、 ( 本大共 12 小，每小 5 分，共 60 分．在每小出的四个中，只有一是符号目要求的 ) 1．已知 a，b，c∈R，那么以下命中正确的选项是() A．若 a>b， ac2>bc2 B．若 ac>bc，a>b C．若 a3>b3 且 ab<0， 1a>1b D．若 a2>b2 且 ab>0， 1a<1b剖析C当c＝0，可知A不正确；当c<0，可知B不正确；由 a3>b3 且 ab<0 知 a>0 且 b<0，因此 1a>1b 建立；当 a<0 且 b<0 ，可知 D不正确． 2 ．若会合 A＝{x||x －2| ≤3，x∈R}， B＝ {y|y ＝1－x2，x∈R}， A∩B＝ () A．[0,1] B．[0 ，＋∞ ) C．[ －1,1] D．?剖析C由|x－2|≤3，得－1≤x≤5，即A＝{x|－1≤x≤5}；B＝{y|y ≤1} ．故 A∩B＝ [ －1,1] ． 3 ．用数学法明“ 1＋2＋22＋⋯＋2n＋2＝2n＋3－1”，在 n＝1 ，左算所得的式子() A ．1 B．1＋2 C．1＋2＋22 D．1＋2＋22＋23剖析D 当 n＝1 ，左＝ 1＋2＋22＋23. 4．已知 x，y，z∈R＋，且 xyz(x＋y＋z) ＝1，(x ＋y)(y ＋z) 的最小是 ( ) A．1 B．2 C．3 D．4剖析 B∵(x ＋ y)(y ＋z) ＝xy＋y2＋xz＋yz＝y(x ＋y＋z) ＋xz＝y×1xyz＋xz＝1xz ＋xz≥21xz?xz＝ 2，当且当 xz＝1，y(x ＋y＋z)＝1 ，取“＝”，∴(x＋y)(y＋z)min＝2. 5．要a2＋b2－1－a2b2≤0，只需明 () A ．2ab－1－a2b2≤0 B． a2＋b2－1－a4＋＋－1－a2b2≤0 D．(a2－1)(b2－1)≥0解析 D 因 a2＋b2－1－a2b2≤0? (a2 －1)(b2 －1) ≥0，故 D.6．于平面α和共面的直 m、n，以下命真命的是() A．若m⊥α，m⊥n， n∥α B．若 m∥α，n∥α， m∥n C．若 m? α，n∥α， m∥n D．若 m、n 与α所成的角相等， m∥n 剖析 C 于平面α和共面的直 m，n，真命是“若 m? α，n∥ α，m∥n”． 7 ．若不等式 2x2＋2kx ＋k4x2＋6x＋3<1 于所有数都成立， k 的取范是 () A. ( －∞，＋∞ ) B. (1,3) C. ( －∞，3) D. ( －∞， 1) ∪(3 ，＋∞ )剖析B∵4x2＋6x＋3＝4x2＋32x ＋3＝4x＋342＋34≥34，∴不等式等价于 2x2＋2kx＋k<4x2＋6x＋3，即2x2＋(6 －2k)x ＋3－k>0 随意的 x 恒建立，∴Δ＝(6 －2k)2 －8(3 －k)<0 ，∴1<k<3. 8．函数 f(x) ＝x2＋x＋a(a>0) 足 f(m)<0 ，f(m ＋1) 的符号是 () A ．f(m ＋1) ≥0 B． f(m ＋1) ≤0 C． f(m＋1)>0 D．f(m ＋1)<0剖析C∵f(x)的称x＝－12，f(0)＝a>0，∴由 f(m)<0 ，得－ 1<m<0，∴m＋1>0，∴ f(m ＋1)>f(0)>0. 9．已知 a>0，b>0， 1a＋1b＋2ab 的最小是 () A．2 B．22 C．4D．5 剖析 C ∵a>0，b>0，∴1a＋1b＋2ab≥21ab＋2ab≥4，当且当 a＝b ＝1 取等号，∴ 1a＋1b＋2abmin＝4. 10 ．使不等式log2x(5x －1)>0 建立的一个必要不充足条件是() A ．x>12B.15<x<25 或 x>12C.15<x<1 D．0<x<12或 x>12剖析D log2x(5x－1)>0? 5x－1>0，2x>1，5x－1>1或 5x－1>0，0<2x<1，5x－1<1? x>15，x>12，x>25 或 x>15，0<x<12，x<25，∴x>12 或 15<x<25. 由 x>12或 15<x<25 建立，可得 x>12 或 0<x<12 建立，反之不建立，故 D. 11．假f(x) ＝x2－4x＋3，若数 x、y 足条件 f(y) ≤f(x) ≤0，点 (x ，y) 所组成的地区的面等于() A. 1 B. 2 C. 3 D. 4解析B由f(y)≤f(x)≤0可得，，即1≤x≤3，－＋y－，画出其表示的平面地区如所示，可得面 S＝2×12×2×1＝ 2，故 B. 12 ． x，y 足束条件 3x－y－6≤0， x－y＋2≥0，x≥0，y≥0，若目函数 z＝ax＋by(a>0 ，b>0) 的最大 12， 2a＋3b 的最小 () A.256 B.83C.113 D．4 剖析 A 作出可行域 ( 四形 OBAC成的地区，包括界 ) 如，作出直 l ：ax ＋by＝0，当直 l 点 A， z＝ax＋b y 获取最大．解 x－y＋2＝0，3x－y－6＝0，得点 A(4,6) ，∴4a＋6b＝12，即 a3＋b2＝1，∴2a＋ 3b＝2a＋3ba3＋b2＝23＋32＋ab＋ba≥23＋ 32＋2＝256，当且当 a ＝b 取等号．二、填空 ( 本大共 4小，每小 5 分，共 20 分．把答案填在中横上 ) 13．已知等差数列 {an}中，有 a11＋a12＋⋯＋ a2010＝a1＋a2＋⋯＋ a3030，在等比数列 {bn} 中，会有似的： ___ _____.剖析由等比数列的性可知， b1b30＝b2b29＝⋯＝ b11b20，∴ 10b11b12⋯b20＝30b1b2⋯b30 .【答案】10b11b12⋯b20＝30b1b2⋯b30 14 ．已知数 x，y 足束条件 x－y＋4≥0， x＋y≥0，x≤3， z＝4x2－y 的最小 ________．剖析作出不等式所表示的可行域( 图略 ) ，z＝4x2－y＝22x?2y＝ 22x＋y，令ω＝2x＋y，可求得ω＝2x＋y 的最小值是－ 2，因此 z＝4x2－y 的最小值为 2－2＝14. 【答案】14 15．某企业租地建库房，每个月占用费 y1 与库房到车站的距离成反比，而每个月库存货物的运费 y2 与库房到车站的距离成正比．若是在距离车站 10 km 处建库房，这项开销 y1 和 y2 分别为 2 万元和 8 万元，那么，要使这两项开销之和最小，库房应建在离车站 ________ km 处．剖析设库房建在离车站 d km处，由已知 y1＝2＝k110，得 k1＝20，∴y1＝20d. 由 y2＝8＝10k2，得 k2＝45，∴y2＝45d. ∴y1＋y2＝20d＋4d5≥220d?4d5＝ 8，当且仅当 20d＝4d5，即 d＝5 时，开销之和最小．【答案】 5 16．在不等边三角形中， a 为最大边，要想获取∠A 为钝角的结论，三边a，b，c 应知足 ________．解析由余弦定理 cos A ＝b2＋c2－a22bc<0，因此 b2＋c2－a2<0，即a2>b2＋c2. 【答案】 a2>b2＋c2 三、解答题 ( 本大题共 6 小题，共70 分．解答应写出文字说明、证明过程或演算步骤) 17 ．(10 分) 已知表中的对数值有且只有两个是错误的. x 1.5 3 5 6 lg x 3a－b ＋c 2a －b a ＋c 1＋a－b－cx 7 8 9 14 27 lg x 2(a＋c) 3(1－a－c) 2(2a－b) 1－a＋2b 3(2a －b) (1)假定上表中lg 3＝2a－b与lg 5＝a＋c都是正确的，试判断 lg 6 ＝1＋a－b－c 可否正确？给出判断过程；(2) 试将两个错误的对象值均指出来并加以更正( 不要求证明 ) ．剖析(1) 由 lg 5＝a＋c 得 lg 2 ＝1－a－c，∴lg 6 ＝ lg 2 ＋lg 3 ＝1－a－c＋2a－b＝1＋a－b－c，知足表中数值，即 lg 6 在假定下是正确的． (2)lg1.5 与 lg 7 是错误的，正确值应为lg 1.5＝lg32＝lg 3－lg 2＝2a －b－1＋a＋c＝3a－b＋c－1. lg 7 ＝lg 14 －lg 2 ＝1－a＋ 2b－1＋a＋c＝2b＋c. 18．(12 分) 已知 f(x) ＝－ 3x2＋a(6 －a)x ＋6. (1) 解对于a 的不等式 f(1)>0 ； (2) 若不等式 f(x)>b 的解集为 ( －1,3) ，求实数 a、b 的值．剖析 (1) ∵f(x) ＝－ 3x2＋a(6 －a)x ＋6，∴f(1) ＝－ 3＋a(6 －a) ＋6＝－ a2＋6a＋3>0 即 a2－ 6a－3<0，解得 3－23<a<3＋23. ∴不等式解集为 {a|3 －23<a<3＋23} ． (2)f(x)>b 的解集为( －1,3) ，即方程－ 3x2＋a(6 － a)x ＋6－b＝ 0 的两根为－ 1,3 ，∴2＝－，－3＝－ 6－b3，解得 a＝3±3，b＝－ 3. 19．(12分)(2011? 南京模 ) 已知数列 {an} 足 a 1＝0，a2＝1，当 n∈N*，an＋2＝an＋1＋an. 求：数列 {an} 的第 4m＋1(m∈N*) 能被 3 整除．剖析 (1) 当 m＝1 ，a4m＋1＝a5＝a4＋a3＝(a3 ＋a2) ＋(a2＋a1) ＝(a2 ＋a 1) ＋2a2＋a1＝3a2＋2a1＝3＋0＝3. 即当 m＝1 ，第4m＋1 能被 3 整除．命建立． (2) 假当 m＝k ，a4k＋1 能被 3 整除，当 m＝k＋1 ， a4(k ＋1) ＋1＝a4k＋5＝a4k＋4＋a4k＋3＝2a4k＋3＋a4k＋2＝2(a4k ＋2＋a4k＋1) ＋a4k＋2＝3a4k＋2＋2a4k＋1. 然， 3a4k＋2 能被 3 整除，又由假知 a4k＋1 能被 3 整除，∴3a4k＋2＋2a4k＋1 能被 3 整除．即当 m＝k＋1 ， a4(k ＋1)＋1 也能被 3 整除．命也建立．由(1) 和(2) 知，于随意 n∈N*，数列{an} 中的第 4m＋1(m∈N*) 能被 3 整除． 20 ．(12 分) 二次函数 f(x) ＝x2＋ax＋a，方程 f(x)－x＝ 0 的两根 x1 和 x2 足0<x1<x2<1. (1) 求数 a 的取范； (2)比 f(0)f(1)－f(0)与 116 的大小，并明原因．剖析 (1)令 g(x) ＝f(x)－x＝x2＋(a －1)x ＋a，由意可得>0，0<1－a2<1，，? a<3－22 或 a>3＋22，－ 1<a<1，a>0 ? 0<a<3－22，故数 a 的取范是 (0,3 －22) ． (2)f(0)f(1) －f(0) ＝g(0)g(1) ＝2a2，令 h(a) ＝2a2，∵当a>0 ，h(a) 增，∴当 0<a<3－22 ，0<h(a)<h(3 －22) ＝2(3－22)2 ＝2(17 －122) ＝2×117＋ 122<116，即 f(0)f(1) －f(0)<116.21．(12 分) 已知 {an} 是正数成的数列， a1＝1，且点 (an ，an＋1)(n ∈N*) 在函数 y＝x2＋1 的象上． (1) 求数列 {an} 的通公式；(2) 若数列 {bn} 足 b1＝1，bn＋1＝bn＋2an，求： bn?bn＋2<b2n＋1.剖析(1)由已知得an＋1＝an＋1，an＋1－an＝1，又a1＝1，因此数列 {an} 是以 1 首， 1 公差的等差数列．故an＝1＋(n －1) ×1＝ n. (2) 由(1) 知，an＝n，进而 bn＋1－bn＝2n. 当 n≥2，bn ＝(bn －bn－1) ＋(bn －1－bn－2) ＋⋯＋ (b2 －b1) ＋b1 ＝2n－1＋2n－2＋⋯＋ 2＋1＝1－2n1－2＝ 2n－1. 又 b1＝1 也适合上式，因此 bn＝2n－1， bn?bn＋2－b2n＋1＝(2n －1)(2n ＋2－1) －(2n ＋1－1)2 ＝(22n ＋2－2n＋2－2n＋1) －(22n ＋2－2?2n＋1＋1 ) ＝－2n<0. 因此 bn?bn＋2<b2n＋1. 22．(12 分) 某养要某个儿童定午餐和晚餐．已知一个单位的午餐含 12 个单位的碳水化合物， 6 个单位蛋白质和 6 个单位的维生素 C；一个单位的晚餐含 8 个单位的碳水化合物， 6 个单位的蛋白质和 10 个单位的维生素 C.其他，该儿童这两餐需要的营养中最少含 64 个单位的碳水化合物， 42 个单位的蛋白质和 54 个单位的维生素 C.若是一个单位的午餐、晚餐的开销分别是2.5 元和 4 元，那么知足上述的营养要求，并且开销最少，应当为该儿童分别预定多少个单位的午餐和晚餐？剖析设该儿童分别预定 x，y 个单位的午餐和晚餐，共需 z 元，则 z＝2.5x ＋4y. 可行域为12x＋8y≥64，6x＋6y≥42，6x＋10y≥54，x≥0，y≥0，即3x＋2y≥16，x＋y≥7，3x＋5y≥27，x≥0，y≥0，作出可行域如图阴影部分所示，因此当 x＝4，y＝3 时，开销最少， zmin＝22 元．因此，分别预定 4 个单位午餐和 3 个单位晚餐，就知足要求了．。

合用优选文件资料分享高三数学不等式、推理与明（答案）2013 届高三数学章末合（12）不等式、推理与明一、：本大共12 小，每小 5 分，共 60 分． 1 ．以下符合三段推理形式的() A．若是 p? q，p 真， q 真 B ．若是b? c，a? b， a? c C．若是 a∥b，b∥c， a∥c D．若是 a＞b，c＞0， ac＞bc 剖析：由三段的推理能够获取 B 三段 . 答案：B2．比平面内正三角形的“三相等，三内角相等”的性，可推出正周围体的以下性，你比适合的是 ( ) ①各棱相等，同一点上的随意两条棱的角都相等；②各个面都是全等的正三角形，相两个面所成的二面角都相等；③各面都是面相等的三角形，同一点上的随意两条棱的角都相等． A ．①B．②C．①②③D．③剖析：由比原理和思想，①②③都是合理、适合的.答案：C 3．用反法明命“ 2＋3是无理数” ，假正确的选项是() A．假 2 是有理数 B ．假 3 是有理数 C．假 2 或 3 是有理数 D．假 2＋3 是有理数剖析：假的反面建立， 2＋3 不是无理数， 2＋3 是有理数 . 答案：D 4．已知 ai ，bi ∈R(i ＝ 1,2,3 ，⋯，n) ，a12＋a22＋⋯＋ an2＝1，b12＋b22＋⋯＋ bn2＝1， a1b1＋a2b2＋⋯＋ anbn 的最大 ( ) A．1 B．2 C．n2 D．2n 剖析：此“ a，b，c，d∈R，a2＋b2＝1，c3＋d2＝1， ac＋bd≤a2＋ c22＋b2＋d22＝1”的实行，比可得 a1b1＋a2b2＋⋯＋ anbn≤a12＋ b122＋a22＋b222＋⋯＋ an2＋bn22＝1.答案：A 5．在以下函数中，最小是 2 的是 () A．y＝x2＋2x B．y ＝x＋2x＋1(x ＞0) C ．y＝sinx ＋1sinx ，x∈(0 ，π2) D ．y＝7x＋7－x 剖析： A中 x 的取未限制，故无最小． D 中，∵ y＝7x＋7－x＝7x＋17x≥2，等号建立的条件是x＝0. B、C均找不到等号建立的条件 . 答案： D 6．一元二次不等式 ax2＋bx＋1＞0 的解集{x| －1＜x＜13} ， ab 的 () A ．－6 B．6 C．－ 5 D．5 解析：∵ax2＋bx＋1＞0 的解集是{x| －1＜x＜13} ，∴－1，13 是方程ax2＋bx＋1＝0 的两根，∴－ 1＋13＝－ ba－1×13＝ 1a? b＝－ 2，a＝－ 3，∴ ab＝－ 3×( － 2) ＝6. 答案： B 7．已知 a＞0，b＞0， 1a＋1b＋2ab 的最小是 () A ．2 B．22 C．4 D．5 剖析：因 1a＋1b＋2ab≥21ab＋ 2ab＝21ab＋ab≥4，当且仅当 1a＝1b，且 1ab ＝ab，即 a＝b＝1 时，取“＝” . 答案： C 8．在直角坐标系中，若不等式组 y≥0，y≤2x，y≤k(x － 1) －1，表示一个三角形地区，则实数 k 的取值范围是 ( ) A ．( －∞，－ 1) B ．( －1,2) C ．( －∞，－1) ∪(2 ，＋∞) D．(2 ，＋∞ ) 剖析：先作出 y≥0，y≤2x，的平面地区如图：若 k＝0 时，显然不能够与阴影部分组成三角形．若 k＞0，将阴影部分的点如 (0,0) 代入 y≤k(x － 1) －1，有 0≤－ k－1，显然不能够与阴影部分组成三角形，因此k＜0；又 y＝k(x －1) －1 是过定点 (1 ，－1) 的直线，由图知，若与阴影部分组成三角形，则有－k－1＞0，故 k＜－ 1 时，原不等式组能组成三角形地区.答案：A 9．如果 a＞b，给出以下不等式，其中建立的是() (1)1a＜1b；(2)a3 ＞b3；(3)a2 ＋1＞b2＋1; (4)2a ＞2b. A．(2)(3)B．(1)(3) C．(3)(4)D．(2)(4)剖析：∵ a、b符号不定，故(1)不正确，(3)不正确．∵y＝x3 是增函数，∴a＞b 时，a3＞b3，故(2) 正确．∴y ＝2x 是增函数，∴ a＞b 时，2a＞2b，故 (4) 正确 . 答案： D 10．设函数 f(x) ＝－ 3(x ＞0) ，x2＋bx＋c (x ≤0) ，若 f( －4) ＝f(0) ，f( －2) ＝0，则对于 x 的不等式 f(x) ≤1的解集为 () A ．( －∞，－3] ∪[ － 1，＋∞ ) B．[ －3，－1]C．[ －3，－1] ∪(0 ，＋∞ ) D．[ －3，＋∞ ) 剖析：当 x≤0时，f(x)＝x2＋bx＋ c 且 f( －4) ＝f(0) ，故对称轴为 x＝－ b2＝－ 2，∴b＝ 4.又 f( －2) ＝4－8＋c＝0，∴c＝4，令 x2＋4x＋4≤1有－ 3≤x≤－ 1；当 x＞0 时， f(x) ＝－ 2≤1显然建立．故不等式的解集为 [ －3，－ 1] ∪(0 ，＋∞ ). 答案： C 11．若直线 2ax＋by－2＝0(a ＞0，b＞0) 均分圆 x2＋y2－2x－4y－6＝0，则2a＋1b 的最小值是 () A ．2－2 B.2 －1 C ．3＋22 D．3－22 解析：由 x2＋y2－2x－4y－6＝0 得 (x －1)2 ＋(y －2)2 ＝11，若 2ax＋by－2＝0 平分圆，∴2a＋2b－2＝0，∴ a＋b＝1，∴2a＋1b＝2(a ＋b)a ＋a＋bb＝3＋2ba＋ab ≥3＋2 2?ba?ab＝3＋22，当且仅当2ba＝ab，且 a＋b＝1，即 a＝2－2，b＝2－1 时取等号 .答案：C 12．某企业租地建库房，每个月土地占用费y1 与库房到车站的距离成反比，而每个月库存货物的运费y2 与库房到车站的距离成正比，若是在距离车站 10 km 处建库房，这两项花销y1 和 y2 分别为 2 万元和 8 万元，那么，要使两用之和最小，建在离站() A．5 kmB ．4 km C．3 km D．2 km剖析：由意可y1＝k1x，y2＝k2x，∴ k1＝xy1，k2＝y2x，把 x＝10，y1＝2 与 x＝10，y2＝8分代入上式得 k1＝20，k2＝0.8 ，∴y1＝ 20x ，y2＝0.8x(x到站的距离 ) ，用之和 y＝ y1＋y2＝0.8x ＋20x≥2 0.8x?20x ＝8，当且当 0.8x ＝20x，即 x＝5 等号建立，故 A. 答案：A 第Ⅱ卷 ( 非共 90 分)二、填空：本大共 4 个小，每小5 分，共 20 分． 13 ．以下，大于或等于 2 的自然数 m的 n 次行以下方式的“分裂”：仿此， 52 的“分裂”中最大的数是，53 的“分裂”中最小的数是 . 剖析：由已知中“分裂”可得故“ 52”的“分裂”中最大的数是 9,53 的“分裂”中最小的数是 21. 答案： 9 21 14 ．由①有面关系：S△PA′B′S△PAB＝PA′?PB′PA?PB，由②有体关系： VP－A′B′C′VP－ ABC＝__________. 剖析：三棱 C′ - PA′B′的高h′， 15 ．已知等比数列 {an} 中，a2＞a3＝1，使不等式 a1－1a1＋a2－1a2＋a3－1a3＋⋯＋ an－1an≥0建立的最大自然数 n 是__________．剖析：∵a2＞ a3＝1，∴0＜ q＝a1a2＜1，a1＝ 1q2＞1，a1－1a1＋a1－1a2＋a3－1a1＋⋯＋ an－1an ＝(a1 ＋a2＋⋯＋ an) －1a1＋1a2＋⋯＋ 1an ＝a1(1 －qn)1 －q－1a11－1qn1－1q＝a1(1 －q4)1 －q－q(1 －qn)a1(1 －q)qn ≥0，∴a1(1 －qn)1 －q≥q(1 －qn)a1(1 －q)qn. 因 0 ＜q＜1，因此，化得： a12≥1qn－ 1，即q4≤qn－ 1，∴4≥n－ 1，n≤5，因此 n 的最大 5. 答案：5 16．数 x，y 足 x－y－2≤0，x＋2y－5≥0， y－2≤0， u＝yx－xy的取范是 __________．剖析：作出x，y 足的可行域如中阴影部分所示，可得可行域内的点与原点的斜率的取范是 13，2，即yx∈13， 2，故令 t ＝yx， u＝t －1t ，依照函数 u＝t －1t在 t ∈13， 2 上增，得 u∈－ 83，32. 答案：－ 83，32 三、解答：本大共6 小，共 7 0 分． 17 ．(10 分) 在三角形中有下面的性： (1) 三角形的两之和大于第三； (2) 三角形的中位等于第三的一半； (3) 三角形的三条内角均分交于一点，且个点是三角形的内心； (4) 三角形的面 S＝12(a ＋b＋c)r(r三角形内切半径，a、b、c 三 ) ．比出周围体的相关相像性．解析： (1) 周围体随意三个面的面之和大于第四个面的面；(2) 四面体的中位面 ( 三条棱的中点的面 ) 的面等于第四个面的面的四分之一；新 ] (3)周围体的六个二面角的均分面交于一点，且个点是周围体内切球的球心； (4) 周围体的体 V ＝13(S1＋S2＋S3＋S4)r(r 周围体内切球的半径， S1、S2、S3、S4 周围体的四个面的面 ) ． 18 ．(12 分) 已知 a＞0，b＞0，求 b2a＋a2b≥a＋ b. 剖析： b2a＋a2b－(a ＋b) ＝b2a－a＋a2b－b ＝(b ＋a)(b －a)a ＋ (a ＋b)(a －b)b＝(a －b)(a ＋b)1b －1a＝1ab(a －b)2(a ＋b) ，∵a＞0，b＞0，∴ b2a＋a2b≥a＋ b. 19 ．(12 分) 响国家大内需的政策，某厂家在 2009 年行促活，算，品的年量 ( 即厂的年量 )x 万件与年促用 t(t ≥0) 万元足 x＝4－k2t ＋1(k 常数 ) ．若是不搞促活，品的年量只能是 1 万件．已知 2009 年生品的固定投入 6 万元，每生 1 万件品需要再投入 12 万元，厂家将每件品的售价钱定每件品平均成本的 1.5 倍( 品成本包括固定投入和再投入两部分 ) ．(1)将厂家 2009 年品的利 y 万元表示年促用 t 万元的函数； (2) 厂家 2009 年的年促用投入多少万元厂家利最大？剖析：(1) 由意有 1＝4－k1，得 k＝3，故 x＝4－32t ＋1. ∴y＝1.5 ×6＋12xx×x－(6 ＋12x) －t ＝3＋6x－t ＝3＋64－3t －1－t ＝27－ 182t ＋1－t(t≥0) ． (2) 由(1) 知： y ＝27－182t ＋1－t ＝27.5 －9t＋12＋t ＋12. 由基本不等式 9t ＋12＋t ＋12≥29t ＋12?t ＋ 12＝6，当且当 9t ＋12＝t ＋12，即 t ＝2.5 ，等号建立，故 y＝27－182t＋1－t ＝27.5 －9t ＋12＋t ＋12≤27.5 － 6＝21.5. 当 t ＝2.5 ， y 有最大 21.5. 因此 2009 年的年促用投入 2.5 万元，厂家利最大． 20 ．(12 分) 数列 {an} 的前 n 和 Sn，且方程 x2－anx－an＝0 有一根 Sn－1，n＝1,2,3 ，⋯ . (1) 求 a1，a2； (2) 猜想数列{Sn} 的通公式．剖析： (1) 当 n＝1 ， x2 －a1x－a1＝0有一根 S1－1＝a1－1，于是 (a1 －1)2 －a1(a1 －1) －a1＝0，解得a1＝12. 当 n＝2 ，x2－a2x－a2＝0 有一根 S2－1＝a2－12，于是 a2－122－a2a2－12－a2＝0，解得 a2 ＝16. (2) 由 (Sn－1)2－a n(Sn－1) －an＝0， Sn2－2Sn＋1－anSn＝0. 当 n≥2 ，an＝Sn－S n－1，代入上式得 Sn －1Sn－2Sn＋1＝0①由 (1) 得 S1＝a1＝12，S2＝a1＋a2＝12＋16＝23. 由①可得 S3＝34，由此猜想 Sn＝ nn＋1，n＝1,2,3 ，⋯ . 21 ．(12 分) 二次函数 f(x) ＝ax2＋b x ＋c 的一个零点是－ 1，且足 [f(x) －x]?f(x) － x2＋12≤0恒建立． (1) 求 f(1)的；(2) 求 f(x) 的剖析式；剖析：(1) 由均不等式得 x2＋12≥2x2＝x，若[f(x) －x]?f(x) －x2＋12≤0恒建立，即 x≤f(x) ≤x2＋ 12恒建立，令 x＝1 得 1≤f(1) ≤12＋ 12＝1，故 f(1) ＝1. (2) 由函数零点－ 1 得 f( －1) ＝0，即 a－b＋c＝0，又由 (1) 知 a＋b＋ c＝1，因此解得 a＋c＝b＝12. 又 f(x) －x＝ax2＋12x＋c－x＝ax2－12x＋c，因f(x) －x≥0恒建立，因此＝14－4ac≤0，因此 ac≥116①于是 a＞0，c＞0. 再由 a＋c＝12，得 ac≤c＋ a22＝116②故 ac＝116，且 a＝c＝14，故 f(x) 的剖析式是 f(x) ＝14x2＋12x2＋12x＋14. 22．(12 分) 某少许民族的刺有着悠久的史，下 (1) 、(2) 、(3) 、(4)她刺最的四个案，些案都由小正方形组成，小正方形数越多刺越漂亮，按同的律刺 ( 小正方形的放律相同 ) ，第n 个形包括 f(n) 个小正方形． (1) 求出 f(5) ； (2)利用合情推理的“ 推理思想” 出f(n+1)与 f(n) 的关系，并依照你获取的关系式求 f(n) 的表达式．剖析：(1)∵f(1)=1 ，f(2)=5 ，f(3)=13 ，f(4)=25 ，∴f(5)=25+4 ×4=41.(2) ∵f(2) - f(1)=4=4 ×1，f(3)- f(2)=8=4 ×2， f(4)- f(3)=12=4 ×3， f(5)-f(4)=16=4 ×4，由上式律得出 f(n+1)- f(n)=4n. ∴f(n)-f(n-1)=4(n-1) ，f(n-1)-f(n-2)=4?(n -2) ， f(n-2)-f(n-3)=4?(n -3) ，⋯f(2)- f(1)=4×1，∴f(n) -f(1)=4[(n-1)+(n-2)+⋯+2+1] =2(n- 1)?n ，∴f(n)=2n2-2n+1.。