指数函数与对数函数问题归类

一、指数函数指数函数的图象和性质二、对数函数对数函数的性质：一、指数函数1．比较大小①较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．练习1：比较下列各组数的大小（1），（2）2、求解有关指数不等式（1） 已知2321(25)(25)x x a a a a -++>++，则x 的取值围是___________． 分析：利用指数函数的单调性求解，注意底数的取值围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x 的取值围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．(2)已知（3）解不等式3．求定义域及值域问题 例3 求函数216x y -=-的定义域和值域．解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-，∞． 令26x t -=，则1y t=-，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数的值域是[)01，． 评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．练习1：函数的定义域为 .练习2 当x练习3 函数(a>0且a 的定义域和值域都是[0,2],则实数a的值为4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a 的值是_______．分析：令x t a =可将问题转化成二次函数的最值问题，需注意换元后t 的取值围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a≤≤，即1t a a≤≤．∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a≤≤，即1a t a≤≤，∴ 1t a=时，2max11214y a ⎛⎫=+-= ⎪⎝⎭，解得13a =或15a =-（舍去），∴a 的值是3或13．评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．练习1：已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x 的最大值和最小值练习2: 设 ，求函数 的最大值和最小值题型五：单调区间问题（主要根据复合函数单调性满足“同增异减”） 例：求函数2222++-=x x y 的定义域，值域和单调区间练习：函数y ＝23231+-⎪⎭⎫⎝⎛x x 的单调区间.二对数函数1.求定义域{求函数的定义域需要从这几个方面入手： （1）分母不为零（2）偶次根式的被开方数非负。

高中数学第四章指数函数与对数函数重难点归纳单选题1、函数f(x)={a x ,(x <0)(a −2)x +3a,(x ≥0)，满足对任意x 1≠x 2，都有f (x 1)−f (x 2)x 1−x 2<0成立，则a 的取值范围是（ ）A ．a ∈(0,1)B ．a ∈[13,1)C ．a ∈(0,13]D ．a ∈[13,2) 答案：C分析：根据条件可知f(x)在R 上单调递减，从而得出{0<a <1a −2<03a ⩽1，解出a 的范围即可．解：∵f(x)满足对任意x 1≠x 2，都有f(x 1)−f(x 2)x 1−x 2<0成立，∴f(x)在R 上是减函数，因为f(x)={a x ,(x <0)(a −2)x +3a,(x ≥0)∴{0<a <1a −2<0(a −2)×0+3a ⩽a 0，解得0<a ⩽13，∴a 的取值范围是(0,13]． 故选：C ．2、已知函数y =a x 、y =b x 、y =c x 、y =d x 的大致图象如下图所示，则下列不等式一定成立的是（ ）A ．b +d >a +cB ．b +d <a +cC ．a +d >b +cD ．a +d <b +c 答案：B分析：如图，作出直线x =1,得到c >d >1>a >b ，即得解.如图，作出直线x=1,得到c>d>1>a>b，所以b+d<a+c.故选：B3、我国某科研机构新研制了一种治疗新冠肺炎的注射性新药，并已进入二期临床试验阶段．已知这种新药在注射停止后的血药含量c（t）（单位：mg/L）随着时间t（单位：h）的变化用指数模型c(t)=c0e−kt描述，假定某药物的消除速率常数k=0.1（单位：ℎ−1），刚注射这种新药后的初始血药含量c0=2000mg/L，且这种新药在病人体内的血药含量不低于1000mg/L时才会对新冠肺炎起疗效，现给某新冠病人注射了这种新药，则该新药对病人有疗效的时长大约为（）（参考数据：ln2≈0.693,ln3≈1.099）A．5.32hB．6.23hC．6.93hD．7.52h答案：C分析：利用已知条件c(t)=c0e−kt=2000e−0.1t，该药在机体内的血药浓度变为1000mg/L时需要的时间为t1，转化求解即可.解：由题意得：c(t)=c0e−kt=2000e−0.1t设该要在机体内的血药浓度变为1000mg/L需要的时间为t1c(t1)=2000e−0.1t1≥1000e−0.1t1≥1 2故−0.1t≥−ln2，t≤ln20.1≈6.93故该新药对病人有疗效的时长大约为6.93ℎ4、函数y =log 2(2x −x 2)的单调递减区间为（ ） A ．(1,2)B ．(1,2] C ．(0,1)D ．[0,1) 答案：A分析：先求出函定义域，再通过换元法利用复合函数“同增异减”的性质得到结果 由2x −x 2>0，得0<x <2， 令t =2x −x 2，则y =log 2t ，t =2x −x 2在(0,1)上递增，在(1,2)上递减， 因为y =log 2t 在定义域内为增函数，所以y =log 2(2x −x 2)的单调递减区间为(1,2)， 故选：A5、化简√−a 3·√a 6的结果为（ ） A ．−√a B ．−√−a C ．√−a D ．√a 答案：A分析：结合指数幂的运算性质，可求出答案. 由题意，可知a ≥0，∴√−a 3·√a 6=(−a )13⋅a 16=−a 13⋅a 16=−a 13+16=−a 12=−√a .故选：A.6、已知2a =5,log 83=b ，则4a−3b =（ ） A ．25B ．5C ．259D ．53 答案：C分析：根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出． 因为2a =5，b =log 83=13log 23，即23b =3，所以4a−3b =4a43b =(2a )2(23b )2=5232=259．7、中国茶文化博大精深，某同学在茶艺选修课中了解到，茶水的口感与茶叶类型和水的温度有关，某种绿茶用80℃左右的水泡制可使茶汤清澈明亮，营养也较少破坏.为了方便控制水温，该同学联想到牛顿提出的物体在常温环境下温度变化的冷却模型：如果物体的初始温度是θ1℃，环境温度是θ0℃，则经过t分钟后物体的温度θ℃将满足θ=θ0+(θ1−θ0)e−kt，其中k是一个随着物体与空气的接触状况而定的正常数.该同学通过多次测量平均值的方法得到初始温度为100℃的水在20℃的室温中，12分钟以后温度下降到50℃.则在上述条件下，100℃的水应大约冷却( )分钟冲泡该绿茶(参考数据：ln2≈0.7，ln3≈1.1)A．3B．3.6C．4D．4.8答案：B分析：根据题意求出k的值，再将θ＝80℃，θ1＝100℃，θ0＝20℃代入θ=θ0+(θ1−θ0)e−kt即可求得t的值.由题可知：50=20+(100−20)e−12k⇒(e−k)12=38⇒e−k=(38)112，冲泡绿茶时水温为80℃，故80=20+(100−20)⋅e−kt⇒(e−k)t=34⇒t⋅lne−k=ln34⇒t=ln 3 4ln(38)112=12(ln3−2ln2)ln3−3ln2≈12(1.1−2×0.7)1.1−3×0.7=3.6.故选：B.8、如图所示：曲线C1，C2，C3和C4分别是指数函数y=a x，y=b x,y=c x和y=d x的图象,则a，b，c，d与1的大小关系是（）A ．a <b <1<c <dB ．a <b <1<d <cC ．b <a <1<c <dD ．b <a <1<d <c 答案：D分析：先根据指数函数的单调性，确定a ，b ，c ，d 与1的关系，再由x =1时，函数值的大小判断. 因为当底数大于1时，指数函数是定义域上的增函数， 当底数小于1时，指数函数是定义域上的减函数， 所以c ，d 大于1，a ，b 小于1，由图知：c 1>d 1 ，即c >d ， b 1<a 1，即 b <a ， 所以b <a <1<d <c ， 故选：D 多选题9、若f (x )满足对定义域内任意的x 1,x 2，都有f (x 1)+f (x 2)=f (x 1⋅x 2)，则称f (x )为“好函数”，则下列函数是“好函数”的是（ ）A ．f (x )=2xB ．f (x )=(12)xC ．f (x )=log 12x D ．f (x )=log 3x答案：CD分析：利用“好函数”的定义，举例说明判断A ，B ；计算判断C ，D 作答.对于A ，函数f (x )定义域为R ，取x 1=1,x 2=2，则f (x 1)+f (x 2)=6，f (x 1⋅x 2)=4， 则存在x 1,x 2，使得f (x 1)+f (x 2)≠f (x 1⋅x 2)，A 不是；对于B ，函数f (x )定义域为R ，取x 1=1,x 2=2，则f (x 1)+f (x 2)=34，f (x 1⋅x 2)=14，则存在x 1,x 2，使得f (x 1)+f (x 2)≠f (x 1⋅x 2)，B 不是；对于C ，函数f (x )定义域{x|x >0}内任意的x 1,x 2，f (x 1)+f (x 2)=log 12x 1+log 12x 2=log 12(x 1x 2)=f (x 1⋅x 2)，C 是；对于D ，函数f (x )定义域{x|x >0}内任意的x 1,x 2，f (x 1)+f (x 2)=log 3x 1+log 3x 2=log 3(x 1x 2)=f (x 1⋅x 2)，D 是． 故选：CD10、下列函数中，有零点且能用二分法求零点的近似值的是（ ） A ．y =2x −3B ．y ={−x +1,x ≥0x +1,x <0C ．y =x 2−3x +3D ．y =|x −2| 答案：AB分析：根据二分法定义，只有零点两侧函数值异号才可用二分法求近似值． 对于选项A ，当x =1时，y =21−3=−1<0，当x =12时，y =212−3=1>0，所以能用二分法求零点的近似值．对于选项B ，当x =2时，y =−2+1=−1<0，当x =12时，y =−12+1=12>0，能用二分法求零点的近似值．对于选项C ，y =x 2−3x +3=(x −32)2+34>0，故不能用二分法求零点的近似值． 对于选项D ，y =|x −2|≥0，故不能用二分法求零点的近似值． 故选：AB ．11、某工厂生产一种溶液，按市场要求该溶液的杂质含量不得超过0.1%，而这种溶液最初的杂质含量为2%，现进行过滤，已知每过滤一次杂质含量减少13，若使这种溶液的杂质含量达到市场要求，则过滤次数可以为（参考数据：lg2≈0.301，lg3≈0.477）（ ） A ．7B ．8C ．9D ．10 答案：BCD分析：由2100×(23)n≤11000解不等式可得答案.设经过n 次过滤，这种溶液的杂质含量达到市场要求，则2100×(23)n≤11000， 即(23)n≤120，两边取对数，得nlg 23≤−lg20，即n (lg2−lg3)≤−(1+lg2)， 得n ≥1+lg2lg3−lg2≈7.4. 故选：BCD.12、下面几个结论正确的是（ ）A ．已知a =(√32)23，b =(45)13，c =ln3，则a <b <cB ．已知a =312，b =√63，c =log 47，则a <c <b C ．已知a =0.32，b =log 20.3，c =20.3，则b <c <a D ．已知log 12a >log 12b >0，则a b <a a <b a答案：AD 分析：对于A ，a =(√32)23=(34)13<(45)13<1，c =ln3>1，即可得到大小关系；对于B ，a 6=(312)6=27，b 6=(√63)6=36可得到a <b ，再选取中间量32，通过比较，得到最终结果；对于C ，b <0，a <1，c >1，可得到大小关系；对于D ，通过构造对数函数和幂函数，利用函数的单调性可得到最终结果.对于A ，a =(√32)23=(34)13<(45)13<1，c =ln3>1，所以a <b <c ；故A 正确；对于B ，a 6=(312)6=27，b 6=(√63)6=36>27∴a <b c =log 47，∵32=log 4432，∵(32)3=278,b 3=6>278∴b >32(432)2=64>72=49∴c <32，∴c <b ∵a >32∴c <a 最终为：c <a <b .故B 错误；对于C ，b =log 20.3<0，a =0.32=0.09<1，c =20.3>20=1∴b <a <c ；故C 错误； 对于D ，当log 12a >log 12b >0时，∵y =log 12x 在定义域内是减函数，故得到0<a <b <1，∵y =a x 是减函数，故得到a b <a a ，又因为y =x α在x >0时是增函数，故得到a a <b a ，故D 正确. 故选：AD.13、给定函数f (x )=2x x 2+1（ ）A ．f (x )的图像关于原点对称B ．f (x )的值域是[−1,1]C ．f (x )在区间[1,+∞)上是增函数D ．f (x )有三个零点 答案：AB分析：对于A ：由函数f (x )的定义域为R ，f (−x )=−f (x )，可判断； 对于B ：当x =0时，f (x )=0，当x ≠0时，f (x )=2x+1x，由x +1x ≥2或x +1x ≤−2，可判断；对于C ：由t =x +1x 在[1,+∞)单调递增可判断；对于D ：令f (x )=0，解方程可判断.解：对于A ：因为函数f (x )的定义域为R ，且f (−x )=2(−x )(−x )2+1=−2xx 2+1=−f (x )，所以函数f (x )是奇函数，所以f (x )的图像关于原点对称，故A 正确； 对于B ：当x =0时，f (x )=0， 当x ≠0时，f (x )=2x+1x，又x +1x≥2或x +1x≤−2，所以0<f (x )≤1或−1≤f (x )<0，综上得f (x )的值域为[−1,1]，故B 正确；对于C ：因为t =x +1x 在[1,+∞)单调递增，所以由B 选项解析得， f (x )在区间[1,+∞)上是减函数，故C 不正确；对于D ：令f (x )=0，即2xx 2+1=0，解得x =0，故D 不正确， 故选：AB. 填空题14、把满足log 23×log 34×⋅⋅⋅×log n+1(n +2)，n ∈N ∗为整数的n 叫作“贺数”，则在区间(1,50)内所有“贺数”的个数是______． 答案：4分析：利用换底公式计算可得log 23×log 34×⋅⋅⋅×log n+1(n +2)=log 2(n +2)，即可判断. 解：因为log 23×log 34×⋅⋅⋅×log n+1(n +2) =lg3lg2×lg4lg3×⋅⋅⋅×lg (n+2)lg (n+1)=lg (n+2)lg2=log 2(n +2)，又log 24=2，log 28=3，log 216=4，log 232=5，log 264=6，……， 所以当n +2=4，8，16，32时，log 2(n +2)为整数， 所以在区间(1,50)内“贺数”的个数是4． 所以答案是：415、函数f (x )=2√2−x+lg (x +3)的定义域为______．答案：(−3,2)分析：根据给定函数有意义列出不等式组，求解即可得原函数定义域. 函数f (x )=2√2−x lg (x +3)有意义，则有{2−x >0x +3>0，解得−3<x <2，所以函数f (x )的定义域为(−3,2). 所以答案是：(−3,2)16、已知125x =12.5y =1000，则y−x xy=________．答案：13分析：先把指数式化为对数式，再由换底公式化为同底数对数运算即可. 解：因为125x =12.5y =1000，所以x =log 1251000，y =log 12.51000，y−xxy =1x −1y =log 1000125−log 100012.5=log 100012512.5=log 100010=13．所以答案是：13.小提示：本题考查指对数互化公式、换底公式和对数运算，属于基础题. 解答题17、已知函数f(x)=log 2(2x +1). （1）求不等式f(x)>1的解集；（2）若函数g(x)=log 2(2x −1)(x >0)，若关于x 的方程g(x)=m +f(x)在[1,2]有解，求m 的取值范围. 答案：（1）{x |x >0}；（2）[log 213,log 235].分析：（1）由f(x)>1可得2x +1>2，从而可求出不等式的解集， （2）由g(x)=m +f(x)，得m =g (x )−f (x )=log 2(1−22x +1)，再由x ∈[1,2]可得log 2(1−22x +1)的范围，从而可求出m 的取值范围（1）原不等式可化为2x +1>2，即2x >1,∴x >0， 所以原不等式的解集为{x |x >0}（2）由g(x)=m +f(x)， ∴m =g (x )−f (x )=log 2(1−22x +1)，当1≤x ≤2时，25≤22x +1≤23，13≤1−22x +1≤35，m ∈[log 213，log 235]18、对于定义在区间[m,n ]上的两个函数f (x )和g (x )，如果对任意的x ∈[m,n ]，均有|f (x )−g (x )|≤1成立，则称函数f (x )与g (x )在[m,n ]上是“友好”的，否则称为“不友好”的．已知函数f (x )=log a (x −3a )，g (x )=log a1x−a(a >0,a ≠1)．(1)若f (x )与g (x )在区间[a +2,a +3]上都有意义，求a 的取值范围； (2)讨论函数f (x )与g (x )在区间[a +2,a +3]上是否“友好”． 答案：(1)(0,1) (2)答案见解析分析：（1）由题意解不等式组{a +2−3a >0a +2−a >0即可；（2）假设存在实数a ，使得f (x )与g (x )在区间[a +2,a +3]上是“友好”的，即|f (x )−g (x )|=|log a (x 2−4ax +3a 2)|≤1，即−1≤log a (x 2−4ax +3a 2)≤1，只需求出函数y =log a (x 2−4ax +3a 2)在区间[a +2,a +3]上的最值，解不等式组即可． （1）若f (x )与g (x )在区间[a +2,a +3]上都有意义，则必须满足{a +2−3a >0a +2−a >0，解得a <1，又a >0且a ≠1，所以a 的取值范围为(0,1)． （2）假设存在实数a ，使得f (x )与g (x )在区间[a +2,a +3]上是“友好”的，则|f (x )−g (x )|=|log a (x 2−4ax +3a 2)|≤1，即−1≤log a (x 2−4ax +3a 2)≤1，因为a ∈(0,1)，则2a ∈(0,2)，a +2>2，所以[a +2,a +3]在x =2a 的右侧，由复合函数的单调性可得y =log a (x 2−4ax +3a 2)在区间[a +2,a +3]上为减函数， 从而当x =a +2时，y max =log a (4−4a )，当x =a +3时，y min =log a (9−6a )，所以{log a(4−4a)≤1log a(9−6a)≥−10<a<1，即{4−4a≥a9a−6a2−1≤00<a<1，解得0<a≤9−√5712，所以当0<a≤9−√5712时，f(x)与g(x)在区间[a+2,a+3]上是“友好”的；当9−√5712<a<1时，f(x)与g(x)在区间[a+2,a+3]上是“不友好”的．。

高考数学中的指数函数与对数函数题详解指数函数和对数函数是高考数学中的重要内容，涉及到的题型和考点较多。

本文将对指数函数和对数函数的基本定义、性质以及解题方法进行详细解析。

一、指数函数指数函数是以指数为自变量的函数，其一般形式为y = a^x （其中a>0且a≠1）。

下面，我们来讨论指数函数的基本性质。

1. 指数函数的定义域和值域指数函数的定义域为实数集R，值域为正实数集(0, +∞)。

2. 指数函数的图像特点当指数a>1时，指数函数的图像在x轴的右侧逐渐增大，形状呈现递增趋势；当0<a<1时，指数函数的图像在x轴的右侧逐渐减小，形状呈现递减趋势。

3. 指数函数的性质(1) 指数函数在定义域内具有严格单调性，即当a>1时为严格递增函数，当0<a<1时为严格递减函数。

(2) 指数函数在定义域内具有连续性，无间断点。

(3) 指数函数在定义域内具有无界性，即当x趋向于正无穷时，函数值也趋向于正无穷。

(4) 指数函数具有经过点(0, 1)的特点。

接下来，我们通过解题的方式来进一步认识指数函数。

例题1：已知方程2^x = 4的解为x = 2，则方程e^(x-1) = 1的解为多少？解题思路：首先，根据指数函数的性质可知，2^x = 4 等价于 x = 2。

然后，代入方程e^(x-1) = 1，得到e^(2-1) = 1，即e^1 = 1，因此方程e^(x-1) = 1的解为x = 1。

二、对数函数对数函数是指以对数为自变量的函数，其一般形式为y = loga(x)（其中a>0且a≠1，x>0）。

下面，我们来探讨对数函数的基本性质。

1. 对数函数的定义域和值域对数函数的定义域为正实数集(0, +∞)，值域为实数集R。

2. 对数函数的图像特点当0<a<1时，对数函数的图像在x轴的右侧逐渐减小，形状呈现递减趋势；当a>1时，对数函数的图像在x轴的右侧逐渐增大，形状呈现递增趋势。

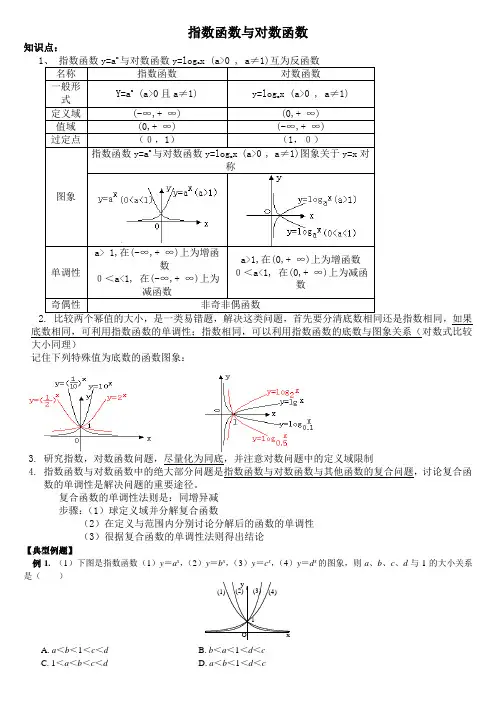
指数函数与对数函数知识点：x比较两个幂值的大小，是一类易错题，解决这类问题，首先要分清底数相同还是指数相同，如果底数相同，可利用指数函数的单调性；指数相同，可以利用指数函数的底数与图象关系（对数式比较大小同理）记住下列特殊值为底数的函数图象：3. 研究指数，对数函数问题，尽量化为同底，并注意对数问题中的定义域限制4. 指数函数与对数函数中的绝大部分问题是指数函数与对数函数与其他函数的复合问题，讨论复合函数的单调性是解决问题的重要途径。

复合函数的单调性法则是：同增异减 步骤：（1）球定义域并分解复合函数（2）在定义与范围内分别讨论分解后的函数的单调性 （3）很据复合函数的单调性法则得出结论【典型例题】例1. （1）下图是指数函数（1）y ＝a x ，（2）y ＝b x ，（3）y ＝c x ，（4）y ＝d x 的图象，则a 、b 、c 、d 与1的大小关系是（ ）y x1O(4)(3)(2)(1)A. a ＜b ＜1＜c ＜dB. b ＜a ＜1＜d ＜cC. 1＜a ＜b ＜c ＜dD. a ＜b ＜1＜d ＜c剖析：可先分两类，即（3）（4）的底数一定大于1，（1）（2）的底数小于1，然后再从（3）（4）中比较c 、d 的大小，从（1）（2）中比较a 、b 的大小。

解法一：当指数函数底数大于1时，图象上升，且底数越大，图象向上越靠近于y 轴；当底数大于0小于1时，图象下降，底数越小，图象向右越靠近于x 轴.得b ＜a ＜1＜d ＜c 。

故选B 。

解法二：令x ＝1，由图知c 1＞d 1＞a 1＞b 1，∴b ＜a ＜1＜d ＜c 。

例2. 已知2x x +2≤（41）x －2，求函数y ＝2x －2－x 的值域。

解：∵2x x +2≤2－2（x －2），∴x 2＋x ≤4－2x ， 即x 2＋3x －4≤0，得－4≤x ≤1。

又∵y ＝2x －2－x 是［－4，1］上的增函数，∴2－4－24≤y ≤2－2－1。

经典例题透析类型一、求函数的反函数例1．已知f(x)=225x - (0≤x ≤4)， 求f(x)的反函数.思路点拨：这里要先求f(x)的范围(值域).解：∵0≤x ≤4，∴0≤x 2≤16， 9≤25-x 2≤25，∴ 3≤y ≤5，∵ y=225x -， y 2=25-x 2，∴ x 2=25-y 2.∵ 0≤x ≤4，∴x=225y - (3≤y ≤5)将x ， y 互换，∴ f(x)的反函数f -1(x)=225x - (3≤x ≤5). 例2．已知f(x)=21(0)1(0)x x x x +≥⎧⎨-<⎩，求f -1(x). 思路点拨：求分段函数的反函数问题，应逐段求其反函数，再合并.解：当x ≥0时，y=x+1≥1，∴y ∈[1，+∞)，∴ f -1(x)=x-1 (x ≥1)；当x<0时，y=1-x 2<1，∴ y ∈(-∞，1)，反解 x 2=1-y ，，∴ f -1； ∴ 综上f -1(x)=1(1)(1)x x x -≥⎧⎪⎨<⎪⎩. 类型二、利用反函数概念解题例3.已知f(x)=112-+x x (x ≥3)， 求f -1(5). 思路点拨：这里应充分理解和运用反函数的自变量就是原函数的函数值，所求的反函数的函数值就是原函数的自变量这一事实，转化成方程问题.解：设f -1(5)=x 0， 则 f(x 0)=5，即 20011x x +-=5 (x 0≥3)∴ x 02+1=5x 0-5， x 02-5x 0+6=0. 解得x 0=3或x 0=2(舍)，∴ f -1(5)=3.举一反三：【变式1】记函数y=1+3-x 的反函数为()y g x =，则g(10)=( ) A ．2 B ．-2 C ．3 D ．-1(法一)依题意，函数13x y -=+的反函数y=-log 3(x-1)，因此g(10)=-2.(法二)依题意，由互为反函数的两个函数的关系，得方程1+3-x=10，解得x=-2，即g(10)=-2.答案B.例4.设点(4，1)既在f(x)=ax 2+b (a<0，x>0)的图象上，又在它的反函数图象上，求f(x)解析式.思路点拨：由前面总结的性质我们知道，点(4，1)在反函数的图象上，则点(1，4)必在原函数的图象上.这样就有了两个用来确定a ，b 的点，也就有了两个求解a ，b 的方程.解： ⎝⎛+⋅=+⋅=)2......(14)1......(4122b a b a 解得.a=-51， b=521，∴ f(x)=-51x+521. 另：这个题告诉我们，函数的图象若与其反函数的图象相交，交点不一定都在直线y=x 上. 例5．已知f(x)=ax b x c ++的反函数为f -1(x)=253x x +-，求a ，b ，c 的值. 思路点拨：注意二者互为反函数，也就是说已知函数f -1(x)=253x x +-的反函数就是函数f(x). 解：求f -1(x)=253x x +-的反函数，令f -1(x)=y 有yx-3y=2x+5. ∴(y-2)x=3y+5 ∴ x=352y y +-(y ≠2)，f -1(x)的反函数为 y=352x x +-.即ax b x c ++=352x x +-，∴ a=3， b=5， c=-2.类型三、互为反函数图象间关系例6.将y=2x的图象先______，再作关于直线y=x 对称的图象，可得到函数y=log 2(x ＋1)的图象( )A ．先向上平行移动一个单位B ．先向右平行移动一个单位C ．先向左平行移动一个单位D ．先向下平行移动一个单位解析：本题是关于图象的平移变换和对称变换，可求出解析式或利用几何直观推断．答案：D总结升华：本题主要考查互为反函数的两个函数的图象的对称关系与函数图象的平移变换等基本知识，以及基本计算技能和几何直观思维能力．举一反三：【变式1】函数y=f(x+1)与函数y=f -1(x+1)的图象( )A.关于直线y=x 对称B.关于直线y=x+1对称C.关于直线y=x-1对称D.关于直线y=-x 对称解：y=f(x+1)与y=f -1(x+1)图象是分别将y=f(x)， y=f -1(x)的图象向左平移一个单位所得，∵ y=f(x)与y=f -1(x)的图象关于直线y=x 对称，y=x 向左平移一个单位而得y=x+1. 故选B.【变式2】已知函数y=log 2x 的反函数是y=f —1(x)，则函数y= f —1(1-x)的图象是( )【答案】由y=log 2x 得f —1(x)＝2x ，所以y=f —1(1-x)＝21-x， 选择C. 【变式3】（2011 四川理7）若()f x 是R 上的奇函数，且当0x >时，1()12xf x ⎛⎫=+ ⎪⎝⎭，则()f x 的反函数的图象大致是（ ）解：当0x >时，函数()f x 单调递减，值域为()1,2，此时，其反函数单调递减且图象在1x =与2x =之间，故选A ．类型四、指数函数和对数函数的综合问题例7.已知函数)2(log )(221x x x f －＝．(1)求函数的单调增区间；(2)求其单调增区间内的反函数．解：复合函数y=f[g(x)]的单调性与y=f(t)，t=g(x)的单调性的关系：同增异减．(1)函数的定义域{x|x<0或x>2}，又t=x 2-2x=(x-1)2-1．∴x ∈(-∞，0)，t 是x 的减函数．而)0(log 21＞＝t t y 是减函数，∴函数f(x)在(-∞，0)为增函数．(2)函数f(x)的增区间为(-∞，0)， 令)2(log 221x x y －＝，则y x x )21(22＝－．∴0)21(22＝－－y x x ，1x ＝∵x<0，∴y x －＋－＝211．∴R)(211)(1∈x x f x －－＋－＝．总结升华：研究函数单调性首先要确定定义域；在函数的每个单调区间内存在反函数，因此要注意反函数存在的条件．。

ｙ＝ｘ＋2的图象之间有什么关系？ 3
01
02
求函数反函数的步骤:
3 求原函数的值域
04
05
2 x与y互换
4 写出反函数及它 的定义域
03
1 反解
y y=2x
结论:
Q(a,b) y=x
(0,1)
O
(1,0)
P(b,a) y=log2x x
点（a,b）在函数y＝f(x)的图像上
b＝f(a)
点（b,a）在反函数y＝f－1(x) 的图像上
a＝f－1(b)
[例4]函数f(x)＝loga (x－1)(a＞0且a≠1)的反函数的图象
经过点(1, 4)，求a的值.
解:依题意,得
1loag(41)
即 :loa3 g1 , a3.
点（a,b）在函数y＝f(x)的图像上 点（b,a）在反函数y＝f－1(x) 的图像上
b＝f(a) a＝f－1(b)
例 5： 已 知 函 数 （ f x） x2（ 1x2） 求 出 f （ 14） 的 值 。
解 ： 令x214， 解 之 得 ： x5 又x2， x5.
点（a,b）在函数y＝f(x)的图像上
b＝f(a)
点（b,a）在反函数y＝f－1(x) 的图像上 a＝f－1(b)
理论迁移
f(x)log2(12x)
例4 已知函数
.
（1）求函数f(x)的定义域和值域；
（2）求证函定义域和值域互换 对应法则互逆
图像关于直线y=x对称
反函数的概念
指数函数y=ax(a>0,a≠1)与 对数函数y=logax(a>0,a≠1) 互为反函数
解：由ｙ＝3ｘ－2（ｘ∈R ）得
ｘ＝ｙ＋2 3

指数函数与对数函数例题和知识点总结一、指数函数的定义与性质指数函数的一般形式为$y ＝ a^x$（＄a ＞ 0$且$a ≠ 1$）。

其中，底数$a$决定了函数的性质。

当$a ＞ 1$时，函数单调递增；当$0 ＜ a ＜ 1$时，函数单调递减。

指数函数的定义域为$R$，值域为$（0, ＋＼infty)＄。

例如，函数$y ＝ 2^x$是一个底数为$2$（大于$1$）的指数函数，它在$R$上单调递增。

二、对数函数的定义与性质对数函数是指数函数的反函数，一般形式为$y ＝＼log_a x$（＄a ＞ 0$且$a ≠ 1$）。

其中，对数的底数$a$同样决定了函数的性质。

当$a ＞ 1$时，函数在$（0, ＋＼infty)＄上单调递增；当$0 ＜ a ＜1$时，函数在$（0, ＋＼infty)＄上单调递减。

对数函数的定义域为$（0, ＋＼infty)＄，值域为$R$。

例如，函数$y ＝＼log_2 x$是一个底数为$2$（大于$1$）的对数函数，它在$（0, ＋＼infty)＄上单调递增。

三、指数函数与对数函数的图象指数函数$y ＝ a^x$（＄a ＞ 0$且$a ≠ 1$）的图象特点：当$a ＞ 1$时，图象过点$（0, 1)＄，从左到右逐渐上升；当$0 ＜ a ＜ 1$时，图象过点$（0, 1)＄，从左到右逐渐下降。

对数函数$y ＝＼log_a x$（＄a ＞ 0$且$a ≠ 1$）的图象特点：当$a ＞ 1$时，图象过点$（1, 0)＄，从左到右逐渐上升；当$0 ＜ a ＜ 1$时，图象过点$（1, 0)＄，从左到右逐渐下降。

四、指数运算与对数运算的性质指数运算性质：1、＄a^m ＼times a^n ＝ a^｛m ＋ n}＄2、＄＼frac{a^m}｛a^n} ＝ a^｛m n}＄3、＄（a^m)＾n ＝ a^｛mn}＄4、＄a^0 ＝ 1$（＄a ≠ 0$）对数运算性质：1、＄＼log_a （MN) ＝＼log_a M ＋＼log_a N$2、＄＼log_a ＼frac{M}｛N} ＝＼log_a M ＼log_a N$3、＄＼log_a M^n ＝ n ＼log_a M$4、＄＼log_a a ＝ 1$5、＄＼log_a 1 ＝ 0$五、例题分析例 1：比较大小比较$2^｛03}＄和$03^2$的大小。

第四章指数函数与对数函数复习总结与检测知识点1：根式1．根式及相关概念（1）a的n次方根定义：如果x n＝a，那么x叫做a的n次方根，其中n>1，且n∈N*.（2）a的n次方根的表示n的奇偶性a的n次方根的表示符号a的取值范围n为奇数na Rn为偶数±na[0，＋∞)（3）根式：式子na叫做根式，这里n叫做根指数，a叫做被开方数．2．根式的性质(n>1，且n∈N*)（1）n为奇数时，na n＝a.（2）n为偶数时，na n＝|a|＝⎩⎪⎨⎪⎧a，a≥0，－a，a<0.（3）n0＝0.（4）负数没有偶次方根．知识归纳知识点2：指数幂及运算1．分数指数幂的意义分数指数幂正分数指数幂规定：n ma＝n a m(a>0，m，n∈N*，且n>1)负分数指数幂规定：nma ＝1amn＝1na m(a>0，m，n∈N*，且n>1) 0的分数指数幂0的正分数指数幂等于0，0的负分数指数幂没有意义2．有理数指数幂的运算性质（1）a r a s＝a r＋s(a>0，r，s∈Q)．（2）(a r)s＝a rs(a>0，r，s∈Q)．（3）(ab)r＝a r b r(a>0，b>0，r∈Q)．3．无理数指数幂一般地，无理数指数幂aα(a>0，α是无理数)是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．知识点3：指数函数的概念、图象与性质1．指数函数的概念一般地，函数y＝a x(a>0，且a≠1)叫做指数函数，其中x是自变量，函数的定义域是R.2．指数函数的图象和性质a的范围a＞10＜a＜1图象性质定义域R值域(0，＋∞)过定点(0,1)，即当x＝0时，y＝1单调性在R上是增函数在R上是减函数奇偶性非奇非偶函数对称性函数y＝a x与y＝a－x的图象关于y轴对称知识点4：对数的概念1．对数（1）指数式与对数式的互化及有关概念：（2）底数a 的范围是a >0，且a ≠1. 2．常用对数与自然对数3．对数的基本性质 （1）负数和零没有对数． （2）log a 1＝0(a >0，且a ≠1)． （3）log a a ＝1(a >0，且a ≠1)． 知识点5：对数的运算1．对数的运算性质如果a >0，且a ≠1，M >0，N >0，那么： （1）log a (MN )＝log a M ＋log a N ； （2）log a MN ＝log a M －log a N ；（3）log a M n ＝n log a M (n ∈R )． 2．对数的换底公式若a >0且a ≠1；c >0且c ≠1；b >0，则有log a b ＝log c blog c a .知识点6：对数函数的概念、图象及性质1．对数函数的概念函数y ＝log a x (a >0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是(0，＋∞)． 2．对数函数的图象及性质(0，＋∞)3．反函数指数函数y ＝a x (a >0，且a ≠1)与对数函数y ＝log a x (a >0且a ≠1)互为反函数．知识点7：三种函数模型的性质知识点8：函数的零点与方程的解1．函数的零点对于函数y＝f(x)，把使f(x)＝0的实数x叫做函数y＝f(x)的零点．2．方程、函数、函数图象之间的关系方程f(x)＝0有实数根∈函数y＝f(x)的图象与x轴有交点∈函数y＝f(x)有零点．3．函数零点存在定理如果函数y＝f(x)在区间[a，b]上的图象是一条连续不断的曲线，且有f(a)f(b)<0，那么，函数y＝f(x)在区间(a，b)内至少有一个零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的解．知识点9：用二分法求方程的近似解1．二分法的定义对于在区间[a，b]上图象连续不断且f(a)·f(b)<0的函数y＝f(x)，通过不断地把它的零点所在的区间一分为二，使所得区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法．2．二分法求函数零点近似值的步骤（1）确定零点x0的初始区间[a，b]，验证f(a)f(b)＜0.（2）求区间(a，b)的中点c.（3）计算f(c)，并进一步确定零点所在的区间：∈ 若f(c)＝0(此时x0＝c)，则c就是函数的零点；∈ 若f(a)f(c)＜0(此时x0∈(a，c))，则令b＝c；∈ 若f(c)f(b)＜0(此时x0∈(c，b))，则令a＝c.（4）判断是否达到精确度ε：若|a－b|＜ε，则得到零点近似值a(或b)；否则重复步骤(2)～(4)．知识点10：函数模型的应用1．常用函数模型常用函数模型（1）一次函数模型y＝kx＋b(k，b为常数，k≠0)（2）二次函数模型y＝ax2＋bx＋c(a，b，c为常数，a≠0)（3）指数函数模型y＝ba x＋c(a，b，c为常数，b≠0，a>0且a≠1)（4）对数函数模型y＝m log a x＋n(m，a，n为常数，m≠0，a>0且a≠1)（5）幂函数模型y＝ax n＋b(a，b为常数，a≠0)（6）分段函数模型y＝⎩⎪⎨⎪⎧ax＋b(x<m)，cx＋d(x≥m)2.建立函数模型解决问题的基本过程题型1：指数与对数的运算【例1】计算：（1）2log32－log3329＋log38－5log53；（2）1.5－⎪⎭⎫⎝⎛-⨯67310＋80.25×42＋(32×3)6－⎝⎛⎭⎫－2323.【解析】(1)原式＝log322×8329－3＝2－3＝－1.(2)原式＝⎝⎛⎭⎫2313＋234×214＋22×33－⎝⎛⎭⎫2313＝21＋4×27＝110.【方法技巧】题型讲解指数、对数的运算应遵循的原则指数式的运算首先注意化简顺序，一般负指数先转化成正指数，根式化为分数指数幂运算，其次若出现分式则要注意分子、分母因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化，前后要等价，熟练地运用对数的三个运算性质并结合对数恒等式，换底公式是对数计算、化简、证明常用的技巧.【针对训练】1．设3x ＝4y ＝36，则2x ＋1y 的值为( )A ．6B ．3C ．2D ．1【解析】D 由3x ＝4y ＝36得x ＝log 336，y ＝log 436， ∈2x ＋1y ＝2log 363＋log 364＝log 369＋log 364＝log 3636＝1.题型2：指数函数、对数函数的图象及应用【例2】（1）若函数y ＝log a x (a >0，且a ≠1)的图象如图所示，则下列函数正确的是( )A B C D（2）已知函数f (x )是定义在R 上的偶函数，当x ≥0时，f (x )＝x⎪⎭⎫ ⎝⎛21∈ 如图，画出函数f (x )的图象；∈ 根据图象写出f (x )的单调区间，并写出函数的值域．【解析】(1)B 由已知函数图象可得，log a 3＝1，所以a ＝3.A 项，函数解析式为y ＝3－x，在R 上单调递减，与图象不符；C 项中函数的解析式为y ＝(－x )3＝－x 3，当x >0时，y <0，这与图象不符；D 项中函数解析式为y ＝log 3(－x )，在(－∞，0)上为单调递减函数，与图象不符；B 项中对应函数解析式为y ＝x 3，与图象相符．故选B.](2)[解] ∈先作出当x ≥0时，f (x )＝⎝⎛⎭⎫12x的图象，利用偶函数的图象关于y 轴对称，再作出f (x )在x ∈(－∞，0)时的图象．∈函数f (x )的单调递增区间为(－∞，0)，单调递减区间为[0，＋∞)，值域为(0,1]． 【方法技巧】1．识别函数的图象从以下几个方面入手： （1）单调性：函数图象的变化趋势； （2）奇偶性：函数图象的对称性； （3）特殊点对应的函数值．2．指数函数与对数函数图象经过定点的实质是a 0＝1，log a 1＝0.【针对训练】2．函数y ＝1＋log 12(x －1)的图象一定经过点( )A ．(1,1)B ．(1,0)C ．(2,1)D ．(2,0)【解析】C 把y ＝log 12x 的图象向右平移1个单位，再向上平移1个单位即可得到y ＝1＋log 12(x －1)的图象，故其经过点(2,1)．题型3：比较大小【例3】 若0<x <y <1，则( )A ．3y <3xB ．log x 3<log y 3C ．log 4x <log 4y D.yx ⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛4141【解析】C 因为0<x <y <1，则对于A ，函数y ＝3x 在R 上单调递增，故3x <3y ，A 错误．对于B ，根据底数a 对对数函数y ＝log a x 的影响：当0<a <1时，在x ∈(1，＋∞)上“底小图高”．因为0<x <y <1，所以log x 3>log y 3，B 错误．对于C ，函数y ＝log 4x 在(0，＋∞)上单调递增，故log 4x <log 4y ，C 正确．对于D ，函数y ＝⎝⎛⎭⎫14x在R 上单调递减，故⎝⎛⎭⎫14x>⎝⎛⎭⎫14y，D 错误．【方法技巧】1．比较两数大小常用的方法有单调性法、图象法、中间值法等．2．当两个数都是指数幂或对数式时，可将其看成某个指数函数、对数函数或幂函数的函数值，然后利用该函数的单调性比较．3．比较多个数的大小时，先利用“0”“1”作为分界点，然后在各部分内再利用函数性质比较大小．4．含参数的问题，要根据参数的取值进行分类讨论． 【针对训练】3．设a ＝log 2π，b ＝log 12π，c ＝π－2，则( )A ．a >b >cB ．b >a >cC ．a >c >bD ．c >b >a【解析】C ∈a ＝log 2π>log 22＝1，b ＝log 12π<log 121＝0，c ＝π－2＝1π2，即0<c <1，∈a >c >b ，故选C.题型4：指数函数、对数函数的性质【例4】（1）设函数f (x )＝ln(1＋x )－ln(1－x )，则f (x )是( )A ．奇函数，且在(0,1)上是增函数B ．奇函数，且在(0,1)上是减函数C ．偶函数，且在(0,1)上是增函数D ．偶函数，且在(0,1)上是减函数 （2）已知a >0，a ≠1且log a 3>log a 2，若函数f (x )＝log a x 在区间[a,3a ]上的最大值与最小值之差为1.∈ 求a 的值；∈ 若1≤x ≤3，求函数y ＝(log a x )2－log a x ＋2的值域．【解析】(1)A [由题意可得，函数f (x )的定义域为(－1,1)，且f (－x )＝ln(1－x )－ln(1＋x )＝－f (x )，故f (x )为奇函数．又f (x )＝ln 1＋x 1－x ＝ln ⎝⎛⎭⎫21－x －1，易知y ＝21－x －1在(0,1)上为增函数，故f (x )在(0,1)上为增函数．](2)[解] ∈因为log a 3>log a 2，所以f (x )＝log a x 在[a,3a ]上为增函数． 又f (x )在[a,3a ]上的最大值与最小值之差为1， 所以log a (3a )－log a a ＝1，即log a 3＝1，所以a ＝3. ∈函数y ＝(log 3x )2－log 3x ＋2＝(log 3x )2－12log 3x ＋2＝⎝⎛⎭⎫log 3x －142＋3116. 令t ＝log 3x ，因为1≤x ≤3， 所以0≤log 3x ≤1，即0≤t ≤1.所以y ＝⎝⎛⎭⎫t －142＋3116∈⎣⎡⎦⎤3116，52， 所以所求函数的值域为⎣⎡⎦⎤3116，52.【方法技巧】1．研究函数的性质要树立定义域优先的原则．2．换元法的作用是利用整体代换，将问题转化为常见问题．该类问题中，常设u ＝log a x 或u ＝a x ，转化为一元二次方程、二次函数等问题．要注意换元后u 的取值范围．题型5：函数的应用【例5】 一种放射性元素，最初的质量为500 g ，按每年10%衰减． （1）求t 年后，这种放射性元素的质量w 的表达式；（2）由求出的函数表达式，求这种放射性元素的半衰期(结果精确到0.1)． 【解析】 (1)最初的质量为500 g. 经过1年，w ＝500(1－10%)＝500×0.9； 经过2年，w ＝500×0.92； 由此推知，t 年后，w ＝500×0.9t . (2)由题意得500×0.9t ＝250，即0．9t ＝0.5，两边同时取以10为底的对数，得 lg 0.9t ＝lg 0.5，即t lg 0.9＝lg 0.5，所以t ＝lg 0.5lg 0.9≈6.6.即这种放射性元素的半衰期约为6.6年． 【方法技巧】指数函数模型的应用在实际问题中，有关人口增长、银行利率、细胞分裂等增长率问题常可以用指数函数模型表示.通常可以表示为y ＝N (1＋p )x (其中N 为基础数，p 为增长率，x 为时间)的形式.【针对训练】4．某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若初时含杂质2%，每过滤一次可使杂质含量减少13，问至少应过滤几次才能使产品达到市场要求？(已知：lg2≈0.301 0，lg 3≈0.477 1)【解析】 设过滤n 次能使产品达到市场要求，依题意，得2100×⎝⎛⎭⎫23n≤11 000，即⎝⎛⎭⎫23n≤120. 则n (lg 2－lg 3)≤－(1＋lg 2)， 故n ≥1＋lg 2lg 3－lg 2≈7.4，考虑到n ∈N ，故n ≥8，即至少要过滤8次才能达到市场要求．指数函数与对数函数(时间：120分钟 满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若a <12，则化简4(2a －1)2的结果是( )A.2a －1 B ．－2a －1 C.1－2aD ．－1－2a【解析】C ∈a <12，∈2a －1<0.于是，原式＝4(1－2a )2＝1－2a . 2．计算：log 225·log 522＝( ) A ．3 B ．4 C ．5D ．6 章节检测【解析】A log 225·log 522＝lg 25lg 2·lg 22lg 5＝2lg 5·lg 232lg 2·lg 5＝2×32＝3.3．函数y ＝x －1·ln(2－x )的定义域为( ) A ．(1,2) B ．[1,2) C ．(1,2]D ．[1,2]【解析】B 要使解析式有意义，则⎩⎪⎨⎪⎧x －1≥0，2－x >0，解得1≤x <2，所以所求函数的定义域为[1,2)．4．下列幂函数中过点(0,0)，(1,1)的偶函数是( ) A ．y ＝x 12 B ．y ＝x 4 C ．y ＝x －2D ．y ＝31x【解析】B 对A ，y ＝x 12的定义域为[0，＋∞)，不是偶函数；C 中，y ＝x －2不过(0,0)点，D 中，y ＝31x 是奇函数，B 中，y ＝x 4满足条件．5．函数f (x )＝21x －x⎪⎭⎫⎝⎛21的零点个数为( )A ．0B ．1C ．2D ．3【解析】B 令f (x )＝0，可得x 12＝⎝⎛⎭⎫12x，在同一平面直角坐标系中分别画出幂函数y ＝x 12和指数函数y ＝⎝⎛⎭⎫12x的图象，如图所示，可得交点只有一个，所以函数f (x )的零点只有一个．6．若log a 3＝m ，log a 5＝n ，则a 2m ＋n的值是( ) A ．15 B ．75 C ．45D ．225【解析】C 由log a 3＝m ，得a m ＝3， 由log a 5＝n ，得a n ＝5， ∈a 2m ＋n ＝(a m )2·a n ＝32×5＝45.7．函数f (x )＝4x ＋12x 的图象( )A ．关于原点对称B ．关于直线y ＝x 对称C ．关于x 轴对称D ．关于y 轴对称【解析】D 易知f (x )的定义域为R ，关于原点对称．∈f (－x )＝4－x ＋12－x ＝1＋4x2x ＝f (x )，∈f (x )是偶函数，其图象关于y 轴对称．8．若log a (a 2＋1)<log a 2a <0，则a 的取值范围是( ) A ．(0,1)B.⎪⎭⎫ ⎝⎛210，C. ⎪⎭⎫⎝⎛1,21 D ．(0,1)∈(1，＋∞)【解析】C 由题意得a >0且a ≠1，故必有a 2＋1>2a . 又log a (a 2＋1)<log a 2a <0，所以0<a <1， 同时2a >1，∈a >12，综上，a ∈⎝⎛⎭⎫12，1. 9．已知a ＝5log 23.4，b ＝5log 43.6，c ＝⎝⎛⎭⎫15log 30.3，则( ) A ．a >b >c B ．b >a >c C ．a >c >bD ．c >a >b【解析】C c ＝5log 3103，只需比较log 23.4，log 43.6，log 3103的大小，又0<log 43.6<1，log 23.4>log 33.4>log 3103>1，所以a >c >b .10．函数f (x )＝a |x ＋1|(a >0，且a ≠1)的值域为[1，＋∞)，则f (－4)与f (1)的关系是( ) A ．f (－4)＝f (1) B ．f (－4)>f (1) C ．f (－4)<f (1)D ．不能确定【解析】B 因为函数f (x )＝a |x ＋1|(a >0，且a ≠1)的值域为[1，＋∞)，所以a >1，又函数f (x )＝a |x ＋1|(a >0，且a ≠1)的图象关于直线x ＝－1对称，所以f (－4)>f (1)．11．已知函数f (x )＝⎩⎪⎨⎪⎧(a －2)x ，x ≥2，⎝⎛⎭⎫12x －1，x <2满足对任意的实数x 1≠x 2都有f (x 1)－f (x 2)x 1－x 2<0成立，则实数a 的取值范围为( )A ．(－∞，2) B.⎝⎛⎦⎤－∞，138 C ．(－∞，2]D.⎣⎡⎭⎫138，2【解析】B [由题意知函数f (x )是R 上的减函数，于是有⎩⎪⎨⎪⎧a －2<0，(a －2)×2≤⎝⎛⎭⎫122－1，由此解得a ≤138，即实数a 的取值范围是⎝⎛⎦⎤－∞，138，选B. 12．函数f (x )＝ax 5－bx ＋1，若f (lg(log 510))＝5，则f (lg(lg 5))的值为( ) A ．－3 B ．5 C ．－5D ．－9【解析】A lg(log 510)＝lg ⎝⎛⎭⎫1lg 5＝－lg(lg 5)， 设t ＝lg(lg 5)，则f (lg(log 510))＝f (－t )＝5. 因为f (x )＝ax 5－bx ＋1， 所以f (－t )＝－at 5＋bt ＋1＝5， 则f (t )＝at 5－bt ＋1， 两式相加得f (t )＋5＝2，则f (t )＝2－5＝－3，即f (lg(lg 5)的值为－3.二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．函数f (x )＝a x －1＋3的图象一定过定点P ，则P 点的坐标是________．【解析】(1,4) 由于函数y ＝a x 恒过(0,1)，而y ＝a x －1＋3的图象可看作由y ＝a x 的图象向右平移1个单位，再向上平移3个单位得到的，则P 点坐标为(1,4)．14．将进货单价为8元的商品按10元一个销售，每天可卖出100个．若每个涨价1元，则日销售量减少10个．为获得最大利润，则此商品日销售价应定为每个________元．【解析】14 设每个涨价x 元，则实际销售价为10＋x 元，销售的个数为100－10x ， 则利润为y ＝(10＋x )(100－10x )－8(100－10x )＝－10(x －4)2＋360(0≤x <10，x ∈N )．因此，当x ＝4，即售价定为每个14元时，利润最大．15．若f (x )＝a ·2x ＋2a －12x ＋1为R 上的奇函数，则实数a 的值为________．【解析】13 因为f (x )＝a ·2x ＋2a －12x ＋1为R 上的奇函数，所以f (0)＝0，即a ·20＋2a －120＋1＝0，所以a ＝13.16．已知125x ＝12.5y ＝1 000，则y －xxy＝________.【解析】13 因为125x ＝12.5y ＝1 000，所以x ＝log 125 1 000，y ＝log 12.5 1 000，y －x xy ＝1x －1y ＝log 1 000 125－log 1 000 12.5＝log 1 00012512.5＝log 1 000 10＝13.三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)求值： (1)⎝⎛⎭⎫21412－(－9.6)0－⎝⎛⎭⎫338－23＋(1.5)－2； (2)log 2512·log 45－log 133－log 24＋5log 52.【解析】(1)⎝⎛⎭⎫21412－(－9.6)0－⎝⎛⎭⎫338－23＋(1.5)－2 ＝⎝⎛⎭⎫9412－1－⎝⎛⎭⎫278－23＋⎝⎛⎭⎫32－2＝32－1－⎝⎛⎭⎫32－2＋⎝⎛⎭⎫232＝32－1－49＋49＝12. (2)log 2512·log 45－log 133－log 24＋5log 52＝－14＋1－2＋2＝34.18．(本小题满分12分)已知指数函数f (x )＝a x (a >0，且a ≠1)过点(－2,9)． (1)求函数f (x )的解析式；(2)若f (2m －1)－f (m ＋3)<0，求实数m 的取值范围．【解析】(1)将点(－2,9)代入f (x )＝a x (a >0，a ≠1)得a －2＝9，解得a ＝13，∈f (x )＝⎝⎛⎭⎫13x . (2)∈f (2m －1)－f (m ＋3)<0， ∈f (2m －1)<f (m ＋3)． ∈f (x )＝⎝⎛⎭⎫13x 为减函数， ∈2m －1>m ＋3，解得m >4， ∈实数m 的取值范围为(4，＋∞)．19．(本小题满分12分)已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ，x ＞0，3x ，x ≤0，且关于x 的方程f (x )＋x －a ＝0有且只有一个实根，求实数a 的取值范围．【解析】如图，在同一坐标系中分别作出y ＝f (x )与y ＝－x ＋a 的图象，其中a 表示直线在y 轴上的截距，由图可知，当a ＞1时，直线y ＝－x ＋a 与y ＝log 2x 只有一个交点．所以实数a 的取值范围是(1，＋∞)．20．(本小题满分12分)已知1≤x ≤4，求函数f (x )＝log 2x 4·log 2x2的最大值与最小值．【解析】 ∈f (x )＝log 2x 4·log 2x2＝(log 2x －2)(log 2x －1) ＝⎝⎛⎭⎫log 2x －322－14， 又∈1≤x ≤4，∈0≤log 2x ≤2，∈当log 2x ＝32，即x ＝232＝22时，f (x )有最小值－14.当log 2x ＝0时，f (x )有最大值2，此时x ＝1. 即函数f (x )的最大值是2，最小值是－14.21．(本小题满分12分)某公司制定了一个激励销售人员的奖励方案：当销售利润不超过15万元时，按销售利润的10%进行奖励；当销售利润超过15万元时，若超过部分为A 万元，则超出部分按2log 5(A ＋1)进行奖励，没超出部分仍按销售利润的10%进行奖励．记奖金总额为y (单位：万元)，销售利润为x (单位：万元)．(1)写出该公司激励销售人员的奖励方案的函数表达式；(2)如果业务员老张获得5.5万元的奖金，那么他的销售利润是多少万元？ 【解析】(1)由题意，得y ＝⎩⎪⎨⎪⎧0.1x ，0<x ≤15，1.5＋2log 5x －14，x >15.(2)∈当x ∈(0,15]时，0.1x ≤1.5， 又y ＝5.5>1.5，∈x >15， ∈1.5＋2log 5(x －14)＝5.5， 解得x ＝39.答：老张的销售利润是39万元． 22．(本小题满分12分)已知函数f (x )＝lg ⎝ ⎛⎭⎪⎫1－x 1＋x .(1)求证：f (x )是奇函数； (2)求证：f (x )＋f (y )＝f ⎝ ⎛⎭⎪⎫x ＋y 1＋xy ；(3)若f ⎝⎛⎭⎪⎫a ＋b 1＋ab ＝1，f ⎝ ⎛⎭⎪⎫a －b 1－ab ＝2，求f (a )，f (b )的值．【解析】(1)证明：由函数f (x )＝lg ⎝⎛⎭⎪⎫1－x 1＋x ，可得1－x 1＋x >0，即x －11＋x <0，解得－1<x <1，故函数的定义域为(－1,1)，关于原点对称．再根据f (－x )＝lg 1＋x 1－x ＝－lg 1－x1＋x＝－f (x )，可得f (x )是奇函数．(2)证明：f (x )＋f (y )＝lg 1－x 1＋x ＋lg 1－y 1＋y ＝lg (1－x )(1－y )(1＋x )(1＋y )，而f ⎝ ⎛⎭⎪⎫x ＋y 1＋xy ＝lg1－x ＋y 1＋xy 1＋x ＋y 1＋xy ＝lg1＋xy －x －y 1＋xy ＋x ＋y ＝lg (1－x )(1－y )(1＋x )(1＋y )，∈f (x )＋f (y )＝f ⎝ ⎛⎭⎪⎫x ＋y 1＋xy 成立．(3)若f ⎝⎛⎭⎪⎫a ＋b 1＋ab ＝1，f ⎝ ⎛⎭⎪⎫a －b 1－ab ＝2，则由(2)可得f (a )＋f (b )＝1，f (a )－f (b )＝2， 解得f (a )＝32，f (b )＝－12.。

高中数学第四章指数函数与对数函数典型例题单选题1、已知a=lg2，10b=3，则log56=（）A．a+b1+a B．a+b1−aC．a−b1+aD．a−b1−a答案：B分析：指数式化为对数式求b，再利用换底公式及对数运算性质变形. ∵a=lg2,0b=3，∴b=lg3，∴log56=lg6lg5=lg2×3lg102=lg2+lg31−lg2=a+b1−a．故选：B．2、函数f(x)=|x|⋅22−|x|在区间[−2,2]上的图象可能是（）A．B．C．D．答案：C分析：首先判断函数的奇偶性，再根据特殊值判断即可；解：∵f(−x)=|x|⋅22−|x|=f(x)，∴f(x)是偶函数，函数图象关于y轴对称，排除A，B选项；∵f(1)=2=f(2)，∴f(x)在[0,2]上不单调，排除D选项．故选：C3、式子√m⋅√m 43√m 56m >0)的计算结果为（ ）A ．1B ．m 120C ．m 512D ．m 答案：D分析：由指数运算法则直接计算可得结果.√m⋅√m 43√m 56=m 12⋅m 43m 56=m 12+43−56=m .故选：D.4、若f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数，实数a 的取值范围是（ ）A ．[1,5]B ．[32,5) C ．(32,5)D ．(1,5) 答案：B分析：由题意得{6−a >1a >1log a 1+3≥(6−a)−a ，解不等式组可求得答案因为f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数，所以{6−a >1a >1log a 1+3≥(6−a)−a ，解得32≤a <5，故选：B5、函数f (x )=√3−x +log 13(x +1)的定义域是（ ）A ．[−1,3)B ．(−1,3)C ．(−1,3]D ．[−1,3] 答案：C分析：由题可得{3−x ≥0x +1>0，即得.由题意得{3−x ≥0x +1>0，解得−1<x ≤3， 即函数的定义域是(−1,3].故选：C.6、下列函数中是增函数的为（ ）A ．f (x )=−xB ．f (x )=(23)xC ．f (x )=x 2D ．f (x )=√x 3答案：D分析：根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ，f (x )=−x 为R 上的减函数，不合题意，舍. 对于B ，f (x )=(23)x为R 上的减函数，不合题意，舍.对于C ，f (x )=x 2在(−∞,0)为减函数，不合题意，舍. 对于D ，f (x )=√x 3为R 上的增函数，符合题意， 故选：D.7、下列计算中结果正确的是（ ） A ．log 102+log 105=1B ．log 46log 43=log 42=12C ．(log 515)3=3log 515=−3D ．13log 28=√log 283=√33答案：A分析：直接根据对数的运算性质及换底公式计算可得；解：对于A ：log 102+log 105=log 10(2×5)=log 1010=1，故A 正确； 对于B ：log 46log 43=log 36，故B 错误；对于C ：(log 515)3=(log 55−1)3=(−log 55)3=−1，故C 错误； 对于D ：13log 28=13log 223=13×3log 22=1，故D 错误； 故选：A8、荀子《劝学》中说：“不积跬步，无以至千里；不积小流，无以成江海．”所以说学习是日积月累的过程，每天进步一点点，前进不止一小点．我们可以把(1+1%)365看作是每天的“进步”率都是1%，一年后是1.01365≈37.7834；而把(1−1%)365看作是每天“退步”率都是1%，一年后是0.99365≈0.0255.若“进步”的值是“退步”的值的100倍，大约经过(参考数据：lg101≈2.0043，lg99≈1.9956) （ ）天．A ．200天B ．210天C ．220天D ．230天 答案：D分析：根据题意可列出方程100×0.99x =1.01x ，求解即可.设经过x 天“进步”的值是“退步”的值的100倍，则100×0.99x=1.01x，即(1.010.99)x =100，∴x =log 1.010.99100=lg lg 1.010.99=lg lg 10199=2lg−lg≈22.0043−1.9956=20.0087≈230．故选：D ． 多选题9、已知函数f(x)=1−2x 1+2x，则下面几个结论正确的有（ ）A ．f(x)的图象关于原点对称B ．f(x)的图象关于y 轴对称C ．f(x)的值域为(−1,1)D ．∀x 1,x 2∈R ，且x 1≠x 2,f (x 1)−f (x 2)x 1−x 2<0恒成立答案：ACD分析：利用奇函数的定义和性质可判断AB 的正误，利用参数分离和指数函数的性质可判断CD 的正误. 对于A ，f(x)=1−2x1+2x ，则f(−x)=1−2−x1+2−x =2x −11+2x =−f(x)， 则f(x)为奇函数，故图象关于原点对称，故A 正确.对于B ，计算f(1)=−13，f(−1)=13≠f(1)，故f(x)的图象不关于y 轴对称，故B 错误. 对于C ，f(x)=1−2x1+2x =−1+21+2x ，1+2x =t,t ∈(1,+∞)，故y =f(x)=−1+2t ，易知：−1+2t ∈(−1,1)，故f(x)的值域为(−1,1),故C 正确. 对于D ，f(x)=1−2x1+2x =−1+21+2x ，因为y =1+2x 在R 上为增函数，y =−1+21+t 为(1,+∞)上的减函数， 由复合函数的单调性的判断法则可得f (x )在R 上单调递减，故∀x 1,x 2∈R ，且x 1≠x 2，f(x 1)−f(x 2)x 1−x 2<0恒成立，故D 正确.故选：ACD.小提示：方法点睛：复合函数的单调性的研究，往往需要将其转化为简单函数的复合，通过内外函数的单调性结合“同增异减”的原则来判断.10、设函数f (x )=ax 2+bx +c (a,b,c ∈R,a >0)，则下列说法正确的是（ ） A ．若f (x )=x 有实根，则方程f(f (x ))=x 有实根 B ．若f (x )=x 无实根，则方程f(f (x ))=x 无实根 C ．若f (−b 2a)<0，则函数y =f (x )与y =f(f (x ))都恰有2个零点D ．若f (f (−b 2a))<0，则函数y =f (x )与y =f(f (x ))都恰有2零点答案：ABD分析：直接利用代入法可判断A 选项的正误；推导出f (x )−x >0对任意的x ∈R 恒成立，结合该不等式可判断B 选项的正误；取f (x )=x 2−x ，结合方程思想可判断C 选项的正误；利用二次函数的基本性质可判断D 选项的正误.对于A 选项，设f (x )=x 有实根x =x 0，则f(f (x 0))=f (x 0)=x 0，A 选项正确； 对于B 选项，因为a >0，若方程f (x )=x 无实根，则f (x )−x >0对任意的x ∈R 恒成立， 故f(f (x ))>f (x )>x ，从而方程f(f (x ))=x 无实根，B 选项正确；对于C 选项，取f (x )=x 2−x ，则f (12)=−14<0，函数y =f (x )有两个零点， 则f(f (x ))=[f (x )]2−f (x )=0，可得f (x )=0或f (x )=1，即x 2−x =0或x 2−x =1. 解方程x 2−x =0可得x =0或1，解方程x 2−x −1=0，解得x =1±√52. 此时，函数y =f(f (x ))有4个零点，C 选项错误；对于D 选项，因为f (f (−b2a ))<0，设t =f (−b2a )，则t =f (x )min ， 因为f (t )<0且a >0，所以，函数f (x )必有两个零点，设为x 1、x 2且x 1<x 2， 则x 1<t <x 2，所以，方程f (x )=x 1无解，方程f (x )=x 2有两解，因此，若f(f(−b))<0，则函数y=f(x)与y=f(f(x))都恰有2零点，D选项正确.2a故选：ABD.小提示：思路点睛：对于复合函数y=f[g(x)]的零点个数问题，求解思路如下：（1）确定内层函数u=g(x)和外层函数y=f(u)；（2）确定外层函数y=f(u)的零点u=u i(i=1,2,3,⋯,n)；（3）确定直线u=u i(i=1,2,3,⋯,n)与内层函数u=g(x)图象的交点个数分别为a1、a2、a3、⋯、a n，则函数y=f[g(x)]的零点个数为a1+a2+a3+⋯+a n.11、(多选题)某市出租车收费标准如下：起步价为8元，起步里程为3km(不超过3km按起步价付费)；超过3km 但不超过8km时，超过部分按每千米2.15元收费；超过8km时，超过部分按每千米2.85元收费，另每次乘坐需付燃油附加费1元.下列结论正确的是（）A．出租车行驶4km，乘客需付费9.6元B．出租车行驶10km，乘客需付费25.45元C．某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用D．某人乘坐一次出租车付费22.6元，则此次出租车行驶了9km答案：BCD分析：根据题意分别计算各个选项的情况，即可得答案.对于A选项：出租车行驶4km，乘客需付费8+1×2.15+1=11.15元，故A错误；对于B选项：出租车行驶10 km，乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元，故B正确；对于C选项：乘出租车行驶5km，乘客需付费8+2×2.15+1=13.30元，乘坐两次需付费26.6元，26.6>25.45，故C正确；对于D选项：设出租车行驶x km时，付费y元，由8+5×2.15+1=19.75<22.6，知x>8，因此由y=8+2.15×5+2.85(x-8)+1=22.6，解得x=9，故D正确.故选：BCD.小提示：本题考查函数模型的应用，解题要点为认真审题，根据题意逐一分析选项即可，属基础题.12、若log2m=log4n，则（）A．n=2m B．log9n=log3mC．lnn=2lnm D．log2m=log8(mn)答案：BCD分析：利用对数运算化简已知条件，然后对选项进行分析，从而确定正确选项.依题意log2m=log4n，所以m>0,n>0,log2m=log22n=12log2n=log2n12，所以m=n 12,m2=n，A选项错误.log9n=log32m2=22log3m=log3m，B选项正确.lnn=lnm2=2lnm，C选项正确.log8(mn)=log23m3=33log2m=log2m，D选项正确.故选：BCD13、在平面直角坐标系中，我们把横纵坐标相等的点称之为“完美点”，下列函数的图象中存在完美点的是（）A．y=﹣2x B．y=x﹣6C．y=3xD．y=x2﹣3x+4答案：ACD分析：横纵坐标相等的函数即y=x，与y=x有交点即存在完美点，依次计算即可.横纵坐标相等的函数即y=x，与y=x有交点即存在完美点，对于A,{y=xy=−2x，解得{x=0y=0，即存在完美点(0,0)，对于B,{y=xy=x−6，无解，即不存在完美点，对于C,{y=xy=3x，解得{x=√3y=√3或{x=−√3y=−√3，即存在完美点(√3,√3)，(−√3,−√3)对于D,{y=xy=x2−3x+4，x2−3x+4=x,即x2−4x+4=0，解得x=2，即存在完美点(2,2).故选：ACD.填空题14、化简(√a−1)2+√(1−a)2+√(1−a)33=________.答案：a-1分析：根据根式的性质即可求解.由(√a−1)2知a-1≥0，a≥1.故原式=a-1+|1-a|+1-a=a-1.所以答案是：a-115、对数型函数f(x)的值域为[0,+∞)，且在(0,+∞)上单调递增，则满足题意的一个函数解析式为______．答案：f(x)=|log2(x+1)|（答案不唯一，满足f(x)=|log a(x+b)|，a>1，b≥1即可）分析：根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f(x)的值域为[0,+∞)，且在(0,+∞)上单调递增，∴满足题意的一个函数是f(x)=|log2(x+1)|．所以答案是：f(x)=|log2(x+1)|（答案不唯一）16、函数y＝log a(x＋1)－2(a>0且a≠1)的图象恒过点________．答案：(0，－2)分析：由对数函数的图象所过定点求解．解：依题意，x+1=1，即x＝0时，y＝log a(0＋1)－2＝0－2＝－2，故图象恒过定点(0，－2)．所以答案是：(0，－2)解答题17、（1）计算0.027−13−(−16)−2+810.75+(19)0−3−1；（2）若x 12+x−12=√6，求x 2+x −2的值．答案：（1）-5；（2）14.分析：（1）由题意利用分数指数幂的运算法则，计算求得结果． （2）由题意两次利用完全平方公式，计算求得结果． （1）0.027−13−(−16)−2+810.75+(19)0−3−1=0.3﹣1﹣36+33+1−13=103−36+27+1−13=−5．（2）若x 12+x −12=√6，∴x +1x +2＝6，x +1x =4，∴x 2+x ﹣2+2＝16，∴x 2+x ﹣2＝14．18、已知函数f (x )=2x −12x +1．(1)判断并证明f (x )在其定义域上的单调性；(2)若f (k ⋅3x )+f (3x −9x +2)<0对任意x ≥1恒成立，求实数k 的取值范围． 答案：(1)f (x )在R 上单调递增；证明见解析 (2)(−∞,43)分析：（1）设x 2>x 1，可整理得到f (x 2)−f (x 1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1)>0，由此可得结论；（2）利用奇偶性定义可证得f (x )为奇函数，结合单调性可将恒成立的不等式化为k <g (x )=3x −23x −1，由g (x )单调性可求得g (x )≥43，由此可得k 的取值范围.（1）f (x )在R 上单调递增，证明如下： 设x 2>x 1，∴f (x 2)−f (x 1)=2x 2−12x 2+1−2x 1−12x 1+1=(2x 2−1)(2x 1+1)−(2x 2+1)(2x 1−1)(2x 2+1)(2x 1+1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1)；∵x 2>x 1，∴2x 2−2x 1>0，又2x 2+1>0，2x 1+1>0，∴f (x 2)−f (x 1)>0， ∴f (x )在R 上单调递增. （2）∵f (−x )=2−x −12−x +1=1−2x1+2x =−f (x )，∴f (x )为R 上的奇函数，由f(k⋅3x)+f(3x−9x+2)<0得：f(k⋅3x)<−f(3x−9x+2)=f(9x−3x−2)，由（1）知：f(x)在R上单调递增，∴k⋅3x<9x−3x−2在[1,+∞)上恒成立；当x≥1时，3x≥3，∴k<3x−23x−1在[1,+∞)上恒成立；令g(x)=3x−23x−1，∵y=3x在[1,+∞)上单调递增，y=23x在[1,+∞)上单调递减，∴g(x)在[1,+∞)上单调递增，∴g(x)≥g(1)=3−23−1=43，∴k<43，即实数k的取值范围为(−∞,43).。

高中数学必修一第四章指数函数与对数函数知识点总结归纳单选题1、设4a =3b =36，则1a+2b =（ ）A ．3B ．1C ．−1D ．−3 答案：B分析：先求出a =log 436,b =log 336，再利用换底公式和对数的运算法则计算求解. 因为4a =3b =36，所以a =log 436,b =log 336， 则1a=log 364,2b=log 369，所以则1a +2b =log 364+log 369=log 3636=1. 故选：B.2、若x 1，x 2是二次函数y =x 2−5x +6的两个零点，则1x 1+1x 2的值为（ ）A ．−12B ．−13C ．−16D ．56 答案：D分析：解方程可得x 1=2,x 2=3，代入运算即可得解. 由题意，令x 2−5x +6=0，解得x =2或3， 不妨设x 1=2,x 2=3，代入可得1x 1+1x 2=12+13=56.故选：D.3、我国在2020年9月22日在联合国大会提出，二氧化碳排放力争于2030年前实现碳达峰，争取在2060年前实现碳中和．为了响应党和国家的号召，某企业在国家科研部门的支持下，进行技术攻关：把二氧化碳转化为一种可利用的化工产品，经测算，该技术处理总成本y （单位：万元）与处理量x （单位：吨）(x ∈[120,500])之间的函数关系可近似表示为y ={13x 3−80x 2+5040x,x ∈[120,144)12x 2−200x +80000,x ∈[144,500] ，当处理量x 等于多少吨时，每吨的平均处理成本最少（ ）A．120B．200C．240D．400答案：D分析：先根据题意求出每吨的平均处理成本与处理量之间的函数关系，然后分x∈[120,144)和x∈[144,500]分析讨论求出其最小值即可由题意得二氧化碳每吨的平均处理成本为S={13x2−80x+5040,x[120,144)1 2x−200+80000x,x∈[144,500]，当x∈[120,144)时，S=13x2−80x+5040=13(x−120)2+240，当x=120时，S取得最小值240，当x∈[144,500]时，S=12x+80000x−200≥2√12x⋅80000x−200=200，当且仅当12x=80000x，即x=400时取等号，此时S取得最小值200，综上，当每月得理量为400吨时，每吨的平均处理成本最低为200元，故选：D4、将进货价为每个80元的商品按90元一个出售时，能卖出400个，每涨价1元，销售量就减少20个，为了使商家利润有所增加，则售价a（元/个）的取值范围应是（）A．90<a<100B．90<a<110C．100<a<110D．80<a<100答案：A分析：首先设每个涨价x元，涨价后的利润与原利润之差为y元，结合条件列式，根据y>0，求x的取值范围，即可得到a的取值范围.设每个涨价x元，涨价后的利润与原利润之差为y元，则a=x+90,y=(10+x)⋅(400−20x)−10×400=−20x2+200x.要使商家利润有所增加，则必须使y>0，即x2−10x<0，得0<x<10,∴90<x+90<100，所以a的取值为90<a<100.故选：A5、已知a=lg2，10b=3，则log56=（）A．a+b1+a B．a+b1−aC．a−b1+aD．a−b1−a答案：B分析：指数式化为对数式求b，再利用换底公式及对数运算性质变形. ∵a=lg2,10b=3，∴b=lg3，∴log56=lg6lg5=lg2×3lg102=lg2+lg31−lg2=a+b1−a．故选：B．6、设f(x)={e x−1,x<3log3(x−2),x≥3，则f(f(11))的值是（）A．1B．e C．e2D．e−1答案：B分析：根据自变量的取值，代入分段函数解析式，运算即可得解.由题意得f(11)=log3(11−2)=log39=2，则f(f(11))=f(2)=e2−1=e.故选：B.小提示：本题考查了分段函数求值，考查了对数函数及指数函数求值，属于基础题.7、已知实数a,b∈(1,+∞)，且log2a+log b3=log2b+log a2，则（）A．a<√b<b B．√b<a<b C．b<√a<a D．√a<b<a答案：B分析：对log2a−log a2<log2b−log b2，利用换底公式等价变形，得log2a−1log2a <log2b−1log2b，结合y=x−1x 的单调性判断b<a，同理利用换底公式得log2a−1log2a<log3b−1log3b，即log2a>log3b，再根据对数运算性质得log2a>log2√b，结合y=log2x单调性，a>√b，继而得解.由log2a+log b3=log2b+log a2，变形可知log2a−log a2<log2b−log b2，利用换底公式等价变形，得log2a−1log2a <log2b−1log2b，由函数f(x)=x−1x在(0,+∞)上单调递增知，log2a<log2b，即a<b，排除C，D；其次，因为log2b>log3b，得log2a+log b3>log3b+log a2，即log2a−log a2>log3b−log b3，同样利用f(x)=x−1x的单调性知，log2a>log3b，又因为log3b=log√3√b>log2√b，得log2a>log2√b，即a>√b，所以√b<a<b.故选：B.8、已知f(x)＝a−x(a>0，且a≠1)，且f(－2)>f(－3)，则a的取值范围是（）A．a>0B．a>1C．a<1D．0<a<1答案：D分析：把f(－2)，f(－3)代入解不等式，即可求得．因为f(－2)＝a2，f(－3)＝a3，f(－2)>f(－3)，即a2>a3，解得：0<a<1．故选：D多选题9、某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=12x2-200x+80000，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.以下判断正确的是（）A．该单位每月处理量为400吨时，才能使每吨的平均处理成本最低B．该单位每月最低可获利20000元C．该单位每月不获利，也不亏损D．每月需要国家至少补贴40000元才能使该单位不亏损答案：AD分析：根据题意，列出平均处理成本表达式，结合基本不等式，可得最低成本；列出利润的表达式，根据二次函数图像与性质，即可得答案.由题意可知，二氧化碳每吨的平均处理成本为yx =12x+80000x−200≥2√12x⋅80000x−200=200，当且仅当12x=80000x，即x=400时等号成立，故该单位每月处理量为400吨时，才能使每吨的平均处理成本最低，最低成本为200元，故A正确；设该单位每月获利为S元，则S=100x−y=100x−(12x2+80000−200x)=−12x2+300x−80000=−12(x−300)2−35000，因为x∈[400,600]，所以S∈[−80000,−40000].故该单位每月不获利，需要国家每月至少补贴40000元才能不亏损，故D正确，BC错误，故选：AD小提示：本题考查基本不等式、二次函数的实际应用，难点在于根据题意，列出表达式，并结合已有知识进行求解，考查阅读理解，分析求值的能力，属中档题.10、已知函数f(x)=log2(2x+8x)−2x，以下判断正确的是（）A．f（x）是增函数B．f（x）有最小值C．f（x）是奇函数D．f（x）是偶函数答案：BD分析：由题设可得f(x)=log2(12x+2x)，根据复合函数的单调性判断f(x)的单调情况并确定是否存在最小值，应用奇偶性定义判断奇偶性.由f(x)=log2(2x+23x)−log222x=log2(12x+2x)，令μ=2x>0为增函数；而t=1μ+μ在(0,1)上递减，在(1,+∞)上递增；所以t在x∈(−∞,0)上递减，在x∈(0,+∞)上递增；又y=log2t在定义域上递增，则y在x∈(−∞,0)上递减，在x∈(0,+∞)上递增；所以f(x)在(−∞,0)上递减，在(0,+∞)上递增，故最小值为f(0)=1，f(−x)=log2(12−x +2−x)=log2(2x+12x)=f(x)，故为偶函数.故选：BD11、为了得到函数y=ln(ex)的图象，可将函数y=ln x的图象（）A．纵坐标不变，横坐标伸长为原来的e倍B．纵坐标不变，横坐标缩短为原来的1eC．向上平移一个单位长度D ．向下平移一个单位长度 答案：BC分析：根据函数图像变换求得结果.解：由题意函数y =lnx 的图象纵坐标不变，横坐标缩短为原来的1e ， 可得到函数y =ln (ex)的图象，则A 错误，B 正确； 因为y =ln (ex)=ln x +1，则将函数y =ln x 的图象向上平移一个单位可得到函数y =ln (ex)的图象， 则C 正确，D 错误. 故选：BC. 填空题12、已知函数f(x)={x +1,x ≤0,log 2x,x >0则函数y =f [f (x )]的所有零点之和为___________.答案：12分析：利用分段函数，分类讨论，即可求出函数y =f [f (x )]的所有零点，从而得解．解：x ⩽0时，x +1=0，x =−1，由f(x)=−1，可得x +1=−1或log 2x =−1，∴x =−2或x =12；x >0时，log 2x =0，x =1，由f(x)=1，可得x +1=1或log 2x =1，∴x =0或x =2； ∴函数y =f [f (x )]的所有零点为−2，12，0，2，所以所有零点的和为−2+12+0+2=12 所以答案是：12．13、对于实数a 和b ，定义运算“∗”：a ∗b ={a 2−ab,b 2−ab, a ≤ba >b ，设f(x)=(2x −1)∗(x −1)，且关于x 的方程为f(x)=m(m ∈R )恰有三个互不相等的实数根，则m 的取值范围是___________. 答案：(0,14)分析：根据代数式2x −1和x −1之间的大小关系，结合题中所给的定义，用分段函数的形式表示函数f (x )的解析式，画出函数的图象，利用数形结合求出m 的取值范围. 由2x −1≤x −1可得x ≤0，由 2x −1>x −1可得x >0，所以根据题意得f (x )={(2x −1)2−(2x −1)(x −1)，x ≤0(x −1)2−(2x −1)(x −1)，x >0，即 f (x )={2x 2−x ，x ≤0x −x 2，x >0，作出函数f (x )的图象如图，当x >0时，f (x )=x −x 2开口向下，对称轴为x =12， 所以当x >0时，函数的最大值为f (12)=12−(12)2=14， 函数的图象和直线y =m (m ∈R )有三个不同的交点． 可得m 的取值范围是(0,14)， 所以答案是：(0,14) 14、函数f(x)=x (12x −a +12)定义域为（﹣∞，1）∪（1，+∞），则满足不等式ax ≥f （a ）的实数x 的集合为______． 答案：{x |x ≥1}分析：由题意可得a ＝2，f(x)=x (12x −2+12)，f(a)=f(2)=2，由ax ≥f （a ），结合指数函数单调性可求x 解：由函数f(x)=x (12x −a +12)定义域为（﹣∞，1）∪（1，+∞），可知a ＝2 ∴f(x)=x (12x −2+12)，f(a)=f(2)=2由ax≥f（a）可得，2x≥2∴x≥1所以答案是：{x|x≥1}解答题15、已知集合A={log52 ,log425,2}，集合B={log25,log319}．记集合A中最小元素为a，集合B中最大元素为b．(1)求A∩B及a，b的值；(2)证明：函数f(x)=x+1x 在[2,+∞)上单调递增；并用上述结论比较a+b与52的大小．答案：(1)A∩B={log25}，a=log52，b=log25；(2)证明见解析，a+b>52分析：（1）根据对数的运算性质以及对数函数的单调性即可解出；（2）根据单调性的定义即可证明函数f(x)=x+1x在[2,+∞)上单调递增，再根据单调性以及对数的性质log a b=1log b a即可比较出大小．（1）因为log425=log25，所以A={log52 ,log25,2}，B={log25,−2}，即A∩B={log25}．因为log52<log525=2=log24<log25，所以a=log52，b=log25．（2）设x1,x2为[2,+∞)上任意两个实数，且2≤x1<x2，则x1−x2<0，x1x2>1，f(x1)−f(x2)=(x1+1x1)−(x2+1x2)=x1−x2+1x1−1x2=(x1−x2)×x1x2−1x1x2<0，即f(x1)<f(x2)，所以f(x)在[2,+∞)上单调递增．所以f(x)>f(2)=52，所以log52+log25=1log25+log25=f(log25)>52．。

专项5 指数函数、对数函数相关的4种题型1.比较大小一般来说，指数、对数比较大小我们采取的思路是：首先，尽量将不同底数的指数、对数或幂函数，通过公式化成同一底数的，底数相同的根据单调性比较大小；其次，对于确实不能化成同一底数的，我们尽量将真数或指数化成相同的，然后我们做出图像，根据指数函数在第一象限内底数越大图像越高的特征、对数函数在第一象限内水平向右底数增大的特征判断大小； 最后，如果全都不相同，我们一般先做出图像，观察图像，判断大小，如果图像仍然不能解决问题，那么我们就应该考虑找中间值进行比较，中间值一般取0，-1,1，比如能否确定所要进行比较的数的正负、与1或-1的大小关系。

通过上述方式一般能解决所有比较大小问题。

1.设0.90.48 1.514,8,()2a b c -===，则（ ） .A c a b >>.B b a c >>.C a b c >>.D a c b >>2.三个数0.32、log 20.3、20.3的大小关系为（ ）A ．0.32<20.3<log 20.3B ．0.32<log 20.3<20.3C ．log 20.3<0.32<20.3D ．log 20.3<20.3<0.323. a log a,log a,log 1,a 0530.5三者的大小关系是则＜＜若（ ）a log a log a log D.a log a log a log C.a log a log a log B.a log a log a log A.530.50.5530.535350.5＞＞＞＞＞＞＞＞4．设a ＞1,且2log (1)log (1),log (2)a a a m a n a p a =+=-=，,则p n m ,,的大小关系为（ ）(A) n ＞m ＞p (B) m ＞p ＞n (C) m ＞n ＞p (D) p ＞m ＞n5.以下四个数中的最大者是（ ）(A) (ln2)2(B) ln(ln2) (C) ln (D) ln26.设12log 3a =，0.213b ⎛⎫= ⎪⎝⎭，132c =，则（ ） A ．a b c << B ．c b a << C ．c a b <<D ．b a c <<7．设a b c ，，均为正数，且122log a a =，121log 2b b ⎛⎫= ⎪⎝⎭，21log 2c c ⎛⎫= ⎪⎝⎭．则（ ） Ａ．a b c << Ｂ．c b a << Ｃ．c a b << Ｄ．b a c <<28.下列大小关系正确的是（ ）A ．20.440.43log 0.3<<；B ．20.440.4log 0.33<<；C ．20.44log 0.30.43<<；D ．0.424log 0.330.4<<9．设2log 3P =，3log 2Q =，23log (log 2)R =，则（ ）Ａ．R Q P << Ｂ．P R Q << Ｃ．Q R P << Ｄ．R P Q <<10. 下列不等式成立的是（ ）A .2lg (lg )e e <<B .2lg (lg )e e <<C .2(lg )lg e e <<D .2(lg )lg e e <<11.已知324log 0.3log 3.4log 3.615,5,()5a b c ===，则（ ） .A a b c >>.B b a c >>.C a c b >>.D c a b >>12.若13(,1),ln ,2ln ,ln x e a x b x c x -∈===，则（ ） .A a b c <<.B c a b <<.C b a c <<.D b c a <<13.设2554log 4,(log 3),log 5,a b c ===则（ ） .A a c b <<.B b c a <<.C a b c <<.D b a c <<2.恒过定点问题指数函数恒过定点（0,1），是指指数函数的指数位置的表达式为0的时候，函数值恒为1；对数函数恒过（1,0），是指对数函数的真数位置的表达式为1的时候，函数值恒为0；对于指数位置或真数位置表达式中含有参数的，应考虑使用公式分离参数。

(名师选题)（精选试题附答案）高中数学第四章指数函数与对数函数重难点归纳单选题1、若函数f(x)=x3+x2−2x−2的一个正零点附近的函数值用二分法计算，其参考数据如下：那么方程x3+x2−2x−2=0的一个近似根（精确度0.1）为（）．A．1.2B．1.4C．1.3D．1.5答案：B分析：根据二分法求零点的步骤以及精确度可求得结果.解：因为f(1)<0,f(1.5)>0，所以f(1)f(1.5)<0，所以函数在(1,1.5)内有零点，因为1.5−1=0.5>0.1，所以不满足精确度0.1；因为f(1.25)<0，所以f(1.25)f(1.5)<0，所以函数在(1.25,1.5)内有零点，因为1.5−1.25=0.25>0.1，所以不满足精确度0.1；因为f(1.375)<0，所以f(1.375)f(1.5)<0，所以函数在(1.375,1.5)内有零点，因为1.5−1.375=0.125>0.1，所以不满足精确度0.1；因为f(1.4375)>0，所以f(1.4375)f(1.375)<0，所以函数在(1.375,1.4375)内有零点，因为1.4375−1.375= 0.0625<0.1，所以满足精确度0.1；所以方程x3+x2−2x−2=0的一个近似根（精确度0.05）是区间(1.375,1.4375)内的任意一个值（包括端点值），根据四个选项可知选B .故选：B2、已知55<84，134<85．设a=log53，b=log85，c=log138，则（）A．a<b<c B．b<a<c C．b<c<a D．c<a<b答案：A分析：由题意可得a 、b 、c ∈(0,1)，利用作商法以及基本不等式可得出a 、b 的大小关系，由b =log 85，得8b =5，结合55<84可得出b <45，由c =log 138，得13c =8，结合134<85，可得出c >45，综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、c ∈(0,1)，a b =log 53log 85=lg3lg5⋅lg8lg5<1(lg5)2⋅(lg3+lg82)2=(lg3+lg82lg5)2=(lg24lg25)2<1，∴a <b ；由b =log 85，得8b =5，由55<84，得85b <84，∴5b <4，可得b <45； 由c =log 138，得13c =8，由134<85，得134<135c ，∴5c >4，可得c >45.综上所述，a <b <c . 故选：A.小提示：本题考查对数式的大小比较，涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用，考查推理能力，属于中等题.3、已知f (x )是定义在R 上的奇函数，当x ≥0时，f(x)=log 2(x +2)+t ，f (−6)=（ ） A ．−2B ．2C ．−4D ．4 答案：A分析：因f (x )是定义在R 上的奇函数，所以f (0)=0，从而可求t ，再由奇函数的定义即可求出f (−6)的值. 解：∵f (x )是定义在R 上的奇函数，又当x ≥0时，f(x)=log 2(x +2)+t ， ∴ f (0)=log 2(0+2)+t =0， ∴t =−1，∴当x ≥0时，f(x)=log 2(x +2)−1，∴f (−6)=−f (6)=−[log 2(6+2)−1]=−(log 223−1)=−2， 故选：A.4、已知函数f(x)=9+x 2x，g(x)=log 2x +a ，若存在x 1∈[3,4]，对任意x 2∈[4,8]，使得f(x 1)≥g(x 2)，则实数a 的取值范围是（ ）A ．(−∞,134]B ．(134,+∞)C ．(0,134)D ．（1，4）答案：A分析：将问题化为在对应定义域内f(x 1)max ≥g(x 2)max ，结合对勾函数和对数函数性质求它们的最值，即可求参数范围.由题意知：f(x)在[3,4]上的最大值大于或等于g(x)在[4,8]上的最大值即可． 当x ∈[3,4]时，f(x)=9x +x ，由对勾函数的性质得：f(x)在[3,4]上单调递增，故f(x)max =f(4)=94+4=254．当x ∈[4,8]时，g(x)=log 2x +a 单调递增，则g(x)max =g(8)=log 28+a =3+a ， 所以254≥3+a ，可得a ≤134．故选：A5、已知y 1=(13)x，y 2=3x ，y 3=10−x ，y 4=10x ，则在同一平面直角坐标系内，它们的图象大致为（ ）A ．B ．C ．D ．答案：A分析：根据指数函数的单调性及图像特征进行比较，即可判断.y 2=3x 与y 4=10x是增函数，y 1=(13)x与y 3=10−x=(110)x是减函数，在第一象限内作直线x =1，该直线与四条曲线交点的纵坐标的大小对应各底数的大小，易知：选A ． 故选：A6、设a =30.7, b =(13)−0.8, c =log 0.70.8，则a,b,c 的大小关系为（ ）A ．a <b <cB ．b <a <cC ．b <c <aD ．c <a <b 答案：D分析：利用指数函数与对数函数的性质，即可得出a,b,c 的大小关系. 因为a =30.7>1， b =(13)−0.8=30.8>30.7=a ，c =log 0.70.8<log 0.70.7=1， 所以c <1<a <b . 故选：D.小提示：本题考查的是有关指数幂和对数值的比较大小问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围.比较指对幂形式的数的大小关系，常用方法：（1）利用指数函数的单调性：y =a x ，当a >1时，函数递增；当0<a <1时，函数递减；（2）利用对数函数的单调性：y =log a x ，当a >1时，函数递增；当0<a <1时，函数递减； （3）借助于中间值，例如：0或1等.7、若32是函数f (x )=2x 2−ax +3的一个零点，则f (x )的另一个零点为（ ）A ．1B ．2C ．（1，0）D ．（2，0） 答案：A分析：由32是函数f (x )=2x 2−ax +3的一个零点，可得a 值，再利用韦达定理列方程解出f (x )的另一个零点． 因为32是函数f (x )=2x 2−ax +3的一个零点，所以f (32)=2×(32)2−a ×32+3=0，解得a =5．设另一个零点为x 0，则x 0+32=52，解得x 0=1，所以f (x )的另一个零点为1． 故选：A ．8、已知0<a <1,b <−1，则函数y =a x +b 的图像必定不经过（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限 答案：A解析：根据指数函数的图象结合图象的平移可得正确的选项. 因为0<a <1，故y =a x 的图象经过第一象限和第二象限， 且当x 越来越大时，图象与x 轴无限接近.因为b <−1，故y =a x 的图象向下平移超过一个单位，故y =a x +b 的图象不过第一象限. 故选：A ．9、设函数f （x ）＝ln |2x +1|﹣ln |2x ﹣1|，则f （x ）（ ） A ．是偶函数，且在 (12，+∞)单调递增B ．是奇函数，且在 (−12，12)单调递增 C ．是偶函数，且在(−∞，−12)单调递增 D ．是奇函数，且在 (−∞，−12)单调递增分析：先求出f (x )的定义域结合奇偶函数的定义判断f (x )的奇偶性，设t ＝|2x+12x−1|，则y ＝ln t ，由复合函数的单调性判断f (x )的单调性，即可求出答案.解：由{2x +1≠02x −1≠0，得x ≠±12．又f （﹣x ）＝ln |﹣2x +1|﹣ln |﹣2x ﹣1|＝﹣（ln |2x +1|﹣ln |2x ﹣1|）＝﹣f （x ）， ∴f （x ）为奇函数，由f （x ）＝ln |2x +1|﹣ln |2x ﹣1|＝ln |2x+12x−1|， ∵2x+12x−1=1+22x−1=1+1x−12．可得内层函数t ＝|2x+12x−1|的图象如图，在（﹣∞，−12），（12，+∞）上单调递减，在（−12，12）上单调递增， 又对数式y ＝lnt 是定义域内的增函数，由复合函数的单调性可得，f （x ）在（−12，12）上单调递增， 在（﹣∞，−12），（12，+∞）上单调递减． 故选：B ．10、设f(x)={e x−1,x <3log 3(x −2),x ≥3，则f(f (11))的值是（ ）A ．1B ．eC ．e 2D ．e −1分析：根据自变量的取值，代入分段函数解析式，运算即可得解. 由题意得f(11)=log 3(11−2)=log 39=2， 则f(f (11))=f (2)=e 2−1=e . 故选：B.小提示：本题考查了分段函数求值，考查了对数函数及指数函数求值，属于基础题. 填空题11、已知log a 13>1，则实数a 的取值范围为______．答案：(13,1).分析：分0<a <1和a >1两种情况求解即可.解：当0<a <1时，由log a13>1，可得log a13>log aa，解得13<a <1；当a >1时，log a 13>1，可得log a13>log aa，得a <13，不满足a >1，故无解.综上所述a 的取值范围为：(13,1). 所以答案是：(13,1).12、已知a ，b 为正数，化简√a 5b 2⋅(a 2b )−1⋅√b 3=_______．答案：a 12b 12分析：根据根式与分数指数幂的互化以及指数幂的运算公式即可求出结果.原式=a 52b 2⋅a −2b −1⋅b 32=a 12b 12． 所以答案是：a 12b 12．13、已知√(a −1)44+1=a ，化简(√a −1)2+√(1−a)2+√(1−a)33=_________． 答案：a −1分析：根据已知条件判断a 的范围，再结合根式的运算性质，即可求得结果. 由已知√(a −1)44+1=a ，即|a −1|=a −1，即a ⩾1，所以(√a −1)2+√(1−a)2+√(1−a)33=(a −1)+(a −1)+(1−a)=a −1， 所以答案是：a −1小提示：本题考查根式的运算性质，属简单题；注意公式的熟练应用即可. 14、函数f （x ）＝3x −3−x 3x +3−x+2，若有f （a ）＋f （a －2）＞4，则a 的取值范围是________.答案：（1，＋∞）分析：构造函数F （x ）＝f （x ）－2，则f （a ）＋f （a －2）＞4等价于F （a ）＋F （a －2）＞0，分析F(x)奇偶性和单调性即可求解.设F （x ）＝f （x ）－2，则F （x ）＝3x −3−x3x +3−x ，易知F （x ）是奇函数，F （x ）＝3x −3−x3x +3−x ＝32x −132x +1＝1－232x +1在R 上是增函数，由f （a ）＋f （a －2）＞4得F （a ）＋F （a －2）＞0， 于是可得F （a ）＞F （2－a ），即a ＞2－a ，解得a ＞1. （1，＋∞）15、已知函数f (x )={x 2+4x x ≥22|x−a | x <2 ，若对任意的x 1∈[2,+∞)，都存在唯一的x 2∈(−∞,2)，满足f (x 2)=f (x 1)，则实数a 的取值范围是______． 答案：0≤a <4分析：由题意可得函数f (x )在[2，＋∞）时的值域包含于函数f (x )在（−∞，2）时的值域，利用基本不等式先求出函数f (x )在x ∈[2，＋∞）时的值域，当x ∈（−∞，2）时，对a 分情况讨论，分别利用函数的单调性求出值域，从而求出a 的取值范围． 解：设函数g (x )=x 2+4x , x ≥2的值域为A ，函数ℎ(x )=2|x−a | , x <2的值域为B ，因为对任意的x 1∈[2,+∞)，都存在唯一的x 2∈(−∞,2)，满足f (x 2)=f (x 1)， 则A ⊆B ，且B 中若有元素与A 中元素对应，则只有一个.当x1∈[2,+∞)时，g(x)=x2+4x =x+4x，因为x+4x ≥2√x⋅4x=4，当且仅当x=4x，即x=2时，等号成立，所以A=[4,+∞)，当x2∈(−∞,2)时，ℎ(x)=2|x−a| , x<2①当a≥2时，ℎ(x)=2a−x , x<2，此时B=(2a−2,+∞)，∴2a−2<4，解得2≤a<4，②当a<2时，ℎ(x)={2a−x,x<a2x−a,a≤x<2，此时ℎ(x)在(−∞,a)上是减函数，取值范围是(1,+∞)，ℎ(x)在[a,2)上是增函数，取值范围是[1,22−a)，∴22−a≤4，解得0≤a<2，综合得0≤a<4.所以答案是：0≤a<4小提示：关键点点睛：本题即有恒成立问题，又有存在性问题，最后可转化为函数值域之间的包含关系问题，最终转化为最值问题，体现了转化与化归的思想.解答题16、已知函数ℎ(x)=|log12x|.(1)求ℎ(x)在[12,a](a>12)上的最大值；(2)设函数f(x)的定义域为I，若存在区间A⊆I，满足:对任意x1∈A，都存在x2∈A(其中A表示A在I上的补集)使得f(x1)=f(x2)，则称区间A为f(x)的“Γ区间”.已知ℎ(x)=|log12x|(x∈[12,2])，若A=[12,a)为函数ℎ(x)的“Γ区间”，求a的最大值.答案：（1）答案见解析；（2）1.解析：（1）作出函数ℎ(x)=|log12x|的图象，分12<a≤2，a>2，利用数形结合法求解.(2)根据对任意x1∈A，都存在x2∈A使得f(x1)=f(x2)，分12<a≤1，1<a≤2，分别求得ℎ(x)在[12,a)和[a,2]上的值域，利用集合法求解.（1）函数ℎ(x)=|log12x|的图象如图所示：当12<a≤2时，ℎ(x)的最大值为ℎ(12)=1，当a>2时，ℎ(x)的最大值为ℎ(a)=−log12a.(2) 当12<a≤1时，ℎ(x)在[12,a)上的值域为(log12a,1]，ℎ(x)在[a,2]上的值域为[0,1]，因为满足:对任意x1∈A，都存在x2∈A使得f(x1)=f(x2)，所以(log12a,1)[0,1]，成立；此时A=[12,a)为函数ℎ(x)的“Γ区间”，当1<a≤2时，ℎ(x)在[12,a)上的值域为[0,1]，ℎ(x)在[a,2]上的值域为[−log12a,1]，当1≤x1<a时，ℎ(x1)<ℎ(a)=−log12a，所以∃x1∈[1,a)，ℎ(x1)∉[−log12a,1]，即存在x1∈A，对任意x2∈A使得f(x1)≠f(x2)，所以A=[12,a)不为函数ℎ(x)的“Γ区间”，所以a的最大值是1.小提示：方法点睛：双变量存在与恒成立问题：若∀x 1∈D 1,∀x 2∈D 2， f (x 1)>g (x 2)成立，则 f (x )min >g (x )max ；若∃x 1∈D 1,∃x 2∈D 2， f (x 1)>g (x 2)成立，则 f (x )max >g (x )min ；若∃x 1∈D 1,∀x 2∈D 2， f (x 1)>g (x 2)成立，则 f (x )max >g (x )max ；若∀x 1∈D 1,∃x 2∈D 2， f (x 1)>g (x 2)成立，则 f (x )miax >g (x )min ；若∀x 1∈D 1,∃x 2∈D 2， f (x 1)=g (x 2)成立，则 f (x )的值域是g (x )的子集；17、（1）计算：(279)12+(lg5)0+(2764)−13； （2）设4a =5b =100，求2(1a +2b )的值．答案：（1）4；（2）2．分析：（1）根据指数的运算性质直接计算即可；（2）通过换底公式可得1a=1log 4100=log 1004，1b =1log 5100=log 1005，进而可得解. （1）原式=(259)12+(lg5)0+[(34)3]−13=53+1+43=4． （2）∵4a =100， ∴a =log 4100．同理可得，b =log 5100，则1a =1log4100=log 1004，1b =1log 5100=log 1005， ∴1a +2b=log 1004+2log 1005=log 100(4×52)=log 100100=1． ∴2(1a +2b )=2．18、已知函数f (x )=log 12x +12x −172．(1)用单调性的定义证明：f (x )在定义域上是减函数；(2)证明：f (x )有零点；(3)设f (x )的零点在区间(1n+1,1n )内，求正整数n ．答案：(1)证明见解析(2)证明见解析(3)10分析：（1）设0<x 1<x 2，则结合对数的运算法则可证得f (x 1)−f (x 2)=(log 12x 1−log 12x 2)+(12x 1−12x 2)>0，则f (x 1)>f (x 2)，由此可得证.（2）结合函数的解析式有f (1)=−8<0，f (116)=72>0，且f (x )在区间(116 ， 1)上连续不断，由零点存在定理可得证.（3）结合函数的解析式可得f (110)f (111)<0，由此可得答案.（1）因为f (x )的定义域为(0,+∞)，设x 1，x 2是(0,+∞)内的任意两个不相等的实数，且x 1<x 2，则f (x 1)−f (x 2)=(log 12x 1−log 12x 2)+(12x 1−12x 2)， 因为x 2−x 1>0，x 1x 2>0，所以log 12x 1−log 12x 2>0，12x 1−12x 2=x 2−x 12x 1x 2>0，所以f (x 1)>f (x 2)，故f (x )在定义域(0,+∞)上是减函数．（2）因为f (1)=0+12−172=−8<0，f (116)=4+8−172=72>0， 所以f (1)⋅f (116)<0，所以f (x )有零点．（3）f (111)=log 12111+112−172=log 211−3>log 28−3=0，f (110)=log 12110+5−172=log 210−72=log 25−52=log 2√25−log 2√32<0，所以f (110)f (111)<0，又f (x )在(0,+∞)上为减函数，所以f (x )的零点在区间(111,110)内，故n ＝10． 19、某校手工爱好者社团出售自制的工艺品，每件的售价在20元到40元之间时，其销售量y （件）与售价x （元/件）之间满足一次函数关系，部分对应数据如下表所示．(1)求此一次函数的解析式；(2)若每件工艺品的成本是20元，在不考虑其他因素的情况下，每件工艺品的售价是多少时，利润最大？最大利润是多少？答案：(1)y =−20x +840(20⩽x ⩽40)(2)每件工艺品的售价为31元时，利润最大，最大利润为2420元分析：（1）设y =ax +b ，任取两级数据代入求得参数值得解析式；（2）由（1）中关系式得出利润与x 的关系，由二次函数的性质得最大值．（1）设y =ax +b ，不妨选择两组数据(20,440)，(22,400)代入，可得{440=20a +b,400=22a +b,解得{a =−20,b =840, ∴一次函数的解析式为y =−20x +840(20⩽x ⩽40)．（2）设利润为S 元，由题意可得S =(−20x +840)(x −20)=−20x 2+1240x −16800=−20(x −31)2+2420，∴当x =31时，S max =2420，∴每件工艺品的售价为31元时，利润最大，最大利润为2420元．。

高中数学第四章指数函数与对数函数知识点梳理单选题1、已知函数f(x)={2,x>mx2+4x+2,x≤m，若方程f(x)−x=0恰有三个根，那么实数m的取值范围是（）A．[−1,2)B．[−1,2]C．[2,+∞)D．(−∞,−1]答案：A分析：由题意得，函数y=f(x)与函数y=x有三个不同的交点，结合图象可得出结果.解：由题意可得，直线y=x与函数f(x)=2(x>m)至多有一个交点，而直线y=x与函数f(x)=x2+4x+2(x≤m)至多两个交点，函数y=f(x)与函数y=x有三个不同的交点，则只需要满足直线y=x与函数f(x)=2(x>m)有一个交点直线y=x与函数f(x)=x2+4x+2(x≤m)有两个交点即可，如图所示，y=x与函数f(x)=x2+4x+2的图象交点为A(−2,−2)，B(−1,−1)，故有m≥−1.而当m≥2时，直线y=x和射线y=2(x>m)无交点，故实数m的取值范围是[−1,2).故选：A.2、已知函数f(x)=9+x2x，g(x)=log2x+a，若存在x1∈[3,4]，对任意x2∈[4,8]，使得f(x1)≥g(x2)，则实数a的取值范围是（）A．(−∞,134]B．(134,+∞)C．(0,134)D．（1，4）答案：A分析：将问题化为在对应定义域内f(x 1)max ≥g(x 2)max ，结合对勾函数和对数函数性质求它们的最值，即可求参数范围.由题意知：f(x)在[3,4]上的最大值大于或等于g(x)在[4,8]上的最大值即可．当x ∈[3,4]时，f (x )=9x +x ，由对勾函数的性质得：f(x)在[3,4]上单调递增，故f (x )max =f (4)=94+4=254．当x ∈[4,8]时，g (x )=log 2x +a 单调递增，则g (x )max =g (8)=log 28+a =3+a ，所以254≥3+a ，可得a ≤134．故选：A3、已知f (x )是定义在R 上的奇函数，当x ≥0时，f(x)=log 2(x +2)+t ，f (−6)=（ ）A ．−2B ．2C ．−4D ．4答案：A分析：因f (x )是定义在R 上的奇函数，所以f (0)=0，从而可求t ，再由奇函数的定义即可求出f (−6)的值. 解：∵f (x )是定义在R 上的奇函数，又当x ≥0时，f(x)=log 2(x +2)+t ，∴f (0)=log 2(0+2)+t =0，∴t =−1，∴当x ≥0时，f(x)=log 2(x +2)−1，∴f (−6)=−f (6)=−[log 2(6+2)−1]=−(log 223−1)=−2，故选：A.4、关于函数f (x )={2x −a,0≤x <2b −x,x ≥2，其中a,b ∈R ，给出下列四个结论： 甲：6是该函数的零点； 乙：4是该函数的零点；丙：该函数的零点之积为0； 丁：方程f (x )=52有两个不等的实根 若上述四个结论中有且只有一个结论错误，则该错误的结论是（ ）A ．甲B ．乙C ．丙D ．丁答案：B分析：由已知函数的单调性判断甲乙中有一个结论错误，假设甲正确，结合丙正确求得a,b 的值，得到函数解析式，再说明丁正确，则答案可求.当x ∈[0,2)时，f (x )=2x −a 为增函数，当x ∈[2,+∞)，f (x )=b −x 为减函数，故6和4只有一个是函数的零点，即甲乙中有一个结论错误，一个结论正确，故丙丁均正确.由两零点之积为0，则必有一个零点为0，则f (0)=20−a =0⇒a =1，①若甲正确，则f (6)=0，即b −6=0，则b =6，可得f (x )={2x −1,0≤x <26−x,x ≥2， 由f (x )=52可得：{0≤x <22x −1=52或{x ≥26−x =52， 解得：x =log 272或x =72，方程f (x )=52有两个不等的实根， 故丁正确，故甲正确，乙错误.②若乙正确，则f (4)=0，即b −4=0，则b =4，可得f (x )={2x −1,0≤x <24−x,x ≥2， 由f (x )=52可得：{0≤x <22x −1=52或{x ≥24−x =52， 解得：x =log 272，方程f (x )=52只有一个实根，故丁错误，不满足题意.故甲正确，乙错误.故选：B.5、已知函数f(x)={log 12x,x >0,a ⋅(13)x ,x ≤0,若关于x 的方程f[f(x)]=0有且只有一个实数根，则实数a 的取值范围是（ ）A ．(−∞,0)∪(0,1)B ．(−∞,0)∪(1,+∞)C ．(−∞,0)D ．(0,1)∪(1,+∞)答案：B分析：利用换元法设t =f (x )，则等价为f (t )=0有且只有一个实数根，分a <0,a =0,a >0 三种情况进行讨论，结合函数的图象，求出a 的取值范围.令f(x)=t ，则方程f[f(x)]=0等价于f(t)=0，当a =0时，此时当x ≤0时，f (x )=a ⋅(13)x =0，此时函数有无数个零点，不符合题意； 当a ≠0，则f(x)=a ⋅(13)x≠0，所以由f(t)=log 12t =0，得t =1，则关于x 的方程f[f(x)]=0有且只有一个实数根等价于关于x 的方程f(x)=1有且只有一个实数根，作出f(x)的图象如图：当a <0时，由图象可知直线y =1与y =f(x)的图象只有一个交点，恒满足条件；当a >0时，要使直线y =1与y =f(x)的图象只有一个交点，则只需要当x ≤0时，直线y =1与f(x)=a ⋅(13)x的图象没有交点，因为x ≤0 时，f (x )=a ⋅(13)x ∈[a,+∞)，此时f (x ) 最小值为a ，所以a >1，综上所述，实数a 的取值范围是(−∞,0)∪(1,+∞)，故选：B.6、已知函数f(x)=11+2x ，则对任意实数x ，有（ ）A ．f(−x)+f(x)=0B ．f(−x)−f(x)=0C ．f(−x)+f(x)=1D ．f(−x)−f(x)=13答案：C分析：直接代入计算，注意通分不要计算错误．f(−x)+f(x)=11+2−x +11+2x=2x1+2x+11+2x=1，故A错误，C正确；f(−x)−f(x)=11+2−x −11+2x=2x1+2x−11+2x=2x−12x+1=1−22x+1，不是常数，故BD错误；故选：C．7、若函数f(x)=x3+x2−2x−2的一个正零点附近的函数值用二分法计算，其参考数据如下：．1.5答案：B分析：根据二分法求零点的步骤以及精确度可求得结果.解：因为f(1)<0,f(1.5)>0，所以f(1)f(1.5)<0，所以函数在(1,1.5)内有零点，因为1.5−1=0.5>0.1，所以不满足精确度0.1；因为f(1.25)<0，所以f(1.25)f(1.5)<0，所以函数在(1.25,1.5)内有零点，因为1.5−1.25=0.25>0.1，所以不满足精确度0.1；因为f(1.375)<0，所以f(1.375)f(1.5)<0，所以函数在(1.375,1.5)内有零点，因为1.5−1.375=0.125> 0.1，所以不满足精确度0.1；因为f(1.4375)>0，所以f(1.4375)f(1.375)<0，所以函数在(1.375,1.4375)内有零点，因为1.4375−1.375=0.0625<0.1，所以满足精确度0.1；所以方程x3+x2−2x−2=0的一个近似根（精确度0.05）是区间(1.375,1.4375)内的任意一个值（包括端点值），根据四个选项可知选B .故选：B8、若√4a2−4a+1=√(1−2a)33，则实数a的取值范围是（）A．[12,+∞)B．(−∞,12]C．[−12,12]D．R答案：B分析：根据根式与指数幂的运算性质，化简得到√(2a−1)2=√(1−2a)33，即可求解.根据根式和指数幂的运算性质，因为√4a 2−4a +1=√(1−2a)33，可化为√4a 2−4a +1=√(1−2a)33，即√(2a −1)2=√(1−2a)33，可得|2a −1|=1−2a ，所以1−2a ≥0，即a ≤12．故选：B.多选题9、已知a ，b 均为正实数，若log a b +log b a =52，a b =b a ，则a b =（ ）A ．12B ．√22C ．√2D ．2答案：AD分析：令t =log a b ，代入可求出t ，可得a 与b 的关系式，再代入a b =b a 即可求出a ，b 的值.令t =log a b ，则t +1t =52，所以2t 2−5t +2=0，即(2t −1)(t −2)=0，解得t =12或t =2，即log a b =12或log a b =2，所以a =b 2或a 2=b ，因为a b =b a ，代入得2b =a =b 2或b =2a =a 2，所以a =4，b =2或a =2，b =4，所以a b =2或a b =12.故选：AD.小提示：本题主要考查了对数的运算及性质，属于中档题.10、已知函数y =f (x )的图象在区间上是一条连续不断的曲线，则下列结论正确的是（）A ．若f (0)⋅f (1)<0，则y =f (x )在(0,1)内至少有一个零点B ．若f (0)⋅f (1)>0，则y =f (x )在(0,1)内没有零点C ．若y =f (x )在(0,1)内没有零点，则必有f (0)⋅f (1)≥0D ．若y =f (x )在(0,1)内有唯一零点，f (0)⋅f (1)<0，则f (x )在(0,1)上是单调函数答案：AC分析：根据零点存在定理逐一判断即可． []0,1因为f(x)在[0，1]上连续，A．f(0)⋅f（1）<0，由零点存在定理可知，y=f(x)在(0,1)内至少有一个零点，故正确；B．当f(x)=x2−x+14时，满足f(0)⋅f（1）>0，但在(0,1)内有一个零点12，故错误；C．y=f(x)在(0,1)内没有零点，则必有f(0)⋅f（1）⩾0等价于f(0)⋅f（1）<0，则y=f(x)在(0,1)内有零点，由零点存在定理可知此命题是真命题，故正确；D．y=f(x)在(0,1)内有唯一零点，f(0)⋅f（1）<0，但f(x)在(0,1)上不一定是单调函数，比如f(x)=14−(x−14)2，故错误．故选：AC．11、某池塘中野生水葫芦的面积与时间的函数关系的图象，如图所示．假设其关系为指数函数，并给出下列说法，其中正确的说法有（）A．野生水葫芦的每月增长率为1B．野生水葫芦从4m2蔓延到12m2只需1．5个月C．设野生水葫芦蔓延到10m2，20m2，30m2所需的时间分别为t1，t2，t3，则有t1+t3<2t2D．野生水葫芦在第1个月到第3个月之间蔓延的平均速度等于在第2个月到第4个月之间蔓延的平均速度答案：AC分析：根据指数函数的图象过点(4,16)，求得函数的解析式，结合指数函数的解析式，逐项判定，即可求解. 设指数函数的解析式为f(x)=a t(a>0,a≠1)，由函数的图象可知图象过点(4,16)，代入可得16=a 4，解得a =2，即f (x )=2t ，则f(n)−f(n−1)f(n−1)=2n −2n−12n−1=1，所以野生水葫芦的每月增长率为1，所以A 正确；由当t =2时，y =4，又由y =12时，可得2t =12，解得t =log 212≠3.5，所以B 不正确；令y =10，可得2t 1=10，解得t 1=log 210，同理可得t 2=log 220,t 3=log 230，则t 1+t 3=log 210+log 230=log 2300，2t 2=2log 220=log 2400，所以t 1+t 3<2t 2，所以C 正确；由平均变化率的定义，可得1月到3月的平均变化率为8−23−1=3， 2月到4月的平均变化率为16−44−2=6，所以D 不正确. 故选：AC.12、已知正数x ，y ，z 满足3x ＝4y ＝6z ，则下列说法中正确的是（ ）A ．1x ＋12y ＝1zB ．3x ＞4y ＞6zC ．x ＋y ＞(32＋√2)z D ．xy ＞2z 2 答案：ACD分析：设3x =4y =6z =t >1，则x =log 3t ，y =log 4t ，z =log 6t ，分别代入选项中，根据对数运算法则化解，判断是否正确即可.设3x =4y =6z =t >1，则x =log 3t ，y =log 4t ，z =log 6t ，则1x +12y =log t 3+12log t 4=log t 6=1z ，故A 正确； 由3x =log 313t ，4y =log 414t ，6z =log 616t ， 又313>414>616，t >1，则3x <4y <6z ，故B 错误；x +y z =log 3t +log 4t log 6t=log 36+log 46=log 32+log 33+log 42+log 43 =log 32+1+12log 23+12=32+log 32+12log 23>32+√2，因此x +y >(32+√2)z ，故C 正确；xy z2=log3t⋅log4tlog6t⋅log6t=log36⋅log46=(log32+log33)⋅(log42+log43)=12(log32+1)⋅(log23+1)=12(2+log32+log23)>2，因此xy>2z2，故D正确；故选：ACD13、已知函数f(x)=x−1，g(x)=2x ．记max{a,b}={a,a≥bb,a<b，则下列关于函数F(x)=max{f(x),g(x)}(x≠0)的说法正确的是（）A．当x∈(0,2)时，F(x)=2xB．函数F(x)的最小值为−2C．函数F(x)在(−1,0)上单调递减D．若关于x的方程F(x)=m恰有两个不相等的实数根，则−2<m<−1或m>1答案：ABD分析：得到函数F(x)={x−1,−1≤x<0或x≥22x,x<−1或0<x<2，作出其图象逐项判断.由题意得：F(x)={x−1,−1≤x<0或x≥22x,x<−1或0<x<2，其图象如图所示：由图象知：当x∈(0,2)时，F(x)=2x，故A正确；函数F(x)的最小值为−2，故正确；函数F(x)在(−1,0)上单调递增，故错误；方程F(x)=m恰有两个不相等的实数根，则−2<m<−1或m>1，故正确；故选：ABD填空题14、若定义域为I=(0,m]的函数f(x)=e x满足：对任意能构成三角形三边长的实数a,b,c∈I，均有f(a)，f(b)，f(c)也能构成三角形三边长，则m的最大值为______．（e≈2.718281828是自然对数的底）答案：ln4##2ln2分析：不妨设三边的大小关系为：0<a≤b≤c，利用函数的单调性，得出f(a)，f(b)，f(c)的大小关系，作为三角形三边则有任意两边之和大于第三边，再利用基本不等式求出边的范围得出m的最大值即可.f(x)=e x在I=(0,m]上严格增，所以f(x)∈(1,e m]，不妨设0<a≤b≤c，因为对任意能构成三角形三边长的实数a,b,c∈I，均有f(a)，f(b)，f(c)也能构成三角形三边长，所以e a+e b>e c,a+b>c，因为e a+e b≥2√e a e b=2√e a+b>e c，所以4e a+b>e2c，因为对任意a,b,c∈I都成立，所以4e c≥e2c，所以e c≤4，所以c≤ln4，所以m≤ln4，所以m的最大值为ln4．所以答案是：ln4.15、设实数x满足log x4−log2x=1，则x=________．答案：14或2分析：结合对数的换底公式整理得(log2x)2+log2x−2=0，求出log2x，结合对数和指数式的互化即可求出x.由于log x4=2log x2=2log2x ，所以原式转化为2log2x−log2x=1，即(log2x)2+log2x−2=0，解得log2x=−2或log2x=1，所以x=14或x=2．故答案为: 14或2.16、已知函数f(x)={e x−1,x≥0，ax2+x+a,x<0恰有2个零点，则a=__________．答案：12##0.5分析：先求得f(x)在[0，+∞)上恰有1个零点，则方程ax2+x+a=0有1个负根，a=0时不成立，a≠0时，由一元二次方程的性质分Δ=0和Δ>0讨论求解即可.当x≥0时，令f(x)=e x−1=0，解得x=0，故f(x)在[0，+∞)上恰有1个零点，即方程ax2+x+a=0有1个负根.当a=0时，解得x=0，显然不满足题意；当a≠0时，因为方程ax2+x+a=0有1个负根，所以Δ=1−4a2≥0.当Δ=1−4a2=0，即a=±12时，其中当a=12时，12x2+x+12=0，解得x=−1，符合题意；当a=−12时，−12x2+x−12=0，解得x=1，不符合题意；当Δ=1−4a2>0时，设方程ax2+x+a=0有2个根x1，x2，因为x1x2=1>0，所以x1，x2同号，即方程ax2+x+a=0有2个负根或2个正根，不符合题意．综上，a=12．所以答案是：0.5.解答题17、已知函数f(x)=a⋅2x−21−x是定义在R上的奇函数.(1)求实数a的值；(2)求不等式f(f(x)−2)>3的解集；(3)若关于x的不等式f(x)>k2x−1+2恒成立，求实数k的取值范围.答案：(1)a=2(2)(1,+∞)(3)(−∞,−54)分析：（1）根据奇函数满足f(−x)+f(x)=0，即可求解；（2）根据f(x)的单调性，即可根据函数值的大小确定自变量的大小，即可转化求解，（3）将恒成立问题转化为最值问题，即可利用二次函数的性质求最值进行求解.（1）因为f(x)=a ⋅2x −21−x 是定义在R 上的奇函数，所以f(−x)+f(x)=0，即a ⋅2−x −21+x +a ⋅2x −21−x =0，即(a −2)(2x +12x )=0，因为2x +12x >0，所以a −2=0，所以a =2（经检验，a =2符合题意） （2）由（1）得f(x)=21+x −21−x ，因为y =21+x 与y =−21−x 在R 上均为增函数，所以f(x)=21+x −21−x 在R 上为增函数， 又f(1)=3，所以f(f(x)−2)>f(1)，所以f(x)−2>1，即f(x)>3=f(1)，所以x >1，所以不等式f[f(x)−2]>3的解集是(1,+∞).（3）因为关于x 的不等式f(x)>k2x−1+2恒成立，即21+x −21−x >k 2x−1+2恒成立，所以k <22x −2x −1恒成立，所以k <(22x −2x −1)min ，因为22x −2x −1=(2x −12)2−54， 所以当2x =12，即x =−1时，22x −2x −1取得最小值−54. 所以k <−54，即实数k 的取值范围是(−∞,−54) 18、已知函数f(x)=log ax ，g(x)=log a (2x +m −2)，其中x ∈[1,3]，a >0且a ≠1，m ∈R .（1）若m =6且函数F (x)=f(x)+g(x)的最大值为2，求实数a 的值.（2）当a >1时，不等式f(x)<2g(x)在x ∈[1,3]时有解，求实数m 的取值范围. 答案：（1）a =√30；（2）m >0.分析：（1）由题设可得F (x )=log a [x (2x +4)]，讨论a >1、0<a <1，结合已知最大值求参数a ，注意判断a 值是否符合题设.（2）由对数函数的性质可得m >0，再由对数函数的单调性可得m >−2x +√x +2，利用二次函数的性质求不等式右边的最小值，即可得m 的取值范围.（1）m=6，g(x)=log a(2x+4)，则F(x)=f(x)+g(x)=log a[x(2x+4)]，x∈[1,3]. 当a>1时，[F(x)]max=F(3)=log a30=2，所以a=√30；当0<a<1时，[F(x)]max=F(1)=log a6=2，所以a=√6，不合题意.综上，a=√30.（2）要使g(x)在[1,3]上有意义，则2+m−2>0，解得m>0.由f(x)<2g(x)，即log a x<log a(2x+m−2)2，又a>1，∴x<(2x+m−2)2，即√x<2x+m−2，得m>−2x+√x+2.令t=√x，t∈[1,√3]，记ℎ(t)=−2t2+t+2，对称轴t=1，4∴[ℎ(t)]min=ℎ(√3)=√3−4，故m>√3−4.综上，m>0.。

指数函数与对数函数真题归类精讲
张爱军
【期刊名称】《中学生数理化（高一版）》
【年(卷),期】2007(000)011
【摘要】@@ 指数函数和对数函数是高中数学的基础知识,也是高考简单题中的常见知识点.同学们在高一学习时就应了解高考命题的方向,下面结合最近两年高考试题,分析一下指数函数与对数函数的考点.
【总页数】3页(P28-30)
【作者】张爱军
【作者单位】无
【正文语种】中文
【中图分类】O1
【相关文献】
1.指数函数、对数函数应用归类例析 [J], 王广燕
2.“指数函数、对数函数、幂函数”自测题B卷 [J], 蔡亚飞
3.“行政职业能力倾向测验”历年真题精讲 [J], 任士
4.2005年国家司法考试部分真题精讲 [J], 佚名
5.“指数函数、对数函数、幂函数”，自测题A卷 [J],
因版权原因，仅展示原文概要，查看原文内容请购买。

指数函数和对数函数复习(有详细知识点和习题详解)一、指数的性质一）整数指数幂整数指数幂的概念是指：a的n次方等于a乘以a的n-1次方，其中a不等于0，n为正整数。

另外，a的-n次方等于1除以a的n次方，其中a不等于0，n为正整数。

整数指数幂的运算性质包括：（1）a的m次方乘以a的n次方等于a的m+n次方；（2）a的n次方的m次方等于a的mn次方；（3）a乘以b的n次方等于a的n次方乘以b的n次方。

其中，a除以a的n次方等于a的n-1次方，a的m-n次方等于a的m除以a的n次方，an次方根的概念是指，如果一个数的n次方等于a，那么这个数叫做a的n次方根，记作x=√a。

例如，27的3次方根等于3，-27的3次方根等于-3，32的5次方根等于2，-32的5次方根等于-2.a的n次方根的性质包括：如果n是奇数，则a的n次方根等于a；如果n是偶数且a大于等于0，则a的正的n次方根等于a，a的负的n次方根等于负的a；如果n是偶数且a小于0，则a的n次方根没有意义，即负数没有偶次方根。

二）例题分析例1：求下列各式的值：（1）3的-8次方；（2）（-10）的2次方；（3）4的（3-π）次方；（4）（a-b）的2次方，其中a大于b。

例2：已知a小于b且n大于1，n为正整数，化简n[（a-b)/(a+b)]。

例3：计算：7+40+7-40.例4：求值：（59/24）+（59-45）/24 + 25×（5-2）/24.解：略。

二）分数指数幂1.分数指数幂当根式的被开方数能被根指数整除时，根式可以写成分数指数幂的形式，例如：$5\sqrt[10]{a^5}=a^{\frac{1}{2}}$，$3\sqrt[12]{a^3}=a^{\frac{1}{4}}$。

当根式的被开方数不能被根指数整除时，根式也可以写成分数指数幂的形式，例如：$\sqrt[4]{a^5}=a^{\frac{5}{4}}$。

规定：1）正数的正分数指数幂的意义是$a^{\frac{p}{q}}=\sqrt[q]{a^p}$。

(名师选题)人教高中数学第四章指数函数与对数函数题型总结及解题方法单选题1、已知a =log 20.6,b =log 20.8,c =log 21.2，则（ ） A ．c >b >a B ．c >a >b C ．b >c >a D ．a >b >c 答案：A分析：由对数函数得单调性即可得出结果. ∵y =log 2x 在定义域上单调递增，∴log 20.6<log 20.8<log 21.2，即c >b >a . 故选：A.2、已知55<84，134<85．设a =log 53，b =log 85，c =log 138，则（ ） A ．a <b <c B ．b <a <c C ．b <c <a D ．c <a <b 答案：A分析：由题意可得a 、b 、c ∈(0,1)，利用作商法以及基本不等式可得出a 、b 的大小关系，由b =log 85，得8b =5，结合55<84可得出b <45，由c =log 138，得13c =8，结合134<85，可得出c >45，综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、c ∈(0,1)，a b =log 53log 85=lg3lg5⋅lg8lg5<1(lg5)2⋅(lg3+lg82)2=(lg3+lg82lg5)2=(lg24lg25)2<1，∴a <b ；由b =log 85，得8b =5，由55<84，得85b <84，∴5b <4，可得b <45； 由c =log 138，得13c =8，由134<85，得134<135c ，∴5c >4，可得c >45. 综上所述，a <b <c . 故选：A.小提示：本题考查对数式的大小比较，涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用，考查推理能力，属于中等题.3、设f (x )是定义域为R 的偶函数，且在(0,+∞)单调递减，则A．f(log31)>f(2−32)>f(2−23)4B．f(log31)>f(2−23)>f(2−32)4C．f(2−32)>f(2−23)>f(log31)4D．f(2−23)>f(2−32)>f(log31)4答案：C解析：由已知函数为偶函数，把f(log31),f(2−32),f(2−23)，转化为同一个单调区间上，再比较大小．4∵f(x)是R的偶函数，∴f(log31)=f(log34)．4∵log34>log33=1,1=20>2−23>2−32,∴log34>2−23>2−32，又f(x)在(0，+∞)单调递减，∴f(log34)<f(2−23)<f(2−32)，∴f(2−32)>f(2−23)>f(log31)，故选C．4小提示：本题主要考查函数的奇偶性、单调性，解题关键在于利用中间量大小比较同一区间的取值．4、如图所示，函数y=|2x−2|的图像是（）A．B．C．D．答案：B分析：将原函数变形为分段函数，根据x=1及x≠1时的函数值即可得解.∵y =|2x−2|={2x −2,x ≥12−2x ,x <1，∴x =1时，y =0,x ≠1时，y >0. 故选：B.5、函数①y =a x ；②y =b x ；③y =c x ；④y =d x 的图象如图所示，a ，b ，c ，d 分别是下列四个数：54，√3，13，12中的一个，则a ，b ，c ，d 的值分别是（ ）A ．54，√3，13，12B ．√3，54，13，12C ．12，13，√3，54，D ．13，12，54，√3， 答案：C分析：根据指数函数的性质，结合函数图象判断底数的大小关系.由题图，直线x =1与函数图象的交点的纵坐标从上到下依次为c ，d ，a ，b ，而√3>54>12>13.故选：C ．6、设alog 34=2，则4−a =（ ） A ．116B ．19C ．18D ．16答案：B分析：根据已知等式，利用指数对数运算性质即可得解 由alog 34=2可得log 34a =2，所以4a =9， 所以有4−a =19，故选：B.小提示：本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目.7、(32)12−100的值为（ ） A ．﹣2B ．2C ．﹣4D ．4 答案：B解析：利用指数幂的运算性质可得计算结果. 解：(32)12−100=3−1=2. 故选：B ．8、若x 1，x 2是二次函数y =x 2−5x +6的两个零点，则1x 1+1x 2的值为（ ）A ．−12B ．−13C ．−16D ．56答案：D分析：解方程可得x 1=2,x 2=3，代入运算即可得解. 由题意，令x 2−5x +6=0，解得x =2或3， 不妨设x 1=2,x 2=3，代入可得1x 1+1x 2=12+13=56.故选：D.9、2021年10月16日，搭载神舟十三号载人飞船的长征二号F 遥十三运载火箭，在酒泉卫星发射中心成功发射升空，载人飞船精准进入预定轨道，顺利将3名宇航员送入太空，发射取得圆满成功．已知在不考虑空气阻力和地球引力的理想状态下，可以用公式v =v 0⋅ln Mm 计算火箭的最大速度v(m/s)，其中v 0(m/s)是喷流相对速度，m(kg)是火箭（除推进剂外）的质量，M(kg)是推进剂与火箭质量的总和，Mm 称为“总质比”．若某型火箭的喷流相对速度为1000m/s ，当总质比为625时，该型火箭的最大速度约为（ ）（附：lge ≈0.434,lg2≈0.301）A ．5790m/sB ．6219m/sC ．6442m/sD ．6689m/s 答案：C分析：根据对数的换底公式运算可得结果.v=v0ln Mm =1000×ln625=1000×4lg5lge=1000×4(1−lg2)lge≈6442m/s.故选：C．10、函数y=|lg(x+1)|的图像是（）A．B．C．D．答案：A分析：由函数y=lgx的图象与x轴的交点是(1,0)结合函数的平移变换得函数y=|lg(x+1)|的图象与x轴的公共点是(0,0)，即可求解.由于函数y=lg(x+1)的图象可由函数y=lgx的图象左移一个单位而得到，函数y=lgx的图象与x轴的交点是(1,0)，故函数y=lg(x+1)的图象与x轴的交点是(0,0)，即函数y=|lg(x+1)|的图象与x轴的公共点是(0,0)，显然四个选项只有A选项满足.故选：A.填空题11、某同学设想用“高个子系数k”来刻画成年男子的高个子的程度，他认为，成年男子身高160cm及其以下不算高个子，其高个子系数k应为0；身高190cm及其以上的是理所当然的高个子，其高个子系数k应为1，请给出一个符合该同学想法､合理的成年男子高个子系数k关于身高x(cm)的函数关系式___________.答案：k={0,0<x≤160, 130(x−160),160<x<190,1,x≥190.，(只要写出的函数满足在区间[160,190]上单调递增，且过点(160,0)和(190,1)即可.答案不唯一)分析：由题意，个数越高，系数k 越大，因此在[160,190]上的函数是增函数即可，初始值(160,0)，(190,1)，设出函数式代入求解．由题意函数k(x)是[160,190]上的增函数，设k(x)=ax +b(a >0)，x ∈[160,190]，由{160a +b =0190a +b =1，解得{a =130b =−163，所以k(x)=130x −163， 所以k ={0,0<x ≤160,130(x −160),160<x <190,1,x ≥190.所以答案是：k ={0,0<x ≤160,130(x −160),160<x <190,1,x ≥190.注：在[160,190]上设其他函数式也可以，只要是增函数，只有两个参数．如y =b −ax (a >0)，y =ax 2+b(a >0)等等．小提示：思路点睛：本题考查函数的应用，解题时注意题目的要求，只要写出的函数满足在区间[160,190]上单调递增，且过点(160,0)和(190,1)即可，因此函数模型可以很多，答案也不唯一． 12、(log 23−log 83)(log 32+log 92)=______．（用数字作答） 答案：1分析：利用对数换底公式及性质计算作答.(log 23−log 83)(log 32+log 92)=(log 23−log 23log 28)(log 32+log 32log 39) =(log 23−13log 23)(log 32+12log 32)=23log 23×32log 32=1.所以答案是：113、已知函数f (x )={e x −1,x ≥0，ax 2+x +a,x <0恰有2个零点，则a =__________．答案：12##0.5分析：先求得f (x )在[0，+∞)上恰有1个零点，则方程ax 2+x +a =0有1个负根，a =0时不成立，a ≠0时，由一元二次方程的性质分Δ=0和Δ>0讨论求解即可.当x≥0时，令f(x)=e x−1=0，解得x=0，故f(x)在[0，+∞)上恰有1个零点，即方程ax2+x+a=0有1个负根.当a=0时，解得x=0，显然不满足题意；当a≠0时，因为方程ax2+x+a=0有1个负根，所以Δ=1−4a2≥0.当Δ=1−4a2=0，即a=±12时，其中当a=12时，12x2+x+12=0，解得x=−1，符合题意；当a=−12时，−12x2+x−12=0，解得x=1，不符合题意；当Δ=1−4a2>0时，设方程ax2+x+a=0有2个根x1，x2，因为x1x2=1>0，所以x1，x2同号，即方程ax2+x+a=0有2个负根或2个正根，不符合题意．综上，a=12．所以答案是：0.5.14、已知函数f(x)=√2x−a的定义域为[2,+∞)，则a=_________．答案：4分析：由已知可得不等式2x−a≥0的解集为[2,+∞)，可知x=2为方程2x−a=0的根，即可求得实数a的值. 由题意可知，不等式2x−a≥0的解集为[2,+∞)，则22−a=0，解得a=4，当a=4时，由2x−4≥0，可得2x≥4=22，解得x≥2，合乎题意.所以答案是：4.15、若alog43=12，则3a+9a=___________；答案：6分析：首先利用换底公式表示a=log32，再代入3a+9a求值.由条件得a=12log34=log32，所以3a+9a=3log32+9log32=3log32+3log34=2+4=6.所以答案是：6解答题16、（1）根据所学知识推导如下的对数运算性质：如果a>0，且a≠1，M>0，那么log a M n=nlog a M(n∈R)；（2）请你运用（1）中的对数运算性质计算lg3lg4(lg8lg9+lg16lg27)的值；（3）因为210=1024∈(103,104)，所以210的位数为4．请判断20222023的位数．（参考数据：lg2022≈3.306，100.038≈1.091）答案：（1）证明见解析；（2）1712；（3）6689．分析：（1）设x=log a M，对数式改写为指数式，等式两边n次方，然后指数式改写为对数式即得；（2）直接利用（1）中性质化简对数后计算即可得；（3）20222023=N，取常用对数，利用（1）求得lgN后可得N的位数．（1）设x=log a M，则M=a x，所以M n=(a x)n=a nx，所以log a M n=log a a nx=nx=nlog a M，得证．（2）lg3lg4(lg8lg9+lg16lg27)=lg3lg22(lg23lg32+lg24lg33)=lg32lg2(3lg22lg3+4lg23lg3)=lg32lg2×17lg26lg3=1712．（3）设20222023=N，则lgN=2023lg2022≈2023×3.306=6688.038，所以N=106688.038=100.038×106688，又1<100.038<10，所以N有6689位数，即20222023的位数为6689．17、首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下进行技术攻关，采取了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本y (元)与月处理量x (吨)之间的函数关系可近似的表示为y=12x2−200x+80000，且处理每吨二氧化碳得到可利用的化工产品价值为100元.(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使单位不亏损？答案：(1)400吨；(2)不获利，需要国家每个月至少补贴40000元才能不亏损.分析：（1）由题设平均每吨二氧化碳的处理成本为yx，应用基本不等式求其最小值，注意等号成立条件. （2）根据获利S=100x−y，结合二次函数的性质判断是否获利，由其值域确定最少的补贴额度.（1）由题意知，平均每吨二氧化碳的处理成本为yx =12x+80000x−200≥2√12x⋅80000x−200=200；当且仅当12x =80000x，即x =400 时等号成立，故该当每月处理量为400吨时，才能使每吨的平均处理成本最低为200元. （2）不获利，设该单位每个月获利为S 元，则S =100x −y =100x −(12x 2−200x +80000)=−12x 2+300x −80000 =−12(x −300)2−35000，因为x ∈[400,600]，则S ∈[−80000,−40000]，故该当单位每月不获利，需要国家每个月至少补贴40000元才能不亏损. 18、已知函数f (x )=12x −1+12．(1)判断f (x )的奇偶性，并加以证明； (2)求函数的值域．答案：(1)f (x )是奇函数；证明见解析 (2)(−∞,−12)∪(12,+∞)分析：（1）首先确定f (x )定义域，根据奇偶性定义可得结论； （2）令t =2x −1，可求得1t 的范围，进而可得f (x )的值域. （1）由2x −1≠0得：x ≠0，∴f (x )定义域为{x |x ≠0}，关于原点对称； ∵f (−x )=12−x −1+12=2x1−2x +12，∴f (−x )+f (x )=12x −1+12+2x1−2x +12=−1+1=0，∴f (x )为奇函数； （2） 令t =2x −1，∵2x −1≠0且2x >0，∴t ∈(−1,0)∪(0,+∞)，∴1t <−1或1t >0， ∴1t +12<−12或1t +12>12，∴f (x )的值域为(−∞,−12)∪(12,+∞).。

关于指数函数与对数函数的问题一、指数函数底数对指数函数的影响：①在同一坐标系内分别作函数的图象，易看出：当 a>l 时，底数越大，函数图象在第一象限越靠近 y 轴；同样地，当 0<a<l 时，底数越小，函数图象在第一象限越靠近 x 轴．②底数对函数值的影响如图．③当 a>0 ，且 a≠l 时，函数与函数y=的图象关于y 轴对称。

利用指数函数的性质比较大小：若底数相同而指数不同，用指数函数的单调性比较：若底数不同而指数相同，用作商法比较；若底数、指数均不同，借助中间量，同时要注意结合图象及特殊值二、对数函数底数对函数值大小的影响：1.在同一坐标系中分别作出函数的图象，如图所示，可以看出：当 a>l 时，底数越大，图象越靠近x 轴，同理，当O<a<l时，底数越小，函数图象越靠近x轴．利用这一规律，我们可以解决真数相同、对数不等时判断底数大小的问题．2.类似地，在同一坐标系中分别作出的图象，如图所示，它们的图象在第一象限的规律是：直线个区域里对数函数的底数都是由右向左逐渐减小，比如x=l把第一象限分成两个区域，分别对应函数每，则必有对数函数的图象与性质：三、对数函数与指数函数的对比：(1) 对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y=x 对称．(2)它们都是单调函数，都不具有奇偶性．当a>l 时，它们是增函数；当O<a<l 时，它们是减函数．(3)指数函数与对数函数的联系与区别：四、关于同底指数函数与对数函数的交点问题一、a 1时方程 a x log a x 的解先求如图 3 所示曲线ya x与ylogax相切时a的值。

设曲线ya x与y log a x 相切于点 M （x, x0），由于曲线y a x在点 M 处的切线斜率为1，a x 0x 0 ,a x0x 0 ,(a x )' |x x0即所以1a x0ln a 1a x 0x 0 , 111则 a ln aln a所以 ln ax 011e,所以 ae e ,此时 x 0 eln a即。