西师版小学所有最全数学知识点及公式

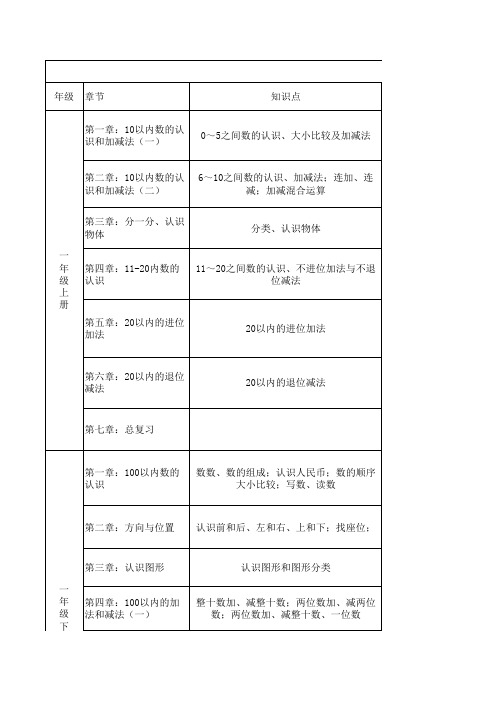
西师版小学数学知识点篇一：西师版小学数学各年级重点西师版小学数学各年级重点一年级（上）1、数的认识及书写（读作、写作）2、 10以内的加减法（连加、连减、加减混合运算、大小于及等于符号的运用）3、 20以内的加减法（连加、连减、加减混合运算、大小于及等于符号的运用）4、认识物体（正方体、长方体、圆柱体、球体；物体的分类）一年级（下）1、100以内数的认识（进位加法、退位减法、连加、连减、加减混合运算、大小于及等于符号的运用）2、人民币的认识与换算3、方向与位置（前、后、上、下、左、右）4、认识图形（圆、三角形、长方形、正方形；图形的拼组）5、认识钟表6、实物分类统计二年级（上）1、乘法口诀表2、角的认识与运用3、测量长度（长度单位的认识与运用，单位间的换算。

1m=10dm=100cm）4、表内除法（除法的意义、平均分、商倍问题）二年级（下）1、万以内数的认识（读作、写作、比较大小）2、认识图形（正方形、长方形、平行四边形、拼组图形）3、三位数的加减法4、长度单位（千米、毫米。

1km=1000m，1cm=10mm）5、有余数的除法（余数必须比除数小）6、时分秒（1时=60分，1分=60s ）7、统计（根据统计回答问题，象形统计）三年级（上）1、二、三位数乘一位数的乘法（口算、估算、笔算、0和任何数相乘都得0，解决问题）2、东南西北的认识（上北下南左西右东，在生活中的运用）3、旋转与平移现象（生活中的旋转与平移）4、周长（周长的意义，正方形、长方形周长的计算。

C正=边长×4，C长=（长+宽）×2。

）5、分数的初步认识6、年月日（大小月、平闰年、24时计时法，时间的计算）三年级（下）1、两位数乘两位数的乘法2、长方形和正方形的面积（S正=边长×边长，S长=长×宽。

单位换算：1m2=100cm2）3、三位数除一位数的除法（口算、估算、笔算）4、统计（简单条形统计）5、小数的初步认识（小数的读写、一位小数的加减法）6、轴对称（生活中的轴对称现象）四年级（上）1、四则混合运算（先括号，再乘除、再加减）2、多位数的认识（多位数的读写，比较大小，近似值）3、多位数的加减法（口算、估算、计算器的运用、加法运算规律。

一.自然数的加减法
1.自然数的加法规则
（1）加法的定义及性质
（2）加法的交换律
（3）加法的结合律
2.自然数的减法规则
（1）减法的定义及性质
（2）有关减法的基本计算方法（3）减法的交换律
二.自然数的乘除法
1.自然数的乘法规则
（1）乘法的定义及性质
（2）乘法的交换律
（3）乘法的结合律
2.自然数的除法规则
（1）除法的定义及性质
（2）有关除法的基本计算方法（3）除法的结合律
三.分数的认识和比较
1.自然数的除法引出分数的概念
2.分数的定义及性质
3.分数的比较
（1）相同分母的比较
（2）相同分子的比较
（3）不同分母的比较
四.分数的加减法
1.分数的加法规则
（1）相同分母的加法
（2）相同分子的加法
（3）不同分母的加法
2.分数的减法规则
（1）相同分母的减法
（2）相同分子的减法
（3）不同分母的减法
五.小数的认识和比较
1.小数的定义及性质
2.小数的大小比较
（1）相同整数部分的比较
（2）整数和小数比较（3）小数之间的比较
六.数的性质和应用
1.奇数和偶数
2.能被2整除的数
3.数的倍数
4.数的约数。

西师版六年级数学知识点总结摘要：一、西师版六年级数学知识点概述二、数的认识与运算1.整数、小数和分数的认识2.数的四则运算规则3.简便运算方法4.乘法结合律与分配律的应用三、几何与测量1.平面图形的性质与分类2.三角形、四边形的面积计算3.圆的相关概念与计算4.测量工具的使用及测量方法四、统计与概率1.数据的收集、整理与分析2.统计图表的绘制与解读3.概率的基本概念与应用五、问题解决与思维训练1.应用题的解题策略2.逻辑思维训练题解析3.数学游戏与趣味数学六、数学素养与价值观1.数学历史的了解2.数学家的故事3.数学在日常生活中的应用4.培养良好的数学学习习惯正文：西师版六年级数学知识点总结一、西师版六年级数学知识点概述六年级数学课程涵盖了数的认识与运算、几何与测量、统计与概率、问题解决与思维训练、数学素养与价值观等多个方面。

学生在学习这些知识点的过程中，不仅能够提高自己的数学素养，还能培养自己的逻辑思维能力和解决问题的能力。

二、数的认识与运算1.整数、小数和分数的认识六年级数学课程中，学生需要对整数、小数和分数有更深入的认识，了解它们之间的关系，掌握它们的基本性质。

2.数的四则运算规则学生需要熟练掌握整数、小数和分数的四则运算规则，并能正确进行计算。

3.简便运算方法学生在掌握四则运算规则的基础上，要学会运用乘法结合律、分配律等简便运算方法，提高运算效率。

4.乘法结合律与分配律的应用学生要学会在实际运算中灵活运用乘法结合律和分配律，简化运算过程。

三、几何与测量1.平面图形的性质与分类学生需要了解平面图形的基本性质，如角、边、面积等，并能对各种平面图形进行分类。

2.三角形、四边形的面积计算学生要学会计算三角形和四边形的面积，并能应用到实际问题中。

3.圆的相关概念与计算学生需要掌握圆的基本概念，如半径、直径、周长等，并能进行相关的计算。

4.测量工具的使用及测量方法学生要学会使用常见的测量工具，如直尺、圆规、量角器等，掌握测量方法，解决实际问题。

西师版小学数学知识点西师版小学数学教材以其科学、系统、全面的特点深受广大学生和教师的喜爱。

本文将介绍一些西师版小学数学教材中的重要知识点，帮助学生更好地掌握数学知识。

一、整数运算整数运算是小学数学的基础，学好整数的运算对学生后续的学习非常重要。

在西师版小学数学教材中，关于整数运算的知识点主要包括四则运算、整数的比较和大小关系等。

学生需要掌握整数的加法、减法、乘法和除法，以及整数之间的比较和大小关系。

二、分数的概念和运算分数是小学数学中的一个难点，但也是非常实用的数学工具。

西师版小学数学教材中对分数的概念和运算进行了详细的介绍。

学生需要理解分数的含义，掌握分数之间的比较、分数的加减乘除等运算法则。

三、面积和周长面积和周长是几何学中的重要概念，也是实际生活中常见的计算问题。

在西师版小学数学教材中，对面积和周长的计算有详细的讲解。

学生需要学会计算矩形、三角形和圆形的面积和周长，掌握相应的计算公式。

四、数据与图表数据和图表的分析能力是数学思维的重要组成部分。

西师版小学数学教材中，涉及数据和图表的内容比较丰富，包括数据的收集和整理、数据的表示和分析等。

学生需要学会提取数据的关键信息，理解图表的含义，并能准确地进行数据分析。

五、空间与几何空间与几何是小学数学的一个重要分支，也是学生感知世界和培养空间想象力的重要手段。

在西师版小学数学教材中，对空间与几何的知识点进行了系统的介绍，包括点、线、面的简单认识、立体图形的认识和分类等。

学生需要学会观察和描述空间中的几何形状，并能进行简单的几何推理。

六、时间和日期时间和日期是孩子们日常生活中需要注意和掌握的内容。

西师版小学数学教材中，设置了一些关于时间和日期的问题。

学生需要学会读表、计算时间间隔，理解常见的日期表达方式等。

总结：通过学习西师版小学数学教材中的重要知识点，学生可以全面而系统地掌握数学的基础知识，为进一步学习打下坚实的基础。

希望同学们能够认真学习，并能灵活运用所学的数学知识解决实际问题。

第一章数和数的运算一、概念和结论〔一〕整数1、整数：自然数和0都是整数。

整数分为正整数、0和负整数。

2、自然数：我们在数物体的时候，用来表示物体个数的0、1、2、3……叫做自然数，一个物体也没有，就用0表示。

0是最小的自然数，自然数包括正整数和0。

3、计数单位：一〔个〕、十、百、千、万、十万、百万、千万、亿……都是计数单位。

每相邻两个计数单位之间的进率都是10。

这样的计数法叫做十进制计数法。

4、数位：计数单位按照一定的顺序排列起来，它们所占的位置叫做数位。

5、数的整除：如果整数a除以整数b(b≠0〕，除得的商是整数而没有余数，我们就说a能被b整除，或者说b能整除a 。

如果数a能被数b〔b≠0〕整除，a就叫做b的倍数，b就叫做a的因数。

倍数和因数是相互依存的。

因为35能被7整除，所以35是7的倍数，7是35的因数。

一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它本身。

例如：10的因数有1、2、5、10，其中最小的因数是1，最大的因数是10。

一个数的倍数的个数是无限的，其中最小的倍数是它本身，没有最大的倍数。

例如：3的倍数有：3、6、9、12……其中最小的倍数是3，没有最大的倍数。

一个数最大的因数和最小的倍数相等，都是它本身。

一个数的所有倍数都是它的所有因数的倍数，一个数的所有因数都是它的所有倍数的因数。

6、能被2、3、5、8、9整除的数的特征：能被2整除的数的特征：个位上是0、2、4、6、8的数，都能被2整除，例如：202、480、304。

能被5整除的数的特征：个位上是0或5的数，都能被5整除，例如：5、30、405。

能被5整除的数的特征：一个数各个数位上的数字之和能被3整除，这个数就能被3整除，例如：204、48.能被9整除的数的特征：一个数各个数位上的数字之和能被9整除，这个数就能被9整除。

例如：234、630.能被4〔或25〕整除的数的特征：一个数的末两位数能被4〔或25〕整除，这个数就能被4〔或25〕整除。

西师版三年级下册数学知识点加数+加数=和一个加数=和-另一个加数被减数-减数=差减数=被减数-差被减数=减数+差因数×因数=积一个因数=积÷另一个因数因数与积的变化规律：一个因数不变，另一个因数扩大到原数的几倍，积就扩大到原数的几倍。

一个因数不变，另一个因数缩小到原数的几倍，积就缩小到原数的几倍。

一个因数扩大几倍，另一个因数缩小几倍，扩大倍数和缩小倍数相同，积就不变。

被除数÷除数=商被除数=商×除数被除数与商的变化规律：除数不变，被除数扩大到原数的几倍，商就扩大到原数的几倍。

除数不变，被除数缩小到原数的几倍，商就缩小到原数的几倍。

被除数不变，除数变大，商就变小。

被除数不变，除数变小，商就变大。

有余数除法：被除数÷除数=商……余数（余数＜除数）被除数=商×除数+余数解决问题常用公式：路程=速度×时间速度=路程÷时间时间=路程÷速度总价=单价×数量单价=总价÷数量数量=总价÷单价工作总量=工作效率×工作时间工作效率=工作总量÷工作时间工作时间=工作总量÷工作效率图形与几何的公式：长方形的周长=（长+宽）×2长+宽=长方形的周长÷2正方形的周长=边长×4边长=正方形的周长÷4长方形的面积=长×宽长=长方形的面积÷宽宽=长方形的面积÷长正方形的面积=边长×边长小数知识点：小数由整数部分和小数部分组成，小数点前面是整数部分，后面是小数部分。

计算一位小数加减法时要注意：笔算一位小数的加减法时，首先要对齐小数点，也就是相同数位对齐，再从十分位算起。

笔算一位小数的加减法和笔算整数加减法相同。

相同数位对齐，从十分位算起；十分位上的数相加满十，向个位进1；十分位上的数不够减，要从个位退1当10再减。

小学数学必备知识点总归纳常用单位换算1、长度单位换算:1千米=1000米1米=10分米1分米=10厘米1米=100厘米 1厘米=10毫米2、面积单位换算:1平方千米=100公顷 1公顷=10000平方米1平方米=100平方分米 1平方分米=100平方厘米1平方厘米=100平方毫米3、体容积单位换算:1立方米=1000立方分米 1立方分米=1000立方厘米 1立方分米=1升 1立方厘米=1毫升 1立方米=1000升4、重量单位换算:1吨=1000千克 1千克=1000克 1千克=1公斤5、人民币单位换算:1元=10角 1角=10分 1元=100分6、时间单位换算:1世纪=100年 1年=12月大月31天有:1\3\5\7\8\10\12月小月30天的有4\6\9\11月平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时 1时=60分 1分=60秒 1时=3600秒常用数量关系等式1、份数:每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、倍数: 1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、路程:速度×时间=路程路程÷速度=时间路程÷时间=速度4、价量: 单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作量: 工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、数据运算: 加数+加数=和和一一个加数=另一个加数被减数一减数=差被减数一差=减数差+减数=被减数因数×因数=积积÷一个因数=另一个因数被除数÷除数=商被除数÷商=除数商×除数=被除数常用图形计算公式1、正方形 C:周长 S:面积 a:边长周长=边长×4 C=4a面积=边长×边长 S=a×a2、正方体 V:体积 a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长 V=a×a×a3、长方形 C:周长 S:面积 a:边长周长=长+宽×2C=2a+b面积=长×宽S=ab4、长方体 V:体积 s:面积 a:长 b:宽 h:高表面积=长×宽+长×高+宽×高×2S =2ab+ah+bh体积=长×宽×高 V=abh5、三角形 s:面积 a:底 h:高面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形 s:面积 a:底 h:高面积=底×高s=ah7、梯形 S:面积 a:上底 b:下底 h:高面积=上底+下底×高÷2s=a+b×h÷28、圆形 S:面积 C:周长 n d=直径 r=半径周长=直径×n=2×n×半径C=nd=2nr面积=半径×半径×n9、圆柱体 v:体积 h:高 s:底面积 r:底面半径 c：底面周长侧面积=底面周长×高=ch2nr或nd表面积=侧面积+底面积×2体积=底面积×高体积=侧面积÷2×半径10、圆锥体 v:体积 h:高 s:底面积 r:底面半径体积=底面积×高÷3奥数常用公式1、平均数总数÷总份数=平均数2、和差问题: 和+差÷2=大数和一差÷2=小数3、和倍问题: 和÷倍数-1=小数小数×倍数=大数或者和一小数=大数4、差倍问题: 差÷倍数-1=小数小数×倍数=大数或小数+差=大数5、相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间6、迫及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间7、流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度8、浓度问题溶质的重量十溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量9、利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=售出价÷成本一1×100%涨跌金额=本金×涨跌百分比利息=本金×利率×时间税后利息=本金×利率×时间×1-20%10、盈亏问题盈+亏÷两次分配量之差=参加分配的份数大盈一小盈÷两次分配量之差=参加分配的份数大亏-小亏÷两次分配量之差=参加分配的份数应特别注意奥数中的植树问题1、非封闭线路上的植树问题,主要可分为以下三种情形：1如果在非封闭线路的两端都要植树,那么：全长=株距×株数-1株距=全长÷株数-12如果在非封闭线路的一端要植树,另一端不要植树,那么：株数=段数=全长÷株距全长=株距×株数株距=全长÷株数3如果在非封闭线路的两端都不要植树,那么：株数=段数-1=全长÷株距-1全长=株距×株数+1株距=全长÷株数+12、封闭线路上的植树问题株数=段数=全长÷株距全长=株距×株数株距=全长÷株数奥数中的常用数据及规律1、圆周率常取数据3.14×1=3.14 3.14×2=6.28 3.14×3=9.42 3.14×4=12.563.14×5=15.7 3.14×6=18.843.14×7=21.983.14×8=25.123.14×9=28.262、常用特殊数的乘积25×3=7525×4=10025×8=200125×3=375125×4=500125×8=1000625×16=1000037×3=1114、常用分数与小数的互化1/2=0.5 1/4=0.25 3/4=0.75 1/5=0.2 2/5=0.43/5=0.6 4/5=0.8 1/8=0.125 3/8=0.3755/8=0.6257/8=0.875 1/20=0.05 3/20=0.15 7/20=0.359/20=0.45 11/20=0.55 1/25=0.04 2/25=0.083/25=0.12 4/25=0.16 6/25=0.245、常用立方数13 =1 23= 8 33= 27 43=64 53=12563=216 73=343 83=512 93= 729小学数学应掌握的基本概念、数理规律及应用第一章数和数的运算一、概念一整数1、整数的意义:自然数和0都是整数2、自然数:我们在数物体的时候,用来表示物体个数的1,2,3,4……叫做自然数.一个物体也没有,用0表示.0也是自然数.3、计数单位: 一个、十、百、千、万、十万、百万、千万、亿……都是计数单位.每相邻两个计数单位之间的进率都是10.这样的计数法叫做十进制计数法.4、数位:计数单位接照一定的顺序排列起来,它们所占的位置叫做数位.5、数的整除:整数a除以整数bb≠0,除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a如果数a能被数bb≠0整除,a就叫做b的倍数,b就叫做a的约数或a的因数.倍数和约数是相互依存的.因为35能被7整除,所以35是7的倍数,7是35的约数.一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身.例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10.一个数的倍数的个数是无限的,其中最小的倍数是它本身.3的倍数有:3、6、9、12……其中最小的倍数是3,没有最大的倍数.个位上是0、2、4、6、8的数,都能被2整除,例如：202、480、304,都能被2整除.个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除.一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除.一个数各位数上的和能被9整除,这个数就能被9整除.能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除.一个数的末两位数能被4或25整除,这个数就能被4或25整除.例如:16、404、1256都能被4整除,50、325、500、1675都能被25整除.一个数的末三位数能被8或125整除,这个数就能被8或125整除.例如:1168、4600、5000、12344都能被8整除,1125、13375、5000都能被125整除.能被2整除的数叫做偶数.不能被2整除的数叫做奇数.0也是偶数.自然数按能否被2整除的特征可分为奇数和偶数.一个数,如果只有1和它本身两个因约数,这样的数叫做质数或素数,100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97.一个数,如果除了1和它本身还有别的因约数,这样的数叫做合数,例如：4、6、8、9、12都是合数.1不是质数也不是合数,自然数除了1外,不是质数就是合数.如果把自然数按其因约数的个数的不同分类,可分为质数、合数和1.每个合数都可以写成几个质数相乘的形式.其中每个质数都是这个合数的因数,叫做这个合数的质因数,例如15=3×5,3和5叫做15的质因数把一个合数用质因数相乘的形式表示出来,叫做分解质因数.例如把28分解质因数几个数公有的约数,叫做这几个数的公约数.其中最大的一个,叫做这几个数的最大公约数,例如12的约数有1、2、3、4、6、12;18的约数有1、2、3、6、9、18.其中,1、2、3、6是12和18的公约数,6是它们的最大公约数.公约数只有1的两个数,叫做互质数,成互质关系的两个数,有下列几种情况：1和任何自然数互质.相邻的两个自然数互质.两个不同的质数互质.当合数不是质数的倍数时,这个合数和这个质数互质.两个合数的公约数只有1时,这两个合数互质,如果几个数中任意两个都互质,就说这几个数两两互质.如果较小数是较大数的约数,那么较小数就是这两个数的最大公约数.如果两个数是互质数,它们的最大公约数就是1.几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,如2的倍数有2、4、6、8、10、12、14、16、18…….3的倍数有3、6、9、12、15、18……其中6、12、18……是2、3的公倍数,6是它们的最小公倍数.如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数.如果两个数是互质数,那么这两个数的积就是它们的最小公倍数.几个数的公约数的个数是有限的,而几个数的公倍数的个数是无限的.二小数1、小数的意义：把整数1平均分成10份、100份、1000份……得到的十分之几、百分之几、千分之几……可以用小数表示.一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几…….一个小数由整数部分、小数部分和小数点部分组成.数中的圆点叫做小数点,小数点左边的数叫做整数部分,小数点右边的数叫做小数部分.在小数里,每相邻两个计数单位之间的进率都是10.小数部分的最高分数单位“十分之一”和整数部分的最低单位“一”之间的进率也是10.2、小数的分类纯小数:整数部分是零的小数,叫做纯小数.例如0.25、0.368都是纯小数.带小数:整数部分不是零的小数,叫做带小数.例如3.25、5.26都是带小数.有限小数:小数部分的数位是有限的小数,叫做有限小数.例如:41.7、25.3、0.23都是有限小数.无限小数:小数部分的数位是无限的小数,叫做无限小数.例如:4.33……3.1415926…….无限不循环小数:一个数的小数部分,数字排列无规律且位数无限,这样的小数叫做无限不循环小数.例如:TT循环小数:一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数.例如：3.555……0.0333……12.109109…….一个循环小数的小数部分,依次不断重复出现的数字叫做这个循环小数的循环节.例如:3.99……的循环节是“9”,0.5454……的循环节是“54”.纯循环小数:循环节从小数部分第一位开始的,叫做纯循环小数.例如:3.111……0.5656…….混循环小数:循环节不是从小数部分第一位开始的,叫做混循环小数.3.1222……0.03333…….写循环小数的时候,为了简便,小数的循环部分只需写出一个循环节,并在这个循环节的首、末位数字上各点一个圆点.如果循环节只有一个数字,就只在它的上面点一个点.例如:3.777……简写作3.7,0.5302302……简写作0.5302.三分数1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数.在分数里,中间的横线叫做分数线;分数线下面的数,叫做分母,表示把单位“1”平均分成多少份;分数线上面的数叫做分子,表示有这样的多少份.把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位.2、分数的分类真分数:分子比分母小的分数叫做真分数.真分数小于1.假分数:分子比分母大或者分子和分母相等的分数,叫做假分数.假分数大于或等于1带分数:假分数可以写成整数与真分数合成的数,通常叫做带分数.3、约分和通分把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分.分子分母是互质数的分数,叫做最简分数.把异分母分数分别化成和原来分数相等的同分母分数,叫做通分.四百分数表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比.百分数通常用“%”来表示.百分号是表示百分数的符号.二、方法一数的读法和写法1.整数的读法:从高位到低位,一级一级地读.读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字.每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零.2.整数的写法:从高位到低位,一级一级地写,哪个数位上一个单位也没有,就在那个数位上写0.3.小数的读法:读小数的时候,整数部分按照整数的读法读,小数点读作“点”,小数部分从左向右顺次读出每一位数位上的数字.4.小数的写法:写小数的时候,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每个数位上的数字.5.分数的读法.读分数时,先读分母再读“分之”然后读分子,分子和分母按照整数的读法来读6.分数的写法:先写分数线,再写分母,最后写分子,按照整数的写法来写.7.百分数的读法:读百分数时,先读百分之,再读百分号前面的数,读数时按照整数的读法来读.8.百分数的写法：百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示.二数的改写一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某一位后面的数,写成近似数.3、四舍五入法：要省略的尾数的最高位上的数是4或者比4小,就把尾数去掉4、大小比较1、比较整数大小：比较整数的大小,位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大；最高位上的数相同,就看下一位,哪一位上的数大那个数就大.2、比较小数大小：先看它们的整数部分,整数部分大的那个数就大；整数部分相同的,十分位上的数大的那个数就大；十分位上的数也相同,百分位上的数大的那个数就大…….3、比较分数的大小：分母相同的分数,分子大的分数比较大;分子相同的数,分母小的分数大.分数的分母和分子都不相同的,先通分,再比较两个数的大小.三数的互化1、小数化成分数：原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分.2、分数化成小数：用分母去除分子.能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数.3、一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数,如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数.。

奇数与偶数：凡是能被2整除的数叫偶数，不能被2整除的数叫奇数。

质数(素数)与合数：一个数的因数只有1和它本身两个因数的数叫做质数，也叫素数，如2。

一个数的因数除了1和它的本身以外，还有其他的因数，这个数就叫合数，如4。

100以内的质数：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97 ，1既不是质数，也不是合数。

最小的质数是2，最小的合数是4。

2的倍数的特征：个位上是0 2 4、6、8的数是2的倍数。

是2的倍数的数叫做偶数，不是2的倍数的数叫做奇数。

5的倍数的特征：个位上是0或5的数是5的倍数。

3的倍数的特征：一个数的各个数字的和是3的倍数，这个数就是3的倍数。

同时是2、3、5的倍数的特征：个位上一定是0。

同时是2、3、5的倍数的最小两位数是30，最小三位数是120。

公历年的平年、闰年：平年：把公历年份除以4(这里不是整百的公历年份)有余数时，就把这一年叫做平年，有365天。

其中二月份有28天。

闰年：把公历年份除以4(这里不是整百的公历年份)没有余数时．就把这一年叫做闰年。

计366天。

其中二月份有29天。

如果年份是整百的，则除以400，再看余数，判断方法同上。

大月31天，小月30天，大月的月份有：1、3、5、7、8、10、12月，小月的月份有：4、6、9、11月。

直线：没有端点，可以向两端无限延长。

射线：只有一个端点，可以向一端无限延长。

直线和射线无法比较长短。

线段：有两个端点。

射线和线段都是直线的一部分。

两点间，线段最短。

平行线：在同一平面内不相交的两条直线叫做平行线。

垂线、垂足：两条直线相交，有一个角是直角时，就说这两条直线互相垂直。

其中一条直线叫做另一条直线的垂线，其交点叫垂足。

从直线外一点到直线所画的线段中，垂线最短。

角：锐角(大于0o小于90o的角)、直角(等于90o的角)、钝角(大于90o而小于180o的角)、平角(等于180o的角)、周角(等于360o的角)。