裂缝计算

裂缝深度计算公式
裂缝深度的计算公式通常取决于裂缝的类型和具体情况。

一般来说，裂缝深度可以通过以下公式进行估算：
裂缝深度 = 裂缝长度× 裂缝宽度 / 裂缝的平均角度。

裂缝深度也可以通过地质勘探和测量来准确测量。

在实际工程中，一般会根据具体情况采用不同的测量方法和公式来计算裂缝深度，以确保准确性和可靠性。

同时，裂缝深度的计算还可能受到地质构造、岩石性质、地下水位等因素的影响，因此在实际工程中需要综合考虑各种因素来确定裂缝深度的计算公式。

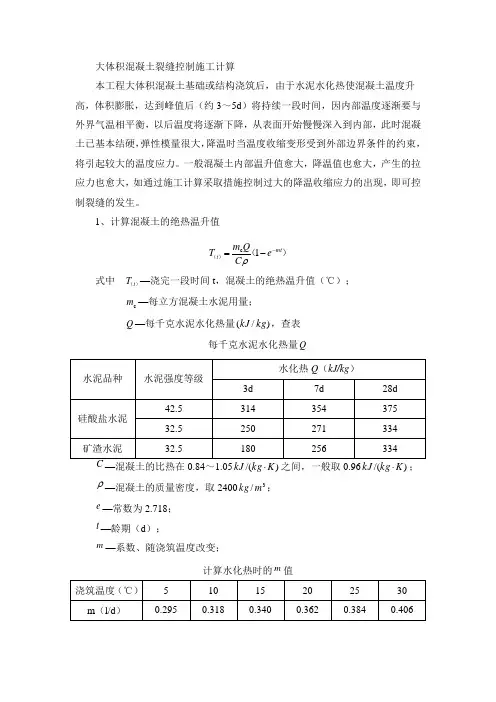
大体积混凝土裂缝控制施工计算本工程大体积混凝土基础或结构浇筑后，由于水泥水化热使混凝土温度升高，体积膨胀，达到峰值后（约3～5d ）将持续一段时间，因内部温度逐渐要与外界气温相平衡，以后温度将逐渐下降，从表面开始慢慢深入到内部，此时混凝土已基本结硬，弹性模量很大，降温时当温度收缩变形受到外部边界条件的约束，将引起较大的温度应力。

一般混凝土内部温升值愈大，降温值也愈大，产生的拉应力也愈大，如通过施工计算采取措施控制过大的降温收缩应力的出现，即可控制裂缝的发生。

1、计算混凝土的绝热温升值）（）（mt t e C Qm T --=1c ρ式中 ）（t T —浇完一段时间t ，混凝土的绝热温升值（℃）； c m —每立方混凝土水泥用量；Q —每千克水泥水化热量)/(kg kJ ，查表每千克水泥水化热量Q水泥品种水泥强度等级水化热Q （kJ/kg ）3d 7d 28d 硅酸盐水泥 42.5 314 354 375 32.5 250 271 334 矿渣水泥32.5180256334C —混凝土的比热在0.84～1.05)/(K kg kJ ⋅之间，一般取0.96)/(K kg kJ ⋅；ρ—混凝土的质量密度，取24003/m kg ；e —常数为2.718；t —龄期（d ）；m —系数、随浇筑温度改变；计算水化热时的m 值浇筑温度（℃） 5 10 15 20 25 30 m （l/d ）0.2950.3180.3400.3620.3840.406实际大体积混凝土基础或结构外表是散热的，混凝土的实际温升低于绝热温升，计算值偏于安全。

℃）（）（00718.2-1240096.0375m T 284.0-c 28=⨯⨯=⨯2、计算各龄期混凝土收缩变形值n bt y t y M M M M e ⨯⋯⨯⨯⨯-=-3210)()1(εε式中 0y ε—标准状态下的最终收缩值（即极限收缩值），取41024.3-⨯；)(t y ε—非标准状态下混凝土任意龄期（d ）的收缩变形值；e —常数为2.718； b —经验系数，取0.01；t —混凝土浇筑后至计算时的天数（d ）；n M M M M ⋯321、、—考虑各种非标准条件，与水泥品种细度、骨料品种、水灰比、水泥浆量、养护条件、环境相对湿度、构件尺寸、混凝土捣实方法、配筋率等有关的修正系数，按表取用。

8．2．2 裂缝宽度计算理论对于裂缝问题，尽管自20世纪30年代以来各国学者做了大量的研究工作，提出了多种计算理论，但至今对于裂缝宽度的计算理论并未取得一致的看法。

这些不同观点反映在各国关于裂缝宽度的计算公式有较大差别。

但我们可以从这些不同的观点中理解和体会影响裂缝宽度的各种因素，为我们有效地控制构件的裂缝宽度提供理论基础。

从目前的裂缝计算模式上看，计算理论大致可以分为四类：第一类是经典的粘结—滑移理论；第二类是无滑移理论；第三类是一般裂缝理论；第四类是试验统计模式。

目前我国《混凝土结构设计规范》（GB50010）采用的是以一般裂缝理论为指导，结合大量试验结果而形成的裂缝计算公式。

而《公路钢筋混凝土与预应力混凝土桥涵设计规范》（JTJ023）结合影响裂缝宽度的各主要因素分析，采用的是以试验统计得到的计算公式。

◆粘结-滑移理论粘结—滑移理论是由R. Saligar于1936年根据钢筋混凝土拉杆试验提出的，一种最早的裂缝理论，直至60年代中期这个理论还一直被广泛的接受应用。

这一理论认为，裂缝的开展是由于钢筋与混凝土之间不再保持变形协调，出现相对滑移而产生的。

因此裂缝宽度等于裂缝间距范围内钢筋和混凝土的变形差。

而裂缝的间距取决于钢筋与混凝土间粘结应力的大小与分布。

粘结应力越大，混凝土拉应力沿构件纵向从零增大到其极限抗拉强度所需的粘结传递长度会越短，裂缝的间距也就越短，裂缝宽度越小，此时裂缝“密而多”；反之，裂缝“疏而稀”，裂缝宽度越大。

由粘结—滑移理论得到的两个基本公式如下（如何根据以上条件推导出来的？）(8-2)(8-3)式中lm --平均裂缝间距；Wm--平均裂缝宽度；d --纵向受拉钢筋直径；ρte--（=As/Ate ）按有效受拉混凝土面积计算的配筋率；,--平均裂缝间距内钢筋和混凝土的平均拉应变。

Ate--有效受拉区混凝土的截面面积，对受弯构件，取二分之一截面高度以下的面积。

对于矩形截面, Ate=0.5bh；倒T形截面，则Ate=0.5bh-(bf-b)hf 。

【钢筋混凝土受弯构件的裂缝宽度和挠度计算】一、引言钢筋混凝土结构是现代建筑中常见的结构形式之一，而受弯构件作为其重要组成部分，其裂缝宽度和挠度的计算是设计过程中的关键内容。

在本文中，我将分析钢筋混凝土受弯构件的裂缝宽度和挠度计算，并对其进行深度探讨，希望能为您提供有价值的信息。

二、裂缝宽度计算1.裂缝宽度计算公式钢筋混凝土受弯构件的裂缝宽度计算可以使用以下公式进行：\[w_k = k \times \frac{f_s}{f_y} \times \frac{M_s}{b \times d}\]其中，\(w_k\)为裂缝宽度，\(k\)为调整系数，\(f_s\)为梁内应力，\(f_y\)为钢筋的屈服强度，\(M_s\)为抗弯强度矩，\(b\)为截面宽度，\(d\)为截面有效高度。

2.裂缝宽度计算包含的因素在裂缝宽度计算中，需要考虑梁内应力、钢筋的屈服强度以及抗弯强度矩等因素。

通过对这些因素的综合考虑，可以准确计算出钢筋混凝土受弯构件的裂缝宽度，从而确保结构的安全性。

三、挠度计算1.挠度计算公式钢筋混凝土受弯构件的挠度计算可以使用以下公式进行：\[f = \frac{5 \times q \times l^4}{384 \times E \times I}\]其中，\(f\)为挠度，\(q\)为荷载，\(l\)为构件长度，\(E\)为弹性模量，\(I\)为惯性矩。

2.挠度计算的影响因素在挠度计算中，荷载、构件长度、弹性模量和惯性矩等因素都会对挠度产生影响。

通过对这些因素进行综合考虑，并结合实际工程情况，可以准确计算出钢筋混凝土受弯构件的挠度，从而满足设计要求。

四、个人观点和理解钢筋混凝土受弯构件的裂缝宽度和挠度计算是结构设计中的重要内容，它直接关系到结构的安全性和稳定性。

在实际工程中，我们需要充分理解裂缝宽度和挠度计算的原理和方法，结合设计规范和实际情况，确保结构设计的合理性和可行性。

五、总结与展望通过本文的分析，我们深入探讨了钢筋混凝土受弯构件的裂缝宽度和挠度计算，并对其进行了详细介绍。

1.计算平均裂缝间距m l通过理论计算并根据实验验证和实际工程经验对参数的修正，得到m l 的计算式为 如下：⎪⎪⎭⎫ ⎝⎛+=te eq m ρβd c l 0.081.9 其中∑∑=iii i i dn dn d υ2eq ，ste teA A ρ=式中 β——系数，对轴心受拉构件，取β=1.1；对偏心轴心受拉构件，取β=1.05；对其他受力构件，取β=1.0；c ——最外层纵向受力钢筋外边缘至受拉区底边的距离（mm ），当c <20mm 时，取c=20mm ；当c>65mm 时，取c=65mm ；te ρ——按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率，当te ρ<0.01时，取te ρ=0.01；te A ——有效受拉混凝土截面面积，可按下列规定取用：对轴心受拉构件取构件截面面积；对受弯、偏心受压和偏心受拉构件，取腹板截面面积的一半与受拉翼缘截面面积之和，即te f f ()0.5A bh b b h =+-，此处f b 、f h 为受拉翼缘的宽度、高度；2.计算平均裂缝宽度m w平均裂缝宽度m w 等于两条相邻裂缝之间（计算时取平均裂缝间距m l ）钢筋的平均伸长与相同水平处构件侧表面混凝土平均伸长的差值m ssq c m l E σψαw =其中，sqte tq f σρψ65.01.1-=，当ψ<0.2时，取ψ=0.2；当ψ>1.0时，取ψ=1.0。

对直接承受重复荷载的构件，取ψ=1.0。

对于不同的受力构件其裂缝截面处的钢筋应力sq σ也不相同。

受弯构件：0870h A .M σS qsq=轴心受拉构件：sq sqA N σ=偏心受拉构件：)('0'ss q sqa h A e N -=σ偏心受压构件：⎪⎭⎫ ⎝⎛-=1z e A N σs q sq3.计算最大裂缝宽度在上述理论分析和试验研究基础上，对于矩形、T 形、倒T 形及工形截面的钢筋混凝土受拉、受弯和偏心受压构件，按荷载效应的标准组合并考虑长期作用影响的最大裂缝宽度w max 按下列公式计算⎪⎪⎭⎫⎝⎛+=te eq s s sq cr ρd .c .E σψαw 08091m ax 4.验算最大裂缝钢筋混凝土构件在正常使用状态下，最大裂缝可按荷载准永久组合并考虑长期作用影响的效应计算，最大裂缝宽度应满足：max lim ωω≤由式（9-16）计算sq d由式（9-17）计算te ρ 计算sq σ由题设条件确定所需计算参数根据构件不同的受力状态选择相应的计算01.0<te ρ开始验算最大裂缝宽度否由式（9-29）计算ψ图9-7最大裂缝宽度验算流程图代入式（9-31）计算最大裂缝宽度max ω结束是 01.0=te ρ m in m ax ωω≤裂缝验算满足要求裂缝验算不满足要求否是。

钢筋混凝土构件的裂缝宽度和挠度计算钢筋混凝土结构是一种广泛应用的建筑结构形式。

在使用的过程中，由于各种因素的影响，钢筋混凝土构件会出现裂缝和挠度。

裂缝宽度和挠度的计算是设计和施工中非常重要的一步，下面将详细介绍钢筋混凝土构件的裂缝宽度和挠度计算的方法。

首先，我们先来了解什么是裂缝宽度。

裂缝宽度是裂缝两侧的最大间隔距离，通常用毫米来表示。

裂缝宽度的计算与构件所承受的荷载大小有关。

弹性模量法是一种基于线弹性理论的裂缝宽度计算方法。

该方法假设构件的截面保持线弹性行为，并且裂缝开口处的应力等于截面中的应力。

根据这个假设，可以通过使用构件的几何特征、材料性质以及荷载情况来进行计算。

弹性模量法的计算步骤如下：1.确定构件的几何特征，包括构件的截面形状、尺寸和钢筋的分布情况。

2.根据构件的截面形状和计算荷载，计算构件的抗弯承载力和抗剪承载力。

3.根据构件的弹性模量、截面的惯性矩和荷载情况，计算出构件所受到的弯矩和剪力。

4.计算裂缝宽度，可以使用一些经验公式或者根据经验计算裂缝宽度的公式，如ACI224R-01中给出的公式。

极限平衡法是一种基于非线性分析的计算方法，广泛用于钢筋混凝土构件的裂缝宽度计算。

该方法考虑了材料的非线性行为和构件在承受荷载过程中的变形情况。

极限平衡法的计算步骤如下：1.确定构件的几何特征和材料性质。

2.将构件的截面划分为若干离散截面，然后使用有限元或其他非线性分析方法计算每个离散截面的受力情况。

3.根据计算出的应力分布，计算裂缝宽度。

可以使用一些经验公式或者根据经验计算裂缝宽度的公式。

除了计算裂缝宽度，钢筋混凝土构件的挠度也是需要考虑的。

挠度是构件在受到荷载作用后产生的弯曲变形，通常用单位长度的偏移量表示。

挠度的计算方法与裂缝宽度计算类似，可以使用弹性模量法和极限平衡法等进行计算。

总而言之，钢筋混凝土构件的裂缝宽度和挠度的计算是设计和施工中的关键步骤。

正确的计算方法能够保证构件的安全性和使用寿命，并且提供准确的数据指导设计和施工。