齿轮弯曲疲劳强度计算

航空发动机Aeroengine收稿日期：2020-05-26基金项目：国家科技重大专项（2017-IV-0012-0049）资助作者简介：滕文爽（1990），女，硕士，工程师，从事航空发动机传动系统设计工作；E-mail ：。

引用格式：滕文爽，郭梅，宋振海.HB 与ISO 标准中锥齿轮轮齿弯曲疲劳强度计算标准比较[J].航空发动机，2022，48（3）：65-69.TENG Wenshuang ，GUO Mei ，SONG parison of calculation standards for bending fatigue strength of bevel gear teeth in HB and ISO standards[J].Aeroengine ，2022，48（3）：65-69.HB 与ISO 标准中锥齿轮轮齿弯曲疲劳强度计算标准比较滕文爽1,2，郭梅1,2，宋振海1,2，庞顺清3，李锦花1,2（1.中国航发沈阳发动机研究所，2.中国航空发动机集团航空发动机动力传输重点实验室：沈阳110015；3.中国航发沈阳黎明航空发动机有限责任公司，沈阳110043）摘要：为正确评估不同标准中的轮齿强度计算结果，分析和比较了航空工业标准（HB ）与国际标准化组织（ISO ）标准计算锥齿轮轮齿弯曲疲劳承载能力。

通过计算方法比较和实例计算对比2种途径，找出了2种标准计算公式的差异、修正系数种类和取值上的差异，及其对计算结果的影响。

结果表明：2种标准考虑的影响因素不同，ISO 标准相较HB 考虑的因素更为全面，特别是在动载系数、应力修正、尺寸系数等参数计算上存在较大差异，使得采用ISO 标准计算齿根应力基本值更小，齿根应力与许用齿根应力更大；ISO 标准中提供的动载系数根据转速区域的不同采用的计算公式不同，提供的尺寸系数考虑了不同组织和热处理工艺对系数取值的影响，对计算结果更有指导意义。

关键词：锥齿轮；轮齿；齿根应力；强度计算；弯曲疲劳；航空工业标准；国际标准化组织标准中图分类号：V233.1文献标识码：Adoi ：10.13477/ki.aeroengine.2022.03.010Comparison of Calculation Standards for Bending Fatigue Strength of Bevel Gear Teethin HB and ISO StandardsTENG Wen-shuang 1，2，GUO Mei 1，2，SONG Zhen-hai 1，2，PANG Shun-qing 3，LI Jin-hua 1，2（1.AECC Shenyang Engine Research Institute ，Shenyang 110015，China ；2.AECC Key Laboratory of Power Transmission Technologyon Aeroengine ，Shenyang 110015，China ；3.AECC Shenyang Liming Aero-engine Co.，Ltd ，Shenyang 110043，China ）Abstract ：In order to correctly evaluate the gear tooth strength calculation results in different standards ，the bending fatigue bearing capacity of bevel gear teeth calculated by Aviation Industry standard (HB)and International Standardization Oganization (ISO)standards were analyzed and compared.Through the comparison of calculation methods and example calculation ，the differences between the two standard calculation formulas ，the types and values of correction coefficients ，and their effects on the calculation results were found out.The results show that the influence factors considered by the two standards are different.The ISO standard is more comprehensive than HB ，es⁃pecially in the calculation of dynamic load coefficient ，stress correction ，size coefficient and other parameters ，which makes the basic value of tooth root stress calculated by ISO standard smaller ，and the tooth root stress and allowable root stress larger.The dynamic load coeffi⁃cient provided in ISO standard adopts different calculation formulas according to different speed regions.The size coefficient provided takes into account the influences of different structures and heat treatment processes on the coefficient value ，which is more instructive tothe calculation results.Key words ：bevel gear ；gear teeth ；tooth root stress ；strength calculation ；bending fatigue ；HB standard ；ISO standard0引言疲劳断齿是航空燃气涡轮发动机附件传动齿轮典型故障形式之一[1]。

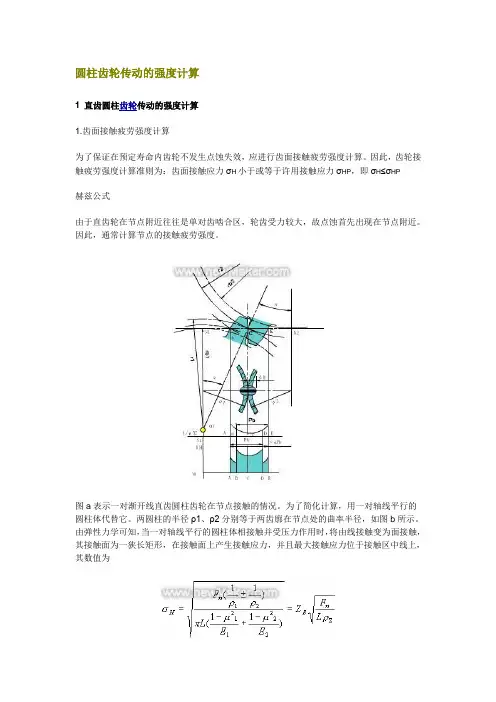
圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

齿面接触强度及齿根弯曲强度核算在设计产品过程中，经常会选用齿轮作为传动力及扭矩的原件。

在大部分成型产品改造或调整过程中，关于齿轮的强度校核这一步骤就可以用类比法代替，从而节省设计人员的精力，缩短了设计周期。

但得出的结果没有书面依据以及理论方面的支持。

所以当进行多次类比之后，所设计出来的齿轮与理论计算得出的齿轮偏差会较大。

其原理类似于累计偏差。

所以应该进行强度校核方面的计算。

齿轮强度校核计算，在实际应用中，主要是两方面的核算：1、齿面接触强度的核算。

2、齿根弯曲强度的核算。

1.齿面接触强度核算-分度圆直径计算参考文献：在初步设计齿轮时，根据齿面接触强度，可按照下列公式估算齿轮传动的尺寸。

(机械设计手册P14-133)a≥A a(μ±1)·√KT1ψaσHP23①d1≥A d·√KT1ψdσHP2·μ±1μ3②公式①为两齿轮中心距的计算；公式②为齿轮分度圆直径的计算。

由于本次计算的是齿轮齿条传动。

所以，中心距a= d1/2其中：d1为齿轮分度圆直径，只需要核算齿轮分度圆直径d1首先，要确定公式②中各个符号代表的含义及数值选取。

d1—齿轮分度圆直径；A d—常系数；K—载荷系数；μ—齿数比；σHP—许用接触应力；ψd—齿宽系数；T1—电机减速机输出扭矩；d1：齿轮分度圆直径，待求；A d：常系数值；A d值在表14-1-65中，通过螺旋角角度β的数值求得。

齿轮的螺旋角β=11.655°,则A d = 756。

载荷系数K，常用值K=1.2～2（机械设计手册P14-133），当载荷平稳，齿宽系数较小，轴承对称布置，轴的刚性较大，齿轮精度较高（6级以上），以及齿轮的螺旋角较大时取较小值；反之取较大值。

根据对比后的结果在K的常用范围内选取。

此次选择K=1.8（载荷平稳，齿宽系数较小，轴为非对称分布，轴的刚性不大，齿轮精度不高）u：传动比。

当齿轮之间为外啮合的时候，选取“+”；当齿轮之间为内啮合的时候，选取“-”，本次计算为齿轮齿条，不影响计算结果。

齿轮弯曲疲劳强度计算公式齿轮弯曲疲劳强度计算公式如下：
Wf = Kf*Yf*Zf*St*J*JL
其中，
Wf：齿轮弯曲疲劳强度，单位为牛/m^2
Kf：载荷系数或安全系数
Yf：应力调整系数
Zf：几何尺寸系数
St：材料疲劳极限强度
J：齿数弯曲系数
JL：载荷系数
其中，载荷系数或安全系数Kf和应力调整系数Yf可以根据不同材料和设计要求进行选择；几何尺寸系数Zf和齿数弯曲系数J也可以通过相关计算公式得出；材料疲劳极限强度St需要根据实验数据或相关标准进行确定；载荷系数JL需要
根据齿轮的实际工作条件进行选择。

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

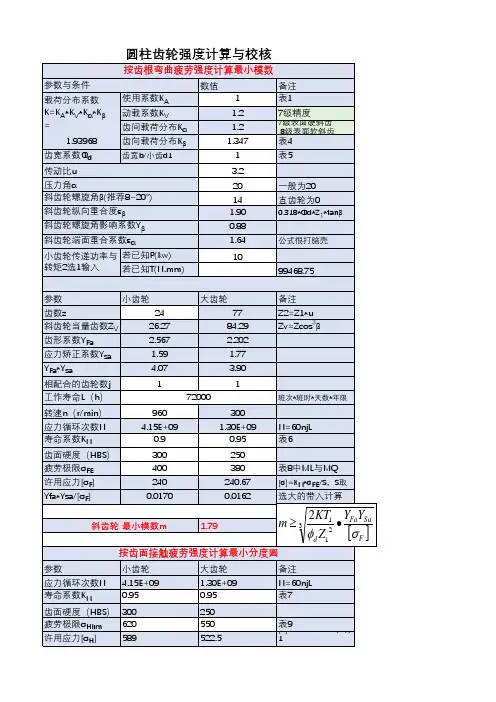
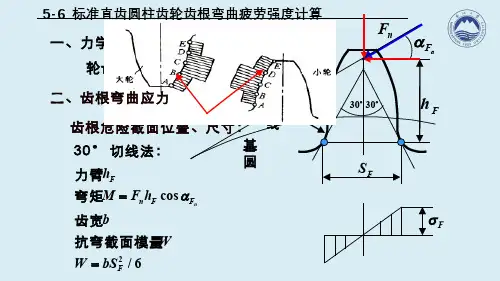
5-6 标准直齿圆柱齿轮齿根弯曲疲劳强度计算 Fh FS 30o 30oaF a nF 基圆过渡曲线Fs 一、力学模型轮齿悬臂梁，F n 作用于齿顶齿根危险截面位置、尺寸：30°切线法：2cos /6n Fn F F F h M F h bWW bS a ==力臂弯矩齿宽抗弯截面模量二、齿根弯曲应力二、齿根弯曲应力12216cos cos 2/6cos aaF F nc F F F F F h F h KT M m W bS bd m S m a a s a ������===������齿根弯曲应力：26cos ,514,cos aa F F F F h mY mS m a a ⎛⎫⎪⎝⎭=-⎛⎫⎪⎝⎭齿形系数图与齿廓形状有关，与模数无关(515)0.750.25sa Y Y e ae -=+应力修正系数图重合度系数2112N/mm a F F sa KT Y Y Y bd mes =齿根弯曲应力：三、标准直齿圆柱齿轮齿根弯曲疲劳强度112:aF F sa F KT Y Y Y bd me s s =≤⎡⎤⎣⎦1.齿根弯曲疲劳强度条件2.分别校核大小齿轮根齿弯曲疲劳强度11111112222122F Fa sa F F Fa sa F KT Y Y Y bd mKT Y Y Y bd me e s s s s =ﾣ����=ﾣ����3.按齿根弯曲疲劳强度设计三、标准直齿圆柱齿轮齿根弯曲疲劳强度()3121312d 14mm12 mm Fa sa a F Fa sa F Y Y Y KT m u z Y Y Y KT m z e eϕs ϕs ≥±⎡⎤⎣⎦≥⎡⎤⎣⎦或1a a 1d 1(1);2d mz u b a b d mz f f f f ﾣ====1122121max ,(2)0.8~1.4,()Fa sa Fa sa Fa sa F F F t ttY Y Y Y Y Y KY KY KY KY m m KY e e ee e s s s ����=����������������==4.设计式的有关说明（）设计式中，设计时，试选。

斜齿轮弯曲强度公式斜齿轮是一种常见的齿轮类型，它在机械传动系统中得到了广泛的应用。

斜齿轮的弯曲强度是机械传动系统设计中的一个重要参数，它反映了斜齿轮在工作中承受弯曲应力的能力。

了解斜齿轮的弯曲强度公式可以帮助我们更好地设计和选型斜齿轮，提高机械传动系统的稳定性和可靠性。

一、斜齿轮的基本概念斜齿轮是指齿轮的齿线方向与齿轮轴线不垂直，而是成一个夹角。

夹角的大小称为螺旋角，用β表示。

根据螺旋角的方向，斜齿轮可分为左旋和右旋两种类型。

二、斜齿轮的弯曲强度斜齿轮在工作中，其齿部受到很大的弯曲应力，这种弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关。

根据弹性力学理论，斜齿轮的弯曲强度可以表示为：σ = K ×σ′× Ym × Zm × [σ]其中，σ表示斜齿轮的弯曲强度；K表示弯曲强度系数，它与齿轮的几何参数、材料等因素有关；σ′表示齿轮的接触应力，即齿轮在接触区内的应力；Ym表示弯曲强度计算系数，它与齿轮的几何参数、转速等因素有关；Zm表示弯曲强度计算系数，它与齿轮的几何参数、转速等因素有关；[σ]表示齿轮材料的许用应力。

三、斜齿轮弯曲强度公式的推导弯曲强度计算系数的确定根据齿轮传动的原理，斜齿轮在工作中主要受到弯曲应力和接触应力两种作用。

弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关，接触应力的大小与齿轮的几何参数、工作压力等因素有关。

因此，弯曲强度系数K可以通过以下公式计算：K = K1 × K2 × K3 × K4其中，K1表示弯曲系数，它与齿轮的几何参数、材料等因素有关；K2表示工作系数，它与工作压力、工作压力位置等因素有关；K3表示转速系数，它与齿轮的转速等因素有关；K4表示温度系数，它与齿轮的工作温度等因素有关。

弯曲强度计算系数的具体值弯曲强度计算系数K的具体值可以根据实际情况查表得到。

根据不同的设计条件和参数，弯曲强度计算系数K可以取不同的值。

######################################################################## ## 渐开线圆柱齿轮疲劳强度计算法## ## ( GB/T3480-97,ISO6336-1996 ) ## ## 2014-03-14 ################郑州机械研究所################ 09:47:49 ##------------------基本输入参数--------------------------小轮总扭矩（N.m）T = 1475.0小轮转速（转/分）RPM1 = 354.0大轮转速（转/分）RPM2 = 91.624实际速比U = 3.8636中心距（mm） A = 275.001法向模数（mm）Mn = 5.0螺旋角（度）β= 11.0法向齿形角（度）αn = 20.0------------------------------------------------------------------------------------------------------小齿轮大齿轮齿轮齿数Z = 22 85总有效齿宽（mm） B = 110.0 110.0变位系数Xn = 0.3886 0.1262齿顶高系数Ha* = 1.0 1.0顶隙系数Cn* = 0.25 0.25------------------齿轮几何参数-----------------------------------------------------------小齿轮大齿轮分度圆直径(mm) D = 112.059 432.955节圆直径(mm) Dp = 113.084 436.917基圆直径(mm) Db = 105.069 405.948顶圆直径(mm) Da = 125.785 444.056根圆直径(mm) Df = 103.445 421.717齿顶厚(mm) Sa = 2.937 4.021滑动率η= 0.991 0.991分度圆线速度(m/s) V = 2.077齿轮精度等级(GB 10095-1988) IQ = 6端面重合度εα= 1.525轴向重合度εβ= 1.336------------------材料及热处理等参数---------------------------------------------------------- 传动类型：减速传动齿轮啮合类型：外啮合螺旋角类型：斜齿修形方式：齿向倒坡或有装配调整小轮材料和热处理类型：渗碳淬火钢大轮材料和热处理类型：渗碳淬火钢设计寿命：10.0 年24小时/每天总设计寿命：86400 小时50 度时润滑油粘度（cSt）= 220.0齿面硬度HB/HRc = 60 58 弹性模量 E = 206000 206000 小齿轮疲劳计算基本载荷(N.m) Tn1 = 1475.0切向力(N) Ft = 26325.456径向力(N) Fr = 9761.02轴向力(N) Fx = 5117.15接触载荷系数(MPa) K = 2.688临界转速比N = 0.038单对齿刚度Cp = 14.543啮合刚度CG = 20.267------------------ 接触强度计算系数--------------------------------------------------------- 使用系数KA = 2.000动载系数Kv = 1.025齿向载荷分布系数KHβ= 1.346齿间载荷分配系数KHα= 1.000节点区域系数ZH = 2.371弹性系数ZE = 189.812重合度系数Zε= 0.810螺旋角系数Zβ= 0.991小齿轮大齿轮寿命系数Znt = 0.896 0.933 润滑系数ZL = 1.057 1.057 速度系数Zv = 0.965 0.965 粗糙度系数Zr = 0.973 0.973 工作硬化系数Zw = 1.000 1.000 尺寸系数Zx = 1.000 1.000 单对齿啮合系数ZBD = 1.000 1.000 ----------------- 弯曲强度计算系数--------------------------------------------------------- 动载系数Kv = 1.025齿向载荷分布系数KFβ= 1.306齿间载荷分配系数KFα= 1.000重合度系数Yε= 0.726螺旋角系数Yβ= 0.908小齿轮大齿轮齿形系数YF = 1.186 1.332应力修正系数YS = 2.235 2.150寿命系数Ynt = 0.880 0.904尺寸系数Yx = 1.000 1.000相对齿根圆角敏感系数Yδrelt = 0.999 1.000相对齿根表面状况系数YRrelt = 1.002 1.002 轮缘系数YBM = 1.000 1.000 齿根圆角半径系数ρF = 0.447 0.450******************** 接触强度计算结果********************************小齿轮大齿轮实验齿轮接触疲劳极限(MPa) σHlim = 1350.00 1350.00 计算齿轮接触极限应力(MPa) σHG = 1199.65 1250.30 许用接触应力(MPa) σHP = 959.72 1000.24 计算接触应力(MPa) σH = 983.65 983.65 计算接触强度安全系数SH = 1.220 1.271 最小接触强度安全系数SHmin = 1.250 1.250 ******************** 弯曲强度计算结果********************************小齿轮大齿轮实验齿轮弯曲疲劳极限(MPa) σFlim = 350.00 350.00 计算齿轮弯曲极限应力(MPa) σFG = 616.33 633.72 许用齿根应力(MPa) σFP = 410.89 422.48 计算齿根应力(MPa) σF = 308.59 333.37 计算弯曲强度安全系数SF = 1.997 1.901 最小弯曲强度安全系数SFmin = 1.500 1.500 --------------------------------------------------------------。

齿面接触疲劳设计公式
齿面接触疲劳设计公式如下：
1. 柯赛尔公式（Koester formula）：
T = K × (p × d)^(1/2)
其中，T表示齿面接触疲劳设计寿命（单位：小时），K为材
料系数，p为齿轮齿数，d为模数。

2. 承载能力公式：
P = K × (b × m × Y) / (d × Fd)
其中，P表示齿面接触疲劳承载能力（单位：N），K为齿轮
系数，b为齿轮宽度（单位：mm），m为模数（单位：mm），Y为弯曲强度几何修正系数，d为齿轮分度圆直径（单位：mm），Fd为齿面接触疲劳强度进给修正系数。

3. 耐疲劳强度公式：
[σ] = σ × (GH × GV)^0.5
其中，[σ]表示齿面接触疲劳强度（单位：MPa），σ为材料疲
劳强度（单位：MPa），GH为齿轮齿高系数，GV为齿轮齿
顶系数。

请注意，以上公式仅供参考，具体的齿面接触疲劳设计需要综合考虑材料特性、工作条件等因素，并结合实际情况进行合理调整。